On Fault Tolerant Single-Shot Logical State Preparation and Robust Long-Range Entanglement
Abstract
Preparing encoded logical states is the first step in a fault-tolerant quantum computation. Standard approaches based on concatenation or repeated measurement incur a significant time overhead. The Raussendorf-Bravyi-Harrington cluster state [23] offers an alternative: a single-shot preparation of encoded states of the surface code, by means of a constant depth quantum circuit, followed by a single round of measurement and classical feedforward [7]. In this work we generalize this approach and prove that single-shot logical state preparation can be achieved for arbitrary quantum LDPC codes. Our proof relies on a minimum-weight decoder and is based on a generalization of Gottesman’s clustering-of-errors argument [12]. As an application, we also prove single-shot preparation of the encoded GHZ state in arbitrary quantum LDPC codes. This shows that adaptive noisy constant depth quantum circuits are capable of generating generic robust long-range entanglement.
Keywords and phrases:
Quantum error correction, fault tolerance, single-shot error correction, logical state preparationCopyright and License:
2012 ACM Subject Classification:
Theory of computation Quantum computation theoryAcknowledgements:
We thank Zhiyang He (Sunny) for helpful discussions. We thank Jong Yeon Lee for helpful discussions and for informing us about an upcoming work with Isaac Kim on single-shot error correction and cluster states. This work was done in part while the authors were visiting the Simons Institute for the Theory of Computing.Funding:
T.B. acknowledges support by the National Science Foundation under Grant No. DGE 2146752. Y.L. is supported by DOE Grant No. DE-SC0024124, NSF Grant No. 2311733, and DOE Quantum Systems Accelerator.Editors:
Raghu MekaSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
Single-shot logical state preparation is a procedure in which a code state (such as the logical or state) of a quantum error correcting code is prepared by a constant depth quantum circuit, followed by one round of single qubit measurements, and an adaptive Pauli correction using classical feedforward. In this paper, we prove that every CSS quantum LDPC code admits a single-shot state preparation procedure with logarithmic space overhead that is fault tolerant against local stochastic noise, generalizing prior work by [7] for the surface code.
The fact that single-shot logical state preparation is feasible is non-trivial: after all, logical states of quantum LDPC codes have circuit lower bounds and cannot be prepared by a constant depth quantum circuit [6, 14, 1]. This issue is circumvented via the additional measurement and classical feedforward. Due to the simplicity of the quantum circuit, there has been a recent theoretical and experimental interest in preparing physically interesting quantum states using these adaptive shallow circuits [22, 20, 21, 8, 25, 10, 28, 16, 24]. Fault tolerance is a key aspect of a faithful experimental preparation of these states, where one must argue that the state is still interesting even though the shallow circuit is noisy. Our result provides a general recipe for fault tolerant state preparation, which can be used for state initialization in fault tolerant quantum computation, as well as a candidate for an experimental demonstration of long-range entangled states using adaptive shallow circuits that is robust to noise.
The intuition behind our result is to realize repeated measurement via measurement-based quantum computation. The standard approach to initialize a quantum LDPC code in the logical state is as follows: first initialize all physical qubits in a code block in the state, then perform repeated and syndrome measurements, and finally perform a Pauli error correction using classical feedforward based on the syndrome measurement outcomes. A key observation here is that the repeated measurements are non-adaptive, thus we can attempt to simulate this process using a cluster state, achieving a space-time trade-off.
This naturally leads to a construction which we refer to as the Alternating Tanner Graph state (Figure 1, also known as a foliated quantum code [3]): there are copies of the code block. A copy of the Tanner graph is placed on each odd layer (simulating syndrome measurements), and a copy of the Tanner graph is placed on each even layer (simulating syndrome measurements). Vertical connections are added between code qubits of neighboring layers, which is used to propagate quantum computation in the time direction. To prepare this cluster state in constant depth, we initialize all qubits in the state and apply a gate on each edge. When applied to the surface code, the is equivalent to the Raussendorf-Bravyi-Harrington (RBH) cluster state [23].
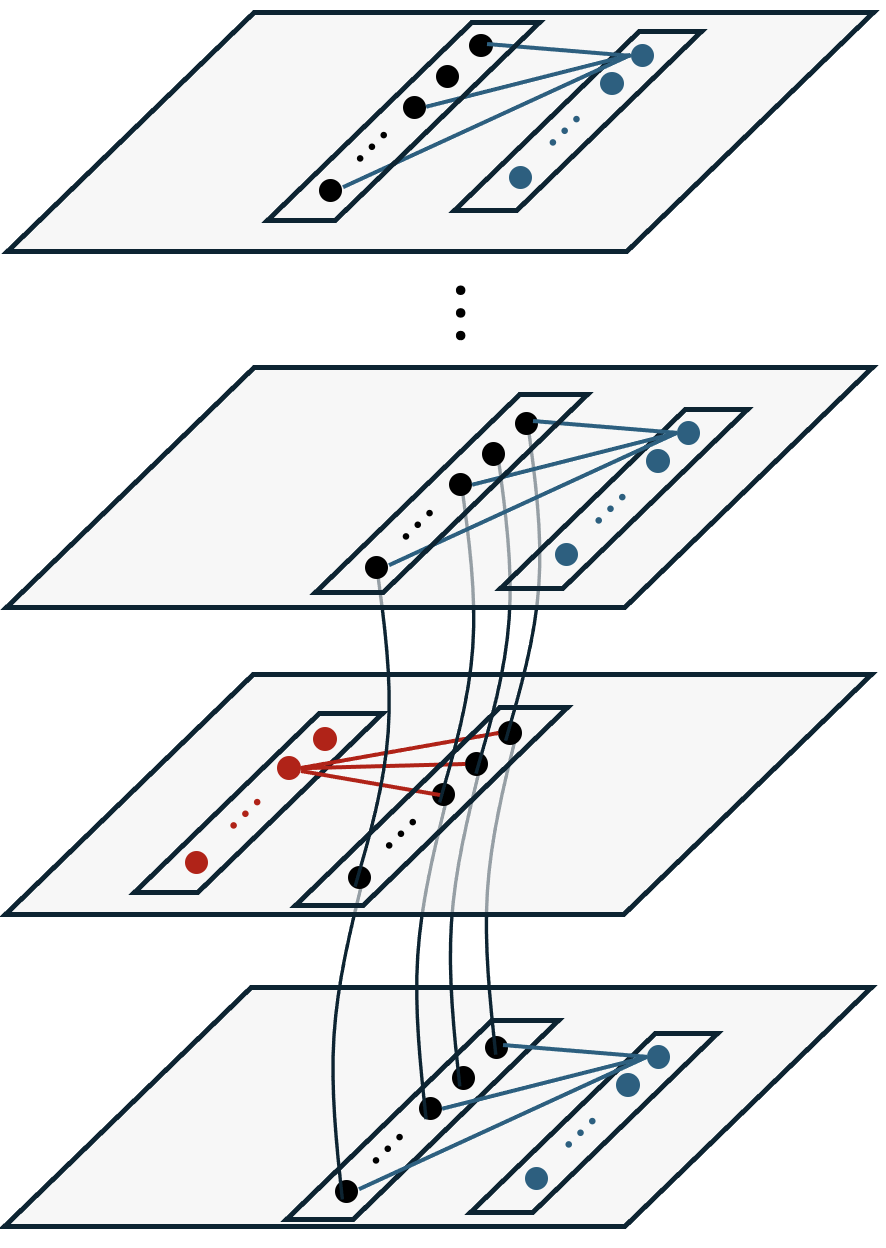

1.1 Results
We start with an informal description of single-shot logical state preparation. Consider a set of noisy qubits divided into two subsystems and . Single-shot logical state preparation is performed via the following procedure:
-
1.
Initialize all qubits in the (noisy) state.
-
2.
Perform a (noisy) constant depth quantum circuit .
-
3.
Measure all qubits in in the Hadamard () basis, obtaining a bitstring . In the absence of noise, the unnormalized post-measurement state equals .
-
4.
Use a classical computer to calculate a Pauli operator (supported on ) based on , and apply to the post-measurement state.111Classical computation is assumed to be performed instantly, such that there is no additional noise on the quantum state during this step of the computation.
In the absence of noise, the final (unnormalized) state is given by
| (1) |
Let us begin by understanding what this procedure can achieve in the absence of noise. With a suitable choice of , one can imagine that step 3 is measuring the stabilizers/parity checks of a quantum LDPC code (where contains code qubits and contains ancilla qubits for syndrome measurement), which collapses the state into a random syndrome subspace (some eigenspace of the code Hamiltonian). Step 4 then performs syndrome decoding and corrects the Pauli error, thus preparing an encoded code state.222What code state are we preparing? For example, assume there is only one logical qubit. Notice that the logical operator of the CSS LDPC code is stabilized by the initial state and commutes with the measurement. Therefore we are able to prepare the encoded state. The encoded state can be prepared similarly by initializing all qubits in .
The key question is what can the above procedure achieve in the noisy setting, where every initial qubit, gate and measurement is subject to some small constant amount of noise (throughout this section, we assume the noise rate is below some constant threshold). Ideally, we would like to achieve fault-tolerant single-shot logical state preparation, which means that the final state in the presence of noise is the desired encoded logical state, up to some residual stochastic noise. This residual noise is benign in the sense that it is correctable with the LDPC code; and the final state (with residual noise) can be used as the initial state of a fault tolerant quantum computation.
The conceptual challenge to achieve fault tolerance here is that the noisy quantum circuit only has constant depth, therefore we cannot hope to correct errors during the state preparation procedure using standard means. The RBH cluster state and its generalization, the ATG [23, 3, 15], is a carefully designed construction where after the bulk of the state is measured, the remaining boundaries/surfaces encode a logical state in the quantum error correcting code up to a Pauli correction. The intuition that this scheme might be fault tolerant lies in the redundancy embedded into the bulk ancilla qubits. Here, we give a general fault-tolerance proof that works for arbitrary quantum LDPC codes.
Theorem 1.
Fix an integer . There exists a fault tolerant, single shot logical state preparation procedure for the encoded states333Note that there are logical qubits, and we can prepare either or . of an arbitrary CSS LDPC code, using ancilla qubits, with success probability at least .
As discussed earlier, the Alternating Tanner Graph (ATG) state (Figure 1) naturally gives rise to redundancies akin to those in a repeated syndrome measurements protocol. Our proof of fault-tolerance leverages an information-theoretic minimum-weight decoder, and is based on the clustering-of-errors argument by [12, 18] for decoding LDPC codes from repeated measurements (see below for a more detailed overview).
Efficient decoding.
In our single-shot logical state preparation result discussed above, the classical decoding procedure (computing from ) relies on an information-theoretic minimum weight decoder, and is not necessarily computationally efficient.444By dynamic programming, the decoding algorithm can be made to run in time. A natural question is whether an efficient decoder that runs in time exists for single-shot logical state preparation, especially if the code is known to have an efficient decoder for quantum error correction.555We emphasize the distinction between a decoder for error-correction, and a decoder for state preparation. Here, we complement our results by showing a simple reduction to the efficient decoding of logical state preparation based on repeated syndrome measurements.
Theorem 2.
If a family of CSS LDPC codes admits an efficient decoder for fault-tolerant logical state preparation based on rounds of repeated syndrome measurements, then it further admits an efficient decoder for a fault-tolerant single shot logical state preparation procedure using ancilla qubits.
In other words, one can tradeoff time for space in logical state preparation. As discussed earlier, this reduction stems from mapping the repeated measurements circuit to a constant depth circuit via measurement based quantum computation, and as we illustrate naturally gives rise to the alternating tanner graph state .
Robust long-range entanglement.
Next we show that the ATG provides a powerful framework that goes beyond the preparation of encoded and as in logical state preparation based on repeated measurements, due to the flexibility in choosing different measurement patterns in the ATG. As an example, we show fault tolerant single-shot preparation of the encoded GHZ state
| (2) |
for any in an arbitrary quantum LDPC code. Here we summarize the algorithm for GHZ state preparation, and then discuss this result from the perspective of robust long-range entanglement and noisy shallow circuits.
To prepare the GHZ state, we measure the ATG in the following pattern, depicted (horizontally) in Figure 2(a): we measure all the check qubits of all code blocks (blue and red in Figure 1), as well as all code qubits in the bulk (blue in Figure 2(a)), with the exception of a careful choice of layers of code qubits (in orange). We prove that the resulting state, after minimum-weight decoding and feedforward, is in fact the encoded GHZ state across the blocks (Figure 2(b)) up to residual stochastic noise.
Theorem 3.
Fix integers . There exists a fault tolerant, single shot logical state preparation procedure for the encoded state of an arbitrary CSS LDPC code, using ancilla qubits, with success probability at least .
This generalizes the RBH construction [23] for the surface code with and , that is, the encoded Bell state in the surface code. Let us review the features of the entanglement in the resulting GHZ state:
-
Noise robust. The preparation procedure uses a noisy constant depth circuit (with noise rate below a constant threshold). Yet, the resulting GHZ state is encoded in a LDPC code and is subject to residual local stochastic noise that is correctable with the code.
-
Generic. The construction works for arbitrary quantum LDPC codes.
-
Long range. There are two aspects of long range entanglement: the first is the entanglement among physical qubits in each code block (which can exhibit topological order), the second is the logical GHZ entanglement that spans code blocks.
Finally, we discuss this result from the perspective of noisy shallow quantum circuits. The first step of this state preparation algorithm is to apply a constant depth circuit on a volume of qubits. At this point, there is no long-range entanglement at all. However, after the bulk (blue in Figure 2(a)) is measured, long-range entanglement is created across the orange blocks (Figure 2(b)): the subsequent decoding and feedforward operations are only used to correct the state into the desired GHZ state, but cannot create entanglement. Therefore, the GHZ-type entanglement is created by the teleportation effect of measurement. Interestingly, this teleportation effect is robust to noise.
Proof of fault tolerance.
The fault-tolerance of our single-shot logical state preparation scheme has two main components. First, we identify the stabilizer structure of . As remarked earlier, the fault tolerance arises from redundancies in the ancilla qubits. Concretely, that manifests in the redundancies of the stabilizers of , which contains certain “meta-checks”. Second, we adapt the clustering arguments by [18, 12] for decoding quantum LDPC codes from random errors to our setting, and develop analogous techniques to argue that the meta-checks contain enough redundancy to be robust against random errors.
The meta-check information. Following [7], inside the (which is a stabilizer state), one can define stabilizers which cleanly factorize into a product of Pauli’s on the bulk of the graph state. We refer to these stabilizers as “meta-checks”, since
1. After measuring the bulk in the basis, they remain stabilizers of the post-measurement state,
2. They inbuild redundancies (“syndrome of syndromes”) into the measured string .
These redundancies will later allow us to use to infer errors that occur on the bulk, and in turn, correctly decode the error for the qubits on the boundary. Here we give an example and defer a rigorous exposition to [2, Section 3.2]. Recall that on every even layer of the , there is a copy of the -Tanner graph lying on the layers and adjacent to it. Now, consider a -check of the code denoted as , and let be the set of qubits it acts on. We show that the following operator
| (3) |
which applies a Pauli- on the copies of the check qubit in layers and , as well as the qubits supported in the check in layer , is a stabilizer of .
While perhaps a bit abstract at first, this operator captures the change in the syndrome after a layer of data-errors on the code and measurement errors on the checks: akin to the redundancy between adjacent syndrome measurements that appear in a repeated syndrome measurement protocol. The fact that these stabilizers factorize cleanly into products of Paulis is non-trivial and depends carefully on the structure of , which we discuss further in [2, Section 3.2].
The clustering argument. [18, 12] showed that any quantum LDPC code can correct random Pauli errors (below a constant threshold noise rate), even in the presence of syndrome measurement errors, by repeating the syndrome measurements times and running an information-theoretic minimum weight decoder. Their proof reasoned that the data-errors and syndrome-errors could be arranged in a low degree graph known as the syndrome adjacency graph, wherein the locations of mismatch errors (where the output of the decoder does not match the true error) clusters into connected components. By a percolation argument on this low-degree graph, one can argue these clusters are unlikely to “contrive” into configurations that induce logical errors on the code. Roughly speaking, the probability of a logical error is upper bounded by
| (4) | ||||
where only clusters of size larger than the code distance can incur logical errors, and is the degree of the graph.666A function only of the locality of the LDPC code. We assumed the noise rate is bounded by a threshold for the geometric series to converge.
Here, we broadly follow this strategy and construct an analogous low-degree syndrome adjacency graph which captures where our min-weight decoder incorrectly guesses a data or check error. Unfortunately, making this argument rigorous is easier said than done. Arguably the main challenge lies in relating the size of clusters of mismatch errors, to the number of true physical errors which lie within the cluster, to properly claim the decay rate with the cluster size. As we discuss in [2, Section 5] and [2, Appendix C], this calculation is highly dependent on the boundary conditions of the syndrome adjacency graph, tailored for Bell states and to GHZ states.
1.2 Discussion and other related works
Fault tolerant shallow circuits.
As a direct corollary, our single-shot logical state preparation can be used as the basis of a fault tolerant implementation of a shallow quantum circuit.
Corollary 4.
Fix an arbitrary quantum LDPC code . Let be a constant depth quantum circuit which uses or or GHZ initial states, gates which are transversal in , and measurements in the standard or Hadamard basis. Then there is a constant depth fault tolerant implementation of which uses a single round of mid-circuit measurement and feedforward.
Here we simply run our single-shot logical state preparation scheme to prepare encoded initial states, and then directly apply transversal gates. Since the logical circuit is constant depth, the residual local stochastic noise still remains local stochastic, and the logical or measurements at the end can be decoded using the code.
A natural question is whether we can remove the mid-circuit measurement and feedforward, and implement an ideal shallow quantum circuit purely via a noisy shallow quantum circuit. Ref. [7] gives such an example: starting from RBH, they directly apply a logical Clifford circuit without correcting the Pauli error . However, since the logical circuit is Clifford, the Pauli error is propagated through the circuit and corrected at the end. Our result similarly implies a more general version:
Corollary 5.
Fix an arbitrary quantum LDPC code . Let be a constant depth quantum circuit which uses or or GHZ initial states, and gates which are Clifford and transversal in , and measurements in the standard or Hadamard basis. Then there is a constant depth fault tolerant implementation of using a noisy circuit (without mid-circuit measurements and feedforward).
Note that we do not address the issue of decoding efficiency. In particular, although Corollary 5 does not need mid-circuit decoding, the decoding at the end of the circuit may still be inefficient. An interesting direction is to explore if Corollary 5 can be the basis of other quantum advantage experiments with noisy shallow quantum circuits against shallow classical circuits, as in [7].
Single-shot preparation of general stabilizer states.
Beyond GHZ state preparation, we show that single-shot logical state preparation can also be achieved for more general stabilizer states, using a combination of the ATG and Steane’s logical measurement. Let be a -qubit stabilizer state with the following structure: there exists a set of stabilizer generators that can be divided into two sets and , such that either or has constant weight and degree. The -qubit GHZ state is such an example, where and . We prove fault tolerant single-shot preparation for any such state encoded across copies of an arbitrary quantum LDPC code. See [2, Appendix D] for more details.
Single-shot quantum error correction.
A closely related concept to our work is single-shot quantum error correction [5]: consider an encoded code block subject to random errors, it is shown that for certain codes a single round of syndrome measurement suffices to correct the error (instead of performing repeated syndrome measurements), even in the presence of syndrome measurement errors. Examples include high-dimensional color codes [4, 5] and toric codes [19], hypergraph product codes [11], quantum Tanner codes [13] and hyperbolic codes [9].
As the ATG is closely related to repeated syndrome measurements, it is natural to ask whether single-shot logical state preparation with constant space overhead exists for those codes, or more generally, for any code with single-shot error correction. While this is proven for 3D gauge color codes [4, 5], it is unclear whether a general reduction from single-shot logical state preparation to single-shot error correction exists. The key issue is that single-shot error correction is defined in the context of correcting errors on an existing encoded code block, while single-shot logical state preparation is about preparing an encoded code state from scratch. We leave further exploration of this issue for future work; it is an interesting question in the context of reducing the spacetime overhead of quantum fault tolerance (also see [27]).
References
- [1] Dorit Aharonov and Yonathan Touati. Quantum circuit depth lower bounds for homological codes, 2018. arXiv:1810.03912.
- [2] Thiago Bergamaschi and Yunchao Liu. On fault tolerant single-shot logical state preparation and robust long-range entanglement, 2024. arXiv:2411.04405.
- [3] A. Bolt, G. Duclos-Cianci, D. Poulin, and T. M. Stace. Foliated quantum error-correcting codes. Phys. Rev. Lett., 117:070501, August 2016. doi:10.1103/PhysRevLett.117.070501.
- [4] H. Bombin. Gauge color codes: optimal transversal gates and gauge fixing in topological stabilizer codes. New Journal of Physics, 17, 2013. URL: https://api.semanticscholar.org/CorpusID:3355844.
- [5] Héctor Bombín. Single-shot fault-tolerant quantum error correction. Phys. Rev. X, 5:031043, September 2015. doi:10.1103/PhysRevX.5.031043.
- [6] S. Bravyi, M. B. Hastings, and F. Verstraete. Lieb-robinson bounds and the generation of correlations and topological quantum order. Phys. Rev. Lett., 97:050401, July 2006. doi:10.1103/PhysRevLett.97.050401.
- [7] Sergey Bravyi, David Gosset, Robert König, and Marco Tomamichel. Quantum advantage with noisy shallow circuits. Nature Physics, 16(10):1040–1045, October 2020. doi:10.1038/s41567-020-0948-z.
- [8] Sergey Bravyi, Isaac Kim, Alexander Kliesch, and Robert Koenig. Adaptive constant-depth circuits for manipulating non-abelian anyons, 2022. arXiv:2205.01933.
- [9] N. P. Breuckmann and Vivien Londe. Single-shot decoding of linear rate ldpc quantum codes with high performance. IEEE Transactions on Information Theory, 68:272–286, 2020. URL: https://api.semanticscholar.org/CorpusID:210157092.
- [10] Edward H. Chen, Guo-Yi Zhu, Ruben Verresen, Alireza Seif, Elisa Bäumer, David Layden, Nathanan Tantivasadakarn, Guanyu Zhu, Sarah Sheldon, Ashvin Vishwanath, Simon Trebst, and Abhinav Kandala. Realizing the nishimori transition across the error threshold for constant-depth quantum circuits, 2023. arXiv:2309.02863.
- [11] Omar Fawzi, Antoine Grospellier, and Anthony Leverrier. Efficient decoding of random errors for quantum expander codes. Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing, 2017. URL: https://api.semanticscholar.org/CorpusID:4390794.
- [12] Daniel Gottesman. Fault-tolerant quantum computation with constant overhead. Quantum Info. Comput., 14(15–16):1338–1372, November 2014. doi:10.26421/QIC14.15-16-5.
- [13] Shouzhen Gu, Eugene Tang, Libor Caha, Shin Ho Choe, Zhiyang He, and Aleksander Kubica. Single-shot decoding of good quantum ldpc codes. ArXiv, abs/2306.12470, 2023. doi:10.48550/arXiv.2306.12470.
- [14] Jeongwan Haah. An invariant of topologically ordered states under local unitary transformations. Communications in Mathematical Physics, 342(3):771–801, March 2016. doi:10.1007/s00220-016-2594-y.
- [15] Timo Hillmann, Guillaume Dauphinais, Ilan Tzitrin, and Michael Vasmer. Single-shot and measurement-based quantum error correction via fault complexes, 2024. arXiv:2410.12963.
- [16] Mohsin Iqbal, Nathanan Tantivasadakarn, Thomas M. Gatterman, Justin A. Gerber, Kevin Gilmore, Dan Gresh, Aaron Hankin, Nathan Hewitt, Chandler V. Horst, Mitchell Matheny, Tanner Mengle, Brian Neyenhuis, Ashvin Vishwanath, Michael Foss-Feig, Ruben Verresen, and Henrik Dreyer. Topological order from measurements and feed-forward on a trapped ion quantum computer. Communications Physics, 7(1):205, June 2024. doi:10.1038/s42005-024-01698-3.
- [17] Alexey A. Kovalev and Leonid P. Pryadko. Improved quantum hypergraph-product ldpc codes. In 2012 IEEE International Symposium on Information Theory Proceedings, pages 348–352, 2012. doi:10.1109/ISIT.2012.6284206.
- [18] Alexey A. Kovalev and Leonid P. Pryadko. Fault tolerance of quantum low-density parity check codes with sublinear distance scaling. Phys. Rev. A, 87:020304, February 2013. doi:10.1103/PhysRevA.87.020304.
- [19] Aleksander Kubica and Michael Vasmer. Single-shot quantum error correction with the three-dimensional subsystem toric code. Nature Communications, 13, 2021. URL: https://api.semanticscholar.org/CorpusID:235352916.
- [20] Jong Yeon Lee, Wenjie Ji, Zhen Bi, and Matthew P. A. Fisher. Decoding measurement-prepared quantum phases and transitions: from ising model to gauge theory, and beyond, 2022. arXiv:2208.11699.
- [21] Jong Yeon Lee, Yi-Zhuang You, and Cenke Xu. Symmetry protected topological phases under decoherence, 2024. arXiv:2210.16323.
- [22] Tsung-Cheng Lu, Leonardo A. Lessa, Isaac H. Kim, and Timothy H. Hsieh. Measurement as a shortcut to long-range entangled quantum matter. PRX Quantum, 3:040337, December 2022. doi:10.1103/PRXQuantum.3.040337.
- [23] Robert Raussendorf, Sergey Bravyi, and Jim Harrington. Long-range quantum entanglement in noisy cluster states. Phys. Rev. A, 71:062313, June 2005. doi:10.1103/PhysRevA.71.062313.
- [24] Nathanan Tantivasadakarn, Ryan Thorngren, Ashvin Vishwanath, and Ruben Verresen. Long-range entanglement from measuring symmetry-protected topological phases. Phys. Rev. X, 14:021040, June 2024. doi:10.1103/PhysRevX.14.021040.
- [25] Nathanan Tantivasadakarn, Ashvin Vishwanath, and Ruben Verresen. Hierarchy of topological order from finite-depth unitaries, measurement, and feedforward. PRX Quantum, 4:020339, June 2023. doi:10.1103/PRXQuantum.4.020339.
- [26] Jean-Pierre Tillich and Gilles Zémor. Quantum ldpc codes with positive rate and minimum distance proportional to the square root of the blocklength. IEEE Transactions on Information Theory, 60(2):1193–1202, 2014. doi:10.1109/TIT.2013.2292061.
- [27] Hengyun Zhou, Chen Zhao, Madelyn Cain, Dolev Bluvstein, Casey Duckering, Hong-Ye Hu, Sheng-Tao Wang, Aleksander Kubica, and Mikhail D. Lukin. Algorithmic fault tolerance for fast quantum computing, 2024. arXiv:2406.17653.
- [28] Guo-Yi Zhu, Nathanan Tantivasadakarn, Ashvin Vishwanath, Simon Trebst, and Ruben Verresen. Nishimori’s cat: Stable long-range entanglement from finite-depth unitaries and weak measurements. Phys. Rev. Lett., 131:200201, November 2023. doi:10.1103/PhysRevLett.131.200201.
