The Computational Complexity of Factored Graphs
Abstract
While graphs and abstract data structures can be large and complex, practical instances are often regular or highly structured. If the instance has sufficient structure, we might hope to compress the object into a more succinct representation. An efficient algorithm (with respect to the compressed input size) could then lead to more efficient computations than algorithms taking the explicit, uncompressed object as input. This leads to a natural question: when does knowing the input instance has a more succinct representation make computation easier?
We initiate the study of the computational complexity of problems on factored graphs: graphs that are given as a formula of products and unions on smaller graphs. For any graph problem, we define a parameterized version that takes factored graphs as input, parameterized by the number of (smaller) ordinary graphs used to construct the factored graph. In this setting, we characterize the parameterized complexity of several natural graph problems, exhibiting a variety of complexities. We show that a decision version of lexicographically first maximal independent set is XP-complete, and therefore unconditionally not fixed-parameter tractable (FPT). On the other hand, we show that clique counting is FPT. Finally, we show that reachability is XNL-complete. Moreover, XNL is contained in FPT if and only if NL is contained in some fixed polynomial time.
Keywords and phrases:
Parameterized Complexity, Fine-grained complexity, Fixed-parameter tractability, Graph algorithmsFunding:
Russell Impagliazzo: Supported by NSF Award AF: Medium 2212136.Copyright and License:
2012 ACM Subject Classification:
Theory of computation Complexity theory and logic ; Theory of computation Complexity classes ; Theory of computation Problems, reductions and completenessAcknowledgements:
We would like to thank Antonina Kolokolova, Anthony Ostuni, and anonymous reviewers for their many helpful comments and suggestions.Editors:
Raghu MekaSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
Traditionally, algorithm design and computational complexity both measure computational time as a function of the input size. Thus, the complexity of computational problems is crucially sensitive to the way the instances are represented as bit sequences. While graphs and abstract data structures can be complex and expressive in the worst case, practical instances are often highly structured or regular. For example, road networks are often organized into repetitive grid patterns. Similarly, in databases, relations frequently inherit underlying structures from previous relations through operations like joins. In molecular geometry, compounds such as graphite are composed of layers of graphene, with each layer forming a regular honeycomb structure. If the input instance has sufficiently regular structure, we might hope to compress the object into a more succinct representation.
An algorithm that is efficient with respect to the size of the succinct encodings would then be able to compute the desired result more efficiently than an algorithm that takes a naive representation of the input. This raises the question: when does knowing that the input instance was created in a uniform way (or has a succinct representation) make computation easier?
To address this question, various formulations of “succinct representation” have been explored. For example, one such formulation is given by a Boolean circuit that can produce any particular input bit [35, 61]. Frequently, the complexity of problems given in this type of succinct format is exponentially more difficult than when the input is given explicitly (see e.g. [35, 31, 49, 48]). However, it’s important to note that the difficulty only increases as a function of the smaller size parameter, and the actual problem has not necessarily become more difficult.
Another type of succinct representation, factored instances, was introduced by [21]. While they give a number of specific problems rather than introduce the concept abstractly, we can generalize by thinking of a fixed set of operations that take pairs of instances to possibly larger instances. For example, one natural operation might be set sum, taking two sets of integers to the set of all sums . Instead of being described directly, the input to a factored problem is given as this operation applied to a pair of possibly smaller instances. If these operations can be computed in polynomial time, the size of the output might be polynomially larger than the input, so this representation might be considerably smaller than the original. For each such set of operations and problem on instances, we can define a parameterized version of the problem on factored instances, where the input is represented as a formula in these (binary) operations over smaller instances, with the parameter being the number of smaller instances. If the underlying problem is polynomial time solvable, then for fixed , the problem remains polynomial time solvable, but with an exponent that potentially grows with . How the compressed representation affects the difficulty of the problems can be formalized in terms of the complexity of such factored problems from the point of view of parameterized complexity. In this paper, we consider such parameterized factored problems for graphs, using standard graph products and union as our operations.
To make this precise, we first review some standard concepts from parameterized complexity. The gold standard for tractability in parameterized complexity is membership in the class of fixed-parameter tractable () problems [25]. Roughly speaking, a factored problem will be fixed-parameter tractable (i.e. in ) if on an instance composed using smaller instances of size at most , there is an algorithm computing the function in time for some fixed function and absolute constant independent of . In these settings, we think of as large and as small, so that any dependence on alone is preferable over an exponent of that grows with . A natural approach to solving problems on factored graphs is to explicitly compute the graph, requiring time and space , and solving the problem on the explicit graph. Such an algorithm has an exponent growing with . Thus such factored problems will always be in 111assuming the problem can be solved in polynomial time on the explicit graph, the class of problems that are polynomial for any particular , but not necessarily in . Even for simple problems with linear time algorithms (on explicit graphs), computing an explicit representation already requires time and so this approach does not put the problem in .
In this work, we initiate the study of the complexity of computational problems on factored graphs. In particular, we consider the question: for a given computational problem, is there an algorithm substantially better than first explicitly computing the factored graph ? This can be formalized as: is the problem in , and, if not, how does the best exponent of possible depend on ?
1.1 Definition of Factored Graphs
We consider a highly natural class of factored problems where the instances are graphs, and the operations are well-studied graph products and unions. Our factored graphs consist of arbitrary combinations of graphs under the following (binary) operations. Unless otherwise stated, all graphs are directed and denotes an edge from to .
-
1.
Cartesian Product. Given , the Cartesian product has vertices for and there is an edge from to if either 1) and , or 2) and .
-
2.
Tensor Product. Given , the tensor product has vertices for and there is an edge from to if and .
-
3.
Union. Given , the union has vertices and there is an edge from to if .
A factored graph can be defined by an ordered tree , where internal nodes are labelled by one of the above three operations and leaves are labelled with (possibly identical) input graphs. Since each operation is associative, we in fact allow the internal nodes to have arbitrary degree.222We require each internal node to have degree greater than 1, as otherwise the operation is the identity. We say that a factored graph is of complexity if the tree has leaves and each input graph has at most vertices. Here, we stress that the we parameterize by the number of leaves in , regardless of the fan-in of specific internal nodes or if a certain input graph appears in multiple leaf nodes. As an example, both and are factored graphs of complexity , where . We illustrate their tree structures in Figure 1.
As another example, any graph can be represented by a factored graph of complexity by taking a union over all edges of the graph.
We define a factored component of , denoted , as follows. is defined by an ordered tree , which is obtained from by deleting every internal node labeled by and attaching exactly one child of to its parent. Another way to understand this is that, since the union and product operations obey the distributive law, we can recursively apply this law to convert a factored graph formula into a union of products. Then, each of these product terms is a factored component. The vertices of are -tuples (note , where is the number of leaves of and is the number of leaves of ). We emphasize that the vertices are flattened tuples and do not preserve the topology of beyond the order of the leaves. We call the dimension of the factored component . The edges of are determined by according to the definition of the graph operations and .
The vertex and edge sets of are then given by the union of the vertex and edge sets of the factored components. While a vertex may belong to multiple factored components, they must all have the same dimension, allowing us to define the dimension of a vertex (Definition 14). We also observe that has at most factored components. We give a more formal definition of factored graphs as well as simple examples in Section 2.
1.2 Our Contributions
Our first result provides an unconditional hardness for a natural parameterized version of the well-studied Lexicographically First Maximal Independent Set (LFMIS) problem. The standard decision version of the LFMIS problem takes as input a graph , where the vertices are indexed as , and a special vertex . The problem asks whether belongs to the LFMIS of . In the parameterized version, the input is given as a factored graph and the vertex indices are provided only for each graph factor . To recover the indices for , recall that each vertex in the factored graph is a flattened tuple of numbers for some , and therefore, we define the vertex indices to be given according to the standard lexicographic order of these tuples, with the index 0 given to the vertex with the lowest lexicographic order. In this work, we show that the LFMIS problem on factored graphs is -complete under -reductions333See Definition 9.3 [27]. Also formally stated in Definition 20 in the context of factored graph problems. and therefore unconditionally not in , providing a lower bound on the best possible exponent as a function of . LFMIS is a natural -complete problem [18], studied by [58, 59, 60] including in the parallel setting [20, 50, 12, 8]. We use the -completeness of this problem as an intuition for why the factored version might be difficult (-complete), but we know of no direct connection between -completeness and hardness of the factored version.
Theorem 1 (-completeness of LFMIS).
The LFMIS problem on factored graphs is -complete under -reductions and not fixed-parameter tractable. In particular, the LFMIS problem on a factored graph of complexity requires time.
While many works in parameterized complexity gave conditional lower bounds against problems in [25], for example completeness for the W-hierarchy [25, 26, 28] or the A-hierarchy [32], unconditional lower bounds against natural problems in are relatively rare [27]. Moreover, although it is known that via a diagonalization argument, the literature on -complete problems remains sparse. The “pebble game” problem was first introduced by Kasai, Adachi, and Iwata [45]. Its parameterized version, the “-pebble game”, was one of the earliest natural combinatorial problems shown to require time and be -complete [1]. As an application of the -pebble game, some other game problems, such as the “cat and mouse game” [13] and the “-peg game”, have also been proven to be -complete via reductions from the -pebble game problem [1]. More recently, Berkholz established an unconditional lower bound of -time for the existential -pebble game [6]. Our result provides yet another natural example of an -complete problem with an explicit lower bound of .
In contrast to the LFMIS problem on factored graphs, we show that the well-studied problem of clique counting [51] is in , solvable in a fixed polynomial of the input graph sizes (where the exponent possibly depends on the size of the clique of interest) times some function on the number of input graphs. Subgraph counting (in particular clique counting) has been studied by a long line of works [51, 16, 11, 42] in a variety of computational models [21, 24, 2, 56, 39]. On graphs with vertices, -cliques can be counted in time (and time is necessary under standard hardness assumptions). We show that counting -cliques on factored graphs of complexity is in time for some fixed (large) function . Note that we do not show clique counting is in with respect to the clique size parameter , but only with respect to the complexity of the factored graph .
Theorem 2 (Counting Clique Subgraphs is in ).
Let be a clique on vertices. Then, computing the number of exact copies of in , denoted , is fixed-parameter tractable. In particular, there is an algorithm computing on factored graphs of complexity in time for some function .
Finally, we turn to the problem of reachability, one of the most fundamental computational problems on graphs. On an explicit graph, algorithms such as depth-first search (DFS) and breadth-first search (BFS) compute reachability in linear time. This raises the question: can reachability on factored graphs be computed efficiently? Moreover, reachability is closely related to classic space complexity classes. The general reachability problem is an important -complete problem [57, 43]; meanwhile, Cook and Mckenzie showed that reachability on a directed acyclic graph of outdegree at most one is -complete [19]. This naturally gives rise to another question: does the completeness of reachability for a classic complexity class extend to its parameterized counterpart when the inputs are given as factored graphs, similar to what we have seen in the case of LFMIS in Theorem 1?
Indeed, we show that the parameterized version of reachability on factored graphs is -complete under -reductions, where is the class of parameterized problems solvable in nondeterministic logarithmic space for any fixed parameter . On the other hand, while we cannot provide a definitive answer to whether reachability on factored graphs is in , we show that answering this question would exactly resolve a major open problem in classical complexity theory. Specifically, we establish a parameterized analog of the well-known open problem that asks whether for some fixed constant .
Theorem 3 (-completeness of Reachability).
Reachability on factored graphs is -complete under -reductions. Furthermore, the following are equivalent:
-
1.
There is a constant such that .
-
2.
.
This result also has several further implications. First, we observe that if reachability is not in , for any space-constructible . On the other hand, if reachability is in then the Exponential Time Hypothesis (ETH) is false. In particular, we claim that since -SUM (determining if in a set of numbers of bits there is a subset of numbers summing to zero) is in , then -SUM can be solved in time, and therefore ETH is false [55].444We need bits to verify that numbers of bits sum to zero. Finally, by combining the above implications, one can also conclude that if ETH is true, then , a result that, to the best of our knowledge, has not been previously established.
Parameterized space complexity classes, including XL and XNL, have also been studied extensively in the literature [10, 17, 33, 29]. Chen, Flum, and Grohe introduced the first complete problems for XL and XNL under parameterized-logspace-reductions555Also known as PL-reductions, a more restrictive notion compared to -reductions [17]. In a related direction, [9] identified a wide variety of problems complete for the class XNLP, which is the class of parameterized problems solvable in nondeterministic logarithmic space and polynomial time for each parameter. Most relevant to our result, Elberfeld, Stockhusen, and Tantau also showed that a parameterized version of reachability with multi-colored edges is complete for the class parameterized-NL-cert under PL-reductions [29].
1.3 Related Work
A long line of work, initiated by [25, 26, 28, 32], has studied the complexity of parameterized problems as a function of their input size and a parameter. Within parameterized complexity, a common theme is to study the complexity of problems given succinct representations of their input. For example, several previous works have investigated the complexity of computing Nash equilibrium of succinct games (represented implicitly) [31, 23, 22, 34, 53, 36]. As another example, [62] considers the complexity of combinatorial problems with succinct representation. Similarly, [52, 63, 40, 41, 49, 48, 14, 15] study the complexity of various computational problems on periodic structures, i.e., travel schedules on a periodic timetable.
Most relevant to this paper, several works have investigated computational problems on graphs with succinct representations such as small circuits [35], distributed graphs described by low complexity agents [4], and factored problems [21]. However, none of these works consider the complexity of factored graphs formed under graph products.
2 Preliminaries
Unless otherwise noted, we work with directed graphs, with edges from to denoted by . For a graph , we denote its vertices by and edges by . For any subset of vertices , let denote the subgraph induced by . For a set , we define to be the power set of .
2.1 Graph Products
We begin with the definitions of the relevant graph operations. Let and be two directed graphs.
Definition 4.
The Cartesian product of and has vertex set and directed edges if and only if either
-
and , or
-
and
As a simple example, note that the Cartesian product of two paths is a grid.
Definition 5.
The tensor product of and has vertex set and directed edges if and only if and .
Definition 6.
The union of and has vertex set and edge set .
While there are many other graph products and operations to consider, such as the or product, or graph negation, we will primarily focus our study of factored graphs under the above three operations.
We note that the above three operations are associative, and observe that the products of higher arity are given as follows.
Definition 7.
The Cartesian product has vertex set and directed edges if and only if there is some index such that and for all .
Definition 8.
The tensor product has vertex set and directed edges if and only if for all .
Definition 9.
The union of and has vertex set and edge set .
2.2 Factored Graph Construction
We now describe how the above operations construct factored graphs. Formally, we define a factored graph by describing how the above graph operations combine the input graphs into a single graph. This motivates the definition of a factored graph according to a tree which specifies the order of operations, or the tree structure of a factored graph.
Definition 10 (Factored Graph Tree Structure).
The factored graph tree structure with leaves, denoted , is an ordered tree with leaves where internal nodes are labelled by an operation (one of , or ) and the leaves are labelled by graphs . Note that are arbitrary and not necessarily distinct. We require that each internal node has degree at least .
Let denote that is the factored graph given by the factored graph tree structure . For convenience, let denote the factored graph tree structure. We say that the factored graph tree structure , or simply , is of complexity if has at most leaves and each leaf is labelled by a graph with at most vertices.
To illustrate our definitions, we will use the following example of a factored graph . Note that there is a natural correspondence between the tree structures of factored graphs and the formulas of the above form, by using parentheses to delineate subtrees of the tree structure. The tree structure of is given in Figure 2.
We now describe how the vertex and edge sets of a factored graph are obtained from its tree structure. First, we define factored components of factored graphs.
Definition 11 (Factored Component).
Let be a factored graph. A factored component of is the factored graph whose tree structure is obtained from the tree structure of by recursively replacing each internal node labelled by with the subtree rooted at one of its children. Note that the internal nodes of are labelled either or .
We say has dimension if has leaves. Suppose the leaves are labelled . Then, . We say every vertex has dimension . The edge set is determined by and following the rules of Cartesian and tensor products.
In our example, the factored components are , and , with dimensions , respectively. Some example tree structures of factored components are given in Figure 3.
Here, we emphasize that the vertex sets of the factored components are flattened products of the vertex sets of the graphs labeling the leaves. For example, the vertex of the factored component has the form not . In particular, the vertex sets do not depend on the topology of the tree beyond the order of the leaves. Finally, the vertex and edge set of is simply the union of the factored components.
Definition 12 (Factored Graph).
Let be a factored graph with tree structure and factored components . Define and .
We note here that different factored graphs can have identical vertex and edge sets. For example, and both have vertex set and edges from to if and only if for all . This aligns with our expectation, as the tensor product is associative.
Note that a single vertex in can belong to multiple factored components. In our running example, if there is a vertex , then the vertex is in the factored components corresponding to and . However, both factored components have dimension . This is formalized in the following lemma, which follows directly from the construction of factored graphs.
Lemma 13.
Suppose is in factored components . Then, .
This allows us to define the dimension of a vertex as the dimension of any factored component it belongs to.
Definition 14 (Vertex Dimension).
Let be a factored graph and be a vertex. The dimension of , denoted by , is the dimension of any factored component that contains .
By construction, the endpoints of any edge must belong to the same factored component.
Lemma 15.
Let be an edge. Then, and belong to the same factored component.
As a corollary, we show that there are no edges between vertices of different dimensions, since vertices in the same factored component necessarily have the same dimension.
Corollary 16.
Let be an edge in . Then, and have the same dimension.
Finally, since every vertex has a unique dimension, it is clear that vertex dimension partitions the vertices of the factored graph. Thus, vertex dimension induces an equivalence relation on .
2.3 Parameterized Complexity
In this section, we review the parameterized complexity classes relevant to this paper with respect to problems on factored graphs. We begin with the definition of fixed-parameter tractability ().
Definition 17 (Fixed-parameter Tractability () for Factored Graph Problems).
A problem on factored graphs is fixed-parameter tractable if there exists an algorithm that solves the problem on factored graph inputs of complexity in time , where is a function of and is a constant independent of .
We also study the parameterized complexity classes and , which correspond to the parameterized version of the classical complexity classes and , respectively. More generally, one can define the parameterized version for any classical complexity class as follows [27]: a parameterized language if and only if for every parameter . Here, is referred to as the -th slice of , which is the subset of consisting of all instances with parameter . We now give the definitions of and in the context of factored graph problems.
Definition 18 ( for Factored Graph Problems).
A problem on factored graphs is in if there exists an algorithm that solves the problem on factored graph inputs of complexity in time , where is a function of .
Definition 19 ( for Factored Graph Problems).
A problem on factored graphs is in if there exists a nondeterministic algorithm that solves the problem on factored graph inputs of complexity in space , where is a function of .
Finally, for - and -completeness, we follow the usual definition that a problem is considered to be complete for a complexity class C if it belongs to C and is hard for C under some suitable notion of reductions. Here, we use the standard notion of parameterized mapping reduction (see Definition 9.3 in [27]), also known as the -reduction [17], under which the class is closed. We now give a definition for - and -hardness under this reduction in the context of factored graph problems.
Definition 20 (-hardness (resp. -hardness) for Factored Graph Problems).
A problem on factored graphs is -hard (resp. -hard) if for every parameterized language (resp. ), there exists a mapping such that for every parameter , mapping reduces to under using time, where is a function of and depends only on .
3 Technical Overview
In this section, we provide a technical overview of our results. Due to space constraints, the proofs are left to the full version of the paper.
3.1 Lexicographically First Maximal Independent Set
Recall that our first main result is the -completeness of the LFMIS problem on factored graphs.
See 1
Theorem 1 is a consequence of a generic reduction from an arbitrary language to the LFMIS problem on factored graphs. Specifically, given a language and the corresponding Turing machine that decides in time, we construct a factored graph of complexity using time, such that solving the LFMIS on simulates the Turing machine . Then, it is fairly straightforward from this reduction that the problem is -complete. Moreover, we also obtain the explicit lower bound of by an application of the Time Hierarchy Theorem to the reduction.
Before proceeding to the detailed explanation, we first provide a high level intuition of this construction. Given a Turing machine, we can encapsulate its computation history in a matrix, where each row represents a configuration of the Turing machine at a specific time. The key idea of the reduction is to construct a graph in such a way that selecting vertices for the LFMIS corresponds to recovering the matrix entries, and thereby simulating the machine. To achieve this, we construct a graph with a grid structure mirroring the matrix. At each grid point, we place a collection of vertices representing all the possible choices for the corresponding matrix entry. The edges are defined according to the machine’s transition function to ensure that the LFMIS chooses the single correct vertex from each grid point that agrees with the computation history of the Turing Machine, effectively allowing us to simulate the Turing machine by solving the LFMIS on the graph. It turns out that this graph has a highly regular structure and therefore can be factorized into a more succinct representation. In the remainder of this (sub)section, we explain this reduction in further detail.
Let be a language in and let be the corresponding Turing machine that decides in time Given an input to , if halts within time , then the entire computation history of on can be represented by a matrix , where the -th row of represents the configuration of at time . To achieve this, each entry contains the following information about the -th tape cell at time : 1) the symbol occupying the cell, 2) whether the tape head is over the cell, and 3) the machine’s current state if the tape head is over the cell. The goal now is to define a graph such that the LFMIS of recovers the computation history , thereby simulating the machine . We modify the Turing machine so that it suffices to query a single vertex in the graph for the halting state of .
Explicit Graph Definition
We begin by defining explicitly as an ordinary graph and then give a factored representation of . Let be the set of vertices corresponding to all possible choices for an entry in the matrix . We define the vertex set of to be copies of , arranged in a grid-like pattern analogous to the matrix . Each copy of is referred to as a supernode, and we use to denote the supernode in the -th row and -th column. Intuitively, the supernode represents all possible choices for the entry . Therefore, we must define the edges of such that the LFMIS includes the single correct vertex, which we call , from each that agrees with the entry .
The edge set of consists of two types of edges: intra-supernode and inter-supernode edges. The intra-supernode edges are designed to ensure that the LFMIS contains at most one vertex within each supernode. This is easily achieved by defining a complete digraph on each supernode. On the other hand, the inter-supernode edges are constructed to ensure that the LFMIS contains the correct vertex from each supernode that agrees with the corresponding entry of . This construction is more subtle and leverages the fact that the configuration at any given time of a deterministic machine uniquely determines the next configuration. Moreover, since the tape head can only move one step left or right at a time, each entry can be uniquely determined given only the three neighboring entries from the previous row: (instead of the entire previous row). To view this from another perspective: the entries , , and each restricts the possible choices for according to the machine’s transition function. We define edges between neighboring supernodes to encode these restrictions. Specifically, for and , a directed edge indicates that, if is chosen to represent the -th tape cell at time , then cannot represent the -th tape cell at the next time step , based on the machine’s transition function. We hope that if the vertices , , and are correctly contained in the LFMIS, then the edges ensure that is the unique vertex in that is not adjacent to or . This will allow us to build the LFMIS inductively. The base case (which corresponds to the first row) is more technical and involves adding horizontal connections between supernodes.
Factored Graph Construction
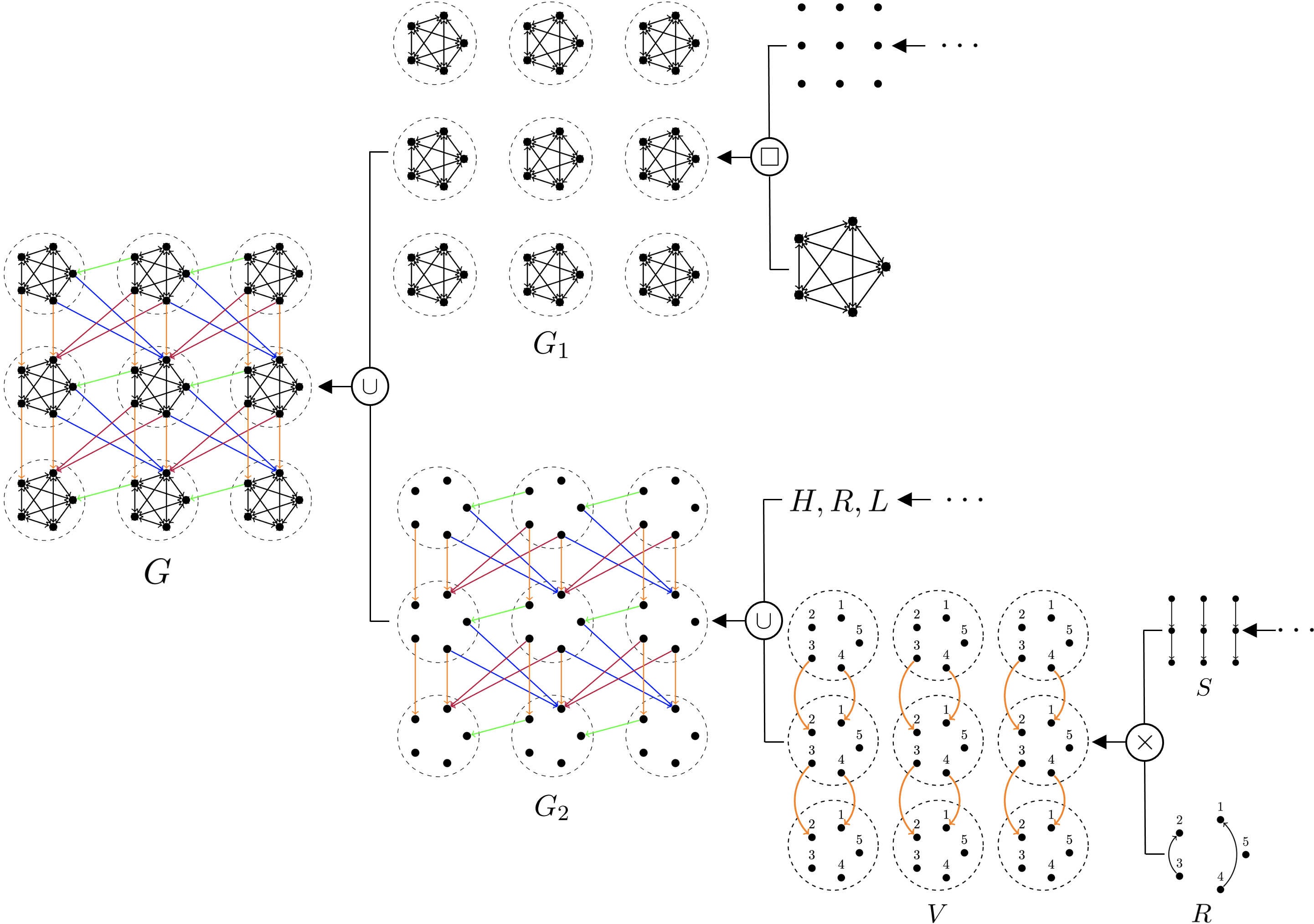
Naively, this graph has vertices, where . However, since the computation rules of are local (depending only on the symbol of the work tape under the head) and repetitive (the same rules apply regardless of the head’s absolute position), we can give a succinct factored representation of . Specifically, we show that has a factored graph representation of complexity . The factorization of is outlined in Figure 4.
The key idea is to break down the graph into regular and repetitive substructures. Following this, we begin by decomposing into two subgraphs, and , such that both subgraphs share the same vertex set as , but contains only the intra-supernode edges and contains only the inter-supernode edges. forms a grid of complete supernodes, which can be represented as the Cartesian product of an empty grid of vertices and a single complete supernode. Similarly, is a grid of supernodes, but with edges connecting neighboring supernodes in four possible directions: vertical , horizontal , diagonally-right , and diagonally-left . We can further decompose into four subgraphs , , , and , which only contain the edges which are in the direction indicated by the name of the subgraph. Each of these subgraphs can be further decomposed into a “structure” graph and a “relation” graph using the tensor product. The structure graph consists of a grid of (ordinary) vertices with edges connecting all neighboring vertices in the corresponding direction of the subgraph. The relation graph encodes the connections between vertices in neighboring supernodes in the corresponding direction. Moreover, the structure graphs themselves can be further factorized. For example, the structure graph for the subgraph can be expressed as the Cartesian product of a path of length and an empty graph on vertices. When the path length is a perfect power (where are integers), it can be further decomposed into a union of factored graphs of complexities . Further details can be found in the full version of the paper.
3.2 Counting -Cliques
In contrast to the first result, our second main result states that counting cliques on factored graphs is in . For this result, we assume that all graphs are undirected.
See 2
In the technical overview, we use edge counting () as an illustrative example. Note that if is an edge, must have the same dimension (Corollary 16), so we may count the edges in each dimension separately. Thus, fix a dimension .
There are at most factored components of dimension . While some edges may belong to multiple factored components, we can use the inclusion-exclusion principle to avoid double-counting such edges. In particular, it suffices to consider counting the number of edges in an arbitrary intersection of factored components . Note that the number of such intersections, while being a large function of , is crucially independent of .
Fix such an intersection and consider a pair of vertices with and . Note that by determining whether are equal or adjacent for all , we can infer from the factored graph tree structure whether . Thus, we can categorize all pairs of vertices into groups based on the relations and . Note also that these groups are disjoint. Next, we collect the subset of groups that form edges in the current intersection . To count the number of edges, it then suffices to sum up the sizes of each group in this collection. For a given group, we can determine its size in time since the relations on each coordinate are independent. In particular, we can count the number of pairs of vertices in each input graph satisfying the relevant constraints and take the product over all input graphs.
3.3 Reachability
Finally, we study the reachability problem on factored graphs.
See 3
We begin with an overview of the proof for the -completeness result, followed by that for the equivalence result. In fact, we will see that both proofs rely on the same major building blocks in slightly different ways.
-completeness
We follow the standard framework for showing that reachability is -complete [57].
Membership in can be established using the same algorithm that shows the ordinary reachability problem is in , even if the input is now given as a factored graph. As in the standard proof, we non-deterministically guess the next vertex in the path and thus only require -space for factored graphs of complexity . Formally, each vertex in can be specified by bits, since each vertex is a tuple of at most coordinates and each coordinate is a vertex in an input graph with at most vertices. Thus, the algorithm requires bits to write down the current vertex and, since the factored graph has at most vertices, at most bits to keep track of the number of steps taken so far.
For -hardness, suppose we have some language . Then, there exists a nondeterministic Turing machine deciding using -space on inputs of length and parameter , for some function of . The standard reduction creates an explicit configuration graph where each vertex encodes a tuple consisting of state, input and work tape positions, and a setting of the work tape. Since the work tape has length , there are at least distinct settings of the work tape. Thus, even though reachability is computable in linear time, the size of the graph already depends exponentially on . However, we are able to exploit the locality of Turing machine operations so that the configuration graph can in fact be encoded by a factored graph of complexity . Given some configuration of on input (a tuple of state, tape head locations and work tape contents), we split the configuration into segments, where each segment only contains contiguous bits of the work tape contents. Note that each segment, even if it encodes a state and tape head locations, only has possible values, since one segment of the work tape only has bits. Thus, we can represent all possible configurations of a segment explicitly using a graph with vertices, while a product of segment graphs can explicitly represent any full configuration of on input .
It remains to express the appropriate transitions between configurations using a factored graph. There are two types of transitions: intra-segment transitions, where the work tape head stays within the same segment, and inter-segment transitions, where the work tape head moves from one segment to another (adjacent) segment. In either case, at most two segments of the work tape are active, where a segment is active during a transition if the work tape head either starts or ends in the segment and inactive otherwise. Thus, we can express individual segments (or pairs of segments) explicitly using input graphs of size . Since the active segments and inactive segments do not interact, we can encode all intra-segment transitions of a single segment using factored graphs of complexity . Similarly, we can encode all inter-segment transitions between a single pair of adjacent segments. Summing over all segments and pairs of adjacent segments, we encode the configuration graph in a factored graph of complexity .
We now briefly describe how the locality of Turing machine computation allows us to express the configuration graph of on using factored graphs. In the overview, we describe only intra-segment transitions. First, note that if the work tape head is not currently placed in a segment, the work tape contents of this segment cannot change. We thus define an inactive graph, where for every possible work tape content, we create a self-loop vertex. If the work tape head is currently placed in the segment, the work tape contents may change. Thus, we define an active graph with all possible configurations on a given segment as nodes, and edges encoding valid transitions. For a given segment, taking the tensor product of the active graph for this segment and the inactive graph for all other segments encodes all intra-segment transitions. A similar construction can be used to construct factored graphs that encode inter-segment transitions.
Equivalence to the Open Problem
For the forward direction, suppose there exists an absolute constant such that . To show that , it now suffices to show reachability on factored graphs is in due to its -completeness under -reductions. Note that the algorithm used in the proof of -membership is in fact an algorithm for each fixed parameter . Thus, if for some independent of , then for any fixed , reachability on factored graphs of complexity can be computed in time (as factored graphs of this complexity have input size ) and is therefore in .
Conversely, if , then in particular, reachability on factored graphs is in . Now, consider any language with its associated nondeterministic Turing machine that decides in space for some constant . Using the same construction as in the proof of -hardness, we construct a factored graph of complexity where solving reachability on simulates . Since reachability on factored graphs is in , it follows that reachability on can be solved in time for some function , where the exponent on is independent of , hence independent of the specific language . This shows that for some absolute constant .
4 Conclusion and Future Work
We have studied the computational complexity of various problems on factored graphs. Even among problems with polynomial time algorithms on explicit graphs, we have shown that their parameterized complexity when the input is represented as a factored graph can differ quite drastically. In the context of parameterized complexity, we have sought to characterize which problems on factored graphs are in . On the positive side, counting the number of copies of a small clique is in . On the negative side, LFMIS is unconditionally not in . Finally, we show that determining whether reachability is in is equivalent to determining whether .
Can the unconditional lower bounds for LFMIS on factored graphs be used to prove similar unconditional lower bounds for other parameterized problems? One obstacle to doing this is the gap in complexity between the -complete LFMIS problem and the easily parallelizable problems that form the bulk of the literature in parameterized complexity. However, reductions in fine-grained complexity often cut across traditional complexity classes, e.g., [46]. So we do not know a reason why this should not also be the case here. Either finding such unconditional results or explaining their impossibility would both be interesting. We could also hope to prove similar results for other -complete problems.
While our lower bounds separate the problems of interest from , they do not rule out significant improvements on the naive algorithm of computing the factored graph explicitly and solving the problem on itself. For example, our LFMIS lower bound only unconditionally rules out algorithms with time . An interesting open problem is to provide a more fine-grained analysis of the complexity of factored graph problems, possibly distinguishing between the number of product and union operations.
In this work, we have chosen to study factored graphs under graph products and unions, specifically the Cartesian and tensor products. A natural extension is to consider other products and operations on graphs, or other interesting objects. Factored problems on bit strings were introduced in [21], and implicitly on integer-valued vectors in [3]. Do similar results hold for factored problems for these input domains and operations?
References
- [1] Akeo Adachi, Shigeki Iwata, and Takumi Kasai. Some combinatorial game problems require omega(n) time. J. ACM, 31(2):361–376, March 1984. doi:10.1145/62.322433.
- [2] Enric Boix Adserà, Matthew S. Brennan, and Guy Bresler. The average-case complexity of counting cliques in erdős-rényi hypergraphs. CoRR, abs/1903.08247:FOCS19–39, 2019. doi:10.48550/arXiv.1903.08247.
- [3] Haozhe An, Mohit Gurumukhani, Russell Impagliazzo, Michael Jaber, Marvin Künnemann, and Maria Paula Parga Nina. The fine-grained complexity of multi-dimensional ordering properties. Algorithmica, 84(11):3156–3191, 2022. doi:10.1007/s00453-022-01014-x.
- [4] Sanjeev Arora, David Steurer, and Avi Wigderson. Towards a study of low-complexity graphs. In Susanne Albers, Alberto Marchetti-Spaccamela, Yossi Matias, Sotiris E. Nikoletseas, and Wolfgang Thomas, editors, Automata, Languages and Programming, 36th International Colloquium, ICALP 2009, Rhodes, Greece, July 5-12, 2009, Proceedings, Part I, volume 5555 of Lecture Notes in Computer Science, pages 119–131. Springer, Springer, 2009. doi:10.1007/978-3-642-02927-1_12.
- [5] Jérémy Barbay, Luca Castelli Aleardi, Meng He, and J. Ian Munro. Succinct representation of labeled graphs. In Takeshi Tokuyama, editor, Algorithms and Computation, 18th International Symposium, ISAAC 2007, Sendai, Japan, December 17-19, 2007, Proceedings, volume 4835 of Lecture Notes in Computer Science, pages 316–328. Springer, Springer, 2007. doi:10.1007/978-3-540-77120-3_29.
- [6] Christoph Berkholz. Lower bounds for existential pebble games and k-consistency tests. In Proceedings of the 27th Annual IEEE Symposium on Logic in Computer Science, LICS 2012, Dubrovnik, Croatia, June 25-28, 2012, pages 25–34. IEEE Computer Society, 2012. doi:10.1109/LICS.2012.14.
- [7] Guy E. Blelloch and Arash Farzan. Succinct representations of separable graphs. In Amihood Amir and Laxmi Parida, editors, Combinatorial Pattern Matching, 21st Annual Symposium, CPM 2010, New York, NY, USA, June 21-23, 2010. Proceedings, volume 6129 of Lecture Notes in Computer Science, pages 138–150. Springer, Springer, 2010. doi:10.1007/978-3-642-13509-5_13.
- [8] Guy E. Blelloch, Jeremy T. Fineman, and Julian Shun. Greedy sequential maximal independent set and matching are parallel on average. In Guy E. Blelloch and Maurice Herlihy, editors, 24th ACM Symposium on Parallelism in Algorithms and Architectures, SPAA ’12, Pittsburgh, PA, USA, June 25-27, 2012, pages 308–317. ACM, 2012. doi:10.1145/2312005.2312058.
- [9] Hans L. Bodlaender, Carla Groenland, Jesper Nederlof, and Céline M. F. Swennenhuis. Parameterized problems complete for nondeterministic FPT time and logarithmic space. CoRR, abs/2105.14882, 2021. doi:10.48550/arXiv.2105.14882.
- [10] Liming Cai, Jianer Chen, Rodney G. Downey, and Michael R. Fellows. Advice classes of parameterized tractability. Ann. Pure Appl. Log., 84(1):119–138, 1997. Asian Logic Conference. doi:10.1016/S0168-0072(95)00020-8.
- [11] Chris Calabro, Russell Impagliazzo, Valentine Kabanets, and Ramamohan Paturi. The complexity of unique k-sat: An isolation lemma for k-cnfs. J. Comput. Syst. Sci., 74(3):386–393, 2008. doi:10.1016/j.jcss.2007.06.015.
- [12] Neil J. Calkin, Alan M. Frieze, and Ludek Kucera. On the expected performance of a parallel algorithm for finding maximal independent subsets of a random graph. Random Struct. Algorithms, 3(2):215–222, 1992. doi:10.1002/rsa.3240030210.
- [13] Ashok K. Chandra and Larry J. Stockmeyer. Alternation. In 17th Annual Symposium on Foundations of Computer Science, Houston, Texas, USA, 25-27 October 1976, pages 98–108. IEEE Computer Society, 1976. doi:10.1109/SFCS.1976.4.
- [14] Hubie Chen. Periodic constraint satisfaction problems: Polynomial-time algorithms. In Francesca Rossi, editor, Principles and Practice of Constraint Programming - CP 2003, 9th International Conference, CP 2003, Kinsale, Ireland, September 29 - October 3, 2003, Proceedings, volume 2833 of Lecture Notes in Computer Science, pages 199–213. Springer, Springer, 2003. doi:10.1007/978-3-540-45193-8_14.
- [15] Hubie Chen. Periodic constraint satisfaction problems: Tractable subclasses. Constraints An Int. J., 10(2):97–113, 2005. doi:10.1007/s10601-005-0551-z.
- [16] Jianer Chen, Xiuzhen Huang, Iyad A. Kanj, and Ge Xia. Strong computational lower bounds via parameterized complexity. J. Comput. Syst. Sci., 72(8):1346–1367, 2006. doi:10.1016/j.jcss.2006.04.007.
- [17] Yijia Chen, Jörg Flum, and Martin Grohe. Bounded nondeterminism and alternation in parameterized complexity theory. In 18th Annual IEEE Conference on Computational Complexity (Complexity 2003), 7-10 July 2003, Aarhus, Denmark, pages 13–29. IEEE Computer Society, 2003. doi:10.1109/CCC.2003.1214407.
- [18] Stephen A. Cook. A taxonomy of problems with fast parallel algorithms. Inf. Control., 64(1-3):2–21, 1985. doi:10.1016/S0019-9958(85)80041-3.
- [19] Stephen A. Cook and Pierre McKenzie. Problems complete for deterministic logarithmic space. J. Algorithms, 8(3):385–394, 1987. doi:10.1016/0196-6774(87)90018-6.
- [20] Don Coppersmith, Prabhakar Raghavan, and Martin Tompa. Parallel graph algorithms that are efficient on average. In 28th Annual Symposium on Foundations of Computer Science, Los Angeles, California, USA, 27-29 October 1987, pages 260–269. IEEE, IEEE Computer Society, 1987. doi:10.1109/SFCS.1987.46.
- [21] Mina Dalirrooyfard, Andrea Lincoln, and Virginia Vassilevska Williams. New techniques for proving fine-grained average-case hardness. In Sandy Irani, editor, 61st IEEE Annual Symposium on Foundations of Computer Science, FOCS 2020, Durham, NC, USA, November 16-19, 2020, pages 774–785. IEEE, IEEE, 2020. doi:10.1109/FOCS46700.2020.00077.
- [22] Constantinos Daskalakis, Alex Fabrikant, and Christos H. Papadimitriou. The game world is flat: The complexity of nash equilibria in succinct games. In Michele Bugliesi, Bart Preneel, Vladimiro Sassone, and Ingo Wegener, editors, Automata, Languages and Programming, 33rd International Colloquium, ICALP 2006, Venice, Italy, July 10-14, 2006, Proceedings, Part I, volume 4051 of Lecture Notes in Computer Science, pages 513–524. Springer, Springer, 2006. doi:10.1007/11786986_45.
- [23] Konstantinos Daskalakis and Christos H. Papadimitriou. The complexity of games on highly regular graphs. In Gerth Stølting Brodal and Stefano Leonardi, editors, Algorithms - ESA 2005, 13th Annual European Symposium, Palma de Mallorca, Spain, October 3-6, 2005, Proceedings, volume 3669 of Lecture Notes in Computer Science, pages 71–82. Springer, Springer, 2005. doi:10.1007/11561071_9.
- [24] Laxman Dhulipala, Quanquan C. Liu, Julian Shun, and Shangdi Yu. Parallel batch-dynamic k-clique counting. In Michael Schapira, editor, 2nd Symposium on Algorithmic Principles of Computer Systems, APOCS 2020, Virtual Conference, January 13, 2021, pages 129–143. SIAM, SIAM, 2021. doi:10.1137/1.9781611976489.10.
- [25] Rodney G. Downey and Michael R. Fellows. Fixed-parameter tractability and completeness I: basic results. SIAM J. Comput., 24(4):873–921, 1995. doi:10.1137/S0097539792228228.
- [26] Rodney G. Downey and Michael R. Fellows. Fixed-parameter tractability and completeness II: on completeness for W[1]. Theor. Comput. Sci., 141(1&2):109–131, 1995. doi:10.1016/0304-3975(94)00097-3.
- [27] Rodney G. Downey and Michael R. Fellows. Parameterized Complexity. Monographs in Computer Science. Springer, 1999. doi:10.1007/978-1-4612-0515-9.
- [28] Rodney G. Downey, Michael R. Fellows, and Kenneth W. Regan. Descriptive complexity and the W hierarchy. In Paul Beame and Samuel R. Buss, editors, Proof Complexity and Feasible Arithmetics, Proceedings of a DIMACS Workshop, New Brunswick, New Jersey, USA, April 21-24, 1996, volume 39 of DIMACS Series in Discrete Mathematics and Theoretical Computer Science, pages 119–134. Citeseer, DIMACS/AMS, 1996. doi:10.1090/dimacs/039/07.
- [29] Michael Elberfeld, Christoph Stockhusen, and Till Tantau. On the space complexity of parameterized problems. In Dimitrios M. Thilikos and Gerhard J. Woeginger, editors, Parameterized and Exact Computation - 7th International Symposium, IPEC 2012, Ljubljana, Slovenia, September 12-14, 2012. Proceedings, volume 7535 of Lecture Notes in Computer Science, pages 206–217, Berlin, Heidelberg, 2012. Springer. doi:10.1007/978-3-642-33293-7_20.
- [30] Arash Farzan and J. Ian Munro. Succinct representations of arbitrary graphs. In Dan Halperin and Kurt Mehlhorn, editors, Algorithms - ESA 2008, 16th Annual European Symposium, Karlsruhe, Germany, September 15-17, 2008. Proceedings, volume 5193 of Lecture Notes in Computer Science, pages 393–404. Springer, Springer, 2008. doi:10.1007/978-3-540-87744-8_33.
- [31] Joan Feigenbaum, Daphne Koller, and Peter W. Shor. A game-theoretic classification of interactive complexity classes. In Proceedings of the Tenth Annual Structure in Complexity Theory Conference, Minneapolis, Minnesota, USA, June 19-22, 1995, pages 227–237. IEEE, IEEE Computer Society, 1995. doi:10.1109/SCT.1995.514861.
- [32] Jörg Flum and Martin Grohe. Fixed-parameter tractability, definability, and model-checking. SIAM J. Comput., 31(1):113–145, 2001. doi:10.1137/S0097539799360768.
- [33] Jörg Flum and Martin Grohe. Describing parameterized complexity classes. Inf. Comput., 187(2):291–319, 2003. doi:10.1016/S0890-5401(03)00161-5.
- [34] Lance Fortnow, Russell Impagliazzo, Valentine Kabanets, and Christopher Umans. On the complexity of succinct zero-sum games. Comput. Complex., 17(3):353–376, 2008. doi:10.1007/s00037-008-0252-2.
- [35] Hana Galperin and Avi Wigderson. Succinct representations of graphs. Inf. Control., 56(3):183–198, 1983. doi:10.1016/S0019-9958(83)80004-7.
- [36] Gianluigi Greco, Enrico Malizia, Luigi Palopoli, and Francesco Scarcello. The complexity of the nucleolus in compact games. ACM Trans. Comput. Theory, 7(1):3:1–3:52, 2014. doi:10.1145/2692372.2692374.
- [37] Shreya Gupta, Boyang Huang, Russell Impagliazzo, Stanley Woo, and Christopher Ye. The computational complexity of factored graphs. CoRR, abs/2407.19102, 2024. doi:10.48550/arXiv.2407.19102.
- [38] Xin He, Ming-Yang Kao, and Hsueh-I Lu. Linear-time succinct encodings of planar graphs via canonical orderings. SIAM J. Discret. Math., 12(3):317–325, 1999. doi:10.1137/S0895480197325031.
- [39] Monika Henzinger, Andrea Lincoln, and Barna Saha. The complexity of average-case dynamic subgraph counting. In Joseph (Seffi) Naor and Niv Buchbinder, editors, Proceedings of the 2022 ACM-SIAM Symposium on Discrete Algorithms, SODA 2022, Virtual Conference / Alexandria, VA, USA, January 9 - 12, 2022, pages 459–498. SIAM, SIAM, 2022. doi:10.1137/1.9781611977073.23.
- [40] Franz Höfting and Egon Wanke. Polynomial algorithms for minimum cost paths in periodic graphs. In Vijaya Ramachandran, editor, Proceedings of the Fourth Annual ACM/SIGACT-SIAM Symposium on Discrete Algorithms, 25-27 January 1993, Austin, Texas, USA, pages 493–499. ACM/SIAM, 1993. URL: http://dl.acm.org/citation.cfm?id=313559.313868.
- [41] Bruce Hoppe and Éva Tardos. The quickest transshipment problem. Math. Oper. Res., 25(1):36–62, 2000. doi:10.1287/moor.25.1.36.15211.
- [42] Shweta Jain and C. Seshadhri. The power of pivoting for exact clique counting. In James Caverlee, Xia (Ben) Hu, Mounia Lalmas, and Wei Wang, editors, WSDM ’20: The Thirteenth ACM International Conference on Web Search and Data Mining, Houston, TX, USA, February 3-7, 2020, pages 268–276. ACM, 2020. doi:10.1145/3336191.3371839.
- [43] Neil D. Jones. Space-bounded reducibility among combinatorial problems. J. Comput. Syst. Sci., 11(1):68–85, 1975. doi:10.1016/S0022-0000(75)80050-X.
- [44] Sampath Kannan, Moni Naor, and Steven Rudich. Implicit representation of graphs. In Janos Simon, editor, Proceedings of the 20th Annual ACM Symposium on Theory of Computing, May 2-4, 1988, Chicago, Illinois, USA, pages 334–343. ACM, 1988. doi:10.1145/62212.62244.
- [45] Takumi Kasai, Akeo Adachi, and Shigeki Iwata. Classes of pebble games and complete problems. SIAM J. Comput., 8(4):574–586, 1979. doi:10.1137/0208046.
- [46] Marvin Künnemann, Ramamohan Paturi, and Stefan Schneider. On the fine-grained complexity of one-dimensional dynamic programming. In Ioannis Chatzigiannakis, Piotr Indyk, Fabian Kuhn, and Anca Muscholl, editors, 44th International Colloquium on Automata, Languages, and Programming, ICALP 2017, July 10-14, 2017, Warsaw, Poland, volume 80 of LIPIcs, pages 21:1–21:15. Schloss-Dagstuhl-Leibniz Zentrum für Informatik, Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2017. doi:10.4230/LIPIcs.ICALP.2017.21.
- [47] Sebastian Maneth and Fabian Peternek. A survey on methods and systems for graph compression. CoRR, abs/1504.00616, 2015. arXiv:1504.00616, doi:10.48550/arXiv.1504.00616.
- [48] Madhav V. Marathe, Harry B. Hunt III, Daniel J. Rosenkrantz, and Richard Edwin Stearns. Theory of periodically specified problems: Complexity and approximability. In Proceedings of the 13th Annual IEEE Conference on Computational Complexity, Buffalo, New York, USA, June 15-18, 1998, page 106. IEEE, IEEE Computer Society, 1998. doi:10.1109/CCC.1998.694596.
- [49] Madhav V. Marathe, Harry B. Hunt III, Richard Edwin Stearns, and Venkatesh Radhakrishnan. Approximation schemes for pspace-complete problems for succinct specifications (preliminary version). In Frank Thomson Leighton and Michael T. Goodrich, editors, Proceedings of the Twenty-Sixth Annual ACM Symposium on Theory of Computing, 23-25 May 1994, Montréal, Québec, Canada, pages 468–477. ACM, 1994. doi:10.1145/195058.195233.
- [50] Satoru Miyano. The lexicographically first maximum subgraph problems: P-completeness and NC algorithms. Math. Syst. Theory, 22(1):47–73, 1989. doi:10.1007/BF02088292.
- [51] Jaroslav Nešetřil and Svatopluk Poljak. On the complexity of the subgraph problem. Commentationes Mathematicae Universitatis Carolinae, 026(2):415–419, 1985. URL: http://eudml.org/doc/17394.
- [52] James B. Orlin. The complexity of dynamic languages and dynamic optimization problems. In Proceedings of the 13th Annual ACM Symposium on Theory of Computing, May 11-13, 1981, Milwaukee, Wisconsin, USA, pages 218–227. ACM, 1981. doi:10.1145/800076.802475.
- [53] Christos H. Papadimitriou and Tim Roughgarden. Computing correlated equilibria in multi-player games. J. ACM, 55(3):14:1–14:29, 2008. doi:10.1145/1379759.1379762.
- [54] Victor Parque and Tomoyuki Miyashita. On succinct representation of directed graphs. In 2017 IEEE International Conference on Big Data and Smart Computing, BigComp 2017, Jeju Island, South Korea, February 13-16, 2017, pages 199–205. IEEE, IEEE, 2017. doi:10.1109/BIGCOMP.2017.7881738.
- [55] Mihai Patrascu and Ryan Williams. On the possibility of faster SAT algorithms. In Moses Charikar, editor, Proceedings of the Twenty-First Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2010, Austin, Texas, USA, January 17-19, 2010, pages 1065–1075. SIAM, SIAM, 2010. doi:10.1137/1.9781611973075.86.
- [56] Jessica Shi, Laxman Dhulipala, and Julian Shun. Parallel clique counting and peeling algorithms. In Michael Bender, John Gilbert, Bruce Hendrickson, and Blair D. Sullivan, editors, Proceedings of the 2021 SIAM Conference on Applied and Computational Discrete Algorithms, ACDA 2021, Virtual Conference, July 19-21, 2021, pages 135–146. SIAM, SIAM, 2021. doi:10.1137/1.9781611976830.13.
- [57] Michael Sipser. Introduction to the theory of computation. SIGACT News, 27(1):27–29, 1996. doi:10.1145/230514.571645.
- [58] Ryuhei Uehara. A measure of parallelization for the lexicographically first maximal subgraph problems. In Rolf H. Möhring, editor, Graph-Theoretic Concepts in Computer Science, 23rd International Workshop, WG ’97, Berlin, Germany, June 18-20, 1997, Proceedings, volume 1335 of Lecture Notes in Computer Science, pages 333–341. Springer, Springer, 1997. doi:10.1007/BFb0024508.
- [59] Ryuhei Uehara. Another measure for the lexicographically first maximal subgraph problems and its threshold value on a random graph. In 1999 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’99), 23-25 June 1999, Fremantle, Australia, pages 350–355. IEEE, IEEE Computer Society, 1999. doi:10.1109/ISPAN.1999.778963.
- [60] Ryuhei Uehara. A measure for the lexicographically first maximal independent set problem and its limits. Int. J. Found. Comput. Sci., 10(4):473–482, 1999. doi:10.1142/S0129054199000332.
- [61] Emanuele Viola and Avi Wigderson. Local expanders. Comput. Complex., 27(2):225–244, 2018. doi:10.1007/s00037-017-0155-1.
- [62] Klaus W. Wagner. The complexity of combinatorial problems with succinct input representation. Acta Informatica, 23(3):325–356, 1986. doi:10.1007/BF00289117.
- [63] Egon Wanke. Paths and cycles in finite periodic graphs. In Andrzej M. Borzyszkowski and Stefan Sokolowski, editors, Mathematical Foundations of Computer Science 1993, 18th International Symposium, MFCS’93, Gdansk, Poland, August 30 - September 3, 1993, Proceedings, volume 711 of Lecture Notes in Computer Science, pages 751–760. Springer, Springer, 1993. doi:10.1007/3-540-57182-5_66.
