On Cascades of Reset Automata

Borelli, Roberto; Geatti, Luca; Montali, Marco; Montanari, Angelo

doi:10.4230/LIPIcs.STACS.2025.20

On Cascades of Reset Automata

Roberto Borelli

University of Udine, Italy Luca Geatti

University of Udine, Italy Marco Montali

Free University of Bozen-Bolzano, Italy Angelo Montanari

University of Udine, Italy

Abstract

The Krohn-Rhodes decomposition theorem is a pivotal result in automata theory. It introduces the concept of cascade product, where two semiautomata, that is, automata devoid of initial and final states, are combined in a feed-forward fashion. The theorem states that any semiautomaton can be decomposed into a sequence of permutation-reset semiautomata. For the counter-free case, this decomposition consists entirely of reset components with two states each. This decomposition has significantly impacted recent research in various areas of computer science, including the identification of a class of transformer encoders equivalent to star-free languages and the conversion of Linear Temporal Logic formulas into past-only expressions (pastification).

The paper revisits the cascade product in the context of reset automata, thus considering each component of the cascade as a language acceptor. First, we give regular expression counterparts of cascades of reset automata. We then establish several expressiveness results, identifying hierarchies of languages based on the restriction of the height (number of components) of the cascade or of the number of states in each level. We also show that any cascade of reset automata can be transformed, with a quadratic increase in height, into a cascade that only includes two-state components. Finally, we show that some fundamental operations on cascades, like intersection, union, negation, and concatenation with a symbol to the left, can be directly and efficiently computed by adding a two-state component.

Keywords and phrases:

Automata, Cascade products, Regular expressions, Krohn-Rhodes theory

Copyright and License:

2012 ACM Subject Classification:

Theory of computation

\rightarrow

Regular languages ; Theory of computation

\rightarrow

Automata extensions

Acknowledgements:

The authors would like to thank Alessio Mansutti for his valuable comments during the preparation of this paper.

Funding:

Luca Geatti and Angelo Montanari acknowledge the support from the 2024 Italian INdAM-GNCS project “Certificazione, monitoraggio, ed interpretabilità in sistemi di intelligenza artificiale”, ref. no. CUP E53C23001670001 and the support from the Interconnected Nord-Est Innovation Ecosystem (iNEST), which received funding from the European Union Next-GenerationEU (PIANO NAZIONALE DI RIPRESA E RESILIENZA (PNRR) – MISSIONE 4 COMPONENTE 2, INVESTIMENTO 1.5 -– D.D. 1058 23/06/2022, ECS00000043). In addition, Marco Montali and Angelo Montanari acknowledges the support from the MUR PNRR project FAIR - Future AI Research (PE00000013) also funded by the European Union Next-GenerationEU.

DOI:

10.4230/LIPIcs.STACS.2025.20

Event:

42nd International Symposium on Theoretical Aspects of Computer Science (STACS 2025)

Editors:

Olaf Beyersdorff, Michał Pilipczuk, Elaine Pimentel, and Nguyễn Kim Thắng

Series and Publisher:

Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik

1 Introduction

The Krohn-Rhodes decomposition theorem is a fundamental result both in automata theory and in semigroup algebra [12]. It relies on the concept of cascade product of two semiautomata, i.e., automata devoid of initial and final states, and thus, ultimately, edge-labeled graphs. In this setup, the first semiautomaton operates on an alphabet $\Sigma$ , while the second one reads symbols belonging to the Cartesian product of $\Sigma$ and the set of states of the first semiautomaton. The key feature of the cascade product, which extends the notion of direct product, is that the second semiautomaton transitions from state $s$ to state $s^{\prime}$ by reading the pair $(\sigma,q)$ if and only if the input symbol is $\sigma$ and the first semiautomaton is in state $q$ .

The Krohn-Rhodes theorem states that any semiautomaton can be decomposed into a cascade (i.e., a sequence of cascade products) of permutation-reset semiautomata.¹¹1Formally, the decomposition is guaranteed to preserve a homomorphism from the cascade to the initial semiautomaton. In such semiautomata, each symbol of the alphabet induces a function on the set of states that is either a permutation, i.e., a bijective function, or a reset, that is, there is a specific state to which all other states are mapped into when reading that symbol. Crucially, if the semiautomaton is counter-free, that is, it does not contain non-trivial cycles [18], the Krohn-Rhodes theorem guarantees the existence of a decomposition that consists of reset automata only, i.e., automata where all symbols induce reset functions (as described above) or the identity function.

The Krohn-Rhodes theorem, in particular the decomposition of counter-free automata into reset automata, had a significant impact on some meaningful problems of current research in computer science. A notable example comes from Angluin et al. [1], who employ the Krohn-Rhodes decomposition theorem to prove that Linear Temporal Logic ( $\mathsf{LTL}$ [19]) is equivalent to transformer encoders with hard attention and strict future masking (see also [13]). Specifically, they show how reset semiautomata can be encoded in B-RASP, a minimal programming language that compiles into transformers. Similarly, studies such as [21, 10, 11] utilized this theorem to analyze the sample complexity of cascades and the expressiveness of Recurrent Neural Networks without circular dependencies. Another example is provided by Maler [14, 15], who used the decomposition theorem to transform any formula of $\mathsf{LTL}$ , interpreted over finite words, into an equivalent formula using only past operators (see also [20]), a problem now known as pastification [2].

In this paper, we revisit the cascade product in the reset automata setting, i.e., language acceptors whose underlying semiautomaton is a reset. We address various expressiveness issues for cascade products by themselves and in relation to regular expressions. These results represent a necessary step towards a more efficient exploitation of Krohn-Rhodes decomposition in pastification, with the ultimate goal of lowering its current, triply exponential upper bound, which is far away from the know, singly exponential lower bound.

The paper consists of three main parts. In the first part, we address the question: given a cascade of reset automata, which is its corresponding regular expression? We begin by focusing on cascades of height $1$ , proving that the language corresponding to a reset automaton over the alphabet $\Sigma$ is always of the form $J\cup(\Sigma^{*}\cdot R\cdot I^{*})$ , for some $I,R\subseteq\Sigma$ , such that $I\cap R=\varnothing$ and either $J=I^{*}$ or $J=\varnothing$ . Then, we extend the analysis to cascades of reset automata of arbitrary height. As a first step, we show that the last level can always be transformed into a two-state automaton, and then, by exploiting such a result, we derive the regular expression corresponding to a generic cascade of reset automata.

In the second part, we build on the previously obtained results and establish several expressiveness results about cascades of reset automata. We structure the analysis into three types of cascades:

(i)

short cascades (whose height is bounded by 2),
(ii)

narrow cascades (where each component has two states, but there is not a height limitation), and
(iii)

general cascades (with no limitations on the height or on the number of states per level).

As for short cascades, we prove that any language $\operatorname{\mathcal{L}}$ over an alphabet $\Sigma$ of cardinality $k$ that is definable by a reset cascade of height $2$ can also be defined by one where the first component has at most $k+1$ states. Additionally, we show that increasing the number of states in the first component results in a strict increase in expressiveness: there exists a family of languages which are definable by a two-reset cascade whose first component has $n$ states, but are not definable if the first component is restricted to $n-1$ states. Similarly, for narrow cascades, we show that increasing the height results in an increase in expressiveness. These two results – the increase in the number of states in the first component for short cascades and the increase in height for narrow cascades – lead to two hierarchies (with infinitely many levels) of languages that are not definable at previous levels. Finally, we show that any general cascade can be transformed into one whose components have all 2 states, with an increase in height of at most a quadratic factor (relative to the height of the original cascade).

In the last part, we deal with closure properties of the languages recognized by reset cascades, and show that some fundamental operations can be computed in an efficient way. More precisely, we prove that the operations of intersection, union, negation, and concatenation with $\Sigma$ to the left (“next operation”) all require the addition of one component with 2 states only.

The paper is structured as follows. Related work is discussed in Section 2. In Section 3, we provide some background knowledge. In Section 4, we introduce the cascades of reset automata, we state some basic results about them, and we provide a characterization of the languages that they recognize in terms of regular expressions. In Section 5, we present some expressiveness results for short, narrow, and general cascades of reset automata. Section 6 focus on closure properties and the efficient computation of some basic operations. Finally, Section 7 provides an assessment of the work done, and it outlines some directions for future research.

2 Related Work

The Krohn-Rhodes theorem and the cascade product turn out be quite useful in understanding the structure and the expressiveness of finite-state systems, in particular in the context of automata and neural networks, and their connection to logic. Various recent contributions have leveraged this foundational theory to explore the expressiveness, modularity, and learning potential of automata in such a context.

A pivotal contribution in this area is the work by Maler on the cascade decomposition of semiautomata [14, 15]. It revisits the Eilenberg’s variant of the Krohn-Rhodes theorem [6] and offers a constructive proof that any semiautomaton can be decomposed into a cascade of elementary (permutation and reset) semiautomata. The paper introduces the holonomy tree as a data structure to represent cascade decompositions and an algorithm to build such a tree. Crucially, the algorithm carefully maps the permutations of the obtained cascade product to non-trivial cycles of the starting semiautomaton: this guarantees that, whenever the starting semiautomaton is counter-free, that is, devoid of non-trivial cycles, the generated cascade decomposition only consists of reset components. An exponential bound on the size of the cascade decomposition in terms of the size of the starting semiautomaton is given. This algorithm can be used to actually translate counter-free automata to temporal logic. More precisely, Maler shows how to translate any cascade product of reset semiautomata into a pure past $\mathsf{LTL}$ formula, that is, a formula featuring only past temporal modalities. Together with the transformation of the future fragment of $\mathsf{LTL}$ , interpreted over finite words, into counter-free automata, this leads to a triply exponential upper bound to the problem of transforming pure-future $\mathsf{LTL}$ over finite words into pure-past $\mathsf{LTL}$ (pastification problem). Equivalently, in the case of $\mathsf{LTL}$ interpreted over infinite words, Maler shows how to use the proposed algorithm to normalize every $\mathsf{LTL}$ formula by mapping it into one belonging to the Reactivity class [16], at a cost of a triply exponential blowup. For both problems, that is, pastification and normalization, the best known lower bounds are singly exponential [3, 17].

The Krohn-Rhodes theorem has also been applied to analyze the complexity of semigroups, as shown in [9]. This study examines semigroups of upper triangular matrices over finite fields and establishes that the Krohn-Rhodes complexity of these semigroups corresponds to $n-1$ , where $n$ is the matrix dimension. These results underline the deep connection between the algebraic structure of semigroups and their matrix representations, providing a measure of how intricate the cascade product representation needs to be for such semigroups.

In [8], the Krohn-Rhodes theorem is used to characterize piecewise testable and commutative languages. The authors define biased reset semiautomata, where the current state changes at most once, and characterize cascades $\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{B}}$ , where $\operatorname{\mathcal{B}}$ is a biased reset semiautomaton. Theorem 4.12 in Section 4 can be seen as a simplification and a generalization (to cascades of unbounded height) of such a characterization. Finally, the authors propose the notion of scope of a cascade, which is used to analyze the dot-depth of star-free languages.

In [21], Ronca builds on the Krohn-Rhodes theorem, proposing automata cascades as a structured and modular framework to describe complex systems. The resulting framework allows automata to be decomposed into components with specific functionalities, enabling fine-grained control of their expressiveness. By focusing on component-based decomposition, the study demonstrates that the sample complexity of learning automata cascades is linear in the number of components and their individual complexities, up to logarithmic factors. This contrasts with traditional state-centric perspectives, where sample complexity scales with the number of states, often limiting the feasibility of learning large systems. The relationships between the cascade product and neural networks are investigated in [10]. Recurrent Neural Cascades (RNCs) are a class of networks with acyclic connections, which naturally align with the cascade product of automata. By exploiting the Krohn-Rhodes theorem, the authors prove that RNCs capture star-free regular languages.

The Krohn-Rhodes theorem also underpins the exploration of transformer models in [13]. While transformers lack recurrence, the paper demonstrates that their layered architecture can simulate the cascade decomposition of finite automata. Leveraging Krohn-Rhodes theory, the authors show that shallow transformers can hierarchically approximate automata computations, enabling polynomial-sized and constant-depth shortcuts for specific automata.

In [1], Angluin et al. draws direct parallels between the expressive power of masked hard-attention transformers and star-free regular languages. These models, constrained by strict future masking, are shown to be equivalent to $\mathsf{LTL}$ and counter-free automata – both closely tied to the Krohn-Rhodes cascade framework. The study underscores how the structured limitations of these transformers, akin to a cascade decomposition, yield expressive yet computationally efficient models.

Together, these contributions extend the applicability of the Krohn-Rhodes theory to neural networks, transformers, and beyond, demonstrating the versatiliy of the cascade framework as a powerful principle in computation.

3 Background

A semiautomaton $\operatorname{\mathcal{A}}$ is a tuple $(\Sigma,Q,\delta)$ such that:

(i)

$\Sigma$ is a (finite) alphabet;
(ii)

$Q$ is a set of states;
(iii)

$\delta:Q\times\Sigma\to Q$ is a transition function.

An automaton $\operatorname{\mathcal{A}}=(\Sigma,Q,\delta,q_{0},F)$ is a semiautomaton extended with an initial state $q_{0}\in Q$ and a set $F\subseteq Q$ of final states. With $\delta^{*}$ we denote the Kleene’s closure of $\delta$ . We say that $\operatorname{\mathcal{A}}$ is two-state iff $|Q|=2$ .

Given an automaton $\operatorname{\mathcal{A}}=(\Sigma,Q,\delta,q_{0},F)$ and a (finite) word $\sigma\coloneqq\langle\sigma_{0},\dots,\sigma_{n}\rangle\in\Sigma^{*}$ , the run $\tau\in Q^{+}$ induced by $\sigma$ is a sequence $\langle q_{0},q_{1},\dots,q_{n+1}\rangle$ such that $\delta(q_{i},\sigma_{i})=q_{i+1}$ , for all $0\leq i\leq n$ . We say that $\tau$ is accepting iff $q_{n+1}\in F$ . A word $\sigma\in\Sigma^{*}$ is accepted by $\operatorname{\mathcal{A}}$ iff the run induced by $\sigma$ is accepting. We define the language of $\operatorname{\mathcal{A}}$ , denoted by $\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}})$ , as the set of accepted words. Given a state $q\in Q$ , let $\operatorname{\mathcal{L}}_{q}(\operatorname{\mathcal{A}})$ be the set of words inducing a run $\tau\coloneqq\langle q_{0},\dots,q_{m}\rangle$ with $q_{m}=q$ . The classic direct product of automata is defined as follows.

Definition 3.1 (Direct product of automata).

Let $\operatorname{\mathcal{A}}=(\Sigma,Q,\delta,q_{0},F)$ and $\operatorname{\mathcal{A}}^{\prime}=(\Sigma,Q^{\prime},\delta^{\prime},q^{% \prime}_{0},$ $F^{\prime})$ be two automata. The direct product of $\operatorname{\mathcal{A}}$ and $\operatorname{\mathcal{A}}^{\prime}$ , denoted by $\operatorname{\mathcal{A}}\times\operatorname{\mathcal{A}}^{\prime}$ , is the automaton $(\Sigma,Q\times Q^{\prime},\delta^{\prime\prime},(q_{0},q^{\prime}_{0}),F% \times F^{\prime})$ such that, for all $(q,q^{\prime})\in Q\times Q^{\prime}$ and for all $a\in\Sigma$ , it holds that $\delta^{\prime\prime}((q,q^{\prime}),a)=(\delta(q,a),\delta^{\prime}(q^{\prime% },a))$ .

The cascade product of semiautomata is defined as follows.

Definition 3.2 (Cascade Product of semiautomata [15, 22]).

Let $\Sigma$ be a finite alphabet and let $\operatorname{\mathcal{A}}=(\Sigma,Q,\delta)$ and $\operatorname{\mathcal{A}}^{\prime}=(\Sigma\times Q,Q^{\prime},\delta^{\prime})$ be two semiautomata over the alphabets $\Sigma$ and $\Sigma\times Q$ , respectively. We define the cascade product between $\operatorname{\mathcal{A}}$ and $\operatorname{\mathcal{A}}^{\prime}$ , denoted with $\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{A}}^{\prime}$ , as the semiautomaton $(\Sigma,Q\times Q^{\prime},\delta^{\prime\prime})$ such that, for all $(q,q^{\prime})\in Q\times Q^{\prime}$ and for all $a\in\Sigma$ :

\delta^{\prime\prime}((q,q^{\prime}),a)=(\delta(q,a),\delta^{\prime}(q^{\prime% },(a,q)))

(2)

We will often simply use “cascade” for “cascade product”.

It is worth noticing that the cascade product of semiautomata is a generalization of the classic direct product: the latter can be recovered by imposing the alphabet of the second semiautomaton to be $\Sigma$ (i.e., the alphabet of the first one) instead of $\Sigma\times Q$ .

The cascade product is an associative operation, meaning that $(\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{A}}^{\prime})\circ% \operatorname{\mathcal{A}}^{\prime\prime}$ is the same semiautomaton as $\operatorname{\mathcal{A}}\circ(\operatorname{\mathcal{A}}^{\prime}\circ% \operatorname{\mathcal{A}}^{\prime\prime})$ . We define the height of the product $\operatorname{\mathcal{A}}_{1}\circ\dots\circ\operatorname{\mathcal{A}}_{n}$ as $n$ .

We now introduce two classes of semiautomata, reset and permutation, depending on the form of their transitions. We first define the notion of function induced by a symbol.

Definition 3.3 (Function induced by a symbol).

Let $\operatorname{\mathcal{A}}=(\Sigma,Q,\delta)$ be a semiautomaton. For each symbol $a\in\Sigma$ , we define the function induced by $a$ in $\operatorname{\mathcal{A}}$ , denoted by $\tau_{a}^{\operatorname{\mathcal{A}}}$ (or simply $\tau_{a}$ when $\operatorname{\mathcal{A}}$ is clear from the context), as the transformation $\tau_{a}:Q\to Q$ such that, for all $q\in Q$ , it holds $\tau_{a}(q)=q^{\prime}$ iff $\delta(q,a)=q^{\prime}$ .

Reset and permutation functions are defined as follows.

Definition 3.4 (Reset and permutation functions).

Let $\tau:Q\to Q$ . We say that $\tau$ is a reset function iff there exists $q^{\prime}\in Q$ such that $\tau(q)=q^{\prime}$ , for all $q\in Q$ . In this case, we say that $\tau$ is a reset on $q^{\prime}$ . If $\tau:Q\to Q$ is a bijection, then it is called a permutation.

On the basis of the functions induced by the symbols of their alphabet, we define the following classes of semiautomata.

Definition 3.5 (Classes of semiautomata).

Let $\operatorname{\mathcal{A}}=(\Sigma,Q,\delta)$ be a semiautomaton. We say that $\operatorname{\mathcal{A}}$ is:

$\blacksquare$

a permutation-reset semiautomaton iff, for each $a\in\Sigma$ , $\tau_{a}$ is either a permutation or a reset.
$\blacksquare$

a permutation semiautomaton iff, for each $a\in\Sigma$ , $\tau_{a}$ is a permutation;
$\blacksquare$

a reset semiautomaton iff, for each $a\in\Sigma$ , $\tau_{a}$ is either the identity function or a reset function;
$\blacksquare$

a pure-reset semiautomaton iff, for each $a\in\Sigma$ , $\tau_{a}$ is a reset function.

We now introduce counter-free semiautomata [18]. Let $\sigma\in\Sigma^{*}$ . From now on, we denote by $(\sigma)^{i}$ the word generated by concatenating $i$ times the word $\sigma$ to itself. A word $\sigma\in\Sigma^{*}$ , with $\sigma\neq\varepsilon$ , defines a nontrivial cycle in a semiautomaton $\operatorname{\mathcal{A}}=(\Sigma,Q,\delta)$ if there exists a state $q\in Q$ such that:

(i)

$\delta^{*}(q,\sigma)\neq q$
(ii)

$\delta^{*}(q,(\sigma)^{i})=q$ , for some $i>1$ .

We say that a semiautomaton $\operatorname{\mathcal{A}}$ is counter-free if there are no words that define a nontrivial cycle. Counter-free automata recognize exactly the set of languages definable by star-free regular expressions, i.e., expressions devoid of Kleene’star. We denote this set by $\operatorname{\mathcal{SF}}$ .

A fundamental result in the field is the Krohn-Rhodes Cascade Decomposition Theorem. The theorem’s initial formulation was expressed in the context of semigroups [12], and its automata-theoretic counterpart [14] can be articulated as follows.

Theorem 3.6 (The Krohn-Rhodes Cascade Decomposition Theorem [12, 14]).

For each semiautomaton $\operatorname{\mathcal{A}}=(\Sigma,Q,\delta)$ , there exists a cascade product of semiautomata $\operatorname{\mathcal{C}}\coloneqq\operatorname{\mathcal{A}}_{1}\circ% \operatorname{\mathcal{A}}_{2}\circ\dots\circ\operatorname{\mathcal{A}}_{n}$ such that:

(i)

$\operatorname{\mathcal{A}}_{i}$ is a permutation-reset semiautomaton, for each $1\leq i\leq n$ ;
(ii)

there is an homomorphism²²2We refer to [12, 14] for a formal definition of homomorphism between semiautomata. from $\operatorname{\mathcal{C}}$ to $\operatorname{\mathcal{A}}$ ;
(iii)

if $\operatorname{\mathcal{A}}$ is counter-free, then $\operatorname{\mathcal{A}}_{i}$ is a two-state reset semiautomaton, for each $1\leq i\leq n$ .

4 Cascades of automata

In this section, we begin our study of the languages recognized by cascades of automata. We start by formally defining them and stating some basic properties. Then, we focus on cascades of reset automata, and provide a characterization of the languages they recognize in terms of regular expressions.

4.1 Definitions and basic properties

To begin with, we generalize the notion of cascade product of semiautomata (Definition 3.2) to automata.

Definition 4.1 (Cascade product of automata).

Let $\Sigma$ be a finite alphabet and let $\operatorname{\mathcal{A}}=(\Sigma,Q,\delta,q_{0},F)$ and $\operatorname{\mathcal{A}}^{\prime}=(\Sigma\times Q,Q^{\prime},\delta^{\prime}% ,q_{0}^{\prime},F^{\prime})$ be two automata over the alphabets $\Sigma$ and $\Sigma\times Q$ , respectively. We define the cascade product of $\operatorname{\mathcal{A}}$ and $\operatorname{\mathcal{A}}^{\prime}$ , denoted by $\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{A}}^{\prime}$ , as the automaton $(\Sigma,Q\times Q^{\prime},\delta^{\prime\prime},(q_{0},q_{0}^{\prime}),F% \times F^{\prime})$ where $\delta^{\prime\prime}$ is defined as in Definition 3.2.

We say that a language $\operatorname{\mathcal{L}}$ is definable by a cascade $\operatorname{\mathcal{C}}$ iff $\operatorname{\mathcal{L}}=\operatorname{\mathcal{L}}(\operatorname{\mathcal{C% }})$ . Figure 1 shows the cascade product of two reset automata defining the language $a\cdot\Sigma^{*}$ .

Figure 1: The reset automaton

\operatorname{\mathcal{A}}_{1}

with set of states

Q=\{q_{0},q_{1}\}

over the alphabet

\Sigma=\{a,b\}

(left). The reset automaton

\operatorname{\mathcal{A}}_{2}

over the alphabet

\Sigma\times Q

(middle). The cascade product

\operatorname{\mathcal{A}}_{1}\circ\operatorname{\mathcal{A}}_{2}

over the alphabet

\Sigma

that recognizes the languages

a\cdot\Sigma^{*}

(right).

In the following, we will use the term cascade to refer both to the component automata and to the resulting automaton.

We now show how to compute the language recognized by a cascade of automata on the basis of the languages recognized by its components. Let $\Sigma_{1}$ and $\Sigma_{2}$ be two alphabets. Let $\sigma^{1}=\sigma^{1}_{1}\dots\sigma^{1}_{n}\in(\Sigma_{1})^{n}$ and $\sigma^{2}=\sigma^{2}_{1}\dots\sigma^{2}_{n}\in(\Sigma_{2})^{n}$ be two words of length $n$ . We define $\operatorname{\mathsf{aug}}(\sigma^{1},\sigma^{2})\in(\Sigma_{1}\times\Sigma_{% 2})^{n}$ as the word $(\sigma^{1}_{1},\sigma^{2}_{1})\dots(\sigma^{1}_{n},\sigma^{2}_{n})$ .

Definition 4.2 (Language of $\operatorname{\mathcal{B}}$ at a state $s$ over $\operatorname{\mathcal{A}}$ ).

Let $\operatorname{\mathcal{A}}=\langle\Sigma,Q,\delta_{A},q_{0},F_{A}\rangle$ and $\operatorname{\mathcal{B}}=\langle\Sigma\times Q,S,\delta_{B},s_{0},F_{B}\rangle$ be two automata. The language of $\operatorname{\mathcal{B}}$ at state $s\in S$ over $\operatorname{\mathcal{A}}$ , denoted by $\operatorname{\mathcal{L}}_{s}(\operatorname{\mathcal{B}})[\operatorname{% \mathcal{A}}]$ , is defined as follows: the empty word only belongs to $\operatorname{\mathcal{L}}_{s_{0}}(\operatorname{\mathcal{B}})[\operatorname{% \mathcal{A}}]$ ; a word $\sigma=\sigma_{1}\dots\sigma_{k}$ , with $k\geq 1$ , belongs to $\operatorname{\mathcal{L}}_{s}(\operatorname{\mathcal{B}})[\operatorname{% \mathcal{A}}]$ if

(i)

$\sigma_{1}\dots\sigma_{k-1}$ induces a run $\tau=\langle q_{0},q_{1}\dots,q_{k-1}\rangle$ on $\operatorname{\mathcal{A}}$ ; and
(ii)

$\operatorname{\mathsf{aug}}(\sigma,\tau)\in\operatorname{\mathcal{L}}_{s}(% \operatorname{\mathcal{B}})$ .

The language of a cascade can be computed from those of its components as follows. Let $\operatorname{\mathcal{C}}=\operatorname{\mathcal{A}}\circ\operatorname{% \mathcal{B}}$ be a cascade. The words forcing $\operatorname{\mathcal{C}}$ to reach a state $(q,s)$ are exactly those words such that:

(i)

they force $\operatorname{\mathcal{A}}$ to reach state $q$ ; and
(ii)

they force $\operatorname{\mathcal{B}}$ to reach state $s$ , when augmented with the run of $\operatorname{\mathcal{A}}$ .

Proposition 4.3 (Language of a cascade in terms of its components).

Let $\operatorname{\mathcal{A}}=\langle\Sigma,Q,\delta_{A},q_{0},$ $F_{A}\rangle$ and $\operatorname{\mathcal{B}}=\langle\Sigma\times Q,S,\delta_{B},s_{0},F_{B}\rangle$ be two automata. It holds that:

1.

$\operatorname{\mathcal{L}}_{(q,s)}(\operatorname{\mathcal{A}}\circ% \operatorname{\mathcal{B}})=\operatorname{\mathcal{L}}_{q}(\operatorname{% \mathcal{A}})\cap\operatorname{\mathcal{L}}_{s}(\operatorname{\mathcal{B}})[% \operatorname{\mathcal{A}}]$ , for all states $q\in Q$ and $s\in S$ ;
2.

$\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}\circ\operatorname{% \mathcal{B}})=\bigcup\limits_{(q,s)\in F}\operatorname{\mathcal{L}}_{(q,s)}(% \operatorname{\mathcal{A}}\circ\operatorname{\mathcal{B}})$ .

We now show that, as it happens with semiautomata, the direct product of automata is just a special case of the cascade product. To this end, we first define the notion of augmentation of an automaton.

Definition 4.4 (Augmentation).

Let $\operatorname{\mathcal{A}}=\langle\Sigma,Q,\delta,q_{0},F\rangle$ and $\operatorname{\mathcal{A}}^{\prime}=(\Sigma^{\prime},Q^{\prime},\delta^{\prime% },q_{0}^{\prime},F^{\prime})$ be two automata such that either $\Sigma^{\prime}=\Sigma$ or $\Sigma^{\prime}=\Sigma\times S$ , for an arbitrary finite set $S$ . We define the augmentation of $\operatorname{\mathcal{A}}^{\prime}$ relative to $\operatorname{\mathcal{A}}$ , denoted by $\operatorname{\mathsf{aug}}(\operatorname{\mathcal{A}},\operatorname{\mathcal{% A}}^{\prime})$ , as the automaton $(\Sigma^{\prime\prime},Q^{\prime},\delta^{\prime\prime},q_{0}^{\prime},F^{% \prime})$ such that:

$\blacksquare$

if $\Sigma^{\prime}=\Sigma$ , then $\Sigma^{\prime\prime}\coloneqq\Sigma\times Q$ and for all $q\in Q^{\prime}$ and all $a\in\Sigma$ , $\delta^{\prime\prime}(q,(a,*))=\delta^{\prime}(q,a)$ ;
$\blacksquare$

if $\Sigma^{\prime}=\Sigma\times S$ , then $\Sigma^{\prime\prime}\coloneqq\Sigma\times Q\times S$ and, for all $q\in Q^{\prime}$ and for all $(a,s)\in\Sigma\times S$ , it holds that $\delta^{\prime\prime}(q,(a,*,s))=\delta^{\prime}(q,(a,s))$ .

Given a cascade $\operatorname{\mathcal{C}}=\operatorname{\mathcal{A}}^{\prime}_{1}\circ\dots% \circ\operatorname{\mathcal{A}}^{\prime}_{n}$ over $\Sigma$ , we define the augmentation of $\operatorname{\mathcal{C}}$ relative to $\operatorname{\mathcal{A}}$ , denoted by $\operatorname{\mathsf{aug}}(\operatorname{\mathcal{A}},\operatorname{\mathcal{% C}})$ , as the cascade $\operatorname{\mathsf{aug}}(\operatorname{\mathcal{A}},\operatorname{\mathcal{% A}}^{\prime}_{1})\circ\dots\circ\operatorname{\mathsf{aug}}(\operatorname{% \mathcal{A}},\operatorname{\mathcal{A}}^{\prime}_{n})$ .

The notion of augmentation can be generalized to a pair of cascades $\operatorname{\mathcal{C}}$ and $\operatorname{\mathcal{C}}^{\prime}$ by treating $\operatorname{\mathcal{C}}$ as a single automaton: from now on, when we will refer to the cascade product of $\operatorname{\mathcal{C}}$ and $\operatorname{\mathcal{C}}^{\prime}$ , we will interpret it as the cascade product of the automaton $\operatorname{\mathcal{A}}$ generated by $\operatorname{\mathcal{C}}$ and $\operatorname{\mathcal{C}}^{\prime}$ .

The next proposition shows that direct product can be simulated by means of augmentation and cascade product.

Proposition 4.5 (Direct product by means of cascade product).

Let $\operatorname{\mathcal{A}}=\langle\Sigma,Q,\delta,q_{0},F\rangle$ be an automaton and let $\operatorname{\mathcal{C}}$ be a cascade over $\Sigma$ . It holds that $\operatorname{\mathcal{A}}\circ\operatorname{\mathsf{aug}}(\operatorname{% \mathcal{A}},\operatorname{\mathcal{C}})=\operatorname{\mathcal{A}}\times% \operatorname{\mathcal{C}}$ .

Furthermore, augmenting an automaton does not affect its property of being reset (or permutation), as stated by the following Proposition 4.6.

Proposition 4.6.

Let $\Sigma$ be a finite alphabet and let $\operatorname{\mathcal{A}}$ be an automaton over $\Sigma$ or $\Sigma\times S$ , for an arbitrary finite set $S$ . If $\operatorname{\mathcal{A}}$ is a reset (resp., permutation) automaton, then, for any automaton $\operatorname{\mathcal{A}}^{\prime}$ over $\Sigma$ , $\operatorname{\mathsf{aug}}(\operatorname{\mathcal{A}}^{\prime},\operatorname{% \mathcal{A}})$ is a reset (resp., permutation) automaton.

It follows that, in particular, if $\operatorname{\mathcal{C}}$ is a cascade of reset (resp., permutation) automata, then $\operatorname{\mathsf{aug}}(\operatorname{\mathcal{A}},\operatorname{\mathcal{% C}})$ is a cascade of reset (resp., permutation) automata. From Propositions 4.5 and 4.6, it follows directly that, given two cascades $\operatorname{\mathcal{C}}$ and $\operatorname{\mathcal{C}}^{\prime}$ of height $m$ and $n$ of reset (resp., permutation) automata, there exists a cascade of height $m+n$ of reset (resp., permutation) automata for $\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})\cap\operatorname{% \mathcal{L}}(\operatorname{\mathcal{C}}^{\prime})$ . In Section 6, we will show how to compute other basic operations on cascades of resets.

4.2 Languages of cascades of resets

In this part, we characterize the language recognized by a cascade of reset automata in terms of regular expressions. We begin with the case of cascades of height $1$ and then we move to cascades of unbounded height.

4.2.1 Cascades of height 1

The study of which regular expressions characterize height-1 cascades of resets coincides with the study of the languages recognized by reset automata. The following theorem gives a characterization of reset automata in terms of regular expressions.

Theorem 4.7 (The languages of reset automata).

Let $\Sigma$ be a finite alphabet. A language $\operatorname{\mathcal{L}}\subseteq\Sigma^{*}$ is recognized by a reset automaton if and only if $\operatorname{\mathcal{L}}=J\cup(\Sigma^{*}\cdot R\cdot I^{*})$ for some $I,R\subseteq\Sigma$ such that $I\cap R=\varnothing$ and either $J=I^{*}$ or $J=\varnothing$ .

Intuitively, an automaton reading a symbol that induces a reset function on a final state is forced to end up in that state, regardless of which state it was in before. Furthermore, it remains in that state if all subsequent symbols induce identity functions. In the case of words containing multiple resets on a final state, only the last of these symbols matters, resulting in words of the form $\Sigma^{*}\cdot R\cdot I^{*}$ . The case of $J=I^{*}$ arises when the initial state is also final. In this scenario, to accept a word, the automaton does not need to read a symbol that induces a reset on a final state (since it is already there), but only needs to stay in the initial state.

A by-product of Theorem 4.7 is that any reset automaton is equivalent to one with two states, only one of which is final. The rationale is as follows:

(i)

the symbols in $R$ induce a reset on the single final state;
(ii)

the symbols in $I$ act as identities; and
(iii)

the symbols neither in $R$ nor in $I$ induce resets on the single non-final state.

Moreover, the initial state is also the final state if and only if $J=I^{*}$ . A graphical account is given in Figure 2.

Proposition 4.8.

For every reset automaton, there exists an equivalent one with two states, exactly one of which is final.

Figure 2: The reset automaton corresponding to a language of the form

J\cup(\Sigma^{*}\cdot R\cdot I^{*})

in the case

J=\varnothing

(on the left) and in the case

J=I^{*}

(on the right).

Theorem 4.7 allows us to establish a first connection between Linear Temporal Logic on finite traces ( $\mathsf{LTLf}$ [5]) formulas and equivalent reset cascades. As highlighted in the introduction, the languages expressible in $\mathsf{LTLf}$ are exactly the star-free languages, that is, those languages that can be represented by regular expressions that do not use the Kleene star, or equivalently, by languages whose minimal automaton is counter-free [18]. By Krohn-Rhodes’ theorem (Theorem 3.6), it follows that the languages definable in $\mathsf{LTLf}$ are precisely those expressible through cascades of resets. Given the relevance of reset cascade decomposition in problems such as pastification [2, 4] and normalization [7] of temporal logic formulas, it is crucial to understand which $\mathsf{LTLf}$ formulas can be expressed with cascades of a specific height. The following result shows that even simple formulas like ${}^{\prime}missing$ (the proposition letter “p” holds at the initial time point) or $p\nobreak\mathbin{\leavevmode\resizebox{}{0.0pt}{$\mathsf{U}$}}^{\prime}missing$ (there is a future point where “q” holds, and until then, “p” remains true) cannot be expressed with cascades of resets of height 1. In fact, the languages they recognize³³3Here, assuming a set of atomic propositions $\mathcal{AP}\coloneqq\{p,q,r,\dots\}$ , the languages of formulas over $\mathcal{AP}$ are defined over the alphabet $\Sigma\coloneqq 2^{\mathcal{AP}}$ . Moreover, given any $p\in\mathcal{AP}$ , we indicate with $\vec{p}$ all the letters $a\in\Sigma$ such that $p\in a$ . are respectively $\vec{p}\cdot\Sigma^{*}$ and $(\vec{p})^{*}\cdot\vec{q}\cdot\Sigma^{*}$ , which are not of the form $J\cup(\Sigma^{*}\cdot R\cdot I^{*})$ , for any choice of $R$ , $I$ , and $J$ . However, the formula $\mathsf{F}^{\prime}missing$ (there exists a point in the future where “p” holds) can be expressed with reset cascades of height 1, as its language is of the form $J\cup(\Sigma^{*}\cdot R\cdot I^{*})$ , choosing $R\coloneqq\vec{p}$ , $I\coloneqq\Sigma\setminus\vec{p}$ , and $J=\varnothing$ .

Corollary 4.9.

The languages defined by the $\mathsf{LTLf}$ formulas ${}^{\prime}missing$ and $p\nobreak\mathbin{\leavevmode\resizebox{}{0.0pt}{$\mathsf{U}$}}^{\prime}missing$ are not definable with height-1 cascades of resets.

4.2.2 Cascades of unbounded-height

In this section we derive regular expressions for cascades of arbitrary height. As a first step, we show that a cascade of height $h$ of reset automata, say $\operatorname{\mathcal{A}}_{1}\circ\dots\circ\operatorname{\mathcal{A}}_{h}$ , can be transformed into an equivalent cascade of the same height, still consisting of reset automata, where the last automaton ( $\operatorname{\mathcal{A}}_{h}$ ) has exactly two states, one of which is the only accepting state. This result forms the basis for Theorem 4.12, which provides the characterization of cascades of arbitrary height.

Lemma 4.10.

Let $\operatorname{\mathcal{A}}$ be an automaton with set of states $Q$ over the alphabet $\Sigma$ , and let $\operatorname{\mathcal{B}}$ be a reset automaton over the alphabet $\Sigma\times Q$ . There exists a 2-states reset automaton $\operatorname{\mathcal{B}}^{\prime}$ , with exactly one final state, such that $\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}\circ\operatorname{% \mathcal{B}})=\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}\circ% \operatorname{\mathcal{B}}^{\prime})$ .

The proof of Lemma 4.10 heavily relies on the characterization of cascades of height 1. More precisely, since $\operatorname{\mathcal{B}}$ is a reset automaton over the alphabet $\Sigma\times Q$ , by Proposition 4.8, there exists an equivalent reset automaton with two states (one of which is the only accepting state) over the same alphabet. Since $\operatorname{\mathcal{B}}$ is at the bottom of the cascade, the language of the cascade $\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{B}}^{\prime}$ is the same as the language of $\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{B}}$ . This is because there are no other automata below $\operatorname{\mathcal{B}}$ in the cascade that can exploit information about $\operatorname{\mathcal{B}}$ ’s current state. As a matter of fact, in Section 5, we will prove that this no longer true when applying the same procedure to $\operatorname{\mathcal{A}}$ : there exist languages definable by a cascade $\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{B}}$ , where $\operatorname{\mathcal{A}}$ has 3 states and $\operatorname{\mathcal{B}}$ has 2 states, that cannot be expressed if the number of states of $\operatorname{\mathcal{A}}$ is limited to 2.

Let us now introduce the notion of filtered automaton, which is obtained from a given automaton by removing (filtering) certain outgoing transitions and possibly changing its initial state.

Definition 4.11 (Filtered Automaton).

Let $\operatorname{\mathcal{A}}=\langle Q,\Sigma,q_{0},\delta,F\rangle$ be an automaton. A filter is pair $(q,H)$ , where $q\in Q$ and $H\subseteq\Sigma\times Q$ . The partial automaton $\operatorname{\mathcal{A}}$ , filtered by $(q,H)$ , denoted as $\operatorname{\mathcal{A}}\downarrow^{q}_{H}$ , is the automaton $(Q,\Sigma,q,\delta^{\prime},F)$ where $\delta^{\prime}(q^{\prime},\sigma)\coloneqq\delta(q^{\prime},\sigma)$ if $(\sigma,q^{\prime})\in H$ , or is undefined otherwise.

Before formally stating Theorem 4.12, that characterizes the languages of cascades of unbounded-height, we give an intuitive account of it. Let $\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{B}}$ be a cascade, with $\operatorname{\mathcal{A}}$ an automaton and $\operatorname{\mathcal{B}}$ a reset automaton, where, w.l.o.g. (Lemma 4.10), $\operatorname{\mathcal{B}}$ has only two states and exactly one final state. Any word accepted by $\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{B}}$ must drive both $\operatorname{\mathcal{A}}$ and $\operatorname{\mathcal{B}}$ to an accepting state. Its language can be captured by analyzing the symbols inducing a reset function that leads to a final state of $\operatorname{\mathcal{B}}$ , and the symbols inducing identities in $\operatorname{\mathcal{B}}$ . The words in the language of $\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{B}}$ are precisely those consisting of

(i)

a prefix that, for any symbol $(\sigma,q)$ inducing a reset on a final state of $\operatorname{\mathcal{B}}$ , drives automaton $\operatorname{\mathcal{A}}$ to state $q$ ;
(ii)

followed by the symbol $\sigma\in\Sigma$ (let $q_{\sigma}$ be the state reached by $\operatorname{\mathcal{A}}$ after reading it);
(iii)

a suffix that forces $\operatorname{\mathcal{B}}$ to remain in its accepting state through its identity functions $I_{B}$ , and forces $\operatorname{\mathcal{A}}$ to reach a final state starting from $q_{\sigma}$ .

In addition, $\operatorname{\mathcal{A}}$ cannot transition from state $q^{\prime}$ when reading a symbol $\sigma^{\prime}$ if the pair $(\sigma^{\prime},q^{\prime})$ does not belong to $\operatorname{\mathcal{B}}$ ’s identity functions, as this would cause $\operatorname{\mathcal{B}}$ to leave its accepting state. Therefore, the suffix corresponds to the language of automaton $\operatorname{\mathcal{A}}$ , filtered by $(\delta_{A}(q,\sigma),I_{B})$ . This is formally expressed by the following theorem.

Theorem 4.12 (Languages of cascades of unbounded-height).

Let $\operatorname{\mathcal{A}}=\langle\Sigma,Q=\{q_{0},\dots,q_{n}\},\delta_{A},$ $q_{0},F_{A}\rangle$ be an automaton and let $\operatorname{\mathcal{B}}=\langle\Sigma\times Q,\{s_{0},s_{1}\},\delta,s_{0},% \{s_{f}\}\rangle$ , with $s_{f}\in\{s_{0},s_{1}\}$ , be a two-state reset automaton with one final state. It holds that:

\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}\circ\operatorname{% \mathcal{B}})=M\cup\bigcup\limits_{(\sigma,q)\in R_{s_{f}}}\operatorname{% \mathcal{L}}_{q}(\operatorname{\mathcal{A}})\cdot\sigma\cdot\operatorname{% \mathcal{L}}\left(\operatorname{\mathcal{A}}\downarrow^{\delta_{A}(q,\sigma)}_% {I_{B}}\right)

(3)

where $R_{s_{f}}$ is the set of symbols in $\Sigma\times Q$ that induce a reset function on state $s_{f}$ , and $M\coloneqq\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}\downarrow^{q_{% 0}}_{I_{B}})$ if $s_{0}=s_{f}$ or $M\coloneqq\varnothing$ otherwise.

Figure 3: On the left and on the center, the reset automata

\operatorname{\mathcal{A}}

and

\operatorname{\mathcal{B}}

, respectively, for the cascade

\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{B}}

recognizing the language

b^{*}\cdot a^{+}

. On the right, the automaton

\operatorname{\mathcal{A}}\downarrow^{s_{1}}_{I_{B}}

, where

I_{B}=\{(a,q_{1}),(b,q_{0})\}

are the identities of automaton

\operatorname{\mathcal{B}}

.

Figure 3 gives an example of application of Theorem 4.12 to a cascade over the alphabet $\Sigma\coloneqq\{a,b\}$ of two reset automata, $\operatorname{\mathcal{A}}$ (on the left) and $\operatorname{\mathcal{B}}$ (on the center), with two states each, recognizing the language $b^{*}\cdot a^{+}$ . Using Theorem 4.12, we have that $\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}\circ\operatorname{% \mathcal{B}})=\operatorname{\mathcal{L}}_{q_{0}}(\operatorname{\mathcal{A}})% \cdot a\cdot\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}\downarrow^{q% _{1}}_{I_{B}})$ , where $\operatorname{\mathcal{A}}\downarrow^{q_{1}}_{I_{B}}$ is the automaton obtained from $\operatorname{\mathcal{A}}$ filtered by the identities $I_{B}=\{(a,q_{1}),(b,q_{0})\}$ of automaton $\operatorname{\mathcal{B}}$ . Since $\operatorname{\mathcal{L}}_{q_{0}}(\operatorname{\mathcal{A}})=b^{*}$ and $\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}\downarrow^{q_{1}}_{I_{B}% })=a^{*}$ , we obtain $\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}\circ\operatorname{% \mathcal{B}})=b^{*}\cdot a^{+}$ . The following is a corollary of Theorem 4.12 in the case in which $\operatorname{\mathcal{B}}$ is a pure-reset automaton.

Corollary 4.13.

Let $\operatorname{\mathcal{A}}=\langle\Sigma,\{q_{0},\dots,q_{n}\},\delta_{A},q_{0% },F_{A}\rangle$ be an automaton and let $\operatorname{\mathcal{B}}=\langle\Sigma\times Q,\{s_{0},s_{1}\},\delta,s_{0},% \{s_{f}\}\rangle$ be a two-state pure-reset automaton with one final state. It holds that

\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}\circ\operatorname{% \mathcal{B}})=M\cup\bigcup\limits_{\begin{subarray}{c}(\sigma,q)\in R_{s_{f}}% \\ \delta_{A}(q,\sigma)\in F_{A}\end{subarray}}\operatorname{\mathcal{L}}_{q}(% \operatorname{\mathcal{A}})\cdot\sigma

(4)

where $M\coloneqq\epsilon$ if $s_{0}=s_{f}$ and $q_{0}\in F_{A}$ , or $M\coloneqq\varnothing$ otherwise.

It is worth noticing that the regular expressions in Theorems 4.12 and 4.13 refer to states of the cascade under consideration. This is a major difference with the characterization of reset cascades of height 1 (Theorem 4.7). In order to prove some undefinability results in the next section, we provide a characterization of the languages recognized by cascades of two-states resets of height $2$ where the second component is pure-reset, based on regular expressions that do not refer to states of the cascade.

Lemma 4.14.

Let $\operatorname{\mathcal{L}}\subseteq\Sigma^{*}$ be a language. $\operatorname{\mathcal{L}}$ is definable by a cascade of height $2$ in which the second component is pure-reset if and only if $\operatorname{\mathcal{L}}=M\cup\bigcup_{i=1}^{n}K_{i}\cdot\sigma_{i}$ for some $M$ , $n$ , $\sigma_{i}$ and $K_{i}$ such that:

(i)

$M$ is either $\phi$ or $\epsilon$ ;
(ii)

$0\leq n\leq 2\cdot|\Sigma|$ ;
(iii)

for all $i=1\dots n$ it holds $\sigma_{i}\in\Sigma$ ;
(iv)

there exists a language $L$ recognizable by a two-state reset automaton such that for all $i=1\dots n$ , either $K_{i}$ is $L$ or $K_{i}$ is $\overline{L}=\Sigma^{*}\setminus L$ .

Notice that the Lemma above can be easily extended to the case in which the first automaton in the cascade has $k$ states, for some $k\geq 2$ . This is done by relaxing (iv) and imposing that $K_{i}$ can be chosen between $k$ languages $K_{1},\dots,K_{k}$ such that $\{K_{1},\dots,K_{k}\}$ is a partition of $\Sigma^{*}$ and each $K_{i}$ is definable by a cascade of resets of height 1. Constraint (ii) is also relaxed to $0\leq n\leq k\cdot|\Sigma|$ .

We will use Theorem 4.12, Corollary 4.13, and Lemma 4.14 in the next section to prove undefinability results of certain languages by cascades of a given height and with a specified number of states at each level.

5 Expressiveness results

In this section, we analyze the expressive power of various types of reset automaton cascades. We begin by defining several language classes, and subsequently structure our analysis into short cascades (where the height is constrained to at most two), narrow cascades (where the height is unbounded but each component contains two states), and general cascades (with no restrictions on either the height or the number of states).

Definition 5.1 (Classes $\mathcal{R}$ and $\mathcal{RPR}$ ).

Let $h\in\mathbb{N}^{>0}$ and let $k_{1},\dots,k_{h}\in\mathbb{N}^{>1}$ . We denote by $\mathcal{R}(k_{1},\dots,k_{h})$ the class of languages definable by a cascade $\operatorname{\mathcal{A}}_{1}\circ\dots\circ\operatorname{\mathcal{A}}_{h}$ of reset automata such that $\operatorname{\mathcal{A}}_{i}$ has $k_{i}$ states, for each $1\leq i\leq h$ . We denote by $\mathcal{RPR}(k_{1},\dots,k_{h})$ the subclass of $\mathcal{R}(k_{1},\dots,k_{h})$ where the last automaton ( $\operatorname{\mathcal{A}}_{h}$ ) is required to be pure-reset. For $h>0$ and $k>1$ , we define $\mathcal{R}^{h}_{k}\coloneqq\bigcup_{2\leq k_{1},\dots,k_{h}\leq k}\mathcal{R}% (k_{1},\dots,k_{h})$ as the set of languages definable by a cascade of height $h$ , where each component has at most $k$ states. We define $\mathcal{R}\coloneqq\bigcup_{h>0,k>1}\mathcal{R}^{h}_{k}$ as the set of languages definable by any cascade of reset automata. The classes $\mathcal{RPR}^{h}_{k}$ and $\mathcal{RPR}$ are defined analogously.

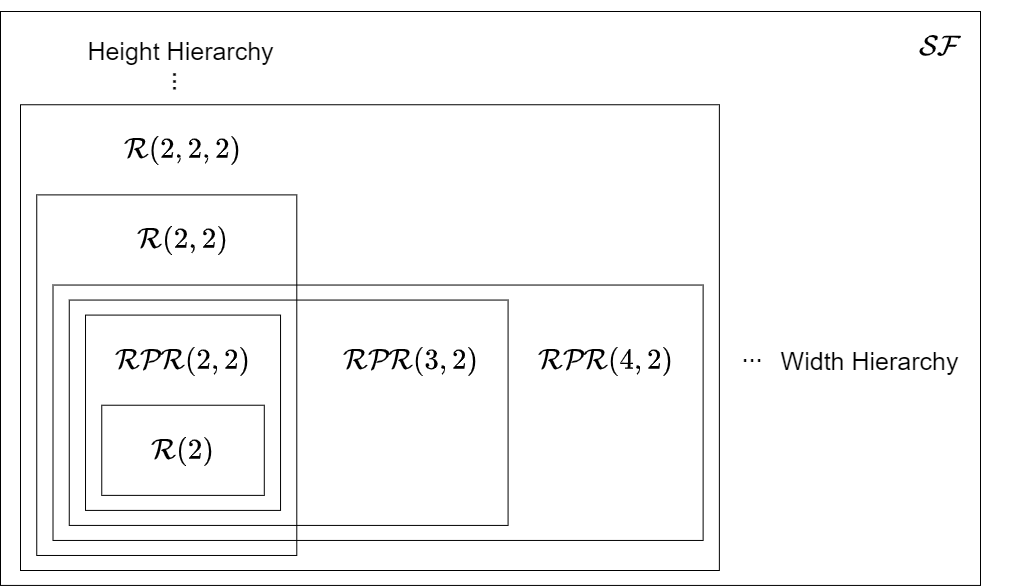
Refer to caption — Figure 4: Summary of (some of) the results in Section 5.

Figure 4 provides an overview of (some of) the results presented in this section. Specifically, it illustrates that increasing the cascade height and increasing the number of states at the first level lead to two distinct language hierarchies.

5.1 Short Cascades

We begin by considering short cascades, i.e. cascades of reset automata of height 2. As a first step, we start by comparing the classes $\mathcal{R}(2),\mathcal{RPR}(2,2)$ and $\mathcal{R}(2,2)$ , and then we focus on $\mathcal{RPR}(k,2)$ and $\mathcal{R}(k,2)$ for every $k>2$ .

We already know that with a single pure-reset automaton we can recognize the set of all words ending with a certain symbol of the alphabet (this follows from Theorem 4.7 in the special case in which $I=\varnothing$ ). As an example, it holds that $\Sigma^{*}a\in\mathcal{RPR}(2)$ . Now, if we introduce an additional pure-reset layer, we can effectively recognize the set of words ending with a two-character suffix. However, we also demonstrate that this is impossible using a single reset automaton.

Lemma 5.2.

Let $L=\Sigma^{*}aa$ . It holds that:

(i)

$L\in\mathcal{RPR}(2,2)$ ;
(ii)

$L\not\in\mathcal{R}(2)$ .

Lemma 5.2 shows that increasing the height of a cascade, even of height $1$ and even with a pure-reset automaton, results into a gain of expressive power.

In the upcoming lemma, we demonstrate that, at the same height, prohibiting identities in the final layer results in a loss of expressive power. To illustrate this, let us consider the language $a\cdot\Sigma^{*}$ . As shown in Figure 1, this language can be defined using a cascade of two reset automata, with the last one specifically containing identities. Building upon Lemma 4.14, we further demonstrate that achieving the same language recognition is not possible when prohibiting identities in the final layer, no matter of the number of states of the first automaton.

Lemma 5.3.

Let $\Sigma$ be an alphabet with at least two symbols, let $L=a\Sigma^{*}$ . It holds that:

(i)

$L\in\mathcal{R}(2,2)$ ;
(ii)

$L\not\in\mathcal{RPR}(k,2)$ , for every $k\geq 2$ .

Figure 5: On the left, the reset automaton

\operatorname{\mathcal{A}}

and on the right the reset automaton

\operatorname{\mathcal{B}}

such that, for

\Sigma=\{a,b,c\}

, the cascade

C\coloneqq\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{B}}

accepts the language

\Sigma^{*}\left(\Sigma^{2}\setminus\{aa,bb,cc\}\right)\cup\{b,c\}

, which precisely corresponds to the language

L_{3}

described in Lemma 5.4. When viewed as a single automaton,

C

is also the minimal automaton for the language

L_{3}

.

In Lemma 4.10, we have shown that the final component of a cascade can always be restricted to two states. A natural question arises: Can the first component also be limited to just two states? The answer is negative, as illustrated by the following example. Consider an alphabet of three symbols and the language $L$ consisting of all words that end with two distinct symbols (e.g. $cb\in L$ but $aa\notin L$ ). As demonstrated in Figure 5, this language can be recognized by a cascade of two reset automata where the first component has three states. However, we will prove that it cannot be recognized if the first component has only two states. Intuitively, the first component’s role is to remember the second-to-last symbol, but with an alphabet of three symbols and only two states, this task becomes impossible. The following Width-Hierarchy Lemma formalizes this intuition, demonstrating the existence of an infinite hierarchy of languages that can be defined using cascades of two resets where the first component contains $k$ states, but cannot be defined when the first component is restricted to $k-1$ states.

Lemma 5.4 (Width-Hierarchy Lemma).

For each $k>2$ , let $\Sigma=\{\sigma_{0},\dots,\sigma_{k-1}\}$ . Let $L_{k}=\Sigma^{*}\left(\Sigma^{2}\setminus\bigcup_{0\leq i<k}\sigma_{i}\sigma_{% i}\right)\cup(\Sigma\setminus\sigma_{0})$ , it holds that:

(i)

$L_{k}\in\mathcal{RPR}(k,2)$ ;
(ii)

$L_{k}\not\in\mathcal{R}(k-1,2)$ .

The following corollary (depicted in Figure 4) follows from Lemmas 5.2, 5.3, and 5.4.

Corollary 5.5.

It holds that:

$\blacksquare$

$\varnothing\subsetneq\mathcal{R}(2)\subsetneq\mathcal{RPR}(2,2)\subsetneq% \mathcal{R}(2,2)$ ;
$\blacksquare$

$\mathcal{RPR}(3,2)\not\subseteq\mathcal{R}(2,2)$ and $\mathcal{R}(2,2)\not\subseteq\mathcal{RPR}(3,2)$ .

Additionally, we prove that for a fixed alphabet $\Sigma$ of cardinality $k$ , any language over $\Sigma$ expressible by a cascade of height 2 can also be expressed by a cascade of height 2 where the first component has at most $k+1$ states. The intuition behind this is that, due to the restriction of transitions to resets or identities, only a finite number of states can be reached from the initial state. This is formalized in the next lemma, which also establishes the optimality of the bound on the number of states of the first component.

Lemma 5.6.

Let $\Sigma$ be a finite alphabet with size $|\Sigma|=k$ . Let $L$ be a language such that $L\subseteq\Sigma^{*}$ . For every $m\in\mathbb{N}^{>0}$ , if $L\in\mathcal{R}(m,2)$ , then $L\in\mathcal{R}(k+1,2)$ . Furthermore, there exists a language $L^{\prime}_{k}\subseteq\Sigma^{*}$ such that $L^{\prime}_{k}\in\mathcal{R}(k+1,2)$ but $L^{\prime}_{k}\not\in\mathcal{R}(k,2)$ .

Figure 6: The cascade

C\coloneqq\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{B}}

accepts the language

L^{\prime}_{3}\coloneqq\Sigma^{*}\left(\Sigma^{2}\setminus\{aa,bb,cc\}\right)

. When treated as a single automaton,

C

consists of 8 states, in contrast to the minimal automaton for

L^{\prime}_{3}

, which has only 7 states.

The language $L^{\prime}_{k}$ used to prove the optimality of the bound in Lemma 5.6 is defined as $\Sigma^{*}\left(\Sigma^{2}\setminus\bigcup_{0\leq i<k}\sigma_{i}\sigma_{i}\right)$ . As an example, Figure 6 shows the case of $L^{\prime}_{3}$ .

5.2 Narrow Cascades

Thus far, our discussion has centered around cascades composed of one or two components. Now, we shift our focus to narrow cascades, i.e. cascades of greater height but in which each components is restricted to have two states (i.e. $\mathcal{R}^{h}_{2}$ ). Just as we have seen that some languages cannot be expressed by cascades of height 1, we will demonstrate that for any given height, there exists a language that cannot be captured at that height, provided the components of the cascade are restricted to two states. We call this the Height-Hierarchy Lemma, and is a counterpart of the Width-Hierarchy Lemma (Lemma 5.4) focused on the height of cascades. It is based on the following family of languages: for each $h\geq 2$ , we consider the language $L_{h}=\Sigma^{h-2}a\Sigma^{*}$ , that is all words that contain symbol “ $a$ ” precisely at position $h-1$ . The Height-Hierarchy Lemma below proves that, for any $h\geq 2$ , the language $L_{h}$ is not definable by cascades of two states reset automata of height less than $h$ .

Lemma 5.7 (Height-Hierarchy Lemma).

For each $h\geq 2$ , let $L_{h}=\Sigma^{h-2}a\Sigma^{*}$ . It holds that:

(i)

$L_{h}\in\mathcal{R}^{h}_{2}$ ;
(ii)

$L_{h}\not\in\mathcal{R}^{h-1}_{2}$ .

Figure 7: Switch automaton.

We briefly explain the intuition behind Lemma 5.7. Regarding point (i) $L_{h}\in\mathcal{R}^{h}_{2}$ , the construction of the two-state reset cascade proceeds as follows. The base case corresponds to Figure 1, while the inductive step for height $h$ involves the use of the two-state reset automaton $\operatorname{\operatorname{\mathcal{A}}_{\mathit{switch}}}$ (illustrated in Figure 7) in cascade with the augmentation of the cascade for the case $h-1$ . Intuitively, $\operatorname{\operatorname{\mathcal{A}}_{\mathit{switch}}}$ recognizes all words containing at least one symbol. Using in cascade $h-2$ copies of $\operatorname{\operatorname{\mathcal{A}}_{\mathit{switch}}}$ together with the cascade in Figure 1, corresponds exactly to the language $\Sigma^{h-2}a\Sigma^{*}$ . In Figure 8, we provide an example of the construction for the case $h=3$ .

Figure 8: A cascade

C_{3}=\operatorname{\mathcal{A}}_{1}\circ\operatorname{\mathcal{A}}_{2}\circ% \operatorname{\mathcal{A}}_{3}

that recognizes the language

\Sigma a\Sigma^{*}

. The first two components enforce that any accepted word contains at least two symbols, as

\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}_{1}\circ\operatorname{% \mathcal{A}}_{2})=\Sigma\Sigma\Sigma^{*}

.

The proof that $L_{h}\not\in\mathcal{R}^{h-1}_{2}$ is more involved and proceeds by induction on $h$ . For the base case ( $h=2$ ), we have $L_{2}=a\Sigma^{*}$ . This case is verified by Lemma 5.3. For the inductive step, assume that the statement holds for every $i\leq h$ . We need to prove that it also holds for $i=h+1$ . Suppose, by contradiction, that $L_{h+1}\in\mathcal{R}^{h}_{2}$ . By definition, this would imply the existence of a cascade $C=\operatorname{\mathcal{A}}_{1}\circ\dots\circ\operatorname{\mathcal{A}}_{h}$ of two-state reset automata such that $\operatorname{\mathcal{L}}(C)=L_{h+1}=\Sigma^{h-1}a\Sigma^{*}$ . However, starting from $C$ , the proof shows how to construct a new cascade $C^{\prime}=\operatorname{\mathcal{B}}_{1}\circ\dots\circ\operatorname{\mathcal% {B}}_{h-1}$ of two-state reset automata such that $\operatorname{\mathcal{L}}(C^{\prime})=\Sigma^{h-2}a\Sigma^{*}=L_{h}$ . The existence of $C^{\prime}$ contradicts the inductive hypothesis, which states that $L_{h}\notin\mathcal{R}^{h-1}_{2}$ . Therefore, the assumption that $L_{h+1}\in\mathcal{R}^{h}_{2}$ must be false, and the cascade $C$ cannot exist.

5.3 General Cascades

In this subsection, we examine cascades of reset automata without imposing restrictions on the number of states in each component or on the total number of components. In the previous part, Lemma 5.6 demonstrates that, for cascade of two resets over the alphabet $\Sigma$ , the maximum expressiveness is achieved when the first component has $|\Sigma|+1$ states. Here, we extend this result to cascades of unbounded height in the Width-Collapse Lemma, that provides lower bounds on the number of states in each component, for which adding states at certain levels does not affect expressiveness.

Lemma 5.8 (Width-Collapse Lemma).

Let $\Sigma$ be a finite alphabet with $|\Sigma|=k\geq 2$ . Let $L\subseteq\Sigma^{*}$ be a language. For any positive integers $h$ and $k_{1},\dots,k_{h}$ , if $L\in\mathcal{R}(k_{1},\dots,k_{h},2)$ , then $L\in\mathcal{R}(f(1),\dots,f(h),2)$ , where $f(i)=\frac{k^{i+1}-1}{k-1}$ .

We now demonstrate how to transform general cascades into narrow cascades. Specifically, we show how any cascade of reset automata (of height $h$ and with $k_{i}$ states at level $i$ , for each $i\in\{1,\dots,h\}$ ) can be transformed into an equivalent narrow cascade (i.e. made of two-state resets), at the cost of increasing its height at most by a factor of $2+\sum_{i=1}^{h-1}\lceil\log_{2}(k_{i})\rceil$ . This result is based on two key points:

1.

Given a general cascade, we can always append a pure-reset automaton at the end without altering its language;
2.

the Narrowing Lemma, which we prove below, demonstrates that any cascade of reset automata, whose final component is pure-reset and containing a component $\operatorname{\mathcal{A}}_{j}$ with $k_{j}$ states (and $k_{j}>2$ ), can be transformed into a new cascade where $\operatorname{\mathcal{A}}_{j}$ is replaced by two new automata, with $2$ and $\lceil\frac{k_{j}}{2}\rceil$ states each.

Instrumental to the Narrowing Lemma, the following result demonstrates that, given a general cascade whose last component is a pure-reset automaton, we can modify this last component to make all the states of the preceding components final, without altering the recognized language.

Lemma 5.9.

Consider a cascade $\operatorname{\mathcal{A}}\circ\operatorname{\mathcal{B}}$ of automata, where $\operatorname{\mathcal{B}}$ is a two-state pure-reset automaton. Let $\operatorname{\mathcal{A}}^{\prime}$ be the automaton obtained from $\operatorname{\mathcal{A}}$ by making all states final. Then, there exists a two-state pure-reset automaton $\operatorname{\mathcal{B}}^{\prime}$ such that $\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}\circ\operatorname{% \mathcal{B}})=\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}}^{\prime}% \circ\operatorname{\mathcal{B}}^{\prime})$ .

The Narrowing Lemma is stated as follows.

Lemma 5.10 (Narrowing Lemma).

Let $C=\operatorname{\mathcal{A}}_{1}\circ\dots\circ\operatorname{\mathcal{A}}_{h}$ be a cascade where $\operatorname{\mathcal{A}}_{i}$ is a reset automaton with $k_{i}$ states for each $1\leq i\leq h-1$ , and $\operatorname{\mathcal{A}}_{h}$ is a pure-reset automaton. Let $j$ be an index such that $1\leq j\leq h-1$ . Then, there exists a cascade $C^{\prime}$ of reset automata

C^{\prime}=\operatorname{\mathcal{A}}^{\prime}_{1}\circ\dots\circ\operatorname% {\mathcal{A}}^{\prime}_{j-1}\circ\operatorname{\mathcal{B}}_{1}\circ% \operatorname{\mathcal{B}}_{2}\circ\operatorname{\mathcal{A}}^{\prime}_{j+1}% \circ\dots\circ\operatorname{\mathcal{A}}^{\prime}_{h}

(5)

such that:

(i)

each $\operatorname{\mathcal{A}}^{\prime}_{i}$ has $k_{i}$ states for $i\neq j$ ;
(ii)

if $\operatorname{\mathcal{A}}_{i}$ is pure-reset (resp., reset), then also $\operatorname{\mathcal{A}}^{\prime}_{i}$ is pure-reset (resp., reset), for $i\neq j$ ;
(iii)

$\operatorname{\mathcal{B}}_{1}$ has $2$ states and $\operatorname{\mathcal{B}}_{2}$ has $\lceil\frac{k_{j}}{2}\rceil$ states; and
(iv)

$\operatorname{\mathcal{L}}(C)=\operatorname{\mathcal{L}}(C^{\prime})$ .

By iteratively applying the Narrowing Lemma to every component with more than two states, we obtain a procedure that, given a cascade of reset automata, produces an equivalent cascade where all components are two-state reset automata. Moreover, it is worth noticing that:

(i)

by Lemma 4.10, w.l.o.g. the last component of any cascades of reset (or pure-resets) has two states, and therefore the Narrowing Lemma does not need to be applied at the last level;
(ii)

if the final component of a cascade is not a pure-reset, a new pure-reset level can always be added without affecting the language of the cascade.

This leads to the following inclusions.

Corollary 5.11.

For each positive $h,k_{1},\dots,k_{h}$ it holds that

1.

$\mathcal{RPR}(k_{1},\dots,k_{h})\subseteq\mathcal{RPR}^{H+1}_{2}$
2.

$\mathcal{R}(k_{1},\dots,k_{h})\subseteq\mathcal{R}^{H+2}_{2}$

where $H=\lceil\log_{2}{k_{1}}\rceil+\dots+\lceil\log_{2}{k_{h-1}}\rceil$ .

Combining Lemma 5.8 and Corollary 5.11, we conclude that if a language $L$ is recognized by a cascade of resets of height $h$ , it can also be recognized by a cascade of height $\Theta(h^{2})$ composed entirely of two-state resets.

Corollary 5.12.

Let $\Sigma$ be an alphabet such that $|\Sigma|=k\geq 2$ and let $L\subseteq\Sigma^{*}$ be a language. If $L$ admits a cascade of reset automata of height $h$ , then $L\in\mathcal{R}^{H}_{2}$ where $H\in\Theta(h^{2})$ . If $k=2$ , then $H=\frac{h^{2}+h+2}{2}$ .

Exploiting the bound for the case $|\Sigma|=2$ , we can prove undefinability of certain languages by general cascades, i.e. without any bound on their height nor on the number of states of its component. As an example, by Lemma 5.7, we know that the language $L=\Sigma^{6}a\Sigma^{*}$ over the alphabet $\Sigma=\{a,b\}$ does not belong to the class $\mathcal{R}^{7}_{2}$ . If $L$ could be recognized by a cascade of height $h=3$ , then it would also be recognized by a two-state cascade of height $H=\frac{h^{2}+h+2}{2}=7$ , leading to the following conclusion: with $\Sigma=\{a,b\}$ , the language $\Sigma^{6}a\Sigma^{*}$ does not admit any cascade of resets of height 3.

Building upon this reasoning, we can formulate the Generalized Height-Hierarchy Lemma. Unlike the original Height-Hierarchy Lemma, which focuses solely on two-state cascades, the generalized version addresses the undefinability of cascades in a broader context, encompassing general cascades.

Lemma 5.13 (Generalized Height-Hierarchy Lemma).

Let $h$ be a positive integer, and define $H=\frac{h^{2}+h+2}{2}+1$ . Consider the language $L_{H}\subseteq\Sigma^{*}$ , where $L_{H}=\Sigma^{H-2}a\Sigma^{*}$ and $\Sigma$ is a two-symbol alphabet. The language $L_{H}$ cannot be recognized by any cascade of reset automata of height $h$ , but it holds that $L_{H}\in\mathcal{R}_{2}^{H}$ .

6 Efficient closure properties of cascades of reset automata

In this section, we present an efficient method for computing specific closure properties of reset cascades. For instance, for the case in which the operation $\otimes$ is binary, given two cascades of resets $\operatorname{\mathcal{C}}$ and $\operatorname{\mathcal{C}}^{\prime}$ (made of only two-states components), we show how it is possible to compute a cascade of two-states resets that recognizes $\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})\otimes\operatorname{% \mathcal{L}}(\operatorname{\mathcal{C}}^{\prime})$ by adding at most one two-state reset automaton (that, in this context, we call brick). We show this for the following operations:

(i)

intersection;
(ii)

complementation;
(iii)

union; and
(iv)

left-concatenation of $\Sigma$ , i.e. given a language $\operatorname{\mathcal{L}}$ to compute $\Sigma\cdot\operatorname{\mathcal{L}}$ .⁴⁴4It is worth noticing that this operation corresponds to compute the closure under the $\mathsf{LTL}$ next modality.

Proposition 4.5 already shows that intersection can be implemented efficiently for cascades of resets: given two reset cascades $\operatorname{\mathcal{C}}$ and $\operatorname{\mathcal{C}}^{\prime}$ (with $m$ and $n$ two-states components, respectively), there exists a cascade for $\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})\cap\operatorname{% \mathcal{L}}(\operatorname{\mathcal{C}}^{\prime})$ with $m+n$ two-state resets.

Before showing the construction for the remaining operations, we give the following key definitions. We define the finalized version of an automaton $\operatorname{\mathcal{A}}$ , denoted with $\operatorname{\mathsf{finv}}(\operatorname{\mathcal{A}})$ , as the automaton obtained from $\operatorname{\mathcal{A}}$ by setting all its states as final. The definition naturally extends to cascades: the finalized version of $\operatorname{\mathcal{C}}$ , denoted with $\operatorname{\mathsf{finv}}(\operatorname{\mathcal{C}})$ , is defined as $\operatorname{\mathsf{finv}}(\operatorname{\mathcal{A}}_{1}){}\circ\dots\circ{% }\operatorname{\mathsf{finv}}(\operatorname{\mathcal{A}}_{n})$ . Clearly, if $\operatorname{\mathcal{C}}$ is a cascade of reset automata, $\operatorname{\mathsf{finv}}(\operatorname{\mathcal{C}})$ is still a cascade of reset automata. We define the reachability set of an automaton relative to a set of states as follows.

Definition 6.1 (Reachability Set).

Let $\operatorname{\mathcal{A}}=\langle\Sigma,Q,\delta,q_{0},F\rangle$ be an automaton. Let $P\subseteq Q$ be a set of states. The reachability set of $\operatorname{\mathcal{A}}$ with respect to $P$ , denoted with $\mathsf{RS}(\operatorname{\mathcal{A}},P)$ , is the set $\{(\sigma,q)\in(\Sigma\times Q):\delta(q,\sigma)\in P\}$ . We denote with $\overline{\mathsf{RS}(\operatorname{\mathcal{A}},P)}$ the set $(\Sigma\times Q)\setminus\mathsf{RS}(\operatorname{\mathcal{A}},P)$ . We write $\mathsf{RS}(\operatorname{\mathcal{A}})$ to refer to $\mathsf{RS}(\operatorname{\mathcal{A}},F)$ .

We now show how to efficiently compute the remaining closure properties.

Complementation

To compute complementation, we introduce the negation brick, whose structure is illustrated in Figure 9 and is formally defined here below.

Figure 9: The negation brick

\operatorname{\mathsf{negb}}(\operatorname{\mathcal{A}})

in the two cases: (a)

\epsilon\in\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}})

(b)

\epsilon\not\in\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}})

.

Definition 6.2 (Negation brick).

Let $\operatorname{\mathcal{A}}=\langle\Sigma,Q,\delta,q_{0},F\rangle$ be an automaton. The negation brick for $\operatorname{\mathcal{A}}$ , denoted with $\operatorname{\mathsf{negb}}(\operatorname{\mathcal{A}})$ , is the two-state pure-reset automaton $\langle\Sigma\times Q,\{n_{0},n_{1}\},\delta,n_{0},\{n_{f}\}\rangle$ such that:

(i)

the final state $n_{f}$ is $n_{1}$ if and only if $\epsilon\in\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}})$ ;
(ii)

the function $\tau$ induced by symbols in $\mathsf{RS}(\operatorname{\mathcal{A}})$ maps all states in the non-final state, i.e. $\tau:\{n_{0},n_{1}\}\mapsto\{n_{0},n_{1}\}\setminus\{n_{f}\}$ ;
(iii)

the function $\tau^{\prime}$ induced by symbols in $\overline{\mathsf{RS}(\operatorname{\mathcal{A}})}$ maps all states in the final one, i.e. $\tau:\{n_{0},n_{1}\}\mapsto\{n_{f}\}$ .

The intuition is that the negation brick, when appended to the end of a cascade $\operatorname{\mathcal{C}}$ , reaches its final state if and only if the underlying cascade $\operatorname{\mathcal{C}}$ is not in a final state. Consequently, by setting all the states of $\operatorname{\mathcal{C}}$ as final, we obtain a cascade that recognizes the complement of $\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})$ , as proved by the following lemma.

Lemma 6.3.

Let $\operatorname{\mathcal{C}}$ be a cascade of automata. The cascade $\operatorname{\mathcal{C}}^{\prime}\coloneqq\operatorname{\mathsf{finv}}(% \operatorname{\mathcal{C}})\circ\operatorname{\mathsf{negb}}(\operatorname{% \mathcal{C}})$ recognizes the language $\overline{\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})}$ . Moreover, if $\operatorname{\mathcal{C}}$ is a cascade of reset automata, then so is $\operatorname{\mathcal{C}}^{\prime}$ .

Interestingly, if the cascade terminates with a pure-reset layer $\operatorname{\mathcal{A}}$ , this automaton can itself serve the function of the negation brick, without the need of an additional component.

Lemma 6.4.

Let $\operatorname{\mathcal{C}}=\operatorname{\mathcal{A}}_{1}\circ\dots\circ% \operatorname{\mathcal{A}}_{n}$ be a cascade of automata such that $\operatorname{\mathcal{A}}_{n}$ is a pure-reset automaton. There exists a cascade $\operatorname{\mathcal{C}}^{\prime}=\operatorname{\mathcal{A}}^{\prime}_{1}% \circ\dots\circ\operatorname{\mathcal{A}}^{\prime}_{n}$ such that:

(i)

$\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}}^{\prime})=\overline{% \operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})}$ ;
(ii)

each automaton $\operatorname{\mathcal{A}}^{\prime}_{i}$ has the same number of states as $\operatorname{\mathcal{A}}_{i}$ ;
(iii)

if $\operatorname{\mathcal{A}}_{i}$ is a reset (resp., pure-reset), then $\operatorname{\mathcal{A}}^{\prime}_{i}$ is also a reset (resp., pure-reset).

Union

Given two cascades $\operatorname{\mathcal{C}}$ and $\operatorname{\mathcal{C}}^{\prime}$ of height $m$ and $n$ , respectively, since $\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})\cup\operatorname{% \mathcal{L}}(\operatorname{\mathcal{C}}^{\prime})=\overline{\overline{% \operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})}\cap\overline{% \operatorname{\mathcal{L}}(\operatorname{\mathcal{C}}^{\prime})}}$ , it is possible to build cascade for $\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})\cup\operatorname{% \mathcal{L}}(\operatorname{\mathcal{C}}^{\prime})$ of height $m+n+3$ , using the previously discussed constructions. In this section, we present a more efficient construction that introduces only one additional component, referred to as the union brick, resulting in a cascade for $\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})\cup\operatorname{% \mathcal{L}}(\operatorname{\mathcal{C}}^{\prime})$ of height $n+m+1$ .

Definition 6.5 (Union brick).

Let $\operatorname{\mathcal{A}}=\langle\Sigma,Q_{A},\delta_{A},q_{0A},F_{A}\rangle$ and $\operatorname{\mathcal{B}}=\langle\Sigma,Q_{B},\delta_{B},q_{0B},F_{B}\rangle$ be two automata. Let $U\subseteq Q_{A}\times Q_{B}$ the set of states $\{(q_{A},q_{B}):q_{A}\in F_{A}\lor q_{B}\in F_{B}\}$ . Let $\operatorname{\mathcal{C}}=\operatorname{\mathcal{A}}\circ\operatorname{% \mathsf{aug}}(\operatorname{\mathcal{A}},\operatorname{\mathcal{B}})$ . The union brick of $\operatorname{\mathcal{A}}$ and $\operatorname{\mathcal{B}}$ , denoted with $\operatorname{\mathsf{unionb}}(\operatorname{\mathcal{A}},\operatorname{% \mathcal{B}})$ , is the two-state pure-reset automaton $\langle\Sigma\times Q,\{u_{0},u_{1}\},\delta,u_{0},\{u_{f}\}\rangle$ such that:

(i)

the final state $u_{f}$ is $u_{0}$ if and only if $\epsilon\in\operatorname{\mathcal{L}}(\operatorname{\mathcal{A}})\cup% \operatorname{\mathcal{L}}(\operatorname{\mathcal{B}})$ ;
(ii)

the function $\tau$ induced by symbols in $\mathsf{RS}(\operatorname{\mathcal{C}},U)$ maps all states in the final one, i.e. $\tau:\{n_{0},n_{1}\}\mapsto\{n_{f}\}$ ;
(iii)

the function $\tau^{\prime}$ induced by symbols in $\overline{\mathsf{RS}(\operatorname{\mathcal{C}},U)}$ maps all states in the non-final state, i.e. $\tau:\{n_{0},n_{1}\}\mapsto\{n_{0},n_{1}\}\setminus\{n_{f}\}$ .

Similarly to the case of complementation, when appended to the end of a cascade $\operatorname{\mathcal{C}}\circ\operatorname{\mathsf{aug}}(\operatorname{% \mathcal{C}},\operatorname{\mathcal{C}}^{\prime})$ , the union brick reaches its final state if and only if either $\operatorname{\mathcal{C}}$ is in a final state or $\operatorname{\mathsf{aug}}(\operatorname{\mathcal{C}},\operatorname{\mathcal{% C}}^{\prime})$ is in a final state. This leads to the following lemma.

Lemma 6.6.

Let $\operatorname{\mathcal{C}}$ and $\operatorname{\mathcal{C}}^{\prime}$ be two cascade of automata. The cascade $\operatorname{\mathcal{C}}^{\prime\prime}\coloneqq\operatorname{\mathsf{finv}}% (\operatorname{\mathcal{C}}\circ\operatorname{\mathsf{aug}}(\operatorname{% \mathcal{C}},\operatorname{\mathcal{C}}^{\prime}))\circ\operatorname{\mathsf{% unionb}}(\operatorname{\mathcal{C}},\operatorname{\mathcal{C}}^{\prime})$ recognizes the language $\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})\cup\operatorname{% \mathcal{L}}(\operatorname{\mathcal{C}}^{\prime})$ . Moreover, if $\operatorname{\mathcal{C}}$ and $\operatorname{\mathcal{C}}^{\prime}$ are cascades of reset automata, then so is $\operatorname{\mathcal{C}}^{\prime\prime}$ .

Also in this case, if one of the two automata corresponds to a cascade terminating with a pure-reset component $\operatorname{\mathcal{A}}$ , the union can be performed without the need for additional layers: the automaton $\operatorname{\mathcal{A}}$ effectively serves as the union brick.

Left-concatenation of $\Sigma$

Given a cascade $\operatorname{\mathcal{C}}$ , we demonstrate how to construct a cascade that recognizes the language $\Sigma\cdot\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})$ , adding only one brick and guaranteeing that the property of being a reset cascade is preserved. As a by-product of this construction, we obtain that, given a cascade of resets of height $h$ equivalent to an $\mathsf{LTL}$ formula $\phi$ (interpreted over finite words), it is possible to construct a cascades of resets for ${}^{\prime}missing(\phi)$ of height $h+1$ , where ${}^{\prime}missing$ is the next modality of $\mathsf{LTL}$ .

We first define the next version of an automaton. The next version of an automaton $\operatorname{\mathcal{A}}$ , denoted as $\operatorname{\mathsf{nextv}}(\operatorname{\mathcal{A}})$ , is defined considering the Cartesian product between the alphabet of $\operatorname{\mathcal{A}}$ and the set $\{\mathsf{off},\mathsf{on}\}$ . Intuitively, if $\operatorname{\mathcal{A}}$ transitions from $q$ to $q^{\prime}$ with a symbols $\sigma$ , so does $\operatorname{\mathsf{nextv}}(\operatorname{\mathcal{A}})$ with the symbol $(\sigma,\mathsf{on})$ . On the contrary, all symbols $(\sigma,\mathsf{off})$ force $\operatorname{\mathsf{nextv}}(\operatorname{\mathcal{A}})$ to transition to the initial state. The formal definition of $\operatorname{\mathsf{nextv}}(\operatorname{\mathcal{A}})$ is given here below.

Definition 6.7 (Next version of an automaton).

Let $\operatorname{\mathcal{A}}=\langle\Sigma^{\prime},Q,\delta,q_{0},F\rangle$ be an automaton such that either $\Sigma^{\prime}=\Sigma$ or $\Sigma^{\prime}=\Sigma\times S$ , for an arbitrary finite set $S$ . We define the next version of $\operatorname{\mathcal{A}}$ , denoted as $\operatorname{\mathsf{nextv}}(\operatorname{\mathcal{A}})$ , as the automaton $(\Sigma^{\prime\prime},Q,\delta^{\prime},q_{0},F)$ such that:

$\blacksquare$

if $\Sigma^{\prime}=\Sigma$ , then $\Sigma^{\prime\prime}\coloneqq\Sigma\times\{\mathsf{off},\mathsf{on}\}$ and, for all $q\in Q$ and for all $a\in\Sigma$ , it holds: $\delta^{\prime}(q,(a,\mathsf{on}))=\delta(q,a)$ and $\delta^{\prime}(q,(*,\mathsf{off}))=q_{0}$ .
$\blacksquare$

if $\Sigma^{\prime}=\Sigma\times S$ , then $\Sigma^{\prime\prime}\coloneqq\Sigma\times\{\mathsf{off},\mathsf{on}\}\times S$ and, for all $q\in Q$ and for all $(a,s)\in\Sigma\times S$ , it holds that: $\delta^{\prime}(q,(a,\mathsf{on},s))=\delta(q,(a,s))$ and $\delta^{\prime}(q,(*,\mathsf{off},*))=q_{0}$ .

Given a cascade $\operatorname{\mathcal{C}}=\operatorname{\mathcal{A}}_{1}\circ\dots\circ% \operatorname{\mathcal{A}}_{n}$ over $\Sigma$ , we define the next version of $\operatorname{\mathcal{C}}$ , denoted with $\operatorname{\mathsf{nextv}}(C)$ , as the cascade $\operatorname{\mathsf{nextv}}(\operatorname{\mathcal{A}}_{1})\circ\dots\circ% \operatorname{\mathsf{nextv}}(\operatorname{\mathcal{A}}_{n})$ over $\Sigma\times\{\mathsf{off},\mathsf{on}\}$ .

Figure 10 shows the next versions of the automata in Figure 1. Crucially, computing the next version of an automaton does not alter its property of being a reset automaton.

Lemma 6.8.

Let $\Sigma$ be a finite alphabet and let $\operatorname{\mathcal{A}}$ be an automaton over $\Sigma$ or over $\Sigma\times S$ for an arbitrary finite set $S$ . If $\operatorname{\mathcal{A}}$ is reset automaton, then also $\operatorname{\mathsf{nextv}}(\operatorname{\mathcal{A}})$ is a reset automaton.

Figure 10: The next version of the two automata in the cascade of Figure 1.

Now, given any cascade $\operatorname{\mathcal{C}}$ , to capture the language $\Sigma\cdot\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})$ , it suffices to consider the automaton $\operatorname{\operatorname{\mathcal{A}}_{\mathit{switch}}}$ (depicted in Figure 7) with the next version of $\operatorname{\mathcal{C}}$ . In fact, considering that initially both $\operatorname{\operatorname{\mathcal{A}}_{\mathit{switch}}}$ and $\operatorname{\mathsf{nextv}}(\operatorname{\mathcal{C}})$ are in their initial states (which, for $\operatorname{\operatorname{\mathcal{A}}_{\mathit{switch}}}$ , is state $\mathsf{off}$ ), reading the first input symbol $\sigma$ forces:

(i)

$\operatorname{\operatorname{\mathcal{A}}_{\mathit{switch}}}$ to transition to state $\mathsf{on}$ ; and
(ii)

$\operatorname{\mathsf{nextv}}(\operatorname{\mathcal{C}})$ to remain in its initial state, because the symbol it reads is $(\sigma,\mathsf{off})$ .

After the first symbol and for all the rest of the input word, $\operatorname{\operatorname{\mathcal{A}}_{\mathit{switch}}}$ remains in state $\mathsf{on}$ , while $\operatorname{\mathsf{nextv}}(\operatorname{\mathcal{C}})$ operates like $\operatorname{\mathcal{C}}$ because it reads symbols of the form $(\sigma^{\prime},\mathsf{on})$ . As shown by the following lemma, this captures exactly $\Sigma\cdot\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})$ .

Lemma 6.9.

Let $\operatorname{\mathcal{C}}$ be a cascade of automata. The cascade $\operatorname{\mathcal{C}}^{\prime}\coloneqq\operatorname{\operatorname{% \mathcal{A}}_{\mathit{switch}}}\circ\operatorname{\mathsf{nextv}}(% \operatorname{\mathcal{C}})$ recognizes the language $\Sigma\cdot\operatorname{\mathcal{L}}(\operatorname{\mathcal{C}})$ . Moreover, if $\operatorname{\mathcal{C}}$ is a cascade of reset automata, then so is $\operatorname{\mathcal{C}}^{\prime}$ .

From Lemma 5.7, it follows the optimality of the construction outlined in Lemma 6.9.

7 Conclusions and Future Work

In this paper, we investigated some fundamental properties of cascades of reset automata. Unlike the approach commonly followed in the literature, where the cascade product is restricted to semi-automata, we focused on the case of automata. This allowed us to study the properties of the recognized languages. As an initial step, we showed how to compute regular expressions equivalent to a cascade. Then, on the basis of such a transformation, we established some meaningful expressiveness results, in particular lower bounds to the height and to the minimum number of states per level of a cascade of resets for specific families of languages. Finally, we showed how to compute the closure of reset cascades under certain basic operations by adding at most one brick to the end of the cascade.

As for the future developments of the work, finding an efficient construction for the closure of reset cascades under the concatenation operation is undoubtedly a crucial direction. This would enable the design of an efficient approach to handling the eventually and until operators of $\mathsf{LTL}$ , providing, together with the results given in the last section of the paper, an efficient decomposition into reset cascades for full $\mathsf{LTL}$ . This would improve the triply-exponential upper bound to such a decomposition achieved by Maler’s algorithm [4, 15]. Last but not least, giving analogous expressiveness and closure results for permutation automata appears to be another promising avenue for further investigation.

References

[1] Dana Angluin, David Chiang, and Andy Yang. Masked hard-attention transformers and boolean RASP recognize exactly the star-free languages. CoRR, abs/2310.13897, 2023. doi:10.48550/arXiv.2310.13897.
[2] Alessandro Artale, Luca Geatti, Nicola Gigante, Andrea Mazzullo, and Angelo Montanari. A Singly Exponential Transformation of LTL[X, F] into Pure Past LTL. In Pierre Marquis, Tran Cao Son, and Gabriele Kern-Isberner, editors, Proceedings of the 20th International Conference on Principles of Knowledge Representation and Reasoning, KR 2023, Rhodes, Greece, September 2-8, 2023, pages 65–74, 2023. doi:10.24963/KR.2023/7.
[3] Alessandro Artale, Luca Geatti, Nicola Gigante, Andrea Mazzullo, and Angelo Montanari. Succinctness issues for LTLf and safety and cosafety fragments of LTL. Information and Computation, 302:105262, 2025. doi:10.1016/j.ic.2024.105262.
[4] Giuseppe De Giacomo, Antonio Di Stasio, Francesco Fuggitti, and Sasha Rubin. Pure-past linear temporal and dynamic logic on finite traces. In Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, pages 4959–4965, 2021.
[5] Giuseppe De Giacomo and Moshe Y. Vardi. Linear Temporal Logic and Linear Dynamic Logic on Finite Traces. In Francesca Rossi, editor, Proceedings of the 23rd International Joint Conference on Artificial Intelligence, pages 854–860. IJCAI/AAAI, 2013. URL: http://www.aaai.org/ocs/index.php/IJCAI/IJCAI13/paper/view/6997.
[6] Samuel Eilenberg. Automata, languages, and machines., B. Pure and applied mathematics. Academic Press, 1976. URL: https://www.worldcat.org/oclc/310535259.
[7] Javier Esparza, Rubén Rubio, and Salomon Sickert. Efficient Normalization of Linear Temporal Logic. J. ACM, 71(2):16:1–16:42, 2024. doi:10.1145/3651152.
[8] Marcus Gelderie. Classifying regular languages via cascade products of automata. In Language and Automata Theory and Applications: 5th International Conference, LATA 2011, Tarragona, Spain, May 26-31, 2011. Proceedings 5, pages 286–297. Springer, 2011. doi:10.1007/978-3-642-21254-3_22.
[9] Mark Kambites. On the krohn-rhodes complexity of semigroups of upper triangular matrices. Int. J. Algebra Comput., 17(1):187–201, 2007. doi:10.1142/S0218196707003548.
[10] Nadezda Alexandrovna Knorozova and Alessandro Ronca. On the expressivity of recurrent neural cascades. In Michael J. Wooldridge, Jennifer G. Dy, and Sriraam Natarajan, editors, Thirty-Eighth AAAI Conference on Artificial Intelligence, AAAI 2024, Thirty-Sixth Conference on Innovative Applications of Artificial Intelligence, IAAI 2024, Fourteenth Symposium on Educational Advances in Artificial Intelligence, EAAI 2014, February 20-27, 2024, Vancouver, Canada, pages 10589–10596. AAAI Press, 2024. doi:10.1609/AAAI.V38I9.28929.
[11] Nadezda Alexandrovna Knorozova and Alessandro Ronca. On the expressivity of recurrent neural cascades with identity. In Pierre Marquis, Magdalena Ortiz, and Maurice Pagnucco, editors, Proceedings of the 21st International Conference on Principles of Knowledge Representation and Reasoning, KR 2024, Hanoi, Vietnam. November 2-8, 2024, 2024. doi:10.24963/KR.2024/82.
[12] Kenneth Krohn and John Rhodes. Algebraic theory of machines. I. Prime decomposition theorem for finite semigroups and machines. Transactions of the American Mathematical Society, 116:450–464, 1965.
[13] Bingbin Liu, Jordan T. Ash, Surbhi Goel, Akshay Krishnamurthy, and Cyril Zhang. Transformers learn shortcuts to automata. In The Eleventh International Conference on Learning Representations, ICLR 2023, Kigali, Rwanda, May 1-5, 2023. OpenReview.net, 2023. URL: https://openreview.net/forum?id=De4FYqjFueZ.
[14] Oded Maler. On the Krohn-Rhodes Cascaded Decomposition Theorem. In Zohar Manna and Doron A. Peled, editors, Time for Verification, Essays in Memory of Amir Pnueli, volume 6200 of Lecture Notes in Computer Science, pages 260–278. Springer, 2010. doi:10.1007/978-3-642-13754-9_12.
[15] Oded Maler and Amir Pnueli. Tight Bounds on the Complexity of Cascaded Decomposition of Automata. In 31st Annual Symposium on Foundations of Computer Science, St. Louis, Missouri, USA, October 22-24, 1990, Volume II, pages 672–682. IEEE Computer Society, 1990. doi:10.1109/FSCS.1990.89589.
[16] Zohar Manna and Amir Pnueli. A hierarchy of temporal properties (invited paper, 1989). In Proceedings of the 9th annual ACM symposium on Principles of distributed computing, pages 377–410, 1990. doi:10.1145/93385.93442.
[17] Nicolas Markey. Temporal logic with past is exponentially more succinct, concurrency column. Bull. EATCS, 79:122–128, 2003.
[18] Robert McNaughton and Seymour A Papert. Counter-Free Automata (MIT research monograph no. 65). The MIT Press, 1971.
[19] Amir Pnueli. The temporal logic of programs. In 18th Annual Symposium on Foundations of Computer Science (sfcs 1977), pages 46–57. IEEE, 1977. doi:10.1109/SFCS.1977.32.
[20] Alessandro Ronca. The transformation logics. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence, IJCAI 2024, Jeju, South Korea, August 3-9, 2024, pages 3549–3557. ijcai.org, 2024. URL: https://www.ijcai.org/proceedings/2024/393.
[21] Alessandro Ronca, Nadezda Alexandrovna Knorozova, and Giuseppe De Giacomo. Automata cascades: Expressivity and sample complexity. In Brian Williams, Yiling Chen, and Jennifer Neville, editors, Thirty-Seventh AAAI Conference on Artificial Intelligence, AAAI 2023, Thirty-Fifth Conference on Innovative Applications of Artificial Intelligence, IAAI 2023, Thirteenth Symposium on Educational Advances in Artificial Intelligence, EAAI 2023, Washington, DC, USA, February 7-14, 2023, pages 9588–9595. AAAI Press, 2023. doi:10.1609/AAAI.V37I8.26147.
[22] Karl-Heinz Zimmermann. On Krohn-Rhodes theory for semiautomata. CoRR, abs/2010.16235, 2020. arXiv:2010.16235.

[bib.bib1] [1] Dana Angluin, David Chiang, and Andy Yang. Masked hard-attention transformers and boolean RASP recognize exactly the star-free languages. CoRR, abs/2310.13897, 2023. doi:10.48550/arXiv.2310.13897.

[bib.bib2] [2] Alessandro Artale, Luca Geatti, Nicola Gigante, Andrea Mazzullo, and Angelo Montanari. A Singly Exponential Transformation of LTL[X, F] into Pure Past LTL. In Pierre Marquis, Tran Cao Son, and Gabriele Kern-Isberner, editors, Proceedings of the 20th International Conference on Principles of Knowledge Representation and Reasoning, KR 2023, Rhodes, Greece, September 2-8, 2023, pages 65–74, 2023. doi:10.24963/KR.2023/7.

[bib.bib3] [3] Alessandro Artale, Luca Geatti, Nicola Gigante, Andrea Mazzullo, and Angelo Montanari. Succinctness issues for LTLf and safety and cosafety fragments of LTL. Information and Computation, 302:105262, 2025. doi:10.1016/j.ic.2024.105262.

[bib.bib4] [4] Giuseppe De Giacomo, Antonio Di Stasio, Francesco Fuggitti, and Sasha Rubin. Pure-past linear temporal and dynamic logic on finite traces. In Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, pages 4959–4965, 2021.

[bib.bib5] [5] Giuseppe De Giacomo and Moshe Y. Vardi. Linear Temporal Logic and Linear Dynamic Logic on Finite Traces. In Francesca Rossi, editor, Proceedings of the 23rd International Joint Conference on Artificial Intelligence, pages 854–860. IJCAI/AAAI, 2013. URL: http://www.aaai.org/ocs/index.php/IJCAI/IJCAI13/paper/view/6997.

[bib.bib6] [6] Samuel Eilenberg. Automata, languages, and machines., B. Pure and applied mathematics. Academic Press, 1976. URL: https://www.worldcat.org/oclc/310535259.

[bib.bib7] [7] Javier Esparza, Rubén Rubio, and Salomon Sickert. Efficient Normalization of Linear Temporal Logic. J. ACM, 71(2):16:1–16:42, 2024. doi:10.1145/3651152.

[bib.bib8] [8] Marcus Gelderie. Classifying regular languages via cascade products of automata. In Language and Automata Theory and Applications: 5th International Conference, LATA 2011, Tarragona, Spain, May 26-31, 2011. Proceedings 5, pages 286–297. Springer, 2011. doi:10.1007/978-3-642-21254-3_22.

[bib.bib9] [9] Mark Kambites. On the krohn-rhodes complexity of semigroups of upper triangular matrices. Int. J. Algebra Comput., 17(1):187–201, 2007. doi:10.1142/S0218196707003548.

[bib.bib10] [10] Nadezda Alexandrovna Knorozova and Alessandro Ronca. On the expressivity of recurrent neural cascades. In Michael J. Wooldridge, Jennifer G. Dy, and Sriraam Natarajan, editors, Thirty-Eighth AAAI Conference on Artificial Intelligence, AAAI 2024, Thirty-Sixth Conference on Innovative Applications of Artificial Intelligence, IAAI 2024, Fourteenth Symposium on Educational Advances in Artificial Intelligence, EAAI 2014, February 20-27, 2024, Vancouver, Canada, pages 10589–10596. AAAI Press, 2024. doi:10.1609/AAAI.V38I9.28929.

[bib.bib11] [11] Nadezda Alexandrovna Knorozova and Alessandro Ronca. On the expressivity of recurrent neural cascades with identity. In Pierre Marquis, Magdalena Ortiz, and Maurice Pagnucco, editors, Proceedings of the 21st International Conference on Principles of Knowledge Representation and Reasoning, KR 2024, Hanoi, Vietnam. November 2-8, 2024, 2024. doi:10.24963/KR.2024/82.

[bib.bib12] [12] Kenneth Krohn and John Rhodes. Algebraic theory of machines. I. Prime decomposition theorem for finite semigroups and machines. Transactions of the American Mathematical Society, 116:450–464, 1965.

[bib.bib13] [13] Bingbin Liu, Jordan T. Ash, Surbhi Goel, Akshay Krishnamurthy, and Cyril Zhang. Transformers learn shortcuts to automata. In The Eleventh International Conference on Learning Representations, ICLR 2023, Kigali, Rwanda, May 1-5, 2023. OpenReview.net, 2023. URL: https://openreview.net/forum?id=De4FYqjFueZ.

[bib.bib14] [14] Oded Maler. On the Krohn-Rhodes Cascaded Decomposition Theorem. In Zohar Manna and Doron A. Peled, editors, Time for Verification, Essays in Memory of Amir Pnueli, volume 6200 of Lecture Notes in Computer Science, pages 260–278. Springer, 2010. doi:10.1007/978-3-642-13754-9_12.

[bib.bib15] [15] Oded Maler and Amir Pnueli. Tight Bounds on the Complexity of Cascaded Decomposition of Automata. In 31st Annual Symposium on Foundations of Computer Science, St. Louis, Missouri, USA, October 22-24, 1990, Volume II, pages 672–682. IEEE Computer Society, 1990. doi:10.1109/FSCS.1990.89589.

[bib.bib16] [16] Zohar Manna and Amir Pnueli. A hierarchy of temporal properties (invited paper, 1989). In Proceedings of the 9th annual ACM symposium on Principles of distributed computing, pages 377–410, 1990. doi:10.1145/93385.93442.

[bib.bib17] [17] Nicolas Markey. Temporal logic with past is exponentially more succinct, concurrency column. Bull. EATCS, 79:122–128, 2003.

[bib.bib18] [18] Robert McNaughton and Seymour A Papert. Counter-Free Automata (MIT research monograph no. 65). The MIT Press, 1971.

[bib.bib19] [19] Amir Pnueli. The temporal logic of programs. In 18th Annual Symposium on Foundations of Computer Science (sfcs 1977), pages 46–57. IEEE, 1977. doi:10.1109/SFCS.1977.32.

[bib.bib20] [20] Alessandro Ronca. The transformation logics. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence, IJCAI 2024, Jeju, South Korea, August 3-9, 2024, pages 3549–3557. ijcai.org, 2024. URL: https://www.ijcai.org/proceedings/2024/393.

[bib.bib21] [21] Alessandro Ronca, Nadezda Alexandrovna Knorozova, and Giuseppe De Giacomo. Automata cascades: Expressivity and sample complexity. In Brian Williams, Yiling Chen, and Jennifer Neville, editors, Thirty-Seventh AAAI Conference on Artificial Intelligence, AAAI 2023, Thirty-Fifth Conference on Innovative Applications of Artificial Intelligence, IAAI 2023, Thirteenth Symposium on Educational Advances in Artificial Intelligence, EAAI 2023, Washington, DC, USA, February 7-14, 2023, pages 9588–9595. AAAI Press, 2023. doi:10.1609/AAAI.V37I8.26147.

[bib.bib22] [22] Karl-Heinz Zimmermann. On Krohn-Rhodes theory for semiautomata. CoRR, abs/2010.16235, 2020. arXiv:2010.16235.

On Cascades of Reset Automata

Abstract

Keywords and phrases:

Copyright and License:

2012 ACM Subject Classification:

Acknowledgements:

Funding:

DOI:

Event:

Editors:

Series and Publisher:

1 Introduction

2 Related Work

3 Background

Definition 3.1 (Direct product of automata).

Definition 3.2 (Cascade Product of semiautomata [15, 22]).

Definition 3.3 (Function induced by a symbol).

Definition 3.4 (Reset and permutation functions).

Definition 3.5 (Classes of semiautomata).

Theorem 3.6 (The Krohn-Rhodes Cascade Decomposition Theorem [12, 14]).

4 Cascades of automata

4.1 Definitions and basic properties

Definition 4.1 (Cascade product of automata).

Definition 4.2 (Language of ℬ at a state s over 𝒜).

Proposition 4.3 (Language of a cascade in terms of its components).

Definition 4.4 (Augmentation).

Proposition 4.5 (Direct product by means of cascade product).

Proposition 4.6.

4.2 Languages of cascades of resets

4.2.1 Cascades of height 1

Theorem 4.7 (The languages of reset automata).

Proposition 4.8.

Corollary 4.9.

4.2.2 Cascades of unbounded-height

Lemma 4.10.

Definition 4.11 (Filtered Automaton).

Theorem 4.12 (Languages of cascades of unbounded-height).

Corollary 4.13.

Lemma 4.14.

5 Expressiveness results

Definition 5.1 (Classes ℛ and ℛ⁢𝒫⁢ℛ).

5.1 Short Cascades

Lemma 5.2.

Lemma 5.3.

Lemma 5.4 (Width-Hierarchy Lemma).

Corollary 5.5.

Lemma 5.6.

5.2 Narrow Cascades

Lemma 5.7 (Height-Hierarchy Lemma).

5.3 General Cascades

Lemma 5.8 (Width-Collapse Lemma).

Lemma 5.9.

Lemma 5.10 (Narrowing Lemma).

Corollary 5.11.

Corollary 5.12.

Lemma 5.13 (Generalized Height-Hierarchy Lemma).

6 Efficient closure properties of cascades of reset automata

Definition 6.1 (Reachability Set).

Complementation

Definition 6.2 (Negation brick).

Lemma 6.3.

Lemma 6.4.

Union

Definition 6.5 (Union brick).

Lemma 6.6.

Left-concatenation of 𝚺

Definition 6.7 (Next version of an automaton).

Lemma 6.8.

Lemma 6.9.

7 Conclusions and Future Work

References

Definition 4.2 (Language of $\operatorname{\mathcal{B}}$ at a state $s$ over $\operatorname{\mathcal{A}}$ ).

Definition 5.1 (Classes $\mathcal{R}$ and $\mathcal{RPR}$ ).

Left-concatenation of $\Sigma$