On Deciding the Data Complexity of Answering Linear Monadic Datalog Queries with LTL Operators
Abstract
Our concern is the data complexity of answering linear monadic datalog queries whose atoms in the rule bodies can be prefixed by operators of linear temporal logic LTL. We first observe that, for data complexity, answering any connected query with operators / (at the next/previous moment) is either in , or in , or -complete, or L-hard and in NL. Then we show that the problem of deciding L-hardness of answering such queries is PSpace-complete, while checking membership in the classes and as well as -completeness can be done in ExpSpace. Finally, we prove that membership in or in , -completeness, and L-hardness are undecidable for queries with operators / (sometime in the future/past) provided that and .
Keywords and phrases:
Linear monadic datalog, linear temporal logic, data complexityCopyright and License:
2012 ACM Subject Classification:
Theory of computation Database query processing and optimization (theory)Editors:
Sudeepa Roy and Ahmet KaraSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
We consider monadic datalog queries, in which atoms in the rule bodies can be prefixed by the temporal operators / (at the next/previous moment) and / (sometime in the future/past) of linear temporal logic LTL [17]. This query language, denoted , is intended for querying temporal graph databases and knowledge graphs in scenarios such as virus transmission [25, 45], transport networks [28], social media [38], supply chains [46], and power grids [37]. In this setting, data instances are finite sets of ground atoms that are timestamped by the moments of time they happen at. The rules in queries are assumed to hold at all times, with time being implicit in the rules and only accessible via temporal operators. We choose LTL for our formalism rather than, say, more expressive metric temporal logic MTL [30, 1] because LTL has been a well established query language in temporal databases since the 1990s (see [39, 41, 14, 32] and the discussion therein on point versus interval-based query languages), also suitable in the context of temporal knowledge graphs as recently argued in [19].
Example 1.
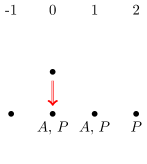
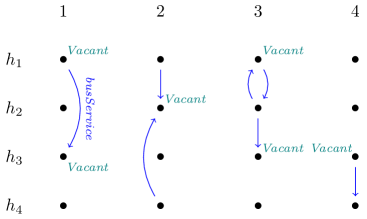
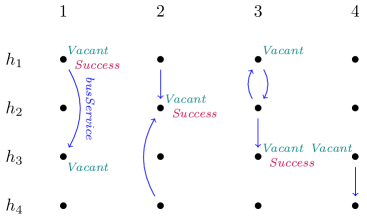
Imagine a PhD student working on a paper while hostel hopping. However, finishing the paper requires staying at the same hostel for at least two consecutive nights. Bus services between hostels, which vary from one day to the next, and hostel vacancies are given by a temporal data instance with atoms of the form and , where , are hostels and a timestamp (see Fig. 1 for an illustration). The following query finds pairs such that having started hopping at hostel on day , the student will eventually submit the paper:
It is readily seen that answering this query is NL-complete for data complexity. If, however, we drop the next-time operator from , it will become equivalent to . The next query simply looks for pairs with having vacancies for two consecutive nights some time later than :
This query can be equivalently expressed as the two-sorted first-order formula
where ranges over objects (hostels) and over time points ordered by . Formulas in such a two-sorted first-order logic, denoted , can be evaluated over finite data instances in for data complexity [26].
Our main concern is the classical problem of deciding whether a given temporal monadic datalog query is equivalent to a first-order query (over any data instance). In the standard, atemporal database theory, this problem, known as predicate boundedness, has been investigated since the mid 1980s with the aim of optimising and parallelising datalog programs [27, 16]. Thus, predicate boundedness was shown to be undecidable for binary datalog queries [24] and 2ExpTime-complete for monadic ones (even with a single recursive rule) [15, 8, 29].
Datalog boundedness is closely related to the more general rewritability problem in the ontology-based data access paradigm [11, 3], which brought to light wider classes of ontology-mediated queries (OMQs) and ultimately aimed to decide the data complexity of answering any given OMQ and, thereby, the optimal database engine needed to execute that OMQ. Answering OMQs given in propositional linear temporal logic LTL is either in , or in , or -complete for data complexity [40], the classes well known from the circuit complexity theory for regular languages. For each of these three cases, deciding whether a given LTL-query falls into it is ExpSpace-complete, even if we restrict the language to temporal Horn formulas and atomic queries [31]. The data complexity of answering atemporal monadic datalog queries comes from four complexity classes [16, 15].
Our 2D query language is a combination of datalog and LTL. It can be seen as the monadic fragment, without negation and aggregate functions, of , a language for reasoning about distributed systems that evolve in time [2]. It is also close in spirit to temporal deductive databases, TDDs [13, 12], extending their monadic fragment with the eventuality operator . The main intriguing question we would like to answer in this paper is whether deciding membership of 2D queries in, say, can be substantially harder than deciding membership in of the corresponding 1D monadic datalog and LTL queries.
With this in mind, we focus on the sublanguage of that consists of linear queries, that is, those that have at most one IDB (intensional, recursively definable) predicate in each rule body. While the full language inherits from TDDs a PSpace-complete query answering problem (for data complexity), we prove that linear queries can be answered in NL. By and we denote the fragments of that only admit the / and / operators, respectively. All of our queries are assumed to be connected in the sense that the graph induced by the body of each rule is connected. These fragments retain practical interest: as argued in [15], atemporal datalog programs used in practice tend to be linear and connected. For example, SQL:1999 explicitly supports linear recursion [20], which together with connectedness is a common constraint in the context of querying graph databases and knowledge graphs [35, 42], where the focus is on path queries [21, 23].
It is known that deciding whether a linear monadic datalog query can be answered in is PSpace-complete [15, 43] (without the monadicity restriction, the problem is undecidable [24]). The same problem for the propositional LTL fragments of and is also PSpace-complete [31].
Our main results in this paper are as follows:
-
Answering queries is NL-complete for data complexity.
-
It is undecidable whether a given -query can be answered in , , or (if ); it is undecidable whether such a query is L-hard (if ).
-
Answering any connected -query is either in or in , or -complete, or L-hard – and anyway it is in NL.
-
It is PSpace-complete to decide whether a connected -query is L-hard; checking whether it is in , or in , or is -complete can be done in ExpSpace.
(Note that dropping the past-time operators and from the languages has no impact on these complexity results.) Thus, the temporal operators / and / exhibit drastically different types of interaction between the object and temporal dimensions. To illustrate the reason for this phenomenon, consider first the following -program:
| (1) | |||
| (2) | |||
| (3) |
Suppose a data instance consists of timestamped atoms , , . We obtain by first applying rule (3) to infer , then rule (2) to infer , and , and finally rule (1) to obtain . Rules (2) and (3) are applied along the timeline of a single object, , while the final application passes from one object, , to another, . To do so, we check whether a certain condition holds for the joint timeline of and , namely, that they are connected by at time 1. However, if we are limited to the operators /, the number of steps that we can investigate along such a joint timeline is bounded by the maximum number of nested / in the program. Therefore, there is little interaction between the two phases of inference that explore the object and the temporal domains. In contrast, rules with / can inspect both dimensions simultaneously as, for example, the rule
| (4) |
In this case, inferring requires checking the existence of an object satisfying and at some arbitrarily distant moment in the future. Given that our programs are monadic, the predicate cannot be expressed using operators / only.
Our positive results are proved by generalising the automata-theoretic approach of [15]. As a by-product, we obtain a method to decompose every connected -query into a plain datalog part and a plain LTL part , which are, however, substantially larger than , so that the data complexity of answering equals the maximum of the respective data complexities of and . This reinforces the “weakness of interaction” between the relational and the temporal parts of the query when the latter is limited to operators /. We also provide some evidence that, in contrast to the atemporal case, the automata-theoretic approach cannot be generalised to the case of disconnected queries. The undecidability of the decision problem for -queries is proved by a reduction of the halting problem for Minsky machines with two counters [33].
The paper is organised as follows. In Section 2, we give formal definitions of data instances and queries, and prove that every temporal monadic datalog query can be answered in P, and in NL if it is linear. In Section 3, we show that checking whether a given query with operator or has data complexity lower than NL is undecidable. Section 4 considers -queries by presenting a generalisation of the automata-theoretic approach of [15], which is then used in Section 5 to provide the decidability results. We conclude with a discussion of future work and our final remarks in Section 6. Detailed proofs can be found in the full version of this paper [4].
2 Preliminaries
A relational schema is a finite set of relation symbols with associated arities . A database over a schema is a set of ground atoms , , is the arity of . We call , , the domain objects or simply objects. We denote by the set of objects occurring in . We denote by the number of atoms in . We denote by the set of integers , where . A temporal database over a schema is a finite sequence of databases over this schema for some , . Each database is called the ’th slice of and is called a timestamp. We denote by . The size of , denoted by , is the maximum between and . The domain of the temporal database is and is denoted by . A homomorphism from as above to is a function that maps to so that if and only if .
We will deal with temporal conjunctive queries (temporal CQs) that are formulas of the form , where are tuples of variables and , the body of the query, is defined by the following BNF:
| (5) |
where and are variables of , and is any of and (the operators / mean “at the next/previous moment” and / “sometime in the future/past”). For brevity, we will use the notation , , for a sequence of symbols if , of symbols if , and an empty sequence if . We call the answer variables of . To provide the semantics, we define for and as follows:
| (6) | |||
| (7) | |||
| (8) | |||
| (9) |
and symmetrically for and . Given a temporal database , a timestamp , and a query , we say that if there exist such that , where .
The problem of answering a temporal CQ is to check, given , , and , whether . Answering temporal CQs is not harder than that for non-temporal CQs. Indeed, we show that any is -rewritable in the sense that there exists an -formula such that for all and as above whenever is true in the two-sorted first-order structure , whose domain is , and where is true whenever and is true whenever (see [5] for details). It follows by [26] that the problem of answering a temporal CQ is in .
We outline the construction of the rewriting. Let . The main issue with the construction is that temporal subformulas of , say , may be true for at , because for . Had that not been the case, we could construct the rewriting for straightforwardly by induction of . To overcome this, let be the number of temporal operators in . We use a property that for all tuples of objects from and subformulas of , we have
| (10) |
Thus, for any subformula of , we construct, by induction, the formulas and for , so that for any , , and any objects ,
For the base case, we set and . For an induction step, e.g., , , for all other , and finally . Here, and are defined in as, respectively, -minimal and -maximal elements in ( is -definable as well). The required rewriting of is then the formula .
Proposition 2.
For a temporal CQ , checking is in for data complexity.
In the non-temporal setting, a body of a CQ (a conjunction of atoms), can be seen as a database (a set of atoms). We have a similar correspondence in the temporal setting, for queries without operators and . Indeed, observe that and . Hence we can assume that any temporal CQ body is a conjunction of temporalised atoms of the form . Given a temporal CQ of this form, let be the least and the greatest number such that and appear in , for some and . Let be a temporal database whose objects are the variables of , and equals if , if , and if . Furthermore, let whenever is in , . Then we can, just as in the non-temporal case, characterise the relation in terms of homomorphisms:
Lemma 3.
For any temporal CQ without and , if and only if there is a homomorphism from to such that , and .
2.1 Temporal Datalog
We define a temporalised version of datalog to be able to use recursion in querying temporal databases. We call this language temporal datalog, or . A rule of over a schema has the form:
| (11) |
where and are relation symbols over and is an arbitrary sequence of temporal operators and . The part of the rule to the left of the arrow is called its head and the right-hand side – its body. All variables from the head must appear in the body.
A program is a finite set of rules. The relations that appear in rule heads constitute its IDB schema, , while the rest form the EDB schema, . A rule is linear if its body contains at most one IDB atom and monadic if the arity of its head is 1. A program is linear (monadic) if so are all its rules. We say that the program is in plain datalog if it does not use the temporal operators and in plain LTL if all its relations have arity 1 and every rule uses just one variable. Recursive rules are those that contain IDB atoms in their bodies, other rules are called initialisation rules. The arity of a program is the maximal arity of its IDB atoms.
Our results are all about connected programs. Namely, define the Gaifman graph of a temporal CQ to be a graph whose nodes are the variables and where two variables are connected by an edge if they appear in the same atom. A rule body is connected if so is its Gaifman graph, and a program is connected when all rules are connected. The size of a program , denoted , is the number of symbols needed to write it down, where every relation symbol is counted as one symbol, and a sequence of operators the form is counted as symbols.
When a program is fixed, we assume that all temporal databases that we work with are defined over . So let be a program and a temporal database. An enrichment of is an (infinite) temporal database over the schema such that and for any and any , if and only if . Thus, the only EDB atoms in are those of , but “enriches” with various IDB atoms at different points of time. We say that is a model of and if is an enrichment of ; and for any rule of , , i.e., for all and any tuples , implies . We write if for every model of and it follows that .
A query is a pair , where is a program and an IDB atom, called the goal predicate. The arity of a query is the arity of . Given a temporal database , a timestamp , a tuple and a query of arity , the pair is a certain answer to over if . The answering problem for a query over a temporal database is that of checking, given a tuple , and , if is a certain answer to over . We use the term “complexity of the query ” to refer to the data complexity of the associated answering problem, and say, e.g., that is complete for polynomial time (for P) or for nondeterministic logarithmic space (NL) if the answering problem for is such.
Our main concern is how the data complexity of the query answering problem is affected by the features of . The following theorem relies on similar results obtained for temporal deductive databases [13, 12] and temporal description logics [6, 7, 22].
Theorem 4.
Answering (monadic) queries is PSpace-complete for data complexity; answering linear (monadic) queries is NL-complete.
Proof (Sketch).
For full , PSpace-completeness can be shown by reusing the techniques for temporal deductive databases [13, 12]. However, we prove that a linear query can be answered in NL. Indeed, fix a linear query . Without loss of generality, we assume that temporalised IDB atoms in rule bodies of have the form , where (the cases of / and consecutive / can be expressed via recursion). Given a temporal database , tuples of objects and from , and , we write if has a rule such that . Analogously, we write if there is an initialisation rule and . Then, given a linear query , we have if and only if , , and there exists a sequence
| (12) |
such that , tuples are from , , for , , and . Let . Using property (10), we observe that a rule either holds or does not hold simultaneously for all , where is the number of temporal operators in , and, similarly, for all . Now, consider a sequence (12) and , where all (the case for is analogous). Any loop of the form in it with can be removed as long as in the resulting sequence
the sum of all remains . This allows us to convert any sequence (12) to a sequence with the same in the beginning, the same in the end, and where all do not exceed , for equal to the maximal arity of a relation in . This means that, for , we can check using timestamps in the range . Clearly, the existence of such a derivation can be checked in NL.
However, individual queries may be easier to answer than in the general case. Since combines features of plain datalog and of linear temporal logic, its queries can correspond to a variety of complexity classes. Recall, for example, queries and from Section 1, the first of which is hard for logarithmic space (L-hard) and the second lies in , the class of problems decidable by unbounded fan-in, polynomial size and constant depth boolean circuits. Furthermore, by using unary relations and operator , one can simulate any regular language, giving rise to queries that lie in , the class obtained from by allowing “MOD ” gates, or are complete for , the class defined similarly for bounded fan-in polynomial circuits of logarithmic depth. Intuitively, the problems in , , and are solvable in short (constant or logarithmic) time on a parallel architecture; see [40] for more details.
In the remainder of the paper we focus on deciding the data complexity for the linear monadic fragment of , denoted . It is well-known that a plain datalog query can be characterised via an infinite set of conjunctive queries called its expansions [34]. We define expansions for and use them as the main tool in our (un)decidability proofs.
2.1.1 Expansions for Linear Monadic Queries
Let be a program and be a unary temporal conjunctive query with a single answer variable and containing a unique IDB atom, say , from . Let be another temporal conjunctive query with a single answer variable, and let be obtained from by substituting by and all other variables with fresh ones. A composition of and , denoted , has the form of with substituted with . We note that the variables of remain present in and is an answer variable of . If contains an IDB atom and is another temporal conjunctive query, the composition can be extended in the same fashion to , and so on. Note that, up to renaming of variables, and are the same queries, so we will omit the brackets and write .
Expansions are compositions of rule bodies of a program . Let be such that is the body of the recursive rule:
| (13) |
and is the body of an initialization rule
| (14) |
The composition is called an expansion of , and is its length. The set of all expansions of is denoted . Moreover, let be the set of all recursive rule bodies of and be the set of all initialization rule bodies. Then each expansion can be regarded (by omitting the symbol ) as a word in , and as a sublanguage of . Adopting a language-theoretic notation, we will use small Latin letters , etc. to denote expansions. To highlight the fact that each expansion is a temporal conjunctive query with the answer variable , we sometimes write .
It is a direct generalization from the case of plain datalog [34] that if and only if there exists such that .
3 Undecidability for Queries with
Our first result about deciding the complexity of a given query is negative.
Theorem 5.
It is undecidable whether a given -query can be answered in , , or (if ). It is undecidable whether the query is L-hard (if ).
The proof is by a reduction from the halting problem of 2-counter machines [33]. Namely, given a 2-counter machine we construct a query that is in if halts and NL-complete otherwise.
Recall, that a 2-counter machine is defined by a finite set of states , with a distinguished initial state , two counters able to store non-negative integers, and a transition function . On each step the machine performs a transition by changing its state and incrementing or decrementing each counter by 1 with a restriction that their values remain non-negative. The next transition is chosen according to the current state and the values of the counters. However, the machine is only allowed to perform zero-tests on counters and does not distinguish between two different positive values. Formally, transitions are given by a partial function :
| (15) |
Let and for all . A computation of is a sequence of configurations:
| (16) |
such that for each , holds and , . We assume that and is such that for all . We call the length of the computation. We say that halts if is not defined in a computation. Thus, either halts after steps or goes through infinitely many configurations.
Let be a 2-counter machine. We construct a connected linear query using the operator only, such that its evaluation is in if halts, but becomes NL-complete otherwise. The construction with the operator instead of is symmetric.
We set the EDB schema of three relations which stand for “transition”, “first counter update”, and “second counter update”, respectively. Intuitively, domain elements of a temporal database represent configurations of , and role triples of , and , arranged according to certain rules described below, will play the role of transitions. A sequence of nodes connected by such triples will thus represent a computation of . Our program will generate an expansion along such a sequence, trying to assign to each configuration an IDB that represents a state of , which will be possible while the placement of the connecting roles on the temporal line follows the rules of . If the machine halts, there is a maximum number of steps we can make, so the check can be done in . If does not halt, however, it has arbitrarily long computations, and the query evaluation becomes NL-complete.
Here are the details. A configuration is represented by an object and three timestamps such that and . The values of the counters and are indicated, respectively, by existence of connections and to some object that is supposed to represent the next configuration in the computation. For the transition to happen, we also require . Given a computation of the form (16), the corresponding computation path is a pair , where for each , there are , , and in the database, with an additional requirement that . Two types of problems may be encountered on such a path. A representation violation occurs when an object has more than one outgoing edge of type , , or . A transition violation of type is detected when there are two consecutive nodes , , and . The program will look for such violations. It will have an IDB relation symbol per each state of . The initialisation rules allow to infer any state IDB from a representation violation, and the IDB from a transition violation of type . The recursive rules then push the state IDB up a computation path following the rules of and tracing “backwards” a computation of . Once infers the initial state IDB at a position with zero counter values, we are done. It remains to give the rules explicitly.
We use a shortcut to mean a “reflexive” version of , i.e. . Clearly, every rule can be rewritten to an equivalent set of rules without it. We need the rules:
| (17) | ||||
| (18) |
to detect representation violations. For transition violations, we first define IDBs , where stand for the respective counter and stands for the change of that counter value in a transition. Each detects situations when a correct transition was not executed, e.g. having , the timestamps and that are marked by an outgoing in consecutive configurations satisfy , , or , which they should not. The rules are the following:
| (19) | ||||
| (20) | ||||
| (21) | ||||
| (22) |
for . Then, again, any state can be inferred from a violation:
| (23) |
for each transition , and for all when is not defined. Finally, we require
| (24) | ||||
| (25) |
This finalises the construction of . Any expansion of starts with the body of the rule (25) and then continues by a sequence of bodies of the rules of the form (24) and ends with a detection either of a representation violation, defined by (17) – (18), or of a transition violation, defined by (23). If halts in steps, it is enough to consider expansions containing no more than bodies of (24). Thus, in this case is in . If, on the contrary, does not halt, we can use expansions representing arbitrarily long prefixes of its computation for a reduction from directed reachability problem, rendering the query NL-hard.
Lemma 6.
If halts, is in . Otherwise, it is NL-hard.
4 Automata-Theoretic Tools for Queries with
From now on, we focus on queries that use operators and only. In this section, we develop a generalisation of the automata-theoretic approach to analysing query expansions proposed in [15]. In Section 5 we use this approach to study the data complexity of this kind of queries.
Recall from Section 2.1.1 the definitions of composition and expansion of rule bodies, alphabets and , and the language . We observe that for any sequence of rule bodies and the compositions and are well-defined. They are words in the languages and , respectively. Note that is a temporal CQ over schema , while is that over , since it contains the IDB atom of . For , is defined as the (temporal) database corresponding to (temporal) CQ , while for we define as the database corresponding to the CQ obtained from by omitting the IDB atom. For either , is over the schema . Having that, we define the language of all words such that .
Plain datalog queries are either in (called bounded), or L-hard (unbounded), and a criterion of unboundedness can be formulated in language-theoretic terms [15]: a connected linear monadic plain datalog query is unbounded if and only if for every there is , , such that its prefix of length is not in .
Example 7.
The query , where is given by the following plain datalog rules, is unbounded.
| (26) | |||
| (27) |
However, if we substitute the rule (27) with another initialisation rule
| (28) |
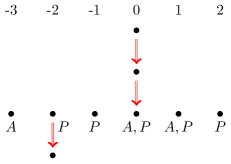
it becomes bounded because for every , its prefix of length is in . To see this, consider the expansions of the query, i.e., given in Figure 2.
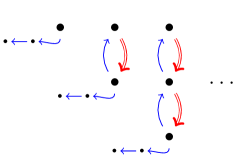
tion , single arrows – the relation .
The authors of [15] construct finite state automata for languages and , the complement of , and use them to check their criterion in polynomial space. Our goal is to generalise this technique to the temporalised case. However, we can not use finite automata to work directly with sequences of rule bodies, since the language , in the presence of time, may be non-regular, as demonstrated by the following example.
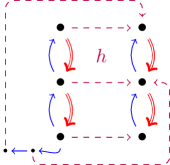
Example 8.
Consider a program
Denote its rule bodies , , and , and the composition . The composition is in , and the corresponding database is given in Figure 3(a). In general, a composition of the form is in if and only if , which, by a simple application of the pumping lemma, is a non-regular language.
To overcome this, we introduce a larger alphabet and define more general versions of the languages and to regain their regularity. Recall that every composition of rule bodies gives rise to a temporal database . Instead of working with , we use an exponentially larger alphabet to describe as a word and define analogues of and over that alphabet. Consider a recursive rule
| (29) |
where is the unique IDB atom in the rule body and . We call such a rule horizontal if and vertical otherwise. In a composition , a vertical (horizontal) segment is a maximal subword that consists of vertical (respectively, horizontal) rule bodies. For every composition we define the description of the respective database as follows. Let , where are vertical segments and are horizontal segments, with and possibly empty. For each we set to be the sequence of singleton sets, each of which contains a vertical rule body. For each , we construct in steps, as follows. Recall that , , has the form , where is the unique IDB atom in . Let and for . Intuitively, is the moment of time where the body lands in the composition . Let be the ordering of the the numbers in the set in the increasing order. We set, to be for ; for ; for ; and for . Additionally, we set for . Now we take .
Finally, . We use the symbol to refer to letters of . We call letters of the form , where is a vertical rule body, vertical letters, and the rest – horizontal letters. Consequently, we can speak of vertical and horizontal segments of , meaning maximal segments composed of vertical (respectively, horizontal) letters only.
Intuitively, describes , which can be seen as composed of , described by , respectively. The symbol , representing a vertical line meeting a horizontal one, marks the point in time where is connected to , while the symbol , analogously, shows where is connected to .
Example 9.
Not every word over correctly describes a temporal database. This motivates the following definition: is correct if (i) every symbol is either a singleton (standing for a vertical rule body) or a set of horizontal rule bodies, with a possible addition of , and (ii) every horizontal segment of preceded by a vertical segment contains exactly one , and every horizontal segment followed by a vertical one – exactly one . A correct word describes a temporal database similarly to how describes . Formally, break into vertical/horizontal segments . For a vertical segment , set . For a horizontal segment , let be the one containing and – containing . Then is the conjunction of rule bodies from , where each is prefixed by , plus, if , an IDB atom . Finally, set for . This will be also useful further.
We are now ready to define languages over that will be useful to study the data complexity of our queries. Let be the language of correct words such that , with , and be its complement. We need to define the language of expansions over the alphabet that we will use together with the language to formulate a criterion for L-hardness similar to the one of [15]. It would be natural to take the language of expansions as . However, it is harder to define an automaton recognising such a language than it is for the language of s as above where each horizontal letter may be extended (as a set) with arbitrary “redundant” rule bodies, and each horizontal segment may be extended, from the left and right, by “redundant” horizontal letters. For example, we will include into the language of expansions the word alongside (30). It turns out that the latter language works for our required criteria as good as the former one. Formally, if , we write if and , where are vertical segments and are horizontal segments, and if , , then there is such that and , . We define to be the set of correct words such that for some .
It is important for our purposes that these languages are regular. For , the rules of the program may be naturally seen as transition rules of a two-way automaton whose states are the IDBs of (plus a final state). The initial state is the one associated with , and the final state is reached by an application of an initialisation rule.
Lemma 10.
For any -query , the language is regular.
The case of is more involved. Generalising from [15], for an automaton to recognise if it suffices to guess (by nondeterminism) an enrichment of , and check that is a model of and that does not contain the atom . Moreover, since is connected, for to be a model it is enough that every piece of of radius , in terms of Gaifman graph, satisfies all the rules. The idea is to precompute the answer for each such piece and encode them in the state-space of the automaton. The problem, specific to the temporalised case, is that enrichments are infinite in the temporal dimension. To resolve this, we observe that there are still finitely many EDB atoms in . Since, once again, is connected, to check that rules with EDBs are satisfied it is enough to consider only those pieces of that contain an EDB atom. For the rest of the rules, it suffices to check if such a finite piece can be extended into an infinitely in time to give a model of . The rules without EDBs can be seen as plain LTL rules, so we can employ satisfiability checking for LTL to perform this check.
Lemma 11.
For any -query , the language is regular.
Corollary 12.
For any -query , the language is regular.
5 Decidability for Connected Linear Queries with
We use the automata introduced in the previous section to prove a positive result.
Theorem 13.
(i) Every connected query is either in , or in , or -complete, or L-hard. (ii) It is PSpace-complete to check whether such a query is L-hard; whether it belongs to , , or is -complete can be decided in ExpSpace.
We first deal with (i). Intuitively, L-hardness is a consequence of the growth of query expansions in the relational domain. If this growth is limited, the query essentially defines a certain temporal property, which can be checked in . Formally, given a word , we define the as the number of vertical letters in . Then, we call a query vertically unbounded if for every there is a word , , such that every prefix of of height is in . Otherwise, the query is called vertically bounded.
Vertically unbounded queries can be shown to be L-hard by a direct reduction from the undirected reachability problem. Namely, take the deterministic automata for and , supplied by Lemma 11 and Corollary 12, and apply the pumping lemma to obtain words such that , and , for all . Then, given a graph and two nodes , use copies of to simulate the edges of , and attach to and to . Thus, you will obtain a temporal database , where if and only if there is a path from to .
Lemma 14.
If a query is vertically unbounded, then it is L-hard.
Observe that whenever for some . If , then , the vertical and horizontal segments of , appear in , starting from at time . Expand to , the -maximal horizontal segment fitting in , and let . Then and . Thus, to check , it suffices to find vertical segments of some , taking -maximal horizontal segments, and check that . If is vertically bounded, there are finitely many vertical segments of interest. Finding vertical segments, as well as extracting -maximal horizontal ones, can be done by an circuit.
Lemma 15.
If is vertically bounded, then the data complexity of coincides with that of checking membership in , modulo reductions computable in .
Recall that is a regular language, so checking membership in it is either in , or , or -complete [40]. This settles the part (i) of Theorem 13: a query is either vertically unbounded and thus L-hard, or vertically bounded and thus belongs to one of the three classes mentioned above.
It remains to address the part (ii) of Theorem 13. By a careful analysis of the proof of Lemma 11 one can show that is recognised by a nondeterministic automaton of size . Further, checking whether its language belongs to , , or is -complete, can be done via the polynomial-space procedure developed in [31]. Thus, given a vertically bounded query, its data complexity can be established in exponential space.
For the vertical boundedness itself, note that substituting with in the respective definition preserves all the results proven so far. For , we can get from Lemma 10 an exponential-size one-way automaton. Checking that the query is vertically unbounded can be done in nondeterministic space logarithmic in the size of the automata for and , as it boils down to checking reachability in their Cartesian product.
Lemma 16.
Checking if a connected query is vertically bounded is in PSpace.
For the lower bound, we show that checking boundedness is already PSpace-hard for connected linear monadic queries in plain datalog. In fact, PSpace-hardness was proved in [15] for program boundedness of disconnected programs. A program is called bounded if is bounded for every IDB in . We were able to regain the connectedness of by focusing on query boundedness (also called predicate boundedness) instead. The idea combines that of [15] with that of Section 3: define an IDB that slides along a computation, this time of a space-bounded Turing machine, looking for an erroneous transition.
Lemma 17.
Deciding boundedness of connected linear monadic queries in plain datalog is PSpace-hard.
Lemmas 14 and 15 bring us to an interesting consideration: to understand the data complexity of a given query one should analyse its behaviour in the relational domain separately from that in the temporal domain. This can be given a precise sense as follows.
Proposition 18.
For every connected query there exist a plain datalog query and a plain LTL query , such that:
-
1.
is vertically bounded if and only if is bounded;
-
2.
if is vertically bounded then its data complexity coincides with that of .
Technically, both and are obtained by simulating the deterministic automaton for the language provided by Corollary 12. In both programs, the IDBs correspond to the states of and EDBs to the letters of . For these EDBs are unary and all the rules are horizontal, so that the expansions unwind fully in the temporal domain. In the case of , the EDBs are binary and every vertical transition of is a step by a binary relation, while the horizontal transitions are skipped (thus, vertical boundedness becomes just boundedness). In both programs, initialisation rules correspond to reaching an accepting state.
We conclude this section with a consideration on disconnected queries. In [15], deciding boundedness is based on the fact that remains regular even when has disconnected rules. This is not the case for , as can be seen from the following example.
Example 19.
Consider the program of four rules:
Let , , and . Then , and, consequently, , whenever . This property is not recognisable by any finite state automaton. For more general classes of automata suitable to recognise or in the disconnected setting, the properties that are to be checked along the lines of [15], such as language emptiness or finiteness, become undecidable. Therefore, disconnected queries possibly require a different approach for analysing the data complexity.
6 Conclusions and Future Work
We have started investigating the complexity of determining the data complexity of answering monadic datalog queries with temporal operators. For linear connected queries with operators /, we have generalised the automata-theoretic technique of [15], developed originally for plain datalog, to establish an classification of temporal query answering and proved that deciding L-hardness of a given query is PSpace-complete, while checking its membership in or can be done in ExpSpace. As a minor side product, we have established PSpace-hardness of deciding boundedness of atemporal connected linear monadic datalog queries. Rather surprisingly and in sharp contrast to the / case, it turns out that checking (non-trivial) membership of queries with operators / in the above complexity classes is undecidable. The results of this paper lead to a plethora of natural and intriguing open questions. Some of them are briefly discussed below.
-
1.
What happens if we disallow applications of to binary EDB predicates in -queries? We conjecture that this restriction makes checking membership in the above complexity classes decidable. In fact, this conjecture follows from a positive answer to the next question.
-
2.
Can our decidability results for be lifted to -queries? Dropping the linearity restriction in the atemporal case results in the extra data complexity class, P, and the higher complexity, 2ExpTime-completeness, of deciding boundedness. The upper bound was obtained using tree automata in [15], and we believe that this approach can be generalised to connected -queries in a way similar to what we have done above.
-
3.
On the other hand, dropping the connectedness restriction might turn out to be trickier, if at all possible, as shown by Example 19. Finding a new automata-theoretic characterisation for disconnected -queries remains a challenging open problem.
-
4.
A decisive step in understanding the data complexity of answering queries mediated by a description logic ontology and monadic disjunctive datalog queries was made in [9, 18] by establishing a close connection with constraint satisfaction problems (CSPs). In our case, quantified CSPs (see, e.g., [47]) seem to be more appropriate. Connecting the two areas might be beneficial to both of them.
- 5.
References
- [1] Rajeev Alur and Thomas A. Henzinger. Real-time logics: Complexity and expressiveness. Inf. Comput., 104(1):35–77, 1993. doi:10.1006/inco.1993.1025.
- [2] Peter Alvaro, William R. Marczak, Neil Conway, Joseph M. Hellerstein, David Maier, and Russell Sears. Dedalus: Datalog in time and space. In Oege de Moor, Georg Gottlob, Tim Furche, and Andrew Jon Sellers, editors, Datalog Reloaded - First International Workshop, Datalog 2010, Oxford, UK, March 16-19, 2010. Revised Selected Papers, volume 6702 of Lecture Notes in Computer Science, pages 262–281. Springer, 2010. doi:10.1007/978-3-642-24206-9_16.
- [3] Alessandro Artale, Diego Calvanese, Roman Kontchakov, and Michael Zakharyaschev. The dl-lite family and relations. J. Artif. Intell. Res., 36:1–69, 2009. doi:10.1613/jair.2820.
- [4] Alessandro Artale, Anton Gnatenko, Vladislav Ryzhikov, and Michael Zakharyaschev. On deciding the data complexity of answering linear monadic datalog queries with LTL operators (extended version), 2025. URL: https://arxiv.org/abs/2501.13762.
- [5] Alessandro Artale, Roman Kontchakov, Alisa Kovtunova, Vladislav Ryzhikov, Frank Wolter, and Michael Zakharyaschev. First-order rewritability of ontology-mediated queries in linear temporal logic. Artif. Intell., 299:103536, 2021. doi:10.1016/j.artint.2021.103536.
- [6] Alessandro Artale, Roman Kontchakov, Vladislav Ryzhikov, and Michael Zakharyaschev. The complexity of clausal fragments of LTL. In Kenneth L. McMillan, Aart Middeldorp, and Andrei Voronkov, editors, Logic for Programming, Artificial Intelligence, and Reasoning - 19th International Conference, LPAR-19, Stellenbosch, South Africa, December 14-19, 2013. Proceedings, volume 8312 of Lecture Notes in Computer Science, pages 35–52. Springer, 2013. doi:10.1007/978-3-642-45221-5_3.
- [7] Alessandro Artale, Roman Kontchakov, Vladislav Ryzhikov, and Michael Zakharyaschev. A cookbook for temporal conceptual data modelling with description logics. ACM Trans. Comput. Log., 15(3):25:1–25:50, 2014. doi:10.1145/2629565.
- [8] Michael Benedikt, Balder ten Cate, Thomas Colcombet, and Michael Vanden Boom. The complexity of boundedness for guarded logics. In 30th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2015, Kyoto, Japan, July 6-10, 2015, pages 293–304. IEEE Computer Society, 2015. doi:10.1109/LICS.2015.36.
- [9] Meghyn Bienvenu, Balder ten Cate, Carsten Lutz, and Frank Wolter. Ontology-based data access: A study through disjunctive datalog, csp, and MMSNP. ACM Trans. Database Syst., 39(4):33:1–33:44, 2014. doi:10.1145/2661643.
- [10] Sebastian Brandt, Elem Güzel Kalayci, Vladislav Ryzhikov, Guohui Xiao, and Michael Zakharyaschev. Querying log data with metric temporal logic. J. Artif. Intell. Res., 62:829–877, 2018. doi:10.1613/jair.1.11229.
- [11] Diego Calvanese, Giuseppe De Giacomo, Domenico Lembo, Maurizio Lenzerini, and Riccardo Rosati. Tractable reasoning and efficient query answering in description logics: The DL-Lite family. J. Autom. Reason., 39(3):385–429, 2007. doi:10.1007/s10817-007-9078-x.
- [12] Jan Chomicki. Polynomial time query processing in temporal deductive databases. In Daniel J. Rosenkrantz and Yehoshua Sagiv, editors, Proceedings of the Ninth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, April 2-4, 1990, Nashville, Tennessee, USA, pages 379–391. ACM Press, 1990. doi:10.1145/298514.298589.
- [13] Jan Chomicki and Tomasz Imielinski. Temporal deductive databases and infinite objects. In Chris Edmondson-Yurkanan and Mihalis Yannakakis, editors, Proceedings of the Seventh ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, March 21-23, 1988, Austin, Texas, USA, pages 61–73. ACM, 1988. doi:10.1145/308386.308416.
- [14] Jan Chomicki, David Toman, and Michael H. Böhlen. Querying ATSQL databases with temporal logic. ACM Trans. Database Syst., 26(2):145–178, 2001. doi:10.1145/383891.383892.
- [15] Stavros S. Cosmadakis, Haim Gaifman, Paris C. Kanellakis, and Moshe Y. Vardi. Decidable optimization problems for database logic programs (preliminary report). In Janos Simon, editor, Proceedings of the 20th Annual ACM Symposium on Theory of Computing, May 2-4, 1988, Chicago, Illinois, USA, pages 477–490. ACM, 1988. doi:10.1145/62212.62259.
- [16] Evgeny Dantsin, Thomas Eiter, Georg Gottlob, and Andrei Voronkov. Complexity and expressive power of logic programming. ACM Comput. Surv., 33(3):374–425, 2001. doi:10.1145/502807.502810.
- [17] Stéphane Demri, Valentin Goranko, and Martin Lange. Temporal Logics in Computer Science: Finite-State Systems. Cambridge Tracts in Theoretical Computer Science. Cambridge University Press, 2016. doi:10.1017/CBO9781139236119.
- [18] Cristina Feier, Antti Kuusisto, and Carsten Lutz. Rewritability in monadic disjunctive datalog, mmsnp, and expressive description logics. Log. Methods Comput. Sci., 15(2), 2019. doi:10.23638/LMCS-15(2:15)2019.
- [19] Valeria Fionda and Giuseppe Pirrò. Characterizing evolutionary trends in temporal knowledge graphs with linear temporal logic. In Jingrui He, Themis Palpanas, Xiaohua Hu, Alfredo Cuzzocrea, Dejing Dou, Dominik Slezak, Wei Wang, Aleksandra Gruca, Jerry Chun-Wei Lin, and Rakesh Agrawal, editors, IEEE International Conference on Big Data, BigData 2023, Sorrento, Italy, December 15-18, 2023, pages 2907–2909. IEEE, 2023. doi:10.1109/BigData59044.2023.10386573.
- [20] International Organization for Standardization. Information technology — database languages — sql — part 2: Foundation (sql/foundation), 1999. URL: https://www.iso.org/standard/23532.html.
- [21] Nadime Francis, Alastair Green, Paolo Guagliardo, Leonid Libkin, Tobias Lindaaker, Victor Marsault, Stefan Plantikow, Mats Rydberg, Petra Selmer, and Andrés Taylor. Cypher: An evolving query language for property graphs. In Gautam Das, Christopher M. Jermaine, and Philip A. Bernstein, editors, Proceedings of the 2018 International Conference on Management of Data, SIGMOD Conference 2018, Houston, TX, USA, June 10-15, 2018, pages 1433–1445. ACM, 2018. doi:10.1145/3183713.3190657.
- [22] Víctor Gutiérrez-Basulto, Jean Christoph Jung, and Roman Kontchakov. Temporalized EL ontologies for accessing temporal data: Complexity of atomic queries. In Subbarao Kambhampati, editor, Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, IJCAI 2016, New York, NY, USA, 9-15 July 2016, pages 1102–1108. IJCAI/AAAI Press, 2016. URL: http://www.ijcai.org/Abstract/16/160.
- [23] Steve Harris and Andy Seaborne. Sparql 1.1 query language. https://www.w3.org/TR/sparql11-query/, 2013. W3C Recommendation, 21 March 2013. URL: https://www.w3.org/TR/sparql11-query/.
- [24] Gerd G. Hillebrand, Paris C. Kanellakis, Harry G. Mairson, and Moshe Y. Vardi. Undecidable boundedness problems for datalog programs. J. Log. Program., 25(2):163–190, 1995. doi:10.1016/0743-1066(95)00051-K.
- [25] Ismail Husein, Herman Mawengkang, Saib Suwilo, and Mardiningsih. Modeling the transmission of infectious disease in a dynamic network. Journal of Physics: Conference Series, 1255(1):012052, August 2019. URL: https://dx.doi.org/10.1088/1742-6596/1255/1/012052.
- [26] Neil Immerman. Descriptive complexity. Graduate texts in computer science. Springer, 1999. doi:10.1007/978-1-4612-0539-5.
- [27] Paris C. Kanellakis. Elements of relational database theory. In Jan van Leeuwen, editor, Handbook of Theoretical Computer Science, Volume B: Formal Models and Semantics, pages 1073–1156. Elsevier and MIT Press, 1990. doi:10.1016/b978-0-444-88074-1.50022-6.
- [28] Kevin Cullinane. Modeling dynamic transportation networks: Bin ran and david boyce springer 1996 isbn 3540611398. Journal of Transport Geography, 6(1):76–78, 1998. doi:10.1016/S0966-6923(98)90041-2.
- [29] Stanislav Kikot, Agi Kurucz, Vladimir V. Podolskii, and Michael Zakharyaschev. Deciding boundedness of monadic sirups. In Leonid Libkin, Reinhard Pichler, and Paolo Guagliardo, editors, PODS’21: Proceedings of the 40th ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems, Virtual Event, China, June 20-25, 2021, pages 370–387. ACM, 2021. doi:10.1145/3452021.3458332.
- [30] Ron Koymans. Specifying real-time properties with metric temporal logic. Real Time Syst., 2(4):255–299, 1990. doi:10.1007/BF01995674.
- [31] Agi Kurucz, Vladislav Ryzhikov, Yury Savateev, and Michael Zakharyaschev. Deciding fo-rewritability of regular languages and ontology-mediated queries in linear temporal logic. J. Artif. Intell. Res., 76:645–703, 2023. doi:10.1613/jair.1.14061.
- [32] Ling Liu and M. Tamer Özsu, editors. Encyclopedia of Database Systems, Second Edition. Springer, 2018. doi:10.1007/978-1-4614-8265-9.
- [33] Marvin L. Minsky. Computation: finite and infinite machines. Prentice-Hall, Inc., USA, 1967. URL: https://dl.acm.org/doi/book/10.5555/1095587.
- [34] Jeffrey F. Naughton. Data independent recursion in deductive databases. J. Comput. Syst. Sci., 38(2):259–289, 1989. doi:10.1016/0022-0000(89)90003-2.
- [35] Juan L. Reutter, Adrián Soto, and Domagoj Vrgoc. Recursion in SPARQL. Semantic Web, 12(5):711–740, 2021. doi:10.3233/SW-200401.
- [36] Vladislav Ryzhikov, Przemyslaw Andrzej Walega, and Michael Zakharyaschev. Data complexity and rewritability of ontology-mediated queries in metric temporal logic under the event-based semantics. In Sarit Kraus, editor, Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI 2019, Macao, China, August 10-16, 2019, pages 1851–1857. ijcai.org, 2019. doi:10.24963/ijcai.2019/256.
- [37] Benjamin Schäfer, Dirk Witthaut, Marc Timme, and Vito Latora. Dynamically induced cascading failures in power grids. Nature Communications, 9(1):1975, May 2018. doi:10.1038/s41467-018-04287-5.
- [38] Brian Skyrms and Robin Pemantle. A dynamic model of social network formation. Proceedings of the National Academy of Sciences, 97(16):9340–9346, 2000. arXiv:https://www.pnas.org/doi/pdf/10.1073/pnas.97.16.9340.
- [39] Richard T. Snodgrass, Ilsoo Ahn, Gad Ariav, Don S. Batory, James Clifford, Curtis E. Dyreson, Ramez Elmasri, Fabio Grandi, Christian S. Jensen, Wolfgang Käfer, Nick Kline, Krishna G. Kulkarni, T. Y. Cliff Leung, Nikos A. Lorentzos, John F. Roddick, Arie Segev, Michael D. Soo, and Suryanarayana M. Sripada. TSQL2 language specification. SIGMOD Rec., 23(1):65–86, 1994. doi:10.1145/181550.181562.
- [40] Howard Straubing. Finite Automata, Formal Logic, and Circuit Complexity. Birkhäuser, Boston, MA, 1994. URL: http://link.springer.com/10.1007/978-1-4612-0289-9.
- [41] David Toman. Point vs. interval-based query languages for temporal databases. In Richard Hull, editor, Proceedings of the Fifteenth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, June 3-5, 1996, Montreal, Canada, pages 58–67. ACM Press, 1996. doi:10.1145/237661.237676.
- [42] Valentina Urzua and Claudio Gutierrez. Linear recursion in G-CORE. In Aidan Hogan and Tova Milo, editors, Proceedings of the 13th Alberto Mendelzon International Workshop on Foundations of Data Management, Asunción, Paraguay, June 3-7, 2019, volume 2369 of CEUR Workshop Proceedings. CEUR-WS.org, 2019. URL: https://ceur-ws.org/Vol-2369/short07.pdf.
- [43] Ron van der Meyden. Predicate boundedness of linear monadic datalog is in PSPACE. Int. J. Found. Comput. Sci., 11(4):591–612, 2000. doi:10.1142/S0129054100000351.
- [44] Dingmin Wang, Pan Hu, Przemyslaw Andrzej Walega, and Bernardo Cuenca Grau. Meteor: Practical reasoning in datalog with metric temporal operators. In Thirty-Sixth AAAI Conference on Artificial Intelligence, AAAI 2022, Thirty-Fourth Conference on Innovative Applications of Artificial Intelligence, IAAI 2022, The Twelveth Symposium on Educational Advances in Artificial Intelligence, EAAI 2022 Virtual Event, February 22 - March 1, 2022, pages 5906–5913. AAAI Press, 2022. doi:10.1609/aaai.v36i5.20535.
- [45] Mincheng Wu, Chao Li, Zhangchong Shen, Shibo He, Lingling Tang, Jie Zheng, Yi Fang, Kehan Li, Yanggang Cheng, Zhiguo Shi, Guoping Sheng, Yu Liu, Jinxing Zhu, Xinjiang Ye, Jinlai Chen, Wenrong Chen, Lanjuan Li, Youxian Sun, and Jiming Chen. Use of temporal contact graphs to understand the evolution of covid-19 through contact tracing data. Communications Physics, 5(1):270, 2022. doi:10.1038/s42005-022-01045-4.
- [46] Mengkai Xu, Srinivasan Radhakrishnan, Sagar Kamarthi, and Xiaoning Jin. Resiliency of mutualistic supplier-manufacturer networks. Scientific Reports, 9, September 2019. doi:10.1038/s41598-019-49932-1.
- [47] Dmitriy Zhuk. vs pspace dichotomy for the quantified constraint satisfaction problem. In 65th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2024, Chicago, IL, USA, October 27-30, 2024, pages 560–572. IEEE, 2024. doi:10.1109/FOCS61266.2024.00043.