Restless Exploration and Token Dissemination in Vertex-Permuted Temporal Graphs
Abstract
In the temporal graph exploration problem, an agent wishes to visit all the vertices of a temporal graph, moving at most one edge in every time step. In restless exploration, the agent is required to move in every step, and cannot wait at a vertex. We study the problem of restless exploration in vertex-permuted graphs, which are a class of temporal graphs in which the topology of the graph stays the same in every time step. In other words, in a vertex permuted temporal graph, in every step , the graph is isomorphic to the same base graph . We give a precise characterization of graphs such that restless exploration is possible in every vertex-permuted graph with base graph . Our technique is based on an a characterization of networks in which there is an online distributed algorithm for restless token dissemination. Finally we describe some families of graphs in which restless exploration is always possible, and some in which it is not.
Keywords and phrases:
Temporal graphs, Vertex permuted graphs, Restless exploration, Periodic graphs, Token disseminationCopyright and License:
2012 ACM Subject Classification:
Theory of computation ; Theory of computation Dynamic graph algorithmsEditors:
Kitty Meeks and Christian ScheidelerSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
Many networks are now understood to be dynamic rather than static, with nodes and edges changing over time. This dynamic nature of networks applies to many real-world scenarios, such as communication networks, transportation networks, social networks, chemical reaction networks, and more. For instance, in wireless networks formed by mobile nodes, such as IoT devices, buses, satellites, or autonomous mobile robots, links are created or broken because of the mobility of nodes. In wireless sensor networks, where sensor nodes are resource-constrained, nodes turn off their batteries to conserve energy, once again causing edges (and nodes) to appear and disappear. In road networks, traffic changes impact the travel time of roads which in turn changes the weights of the links. The dynamic nature of such networks greatly increases the challenge of solving problems that are well-understood in the static setting.
Many models of dynamic networks [25] have been studied in the last two decades, which have been variously referred to as time-varying graphs [7, 16], fixed schedule dynamic networks [27], evolving graphs [15], and temporal graphs [20]. For our purposes, a temporal graph is defined as a sequence of graphs , where each is a static undirected graph, and all graphs in the sequence have the same vertex set , but possibly different edge sets. The number is called the lifetime of the temporal graph. A temporal walk is a time-respecting walk in a temporal graph, that is a sequence of time-vertex pairs such that for each , the edge is in the graph and [11]. An exploration schedule is a temporal walk that visits all vertices of the graph [11, 22]. A temporal graph is called explorable if it admits an exploration schedule starting at any vertex; it is unexplorable otherwise.
The process of exploration can be described as an agent, starting at a source vertex, and traveling at most one edge in the temporal graph in each time step, and visiting every vertex in the graph. The term “agent” is used to refer to a mobile agent or a process or a packet that travels through the graph.
The notion of restless exploration was introduced in [5]: in -restless exploration, the agent must leave a vertex within at most steps after arriving, that is, . In -restless exploration, the agent cannot wait at a vertex, and must leave in the step after it arrives. Such a restriction has also been studied in the context of communication networks and is motivated by constraints on buffer space. In particular, in hot-potato routing or deflection routing [4, 6, 14, 23], an intermediate node has to forward a packet to a neighboring node as soon as it receives it, and cannot store it in order to wait for the best link to become available.
The notion of restless exploration was introduced in [5]: in -restless exploration, the agent must leave a vertex within at most steps after arriving, that is, . In -restless exploration, the agent cannot wait at a vertex, and must leave in the step after it arrives. Such a restriction has also been studied in the context of communication networks and is motivated by constraints on buffer space. In particular, in hot-potato routing or deflection routing [4, 6, 14, 23], an intermediate node has to forward a packet to a neighboring node as soon as it receives it, and cannot store it in order to wait for the best link to become available.
In [22], it was shown that any temporal graph that is connected in every step, and has a lifetime of at least is explorable. However, not all such graphs are 1-restless explorable. For example, consider a 2-periodic temporal graph with 3 vertices ; in odd steps, the edge set is , and in even steps, the edge set is . Starting at vertex 1, in odd steps, due to the restless constraint, the agent must move from vertex 1 to vertex 2, and in even steps, it must move from vertex 2 to vertex 1, and vertex 3 is never visited. Bellito et al [5] showed that 1-restless explorability is NP-hard to determine in a 3-periodic temporal graph, while it can be determined in polynomial time in a 2-periodic graph.
In this paper, we study 1-restless exploration in a specific type of temporal graph, referred to as a Vertex Permuted Graph (VPG), introduced in [2]. A VPG is a temporal graph in which the structure of the graph remains fixed at each time step throughout the graph’s lifetime, though the vertices may assume different positions in the graph. For example, birds flying in formation are known to swap positions to share ’lift’ while maintaining the same structure of the formation. Similarly, elite cyclists who ride in pelotons, swap their positions after specific intervals to share the fatigue of being in front of the formation. In the context of sensor networks, different nodes may periodically assume the role of clusterhead, with the cluster having a star topology, in order to balance energy consumption across cluster members. All the above are examples of vertex-permuted graphs. While only ring topologies are studied in [2], we study VPGs with arbitrary connected topologies.
1.1 Our Contributions
We give a precise characterization of graphs such that every vertex-permuted graph with base graph is 1-restlessly explorable. If the base graph has more than one connected component, then clearly the vertex-permuted graph where the permutation remains the same in every step is not explorable. So it is necessary that the base graph is connected. We show that every vertex-permuted graph with base graph is 1-restlessly explorable if and only if does not have a so-called blocking set of size less than . Our result relies on a distributed restless algorithm for token dissemination that we prove is successful on any temporal graph based on a graph that does not have a blocking set. On the other hand, if the graph does have a blocking set, then there exists a vertex-permuted graph based on in which 1-restless token dissemination is impossible.
We then consider 1-restless explorability of specific families of graphs. We show that all VPGs with base graphs that are regular graphs and grids of even length are 1-restlessly explorable, while graphs containing a vertex of degree 1, and some bipartite graphs, including grids of odd length, are not 1-restlessly explorable.
1.2 Related Work
The exploration of temporal graphs, introduced by Michail and Spirakis [22], addresses the problem of designing temporal walks that visit all vertices of a dynamic graph. They established that any temporal graph with vertices that is connected in every step, can be explored in time steps, a bound later confirmed to be tight by Erlebach et al. [11]. Improved bounds have been given for specific graph classes, such as planar graphs, cycles, grids, and graphs with bounded treewidth [11]. Several studies have explored different facets of temporal graph exploration, including periodically varying graphs [16], parameterized and non-strict exploration problems [12, 13], delay-robust routing under unreliable connections [17], and exploration of temporal graphs with a certain structural property [9, 19].
Bellitto et al. [5] introduced the problem of k-restless exploration, where an agent cannot remain at any vertex for more than time steps. They characterized the complexity of determining if -restless exploration is possible in -periodic graphs; proving that it is solvable in polynomial time for but NP-hard for . The restless property has also been studied in the context of temporal reachability and path-finding problems [8, 26, 28], where the objective is to find time-respecting paths under bounded waiting times.
In the problem of -token dissemination, or -gossip, there are tokens initially present at some of the nodes of the network, and the problem is to disseminate the tokens to all nodes in the network. Token dissemination in dynamic networks was first proposed in [21], where a simple flooding algorithm was shown to work in steps, under the constraint that the network is always connected. Subsequent work has focused on upper and lower bounds on the number of rounds required for token dissemination for both deterministic and randomized algorithms, under different connectivity constraints, different adversarial models, and the ability/inability to combine tokens [3, 1, 18, 24, 10]. As far as we are aware, there is no prior work on token dissemination under restless constraints. We study token dissemination under restless constraints on vertex-permuted temporal graphs.
In the problem of -token dissemination, or -gossip, there are tokens initially present at some of the nodes of the network, and the problem is to disseminate the tokens to all nodes in the network. Token dissemination in dynamic networks was first proposed in [21], where a simple flooding algorithm was shown to work in steps, under the constraint that the network is always connected. Subsequent work has focused on upper and lower bounds on the number of rounds required for token dissemination for both deterministic and randomized algorithms, under different connectivity constraints, different adversarial models, and the ability/inability to combine tokens [3, 1, 18, 24, 10]. As far as we are aware, there is no prior work on token dissemination under restless constraints. In this paper, we show the connection between restless token dissemination and restless graph exploration in vertex-permuted temporal graphs.
In [2], the notion of vertex permutation dynamism was introduced, and the authors gave an algorithm for dispersion of mobile agents in vertex-permuted rings. Vertex-permuted graphs of other topologies were not studied. We study restless exploration in vertex-permuted graphs of arbitrary topologies.
1.3 Organization of the paper
In Section 2, we describe the notation we use and give some preliminary definitions. Section 3 contains our main result: a characterization of vertex permuted graphs that are restlessly explorable. In Section 4, we use the characterization to determine the explorability of vertex-permuted graphs based on many well-known classes of graphs. We discuss future directions in Section 5.
2 Preliminaries and Definitions
For our purposes, a temporal graph is a sequence of graphs , where each is a static undirected graph, and all have the same vertex set , but possibly different edge sets. The number is called the lifetime of the temporal graph. Each graph corresponds to the state of the temporal graph at time step , with an edge representing a connection between two vertices that is available at time . The sequence of graphs models the evolution of a network over time [11]. A temporal graph with lifetime is called periodic with a fixed period if for every .
Given a temporal graph , with , a temporal walk in the graph is an alternating sequence of time-vertex pairs such that for each , the edge is in the graph and [11]. In this paper, we only consider strict temporal walks, in which at most one edge can be traversed in a time step. A temporal walk is -restless if for every , we have . In this paper, we focus exclusively on 1-restless walks, that is, , and in the sequel, we use restless to mean -restless.
Given a source vertex , an exploration schedule is a temporal walk that starts with and visits every vertex in the graph. Note that a vertex may be visited more than once. A restless exploration schedule is a restless temporal walk that visits every vertex in the graph. We say a graph is restlessly explorable if there exists a restless exploration schedule starting from every vertex in the graph.
Vertex-Permuted Graphs (VPGs) are a class of temporal graphs where the vertices are permuted at each time step, but the underlying structure of the graph remains unchanged. Formally:
Definition 1 (Vertex Permuted Graph).
Given a graph and a permutation sequence where each is a permutation of , the vertex permuted graph is a temporal graph in which , where , that is, for all , the graph is isomorphic to graph where the isomorphism is defined by the permutation . The graph is called the base graph of ; we also say that is based on .
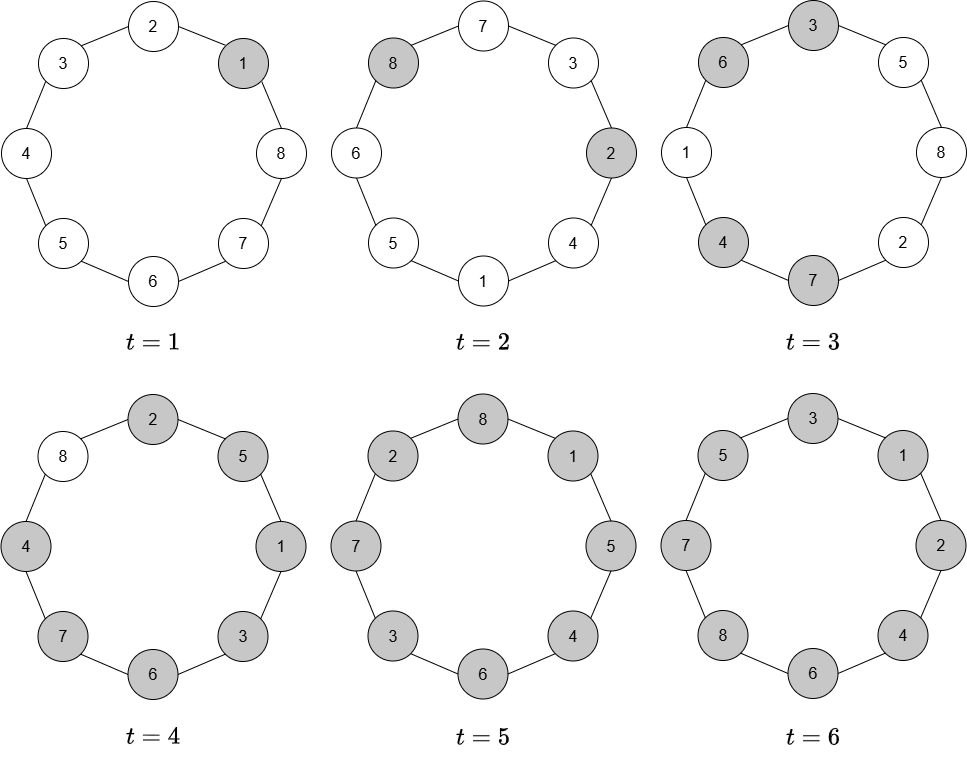
A Vertex Permuted Cycle (VPC) with vertices is a vertex permuted graph whose base graph is . Figure 1 illustrates six consecutive time steps of a VPC. Observe that in contrast to the model of a temporal cycle in which a different edge may be unavailable in each step, but all other connections between nodes remain the same [11], in a VPC, the connections between nodes can vary arbitrarily, while still maintaining a cycle topology.
In this paper, we study the restless explorability of vertex-permuted graphs. As already mentioned, we restrict ourselves to base graphs that are connected. We first describe an online and distributed token dissemination procedure, and then introduce the concepts of tokenizable and untokenizable graphs.
Restless Token Dissemination Procedure
Given a VPG with vertices, and a starting node , the token dissemination procedure proceeds as follows:
-
At time step , the starting vertex is assigned a token (henceforth, a vertex with a token is referred to as a token holder).
-
For every , any vertex that has the token sends it to all its neighbors (it does not keep the token). In other words, a vertex becomes a token holder at time if it is adjacent to at least one token holder at time step .
Observe that the above token dissemination procedure is simply a flooding algorithm under the restless constraint, unlike the -token dissemination algorithms in [21], in which a vertex repeatedly broadcasts the token, once it receives it. It is online in the sense that a vertex has no knowledge of future graphs in the sequence in order to determine the action at time step . Note also that a vertex can both send and receive tokens in the same time step, in which case it remains a token-holder in the following time step. To illustrate, consider our token dissemination procedure applied to the VPC in Figure 1. The propagation of tokens in every time step is shown in Figure 1. Starting from vertex , tokens propagate based on the adjacency of token holders at each time step. As the vertices permute at each step, tokens continue to spread across the graph. At time step , vertices and become token holders, as they were the neighbors of vertex in time step 1, which was the only token holder at that time. At time step , vertices , , , and become token holders, as they were neighbors of the holders in time step . By continuing this process, all vertices become token holders by time step .
For the token dissemination procedure initiated at time step from the starting vertex in the graph , we use the following notations throughout this paper:
-
refers to the set of token holders at time step .
-
denotes the number of token-holders at time step , that is,
. -
is the set of all vertices in that have held a token at at some time step with , that is, .
For example, for the token dissemination procedure shown in Figure 1, we have , and . Also for every vertex permuted graph , and any start vertex , we have and .
We now present the definition of a tokenizable graph.
Definition 2 (Tokenizable graph).
A graph with vertices is called tokenizable if, for every starting vertex and every permutation sequence , we have . Furthermore, if is tokenizable and there exists a starting vertex and a permutation sequence such that , then is partially tokenizable; otherwise, it is fully tokenizable.
A graph is called untokenizable, if it is not tokenizable. Formally:
Definition 3 (Untokenizable graph).
A graph is called untokenizable if there exists a series of permutations and a start vertex such that .
We will show later that it is enough to restrict to the first graphs in : if there exists a vertex that does not receive the token before time , then it can never receive the token in . Figure 1 showed a VPC with 8 vertices in which all vertices become token holders at time step 5 and will remain token holders afterwards. However, as shown in Figure 2, there exist VPCs with 8 vertices such that there is no time step in which all vertices simultaneously hold a token, even though every vertex has received a token at or before time step 4. Furthermore, the permutation sequence for this VPC is 2-periodic. This shows that a cycle of 8 vertices is not fully tokenizable. We will show in the upcoming section that all cycles are either fully or partially tokenizable.
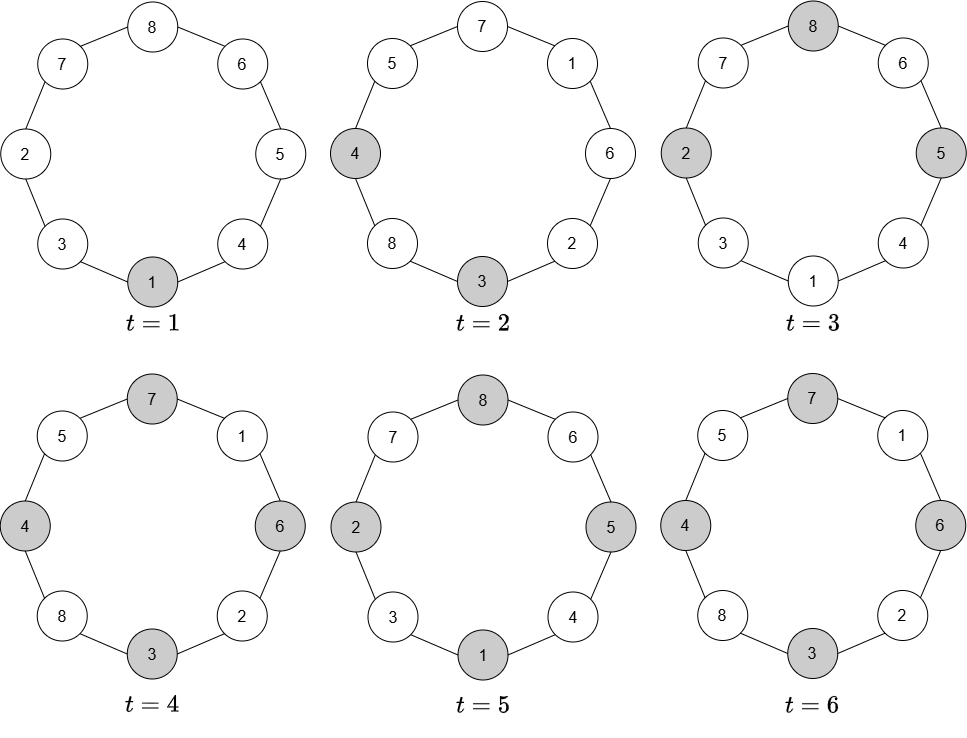
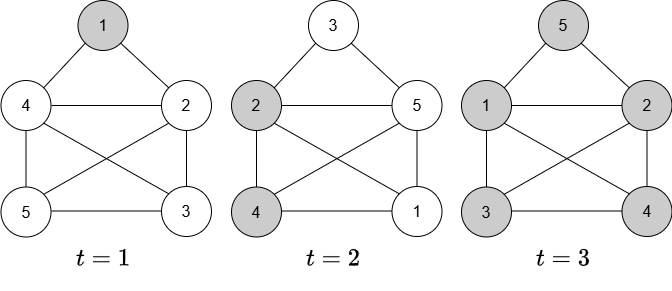
Figure 3 gives an example of a VPG and the token dissemination procedure starting at vertex 1. We will show in Theorem 12 that the base graph shown in Figure 3 is fully tokenizable; that is, under all permutation sequences and all possible start vertices, there will always be 5 token holders after at most 5 steps.
Note that if a graph is disconnected, then it is untokenizable, as under the identity permutation sequence, tokens cannot be sent between two different connected components in the VPG . In Figure 4, we present an example of a vertex-permuted graph based on an untokenizable graph . When starting the token dissemination procedure from vertex 5, vertex will never become a token holder under the given permutation sequence. Notably, the sequence shown is 2-periodic, and satisfies and , and even if this pattern continues indefinitely, node will remain without a token.
.drawio.png)
For any subset , let denote the set of neighbors of vertices in .
Definition 4 (Blocking Set (BS) and Minimum Blocking Set (MBS)).
Given a graph , a blocking set (BS) of is an independent set of vertices such that . Furthermore, if is the smallest such set, then it is called a minimum blocking set (MBS) of .
Note that for a graph with vertices, any blocking set can be of size at most . In Figure 5, the graph in part (b) contains 4 blocking sets: , , , and . Among these, the minimum blocking set is . In contrast, in part (a) the graph has three blocking sets , , , all of which are MBS .
.drawio%20(1).png)
3 Restless explorability in vertex permuted graphs
This section addresses the restless explorability problem in vertex-permuted graphs. We investigate the connection between tokenizability and the existence of a blocking set and provide a characterization of the structure of graphs that can be explored under restless constraints and vertex permutations.
3.1 A characterization of tokenizable graphs
In this subsection, we give a structural characterization of tokenizable graphs by showing the relationship of tokenizability to the existence of a blocking set. First, we establish several lemmas that will support the proofs of the main results. Recall that is the set of neighbors of vertices in for any .
.png)
Lemma 5.
If a connected graph contains a subset that is an independent set such that , then there exists a blocking set with .
Proof.
If , then the lemma follows trivially, since is the blocking set. If , we prove the claim by giving a simple iterative procedure to find such a subset.
While , remove an arbitrary vertex from and update . At each step, the size of decreases by 1, while the size of does not increase. Since is connected, is never empty, ensuring that the process terminates with , where is the required blocking set. This concludes the proof.
Figure 6 illustrates an example of this procedure: is an independent set with 5 vertices, and is set of neighbors of vertices in . Since , we start by removing vertex from , which causes the removal of vertices and from . The updated sets are and . In the next step, we remove vertex from but remains unchanged since and have other neighbors in . Similarly, removing vertex does not alter . At this point, the process terminates with , forming a blocking set. Note that selecting different vertices during the steps may lead to different blocking sets.
Lemma 6.
Suppose for a connected graph there exists a sequence of permutations , a start vertex , and some time step such that . Then at time , there exists a non-empty independent set of token holders such that .
Proof.
Let . Denote as and let . So the set of vertices that are holders as well as neighbors of holders is . Denote and to be the set of neighbors of vertices in , that is . See Figure 7 for an illustration.

Observe that is an independent set. We claim that is not empty. If instead, every vertex in is also a neighbor of a vertex in , all these vertices will also be token holders in time step . Since the graph is connected, and since , at least one more vertex will also be token holder at time , implying that , a contradiction. This proves the claim.
Next, consider , the set of neighbors of . Observe that is not empty, if so, would be disconnected from the rest of the graph. Also clearly . We claim that . Suppose instead that . Consider the token holders at time . Every node (if any) in will be a token holder at time . Also all nodes in will be token holders at time . Therefore
a contradiction to .
Therefore as claimed.
In the token dissemination procedure for any VPG based on , unless there is a blocking set in , the number of vertices that have received a token increase in every time step until the number of token holders is . Lemma 7 formalizes this observation.
Lemma 7.
Suppose for a connected graph there exists a sequence of permutations , a start vertex , and some time step such that . Then has a blocking set . Moreover .
Proof.
Lemma 8.
If a connected graph doesn’t have a BS, then it is fully tokenizable.
Proof.
From Lemma 7, we can deduce that if the graph does not have a blocking set, then the number of token holders keeps increasing in every time step until it equals . So is fully tokenizable.
An important observation in the token dissemination procedure for a graph with a MBS is as follows: the number of token holders continues to increase in every step until it reaches ; after this time step, the number of token holders will remain at least in all subsequent time steps. This behavior is formalized and proven in the following lemma.
Lemma 9.
Suppose a connected graph has a MBS of size , then for every sequence of permutations , and start vertex and time step , if then . Moreover, if for some time step , then .
Proof.
For the first part, suppose as a contradictory assumption that there exists some , , and such that, , then from Lemma 7, there must exist a blocking set such that , which contradicts the assumption that the size of the minimum blocking set is . Therefore, for every , if , it follows that .
For the second part, suppose and . Once again, by Lemma 7, this would imply the existence of an MBS such that , which contradicts the assumption that the size of the MBS is .
Building on the lemmas and observations established so far, we now present a characterization of untokenizable, partially tokenizable, and fully tokenizable graphs. The following theorems precisely describe the conditions under which a graph is untokenizable or partially tokenizable based on the properties of its MBS.
Theorem 10.
A connected graph G with vertices is untokenizable if and only if it contains a blocking set such that .
Proof.
First we prove that if there is a MBS such that , then is untokenizable. Let , and let . We describe a sequence of permutations and a start vertex such that vertices in will never hold a token in . Since is a MBS of and , we have and . Wlog let , , and . Our temporal graph will be a -periodic graph such that in the odd time steps, we have the original graph and in the even steps we use the following permutation:
With this permutation , observe that the subgraph induced by is not connected to in odd steps, and is not connected to vertices in in even steps. To prevent from ever obtaining a token, it is sufficient to start the token procedure at some vertex in . Then in time step , a subset of the vertices in will hold the token, and none of the vertices in have the token. Since the subgraph induced by is not connected to any vertex in in time step 2, there is no way for the vertices in to become token holders in the following step. Inductively, it is straightforward to see that for odd and for even . This ensures that none of the vertices in will ever hold a token, making the graph untokenizable.
Next we prove the other direction. Suppose that with vertices is untokenizable. This means there exists an initial vertex and a sequence of permutations such that . This implies that the maximum number of token holders at any step must be some , and hence, there must exist some time step in which and . By Lemma 6, at time , there there exists a non-empty independent set of token holders such that .
Furthermore, since is untokenizable, and therefore . By Lemma 5, has a blocking set of size as desired.
Theorem 11.
A connected graph G with vertices is partially tokenizable if and only if it contains a MBS such that .
Proof.
First, we will prove that if there exists a MBS with , then the graph is partially tokenizable. Since , the graph is tokenizable by Theorem 10.
Now, let be the MBS , wlog let . Our temporal graph will be a -periodic graph; in odd steps, we have the original graph , and in even steps, we use the permutation . Let be the number of tokens in step . By Lemma 9, keeps increasing until for some time step we have . After this step, all vertices in the set are holders in odd steps, and all remaining vertices are holders in even steps and NoT. This proves that is partially tokenizable.
Conversely, suppose for graph , there does not exist an MBS with . Then either does not have a blocking set at all, or it has an MBS of size (since any blocking set has to be of size ). In the first case, by Theorem 8, is fully tokenizable, and in the second case, by Theorem 10, it is untokenizable.
Theorem 12.
A connected graph with vertices is fully tokenizable if and only if does not contain any BS.
Proof.
If does not contain any BS, then by Lemma 8, is fully tokenizable. For the converse, assume for the purpose of contradiction that is fully tokenizable, and that contains a BS. Let be a MBS of . Then either or .
In both cases, is not fully tokenizable, a contradiction to the assumption. Therefore, does not contain a .
3.2 Restless token dissemination
In this section, we present a straightforward consequence of our characterization of tokenizable graphs.
Theorem 13.
There is a distributed algorithm for restless token dissemination in every vertex permuted graph based on a connected graph in steps, if and only if has no MBS of size .
Proof.
Suppose has no MBS of size . Then Theorems 12 and 11 imply that under any permutation sequence , and from any start vertex, the token dissemination procedure will ensure that all vertices in become token holders in steps, ensuring restless token dissemination in . Conversely, suppose there is a distributed algorithm for token dissemination in every vertex-permuted graph based on . Fix a vertex-permuted graph based on , and suppose there exists a schedule for restless token dissemination in . It must be a subset of the schedule implied by our token dissemination procedure, in which every vertex sends the token to all its neighbors in the step immediately after it receives it. Therefore our token dissemination procedure will also ensure that tokens are restlessly disseminated to all vertices in . Since this is true for every based on , it follows that is tokenizable, and by Theorem 10, has no MBS of size .
We note that if has an MBS of size exactly , there are VPGs based on , in which the token will never be held simultaneously by all nodes in the restless setting, whereas if has no blocking set, then for every VPG based on , the token dissemination procedure described in Section 3.1 results in every node simultaneously holding the token.
3.3 Restless exploration
Next, we outline the relationship between tokenizability of a graph and explorability of vertex-permuted graphs based on .
Theorem 14.
A connected graph is tokenizable if and only if every temporal graph with base graph and lifetime is restless explorable, where .
Proof.
Suppose is tokenizable. Let be an arbitrary VPG based on the graph , and of lifetime . By the definition of tokenizability, for every , . That is, for any vertex , we have . This implies that there exists a restless temporal walk from to in at most time steps. Using the standard technique of concatenating temporal walks between pairs of vertices into an exploration schedule, it follows that there is a restless exploration schedule of length at most in starting at any vertex .
Conversely, suppose is untokenizable. Then by Theorem 10, has an MBS of size . Similarly to the proof of Theorem 10, we define a 2-periodic VPG (of infinite lifetime) based on , in which for odd , and in even time steps, the vertices in change places with the vertices in . Let be an arbitrary vertex in and let be an arbitrary vertex in . Since , there exists at least one such . It is clear that there is no temporal walk (of any length) from to in this graph. Therefore is unexplorable.
We note that the exploration schedule mentioned above can be constructed in an offline and centralized manner, and is not necessarily an optimal schedule; we only claim that a schedule of length at most exists.
4 Restless explorability of some graph families
In this section, we study the explorability of some specific families of graphs. Observe that cliques are clearly restlessly explorable: a vertex-permuted clique is actually a static graph, since in every step, the graph is the same: every vertex is connected to every other vertex.
Theorem 15.
Every VPG whose base graph is a connected regular graph is restlessly explorable.
Proof.
Assume for the purpose of contradiction that there exists an unexplorable VPG with base graph a -regular graph . By Theorem 14 and 10, we conclude that contains a MBS such that . Note that and since , there is at least one vertex, say , in .
Let be the set of edges incident on . Since is -regular, we have . Since the edges in are also incident on , we conclude that the only neighbors of are vertices in . However, this means the subgraph induced by is not connected to , a contradiction to being connected. Thus, must be explorable.
The following corollary is immediate.
Corollary 16.
Every VPG whose base graph is a cycle, -dimensional torus, or a connected regular bipartite graph, is restlessly explorable.
We note that cycles and tori with odd numbers of vertices are fully tokenizable, while those with an even number of vertices are partially tokenizable.
Next, we consider some base graphs that are not regular.
Theorem 17.
Let be a vertex-permuted grid with vertices where is even. Then is restlessly explorable.
Proof.
Assume without loss of generality that the base grid has columns where is even. We show that has no blocking set with vertices by showing that for any independent set with . In particular, we show that there is a matching of size between and and show that there is at least one element of that is unmatched.
Consider an independent set with , and denote the subset of elements of in the row by . Clearly, since is an independent set and the row has an even number of vertices, there is always a matching between and the elements of in row . Since , there must be a row such that . First, suppose there exists a row that has no elements from at all; in this case, we take a row such that , and it is adjacent to a row with . Such a row must exist, and clearly, there is at least one neighbor of a vertex in in the row that is not matched, and we are done. Therefore in what remains, we assume that every row has at least one element of , and we consider a row such that .
Let denote the 0-1 string representing the vertices in row , where the -th symbol is 1 if the -th vertex is in and otherwise. Note that the number of 0’s in must be at least two more than the number of 1’s, since . We first consider the following three cases:
- has a prefix in
-
: in this case, for each pair (01) in the prefix, we match the corresponding vertices to each other, and find an arbitrary matching in the corresponding suffix (which must have at least as many 0s as 1s). Let be the vertex corresponding to the second-last symbol of the prefix. Then and is unmatched.
- has a suffix in :
-
We match each pair as in the previous case, and let be the vertex corresponding to the second symbol in the suffix; we note that is unmatched.
- has a substring in :
-
The argument is identical to the previous case; the vertex corresponding to the second symbol in the substring is in and is unmatched.
Thus in all the above cases, we have the required matching and unmatched element of as needed. It remains to consider the situation when for every row with , none of the three conditions listed above is satisfied. Let be such a row and the corresponding string. Since does not have a prefix in , it either starts with 00 or starts with 1. If it starts with 1, it must be either of the form (Type A) or of the form (Type B), since it does not satisfy the second and third conditions. If instead it starts with 00, it must be of the form (Type C). For any of these types, we match the vertices corresponding to each (01) pair. We now identify an unmatched vertex for each type. Let be a row adjacent to .
- Type A.
-
: If or if is of types A, B, or C, then must end with or start with a 1, which implies that two elements of are adjacent, a contradiction.
- Type B.
-
: Then as in the previous case, it cannot be that is of Type A or B. So must be of type , or and . Let be the last vertex in row ; it is adjacent to the last vertex in row which is in ; note that is unmatched.
- Type C.
-
: Symmetric to the previous case, must be of type B, or and . Then let be the first vertex in row ; it is adjacent to the first vertex in row , which is in ; note that is unmatched.
The above analysis is exhaustive: we showed that if , there exists a matching of size between and and a vertex that is unmatched. That is, , which implies that is not a blocking set. Therefore, by Theorems 10 and 14, is restlessly explorable.
Finally, we present some examples of untokenizable graphs. Recall that for an untokenizable graph , there may be some VPGs with base graph that are explorable, and others that are not explorable; see for example Figure 8 part (b).
Theorem 18.
Any connected graph with that contains a vertex of degree is untokenizable. Therefore, there exist VPGs based on that are not restlessly explorable.
Proof.
Let be the vertex with degree , and let be its only neighbor. Since has no other connections, it forms an independent set of size , with . This implies that constitutes a MBS of size , satisfying . By Theorem 10, is untokenizable, and by Theorem 14, there exist VPGs based on that are not restlessly explorable.
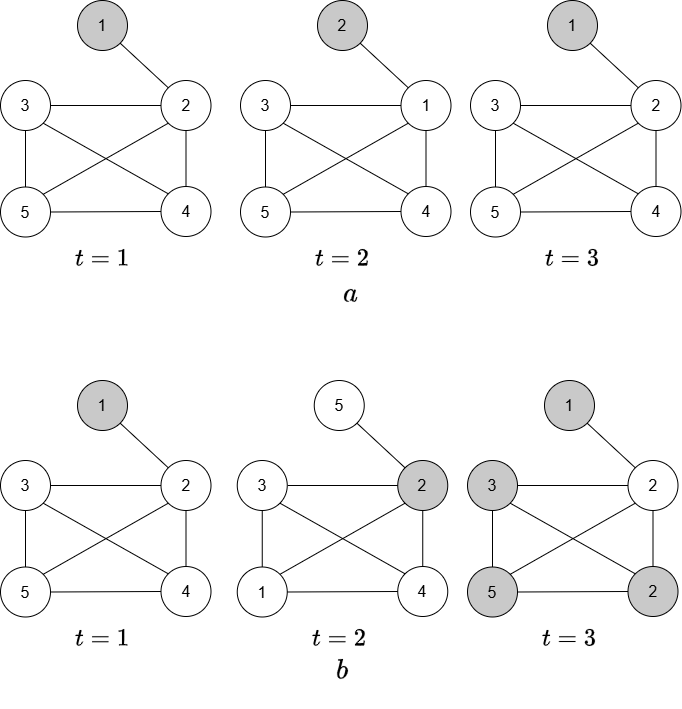
Corollary 19.
There exist VPGs with base graph a path or a star-graph that are not restlessly explorable.
Figure 8 illustrates two VPGs with the same base graph . Note that by Theorem 18, the base graph is untokenizable. In part (a), the first three time steps of a 2-periodic VPG based on are shown; in odd and even time steps the vertices 1 and 2 swap places. Consequently, for odd , and for even . For all , , and it is clear that restless token dissemination or exploration are not possible in this VPG. In contrast, in part (b), a different 2-periodic VPG based on the same base graph is shown, in which the token reaches all vertices in 3 time steps.
Theorem 20.
For every bipartite graph such that , there exist VPGs based on that are not restlessly explorable.
Proof.
Without loss of generality, assume . By Lemma 5, there exists a blocking set such that . Since , it follows that . By Theorem 10, is untokenizable, and by Theorem 14, there exist VPGs based on that are not restlessly explorable.
As a direct consequence of Theorem 20, we have the following:
Corollary 21.
For every grid with an odd number of vertices, there exists VPGs based on that are not restlessly explorable.
5 Open Problems
In this paper, we studied restless exploration in vertex-permuted graphs, and showed that unless a graph has a blocking set of size , all vertex-permuted graphs with base graph are explorable. The complexity of determining whether such a blocking set exists in a given graph remains an open computational problem. While a graph may be untokenizable, it is possible that a specific VPG is still -restlessly explorable. The complexity of determining if a specific VPG is 1-restlessly explorable is an interesting open question. Extending our results to the -restless setting is another direction of research.
References
- [1] Sebastian Abshoff, Markus Benter, Andreas Cord-Landwehr, Manuel Malatyali, and Friedhelm Meyer auf der Heide. Token dissemination in geometric dynamic networks. In International Symposium on Algorithms and Experiments for Sensor Systems, Wireless Networks and Distributed Robotics, pages 22–34. Springer, 2013. doi:10.1007/978-3-642-45346-5_3.
- [2] Ankush Agarwalla, John Augustine, William K Moses Jr, Sankar K Madhav, and Arvind Krishna Sridhar. Deterministic dispersion of mobile robots in dynamic rings. In Proceedings of the 19th International Conference on Distributed Computing and Networking, pages 1–4, 2018. doi:10.1145/3154273.3154294.
- [3] Mohamad Ahmadi, Fabian Kuhn, Shay Kutten, Anisur Rahaman Molla, and Gopal Pandurangan. The communication cost of information spreading in dynamic networks. In IEEE 39th International Conference on Distributed Computing Systems (ICDCS), pages 368–378, 2019. doi:10.1109/ICDCS.2019.00044.
- [4] Amotz Bar-Noy, Prabhakar Raghavan, Baruch Schieber, and Hisao Tamaki. Fast deflection routing for packets and worms. In Proceedings of the Twelfth Annual ACM Symposium on Principles of Distributed Computing, pages 75–86, 1993.
- [5] Thomas Bellitto, Cyril Conchon-Kerjan, and Bruno Escoffier. Restless exploration of periodic temporal graphs. In 2nd Symposium on Algorithmic Foundations of Dynamic Networks (SAND 2023), pages 13:1–13:15, 2023. doi:10.4230/LIPICS.SAND.2023.13.
- [6] Costas Busch, Maurice Herlihy, and Rogert Wattenhofer. Routing without flow control. In Proceedings of the Thirteenth Annual ACM Symposium on Parallel Algorithms and Architectures, pages 11–20, 2001. doi:10.1145/378580.378582.
- [7] Arnaud Casteigts, Paola Flocchini, Walter Quattrociocchi, and Nicola Santoro. Time-varying graphs and dynamic networks. International Journal of Parallel, Emergent and Distributed Systems, pages 387–408, 2012. doi:10.1080/17445760.2012.668546.
- [8] Arnaud Casteigts, Anne-Sophie Himmel, Hendrik Molter, and Philipp Zschoche. Finding temporal paths under waiting time constraints. Algorithmica, pages 2754–2802, 2021. doi:10.1007/S00453-021-00831-W.
- [9] Konstantinos Dogeas, Thomas Erlebach, Frank Kammer, Johannes Meintrup, and William K Moses Jr. Exploiting automorphisms of temporal graphs for fast exploration and rendezvous. In 51st International Colloquium on Automata, Languages, and Programming, ICALP, pages 55:1–55:18, 2024. doi:10.4230/LIPICS.ICALP.2024.55.
- [10] Chinmoy Dutta, Gopal Pandurangan, Rajmohan Rajaraman, Zhifeng Sun, and Emanuele Viola. On the complexity of information spreading in dynamic networks. In Proceedings of the Twenty-Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, pages 717–736, 2013. doi:10.1137/1.9781611973105.52.
- [11] Thomas Erlebach, Michael Hoffmann, and Frank Kammer. On temporal graph exploration. Journal of Computer and System Sciences, 119:1–18, 2021. doi:10.1016/J.JCSS.2021.01.005.
- [12] Thomas Erlebach and Jakob T Spooner. Non-strict temporal exploration. In International Colloquium on Structural Information and Communication Complexity, pages 129–145, 2020. doi:10.1007/978-3-030-54921-3_8.
- [13] Thomas Erlebach and Jakob T Spooner. Parameterised temporal exploration problems. Journal of Computer and System Sciences, 135:73–88, 2023. doi:10.1016/J.JCSS.2023.01.003.
- [14] U. Feige and P. Raghavan. Exact analysis of hot-potato routing. In Proceedings, 33rd Annual Symposium on Foundations of Computer Science, pages 553–562, 1992.
- [15] Afonso Ferreira. Building a Reference Combinatorial Modelfor Dynamic Networks: Initial Results in Evolving Graphs. PhD thesis, INRIA, 2003.
- [16] Paola Flocchini, Bernard Mans, and Nicola Santoro. Exploration of periodically varying graphs. In Algorithms and Computation: 20th International Symposium, ISAAC 2009, pages 534–543, 2009. doi:10.1007/978-3-642-10631-6_55.
- [17] Eugen Füchsle, Hendrik Molter, Rolf Niedermeier, and Malte Renken. Delay robust routes in temporal graphs. In 39th International Symposium on Theoretical Aspects of Computer Science (STACS 2022), pages 30:1–30:15, 2022. doi:10.4230/LIPICS.STACS.2022.30.
- [18] Bernhard Haeupler. Analyzing network coding gossip made easy. In Proceedings of the Forty-Third Annual ACM Symposium on Theory of Computing, pages 293–302, 2011. doi:10.1145/1993636.1993676.
- [19] David Ilcinkas, Ralf Klasing, and Ahmed Mouhamadou Wade. Exploration of constantly connected dynamic graphs based on cactuses. In International Colloquium on Structural Information and Communication Complexity, pages 250–262. Springer, 2014. doi:10.1007/978-3-319-09620-9_20.
- [20] David Kempe, Jon Kleinberg, and Amit Kumar. Connectivity and inference problems for temporal networks. Journal of Computer and System Sciences, pages 820–842, 2002. doi:10.1006/JCSS.2002.1829.
- [21] Fabian Kuhn, Nancy Lynch, and Rotem Oshman. Distributed computation in dynamic networks. In Proceedings of the Forty-Second ACM Symposium on Theory of Computing, pages 513–522, 2010. doi:10.1145/1806689.1806760.
- [22] Othon Michail and Paul G Spirakis. Traveling salesman problems in temporal graphs. Theoretical Computer Science, 634:1–23, 2016. doi:10.1016/J.TCS.2016.04.006.
- [23] Thomas Moscibroda and Onur Mutlu. A case for bufferless routing in on-chip networks. In Proceedings of the 36th Annual International Symposium on Computer Architecture, pages 196–207, 2009. doi:10.1145/1555754.1555781.
- [24] Regina O’Dell and Rogert Wattenhofer. Information dissemination in highly dynamic graphs. In Proceedings of the 2005 Joint Workshop on Foundations of Mobile Computing, pages 104–110, 2005. doi:10.1145/1080810.1080828.
- [25] Christian Scheideler. Models and techniques for communication in dynamic networks. In Annual Symposium on Theoretical Aspects of Computer Science, pages 27–49, 2002. doi:10.1007/3-540-45841-7_2.
- [26] Suhas Thejaswi, Juho Lauri, and Aristides Gionis. Restless reachability problems in temporal graphs. Knowledge and Information Systems, pages 1–47, 2025.
- [27] B Bui Xuan, Afonso Ferreira, and Aubin Jarry. Computing shortest, fastest, and foremost journeys in dynamic networks. International Journal of Foundations of Computer Science, pages 267–285, 2003.
- [28] Philipp Zschoche. Restless Temporal Path Parameterized Above Lower Bounds. In 40th International Symposium on Theoretical Aspects of Computer Science (STACS 2023), pages 55:1–55:16, 2025.
