On Palindromic Periodicities

Fici, Gabriele; Shallit, Jeffrey; Simpson, Jamie

doi:10.4230/LIPIcs.CPM.2025.11

On Palindromic Periodicities

Gabriele Fici

Dipartimento di Matematica e Informatica, University of Palermo, Italy Jeffrey Shallit

School of Computer Science, University of Waterloo, Canada Jamie Simpson

130 Preston Point Rd, East Fremantle, WA 6158, Australia

Abstract

We say a finite word $x$ is a palindromic periodicity if there exist two palindromes $p$ and $s$ such that $|x|\geq|ps|$ and $x$ is a prefix of the infinite periodic word $(ps)^{\omega}=pspsps\cdots$ . In this paper we examine the palindromic periodicities occurring in some classical infinite words, such as Sturmian words, episturmian words, the Thue–Morse word, the period-doubling word, the Rudin–Shapiro word, the paperfolding word, and the Tribonacci word, and prove a number of results about them. We also prove results about words with the smallest number of distinct palindromic periodicities.

Keywords and phrases:

Combinatorics on words, Palindrome, Symmetric word, Palindromic periodicity, Walnut, Thue-Morse word, Sturmian word, Episturmian word

Funding:

Gabriele Fici: Project MUR PRIN 2022 APML – 20229BCXNW.

Jeffrey Shallit: Funded by NSERC under grants 2018-04118 and 2024-03725.

Copyright and License:

2012 ACM Subject Classification:

Mathematics of computing

\rightarrow

Combinatorics on words

DOI:

10.4230/LIPIcs.CPM.2025.11

Event:

36th Annual Symposium on Combinatorial Pattern Matching (CPM 2025)

Editors:

Paola Bonizzoni and Veli Mäkinen

Series and Publisher:

Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik

1 Introduction

Recently, the third author introduced the notion of palindromic periodicity [33]. A finite word $x$ is called a palindromic periodicity if there exist two palindromes $p$ and $s$ such that $|x|\geq|ps|$ and $x$ is a prefix of the word $(ps)^{\omega}=pspsps\cdots$ . He proved a number of interesting results about these words. As an example, $x=121344312134$ is a palindromic periodicity, as can be seen by taking $p=121$ , $s=3443$ . Note that in this example, $x$ itself is not the product of two palindromes. A shortest binary word that is not a palindromic periodicity is $x=001011$ (cf. [16]).

Words that are products of two palindromes were studied, for example, by Kemp [22], Brlek et al. [3], Guo et al. [20], and Borchert and Rampersad [2]. In particular, a word is a product of two palindromes if and only if it is symmetric, i.e., a conjugate (cyclic shift) of its reverse. Note that if a word is symmetric, all its conjugates are symmetric too.

Particular cases of symmetric words are the words that have a perfectly clustered Burrows–Wheeler transform – this was proved independently by the third author with Simon Puglisi [34] and by Restivo and Rosone [29]. As a consequence, every word that has a perfectly clustered Burrows–Wheeler transform is a palindromic periodicity. Recall that the Burrows–Wheeler transform of a word $w$ is the word $\operatorname{BWT}(w)$ obtained by concatenating the last letters of the conjugates of $w$ sorted in ascending lexicographic order. A word $w$ over the ordered alphabet $\Sigma=\{0,1,\ldots,k-1\}$ is said to have perfectly clustered Burrows–Wheeler transform if $\operatorname{BWT}(w)$ belongs to $(k-1)^{*}\cdots 1^{*}0^{*}$ . A combinatorial characterization of words with perfectly clustered Burrows–Wheeler transform has been recently found by Lapointe and Reutenauer [23].

In this note we prove a number of new results about the concept of palindromic periodicity. We first observe that being a palindromic periodicity is equivalent to having a symmetric word-period. In particular, the class of words whose fractional root (shortest word-period) is symmetric is a subclass of the class of palindromic periodicities. As we prove in this paper, in this sublcass we have all finite factors of Sturmian words and, more generally, all trapezoidal (or stiff) words, that are words with at most $n+1$ distinct factors of length $n$ for any $n$ – notice that by definition trapezoidal words are binary words – and also all prefixes (but not all factors) of standard episturmian words. All these words are therefore palindromic periodicities.

Then, using the free software tool Walnut [28, 31], we examine the palindromic periodicities occurring in certain classic generalized automatic words, such as the Thue–Morse word, Rudin–Shapiro word, period-doubling word, paperfolding word, and Tribonacci word.

Finally, we give some results on words with the smallest number of distinct palindromic periodicities, proving bounds in the binary case and in the case of alphabets of size at least $3$ . All the bounds are optimal, and we provide examples realizing them.

2 Preliminaries

A contiguous block in a word $w$ is called a factor of $w$ . It is a prefix of $w$ if it occurs at the beginning of $w$ , and a suffix of $w$ if it occurs at the end of $w$ . We say that a nonempty word $z$ is a word-period of a word $w$ if $w$ is a prefix of $z^{\omega}=zzz\cdots$ . The shortest word-period of a word is called its fractional root and is denoted $z_{w}$ . For example, ent and entent are word-periods of the French word entente and the former is also its fractional root. The length of a word-period of a word $w$ is called a period of $w$ . We call the length of the fractional root of $w$ the period of $w$ . A word $v$ is a border of a word $w$ if $v$ is both a prefix and a suffix of $w$ . A word $w$ is unbordered if it does not have non-trivial borders (i.e., its only borders are the empty word $\varepsilon$ and the word $w$ itself). A word is unbordered if and only if it coincides with its fractional root. The reverse of a finite word $w$ is denoted $w^{R}$ . If $w=w^{R}$ , then $w$ is a palindrome. Two words $w$ and $w^{\prime}$ are conjugates if one is a cyclic shift of the other, i.e., there exist words $u$ and $v$ such that $w=uv$ and $w^{\prime}=vu$ . A word of length $n>0$ is primitive if it has $n$ distinct conjugates. A word is called symmetric if it is a conjugate of its reverse; or, equivalently, if it is the product of two palindromes [3]. A palindrome is a particular case of a symmetric word, in which one of the two palindromes is the empty word.

Note that every symmetric word is a palindromic periodicity. Actually, it follows from the definition that a word $w$ is a palindromic periodicity if and only if $w$ has a symmetric word-period. In particular, if the fractional root of $w$ is symmetric, then $w$ is a palindromic periodicity. However, $0100110$ is a palindromic periodicity (since it is symmetric), yet its fractional root $010011$ is not symmetric, so the converse does not hold in general.

$\blacktriangleright$ Remark 1.

A word $w$ is symmetric if and only if $w^{n}$ is symmetric for any integer $n>1$ . Indeed, if $w=uv$ , with $u, v$ palindromes, then $w^{n}=(uv)^{n-1}uv$ , and $(uv)^{n-1}u$ is a palindrome.

An analogous property does not hold for palindromic periodicities. For example, $w=010110$ is a palindromic periodicity, but $w^{2}=010110010110$ is not.

By the previous remark, we can suppose that the symmetric word-period of a nonempty palindromic periodicity is primitive. Since a word $w$ cannot have two distinct primitive word-periods both shorter than half the length of $w$ (as a consequence of the Fine and Wilf theorem [17]), it follows that if the fractional root of a palindromic periodicity $w$ is not symmetric, then $w$ has a symmetric word-period that is longer than half the length of $w$ .

3 Results for certain classes of words

In this section, we prove that for certain classes of words the fractional root is always symmetric. As we saw in the previous section, this implies in particular that these words are palindromic periodicities.

3.1 Sturmian and trapezoidal words

Recall that an infinite binary word is called Sturmian if it has exactly $n+1$ distinct factors of length $n$ , for all $n\geq 0$ . An example of Sturmian word is the Fibonacci word $f=0100101001001\cdots$ , fixed point of the morphism $0\rightarrow 01$ , $1\rightarrow 0$ . A finite binary word is called Sturmian if it is a factor of an infinite Sturmian word. A finite Sturmian word $u$ is a central word if $0u0$ , $0u1$ , $1u0$ and $1u1$ are all Sturmian words. A finite Sturmian word is standard if it is of the form $u01$ or $u10$ , where $u$ is a central word. In particular, the words $u01$ and $u10$ are conjugates [26] and therefore a standard word is a conjugate of its reverse, i.e., it is symmetric. de Luca and De Luca proved that a finite word is Sturmian if and only if its fractional root is a conjugate of a standard Sturmian word [25]. Thus, every finite Sturmian word has a symmetric fractional root. As a consequence, we have the following result, which was originally conjectured by the second author.

Theorem 2.

Every nonempty factor of a Sturmian word is a palindromic periodicity.

Notice that not every palindromic periodicity is a factor of a Sturmian word, with $0011$ being a smallest example.

A finite word is trapezoidal [27] (or stiff [21]) if it has at most $n+1$ distinct factors of length $n$ for every $n$ . Trapezoidal words are binary words by definition. All finite Sturmian words are trapezoidal, but there are trapezoidal words that are not Sturmian (e.g., $0011$ ).

A binary word $w$ is not Sturmian if and only if there exists a word $u$ such that both $0u0$ and $1u1$ are factors of $w$ [8]. The pair $(0u0,1u1)$ is called a pathological pair. Moreover, it is possible to prove that the word $u$ in a pathological pair of minimal length is a central word [6]. The structure of non-Sturmian trapezoidal words was described by D’Alessandro in [9]: Let $w$ be a binary word that is not Sturmian. Then $w$ is trapezoidal if and only if $w=pq$ , where the fractional roots of $p^{R}$ and $q$ are $z_{0u0}$ and $z_{1u1}$ , where $(0u0,1u1)$ is the pathologial pair of minimal length of $w$ . Moreover, $p$ and $q$ are Sturmian words.

Example 3.

The word $w=00001010$ is trapezoidal but not Sturmian. Its pathological pair of minimal length is $(000,101)$ , so that $z_{000}=0$ and $z_{101}=10$ . The word $w$ can be written as $w=pq$ , with $p=0000$ and $q=1010$ , where $z_{p^{R}}=z_{000}$ and $z_{q}=z_{101}$ .

Theorem 4.

Every trapezoidal word has a symmetric fractional root. In particular, then, it is a palindromic periodicity.

Before proving Theorem 4, we need to recall some preliminary results.

Proposition 5 ([11, 9]).

Let $u$ be a word. Then $u$ is central if and only if $u$ is a power of a single letter or there exist central words $P$ and $Q$ , with $P$ a proper prefix of $Q$ , such that $u=PxyQ=QyxP$ , where $\{x,y\}=\{0,1\}$ .

Moreover, $Q=(Pxy)^{\ell}P^{\prime}=P^{\prime}(yxP)^{\ell}$ , for some $\ell>0$ and $P^{\prime}$ is a palindrome such that either $P^{\prime}=Px$ or $P^{\prime}y$ is a prefix of $P$ .

Proposition 6 ([9]).

Let $u=PxyQ=QyxP$ , with $|P|<|Q|$ , be a central word that is not a power of a single letter. Then the fractional root of $x u x$ is $x Q y$ , and the fractional root of $y u y$ is $y P x$ .

Proof of Theorem 4.

Let $w$ be a trapezoidal word. Since for Sturmian words the statement is true by Theorem 2, we can suppose that $w$ is not Sturmian.

By the characterization of non-Sturmian trapezoidal words, $w$ contains a pathological pair of minimal length $(0u0,1u1)$ , where $u$ is a central word, and $w$ can be written as $w=pq$ , where the fractional roots of $p^{R}$ and $q$ are $z_{0u0}$ and $z_{1u1}$ .

If $u$ is a power of a letter, the statement is readily verified. So suppose $u$ is not a power of a letter. By Proposition 6, there exist central words $P$ and $Q$ , with $P$ a proper prefix of $Q$ , such that $u=PxyQ=QyxP$ and $z_{xux}=xQy$ and $z_{yuy}=yPx$ , with $\{x,y\}=\{0,1\}$ .

So, either $w$ is a factor of a word in

(yQx)^{*}(yPx)^{*}

or a factor of a word in

(xPy)^{*}(xQy)^{*}.

Suppose first that $w$ is minimal, in the sense that it coincides with the concatenation of its pathological pair of minimal length $\{p,q\}=\{xux,yuy\}$ , so that $w$ is equal to $w=xuxyuy$ or to $y u y x u x$ . Then $w=z_{w}$ since $w$ is unbordered, and in this case the statement is true.

Let $w^{\prime}=pq^{\prime}$ be the shortest word that has $w$ as a prefix and has root $z_{w^{\prime}}\neq z_{w}$ . For every proper prefix of $w^{\prime}$ the statement is verified since the root has not changed. So we have $w^{\prime}=z_{w^{\prime}}$ , and we claim that $w^{\prime}=xuxyu^{\prime}y$ or $w^{\prime}=yuyxu^{\prime}x$ for a central word $u^{\prime}$ , so that $z_{w^{\prime}}$ is symmetric and the statement is proved for $w^{\prime}$ .

Suppose first that $w=yuyxux$ , so that $w$ and $w^{\prime}$ are words in $(xPy)^{*}(xQy)^{*}$ . In this case, we have $w^{\prime}=w\cdot yQx$ . In fact, by the characterization of non-Sturmian trapezoidal words, $q^{\prime}$ must have fractional root $x Q y$ , and indeed $q^{\prime}=xux\cdot xQy=xQyxPx\cdot yQx=xQyxQyxPx$ , and $P x$ is a prefix of $Q$ by Proposition 5. Since $y Q y$ is a prefix of $p=yQyxPy$ , and hence of $w^{\prime}$ , we have that $w\cdot yQx$ is the shortest right extension of $w$ that has a fractional root different from that of $w$ . Finally, $q^{\prime}=xux\cdot yQx=xQyxPxyQx$ and the word $u^{\prime}=QyxPxyQ$ is a central word by Proposition 5 since it can be written as $uxyQ=Qyxu$ .

Let us now assume $w=xuxyuy$ , so that $w$ and $w^{\prime}$ are words in $(yQx)^{*}(yPx)^{*}$ . In this case we have $w^{\prime}=w\cdot xPy$ . In fact, by the characterization of non-Sturmian trapezoidal words, the word $q^{\prime}$ must have fractional root $y P x$ , and indeed

q^{\prime}=yuy\cdot xPy=yPxyQyxPy\cdot yQx=yPxyPxyQy=yPxyPxy(Pxy)^{\ell}P^{% \prime}y,

and $P^{\prime}y$ is a prefix of $P x y$ by Proposition 5. Since $x P x$ is a prefix of $p=xPxyQx$ , and hence of $w^{\prime}$ , we have that $w\cdot xPy$ is the shortest right extension of $w$ that has a fractional root different from that of $w$ . Finally, $q^{\prime}=yuy\cdot xPy=yPxyQyxPy$ and the word $u^{\prime}=PxyQyxP$ is a central word by Proposition 5 since it can be written as $Pxyu=uyxP$ .

Let us now consider the extensions on the left of $w^{\prime}$ . Again, the extension is unique by the characterization of non-Sturmian trapezoidal words. But in this case, for each letter we add to the left, the fractional root will change. In particular, if the length of the fractional root does not change, the new fractional root is just a conjugate of the previous one, and the statement is verified. So let $w^{\prime\prime}=p^{\prime}q^{\prime}$ be the shortest left extension of $w^{\prime}$ (i.e., such that $p$ is a suffix of $p^{\prime}$ ) that has a fractional root longer than that of $w^{\prime}$ . We claim that $w^{\prime\prime}=xu^{\prime\prime}xyu^{\prime}y$ for a central word $u^{\prime\prime}$ .

Suppose first that $w^{\prime\prime}\in(yQx)^{*}(yPx)^{*}$ . By the characterization of non-Sturmian trapezoidal words, $(p^{\prime})^{R}$ must have fractional root $(xQy)^{R}=yQx$ , and indeed $p^{\prime}=xQy\cdot p=xQyxux=xQyxPxyQx=xPxyQxyQx$ and $x P$ is a suffix of $Q$ by Proposition 5. Since $z_{w^{\prime}}$ ends in $y Q y$ , we have that $xQyw^{\prime}$ is the shortest left extension of $w^{\prime}$ that has a different fractional root. Finally, $z_{w^{\prime\prime}}=w^{\prime\prime}=p^{\prime}q^{\prime}$ and $p^{\prime}=xQy\cdot p=xQyxux=xQyxPxyQx=xu^{\prime\prime}x$ with $u^{\prime\prime}=Qyxu=uxyQ$ , and $u^{\prime\prime}$ is a central word by Proposition 5.

If instead $w^{\prime\prime}\in(xPy)^{*}(xQy)^{*}$ , then $p^{\prime}$ must have fractional root $(xPy)^{R}=yPx$ , and indeed $p^{\prime}=yPx\cdot p=yPxyuy=yPxyPxyQy=yPxyPxy(Pxy)^{\ell}P^{\prime}y$ , and $P^{\prime}y$ is a prefix of $P x y$ by Proposition 5. Since $z_{w^{\prime}}$ ends in $y P y$ , we have that $yPxw^{\prime}$ is the shortest left extension of $w^{\prime}$ that has a different fractional root. Finally, $z_{w^{\prime\prime}}=w^{\prime\prime}=p^{\prime}q^{\prime}$ and $p^{\prime}=yPx\cdot p=yPxyQyxPy=yu^{\prime\prime}y$ with $u^{\prime\prime}=Pxyu=uyxP$ , and $u^{\prime\prime}$ is a central word by Proposition 5.

Since by D’Alessandro’s characterization, every non-Sturmian trapezoidal word is obtained by extending a word of the form $x u x y u y$ or $y u y x u x$ periodically on the right and on the left, the proof is complete. $\hfill\blacktriangleleft$

Example 7.

The word $w=010001000100010010010010010$ is a non-Sturmian trapezoidal word. Its fractional root is $z_{w}=010001000100010010010010$ (and we have $w=z_{w}010$ ). The pathological pair of minimal length of $w$ is $(0001000,1001001)=(0u0,1u1)$ , where $u=00100$ . The fractional root of $0u0$ is $z_{0u0}=0001$ , while the fractional root of $1u1$ is $z_{1u1}=100$ .

The fractional root $z_{w}$ of $w$ is a conjugate of $z^{\prime}=100010001000100100100100=(1000)^{3}(100)^{4}=(z_{0u0}^{R})^{3}(z_{1% u1})^{4}$ . The word $z^{\prime}=1000100010001\cdot 00100100100$ is symmetric; hence $z_{w}$ is symmetric too.

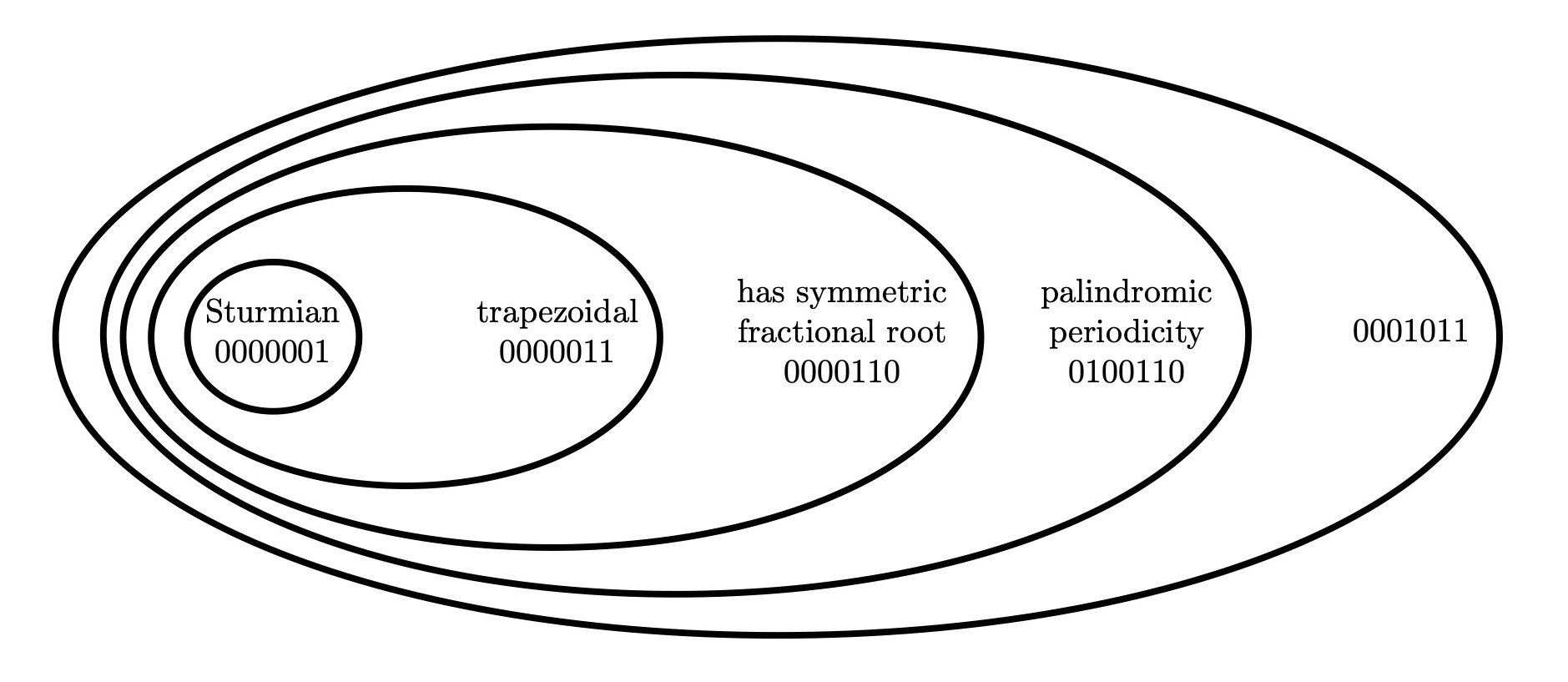
The classes of Sturmian, trapezoidal, having symmetric fractional root, and palindromic periodicity form a strict inclusion hierarchy within the set of all finite binary words, as illustrated in Figure 1.

Refer to caption — Figure 1: The inclusion hierarchy.

3.2 Rich words

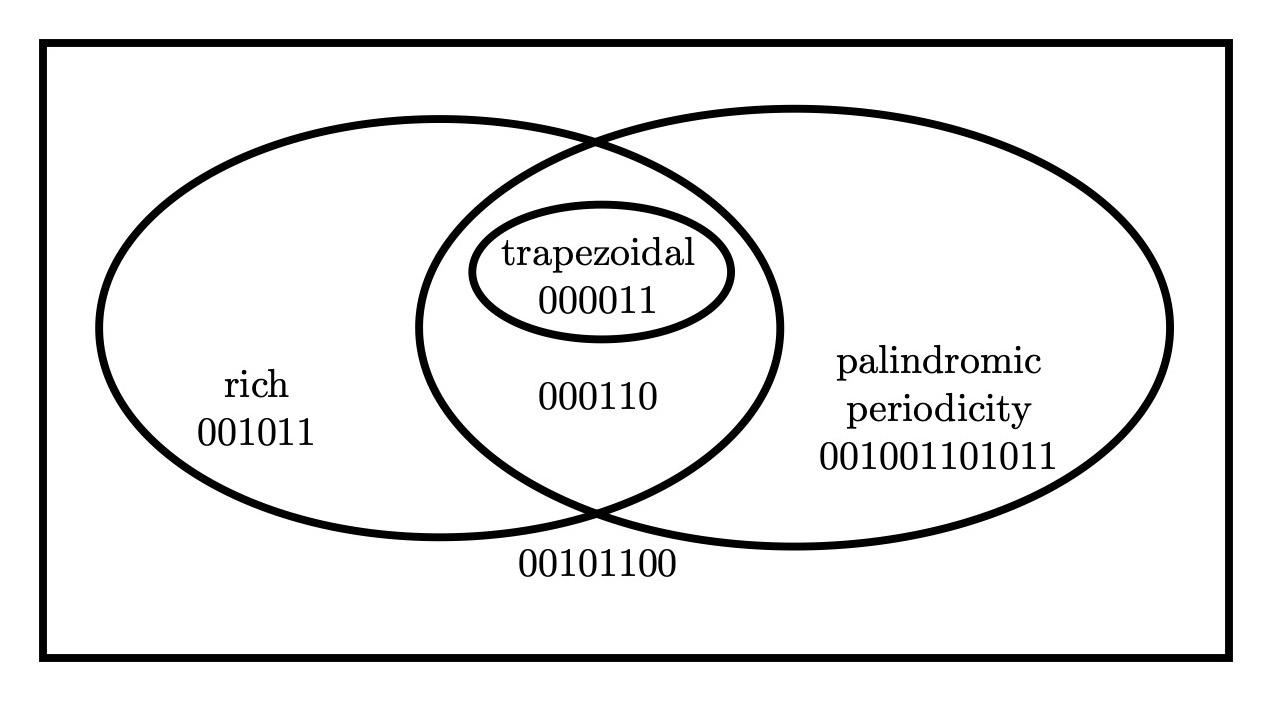
Recall that a word of length $n$ contains at most $n$ nonempty distinct palindromic factors [13]. A word of length $n$ is called rich if it contains $n$ distinct palindromic factors [18]. Every trapezoidal word is rich [12]. But there are rich words that are not palindromic periodicities, e.g., $001011$ . On the other hand, there are palindromic periodicities that are not rich, a shortest example being $001001101011$ . This is illustrated in Figure 2.

However, if a word is rich and closed, then one can prove that it is a palindromic periodicity. A word is called closed [15] (or periodic-like [7]) if it has length $1$ or it has a factor that appears only as a prefix and as a suffix, i.e., without internal occurrences. For example, $00$ , $0110$ , and $01010$ are closed, while $01$ , $0010$ , and $0101001$ are not. Bucci, de Luca, and De Luca [5] proved that if a word is rich and closed, then its fractional root is symmetric. In particular, then, we have the following

Proposition 8.

If a word is rich and closed, then it is a palindromic periodicity.

Notice that the language of rich words is factorial (closed under taking factors) while the language of palindromic periodicities is not.

3.3 Episturmian words

Let us now consider larger alphabets. Recall that an infinite word is episturmian if its set of finite factors is closed under reverse and it has at most one left special factor (i.e., a factor that occurs preceded by at least two different letters) of each length. Moreover, an episturmian word is standard if all of its left special factors are prefixes of it. Episturmian words are a generalization of Sturmian words to larger alphabets. See [19] for a survey.

In [24], de Luca and De Luca proved that for every nonempty prefix $w$ of a standard episturmian word, the fractional root of $w$ is symmetric. As a consequence, we have the following

Theorem 9.

Every nonempty prefix of a standard episturmian word is a palindromic periodicity.

In particular, then, all nonempty prefixes of the Tribonacci word, the fixed point of the morphism $0\rightarrow 01$ , $1\rightarrow 02$ , $2\rightarrow 0$ , are palindromic periodicities. However, not all factors of the Tribonacci word are palindromic periodicities, $102$ being a smallest example. See Section 5.5 for more discussion.

4 Results for generalized automatic words

In this section we discuss the case of generalized automatic words, that is, the $n$ ’th term is generated by a finite-state machine when the input is the representation of $n$ in an appropriate numeration system. See [31] for more details.

Let $\operatorname{pp}_{\bf x}(n)$ denote the number of distinct length- $n$ factors of an infinite word $\bf x$ that are palindromic periodicities.

Theorem 10.

Let $\bf x$ be a generalized automatic infinite word. Then there exists a finite automaton taking two inputs $i$ and $n$ in parallel, and accepting if and only if ${\bf x}[i..i+n-1]$ is a palindromic periodicity.

Proof.

The idea is to create a first-order logical formula that evaluates to TRUE if ${\bf x}[i..i+n-1]$ is a palindromic periodicity. We do this in several steps:

$\blacksquare$

$\operatorname{\textsc{Per}}(i,n,p)$ asserts that ${\bf x}[i..i+n-1]$ has period $p$ ;
$\blacksquare$

$\operatorname{\textsc{Pal}}(i,n)$ asserts that ${\bf x}[i..i+n-1]$ is a palindrome;
$\blacksquare$

$\operatorname{\textsc{Paltwo}}(i,n)$ asserts that ${\bf x}[i..i+n-1]$ is the product of two (possibly empty) palindromes;
$\blacksquare$

$\operatorname{\textsc{Ispp}}(i,n)$ asserts that ${\bf x}[i..i+n-1]$ is a palindromic periodicity.

These can be defined as follows:

	$\displaystyle\operatorname{\textsc{Per}}(i,n,p)$	$\displaystyle:=\forall t\ (t\geq i\,\wedge\,t<i+n-p)\implies{\bf x}[t]={\bf x}% [t+p]$
	$\displaystyle\operatorname{\textsc{Pal}}(i,n)$	$\displaystyle=\forall t,u\ (t\geq i\,\wedge\,t<i+n\,\wedge\,t+u=2i+n-1)% \implies{\bf x}[t]={\bf x}[u]$
	$\displaystyle\operatorname{\textsc{Paltwo}}(i,n)$	$\displaystyle=\exists m\ m\leq n\,\wedge\,\operatorname{\textsc{Pal}}(i,m)\,% \wedge\,\operatorname{\textsc{Pal}}(i+m,n-m)$
	$\displaystyle\operatorname{\textsc{Ispp}}(i,n)$	$\displaystyle:=\exists p\ p\geq 1\,\wedge\,p\leq n\,\wedge\,n\geq 1\,\wedge\,% \operatorname{\textsc{Per}}(i,n,p)\,\wedge\,\operatorname{\textsc{Paltwo}}(i,p).$

Now, by the classic result of Bruyère et al. [4], we know there is an algorithm to convert these first-order statements to the desired automata. $\hfill\blacktriangleleft$

Corollary 11.

Let $\bf x$ be a generalized automatic infinite word. There is an algorithm that, given the automaton computing $\bf x$ , decides whether $\bf x$ contains arbitrarily long palindromic periodicities.

Proof.

It suffices to define the appropriate first-order formula, which is

\forall m\ \exists i,n\ n>m\,\wedge\,\operatorname{\textsc{Ispp}}(i,n).

This can then be translated into an automaton of one state that either accepts everything (and so $\bf x$ contains arbitrarily long palindromic periodicities) or nothing (and so $\bf x$ does not). $\hfill\blacktriangleleft$

Recall that a linear representation for a function $f:\mathbb{N}\rightarrow\mathbb{Z}$ is a triple $(v,\mu,w)$ where $v$ is a row vector, $w$ is a column vector, and $\mu$ is a matrix-valued morphism. Then $f(n)=v\cdot\mu(x)\cdot w$ , where $x$ is a representation of $n$ in the appropriate numeration system (e.g., base $k$ for $k\geq 2$ , or Fibonacci, or Tribonacci, etc.).

Corollary 12.

Let $\bf x$ be a generalized automatic infinite word. Then the number $\operatorname{pp}_{\bf x}(n)$ of length- $n$ factors that are palindromic periodicities is a regular sequence, and furthermore there is an algorithm to compute a linear representation for it.

Proof.

We need three additional automata, computable from the following first-order statements:

$\blacksquare$

$\operatorname{\textsc{Faceq}}(i,j,n)$ asserts that ${\bf x}[i..i+n-1]={\bf x}[j..j+n-1]$
$\blacksquare$

$\operatorname{\textsc{Novel}}(i,n)$ asserts that the first occurrence of the factor ${\bf x}[i..i+n-1]$ is at position $i$ of $\bf x$
$\blacksquare$

$\operatorname{\textsc{Countpp}}(i,n)$ asserts that ${\bf x}[i..i+n-1]$ is a palindromic periodicity and is the first appearance of this factor in $\bf x$ .

These can be defined as follows:

	$\displaystyle\operatorname{\textsc{Faceq}}(i,j,n)$	$\displaystyle=\forall u,v\ (u\geq i\,\wedge\,u<i+n\,\wedge\,u-i=v-j)\implies{% \bf x}[u]={\bf x}[v]$
	$\displaystyle\operatorname{\textsc{Novel}}(i,n)$	$\displaystyle=\forall j\ (j<i)\implies\neg\operatorname{\textsc{Faceq}}(i,j,n)$
	$\displaystyle\operatorname{\textsc{Countpp}}(i,n)$	$\displaystyle=\operatorname{\textsc{Novel}}(i,n)\,\wedge\,\operatorname{% \textsc{Ispp}}(i,n).$

We can now form the linear representation for $\operatorname{pp}_{\bf x}(i,n)$ directly from the automaton for $\operatorname{\textsc{Countpp}}$ , as described in [31, §4.9 and Chap. 9]. $\hfill\blacktriangleleft$

5 Results for some famous infinite words

We now use the results of the previous section to prove a number of results about the palindromic periodicities occurring in some famous infinite words. Due to space constraints, we refer the reader to the full version of the paper for details of the results stated in this section.

5.1 The period-doubling word

Recall that the period-doubling word ${\bf pd}=1011101010111011\cdots$ is the fixed point of the morphism $1\rightarrow 10$ , $0\rightarrow 11$ .

Theorem 13.

Define $f(0)=0$ and $f(1)=2$ . If $n\geq 2$ , write $n=2^{k}+r$ for $0\leq r<2^{k}$ and define

f(n)=\begin{cases}3\cdot 2^{k-1},&\text{if $0\leq r<2^{k-2}$;}\\ 2^{k+1},&\text{if $2^{k-2}\leq r<2^{k-1}$; }\\ 6\cdot 2^{k-1}-r,&\text{if $2^{k-1}\leq r<3\cdot 2^{k-2}$;}\\ 7\cdot 2^{k-1}-r,&\text{if $3\cdot 2^{k-2}\leq r<2^{k}$.}\end{cases}

Then $f(n)=\operatorname{pp}_{\bf pd}(n)$ for all $n\geq 0$ .

Corollary 14.

We have $\operatorname{pp}_{\bf pd}(n)\leq 5n/3$ for $n\geq 2$ and $\operatorname{pp}_{\bf pd}(n)\geq(6n+6)/5$ for $n\geq 3$ , and both bounds are tight, in the sense that they hold with equality infinitely often.

5.2 The Thue–Morse word

Recall that the Thue–Morse word ${\bf t}=0110100110010110\cdots$ is the fixed point starting with $0$ of the morphism $0\rightarrow 01$ , $1\rightarrow 10$ .

Theorem 15.

Let $n\geq 3$ and write $n=2^{k}+r$ , where $0\leq r<2^{k}$ . If $k$ is even, then

\operatorname{pp}_{\bf t}(n)=\begin{cases}2^{k+1}+2-2r,&\text{if $0\leq r<2^{k% -2}$;}\\ 3\cdot 2^{k}+2-2r,&\text{if $2^{k-2}\leq r\leq 2^{k-1}$;}\\ 2^{k+2}+4-4r,&\text{if $2^{k-1}<r<3\cdot 2^{k-2}$;}\\ 10\cdot 2^{k-1}+4-4r,&\text{if $3\cdot 2^{k-2}\leq r<2^{k}$}.\end{cases}

If $k$ is odd, then

\operatorname{pp}_{\bf t}(n)=\begin{cases}3\cdot 2^{k-1}+2-2r,&\text{if $0\leq r% <2^{k-3}$;}\\ 2^{k+1}+2-2r,&\text{if $2^{k-3}\leq r<2^{k-1}$;}\\ 2^{k+2}-2,&\text{if $r=2^{k-1}$};\\ 3\cdot 2^{k+1}+4-4r,&\text{if $2^{k-1}\leq r<2^{k}$}.\end{cases}

Corollary 16.

We have $\operatorname{pp}_{\bf t}(n)\geq(n+17)/2$ for $n\geq 12$ and $\operatorname{pp}_{\bf t}(n)\leq(8n-6)/3$ for $n\geq 6$ . Furthermore, these bounds are sharp, in the sense that the bounds are achieved for infinitely many $n$ . The lower bound is achieved for $n=2\cdot 4^{k}-1$ , $k\geq 1$ , and the upper bound is achieved for $n=3\cdot 4^{k}$ , $k\geq 0$ .

5.3 The Rudin–Shapiro word

Recall that the Rudin–Shapiro word $00010010000111010001001\cdots$ counts the number of $11$ ’s occurring in the base- $2$ representation of $n$ , taken modulo $2$ [30, 32].

Theorem 17.

For $n\geq 25$ there are no length- $n$ factors of the Rudin–Shapiro word that are palindromic periodicities. The bound $25$ is optimal, as witnessed by the length- $24$ factor $011110110111100010000100$ .

5.4 The regular paperfolding word

Recall that the regular paperfolding word $001001100011011000100111\cdots$ is defined by the limit of the sequence of words $p_{0}=0$ and $p_{n+1}=p_{n}\,0\,\overline{p_{n}}^{R}$ , where $\overline{w}$ denotes the binary complement of $w$ . See [10].

Theorem 18.

For $n\geq 22$ there are no length- $n$ factors of the regular paperfolding word that are palindromic periodicities. The bound $22$ is optimal, as witnessed by the length- $21$ factor $011000110111001001110$ .

5.5 The Tribonacci word

Recall that the Tribonacci word $0102010010201010201001\cdots$ is the fixed point of the morphism $0\rightarrow 01$ , $1\rightarrow 02$ , $2\rightarrow 0$ . See, e.g., [1].

Not all factors of $\bf tr$ are palindromic periodicities; e.g., $102$ , but many of them are. For example, we can verify that all prefixes are (see Theorem 4 above):

We now compute an explicit formula for the number of length- $n$ factors of $\bf tr$ that are palindromic periodicities. Define, as usual, the Tribonacci numbers by $T_{0}=0$ , $T_{1}=1$ , $T_{2}=2$ and $T_{n}=T_{n-1}+T_{n-2}+T_{n-3}$ for $n\geq 3$ . We also set $T_{i}=0$ for $i<0$ .

Theorem 19.

Let $n\geq 0$ and $T_{k}\leq n<T_{k+1}$ . Then

\operatorname{pp}_{\bf tr}(n)=\begin{cases}2n+1,&\text{if $n\leq(T_{k+1}-T_{k-% 1}-1)/2$;}\\ 2T_{k+1}+2T_{k-1}-(2n+1),&\text{if $(T_{k+1}-T_{k-1}-1)/2<n<T_{k}+T_{k-1}$};\\ T_{k+1}+T_{k-1},&\text{otherwise.}\end{cases}

Corollary 20.

We have $\operatorname{pp}_{\bf tr}(n)\leq 2n+1$ and $\operatorname{pp}_{\bf tr}(n)>\alpha n$ , where $\alpha\doteq 1.0873780253841527$ is the real zero of $X^{3}+2X^{2}+4X-8$ .

6 Words with few palindromic periodicities

When we count palindromic periodicities in this section, we do not count the empty word.

As we have seen above, both the Rudin–Shapiro word and the regular paperfolding word have only finitely many palindromic periodicities as factors. Indeed, using the linear representation for counting the number of palindromic periodicities of length $n$ , we can show that the Rudin–Shapiro word has exactly $334$ palindromic periodicities, and the paperfolding word has exactly $255$ palindromic periodicities. This suggests the question of finding words with the minimum possible number of palindromic periodicities.

We say a word is aperiodic if it is not ultimately periodic.

Theorem 21.

Let $\Sigma=\{0,1,\ldots,k-1\}$ be an alphabet of size at least $3$ .

(a)

No infinite word over $\Sigma$ has fewer than $6$ distinct palindromic periodicities.
(b)

The bound $6$ is optimal because $(012)^{\omega}$ has $6$ .
(c)

No aperiodic infinite word over $\Sigma$ has $\leq 8$ palindromic periodicities.
(d)

The bound $8$ is optimal, because the image of the Fibonacci word $\bf f$ , fixed point of the morphism $0\rightarrow 01$ , $1\rightarrow 0$ , under the map $\tau:0\rightarrow 0$ , $1\rightarrow 12$ , has $9$ palindromic periodicities, namely $\{0,1,2,01,12,20,00,001,200\}$ .

The word $\tau({\bf f})$ was previously studied by the first author and Luca Zamboni [14].

Proof.

(a)

Without loss of generality we may assume that the first occurrence of a letter $i$ precedes the first occurrence of $j$ for all $i<j$ . Then breadth-first search, where we allow the alphabet to grow with the size of the word, demonstrates that the longest such word with $\leq 5$ palindromic periodicities is of length $5$ , namely $00000$ .
(b)

It is easy to see the only palindromic periodicities of $(012)^{\omega}$ are $0,1,2,01,12,20$ .
(c)

Again, without loss of generality, we assume that the first occurrence of a letter $i$ precedes the first occurrence of $j$ for all $i<j$ . With this assumption, we claim that if $w$ is of length at least $9$ and has $\leq 8$ palindromic periodicities, then $w$ is of one of the following forms:

$0(012)^{i}\{\epsilon,0,01\}$ ,

$(012)^{i}\{\epsilon,0,2,3,00,01,03,011,013\}$ ,

$(0123)^{i}\{\epsilon,0,01,012\}$ ,

$0(123)^{i}\{\epsilon,1,12\}$ .

The claim can be easily verified for $9\leq|w|\leq 12$ . It is easy to check that all words with the stated property of length $12$ can be written uniquely in the form $xy^{i}z$ with $i\geq 2$ $x\in\{\epsilon,0\}$ , $y\in\{012,123,0123\}$ , and $|z|\leq 3$ . Let $w$ be a shortest counterexample to the claim with $|w|>12$ . Let $xy^{i}z$ be the unique factorization of the prefix of $w$ of length $12$ ; then $i\geq 2$ . Write $w=xy^{j}z^{\prime}$ with $j$ as large as possible. It is now easy to check, by considering the possible suffixes $y^{2}z^{\prime}$ of $w$ , that either $z^{\prime}$ begins with $y$ (so $j$ was not maximal, a contradiction), or $z^{\prime}$ is one of the words given in the characterization, a contradiction.

(d)

We use Walnut. Here it is possible to compute an automaton for $\tau({\bf f})$ because the number of occurrences of $0$ (resp., $1$ ) in a prefix of length $n$ of $\bf f$ is synchronized; see [31, Sect. 10.11]. The following Walnut code checks that $\tau({\bf f})$ has no palindromic periodicities of length $>3$ ; it is then easy to enumerate them by hand. The code for the first five automata is taken from [31, Sect. 10.11].

reg shift {0,1} {0,1} "([0,0]|[0,1][1,1]*[1,0])*":
def phin "?msd_fib (s=0 & n=0) | Ex $shift(n-1,x) & s=x+1":
def noverphi "?msd_fib Et $phin(n,t) & s+n=t":
def fibpref0 "?msd_fib $noverphi(n+1,s)":
def fibpref1 "?msd_fib Eu $fibpref0(n,u) & n=s+u":

def img "?msd_fib Ew,x,y,z $fibpref0(q,x) & $fibpref1(q,y) &
   $fibpref0(q+1,w) & $fibpref1(q+1,z) & x+2*y<=n & w+2*z>n &
   r+x+2*y=n":
# img(n) = (q,r) means the n’th position of the image
# tau(f) is the r’th letter of phi(f[q])

def img0 "?msd_fib Eq,r $img(n,q,r) & F[q]=@0":
def img1 "?msd_fib Eq,r $img(n,q,r) & F[q]=@1 & r=0":
def img2 "?msd_fib Eq,r $img(n,q,r) & F[q]=@1 & r=1":
combine NF img0=0 img1=1 img2=2:

def nfper "?msd_fib At (t>=i & t+p<i+n) => NF[t]=NF[t+p]":
def nfpal "?msd_fib At,u (t>=i & t<i+n & t+u+1=2*i+n) => NF[t]=NF[u]":
def nf2pal "?msd_fib Em m<=n & $nfpal(i,m) & $nfpal(i+m,n-m)":
def nfpp "?msd_fib Ep p>=1 & p<=n & n>=1 & $nfper(i,n,p) & $nf2pal(i,p)":
eval nfpp3 "?msd_fib Ai,n $nfpp(i,n) => n<=3":

and Walnut returns TRUE for the last assertion. To check that $\tau({\bf f})$ is aperiodic, we check that it has no $4$ th powers:

eval no4 "?msd_fib ~Ei,n,p n>=1 & p>=1 & $nfper(i,n,p) & n>=4*p":

$\hfill\blacktriangleleft$

The binary case is similar but a bit more complicated.

Theorem 22.

Let $\Sigma=\{0,1\}$ .

(a)

No infinite word over $\Sigma$ has fewer than $30$ distinct palindromic periodicities.
(b)

The bound $30$ is optimal because $(001011)^{\omega}$ has $30$ .
(c)

No aperiodic infinite binary word has $\leq 43$ palindromic periodicities.
(d)

The bound $43$ is optimal, because the image of the Fibonacci word $\bf f$ under the map $\varphi:0\rightarrow 0$ , $1\rightarrow 01101$ has $44$ palindromic periodicities.

The word $\varphi({\bf f})$ was previously studied by the first author and L. Zamboni [14].

Proof sketch..

(a)

Breadth-first search shows that the longest binary words with $\leq 29$ palindromic periodicities are of length $29$ ; namely, $0^{29}$ and $1^{29}$ .
(b)

It is easy to check that the only palindromic periodicities in $(001011)^{\omega}$ are

$\displaystyle 0,1,00,01,10,11,001,010,011,100,101,110,0010,0101,0110,1001,1011,$

$\displaystyle 1100,00101,01011,01100,10010,10110,11001,010110,011001,100101,$

$\displaystyle 0110010,1011001,10010110.$
(c)

We claim that every sufficient large finite binary word having $\leq 43$ palindromic periodicities is of the form $xy^{i}z$ where $|x|,|z|\leq 5$ and $y$ is a conjugate of one of members of the set $B$ , where

$\displaystyle B$ $\displaystyle=\{001011,001101,0001011,0001101,0010111,0011101,00001011,00001101,$

$\displaystyle\quad\quad 00010111,00011101,00101011,00101111,00110101,00111101\}.$

The argument is similar as for the previous theorem.

(d)

We use Walnut. Again, it is possible to compute an automaton for $\varphi({\bf f})$ . The following Walnut code checks that $\varphi({\bf f})$ has no palindromic periodicities of length $>9$ ; it is then easy to enumerate them by hand.

def img2 "?msd_fib Ew,x,y,z $fibpref0(q,x) & $fibpref1(q,y) &
   $fibpref0(q+1,w) & $fibpref1(q+1,z) & x+5*y<=n & w+5*z>n & r+x+5*y=n":
# img2(n) = (q,r) means the n’th position of the image
# phi(f) is the r’th letter of phi(f[q])

def img20 "?msd_fib Eq,r $img2(n,q,r) & ((F[q]=@0)|(F[q]=@1 & (r=0|r=3)))":
def img21 "?msd_fib Eq,r $img2(n,q,r) & F[q]=@1 & (r=1|r=2|r=4)":
combine QF img20=0 img21=1:
# 61 states

def qfper "?msd_fib At (t>=i & t+p<i+n) => QF[t]=QF[t+p]":
#17157 states
def qfpal "?msd_fib At,u (t>=i & t<i+n & t+u+1=2*i+n) => QF[t]=QF[u]":
#119 states, largest intermediate automaton was 58110620 states!
def qf2pal "?msd_fib Em m<=n & $qfpal(i,m) & $qfpal(i+m,n-m)":
#187 states
def qfpp "?msd_fib Ep p>=1 & p<=n & n>=1 & $qfper(i,n,p) & $qf2pal(i,p)":
#203 states

eval nqpp9 "?msd_fib Ai,t $qfpp(i,t) => t<=9":

We can also check that $\varphi({\bf f})$ is aperiodic.

eval no42 "?msd_fib ~Ei,n,p n>=1 & p>=1 & $qfper(i,n,p) & n>=4*p":

$\hfill\blacktriangleleft$

7 Conclusions and open problems

We discussed palindromic periodicities in relation to known classes of finite and infinite words. In particular, we discussed the case of Sturmian words and their generalizations (trapezoidal words and episturmian words), and the case of generalized automatic words. We also gave optimal bounds on the minimal number of distinct palindromic periodicities occurring in an infinite word, both in the case of a binary alphabet and of alphabets of size at least $3$ .

A question we leave for further research is: asymptotically, how many palindromic periodicities of length $n$ are there for binary words? The first few values of the sequence are:

\displaystyle 2,4,8,16,32,58,108,190,336,560,948,1574,2568,4116,6596,10444,163% 20,25488,39216.

It is sequence A374495 in the On-Line Encyclopedia of Integer Sequences [35]. More terms there have now been computed by Michael S. Branicky. Obviously, the growth rate of the language of palindromic periodicities is at least $\Omega(2^{n/2})$ , since palindromes are particular cases of palindromic periodicities.

Finally, we think the notion of palindromic periodicity may find applications in the domain of string processing. However, in this paper we did not delve into the algorithmic aspects, since our focus was purely combinatorial.

References

[1] E. Barcucci, L. Bélanger, and S. Brlek. On Tribonacci sequences. Fibonacci Quart., 42:314–319, 2004.
[2] A. Borchert and N. Rampersad. Words with many palindrome pair factors. Electronic J. Combinatorics, 22, 2015. Available at tinyurl.com/2p87wsrz.
[3] Srecko Brlek, Sylvie Hamel, Maurice Nivat, and Christophe Reutenauer. On the palindromic complexity of infinite words. Internat. J. Found. Comp. Sci., 15(2):293–306, 2004. doi:10.1142/S012905410400242X.
[4] V. Bruyère, G. Hansel, C. Michaux, and R. Villemaire. Logic and $p$ -recognizable sets of integers. Bull. Belgian Math. Soc., 1:191–238, 1994. Corrigendum, Bull. Belgian Math. Soc. 1 (1994), 577.
[5] M. Bucci, A. de Luca, and A. De Luca. Rich and periodic-like words. In V. Diekert and D. Nowotka, editors, DLT 2009, volume 5583 of Lecture Notes in Computer Science, pages 145–155. Springer-Verlag, 2009. doi:10.1007/978-3-642-02737-6_11.
[6] Michelangelo Bucci, Alessandro De Luca, and Gabriele Fici. Enumeration and structure of trapezoidal words. Theor. Comput. Sci., 468:12–22, 2013. doi:10.1016/J.TCS.2012.11.007.
[7] Arturo Carpi and Aldo de Luca. Periodic-like words, periodicity, and boxes. Acta Informatica, 37(8):597–618, 2001. doi:10.1007/PL00013314.
[8] Ethan M. Coven and G. A. Hedlund. Sequences with minimal block growth. Math. Syst. Theory, 7(2):138–153, 1973. doi:10.1007/BF01762232.
[9] Flavio D’Alessandro. A combinatorial problem on trapezoidal words. Theor. Comput. Sci., 273(1-2):11–33, 2002. doi:10.1016/S0304-3975(00)00431-X.
[10] C. Davis and D. E. Knuth. Number representations and dragon curves–I, II. J. Recreational Math., 3:66–81, 133–149, 1970.
[11] Aldo de Luca. Sturmian words: Structure, combinatorics, and their arithmetics. Theor. Comput. Sci., 183(1):45–82, 1997. doi:10.1016/S0304-3975(96)00310-6.
[12] Aldo de Luca, Amy Glen, and Luca Q. Zamboni. Rich, sturmian, and trapezoidal words. Theor. Comput. Sci., 407(1-3):569–573, 2008. doi:10.1016/J.TCS.2008.06.009.
[13] Xavier Droubay, Jacques Justin, and Giuseppe Pirillo. Episturmian words and some constructions of de Luca and Rauzy. Theor. Comput. Sci., 255(1-2):539–553, 2001. doi:10.1016/S0304-3975(99)00320-5.
[14] G. Fici and L. Q. Zamboni. On the least number of palindromes contained in an infinite word. Theoret. Comput. Sci., 481:1–8, 2013. doi:10.1016/J.TCS.2013.02.013.
[15] Gabriele Fici. A classification of trapezoidal words. In Petr Ambroz, Stepan Holub, and Zuzana Masáková, editors, Proceedings 8th International Conference Words 2011, Prague, Czech Republic, 12-16th September 2011, volume 63 of EPTCS, pages 129–137, 2011. doi:10.4204/EPTCS.63.18.
[16] Gabriele Fici. The shortest interesting binary words. CoRR, abs/2412.21145, 2024. doi:10.48550/arXiv.2412.21145.
[17] N. J. Fine and H. S. Wilf. Uniqueness theorems for periodic functions. Proc. Amer. Math. Soc., 16:109–114, 1965.
[18] A. Glen, J. Justin, S. Widmer, and L. Q. Zamboni. Palindromic richness. European J. Combinatorics, 30:510–531, 2009. doi:10.1016/J.EJC.2008.04.006.
[19] Amy Glen and Jacques Justin. Episturmian words: a survey. RAIRO Theor. Informatics Appl., 43(3):403–442, 2009. doi:10.1051/ITA/2009003.
[20] C. Guo, J. Shallit, and A. M. Shur. On the combinatorics of palindromes and antipalindromes. ArXiv preprint arXiv:1503.09112 [cs.FL], available at https://arxiv.org/abs/1503.09112, 2015. arXiv:1503.09112.
[21] Alex Heinis. Arithmetics and combinatorics of words of low complexity. PhD thesis, Leiden University, 2001.
[22] R. Kemp. On the number of words in the language $\{w\in{\Sigma^{*}}\mid w=w^{R}\}^{2}$ . Discrete Math., 40:225–234, 1982.
[23] M. Lapointe and C. Reutenauer. Characterizations of perfectly clustering words. ArXiv preprint arXiv:2407.19140 [math.CO], available at https://arxiv.org/abs/2407.19140, 2024.
[24] A. de Luca and A. De Luca. Pseudopalindrome closure operators in free monoids. Theoret. Comput. Sci., 362:282–300, 2006. doi:10.1016/J.TCS.2006.07.009.
[25] A. de Luca and A. De Luca. Some characterizations of finite Sturmian words. Theoret. Comput. Sci., 356:118–125, 2006. doi:10.1016/J.TCS.2006.01.036.
[26] A. de Luca and F. Mignosi. Some combinatorial properties of Sturmian words. Theoret. Comput. Sci., 136:361–385, 1994.
[27] Aldo de Luca. On the combinatorics of finite words. Theor. Comput. Sci., 218(1):13–39, 1999. doi:10.1016/S0304-3975(98)00248-5.
[28] H. Mousavi. Automatic theorem proving in Walnut. Arxiv preprint arXiv:1603.06017 [cs.FL], available at http://arxiv.org/abs/1603.06017, 2016. arXiv:1603.06017.
[29] Antonio Restivo and Giovanna Rosone. Burrows-Wheeler transform and palindromic richness. Theor. Comput. Sci., 410(30-32):3018–3026, 2009. doi:10.1016/J.TCS.2009.03.008.
[30] W. Rudin. Some theorems on Fourier coefficients. Proc. Amer. Math. Soc., 10:855–859, 1959.
[31] J. Shallit. The Logical Approach To Automatic Sequences: Exploring Combinatorics on Words with Walnut, volume 482 of London Math. Soc. Lecture Note Series. Cambridge University Press, 2023.
[32] H. S. Shapiro. Extremal problems for polynomials and power series. Master’s thesis, MIT, 1952.
[33] J. Simpson. Palindromic periodicities. ArXiv preprint arXiv:2402.05381 [math.CO]. Available at https://arxiv.org/abs/2402.05381., 2024.
[34] Jamie Simpson and Simon J. Puglisi. Words with simple Burrows-Wheeler transforms. Electronic J. Combinatorics, 15(1):#R83, 2008. URL: http://www.combinatorics.org/Volume_15/Abstracts/v15i1r83.html.
[35] N. J. A. Sloane et al. The On-Line Encyclopedia of Integer Sequences. Electronic resource, available at https://oeis.org, 2024.

[bib.bib1] [1] E. Barcucci, L. Bélanger, and S. Brlek. On Tribonacci sequences. Fibonacci Quart., 42:314–319, 2004.

[bib.bib2] [2] A. Borchert and N. Rampersad. Words with many palindrome pair factors. Electronic J. Combinatorics, 22, 2015. Available at tinyurl.com/2p87wsrz.

[bib.bib3] [3] Srecko Brlek, Sylvie Hamel, Maurice Nivat, and Christophe Reutenauer. On the palindromic complexity of infinite words. Internat. J. Found. Comp. Sci., 15(2):293–306, 2004. doi:10.1142/S012905410400242X.

[bib.bib4] [4] V. Bruyère, G. Hansel, C. Michaux, and R. Villemaire. Logic and $p$ -recognizable sets of integers. Bull. Belgian Math. Soc., 1:191–238, 1994. Corrigendum, Bull. Belgian Math. Soc. 1 (1994), 577.

[bib.bib5] [5] M. Bucci, A. de Luca, and A. De Luca. Rich and periodic-like words. In V. Diekert and D. Nowotka, editors, DLT 2009, volume 5583 of Lecture Notes in Computer Science, pages 145–155. Springer-Verlag, 2009. doi:10.1007/978-3-642-02737-6_11.

[bib.bib6] [6] Michelangelo Bucci, Alessandro De Luca, and Gabriele Fici. Enumeration and structure of trapezoidal words. Theor. Comput. Sci., 468:12–22, 2013. doi:10.1016/J.TCS.2012.11.007.

[bib.bib7] [7] Arturo Carpi and Aldo de Luca. Periodic-like words, periodicity, and boxes. Acta Informatica, 37(8):597–618, 2001. doi:10.1007/PL00013314.

[bib.bib8] [8] Ethan M. Coven and G. A. Hedlund. Sequences with minimal block growth. Math. Syst. Theory, 7(2):138–153, 1973. doi:10.1007/BF01762232.

[bib.bib9] [9] Flavio D’Alessandro. A combinatorial problem on trapezoidal words. Theor. Comput. Sci., 273(1-2):11–33, 2002. doi:10.1016/S0304-3975(00)00431-X.

[bib.bib10] [10] C. Davis and D. E. Knuth. Number representations and dragon curves–I, II. J. Recreational Math., 3:66–81, 133–149, 1970.

[bib.bib11] [11] Aldo de Luca. Sturmian words: Structure, combinatorics, and their arithmetics. Theor. Comput. Sci., 183(1):45–82, 1997. doi:10.1016/S0304-3975(96)00310-6.

[bib.bib12] [12] Aldo de Luca, Amy Glen, and Luca Q. Zamboni. Rich, sturmian, and trapezoidal words. Theor. Comput. Sci., 407(1-3):569–573, 2008. doi:10.1016/J.TCS.2008.06.009.

[bib.bib13] [13] Xavier Droubay, Jacques Justin, and Giuseppe Pirillo. Episturmian words and some constructions of de Luca and Rauzy. Theor. Comput. Sci., 255(1-2):539–553, 2001. doi:10.1016/S0304-3975(99)00320-5.

[bib.bib14] [14] G. Fici and L. Q. Zamboni. On the least number of palindromes contained in an infinite word. Theoret. Comput. Sci., 481:1–8, 2013. doi:10.1016/J.TCS.2013.02.013.

[bib.bib15] [15] Gabriele Fici. A classification of trapezoidal words. In Petr Ambroz, Stepan Holub, and Zuzana Masáková, editors, Proceedings 8th International Conference Words 2011, Prague, Czech Republic, 12-16th September 2011, volume 63 of EPTCS, pages 129–137, 2011. doi:10.4204/EPTCS.63.18.

[bib.bib16] [16] Gabriele Fici. The shortest interesting binary words. CoRR, abs/2412.21145, 2024. doi:10.48550/arXiv.2412.21145.

[bib.bib17] [17] N. J. Fine and H. S. Wilf. Uniqueness theorems for periodic functions. Proc. Amer. Math. Soc., 16:109–114, 1965.

[bib.bib18] [18] A. Glen, J. Justin, S. Widmer, and L. Q. Zamboni. Palindromic richness. European J. Combinatorics, 30:510–531, 2009. doi:10.1016/J.EJC.2008.04.006.

[bib.bib19] [19] Amy Glen and Jacques Justin. Episturmian words: a survey. RAIRO Theor. Informatics Appl., 43(3):403–442, 2009. doi:10.1051/ITA/2009003.

[bib.bib20] [20] C. Guo, J. Shallit, and A. M. Shur. On the combinatorics of palindromes and antipalindromes. ArXiv preprint arXiv:1503.09112 [cs.FL], available at https://arxiv.org/abs/1503.09112, 2015. arXiv:1503.09112.

[bib.bib21] [21] Alex Heinis. Arithmetics and combinatorics of words of low complexity. PhD thesis, Leiden University, 2001.

[bib.bib22] [22] R. Kemp. On the number of words in the language $\{w\in{\Sigma^{*}}\mid w=w^{R}\}^{2}$ . Discrete Math., 40:225–234, 1982.

[bib.bib23] [23] M. Lapointe and C. Reutenauer. Characterizations of perfectly clustering words. ArXiv preprint arXiv:2407.19140 [math.CO], available at https://arxiv.org/abs/2407.19140, 2024.

[bib.bib24] [24] A. de Luca and A. De Luca. Pseudopalindrome closure operators in free monoids. Theoret. Comput. Sci., 362:282–300, 2006. doi:10.1016/J.TCS.2006.07.009.

[bib.bib25] [25] A. de Luca and A. De Luca. Some characterizations of finite Sturmian words. Theoret. Comput. Sci., 356:118–125, 2006. doi:10.1016/J.TCS.2006.01.036.

[bib.bib26] [26] A. de Luca and F. Mignosi. Some combinatorial properties of Sturmian words. Theoret. Comput. Sci., 136:361–385, 1994.

[bib.bib27] [27] Aldo de Luca. On the combinatorics of finite words. Theor. Comput. Sci., 218(1):13–39, 1999. doi:10.1016/S0304-3975(98)00248-5.

[bib.bib28] [28] H. Mousavi. Automatic theorem proving in Walnut. Arxiv preprint arXiv:1603.06017 [cs.FL], available at http://arxiv.org/abs/1603.06017, 2016. arXiv:1603.06017.

[bib.bib29] [29] Antonio Restivo and Giovanna Rosone. Burrows-Wheeler transform and palindromic richness. Theor. Comput. Sci., 410(30-32):3018–3026, 2009. doi:10.1016/J.TCS.2009.03.008.

[bib.bib30] [30] W. Rudin. Some theorems on Fourier coefficients. Proc. Amer. Math. Soc., 10:855–859, 1959.

[bib.bib31] [31] J. Shallit. The Logical Approach To Automatic Sequences: Exploring Combinatorics on Words with Walnut, volume 482 of London Math. Soc. Lecture Note Series. Cambridge University Press, 2023.

[bib.bib32] [32] H. S. Shapiro. Extremal problems for polynomials and power series. Master’s thesis, MIT, 1952.

[bib.bib33] [33] J. Simpson. Palindromic periodicities. ArXiv preprint arXiv:2402.05381 [math.CO]. Available at https://arxiv.org/abs/2402.05381., 2024.

[bib.bib34] [34] Jamie Simpson and Simon J. Puglisi. Words with simple Burrows-Wheeler transforms. Electronic J. Combinatorics, 15(1):#R83, 2008. URL: http://www.combinatorics.org/Volume_15/Abstracts/v15i1r83.html.

[bib.bib35] [35] N. J. A. Sloane et al. The On-Line Encyclopedia of Integer Sequences. Electronic resource, available at https://oeis.org, 2024.

	$\displaystyle 0,1,00,01,10,11,001,010,011,100,101,110,0010,0101,0110,1001,1011,$
	$\displaystyle 1100,00101,01011,01100,10010,10110,11001,010110,011001,100101,$
	$\displaystyle 0110010,1011001,10010110.$

	$\displaystyle B$	$\displaystyle=\{001011,001101,0001011,0001101,0010111,0011101,00001011,00001101,$
		$\displaystyle\quad\quad 00010111,00011101,00101011,00101111,00110101,00111101\}.$

On Palindromic Periodicities

Abstract

Keywords and phrases:

Funding:

Copyright and License:

2012 ACM Subject Classification:

DOI:

Event:

Editors:

Series and Publisher:

1 Introduction

2 Preliminaries

▶ Remark 1.

3 Results for certain classes of words

3.1 Sturmian and trapezoidal words

Theorem 2.

Example 3.

Theorem 4.

Proposition 5 ([11, 9]).

Proposition 6 ([9]).

Proof of Theorem 4.

Example 7.

3.2 Rich words

Proposition 8.

3.3 Episturmian words

Theorem 9.

4 Results for generalized automatic words

Theorem 10.

Proof.

Corollary 11.

Proof.

Corollary 12.

Proof.

5 Results for some famous infinite words

5.1 The period-doubling word

Theorem 13.

Corollary 14.

5.2 The Thue–Morse word

Theorem 15.

Corollary 16.

5.3 The Rudin–Shapiro word

Theorem 17.

5.4 The regular paperfolding word

Theorem 18.

5.5 The Tribonacci word

Theorem 19.

Corollary 20.

6 Words with few palindromic periodicities

Theorem 21.

Proof.

Theorem 22.

Proof sketch..

7 Conclusions and open problems

References

$\blacktriangleright$ Remark 1.