Linear-Space LCS Enumeration for Two Strings
Abstract
Suppose we want to seek the longest common subsequences (LCSs) of two strings as informative patterns that explain the relationship between the strings. The dynamic programming algorithm gives us a table from which all LCSs can be extracted by traceback. However, the need for quadratic space to hold this table can be an obstacle when dealing with long strings. A question that naturally arises in this situation would be whether it is possible to exhaustively search for all LCSs one by one in a time-efficient manner using only a space linear in the LCS length, where we treat read-only memory for storing the strings as excluded from the space consumed. As a part of the answer to this question, we propose an -space algorithm that outputs all distinct LCSs of the strings one by one each in time, where the strings are both of length and is the LCS length of the strings.
Keywords and phrases:
algorithms, longest common subsequence, enumerationFunding:
Yoshifumi Sakai: This work was supported by JSPS KAKENHI Grant Number JP23K10975.2012 ACM Subject Classification:
Theory of computation Pattern matchingEditors:
Paola Bonizzoni and Veli MäkinenSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
Comparing two strings to find common patterns that would be most informative of their relationships is a fundamental task in parsing them. The longest common subsequences (LCSs) are regarded as such common patterns, and the problem of efficiently finding one of them has long been studied [2, 3, 5, 6, 7, 8, 9, 10, 11, 13]. Here, a subsequence of a string is the sequence obtained from the string by deleting any number of elements at any position that is not necessarily contiguous. Hence, an LCS of two strings is a common subsequence obtained by deleting the least possible number of elements from the strings. For example, if and are the target strings, then is one of the seven distinct LCSs of and . The six other LCSs are , , , , , and .
Given a pair of strings and both of length and a string of length less than , it is easy to determine whether is a common subsequence of and in time. In comparison, it is hard to determine whether is an LCS of and . The reason is that we need to know the LCS length in advance. It was revealed [1, 4] that unless the strong exponential time hypothesis (SETH) does not hold, no algorithm can determine the LCS length of and in time for any positive constant . Therefore, we cannot find any LCS in time under SETH.
On the other hand, as is well known, finding an arbitrary LCS of and is possible in time and space by the dynamic programming (DP) algorithm [13]. The space of size consumed to store the LCS lengths for all pairs of a prefix of and a prefix of can be treated as constituting a particular directed acyclic graph (DAG) such that any path from the source to the sink represents an LCS of and . This DAG is also useful in applications other than seeking a single arbitrary LCS because each LCS is represented by at least one of the paths from the source to the sink. If one considers only the problem of finding a single arbitrary LCS without intending a data structure representing all LCSs, Hirschberg [7] showed that space is sufficient to solve the problem in the same time as the DP algorithm. Excluding the read-only memory storing and , his algorithm with a slight modification performs only in space, where denotes the LCS length of and .
The advantage of -space algorithms for finding an arbitrary LCS is that they perform without reserving space, the size of which becomes pronounced when is large. Thus, a natural question that would come to mind is whether it is possible to design -space algorithms that are as accessible to all LCSs as the DP algorithm in addition to the above advantage. As a part of the answer to this question, this article shows that an -space algorithm is capable of enumerating all distinct LCSs with a delay time not significantly inferior to the running time of Hirschberg’s -space algorithm [7] for finding a single arbitrary LCS. More precisely, the algorithm proposed in this article outputs each LCS in time after the previous LCS is output, if any, which is inferior by a logarithmic factor of . Enumeration is done by introducing a DAG, called the all-LCS graph, with each path from the source to the sink corresponding to a distinct LCS and vice versa. Since the size of the all-LCS graph is , which exceeds , we design the proposed algorithm to somehow perform a depth-first search without explicitly constructing it.
2 Preliminaries
For any sequences and , let denote the concatenation of followed by . For any sequence , let denote the length of , i.e., the number of elements in . For any index with , let denote the th element of , so that . A subsequence of is obtained from by deleting zero or more elements at any positions not necessarily contiguous, i.e., the sequence for some length with and some indices with . For any indices and with , let denote the contiguous subsequence of , where with represents the empty subsequence. If (resp. ), then is called a prefix (resp. suffix) of .
A string is a sequence of characters over an alphabet set. For any strings and , a common subsequence of and is a subsequence of that is a subsequence of . Let denote the maximum of over all common subsequences of and . Any common subsequence of and with is called a longest common subsequence (an LCS) of and . The following lemma gives a typical recursive expression for the LCS length.
Lemma 1 (e.g., [13]).
For any strings and , if at least one of and is empty, then ; otherwise, if , then ; otherwise, , where and . The same also holds for the case where and .
Let any algorithm that takes certain information, specified later, of an arbitrary pair of non-empty strings and as input and uses only space to output all distinct LCSs of and , each represented by a specific form, one by one be called a linear-space LCS enumeration algorithm. We assume that the information of and given to the algorithm consists of , , and -time access to check whether or not for any pair of indices and with and with no space consumption. The worst-case time between outputting one LCS and the next LCS is called the delay time of the algorithm. This article aims to propose a linear-space LCS enumeration algorithm with delay time.
Let any index pair such that , , and be called a match. For convenience, we sometimes treat and (resp. and as virtual elements of and , respectively, both of which are identical to a virtual character, say (resp. ), that appears in neither nor , so that (resp. ) can be treated as a virtual match. We use src and snk to denote and , respectively. For any match , let and denote the indices such that . Furthermore, let the diagonal coordinate of be , by treating any match as a grid point on a two-dimensional plane. For any matches and , let (resp. ) mean that both and (resp. and ). For any non-virtual match , we call the character that is identical to both and the character corresponding to . Similarly, for any sequence of non-virtual matches, we call the concatenation of the characters corresponding to for all indices from to in this order the string corresponding to .
Let us call any sequence of non-virtual matches with an LCS-match sequence, because the string corresponding to is an LCS of and . For convenience, we sometimes treat and as virtual elements and of any LCS-match sequence , respectively. Although any LCS of and has at least one LCS-match sequence with as the corresponding string, two or more such LCS-match sequences may exist. Hence, the problem of enumerating LCSs is not equivalent to the problem of enumerating LCS-match sequences. As the representative of LCS-match sequences having the same corresponding strings, we consider the one such that for any index with , and are the shortest prefixes of and with the string corresponding to as a subsequence, respectively. We call any such LCS-match sequence front-leaning. Since any LCS of and has exactly one front-leaning LCS-match sequence with as the corresponding string, the problem of enumerating LCSs is equivalent to the problem of enumerating front-leaning LCS-match sequences. Based on this observarion, we design the proposed linear-space LCS enumeration algorithm to output all distinct front-leaning LCS-match sequences one by one instead of outputting the corresponding LCSs.
3 Algorithm
This section proposes a linear-space LCS enumeration algorithm that outputs all distinct front-leaning LCS-match sequences of and each in time.
Our approach to designing the algorithm considers a particular directed acyclic graph (DAG), which we call the all-LCS graph, such that each path from vertex to vertex represents a distinct front-leaning LCS-match sequence and vice versa, where each vertex in the graph is a different particular match. Relying on this DAG, we can enumerate LCSs by enumerating all paths from src to snk in a straightforward manner using depth-first search (DFS). The all-LCS graph we introduce is of size , which exceeds the size of space allowed for any linear-space LCS enumeration algorithm. Our proposed algorithm overcomes this situation by simulating DFS on the all-LCS graph without explicitly constructing it. We define the all-LCS graph in Section 3.1 and propose a linear-space LCS enumeration algorithm by presenting how to simulate the DFS in Section 3.2.
3.1 All-LCS graph
Conceptually speaking, the all-LCS graph is the union of the path from src to snk that passes through vertices in this order over all front-leaning LCS-match sequences , where we recall that and . The correctness of the definition can be verified because for any front-leaning LCS-match sequences that share an element, exchanging their prefixes ending at the element also yields front-leaning LCS-match sequences. However, since we need to use the all-LCS graph without knowing what front-leaning LCS-match sequences exist, the current definition is not specific enough for our situation. To address this issue, we redefine the all-LCS graph as inductively defined.
For simplicity, for any match , let and denote and , respectively. The key idea to redefine the all-LCS graph is to focus only on particular matches introduced below.
Definition 2 (valid match).
Let any match such that be called -valid, or simply valid.
Definition 3 (follower).
For any valid match , let any -valid match that is the only match with be called a -follower. Let denote the sequence of all -followers such that (and hence ). Adopting the order of elements in , let the th -follower be and let the next -follower of be , unless .
Definition 2 is conceived from the fact that for any LCS-match sequence and any index with , both and . On the other hand, Definition 3 comes from the observation that for any front-leaning LCS-match sequence and any index with , is -valid, is -valid, and is the only match such that . Sequence introduced in Definition 3 makes sense because for any distinct -followers and , if at least or , then both and ; otherwise, both and , due to condition that (resp. ) is the only match with (resp. ). Our inductive definition of the all-LCS graph is as follows (see Figure 1).
Definition 4 (all-LCS graph).
The all-LCS graph is defined inductively to be the DAG such that is a vertex and for any vertex , all -followers are vertices and any -follower is connected with by an edge from to .
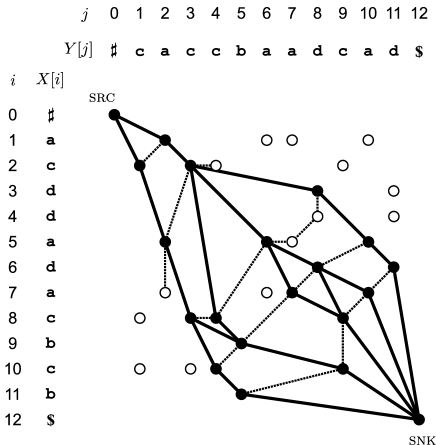
The following lemma claims that Definition 4 defines the all-LCS graph well.
Lemma 5.
The all-LCS graph has a path from vertex src to vertex snk that passes through vertices in this order if and only if is a front-leaning LCS-match sequence.
Proof.
Let be an arbitrary front-leaning LCS-match sequence, so that for any index with , is a -follower. Since src is a vertex of the all-LCS graph, induction proves that for any index with , the all-LCS graph has an edge from to , completing the “if” part of the lemma.
Consider the path of the all-LCS graph in the lemma. Since src is -valid, is a follower for any index with , and snk is -valid, we have that . Induction proves that for any index with , and are the shortest prefixes of and with the string corresponding to as a subsequence, respectively, completing the proof of the “only if” part.
The size of the all-LCS graph is as stated in the following lemma.
Lemma 6.
The number of edges in the all-LCS graph is at most .
Proof.
The number of edges in the all-LCS graph is equal to the sum of over all vertices in the graph, where is the sequence of all -followers introduced in Definition 3. For any vertex and any index with , it follows from (resp. ) that (resp. ). On the other hand, since is a -follower, is the only match with . Thus, is not a match. This implies that each is a distinct non-match index pair with and because is a match and include no match. In addition, each vertex having an odd number of -followers other than src is a distinct match with and . Therefore, the lemma holds because there exist index pairs with and .
Remark 7.
If an space is available, then as an implementation of the all-LCS graph, it is not difficult to design an -time algorithm that constructs the two-dimensional array such that each element with and is the sequence of all -followers in ascending order of the diagonal coordinate, if is a vertex of the all-LCS graph, or the empty sequence, otherwise. Once is available, we can enumerate LCSs with delay time by finding each distinct path in the all-LCS graph from src to snk in time by performing DFS.
3.2 Proposed linear-space LCS enumeration algorithm
As mentioned earlier, the linear-space LCS enumeration algorithm we propose simulates DFS on the all-LCS graph without explicitly constructing it, because the algorithm can use only space while the size of the all-LCS graph is .
3.2.1 Algorithm overview
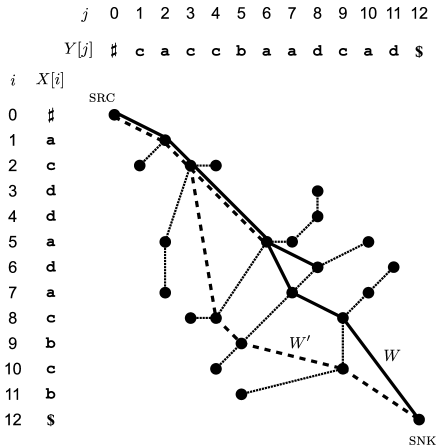
The proposed algorithm outputs each distinct front-leaning LCS-match sequence in lexicographical order of the sequence , where is the th -follower (see Definition 3). Due to this output order setting, the following index and match immediately provide the subsequent lemma, based on which we design the proposed algorithm.
Definition 8 (branching position and match).
For any front-leaning LCS-match , let the greatest index with such that is not the last -follower be called the branching position of , if any. In addition, let the next -follower of be called the branching match of , if the branching position of exists.
Lemma 9.
For any front-leaning LCS-match sequence , is the last output one if and only if has no branching position. If is the first output one, then for any index with , is the first -follower. Otherwise, , is the branching match of , and for any index with , is the first -follower, where is the last output front-leaning LCS-match sequence before and is the branching position of .
Example 10.
Consider the third and fourth output front-leaning LCS-match sequences as and , respectively, for the same and as Figure 1 (see Figure 2). Since is with , , , , , and , the branching position of is and the branching match of is . Thus, it follows from Lemma 9 that and . In addition, due to , and due to . Hence, is determined as .
The proposed algorithm denoted enumLCS obtains each distinct front-leaning LCS-match sequence using variables and . These variables are to maintain and the existing branching position of , respectively. After initializing to , for each front-leaning LCS-match sequence according to our output order setting, the algorithm executes procedure updateW to set to , outputs as , and executes procedure findBranch to set and to the branching position and match of , respectively, if existing. If the branching position of does not exist, then is set to a dummy index, indicating that is the last output one. Due to Lemma 9, induction proves that the algorithm outputs all distinct front-leaning LCS-match sequences of and one after another. A pseudo-code of enumLCS is given as Algorithm 1.
3.2.2 Space-efficient search for locally valid matches
Before presenting the details of procedures updateW and findBranch, we generalize the validity of matches to the local case and develop an algorithm that generates the stream of all the “locally” -valid matches in ascending order of the diagonal coordinate. The reason is that both updateW and findBranch are designed to simulate this algorithm.
For any valid matches and with and any match with , let denote and let denote , so that and . We define locally valid matches as follows.
Definition 11 (locally valid match).
For any valid matches and with , let any match with and be called -locally -valid, or simply -locally valid.
Note that for any valid matches , , and with , is not necessarily -locally valid. For example, , , and for the same and as Figure 2 are valid matches with but is not -locally valid. In contrast, any -locally -valid match is -valid, because and due to , , and .
The number of -locally -valid matches is , which may exceed . However, the stream of all -locally -valid matches in ascending order of the diagonal coordinate can be generated by executing the -space algorithm genStream presented as Algorithm 2.
| output matches | ||||||
|---|---|---|---|---|---|---|
| 1 | empty | |||||
| 2 | empty | |||||
| 3 | empty | |||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | ||||||
| 9 |
Lemma 12.
For any indices , , and with and any pair of an -valid match and an -valid match with , outputs all -locally -valid matches one by one in ascending order of the diagonal coordinate in time and space.
Proof.
For any index with and any index with , let and denote and , respectively, so that for any match with , and .
To find all -locally -valid matches, genStream maintains two index variables and with and . After initializing and to and , respectively, the algorithm repeatedly updates and by either increasing by one or decreasing by one and outputs as a distinct -locally -valid match, if , , and , until or . Hence, the -locally -valid matches output by the algorithm are in ascending order of the diagonal coordinate (see Table 1).
At each iteration of the algorithm, at least or . This is because otherwise there exist matches and with , , and , which implies that , a contradiction. Therefore, if , then any match with is not -locally -valid due to ; otherwise, any match with is not -locally -valid due to . Based on this fact, in each iteration of the algorithm, if , then is increased by one; otherwise, is decreased by one.
The algorithm accomplishes the above by maintaining a sequence variable of at most indices so that and for any index with , is the least index with such that . Analogously, a sequence variable of at most indices is maintained so that and for any index with , is the greatest index with such that . The algorithm executes procedure incJ (lines 9 through 13 of Algorithm 2) to increase by one and update in a straightforward way based on Lemma 1 in time and executes procedure decI (lines 14 through 18) to decrease by one and update in time symmetrically.
It follows from that both and hold if and only if all of , , , and hold. On the other hand, if and only if or . Thus, all distinct -locally -valid matches are output by the algorithm successfully in ascending order of the diagonal coordinate. Since incJ is executed at most times and decI is executed at most times, the algorithm runs in time and space.
3.2.3 Ideas for speeding up the naive method
In what follows, for simplicity, we use to represent the index maintained by enumLCS, when is output as by line 6 of Algorithm 1, where is an arbitrary front-leaning LCS-match sequence. Hence, if is the first output one, then ; otherwise, is the branching position of the last output front-leaning LCS-match sequence before . When mentioning , it is often the case that and are obvious from and , respectively. In such cases, for the sake of readability, and are omitted from the specification, and we denote it by .
A naive -space procedure completes the task of updateW and findBranch simultaneously in time as follows. For each index from to in this order, by simulating in time, we can obtain the existing next -follower of as a candidate of the branching match of , if , or otherwise, we can obtain both the first and existing second -followers of as and a candidate of the branching match, respectively. The existing last found candidate is the branching match of , based on which the branching position of can also be determined.
We reduce the execution time of the naive procedure to by considering an approximation of that can be obtained faster than and transformed into easily. The definition of is as follows.
Definition 13 (approximation of ).
For any front-leaning LCS-match sequence , let denote the sequence such that and for any index with , is the -locally -valid match with the least diagonal coordinate.
Example 14.
The difference between and that allows us to obtain faster than is that each element of with is defined dependent on while the corresponding element of is defined independent of . That is, unlike the case of , where each element of must be determined in ascending order of from to , each element of can be determined in any order. Procedure updateW obtains by recursively decomposing the problem of determining into the problems of determining and determining , which is done by simulating until the first match is output to determine . The following lemma guarantees that our approach works by claiming that because this implies that is -locally -valid.
Lemma 15.
For any front-leaning LCS-match sequence , is an LCS-match sequence.
Proof.
Since , it suffices to show that for any index with , . Since is -locally -valid, there exists a -locally -valid match with . It follows from and neither nor that . This implies that because . Symmetrically, there exists a -locally -valid match with , which satisfies that . Thus, .
The conversion from to is possible in time by determining using and for each index from to in this order based on the following Lemma.
Lemma 16.
For any front-leaning LCS-match sequence and any index with , is the match with the least index that is greater than .
Proof.
It follows from Lemma 15 that . Due to definition of , there exists no -valid match with such that . Therefore, if , then the match in the lemma is , i.e., the first -follower. In addition, because is a match. This implies from due to Lemma 15 that if , then . Thus, induction proves the lemma.
| 1 | |||||
|---|---|---|---|---|---|
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 | |||||
| 10 | |||||
| 11 | empty | empty |
The reason for splitting the naive procedure into updateW and findBranch is that once is available, we can efficiently determine the existing branching match of it as follows. As long as searching only for the branching match, iterative updates of in execution of can start from rather than from , if and are appropriately maintained. Let denote execution of the modified genStream as above and let denote maintained in . A key observation for improving time efficiency is that can be used as for any index because is a prefix of (see Table 2). This immediately implies that adopting as maintained in instead of and doing for each from to in descending order allow to initialize not from scratch but staring from the resulting after doing , unless . Another crucial observation is that only the first element of is sufficient to be maintained in each and update of can be done by scanning instead of . Based on these observations, we design findBranch as a modification of .
3.2.4 Procedures updateW and findBranch
Based on Lemmas 15 and 16, updateW obtains and transform it to for each front-leaning LCS-match sequence . Algorithm 3 presents a pseudo-code of updateW, in which recursive decomposition of the problem of determining is implemented as a sequential process. The following lemma assures that this procedure works well.
Lemma 17.
For any front-leaning LCS-match sequence , if is given as , then updateW determines as in time and space.
Proof.
Lines 1 through 8 of updateW implemented as Algorithm 3 determines , i.e., the -locally -valid match having the least diagonal coordinate, as for each index with . This can be verified because it follows from Lemma 15 that is the -locally -valid match with the least diagonal coordinate, implying that can be obtained as the first match output by due to Lemma 12. Execution of lines 1 through 8 completes in time because the number of iterations of lines 2 through 8 is and it follows from Lemma 12 that each iteration executes in time. Once is available as , for each index from to in this order, lines 10 through 12 determine as from and in time based on Lemma 16.
As mentioned in Section 3.2.3, we adopt a modification of as findBranch to determine the existing branching match of in time. A pseudo-code of findBranch is presented as Algorithm 4. Note that incJ in findBranch (lines 12 through 15) maintains only the first element of maintained by in a straightforward way. In contrast, decI in findBranch (lines 16 through 20) is the same as decI in , which implies that maintained by is a prefix of maintained by findBranch. The following lemma claims that findBranch works successfully.
Lemma 18.
For any front-leaning LCS-match sequence given as , findBranch determines the branching position and match of as and , respectively, if existing, or sets to a dummy index, otherwise, in time and space.
Proof.
After initialization of variables , , , and by line 1 of findBranch implemented as Algorithm 4, for each index from to in this order, lines 3 through 11 search for the next -follower of . In this process for , is initialized to by line 3 and is initialized to by line 4. Since and are also updated appropriately by lines 3 and 4, respectively, lines 5 through 11 simulate execution of until the -locally -valid match with and having the least diagonal coordinate is found. If found, then line 7 terminates the execution of findBranch after setting to as the branching position of and setting to , instead of , as the branching match of due to an argument similar to the proof of Lemma 16.
For any index with , the process for implemented by lines 2 though 11 executes incJ times each in time. On the other hand, for each index with , decI is executed at most once in time throughout the execution of findBranch. Thus, findBranch runs in time and space.
Theorem 19.
Algorithm enumLCS with procedures updateW and findBranch works as a linear-space LCS enumeration algorithm that outputs all distinct front-leaning LCS-match sequences of and each in time.
4 Concluding remarks
This article proposed an algorithm that takes strings and as input and uses space, excluding the space for storing and , to enumerate all distinct LCSs of and each in time. The all-LCS graph, of size , introduced in Section 3.1 allows us to determine all distinct LCSs each in time. Given this, whether we can remove the logarithmic factor of from the delay time achieved by the proposed algorithm is a natural question arising from a space-delay tradeoff perspective. The author recently claimed in [12] that adopting a variant of the linear-space LCS-finding algorithm of Hirschberg [7] as an alternative of our -time procedure updateW can resolve this question in the affirmative.
References
- [1] Amir Abboud, Arturs Backurs, and Virginia Vassilevska Williams. Tight hardness results for lcs and other sequence similarity measures. In 2015 IEEE 56th Annual Symposium on Foundations of Computer Science, pages 59–78. IEEE, 2015. doi:10.1109/FOCS.2015.14.
- [2] Alberto Apostolico. Improving the worst-case performance of the hunt-szymanski strategy for the longest common subsequence of two strings. Information Processing Letters, 23(2):63–69, 1986. doi:10.1016/0020-0190(86)90044-X.
- [3] Alberto Apostolico and Concettina Guerra. The longest common subsequence problem revisited. Algorithmica, 2:315–336, 1987. doi:10.1007/BF01840365.
- [4] Karl Bringmann and Marvin Künnemann. Quadratic conditional lower bounds for string problems and dynamic time warping. In 2015 IEEE 56th Annual Symposium on Foundations of Computer Science, pages 79–97. IEEE, 2015. doi:10.1109/FOCS.2015.15.
- [5] Yo-lun Chin, Chung-kwong Poon, et al. A fast algorithm for computing longest common subsequences of small alphabet size. University of Hong Kong, Department of Computer Science, 1990.
- [6] Jun-Yi Guo and Frank K Hwang. An almost-linear time and linear space algorithm for the longest common subsequence problem. Information processing letters, 94(3):131–135, 2005. doi:10.1016/j.ipl.2005.01.002.
- [7] Daniel S. Hirschberg. A linear space algorithm for computing maximal common subsequences. Communications of the ACM, 18(6):341–343, 1975. doi:10.1145/360825.360861.
- [8] James W Hunt and Thomas G Szymanski. A fast algorithm for computing longest common subsequences. Communications of the ACM, 20(5):350–353, 1977. doi:10.1145/359581.359603.
- [9] Costas S Iliopoulos and M Sohel Rahman. A new efficient algorithm for computing the longest common subsequence. Theory of Computing Systems, 45(2):355–371, 2009. doi:10.1007/s00224-008-9101-6.
- [10] William J Masek and Michael S Paterson. A faster algorithm computing string edit distances. Journal of Computer and System sciences, 20(1):18–31, 1980. doi:10.1016/0022-0000(80)90002-1.
- [11] Narao Nakatsu, Yahiko Kambayashi, and Shuzo Yajima. A longest common subsequence algorithm suitable for similar text strings. Acta Informatica, 18:171–179, 1982. doi:10.1007/BF00264437.
- [12] Yoshifumi Sakai. Linear-space LCS enumeration with quadratic-time delay for two strings. arXiv preprint arXiv:2504.05742, 2025. doi:10.48550/arXiv.2504.05742.
- [13] Robert A Wagner and Michael J Fischer. The string-to-string correction problem. Journal of the ACM (JACM), 21(1):168–173, 1974. doi:10.1145/321796.321811.
