Geometric Bipartite Matching Based Exact Algorithms for Server Problems
Abstract
For any given metric space, obtaining an offline optimal solution to the classical -server problem can be reduced to solving a minimum-cost partial bipartite matching between two point sets and within that metric space.
For -dimensional metric space, we present an time algorithm for solving this instance of minimum-cost partial bipartite matching; here, represents the spread of the point set, and is the query/update time of a -dimensional dynamic weighted nearest neighbor data structure. Our algorithm improves upon prior algorithms that require at least time. The design of minimum-cost (partial) bipartite matching algorithms that make sub-quadratic queries to a weighted nearest-neighbor data structure, even for bounded spread instances, is a major open problem in computational geometry. We resolve this problem at least for the instances that are generated by the offline version of the -server problem.
Our algorithm employs a hierarchical partitioning approach, dividing the points of into rectangles. It maintains a partial minimum-cost matching where any point is either matched to another point or to the boundary of the rectangle it is located in. The algorithm involves iteratively merging pairs of rectangles by erasing the shared boundary between them and recomputing the minimum-cost partial matching. This continues until all boundaries are erased and we obtain the desired minimum-cost partial matching of and . We exploit geometry in our analysis to show that each point participates in only number of augmenting paths, leading to a total execution time of .
We also show that, for the norm and dimensions, any algorithm that can solve instances of the offline -server problem with an exponential spread in time can be used to compute minimum-cost bipartite matching in a complete graph defined on two -dimensional point sets under the norm within time. This suggests that removing spread from the execution time of our algorithm may be difficult as it immediately results in a sub-quadratic algorithm for bipartite matching under the norm.
Keywords and phrases:
Minimum-Cost Bipartite Matching, Server Problems, Primal-Dual ApproachCopyright and License:
2012 ACM Subject Classification:
Theory of computation Computational geometryFunding:
This research was supported by NSF grants CCF 2514753 and CCF 2223871.Editors:
Oswin Aichholzer and Haitao WangSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
This paper considers two classical optimization problems: the offline -server problem and the minimum-cost bipartite matching problem in geometric settings.
Offline -server problem and its variant.
Consider a sequence of requests in a metric space equipped with the cost function . The cost of a single server servicing the requests in is the sum of the distances between every consecutive pair of points in the sequence, i.e., . Given a sequence of requests and an integer , the -sequence partitioning problem (or simply the -SP problem) requires partitioning the requests in into subsequences so that is minimized. The optimal solution for the -sequence partitioning problem is the cheapest way for servers to service all of the requests in . We also consider a variant: the -sequence partitioning with initial locations problem (or the -SPI problem). Here, in addition to the requests , we are also given the initial locations for the servers. The objective of this problem is to partition into subsequences so that the initial location of server appears in the first element of the subsequence and the cost is minimized. The optimal solution to the -SPI problem is the offline optimal solution to the well-known -server problem.
We assume that the requests in and the initial locations in are scaled and translated so that they are contained inside the unit hypercube . Such scaling and translation do not impact the optimal solutions for the -SP and -SPI problems. We define the diameter to be the largest distance between any two request locations in and the closest pair distance, denoted by , to be the smallest non-zero distance between any two requests in . The spread, denoted by , is the ratio of the diameter to the closest-pair distance, i.e., .
Minimum-cost bipartite matching.
Consider a weighted bipartite graph , where each edge between and is assigned a real-valued cost. Let . A matching of size , or simply a -matching, is a set of edges in that are vertex-disjoint. The cost of any matching is the sum of the costs of its edges. Given a parameter , the minimum-cost bipartite -matching problem seeks to find a -matching with a minimum cost. When , a matching of size is called a perfect matching. When and are -dimensional point sets and the cost of any edge between and is the distance , the problem of finding the minimum-cost bipartite -matching is also called the (partial) geometric bipartite matching problem.
Relating the two problems.
Chrobak et al. [4] established a reduction from the minimum-cost bipartite -matching problem to the -SPI problem.
Lemma 1 ([4, Theorem 11]).
Any algorithm that computes an optimal solution to the -SPI in an arbitrary metric space in time can also find, in time, a minimum-cost perfect matching in any complete bipartite graph with real-valued costs.
We strengthen the connection between the two problems by showing a reduction in the reverse direction, i.e., we reduce the -SP (resp. -SPI) problem to the minimum-cost bipartite -matching problem. Given an input sequence of requests to the -SP problem, we construct a bipartite graph with a vertex set and a set of edges as follows. Vertex Set: For each request , we create a vertex (resp. ) in (resp. ) and designate it as the entry (resp. exit) gate for request . Edge Set: The exit gate of request is connected to the entry gate of every subsequent request with with an edge. The cost of this edge is . Any minimum-cost -matching in can be used to find an optimal solution to the -SP problem. See Figure 1.
For the -SPI problem, for each server , we add a vertex at the initial location to and connect to the entry gate of every request in . The cost of this edge is . A minimum-cost -matching in this graph can be converted to an optimal solution for the -SPI problem.
A different reduction from -SP and -SPI problems to the minimum-cost flow problem has been presented in previous works [4, 22, 24], leading to the development of time algorithm. However, unlike our reduction, their approach generates instances that include edges whose costs are and fails to maintain the metric properties of costs.
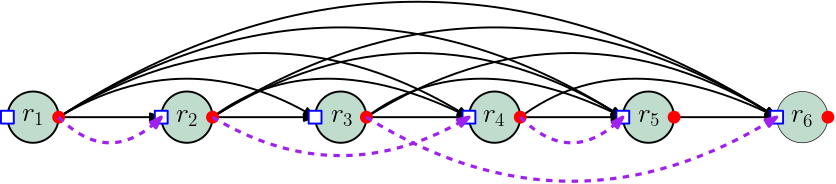
Lemma 2.
An optimal solution for an instance (resp. ) of -SP (resp. -SPI) problem can be found by computing a minimum-cost matching of size (resp. ) in (resp. ).
Finally, we extend the reduction Chrobak et al. [4] to geometric settings and provide a reduction from the geometric minimum-cost matching problem under the -norm to the geometric version of the -SPI problem. This reduction, however, creates an instance of the -SPI problem with a spread of . Lemma 3 follows directly from this reduction.
Lemma 3.
Any algorithm that can solve the -dimensional -SPI problem under the costs in time can also be used to solve an instance of minimum-cost bipartite matching under the costs on a complete graph in time.
Related work.
For a graph with edges and vertices, the classical Hungarian algorithm computes a minimum-cost -matching for all values of [11, 16]. Starting with an empty matching, the Hungarian algorithm iteratively builds a minimum-cost -matching from the maintained minimum-cost -matching in time by finding a minimum net-cost augmenting path, i.e., an augmenting path that increases the matching cost by the smallest value. The overall execution time of the Hungarian algorithm is , or when . Despite substantial efforts, this remains the most efficient algorithm for the problem. Notable exceptions include specialized cases, such as graphs with small vertex separators [13] or integer edge weights [2, 5, 6].
In geometric settings, Vaidya showed that each iteration of the Hungarian algorithm can be implemented in time, where represents the query/update time of a dynamic weighted nearest neighbor (DWNN) data structure. Thus, the minimum-cost -matching can be computed in time, which is sub-cubic in provided is sub-linear. For instance, for the norm and dimensions, [27] and for the norm and dimensions, [8]. In these cases, the Hungarian algorithm can be implemented in near-quadratic time.
Designing algorithms that compute a minimum-cost matching using sub-quadratic DWNN queries remains a central open problem in computational geometry. There are three notable exceptions. First, for points with integer coordinates and the and norms, Sharathkumar and Agarwal [26] adapted a cost-scaling algorithm [5] and presented an algorithm that executes in time. Second, Sharathkumar [25] extended this result to 2-dimensional point sets with integer coordinates and the costs. Their result, however, relies on planarity as well as the edge costs being the square root of integers and does not extend to -dimensional points with real-valued coordinates. Third, Gattani et al. [7] presented a divide-and-conquer algorithm (GRS algorithm) with a worst-case runtime of , where is the spread of the points. For 2-dimensional stochastic points drawn from an unknown distribution, however, the expected runtime of the GRS algorithm improves to .
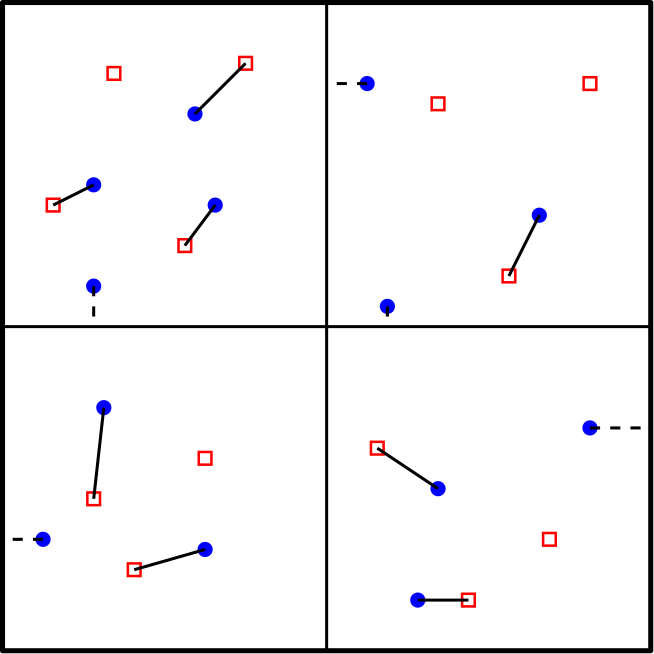
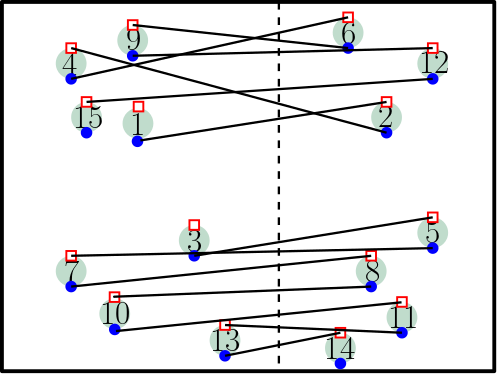
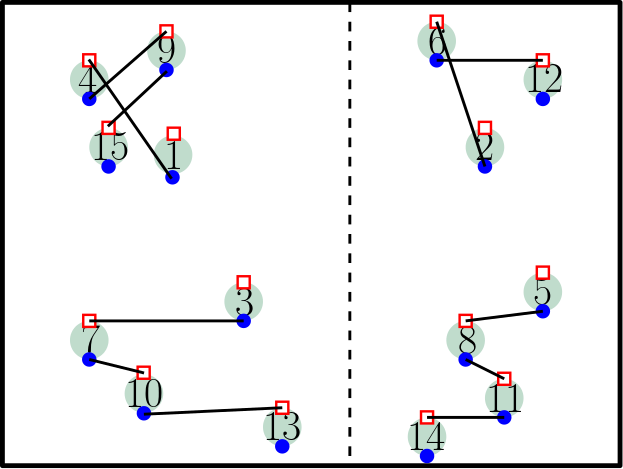
The GRS algorithm uses a randomly-shifted quadtree to divide the problem into smaller subproblems. Within each square of the quadtree, it recursively computes a minimum-cost extended matching, allowing each point of in to match either to a point of in or to the boundaries of (Figure 2(left)). The algorithm then combines the matchings of the child squares by erasing their common boundaries, freeing points of that were matched to those boundaries (Figure 2(middle)), and then it iteratively matches the freed points.
Gattani et al. [7] showed that for stochastic point sets and , most points in will match to a close-by point in and only points will match to boundaries. Thus, erasing these boundaries creates free points, each again matched in time, resulting in an overall runtime of . However, this efficiency does not extend to arbitrary point sets. For instance, if all points in lie in one child and all points in lie in another child , then all edges of a minimum-cost matching cross the boundaries. In this case, the minimum-cost extended matching in matches all points in to its boundary (Figure 2(right)), and erasing the boundary creates free points. Hence, the merge step takes time. Furthermore, unlike the Hungarian algorithm, the GRS algorithm does not guarantee optimal intermediate matchings and cannot compute minimum-cost -matchings.
Our results.
The optimal solutions to the -SP (resp. -SPI) problems can be computed in time by non-trivially adapting the Hungarian algorithm to find a minimum-cost -matching (resp. -matching) in (resp. ). This algorithm, however, makes quadratic queries to a DWNN data structure when . The main contribution of this paper is the design of a novel algorithm that, for any , computes the optimal solution to the -SP and -SPI problems using only a sub-quadratic number of DWNN queries.
Theorem 4.
Given any sequence (resp. ) of requests (resp. requests and initial server locations) in dimensions with a spread of , and a value , there exists a deterministic algorithm that computes the optimal solution for the instance of -SP (resp. -SPI) problem under the norm in time.
Our algorithm also extends to higher dimensions, and for any dimension , it computes optimal solutions to the -SP and -SPI problems in time.
Designing geometric bipartite matching algorithms that perform a sub-quadratic number of queries to a DWNN data structure is challenging. Nevertheless, Theorem 4 shows that the bipartite matching instances generated by -SP and -SPI problems with bounded spread can be solved using sub-quadratic DWNN queries. For unbounded spread cases, the challenge remains elusive, at least for the -SPI problem since, by Lemma 3, such an algorithm yields a sub-quadratic solution for the -dimensional minimum-cost bipartite matching problem under costs.
Our algorithm uses a hierarchical partitioning tree, whose nodes (referred to as cells) are axis-parallel rectangles with an aspect ratio of at most , and each cell splits into two smaller rectangles, forming its children. Our algorithm maintains a set of current cells that partition the input points and computes a minimum-cost extended -matching, where the points in are allowed to match to the cell boundaries. It then replaces a pair of sibling rectangles in with their parent, effectively erasing their shared boundary and creating additional free points. These free points are then matched again by finding minimum net-cost augmenting paths. When all the boundaries are erased, the algorithm terminates with the desired minimum-cost -matching.
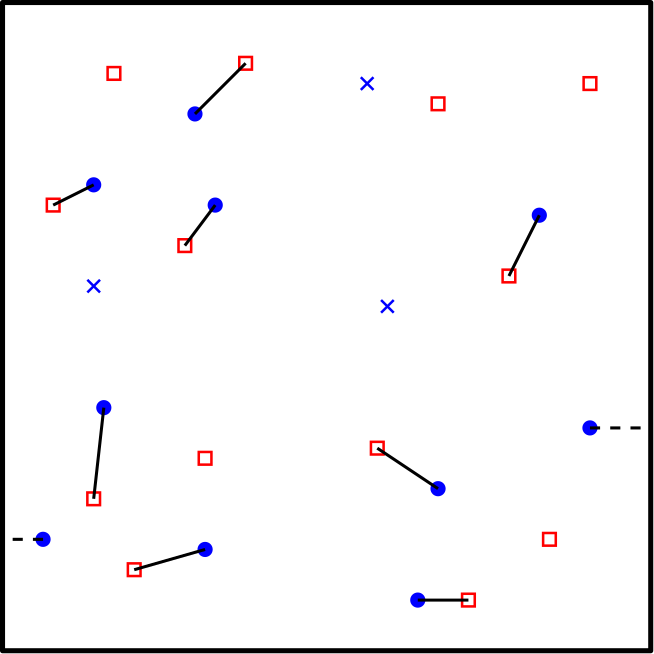
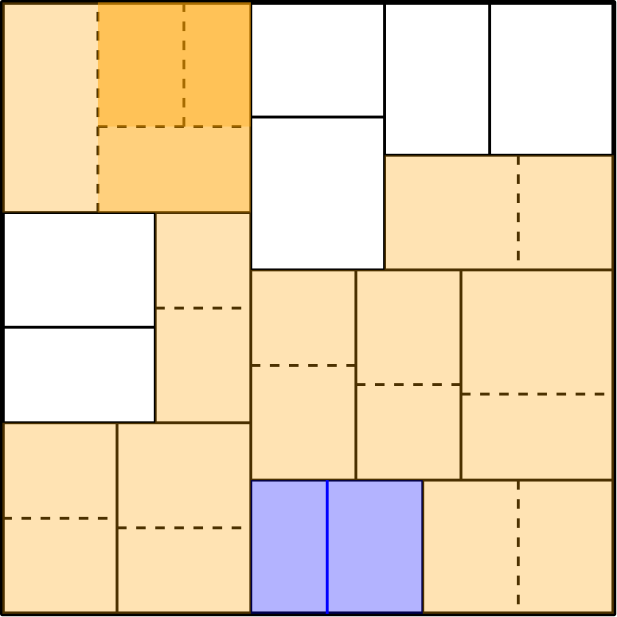
Our efficiency analysis faces three main hurdles. First, while finding a minimum net-cost augmenting path typically requires a search on the entire graph, we show that for extended matchings, such paths lie entirely within a current cell, allowing efficient local searches inside each current cell and selecting the global minimum across cells. Second, bounding the time to merge two cells is challenging, especially since some current cells may hold points, where each point is matched to a far away point in the optimal solution (Figure 3(left)). We address this challenge by showing that any minimum-cost extended matching has only points matched to the shared boundary. To establish this, we critically use the fact that every sub-problem has a hidden low-cost high-cardinality matching with sub-linearly many free points (see Figure 3 (right)). Finally, the free points in our extended matching may differ from those in the minimum-cost -matching . For instance, a point may be free in but matched to the boundary in , leaving another point unmatched. While correcting such mismatches via alternating and augmenting paths can take time each (leading to a naïve bound of ), we use geometry to show that only such corrections occur for each cell, yielding an overall runtime to .
Our proof techniques also refine the analysis of the GRS algorithm when the cost between points and is for any . Prior work showed that the GRS algorithm computes the minimum-cost perfect matching between two 2-dimensional stochastic point sets in time [7], which implies a quadratic number of queries to the DWNN data structure as . Raghvendra et al. [20] observed that, for any , there exists a low-cost, high-cardinality matching with sublinear free points. Building on a similar observation and our novel analysis techniques, we show that the GRS algorithm makes only a sub-quadratic number of DWNN queries, regardless of the value of .
Theorem 5.
Suppose is a set of points inside the unit square and is a subset chosen uniformly at random from all subsets of size . Let . Then, there exists an algorithm that computes the minimum-cost perfect matching on the complete bipartite graph on and under costs in expected time.
The setting originally considered in the analysis of the GRS algorithm [7], where and are samples from the same distribution, is a special case of randomly partitioning a set of points into two sets and of points, considered in Theorem 5.
Due to space limitations, we restrict the description of our algorithm and its analysis to the -SP problem in dimensions. All other results, including extensions to higher dimensions, are presented in the full version of our paper.
2 Geometric Primal-Dual Framework
Let be an input to the -SP problem, where the distance between two locations and is given by . In this section, we introduce a primal-dual framework based on hierarchical partitioning to compute a minimum-cost -matching in . We begin by describing the hierarchical partitioning scheme.
2.1 Hierarchical Partitioning
Using , we construct a hierarchical partitioning recursively. Each node of is an axis-parallel rectangle, referred to as a cell. The root node, , contains all points in . For each node , let and be the points of and inside and let . If (i.e., is empty or contains the entry and exit gates of a single request), then is marked as a leaf node. Otherwise, we partition into two smaller rectangles as follows. Let be the larger of the length and width of rectangle . Without loss of generality, assume that is the width of and let be the -coordinate of the bottom-left corner of . For any value , define ; here, denotes the coordinate of the point . Let . We partition into two smaller rectangles by using a vertical line defined by and add them as the children of to . We refer to the segment partitioning into its two children as its divider and denote it by . See Figure 4(left). For any cell , the four sides of its rectangle are defined by the dividers of its ancestor or the boundaries of the root square. This completes the construction of . Note that the height of the tree is . A simple sweep-line algorithm can compute in time. Using this procedure, we construct in time.


Lemma 6.
For each cell of , the ratio of the largest to the smallest side of is at most . Furthermore, the number of points of with a distance smaller than to the divider is .
Recollect that a matching in is a subset of vertex-disjoint edges. We refer to a point as unmatched in if it does not have an edge of incident on it and matched otherwise. The following structural property of the -SP problem will be critical in bounding the efficiency of our algorithm.
Lemma 7.
For any cell of , there exists a matching between that matches all except points of and has a cost .
2.2 Extended Bipartite Matching
Suppose we are given a subset of cells from that partitions , i.e., the cells of are interior disjoint and these cells cover the root square . Let denote the shortest distance from to the boundaries of the cell . For any point inside , let be the cell of that contains . We define . We extend the definition of matching to allow points in to match to the boundaries of cells in . A -extended matching consists of a matching as well as a subset of points of that are unmatched in but instead matched to the boundaries of the cells of that contain them. See Figure 4(right). The cost of a -extended matching is
| (1) |
We refer to all points of as boundary-matched. All points of that are neither matched in nor boundary-matched are considered free. All points of that are not matched in are also considered free. The size of is equal to . When is clear from the context, we refer to as an extended matching. An extended matching of size with the minimum cost is called a minimum-cost -extended -matching.
Consider the partitioning , where is the root cell of . Using the fact that the input points are far from the boundaries of , we show in Lemma 8 below that any minimum-cost -extended matching of size is also a minimum-cost -matching, i.e., no point of is boundary-matched in .
Lemma 8.
Suppose , where is the root cell of . Let be a minimum-cost extended -matching on , for . Then, the matching is a minimum-cost -matching.
Let denote a -extended matching. Any path on the graph whose edges alternate between matching and non-matching edges in is called an alternating path. An alternating path is called an augmenting path if starts from a free point and ends with either (i) a free point , or (ii) a point . We augment the extended matching along an augmenting path by updating its matching and for case (ii), we match to the boundary and update to include . The net-cost of in case (i) is , and in case (ii) is
From Lemma 8, given a sequence of requests in the unit square, one can compute an optimal solution to the -SP problem on by computing a minimum-cost -extended -matching on . Given a partitioning , to compute a minimum-cost -extended -matching, similar to the Hungarian algorithm, one can start from an empty extended matching and iteratively augment along a minimum net-cost augmenting path. In the next section, we present a primal-dual framework that our algorithm uses to efficiently compute minimum net-cost augmenting paths.
2.3 A Constrained Dual Formulation for Extended Matchings
Suppose is a set of cells of partitioning the root cell . Consider a -extended matching on along with a set of non-negative dual weights . Let be the set of free points of with respect to . We say that is feasible if,
| (2) | ||||||
| (3) | ||||||
| (4) | ||||||
| (5) | ||||||
| (6) |
For any edge , the slack of is defined as . The edge is admissible if . For any point , the slack of is defined as . For any feasible extended matching , the slack of every edge as well as every point is non-negative. Recall that an augmenting path starts at a free point and ends at (i) a free point or (ii) a point . The path is admissible if all edges of are admissible and in case (ii), the slack of the end-point is . The following properties of extended feasible matchings are critical in the design of an efficient and correct algorithm.
Lemma 9.
Given a feasible -extended -matching and a set of non-negative dual weights on , let be a minimum net-cost augmenting path with respect to . Let, for any , . Then,
-
(a)
all points of lie inside a single cell of , and
-
(b)
if, for every cell , and for all free points , , then is a minimum-cost extended -matching.
The property described in Lemma 9(a) is important for the design of an efficient algorithm. Unlike the Hungarian algorithm, which searches the entire graph for the minimum net-cost augmenting path, our algorithm can find the minimum net-cost augmenting path by searching for the cheapest augmenting path inside each cell and then taking the smallest among them. Thus, we can replace a global search with a search inside each cell of . The property in Lemma 9(b) is important for the design of a correct algorithm since it provides conditions under which an extended matching is a minimum-cost extended matching. Our algorithm is designed to maintain these conditions as invariants during its execution. Lemma 10 provides a method to update the dual weights, which is essential during the process of merging cells.
Lemma 10.
Suppose is a feasible -extended matching and is a minimum net-cost augmenting path. For any cell , define , and suppose and for all free points . Then, one can update the dual weights in time such that remains feasible, for all , and for all free points .
The next lemma provides critical properties that allow for correctly and efficiently merging cells in .
Lemma 11.
For a cell of , suppose and denote its two children, and let denote a partitioning containing and . Let . Given a feasible -extended matching , let denote the subset of boundary-matched points that are matched to the divider of . Then,
-
(a)
the -extended matching is also feasible, and,
-
(b)
.
From Lemma 11(a), erasing a divider does not cause the feasibility conditions to be violated. The proof of Lemma 11(a) relies on the fact that when we erase the divider of a cell in , the RHS of (4) will only increase and so it is not violated. Despite preserving the feasibility conditions, erasing the boundary may result in the violation of Lemma 9(b), i.e., the matching may no longer be a minimum-cost extended matching. In our algorithm in Section 3, we describe a process to adjust the matching and dual weights and obtain a minimum-cost extended matching.
Residual Graph.
Similar to the Hungarian algorithm, we define a residual graph that assists in finding the minimum net-cost augmenting path. Consider a feasible -extended matching along with a set of dual weights on points of . For each cell , we define a residual graph . The vertex set of is a source vertex and the points in . For any edge inside , if (resp. ), there is an edge directed from to (resp. from to ) with a weight in . Furthermore, there is an edge directed from to every free point with a weight .
3 A Sub-Quadratic Algorithm for the -SP Problem
In this section, we describe an algorithm that, given a sequence of requests in -dimensions, computes the optimal solution to the -SP problem in time.
3.1 Algorithm
Initialize to the leaf cells of . Let be the extended matching maintained by the algorithm and initialized to and . For each point , let denote its dual weight initialized to . Let , initialized to , be the free points of with respect to . For each cell that contains at least one free point , let denote the minimum net-cost augmenting path inside . Initially, since is a leaf of , it contains only one point , and therefore, is this point with a net-cost equal to . Our algorithm maintains a priority queue storing every leaf cell with at least one free vertex with a key of . At any time during the execution of our algorithm, let be the cell with the smallest key in and let be the key of . Execute the following steps until becomes empty:
-
While ,
-
–
Extended Hungarian search step: Extract the cell with the minimum key of from . Augment the matching along and update the key of in (See Section 3.1.1 for details).
-
–
-
Merge step: If , remove from and return the matching of . Otherwise, pick a cell with the smallest perimeter and let and be the parent and sibling of in , respectively. Erase the divider of , i.e., set . We execute a Merge procedure that updates the matching inside the cell so that is at least (See Section 3.1.2 for details). At this point, the size of the updated extended matching may not be , i.e., there may be more than free points.
Invariants.
For each cell , let . During the execution of our algorithm,
-
(I1)
the extended matching is feasible,
-
(I2)
For each cell , and for all free point , , and,
-
(I3)
The -value is non-decreasing. Furthermore, after each step of the algorithm, denotes the smallest net-cost of all augmenting paths with respect to .
3.1.1 Details of the Extended Hungarian Search Step
Given a feasible extended matching and a cell , the extended Hungarian search procedure computes the minimum net-cost augmenting path and augments along . It then computes the new minimum net-cost augmenting path and updates the key of in to be its net-cost. This procedure is similar to the classical Hungarian search procedure executed on and is mildly modified to include the augmenting paths that end at the boundary of . Details of the procedure are as follows.
-
1.
Update duals: With as the source vertex, execute Dijkstra’s shortest path algorithm on the residual graph . Let be the shortest path from to each and let be the cost of . Let
(7) For any , if , set .
-
2.
Augment: Let be the point realizing the minimum distance in Equation (7). Let be the augmenting path obtained by removing . Augment along .
-
3.
Update key: If has no free points, then remove from . Otherwise,
-
(a)
Recompute the residual graph with respect to the updated matching,
-
(b)
With as the source, execute the Dijkstra’s shortest path algorithm on . For each , let be the distance from to .
-
(c)
Update the key of in to .
-
(a)
Lemma 12 establishes the properties of the extended Hungarian search procedure.
Lemma 12.
After the execution of the extended Hungarian search procedure for a cell , the extended matching remains feasible, for all points , and for all free points . Furthermore, the path computed by the procedure is a minimum net-cost augmenting path inside . After augmenting along , the updated key for is the smallest net-cost of all augmenting paths inside and is at least .
3.1.2 Details of the Merge Step
Given a feasible extended matching , any cell of where both of its children and are in , and a value , the merge procedure uses the algorithm in Lemma 10 to update the dual weights inside (resp. ) so that remains feasible, the dual weights of all points in (resp. ) are at most , and the dual weight of all free points (resp. ) is (resp. ). The procedure then updates and makes the points matched to the divider free. While there exists a free point with ,
-
1.
With as the source, execute Dijkstra’s shortest path algorithm on the residual graph . For each , let be the shortest path from to in and let be its cost. Define
(8) -
2.
Let be the point realizing the minimum value in Equation (8). Let be the path obtained by removing from the path .
-
(a)
If and (i.e., is determined by the third element in the RHS of Equation (8)), then is a path from a free point to the matched point . For each , if , update its dual weight to . The path is an admissible alternating path with respect to the updated dual weights. Set . Note that is now a free point with .
-
(b)
Otherwise, is an augmenting path. For each , if , update its dual weight to . The path is an admissible augmenting path with respect to the updated dual weights. Augment along .
-
(a)
At the end of this execution, all free points of in have a dual weight of . Finally, we update the key for by executing steps 3(a)–(c) from the extended Hungarian search step.
The following lemma states the useful properties of the merge step.
Lemma 13.
After the execution of the merge procedure on a cell , the updated extended matching is feasible, the dual weights for every is at most , and for all free points . Furthermore, the updated key for is the smallest net-cost of all augmenting paths within and is at least .
3.2 Analysis
We begin by showing in Section 3.2.1 that the three invariants (I1)–(I3) hold during the execution of our algorithm and use them to show the correctness of our algorithm. We then show in Section 3.2.2 that the running time of our algorithm is .
3.2.1 Correctness
Our algorithm initializes with a feasible -extended matching and sets all dual weights and to . Therefore, (I1) and (I2) hold at the start of the algorithm. The extended Hungarian search (Lemma 12) as well as the merge step (Lemma 13) do not violate the feasibility of the extended matching and therefore (I1) holds during the execution of the algorithm. The extended Hungarian search (Lemma 12) and the merge (Lemma 13) procedures keep the dual weight of every point inside at or below , while ensuring that the dual weight of free points inside is ; hence, (I2) holds. Finally, both the extended Hungarian search (Lemma 12) and the merge (Lemma 13) procedures update the key of to the smallest net-cost of all augmenting paths inside and do not decrease the key of any cell. From this observation, (I3) follows in a straightforward way.
From (I1) and (I2), our algorithm maintains a feasible -extended matching where, for each cell , . From (I3), is equal to the minimum net-cost of all augmenting paths with respect to ; combining this with Lemma 9(b), we conclude that is a minimum-cost -extended matching. Upon termination, the algorithm returns a minimum-cost -extended -matching for , which from Lemma 8 has no boundary-matched points. Therefore, this matching is also a minimum-cost -matching, as desired.
3.2.2 Efficiency
Both the merge step and the extended Hungarian search step require an execution of Dijkstra’s shortest path algorithm on . In the full version of our paper, we show that this execution takes time. Using this, we analyze the execution time.
We begin by establishing a bound on the execution time of the merge step, which combines and into a single cell . At the start of this step, the dual weight of all free points in and are raised to (from Lemma 10). As a result, once the divider is removed, the only free points with dual weights below are those that are matched to the divider . From Lemma 11(b), the number of points matched to is . Therefore, the while-loop in the merge procedure executes only times. Since each iteration takes time, the total execution time of a single execution of the merge step is . Given that each point is in only many cells of , the total time taken by the merge step across all cells of is .
Similarly, if the execution time for the extended Hungarian search within a single cell is bounded by , then the cumulative execution time of the extended Hungarian search across all cells – and consequently, the total runtime of the entire algorithm – can be bounded by . In the remainder of our analysis, we establish a bound of for the time taken by the extended Hungarian search within a single cell . Recall that the algorithm selects a cell containing the minimum net-cost augmenting path from the priority queue and performs an extended Hungarian search procedure within , requiring time. To analyze the total execution time of the extended Hungarian search procedure, we show that any cell can be selected by the algorithm at most times. In particular, we categorize the selection of as a low-net-cost case if and a high-net-cost case otherwise. First, we show that in the high-net-cost case (), the number of free points remaining in is , and as a result, the total number of high-net-cost selections of is .
Lemma 14.
Given a feasible extended matching and any cell , if the net-cost of the minimum net-cost augmenting path inside is greater than , then the number of free points of is .
Next, we bound the number of low-net-cost selections of . Define as the set of all cells that are processed by the merge procedure while and (Figure 5). Our algorithm always picks the smallest perimeter cells to merge, and as a result, we obtain the following lemma.
Lemma 15.
For any non-leaf cell in and any cell , .
For any cell , the merge step erases the divider and makes the points that are matched to free. Each of these new free points might cause to be selected by the algorithm. Therefore, to bound the number of low-net-cost selections of , we show that the total number of points that are matched to the dividers of the cells in is at most . For any cell , let denote the set of points of that are matched to the divider when our algorithm starts the merge step on . Thus, we have to bound by . By invariant (I2), for each point , . Furthermore, by Condition (5), . Therefore, the point is within a distance from the divider .
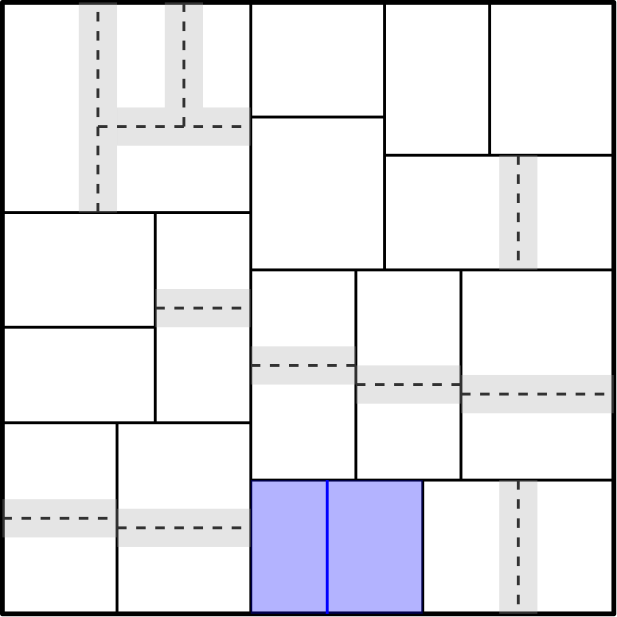
From Lemma 15, for each cell and each point , the point is within a distance from the divider , and from the construction of (Lemma 6), . Furthermore, from Lemma 15 and the construction of , each point can lie inside a constant number of cells in ; hence, . Therefore, the total number of low-net-cost selections of by the extended Hungarian search procedure is .
4 Conclusion and Open Questions
We presented an exact algorithm for the -SP and -SPI problems on -dimensional point sets with bounded spread , achieving sub-quadratic queries to a DWNN data structure and only logarithmic dependence on . We highlight two open directions: First, can the dependence be removed? This would yield sub-quadratic algorithms for geometric bipartite matching, addressing a central open problem in computational geometry. Second, our reductions frame the -server problem as a mild variant of online metric matching. This connects with extensive work on the online -server problem [1, 3, 9, 10, 12, 14, 21, 23]. The reduction suggests simplifications and improvements to work function-based implementations, including the scalable algorithm by Raghvendra and Sowle [21]. Moreover, can we adapt the RM algorithm [15, 17, 18], which is the best-known online metric algorithm, to establish tighter bounds on its competitive ratio for -server?
References
- [1] Sébastien Bubeck, Michael B Cohen, Yin Tat Lee, James R Lee, and Aleksander Mądry. K-server via multiscale entropic regularization. In Proc. 50th Annual ACM SIGACT Symposium on Theory of Computing, pages 3–16, 2018.
- [2] Li Chen, Rasmus Kyng, Yang P Liu, Richard Peng, Maximilian Probst Gutenberg, and Sushant Sachdeva. Maximum flow and minimum-cost flow in almost-linear time. In Proc. 63rd IEEE Annual Sympos. Foundations of Computer Science, pages 612–623. IEEE, 2022. doi:10.1109/FOCS54457.2022.00064.
- [3] M. Chrobak and L. L. Larmore. An optimal on-line algorithm for k servers on trees. SIAM Journal of Computing, 20(1):144–148, 1991. doi:10.1137/0220008.
- [4] Marek Chrobak, H Karloof, Tom Payne, and Sundar Vishwnathan. New results on server problems. SIAM Journal on Discrete Mathematics, 4(2):172–181, 1991. doi:10.1137/0404017.
- [5] H. N. Gabow and R. E. Tarjan. Faster scaling algorithms for network problems. SIAM Journal of Computing, 18(5):1013–1036, October 1989. doi:10.1137/0218069.
- [6] Harold N. Gabow and Robert Endre Tarjan. Faster scaling algorithms for general graph-matching problems. Journal ACM, 38(4):815–853, 1991. doi:10.1145/115234.115366.
- [7] Akshaykumar Gattani, Sharath Raghvendra, and Pouyan Shirzadian. A robust exact algorithm for the Euclidean bipartite matching problem. Advances in Neural Information Processing Systems, 36, 2024.
- [8] Haim Kaplan, Wolfgang Mulzer, Liam Roditty, Paul Seiferth, and Micha Sharir. Dynamic planar Voronoi diagrams for general distance functions and their algorithmic applications. Discrete & Computational Geometry, 64:838–904, 2020. doi:10.1007/S00454-020-00243-7.
- [9] E. Koutsoupias. The k-server problem. Computer Science Review, 3(2):105–118, 2009. doi:10.1016/J.COSREV.2009.04.002.
- [10] Elias Koutsoupias and Christos H. Papadimitriou. On the k-server conjecture. Journal of the ACM, 42(5):971–983, 1995. doi:10.1145/210118.210128.
- [11] Harold W Kuhn. The Hungarian method for the assignment problem. Naval Research Logistics Quarterly, 2(1-2):83–97, 1955.
- [12] James R. Lee. Fusible HSTs and the randomized k-server conjecture. In Mikkel Thorup, editor, Proc. 59th IEEE Annual Symposium on Foundations of Computer Science, pages 438–449, 2018. doi:10.1109/FOCS.2018.00049.
- [13] Richard J Lipton and Robert Endre Tarjan. Applications of a planar separator theorem. SIAM Journal on Computing, 9(3):615–627, 1980. doi:10.1137/0209046.
- [14] Mark S. Manasse, Lyle A. McGeoch, and Daniel D. Sleator. Competitive algorithms for server problems. Journal of Algorithms, 11(2):208–230, 1990. doi:10.1016/0196-6774(90)90003-W.
- [15] Krati Nayyar and Sharath Raghvendra. An input sensitive online algorithm for the metric bipartite matching problem. In Proc. 58th IEEE Annual Symposium on Foundations of Computer Science, pages 505–515, 2017. doi:10.1109/FOCS.2017.53.
- [16] Abhijeet Phatak, Sharath Raghvendra, Chittaranjan Tripathy, and Kaiyi Zhang. Computing all optimal partial transports. In Proc. 11th Internat. Conference on Learning Representations, 2022.
- [17] Sharath Raghvendra. A robust and optimal online algorithm for minimum metric bipartite matching. In Approximation, Randomization, and Combinatorial Optimization, 2016.
- [18] Sharath Raghvendra. Optimal analysis of an online algorithm for the bipartite matching problem on a line. In 34th International Symposium on Computational Geometry, pages 67:1–67:14, 2018. doi:10.4230/LIPICS.SOCG.2018.67.
- [19] Sharath Raghvendra, Pouyan Shirzadian, and Rachita Sowle. Geometric bipartite matching based exact algorithms for server problems, 2025. arXiv:2504.06079.
- [20] Sharath Raghvendra, Pouyan Shirzadian, and Kaiyi Zhang. A new robust partial p-Wasserstein-based metric for comparing distributions. In 41st Internat. Conference on Machine Learning, 2024.
- [21] Sharath Raghvendra and Rachita Sowle. A scalable work function algorithm for the k-server problem. In 18th Scandinavian Symposium and Workshops on Algorithm Theory, volume 227, 2022. doi:10.4230/LIPICS.SWAT.2022.30.
- [22] Tomislav Rudec, Alfonzo Baumgartner, and Robert Manger. A fast implementation of the optimal off-line algorithm for solving the k-server problem. Mathematical Communications, 14(1):119–134, 2009.
- [23] Tomislav Rudec, Alfonzo Baumgartner, and Robert Manger. A fast work function algorithm for solving the k-server problem. Central European Journal of Operations Research, 21:187–205, 2013. doi:10.1007/S10100-011-0222-7.
- [24] Tomislav Rudec and Robert Manger. A new approach to solve the k-server problem based on network flows and flow cost reduction. Computers & operations research, 40(4):1004–1013, 2013. doi:10.1016/J.COR.2012.11.006.
- [25] R. Sharathkumar. A sub-quadratic algorithm for bipartite matching of planar points with bounded integer coordinates. In Proc. 29th Annual Symposium on Computational Geometry, pages 9–16, 2013. doi:10.1145/2462356.2480283.
- [26] R Sharathkumar and Pankaj K Agarwal. Algorithms for the transportation problem in geometric settings. In Proc. 23rd Annual ACM-SIAM Sympos. on Discrete Algorithms, pages 306–317, 2012. doi:10.1137/1.9781611973099.29.
- [27] Pravin M Vaidya. Geometry helps in matching. SIAM Journal of Computing, 18(6):1201–1225, 1989. doi:10.1137/0218080.
