Abstract 1 Introduction 2 Features References

AmoebotSim 2.0: A Visual Simulation Environment for the Amoebot Model with Reconfigurable Circuits and Joint Movements

Matthias Artmann ORCID Paderborn University, Germany Tobias Maurer111In memoriam, † 2023 Paderborn University, Germany Andreas Padalkin ORCID Paderborn University, Germany Daniel Warner ORCID Paderborn University, Germany Christian Scheideler ORCID Paderborn University, Germany
Abstract

We present AmoebotSim 2.0, a simulation environment for the geometric amoebot model of programmable matter that supports the reconfigurable circuit and joint movement extensions of the model. In the geometric amoebot model, we consider systems of simple computational entities called amoebots in a regular triangular grid environment. We are interested in distributed algorithms that solve coordination and shape formation problems. The reconfigurable circuit and joint movement extensions of the model allow the amoebots to communicate over greater distances and perform more complex movements, overcoming some limitations of the original model. AmoebotSim 2.0 is an open-source simulation environment that supports these extensions and provides a rich graphical interface, flexible simulation features, an extensive API, and comprehensive documentation.

Keywords and phrases:
Programmable matter, amoebot model, reconfigurable circuits, joint movements, simulator
Category:
Media Exposition
Copyright and License:
[Uncaptioned image] © Matthias Artmann, Tobias Maurer, Andreas Padalkin, Daniel Warner, and
Christian Scheideler; licensed under Creative Commons License CC-BY 4.0
2012 ACM Subject Classification:
Theory of computation → Computational geometry ; Theory of computation → Distributed computing models ; Theory of computation → Self-organization
Supplementary Material:

Software  (Source Code): https://github.com/martmannupb/AmoebotSim-2.0 [1]
  archived at Software Heritage Logo swh:1:dir:41a83f85a3e7c6c1d5a2fec79533bef04c7ff770
Other  (Website): https://cs.uni-paderborn.de/en/ti/forschung/open-source-projekte/amoebotsim-2
InteractiveResource  (Web App): https://groups.uni-paderborn.de/fg-ti/AmoebotSim2.0/
Funding:
This work was supported by the DFG Project SCHE 1592/10-1.
DOI:
10.4230/LIPIcs.SoCG.2025.81
Event:
41st International Symposium on Computational Geometry (SoCG 2025)
Editors:
Oswin Aichholzer and Haitao Wang
Series and Publisher:
LIPIcs Logo Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik

1 Introduction

Programmable matter envisions materials that can change their physical properties like shape, elasticity, conductivity, and color in a programmable fashion and react autonomously to external influences [10]. Potential application areas include minimally invasive medical treatment, maintenance, exploration, and manufacturing. We typically view such materials as systems of many identical nano-scale computational entities with minimal individual movement and communication abilities.

We consider the geometric amoebot model [5, 4], where a set of n entities, called amoebots, is placed on the nodes of the infinite equilateral triangular grid graph (see Fig. 1a). The set of occupied nodes must be connected and every node can be occupied by at most one amoebot. By performing an expansion, an amoebot occupying one node can expand its body onto an adjacent unoccupied node. An expanded amoebot can contract into either of the two occupied nodes. By repeated expansion and contraction, the amoebots can move along the edges of the grid. Two amoebots occupying adjacent nodes can sense each other and exchange simple messages. The amoebots are controlled by anonymous, identical finite state machines with a constant number of states that is fixed by the algorithm. We consider a fully synchronous execution model where time proceeds in discrete rounds and in each round, all amoebots are activated simultaneously.

The reconfigurable circuit extension [6] allows amoebots to construct communication networks by placing pins on the amoebots’ borders (see Fig. 1b). The pins of adjacent amoebots connect to form communication channels. Each amoebot can internally connect arbitrary disjoint subsets of its pins into partition sets. Using partition sets as nodes and connections between pins of adjacent amoebots as edges, we define a graph. We call the connected components of this graph circuits. Amoebots can use circuits as communication channels on which they can broadcast primitive signals called beeps. A beep carries no information about its origin and is always received by all amoebots on a circuit. Using circuits, many coordination problems can be solved in polylogarithmic time [6, 9, 8, 2].

The joint movement extension [7] enables amoebots to perform more complex movements by pushing and pulling each other during expansions and contractions (see Fig. 1c). By combining their local movements, amoebots can rapidly reconfigure and move their structure.

Figure 1: (a) Contracted and expanded amoebots (blue) in the triangular grid. Adjacent amoebots are connected by red edges. (b) The reconfigurable circuit extension. Amoebots are drawn as hexagons, pins are black circles on their borders and partition sets are drawn as black circles inside the hexagons. The partition sets are connected to the pins they contain. Partition sets in the same circuit have lines of the same color. (c) Amoebots before and after a joint movement.

In this paper, we present AmoebotSim 2.0, a visual simulator for algorithms in the geometric amoebot model that supports both model extensions. The source code is available on GitHub222https://github.com/martmannupb/AmoebotSim-2.0, and there is a website333https://cs.uni-paderborn.de/en/ti/forschung/open-source-projekte/amoebotsim-2 showcasing the main features, some example simulations, and a browser-based demo. The simulator was developed for the Unity444https://unity.com/ game engine, which provides a platform for a highly interactive user interface and efficient rendering of complex simulations. The project can only be opened and executed within Unity’s editor. Our simulator was inspired by AmoebotSim [3], a simulator for the original amoebot model. The main difference between the two simulators is that AmoebotSim uses a sequential execution model, while the extensions supported by our simulator require a synchronous model.

2 Features

User Interface.

The simulator’s user interface (see Fig. 2) consists of a central viewport showing the amoebot structure, a top toolbar with visualization options and general controls, a bottom toolbar with simulation controls, a collapsible log, and two collapsible side panels. The left panel displays the state variables of a selected amoebot, which can be edited while the simulation is paused, and the right panel either displays advanced visualization settings or algorithm parameters, depending on the current mode. When launched, the simulator starts in initialization mode, where the algorithm can be selected and the amoebot structure is initialized. Starting the simulation switches to simulation mode, where the simulation controls are enabled and the selected algorithm is executed.

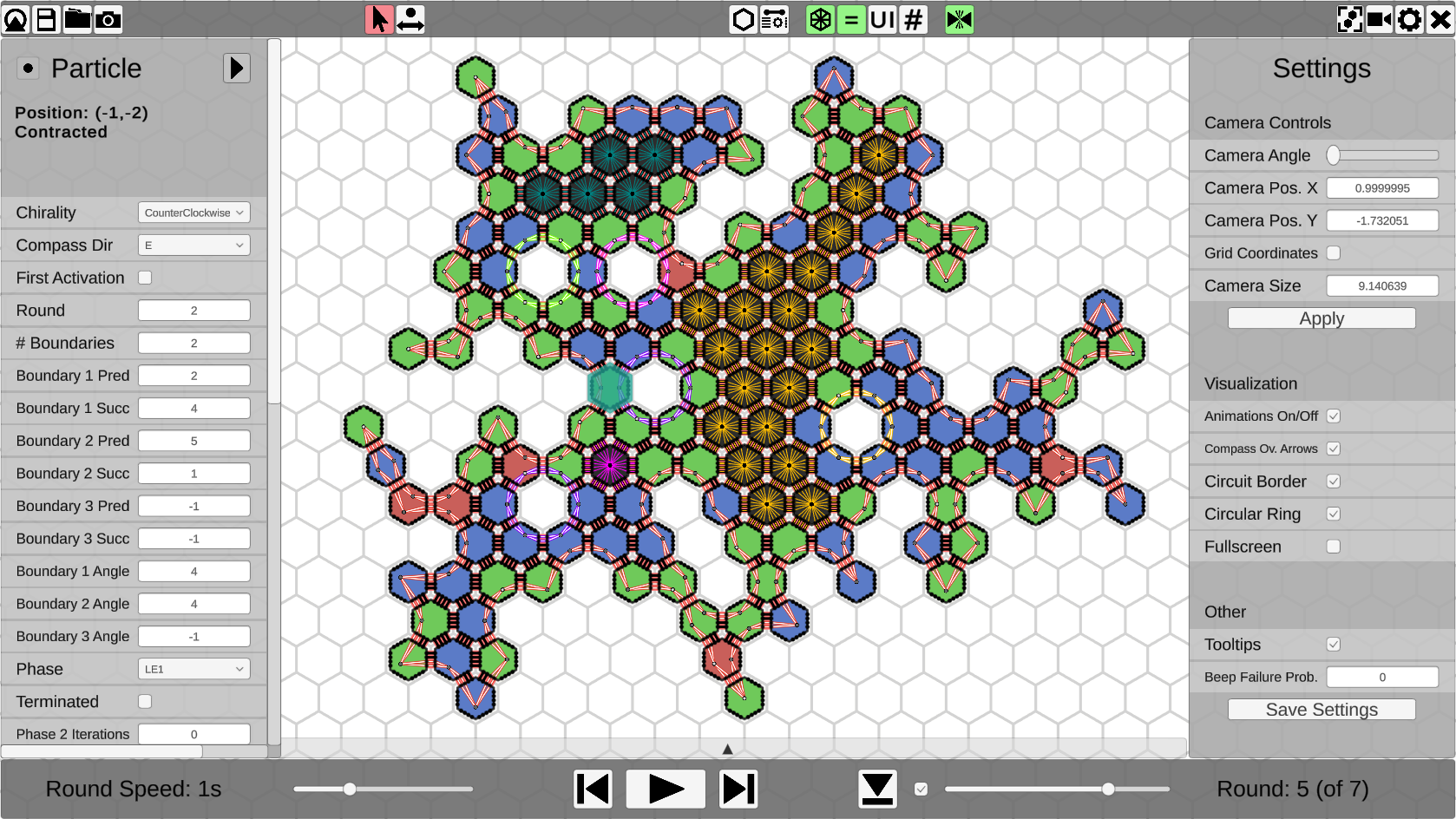
Refer to caption
Figure 2: The AmoebotSim 2.0 user interface.

Visualization Options.

Visualizing amoebot states and complex circuit configurations is the main task of AmoebotSim 2.0. Therefore, each amoebot can control its color, the colors of its circuits, and the placement of its partition sets. Using the top toolbar, the amoebot visualization can be switched between three different modes, and circuits and joint movement bonds can be toggled off. To visualize the dynamics of a simulation, all movements are animated and beeps are highlighted with a flashing effect. The animation speed can be adjusted and the animations can be turned off if desired. Additional UI elements like lines and arrows can be drawn on top of the amoebots to display structures like spanning trees.

Algorithm Development.

Algorithms are developed as C# classes that inherit from a base class and implement or override certain methods and fields. The simulation environment provides an algorithm creation tool that generates a functional template file with one click. Inheriting from the base class allows the simulator to detect the algorithm class by reflection, so no further registration in the core system is necessary. The base class and additional utilities provide a variety of methods and constants for all possible amoebot actions and information retrieval, e. g., discovering neighbors, manipulating direction values, setting up pin configurations, performing movements, etc. An algorithm can also be developed as a subroutine, allowing it to be reused by other algorithms and subroutines. A library of subroutines for some basic algorithms like leader election and boundary identification is provided. In addition to the documentation comments annotating all API source code, a comprehensive documentation with installation and usage instructions is hosted on GitHub.

Initialization.

Every algorithm can implement an initialization procedure with custom parameters to place and initialize the amoebots. Using a global view of the structure, developers can establish any initial conditions, e. g., elect a leader amoebot, ensure hole-freeness, and provide input data. Afterwards, the amoebot structure can be edited manually by using the top toolbar and left side panel to add, remove, move, and edit amoebots.

Simulation History.

The simulator records all rounds of a simulation. Using the bottom toolbar, any part of the recorded history can be reviewed and replayed. The history can also be cut off after the selected round so that the next rounds can be simulated again, possibly leading to a different outcome if the algorithm is randomized or some amoebot states were edited. Simulations can be stored in JSON files and loaded later.

References

  • [1] Matthias Artmann, Tobias Maurer, Andreas Padalkin, Daniel Warner, and Christian Scheideler. AmoebotSim 2.0. Software, version 1.8.4., DFG-SCHE 1592/10-1, swhId: swh:1:dir:41a83f85a3e7c6c1d5a2fec79533bef04c7ff770 (visited on 2025-06-02). URL: https://github.com/martmannupb/AmoebotSim-2.0, doi:10.4230/artifacts.23289.
  • [2] Matthias Artmann, Andreas Padalkin, and Christian Scheideler. On the shape containment problem within the amoebot model with reconfigurable circuits. CoRR, abs/2501.16892, 2025. doi:10.48550/arXiv.2501.16892.
  • [3] Joshua J. Daymude, Robert Gmyr, and Kristian Hinnenthal. AmoebotSim: A Visual Simulator for the Amoebot Model of Programmable Matter. Available online at https://github.com/SOPSLab/AmoebotSim, 2021.
  • [4] Joshua J. Daymude, Andréa W. Richa, and Christian Scheideler. The canonical amoebot model: Algorithms and concurrency control. Distributed Computing, 36(2):159–192, 2023. doi:10.1007/s00446-023-00443-3.
  • [5] Zahra Derakhshandeh, Shlomi Dolev, Robert Gmyr, Andréa W. Richa, Christian Scheideler, and Thim Strothmann. Brief Announcement: Amoebot – A New Model for Programmable Matter. In Proceedings of the 26th ACM Symposium on Parallelism in Algorithms and Architectures, pages 220–222, Prague, Czech Republic, 2014. ACM. doi:10.1145/2612669.2612712.
  • [6] Michael Feldmann, Andreas Padalkin, Christian Scheideler, and Shlomi Dolev. Coordinating Amoebots via Reconfigurable Circuits. Journal of Computational Biology, 29(4):317–343, 2022. doi:10.1089/cmb.2021.0363.
  • [7] Andreas Padalkin, Manish Kumar, and Christian Scheideler. Reconfiguration and Locomotion with Joint Movements in the Amoebot Model. In Arnaud Casteigts and Fabian Kuhn, editors, 3rd Symposium on Algorithmic Foundations of Dynamic Networks (SAND 2024), volume 292 of Leibniz International Proceedings in Informatics (LIPIcs), pages 18:1–18:20, Dagstuhl, Germany, 2024. Schloss Dagstuhl – Leibniz-Zentrum für Informatik. doi:10.4230/LIPIcs.SAND.2024.18.
  • [8] Andreas Padalkin and Christian Scheideler. Polylogarithmic Time Algorithms for Shortest Path Forests in Programmable Matter. In Ran Gelles, Dennis Olivetti, and Petr Kuznetsov, editors, 43rd ACM Symposium on Principles of Distributed Computing, PODC ’24, pages 65–75, New York, NY, USA, 2024. ACM. doi:10.1145/3662158.3662776.
  • [9] Andreas Padalkin, Christian Scheideler, and Daniel Warner. The Structural Power of Reconfigurable Circuits in the Amoebot Model. In Thomas E. Ouldridge and Shelley F. J. Wickham, editors, 28th International Conference on DNA Computing and Molecular Programming (DNA 28), volume 238 of Leibniz International Proceedings in Informatics (LIPIcs), pages 8:1–8:22, Dagstuhl, Germany, 2022. Schloss Dagstuhl – Leibniz-Zentrum für Informatik. doi:10.4230/LIPIcs.DNA.28.8.
  • [10] Tommaso Toffoli and Norman Margolus. Programmable Matter: Concepts and Realization. International Journal of High Speed Computing, 05(02):155–170, 1993. doi:10.1142/S0129053393000086.