Abstract 1 Introduction 2 Software 3 Results and Discussion References

Finding Shortest Reconfiguration Sequences for Modular Robots

UML Modular Robotics Group University of Massachusetts Lowell, MA, USA Hugo A. Akitaya ORCID University of Massachusetts Lowell, MA, USA Andrew Clements University of Massachusetts Lowell, MA, USA Sam Downey University of Massachusetts Lowell, MA, USA Jonathan Eisenbies University of Massachusetts Lowell, MA, USA Soham Samanta Greater Commonwealth Virtual School, Medford, MA, USA Gabriel Shahrouzi University of Massachusetts Lowell, MA, USA Frederick Stock ORCID University of Massachusetts Lowell, MA, USA
Abstract

This paper introduces a set of tools built to help researchers design algorithms for modular robots. These tools can brute force solutions to specific reconfigurations, visualize movements of modular robots, and can be used to design specific configurations of robots. Multiple models of modular robots are supported, and can be added by users.

Keywords and phrases:
modular reconfigurable robots, sliding cube model, reconfiguration
Category:
Media Exposition
Copyright and License:
[Uncaptioned image] © UML Modular Robotics Group, Hugo A. Akitaya, Andrew Clements, Sam Downey,
Jonathan Eisenbies, Soham Samanta, Gabriel Shahrouzi, and Frederick Stock; licensed under Creative Commons License CC-BY 4.0
2012 ACM Subject Classification:
Theory of computation → Computational geometry
Funding:
Research supported by the NSF award CCF-2348067.
DOI:
10.4230/LIPIcs.SoCG.2025.85
Event:
41st International Symposium on Computational Geometry (SoCG 2025)
Editors:
Oswin Aichholzer and Haitao Wang
Series and Publisher:
LIPIcs Logo Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik

1 Introduction

In Modular Robotic Systems (MRS) a “robot” consists of several small independent robotic units (called modules) that can move around each other (re-configure) to change the overall shape of the robot. This gives the system flexibility to adapt to different situations and resilience since modules are interchangeable. In many MRS models, a configuration of the system is a polyform composed of lattice-aligned modules. A move transforms a configuration C into another configuration C′, where C and C′ differ by the position of a single module m. A sequence of configurations C0,C1,C2,C3,… where each Ci+1 is obtained by applying a single move to Ci is called a reconfiguration sequence. The single backbone condition [6] is often required, to move a module m in a configuration C, C∖{m} must be connected.

A moving module must not collide with a stationary module. The free space requirements define the local arrangement of modules required to prevent collisions. Many models are defined by their free space requirements, such as sliding [5, 7] or pivoting [3, 8] cubes. These two models and their 2D analogs (sliding and pivoting squares) are the focus of this paper. Their free-space requirements are shown in Figure 1.

Figure 1: Free space requirements different movement models. Cubes with x’s must be empty, the blue cube is the moving module. (a) sliding cube model (b) the restricted pivoting cube (c) “leapfrog” and “monkey” moves from [1].

A model is universal if any configuration can be reconfigured into any other. Clearly, MRS models that admit universal reconfiguration are particularly desirable. However, this is not a common property, and small changes in free space requirements can affect whether a MRS model is universal or not. For example, the sliding square and cube models are universal [2, 5], while the pivoting square model is not. Further, it is PSPACE-complete to decide whether two given configurations can even be reconfigured into each other [1].

Contribution.

This paper introduces three new tools built to ease this process. A user can define a modular robot model and define starting and ending configurations and then via brute-force search (taking exponential time), find the shortest reconfiguration sequence between them. This can not only find optimal reconfiguration sequences but also be used to verify the correctness of a meta-module.111The source code is available at https://github.com/Modular-Robotics-Group/modular-robotics/. This work would be presented at CG Week via a live demonstration. At the time of writing this is an active research project, hence the software maybe updated, the linked GitHub will have updated documentation.

2 Software

Tiler.

Our tool “3D Tiler” is a web-based application designed to create and manipulate 3D polyforms, inspired by the SVG Painter by Erik Demaine222Available at https://erikdemaine.org/svgpainter/. It supports the cube and rhombic dodecahedron lattices. The tool provides a variety of controls for users to interact with their designs. Layer controls allow users to move up or down layers and highlight the current layer, while color controls enable changing the color. The interface is illustrated in Figure 2. Additionally, 3D Tiler offers export options to JSON and OBJ formats, facilitating the sharing and utilization of designs in other applications. Importing designs from JSON files is also supported, making collaboration and modification straightforward.

Figure 2: 3D Tiler interface.

Pathfinder.

We built a tool “Pathfinder” which finds the shortest reconfiguration sequence between two configurations. Move definitions (free space requirements), and initial and final configurations are specified as input JSON files. A variety of cube/square models, as well as rhombic dodechahedra are supported “out of the box” and users can specify their own models.

It natively supports two search algorithms to explore and find shortest paths in the configuration space. We are given initial and final configurations333https://github.com/Modular-Robotics-Group/modular-robotics/wiki/Pathfinder#state-definitions together with a description of the allowed moves444https://github.com/Modular-Robotics-Group/modular-robotics/wiki/Move-Definitions. The pathfinder tool uses a shortest path algorithm to incrementally build the configuration graph G. At each step, starting with the initial configuration, we check whether each non-cut, non-static module has a valid move, each producing a new configuration added to G, which we then recurse into, in an order specified by the selected shortest path algorithm. Once a move generates the desired configuration, a file is produced for use in the visualization tool demonstrating the corresponding reconfiguration sequence.

BFS.

New states are added to a queue and processed in a FIFO order. Each new state is kept in a hash table, so states can be checked if they have been previously visited. While a state is being processed, all new states reachable from the current state are generated and added to the queue. When the hash for the current state matches the hash for the final state, the algorithm terminates and returns the path from the start state to the end state.

A* search.

A* search algorithm was implemented with various heuristics to improve search times. This search works almost identically to BFS, with the only difference being the use of a priority queue to store adjacent states. States are then processed in an order based on their depth added to a weight assigned to them by a heuristic. The advantages of the A* search are most clear when testing scenarios in 3D space, where the number of possible moves is far greater, and the heuristic tends to avoid irrelevant configurations.

Visualization.

“WebVis” is an interactive, browser-based tool to visualize configurations and move sequences, as well as help to conceptualize potential new meta-module configurations. The tool takes a “scenario” file as input, which specifies a reconfiguration sequence and additional data such as module color, size, and shape. There are controls available to step forward and backward through the move sequence, change the animation speed, load in example scenarios, move the camera, and change the camera projection scheme (perspective versus orthographic). Details of input file specification can be found on the project wiki.

Figure 3: An initial, intermediate, and final configuration in the pivoting square model.

3 Results and Discussion

Pivoting to Sliding Meta-module.

We analyzed the meta-module shown in Figure 3 made of pivoting square modules which simulate a sliding square module, demonstrating its correctness. The animation of the reconfiguration shown can be found in the repository.

Heuristics.

Table 1 shows the differences between search algorithms utilized.

Table 1: Search methods used on the initial and final configurations in Figure 3. All methods found a path of length 14.
Search Method: BFS A* (Manhattan Distance) A* (Symmetric Difference)
Duplicate States Avoided: 148407 40783 58172
Unique States Visited: 24770 13114 14820
Average Time: 1123.67ms 455.33ms 756.67ms

Rhombic Dodecahedron Pivoting Model.

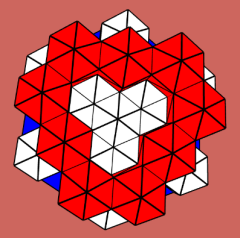
In the young researchers’ forum at SOCG 2023 Akitaya & Stock [4] showed that Rhombic Dodecahedral Modular Robots admit super-rigid configurations (Fig. 4), meaning that there are rigid configurations that remain rigid even with the addition of helper modules. Although the claims in [4] were proven, the proof requires a lot of casework, a technique prone to error. With our tool, we verified the validity of their results.

Refer to caption
Figure 4: An example of a super rigid configuration from [4].

References

  • [1] Hugo A. Akitaya, Erik D. Demaine, Andrei Gonczi, Dylan H. Hendrickson, Adam Hesterberg, Matias Korman, Oliver Korten, Jayson Lynch, Irene Parada, and Vera Sacristán. Characterizing Universal Reconfigurability of Modular Pivoting Robots. In Kevin Buchin and Éric Colin de Verdière, editors, 37th International Symposium on Computational Geometry (SoCG 2021), volume 189 of Leibniz International Proceedings in Informatics (LIPIcs), pages 10:1–10:20, Dagstuhl, Germany, 2021. Schloss Dagstuhl – Leibniz-Zentrum für Informatik. doi:10.4230/LIPICS.SOCG.2021.10.
  • [2] Zachary Abel, Hugo A. Akitaya, Scott Duke Kominers, Matias Korman, and Frederick Stock. A universal in-place reconfiguration algorithm for sliding cube-shaped robots in a quadratic number of moves. In Wolfgang Mulzer and Jeff M. Phillips, editors, 40th International Symposium on Computational Geometry (SoCG 2024), pages 1:1–1:14. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2024. doi:10.4230/LIPIcs.SoCG.2024.1.
  • [3] Hugo A. Akitaya, Esther M. Arkin, Mirela Damian, Erik D. Demaine, Vida Dujmović, Robin Flatland, Matias Korman, Belen Palop, Irene Parada, André van Renssen, and Vera Sacristán. Universal reconfiguration of facet-connected modular robots by pivots: the O(1)-musketeers. Algorithmica, 83(5):1316–1351, 2021. doi:10.1007/S00453-020-00784-6.
  • [4] Hugo A. Akitaya and Frederick Stock. Reconfiguration of 3D pivoting modular robots. arXiv preprint arXiv:2304.09990, 2023. doi:10.48550/arXiv.2304.09990.
  • [5] Adrian Dumitrescu and János Pach. Pushing Squares Around. In Proceedings of the twentieth annual symposium on Computational geometry, pages 116–123, 2004. doi:10.1145/997817.997838.
  • [6] Adrian Dumitrescu, Ichiro Suzuki, and Masafumi Yamashita. Motion planning for metamorphic systems: feasibility, decidability, and distributed reconfiguration. IEEE Transactions on Robotics and Automation, 20(3):409–418, 2004. doi:10.1109/TRA.2004.824936.
  • [7] Robert Fitch, Zack Butler, and Daniela Rus. Reconfiguration planning for heterogeneous self-reconfiguring robots. In Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003)(Cat. No. 03CH37453), volume 3, pages 2460–2467. IEEE, 2003. doi:10.1109/IROS.2003.1249239.
  • [8] Cynthia Sung, James Bern, John Romanishin, and Daniela Rus. Reconfiguration planning for pivoting cube modular robots. In 2015 IEEE international conference on robotics and automation (ICRA), pages 1933–1940. IEEE, 2015. doi:10.1109/ICRA.2015.7139451.