New and Improved Bounds for Markov Paging

Pabbaraju, Chirag; Vakilian, Ali

doi:10.4230/LIPIcs.ICALP.2025.123

New and Improved Bounds for Markov Paging

Chirag Pabbaraju

Stanford University, CA, USA Ali Vakilian

Toyota Technological Institute at Chicago, IL, USA

Abstract

In the Markov paging model, one assumes that page requests are drawn from a Markov chain over the pages in memory, and the goal is to maintain a fast cache that suffers few page faults in expectation. While computing the optimal online algorithm $(\mathrm{OPT})$ for this problem naively takes time exponential in the size of the cache, the best-known polynomial-time approximation algorithm is the dominating distribution algorithm due to Lund, Phillips and Reingold (FOCS 1994), who showed that the algorithm is $4$ -competitive against $\mathrm{OPT}$ . We substantially improve their analysis and show that the dominating distribution algorithm is in fact $2$ -competitive against $\mathrm{OPT}$ . We also show a lower bound of $1.5907$ -competitiveness for this algorithm – to the best of our knowledge, no such lower bound was previously known.

Keywords and phrases:

Beyond Worst-case Analyis, Online Paging, Markov Paging

Category:

Track A: Algorithms, Complexity and Games

Funding:

Chirag Pabbaraju: Supported by Moses Charikar and Gregory Valiant’s Simons Investigator Awards.

Copyright and License:

2012 ACM Subject Classification:

Theory of computation

\rightarrow

Online algorithms ; Theory of computation

\rightarrow

Approximation algorithms analysis

Related Version:

Full Version: https://arxiv.org/abs/2502.05511 [20]

Acknowledgements:

The authors would like to thank Avrim Blum for helpful pointers.

DOI:

10.4230/LIPIcs.ICALP.2025.123

Event:

52nd International Colloquium on Automata, Languages, and Programming (ICALP 2025)

Editors:

Keren Censor-Hillel, Fabrizio Grandoni, Joël Ouaknine, and Gabriele Puppis

Series and Publisher:

Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik

1 Introduction

The online paging problem is a fundamental problem in online algorithms. There are $n$ pages in slow memory, and requests for these pages arrive sequentially. We are allowed to maintain a fast cache of size $k$ , which initially comprises of some $k$ pages. At time step $t$ , if the page requested, say $p_{t}$ , exists in the cache, a cache hit occurs: we suffer no cost, the cache stays as is, and we move to the next request. Otherwise, we incur a cache miss/page fault, suffer a unit cost, and have to evict some page from the cache so as to bring $p_{t}$ from memory into the cache. A paging algorithm/policy is then specified by how it chooses the page to evict whenever it suffers a cache miss.

An optimal offline algorithm for this problem is the algorithm that has entire knowledge of the page request sequence, and makes its eviction choices in a way that minimizes the total number of cache misses it incurs. The classical Farthest-in-Future algorithm [3], which at any cache miss, evicts the page that is next requested latest in the remainder of the sequence, is known to be an optimal offline policy. In the spirit of competitive analysis as introduced by [22], one way to benchmark any online algorithm (i.e., one which does not have knowledge of the page request sequence) is to compute the ratio of the number of page faults that the algorithm suffers, to the number of page faults that the optimal offline algorithm suffers, on a worst-case sequence of page requests. It is known that any deterministic online algorithm has a worst-case ratio that is at least $k$ , while any randomized online algorithm has a worst-case ratio of $\Omega(\log k)$ .

Taking a slightly more optimistic view, one can also consider benchmarking an algorithm against the best online algorithm, that does not know beforehand the realized sequence of page requests. Additionally, in the context of beyond worst-case analysis, one can impose assumptions on the sequence of page requests to more accurately model the behavioral characteristics of real-world page requests on computers. For example, page requests generally follow the locality of reference principle, either in time (the next time a particular page is requested is close to its previous time) or in space (the page that will be requested next is likely to be in a nearby memory location).

The Markov Paging model, introduced by [14], is one of the ways to model locality of reference in the page requests. The model assumes that page requests are drawn from a (known) Markov chain over the $n$ pages. With this distributional assumption, one can ask how an online paging algorithm fares, in comparison to the optimal online algorithm that suffers the smallest number of page misses in expectation over the draw of a page sequence from the distribution. Indeed, one can compute an optimal online algorithm, but only in time exponential in the cache size $k$ . Therefore, one seeks efficient polynomial-time algorithms that are approximately optimal.

In 1994, [16] proposed an elegant randomized algorithm for the Markov Paging problem, known as the dominating distribution algorithm. The dominating distribution algorithm, whenever it suffers a cache miss, evicts a random page drawn from a special distribution, which has the property that a randomly drawn page is likely to be next requested latest among all the existing pages in the cache. This algorithm, which has since become a popular textbook algorithm due to its simplicity (e.g., see Chapter 5 in [4], or the lecture notes by [21]), runs in time polynomial in $k$ ; furthermore, [16] show that the algorithm suffers only 4 times more cache misses in expectation than the optimal online algorithm. Since then, this has remained state-of-the-art – we do not know any other polynomial-time algorithms that achieve a better performance guarantee. It has nevertheless been conjectured that the above guarantee for the dominating distribution algorithm is suboptimal (e.g., see Section 6.2 in [21]).

Our main result improves this bound for the dominating distribution algorithm.

Theorem 1.

The dominating distribution algorithm suffers at most 2 times more cache misses in expectation compared to the optimal online algorithm in the Markov Paging model.

In fact, as mentioned in [16], our guarantee for the performance of the dominating distribution algorithm holds more generally for pairwise-predictive distributions. These are distributions for which one can compute any time, for any pair of pages $p$ and $q$ in the cache, the probability that $p$ is next requested before $q$ in the future (conditioned on the most recent request).

While the dominating distribution algorithm is a randomized algorithm, [16] also propose a simple deterministic algorithm for the Markov Paging model, known as the median algorithm. On any cache miss, the median algorithm evicts the page in cache that has the largest median time at which it is requested next. [16] show that the median algorithm suffers at most 5 times more cache misses in expectation than the optimal online algorithm – to the best of our knowledge, this is the state of the art for deterministic algorithms. As a convenient consequence of our improved analysis, we can also improve this guarantee for the median algorithm.

Theorem 2.

The median algorithm suffers at most 4 times more cache misses in expectation compared to the optimal online algorithm in the Markov Paging model.

Given the improved performance guarantee in Theorem 1, one can ask: is this the best bound achievable for the dominating distribution algorithm? Or can we show that it is the optimal online algorithm? A detail here is that the dominating distribution algorithm is defined as any algorithm satisfying a specific property (see (3)); in particular, there can exist different dominating distribution algorithms. Our upper bound (Theorem 1) holds uniformly for all dominating distribution algorithms. Our next theorem shows a lower bound that at least one of these is suboptimal.

Theorem 3.

There exists a dominating distribution algorithm that suffers at least $1.5907$ times more cache misses in expectation compared to the optimal online algorithm in Markov Paging.

Theorem 3 shows that one cannot hope to show optimality uniformly for all dominating distribution algorithms. To the best of our knowledge, no such lower bounds for the dominating distribution algorithm have been previously shown. While we believe that the bound in Theorem 1 is the correct bound, it would be interesting to close the gap between the upper and lower bound.

Finally, we also consider a setting where the algorithm does not exactly know the Markov chain generating the requests, but only has access to a dataset of past requests. In this case, one can use standard estimators from the literature to approximate the transition matrix of the Markov chain from the dataset. But can an approximate estimate of the transition matrix translate to a tight competitive ratio for a paging algorithm, and if so, how large of a dataset does it require? The robustness of the analysis¹¹1In fact, we borrow this robustness from the original analysis of [16]. of Theorem 1 lends a precise learning-theoretic result (Theorem 17 in Section 7) showing that the dominating distribution algorithm, when trained on a dataset of size $O(n^{2}/\varepsilon^{2})$ , is no more than $\frac{2}{1-2\varepsilon}$ times worse than the optimal online algorithm on a fresh sequence.

This result is especially relevant in the context of data-driven and learning-augmented algorithms. For instance, by treating the learned Markov chain as a learned oracle and combining it with a worst-case approach, such as the Marker algorithm, similarly to the approach proposed in [19, 18], the resulting algorithm achieves $O(1)$ -consistency and $O(\log k)$ -robustness guarantees for the online paging problem.

Table 1: State of the art for Markov Paging (best-known bounds are in bold). Both the median and the dominating distribution algorithm are due to [16].

Algorithm	Reference	Upper Bound	Lower Bound
	[16]	4	-
Dominating Distribution	[16]	(Theorem 3.5)	-
(Randomized)	This Work	2	1.5907
	This Work	(Theorem 1)	(Theorem 3)
	[16]	5	1.511²²2[16] only provide a proof for a lower bound of 1.4, but mention that they also obtained 1.511.
Median	[16]	(Theorem 2.4)	(Theorem 5.4)
(Deterministic)	This Work	4	-
	This Work	(Theorem 2)	-

1.1 Other Related Work

There is a rich literature by this point on studying the online paging problem under assumptions on the permissible page requests that are supposed to model real-world scenarios (see e.g., the excellent surveys by [12] and [7]). In particular, several models are motivated by the aforementioned locality of reference principle. The access graph model, proposed originally by [5], and developed further in the works of [13], [8] and [9], assumes an underlying graph on the pages, which a request sequence is supposed to abide by. Namely, if a page $p_{t}$ has been requested at time $t$ , then only the neighbors of $p_{t}$ in the graph may be requested at time $t+1$ . In this sense, the Markov Paging model can be thought of as a probabilistic variant of the access graph model. [23] models locality of reference based on the “working sets” concept, introduced by [6], and also shows how a finite lookahead of the page sequence can be used to obtain improved guarantees. A related form of competitive analysis, proposed by [15], assumes that there is a family of valid distributions, and page sequences are drawn from some distribution belonging to this family. The goal is to be simultaneously competitive with the optimal algorithm for every distribution in the family. A particular family of interest suggested by [15] (which is incomparable to the Markov Paging model) is that of diffuse adversaries, which has since been developed further in follow-up works by [25, 26] and [2]. Finally, [1] study paging under the bijective analysis framework, which compares algorithms under bijections on page request sequences.

2 Background and Setup

2.1 Markov Paging

The Markov Paging model assumes that the page requests are drawn from a time-homogeneous Markov chain, whose state space is the set of all pages. More precisely, the Markov Paging model is specified by an initial distribution on the $n$ pages, and a transition matrix $M\in[0,1]^{n\times n}$ , where $M_{i,j}$ specifies the probability that page $j$ is requested next, conditioned on the most recently requested page being $i$ . The form of the initial distribution will not be too important for our purposes, but for concreteness, we can assume it to be the uniform distribution on the $n$ pages. It is typically assumed that the transition matrix $M$ is completely known to the paging algorithm/page eviction policy – however, the realized page sequence is not. Upon drawing $T$ page requests from the Markov chain, the objective function that a page eviction policy $\mathcal{A}$ seeks to minimize is:

\displaystyle\operatorname{{\mathds{E}}}[\mathrm{Cost}(\mathcal{A},T)]

\displaystyle=\operatorname{{\mathds{E}}}_{M,\mathcal{A}}\left[\sum_{t=1}^{T}% \mathds{1}[\text{$\mathcal{A}$ suffers a cache miss at time $t$}]\right],

(1)

where the expectation is with respect to both the random page request sequence drawn from $M$ , and the randomness in the policy $\mathcal{A}$ . We denote by $\mathrm{OPT}$ the policy that minimizes the objective in (1). For $c\geq 1$ , an eviction policy $\mathcal{A}$ is said to $c$ -competitive against $\mathrm{OPT}$ if for every $T$ , $\operatorname{{\mathds{E}}}[\mathrm{Cost}(\mathcal{A},T)]\leq c\cdot% \operatorname{{\mathds{E}}}[\mathrm{Cost}(\mathrm{OPT},T)]$ .

It is worth emphasizing that the competitive analysis above is with respect to the optimal online strategy, in that $\mathrm{OPT}$ does not know beforehand the realized sequence of requests. As mentioned previously, the Farthest-in-Future policy [3] is known to be an optimal offline policy.

It is indeed possible to compute $\mathrm{OPT}$ exactly – however, the best known ways do this are computationally very expensive, requiring an exponential amount of computation in $k$ .

Theorem 4 (Theorems 1, 2 in [14]).

The optimal online policy that minimizes $\lim_{T\to\infty}\frac{1}{T}\cdot\operatorname{{\mathds{E}}}[\mathrm{Cost}(% \mathcal{A},T)]$ over all policies $\mathcal{A}$ can be computed exactly by solving a linear program in $n\binom{n}{k}$ variables. Furthermore, for any finite $T$ , an optimal online policy that minimizes $\operatorname{{\mathds{E}}}[\mathrm{Cost}(\mathcal{A},T)]$ can be computed in time $T\cdot n^{\Omega(k)}$ .

Unfortunately, we do not know of any better algorithms that are both optimal and run in polynomial time in $k$ . Therefore, one seeks efficient polynomial time (in $k$ ) algorithms that are approximately optimal, i.e., achieve $c$ -competitiveness with $\mathrm{OPT}$ for $c$ as close to $1$ as possible.

Towards this, [14] showed that several intuitive eviction policies are at least an $\Omega(k)$ factor suboptimal compared to $\mathrm{OPT}$ . They then showed a policy $\mathcal{A}$ that is provably $O(1)$ -competitive against $\mathrm{OPT}$ ; however, the constant in the $O(1)$ is somewhat large. Thereafter, [17]³³3We reference the journal version [17] in lieu of the conference version [16] hereafter. proposed an elegant polynomial-time policy, referred to as the dominating distribution algorithm, and showed that it is $4$ -competitive against $\mathrm{OPT}$ . We describe this policy ahead.

2.2 Dominating Distribution Algorithm

The dominating distribution algorithm, proposed by [17] and denoted $\mathcal{A}_{\mathrm{dom}}$ hereon, operates as follows. At any page request, if $\mathcal{A}_{\mathrm{dom}}$ suffers a cache miss, it computes a so-called dominating distribution $\mu$ over the currently-existing pages in the cache. Thereafter, it draws a page $p\sim\mu$ , and evicts $p$ . First, we will specify the properties of this dominating distribution.

Intuitively, we want $\mu$ to be a distribution such that a typical page drawn from $\mu$ will be highly likely to be next requested later than every other page in the cache. Formally, suppose that the most recently requested page (that caused a cache miss) is $s$ . Fix any two pages $p$ and $q$ and let

\displaystyle\alpha(p<q|s):=\operatorname{{Pr}}_{M}[\text{$p$ is next % requested before $q$ }|\text{ $s$ is the most recently requested page}],

(2)

and let $\alpha(p<p|s)=0$ for all pages $p$ . Here, the probability is only over the draw of page requests from the Markov chain. It is possible to compute $\alpha(p<q|s)$ values for all pairs $p, q$ in cache by solving linear systems (i.e., in time $\mathrm{poly}(n)$ ), provided that we know the transition matrix $M$ (see Appendix A). For notational convenience, we will hereafter frequently denote $\alpha(p<q|s)$ simply by $\alpha(p<q)$ , implicitly assuming conditioning on the most frequently requested page.

Equipped with all these $\alpha(p<q)$ values, let us define $\mu$ to be a distribution over the pages in the cache satisfying the following property: for every fixed page $q$ in the cache,

\displaystyle\operatorname{{\mathds{E}}}_{p\sim\mu}[\alpha(p<q)]\leq\frac{1}{2}.

(3)

This is the required dominating distribution. A somewhat surprising fact here is that such a dominating distribution provably always exists, and furthermore can be constructed efficiently by solving a linear program with just $O(k)$ variables (i.e., in $\mathrm{poly}(k)$ time).

Theorem 5 (Theorem 3.4 in [17]).

A distribution $\mu$ satisfying the condition in (3) necessarily exists and can be computed by solving a linear program in $O(k)$ variables.

Thus, the total computation required by $\mathcal{A}_{\mathrm{dom}}$ at each cache miss is only $\mathrm{poly}(k)$ (to solve the linear program that constructs $\mu$ ), assuming all $\alpha(p<q)$ values are precomputed initially. In summary, the overall computation cost of $\mathcal{A}_{\mathrm{dom}}$ across $T$ page requests is at most $T\cdot\mathrm{poly}(n,k)$ .

It remains to argue that if $\mathcal{A}_{\mathrm{dom}}$ evicts $p\sim\mu$ on a cache miss, it compares well with $\mathrm{OPT}$ . The following claim, whose proof follows from the definition of $\mu$ , will be useful.

Claim 6.

Let $s$ be the most recently requested page. The dominating distribution $\mu$ satisfies the following property: for every fixed page $q$ in the cache, we have that

\displaystyle\operatorname{{Pr}}_{p\sim\mu,M}[\text{$q$ is next requested no % later than $p$ }|\text{ $s$ is the most recently requested page}]\geq\frac{1}{% 2}.

(4)

Using this property of $\mu$ , [17] show that $\mathcal{A}_{\mathrm{dom}}$ incurs only $4$ times as many cache misses as $\mathrm{OPT}$ in expectation. The following section provides this part of their result.

3 4-competitive Analysis of [17]

We restate and provide a detailed proof of the crucial technical lemma from [17], which is particularly useful for our improved $2$ -competitive analysis in Section 5.

Lemma 7 (Lemma 2.5 in [17]).

Let $\mathcal{A}$ be a paging algorithm. Suppose that whenever $\mathcal{A}$ suffers a cache miss, the page $p$ that it chooses to evict is chosen from a distribution such that the following property is satisfied: for every page $q$ in the cache, the probability (over the choice of $p$ and the random sequence ahead, conditioned on the most recently requested page) that $q$ is next requested no later than the next request for $p$ is at least $1/c$ . Then $\mathcal{A}$ is $2c$ -competitive against $\mathrm{OPT}$ .

Proof.

Consider an infinite sequence of page requests, and consider running $\mathcal{A}$ and $\mathrm{OPT}$ (independently) on this sequence. At any time $t$ that $\mathcal{A}$ suffers a cache miss (say on a request to page $s$ ), suppose that $\mathcal{A}$ chooses to evict page $p$ . Let $\mathcal{A}^{-}$ denote the contents in the cache of $\mathcal{A}$ just before the request. Similarly, let $\mathrm{OPT}^{+}$ denote the contents in the cache of $\mathrm{OPT}$ just after the request.

The proof uses a carefully designed charging scheme:⁴⁴4The charging scheme is purely for analysis purposes. if $\mathcal{A}$ has to evict a page $p$ at time $t$ (due to a request for page $s$ ), $p$ assigns a charge to a page $c(p)$ that is not in the cache of $\mathrm{OPT}$ after the request at time $t$ . Ideally, this page $c(p)$ will be requested again before $p$ , causing $\mathrm{OPT}$ to incur a cache miss at that later time. The specific charging scheme is as follows:

Algorithm 1 Charging Scheme.

Suppose that at time $t$ , there is a request for page $s$ .

1.

Set $c(s)=\emptyset$ .
2.
If $\mathcal{A}$ evicts some page $p$ , $c(p)$ is selected as follows:
1. (a)
  
  If $p\notin\mathrm{OPT}^{+}$ , set $c(p)=p$ .
2. (b)
  
  If $p\in\mathrm{OPT}^{+}$ , find a page $q\in\mathcal{A}^{-}\setminus\mathrm{OPT}^{+}$ that has no charges from $\mathrm{OPT}^{+}\setminus\mathcal{A}^{-}$ . Set $c(p)=q$ .⁵⁵5for any page $p$ that $\mathcal{A}$ might evict which satisfies the condition $p\notin\mathrm{OPT}^{+}$ , we make the same choice of $q$ .
3.

If $\mathrm{OPT}$ evicts some page $p$ and $c(p)\neq p$ , set $c(p)=p$ .

At any time for any page $p$ , $c(p)$ will either be $\emptyset$ , or some (single) page. Furthermore, before the request at any time, $c(p)\neq\emptyset$ if and only if $p$ is not currently in the cache of $\mathcal{A}$ .

The first action (Item 1) at the time of any page request is the clearing of charges: when a page $s$ is requested, if $s$ was giving a charge (either to itself or another page), it is duly cleared. If $\mathcal{A}$ suffers a cache miss, and evicts $p$ , then our task is to find a page which is not going to be in the cache of $\mathrm{OPT}$ just after time $t$ , and assign a charge from $p$ to this page.

If $p$ is not in $\mathrm{OPT}^{+}$ (Item 2a), we assign $p$ ’s charge to itself. Otherwise, $p$ is in $\mathrm{OPT}^{+}$ (i.e., $p$ is a page in $\mathcal{A}^{-}\cap\mathrm{OPT}^{+}$ ), and we need to find a different page to charge. In this case, we will argue the existence of a page $q$ that satisfies the condition in Item 2b, for $p$ that fall into this case. Let us remove the common set $\mathcal{A}^{-}\cap\mathrm{OPT}^{+}$ from each of $\mathcal{A}^{-}$ and $\mathrm{OPT}^{+}$ , and consider the sets $\mathcal{A}^{-}\setminus\mathrm{OPT}^{+}$ , $\mathrm{OPT}^{+}\setminus\mathcal{A}^{-}$ . Note that both these sets have the same size, and $s$ is in $\mathrm{OPT}^{+}\setminus\mathcal{A}^{-}$ , but not in $\mathcal{A}^{-}\setminus\mathrm{OPT}^{+}$ . Furthermore, in our initial step, we set $c(s)=\emptyset$ . Thus, even if every page in $\mathrm{OPT}^{+}\setminus\mathcal{A}^{-}$ other than $s$ assigns a charge to a page in $\mathcal{A}^{-}\setminus\mathrm{OPT}^{+}$ , at least one page remains unassigned. We select this page (say the first one in a natural ordering) as $q$ , the required charge recipient for $p$ . Either way, note that $c(p)$ is not in $\mathrm{OPT}^{+}$ , and if $c(p)$ is requested before $p$ , then $\mathrm{OPT}$ incurs a cache miss. In this sense, $c(p)$ can be thought of as the “savior” page for $p$ .

Item 3 simply reassigns the charge that a page gives if it is eventually evicted from $\mathrm{OPT}$ . Specifically, $p$ may have initially set $c(p)=q\neq p$ when $\mathcal{A}$ evicted $p$ , as $p$ still remained in $\mathrm{OPT}$ ’s cache. However, if $\mathrm{OPT}$ later evicts $p$ , we can safely transfer the responsibility back from $q$ to $p$ .

The nice property about this charging scheme is that no page ever has more than $2$ charges on it. Specifically, a page can hold at most one charge from itself and at most one charge from another page (because of Item 2b and Item 3). In fact, the only way a page can have two charges is if it first receives a charge from another page and later gets evicted by $\mathcal{A}$ , assigning itself a self-charge.

Now, fix a finite time horizon $T$ : we will reason about the number of cache misses suffered by $\mathcal{A}$ and $\mathrm{OPT}$ over the course of the $T$ page requests at $t=1,\dots,T$ . First, let $\mathcal{I}$ denote the random variable that is the number of pages $s$ that were not present in the cache initially⁶⁶6Note that both $\mathrm{OPT}$ and $\mathcal{A}$ start with the same initial cache., but were requested at some $t\leq T$ : $\mathrm{OPT}$ suffers a cache miss for each of these pages.

Next, let $r(t,p)$ denote the first time after $t$ that there is a request for page $p$ . Define:

$\displaystyle\alpha(t)$	$\displaystyle=\mathds{1}[\text{$\mathcal{A}$ is forced to evict at time $t$}],$	(5)
$\displaystyle\beta(t)$	$\displaystyle=\mathds{1}[\text{$\mathcal{A}$ is forced to evict at time $t$ % and the page $\boldsymbol{p}$ it evicts satisfies that $c(\boldsymbol{p})$\ is}$
	$\displaystyle\qquad\qquad\text{requested no later than $r(t,\boldsymbol{p})$}],$	(6)

where $\boldsymbol{p}$ is a random variable denoting the evicted page. Note that $\mathrm{Cost}(\mathcal{A},T)=\sum_{t\leq T}\alpha(t)$ .

Observe that the indicator $\beta(t)$ represents a cache miss for $\mathrm{OPT}$ (in the infinite sequence of requests) due to a request for the savior page $c(\boldsymbol{p})$ . Note, however, that a request to the savior page $c(\boldsymbol{p})$ might occur after the time horizon $T$ . This can be addressed by counting the number of open charges remaining after the request at time $T$ . Specifically, let $\mathcal{O}$ denote the number of charges assigned by pages that are not in $\mathcal{A}$ ’s cache after the request at time $T$ . Upon subtraction of $\mathcal{O}$ , the quantity $\sum_{t\leq T}\beta(t)-\mathcal{O}$ counts the number of cache misses suffered by $\mathrm{OPT}$ due to requests to savior pages. A final detail is that a savior page could potentially have two charges on it, and hence we may count the same cache miss for $\mathrm{OPT}$ twice in the above calculation. Concretely, suppose at time $t_{1}$ , $p$ gets evicted by $\mathcal{A}$ , and assigns a charge to $c(p)=q\neq p$ . Then, suppose that at time $t_{2}>t_{1}$ but $t_{2}<r(t_{1},p)$ , $q$ is itself evicted by $\mathcal{A}$ , resulting also in a charge $c(q)=q$ . Now, suppose that $q$ gets requested after $t_{2}$ but before $r(t_{1},p)$ . In this case, we have that both $\beta(t_{1})=1$ and $\beta(t_{2})=1$ , but these are really the same cache miss in $\mathrm{OPT}$ . Thus, we need to account for a possible double-counting of cache misses in $\mathrm{OPT}$ – one way to (very conservatively) do this is simply dividing the expression by 2. In total, we obtain that

\displaystyle\mathrm{Cost}(\mathrm{OPT},T)

\displaystyle\geq\frac{1}{2}\left(\sum_{t\leq T}\beta(t)-\mathcal{O}\right)+% \mathcal{I},

(7)

and hence

\displaystyle\operatorname{{\mathds{E}}}[\mathrm{Cost}(\mathrm{OPT},T)]

\displaystyle\geq\frac{1}{2}\sum_{t\leq T}\operatorname{{\mathds{E}}}[\beta(t)% ]+\operatorname{{\mathds{E}}}\left[\mathcal{I}-\frac{\mathcal{O}}{2}\right]% \geq\frac{1}{2}\sum_{t\leq T}\operatorname{{\mathds{E}}}[\beta(t)]+% \operatorname{{\mathds{E}}}\left[\mathcal{I}-\mathcal{O}\right].

The expectation on the left side above is only with respect to the randomness in the sequence of page requests and $\mathrm{OPT}$ , whereas the expectation on the right side is over the randomness in the sequence of requests, $\mathrm{OPT}$ as well as $\mathcal{A}$ . From here, using the defining property of the algorithm from the lemma statement, we can show that $\operatorname{{\mathds{E}}}[\beta(t)]\geq\frac{1}{c}\cdot\operatorname{{% \mathds{E}}}[\alpha(t)]$ . Furthermore, we can also argue that the random variable $\mathcal{I}-\mathcal{O}$ is always non-negative. Both these together imply the lemma. We defer the details of these last two steps to Appendix B. $\hfill\blacktriangleleft$

Corollary 8.

The dominating distribution algorithm $\mathcal{A}_{\mathrm{dom}}$ is 4-competitive against $\mathrm{OPT}$ .

Proof.

This follows from Lemma 7 and Claim 6. $\hfill\blacktriangleleft$

$\blacktriangleright$ Remark 9.

Consider setting $c=1$ in Lemma 7: this corresponds to $\mathcal{A}$ effectively being an offline algorithm, that knows the page in cache that is going to next be requested farthest in the future. We already know that such an algorithm is optimal, i.e., is 1-competitive against $\mathrm{OPT}$ . However, the guarantee given by Lemma 7 for such an algorithm is still only $2$ -competitiveness. This at least suggests that there is scope to improve the guarantee to $c$ -competitiveness.

4 Sources of Looseness in the Analysis

We systematically identify the sources of looseness in the above analysis with illustrative examples, before proceeding to individually tighten them in the subsequent section.

4.1 A Conservative Approach to Handling Doubly-Charged Pages

Recall that in the summation $\sum_{t\leq T}\beta(t)$ above, a cache miss for $\mathrm{OPT}$ may be double-counted if the same page is assigned two charges. Although one way to address this overcounting is to divide the summation by 2, this approach is overly conservative, as it undercounts every cache miss in $\mathrm{OPT}$ that results from a request to a singly-charged page. For instance, consider the following situation:

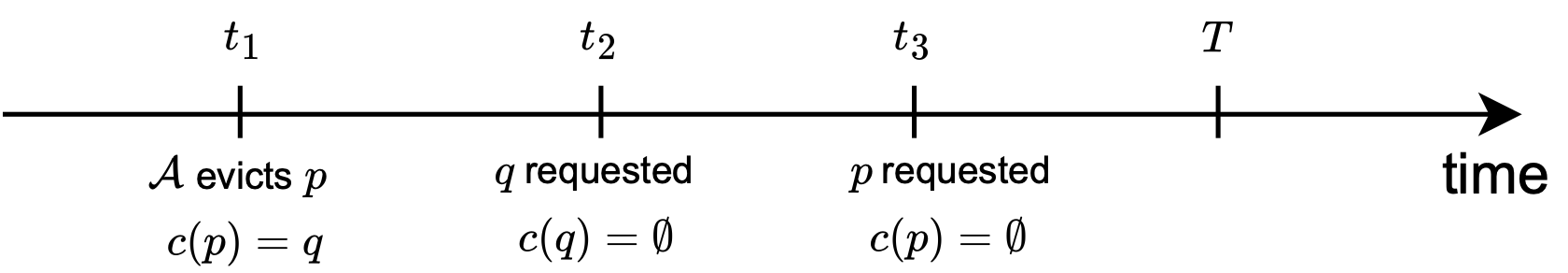
Refer to caption — Figure 1: Request for $q$ (a singly charged page) at $t_{2}$ constitutes a unit cache miss for $\mathrm{OPT}$ , but the division by 2 undercounts this (and every other singly-charged cache miss in $\mathrm{OPT}$ ).

Here, at time $t_{1}$ , $\mathcal{A}$ evicts a page $p$ . Suppose that $p$ continues to live in the cache of $\mathrm{OPT}$ after the request at $t_{1}$ , and hence $c(p)$ is assigned to some $q$ in $\mathcal{A}$ ’s cache. Now, say that $q$ is requested at time $t_{2}$ , which is before $t_{3}=r(t_{1},p)$ . Furthermore, assume that at $t_{2}$ , $q$ only had the single charge on itself (by $p$ ), i.e., $q$ was not evicted by $\mathcal{A}$ in the time between $t_{1}$ and $t_{2}$ . Then, $\beta(t_{1})=1$ , but we are wastefully dividing it by 2 in our calculation.

4.2 Inexhaustive Clearing of Charges upon a Page Request

Consider the first item in the charging scheme (Item 1) – whenever a page $s$ is requested, any charges that $s$ might be giving are cleared (i.e., $c(s)=\emptyset$ ). Intuitively, this is supposed to account for the fact that, while $s$ was holding some page $c(s)$ responsible for being requested before $s$ itself, either this did happen, in which case we happily clear the already-paid charge, or this did not quite happen and $s$ got requested before $c(s)$ , in which case we should let go of the charge and focus on the future. However, consider instead the case where $s$ does not have a charge on any other page, but is itself the bearer of a charge by some other page, say $p$ . In this case, $s$ has successfully paid the charge that was expected of it – but this charge would only be cleared upon the next request to $p$ ! If it so happens that $p$ is next requested after the time horizon $T$ , then even if $s$ successfully paid the charge due to $p$ , since this charge was not cleared when it was requested, it would be counted in $\mathcal{O}$ as part of the open charges post time $T$ , and wastefully subtracted in the calculation. This is concretely illustrated in the situation below:

This suggests that whenever a page is requested, we should clear not only the charges it gives but also any charges it bears, preventing unnecessary inclusion in $\mathcal{O}$ . This approach ensures that a page discards its imposed charge immediately upon “paying it off” rather than with a delay.

4.3 No Accounting for Uncharged, Non-first-timer Pages

Finally, observe that in the accounting of cache misses for $\mathrm{OPT}$ , we only count those that occur due to requests to charged/savior pages (as counted by the $\beta(t)$ ’s), and those that occur due to first-time requests to pages not initially in the cache (as counted by $\mathcal{I}$ ). However, $\mathrm{OPT}$ can also suffer cache misses due to a request to an uncharged page. Namely, if there is a request to a page $q$ that was previously evicted by $\mathrm{OPT}$ , but at the time that it is requested, $q$ is bearing no charges at all, then the cache miss due to $q$ is not being counted in the calculation. This is illustrated below:

$\mathcal{A}$ evicts $p$ at time $t_{1}$ and assigns a charge to $q\neq p$ , implying that $q$ is not in the cache of $\mathrm{OPT}$ after the request at $t_{1}$ (but was instead previously evicted by $\mathrm{OPT}$ ). Next, at $t_{2}$ , $p$ is requested, and this clears the charge it had on $q$ . Since $p$ got requested before $q$ , $\beta(t_{1})=0$ . Then, at $t_{3}$ , $q$ is requested – $q$ has no charges on it at this point. Notice that this still causes a cache miss for $\mathrm{OPT}$ at $t_{3}$ . However, this cache miss is not accounted for in our calculation, either by $\beta(t_{1})$ , or by $\mathcal{I}$ (since this is not the first time that $q$ is being brought into the cache).

5 Tightening the Analysis to 2-competitiveness

Having identified the loose ends in the analysis of [17] above, we are able to tighten their analysis and prove the following lemma:

Lemma 10.

Let $\mathcal{A}$ be a paging algorithm. Suppose that whenever $\mathcal{A}$ suffers a cache miss, the page $p$ that it chooses to evict is chosen from a distribution such that the following property is satisfied: for every page $q$ in the cache, the probability (over the choice of $p$ and the random sequence ahead, conditioned on the most recently requested page) that $q$ is next requested no later than the next request for $p$ is at least $1/c$ . Then $\mathcal{A}$ is $c$ -competitive against $\mathrm{OPT}$ .

Proof.

We make one small change (highlighted in green) to Item 1 in the charging scheme (Algorithm 1) from the analysis of [17] – whenever a new page is requested, any charges that this page might be giving are cleared, but also any charges that other pages might be having on the requested page are also cleared. This fixes the issue about uncleared charges from Section 4.2.

Algorithm 2 Updated Charging Scheme.

Suppose that at time $t$ , there is a request for page $s$ .

1.
1. (a)
  
  Set $c(s)=\emptyset$ .
2. (b)
  
  For any page $p$ that has $c(p)=s$ , set $c(p)=\emptyset$ .
2.
If $\mathcal{A}$ evicts some page $p$ , $c(p)$ is selected as follows:
1. (a)
  
  If $p\notin\mathrm{OPT}^{+}$ , set $c(p)=p$ .
2. (b)
  
  If $p\in\mathrm{OPT}^{+}$ , find a page $q\in\mathcal{A}^{-}\setminus\mathrm{OPT}^{+}$ that has no charges from $\mathrm{OPT}^{+}\setminus\mathcal{A}^{-}$ . Set $c(p)=q$ .
3.

If $\mathrm{OPT}$ evicts some page $p$ and $c(p)\neq p$ , set $c(p)=p$ .

Let $\alpha(t)$ and $\beta(t)$ be the same random variables as defined in (5), (3) in the proof of Lemma 7. Further, let $\mathcal{I}$ and $\mathcal{O}$ be the same random variables as defined there as well. Note that even with the slightly-changed charging scheme, $\mathcal{I}$ remains quantitatively the same; the random variable $\mathcal{O}$ however changes – in particular, it potentially becomes a smaller number, because we are clearing charges more aggressively. The random variable $\sum_{t\leq T}\beta(t)-\mathcal{O}$ nevertheless still counts the cache misses suffered by $\mathrm{OPT}$ due to requests to savior pages, while potentially double-counting a few misses. However, to account for this double-counting, instead of dividing every miss by 2 (which was the issue discussed in Section 4.1), we explicitly keep track if some $\beta(t)$ corresponds to a request to a doubly-charged page, and subtract it from our calculation. Formally, let

\displaystyle\mathcal{D}=\sum_{t\leq T}\mathds{1}[\text{Page $\boldsymbol{p}$ % requested at time $t$ has two charges on it}].

(8)

Then, the quantity $\sum_{t\leq T}\beta(t)-\mathcal{D}-\mathcal{O}$ counts the cache misses suffered by $\mathrm{OPT}$ due to requests to savior pages more precisely, and without double-counting any miss. This crucially allows us to avoid an unnecessary factor of $2$ .

Lastly, in order for the analysis to go through, we have to also fix the final issue regarding requests to uncharged pages described in Section 4.3. We simply do this by keeping track of an additional quantity that counts this, and add it to our calculation. Namely, let

	$\displaystyle\mathcal{U}=\sum_{t\leq T}\mathds{1}[$	Page $\boldsymbol{p}$ requested at time $t$ does not exist in $\mathrm{OPT}$ ’s cache at this time
		$\displaystyle\text{because it was previously evicted by $\mathrm{OPT}$, and $% \boldsymbol{p}$ has no charges on it}].$		(9)

Then, combining all of the above, we have that

\displaystyle\mathrm{Cost}(\mathrm{OPT},T)

\displaystyle\geq\sum_{t\leq T}\beta(t)-\mathcal{D}-\mathcal{O}+\mathcal{U}.

(10)

Comparing this to the accounting in (7), it at least seems plausible that by not halving, we might be able to save a factor of 2. Namely, taking expectations, we obtain that

	$\displaystyle\hskip-1.0pt\operatorname{{\mathds{E}}}[\mathrm{Cost}(\mathrm{OPT% },T)]$	$\displaystyle\geq\sum_{t\leq T}\operatorname{{\mathds{E}}}[\beta(t)]+% \operatorname{{\mathds{E}}}[\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}]$
		$\displaystyle\geq\frac{1}{c}\sum_{t\leq T}\operatorname{{\mathds{E}}}[\alpha(t% )]+\operatorname{{\mathds{E}}}[\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}% ]=\frac{1}{c}\operatorname{{\mathds{E}}}[\mathrm{Cost}(\mathcal{A},T)]+% \operatorname{{\mathds{E}}}[\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}],$

where the first inequality follows from the same analysis that we did in the proof of Lemma 7. It remains to argue that the quantity $\operatorname{{\mathds{E}}}[\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}]$ is nonnegative. Note that the random variable $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ starts out being $0$ before the very first request at time $t=1$ . We will argue that it always stays nonnegative thereafter via two following two claims.

Claim 11.

If the page $s$ requested at time $t$ satisfies the following condition: $s$ exists in $\mathrm{OPT}$ ’s cache and $s$ does not exist in $\mathcal{A}$ ’s cache and $s$ is not giving a charge and $s$ is not bearing any charges, then the random variable $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ decreases by 1 from $t$ to $t+1$ . Furthermore, if the page $s$ requested at time $t$ does not satisfy this condition, then $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ either increases or stays the same from $t$ to $t+1$ .

The proof of this claim involves straightforward but exhaustive casework; it is deferred to Appendix C. In particular, for the latter part of the claim, we need to show that if the requested page $s$ violates any part of the condition, $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ cannot decrease.

Claim 12.

If the page $s$ requested at time $t$ satisfies the condition: $s$ exists in $\mathrm{OPT}$ ’s cache and $s$ does not exist in $\mathcal{A}$ ’s cache and $s$ is not giving a charge and $s$ is not bearing any charges, then $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ is strictly positive just before this request.

Proof.

Consider any time $t$ where the requested page $s$ satisfies the condition. We can associate to the page $s$ two past events occurring at times $t_{1}$ and $t_{2}$ (where $t_{1}<t_{2}<t$ ) such that: (1) $\mathcal{A}$ evicts $s$ at $t_{1}$ , but $s$ continues to live in $\mathrm{OPT}$ ’s cache, resulting in $s$ giving a charge to some other page $q$ in $\mathcal{A}$ ’s cache (Item 2b), and (2) $q$ gets requested at $t_{2}$ , before the request to $s$ at $t$ , thereby clearing the charge by $s$ on $q$ (as per Item 1b). Observe that these two past events need to necessarily occur for $s$ to satisfy the condition. Now observe that when $q$ gets requested at $t_{2}$ , $q$ is the bearer of a single charge. Thus, over the course of this request to $q$ , $\mathcal{I},\mathcal{D},\mathcal{U}$ remain unchanged. Because $s$ ’s charge on $q$ gets cleared, $\mathcal{O}$ decreases by $1$ . Finally, because $q$ is in $\mathcal{A}$ ’s cache at this time, no new charges are added to $\mathcal{O}$ . Thus, $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ strictly increases by 1 at step (2). Also, note that for each distinct time step where the requested page $s$ satisfies the condition, there is a distinct associated (past) step (2).

Now consider the first time $t_{0}$ where the requested page $s$ satisfies the condition. Then, by Claim 11, at every previous time step, $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ either increased or remained the same. Given that $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ started out being 0, and recalling that step (2) (which happened before $t_{0}$ ) caused a strict increase in the quantity, we have that $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ is strictly positive at $t_{0}$ .

Just after the request at $t_{0}$ , $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ decreases by 1 (by Claim 11), and is now only guaranteed to be nonnegative, instead of positive. Then, consider the next time $t$ when a page $s$ satisfying the condition is requested. We can again trace its associated (distinct) step (2) that happened in the past. If this happened before $t_{0}$ , then $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ stayed positive after the request at $t_{0}$ . Alternatively, if this happened in between $t_{0}$ and $t$ , $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ still turns positive (if it ever became zero at all). In either case, $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ is positive before the request at $t$ . The claim follows by induction. $\hfill\vartriangleleft$

The above two claims establish that if $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}=0$ at any time $t$ , then $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ cannot decrease at time $t+1$ . Furthermore, if at all $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ does decrease (from being a positive number), it only decreases by 1. Together, this means that $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ is always nonnegative, and hence it is nonnegative in expectation. This concludes the proof of Lemma 10 $\hfill\blacktriangleleft$

Corollary 13.

The dominating distribution algorithm $\mathcal{A}_{\mathrm{dom}}$ is 2-competitive against $\mathrm{OPT}$ .

Proof.

This follows from Lemma 10 and Claim 6. $\hfill\blacktriangleleft$

$\blacktriangleright$ Remark 14.

As in Remark 9, if we set $c=1$ in Lemma 10, our lemma says that a policy that has essentially seen the future and evicts the page that is next scheduled to be requested latest is 1-competitive against $\mathrm{OPT}$ , i.e., it is optimal. Thus, our analysis, while establishing the best-possible guarantee for algorithms satisfying the condition of the lemma, additionally recovers an alternate, charging-scheme-based proof of the optimality of the Farthest-in-Future eviction policy.

$\blacktriangleright$ Remark 15.

The factor of 4 in the analysis of [16] constituted a factor of 2 arising due to doubly-charged pages, and a factor of 2 arising from the property of the dominating distribution algorithm. While we got rid of the first factor, the second factor seems inherent to the dominating distribution algorithm; it would be interesting to see if this factor could be improved as well.

Lemma 10 also allows us to improve the approximation guarantee for another intuitive deterministic algorithm considered by [17], namely the median algorithm. At any cache miss, the median algorithm evicts the page in cache that has the largest median time of next request. For deterministic algorithms satisfying the condition of Lemma 7, [17] employ a slightly more specialized analysis of the charging scheme in Algorithm 1 (Lemma 2.3 in [17]) to obtain a $(c+1)$ -competitive guarantee against $\mathrm{OPT}$ (instead of $2c$ -competitiveness). Thereafter, by arguing that the median algorithm satisfies the condition with $c=4$ , (Theorem 2.4 in [17]), they are able to show that the median algorithm is 5-competitive against $\mathrm{OPT}$ . Our tighter analysis in Lemma 10 applies to any algorithm (deterministic/randomized), and hence also improves the guarantee for deterministic algorithms obtained by [17]. More importantly, it improves the performance guarantee that we can state for the median algorithm.

Corollary 16.

The median algorithm is 4-competitive against $\mathrm{OPT}$ .

6 Lower Bound for Dominating Distribution Algorithms

We now show that there exist problem instances where a dominating distribution algorithm⁸⁸8Note that we cannot hope to prove a lower bound that applies to all dominating distribution algorithms, since the optimal Farthest-in-Future algorithm is technically also a dominating distribution algorithm. can provably be at least $c$ times worse than $\mathrm{OPT}$ , for $c\geq 1.5907$ . We present a simpler bound of $c=1.5$ here, and defer the proof of the improved bound to the full version.

Consider a simple Markov cain on 3 total pages, and a cache of size 2. At each time step independently, page 1 is requested with probability $1-\varepsilon$ , and page 2 and 3 are requested each with probability $\varepsilon/2$ . This corresponds to the Markov chain with the transition matrix

\displaystyle\begin{bmatrix}1-\varepsilon&\varepsilon/2&\varepsilon/2\\ 1-\varepsilon&\varepsilon/2&\varepsilon/2\\ 1-\varepsilon&\varepsilon/2&\varepsilon/2\end{bmatrix}.

We start with the initial cache being $[1,2]$ . The reference algorithm $\mathcal{A}_{\mathrm{ref}}$ we will compete against always keeps page 1 in its cache. If it suffers a cache miss, it swaps out the other page with the requested page. At any time $t$ , the probability that $\mathcal{A}_{\mathrm{ref}}$ suffers a miss is therefore exactly $\varepsilon/2$ , and hence the expected total number of misses through $T$ timesteps is $\varepsilon T/2$ .

Now, consider $\mathcal{A}_{\mathrm{dom}}$ . We want to capitalize on the fact that $\mathcal{A}_{\mathrm{dom}}$ evicts page 1 with some positive probability, in contrast to $\mathcal{A}_{\mathrm{ref}}$ . Namely, observe that

$\displaystyle\operatorname{{Pr}}[\text{$\mathcal{A}_{\mathrm{dom}}$ has miss % at $t$}]$	$\displaystyle=\operatorname{{Pr}}[\text{$1$ in cache of $\mathcal{A}_{\mathrm{% dom}}$ at $t$}]\cdot\frac{\varepsilon}{2}$
	$\displaystyle\quad+\operatorname{{Pr}}[\text{$1$ not in cache of $\mathcal{A}_% {\mathrm{dom}}$ at $t$}]\cdot(1-\varepsilon)$
	$\displaystyle=p_{t}\cdot\frac{\varepsilon}{2}+(1-p_{t})\cdot(1-\varepsilon),$	(11)

where we denote $p_{t}=\operatorname{{Pr}}[\text{$1$ in cache of $\mathcal{A}_{\mathrm{dom}}$ % at $t$}]$ . The latter probability is non-zero for $\mathcal{A}_{\mathrm{dom}}$ , which already makes its expected total number of misses larger than that of $\mathcal{A}_{\mathrm{ref}}$ . We will therefore aim to maximize this difference. Observe that

	$\displaystyle p_{t}$	$\displaystyle=\operatorname{{Pr}}[\text{$1$ requested at $t-1$}]+\operatorname% {{Pr}}[\text{$1$ in cache of $\mathcal{A}_{\mathrm{dom}}$ at $t-1$}]$
		$\displaystyle\quad\cdot\operatorname{{Pr}}[\text{$1$ not requested at $t-1$}]$
		$\displaystyle\quad\cdot\operatorname{{Pr}}[\text{$1$ not evicted by $\mathcal{% A}_{\mathrm{dom}}$ at $t-1\leavevmode\nobreak\ \big{\|}$ $1$ not requested, $1$% in cache of $\mathcal{A}_{\mathrm{dom}}$ at $t-1$}]$
		$\displaystyle=1-\varepsilon+p_{t-1}\cdot\varepsilon$
		$\displaystyle\quad\cdot\operatorname{{Pr}}[\text{$1$ not evicted by $\mathcal{% A}_{\mathrm{dom}}$ at $t-1\leavevmode\nobreak\ \big{\|}$ $1$ not requested, $1$% in cache of $\mathcal{A}_{\mathrm{dom}}$ at $t-1$}].$

We can analytically calculate the last probability. Say the cache of $\mathcal{A}_{\mathrm{dom}}$ at $t-1$ is, without loss of generality, $[1,2]$ . Given that $1$ is not requested, we have that either of $2$ or $3$ are requested, each with probability $1/2$ . If $2$ is requested, there is no cache miss. If on the other hand, $3$ is requested, $\mathcal{A}_{\mathrm{dom}}$ calculates a dominating distribution $\mu$ over $[1,2]$ . This can be easily calculated. Let $\alpha(p<q)$ again be the probability that $p$ is requested next before $q$ (conditioned on the current page, which in this case, does not matter since the distributions at every time step are independent and identical). We have that

	$\displaystyle\alpha(1<1)=\alpha(2<2)=0,$
	$\displaystyle\alpha(2<1)=\varepsilon/2+\varepsilon/2\cdot\alpha(2<1)\implies% \quad\alpha(2<1)=\frac{\varepsilon/2}{1-\varepsilon/2},$
	$\displaystyle\alpha(1<2)=1-\varepsilon+\varepsilon/2\cdot\alpha(1<2)\implies% \quad\alpha(1<2)=\frac{1-\varepsilon}{1-\varepsilon/2}.$

The condition for the dominating distribution is that, for every fixed page $q$ in the cache, $\operatorname{{\mathds{E}}}_{p\sim\mu}[\alpha(p<q)]\leq 1/2$ . Letting $\mu(1)=x$ so that $\mu(2)=1-x$ , this translates to

\displaystyle(1-x)\cdot\alpha(2<1)\leq 1/2,\qquad x\cdot\alpha(1<2)\leq 1/2% \qquad\implies\qquad\frac{3\varepsilon-2}{2\varepsilon}\leq x\leq\frac{2-% \varepsilon}{4-4\varepsilon}.

We want $x$ to be large as possible, because we want $\mathcal{A}_{\mathrm{dom}}$ to evict $1$ with the highest feasible probability, so that it will suffer a lot of cache misses. Thus, we set $x=\frac{2-\varepsilon}{4-4\varepsilon}$ . This gives us that,

	$\displaystyle\operatorname{{Pr}}[\text{$1$ not evicted by $\mathcal{A}_{% \mathrm{dom}}$ at $t-1\leavevmode\nobreak\ \big{\|}$ $1$ not requested, $1$ in % cache of $\mathcal{A}_{\mathrm{dom}}$ at $t-1$}]$
	$\displaystyle=\frac{1}{2}+\frac{1}{2}\cdot(1-x)=1-\frac{x}{2}=\frac{6-7% \varepsilon}{8-8\varepsilon}.$

Plugging this in our calculation for $p_{t}$ from above, we get that

\displaystyle p_{t}

\displaystyle=\underbrace{1-\varepsilon}_{c}+p_{t-1}\cdot\underbrace{\frac{% \varepsilon(6-7\varepsilon)}{8-8\varepsilon}}_{d}.

Unrolling the recurrence, and using that $p_{1}=1$ , we obtain that for $t\geq 2$ ,

\displaystyle p_{t}

\displaystyle=c(1+d+\dots+d^{t-2})+d^{t-1}=c\cdot\frac{1-d^{t-1}}{1-d}+d^{t-1}.

Summing up $\eqref{eqn:misses-A-dom}$ until $T$ , and substituting $p_{t}$ from above, we get that

	$\displaystyle\operatorname{{\mathds{E}}}[\mathrm{Cost}(\mathcal{A}_{\mathrm{% dom}},T)]$	$\displaystyle=T(1-\varepsilon)+\left(\frac{3\varepsilon}{2}-1\right)\sum_{t=1}% ^{T}p_{t}$
		$\displaystyle=T(1-\varepsilon)+\left(\frac{3\varepsilon}{2}-1\right)\left[% \frac{c}{1-d}\left(T-\frac{1-d^{T}}{1-d}\right)+\frac{1-d^{T}}{1-d}\right].$

Taking the limit as $T\to\infty$ , we get that

\displaystyle\lim_{T\to\infty}\frac{\operatorname{{\mathds{E}}}[\mathrm{Cost}(% \mathcal{A}_{\mathrm{dom}},T)]}{\operatorname{{\mathds{E}}}[\mathrm{Cost}(% \mathcal{A}_{\mathrm{ref}},T)]}

\displaystyle=\frac{1-\varepsilon+\left(\frac{3\varepsilon}{2}-1\right)\left(% \frac{c}{1-d}\right)}{\varepsilon/2}.

Substituting the values of $c$ and $d$ , and taking the limit as $\varepsilon\to 0$ , the ratio above converges to $1.5$ .

7 Learning the Markov Chain from Samples

It is worth pointing out that the form of Lemma 10 allows us to obtain performance guarantees even when we only have approximate estimates of the $\alpha(p<q)$ values, as also noted in passing by [17]. In particular, suppose that we only have $\varepsilon$ -approximate (multiplicate or additive) estimates $\hat{\alpha}(p<q)$ of $\alpha(p<q)$ , that still satisfy $\hat{\alpha}(p<q)+\hat{\alpha}(q<p)=1$ , and $\hat{\alpha}(p<p)=0$ . Suppose that at each cache miss, we use these $\hat{\alpha}(p<q)$ values to compute a dominating distribution $\hat{\mu}$ , and draw the page $p$ to evict from $\hat{\mu}$ . Even with such an approximate dominating distribution, we can still guarantee either $\frac{2}{1-2\varepsilon}$ -competitiveness (in the case that $\hat{\alpha}(p<q)\in[\alpha(p<q)-\varepsilon,\alpha(p<q)+\varepsilon]$ ), or $\frac{2-2\varepsilon}{1-2\varepsilon}$ -competitiveness (in the case that $\hat{\alpha}(p<q)\in[(1-\varepsilon)\alpha(p<q),(1+\varepsilon)\alpha(p<q)]$ ). This follows as a direct consequence of Claim 6 and Lemma 10.

Perhaps the first scenario to consider here is when we do not assume prior knowledge of the transition matrix $M$ , but only have access to samples previously drawn from the Markov chain. For example, we can imagine that the algorithm designer has available a large training dataset of past page requests. This dataset can be used to derive estimates of the entries in the transition matrix $M$ , for instance, using one of the several existing estimators [10, 24, 11]. In fact, recall that the computation of the $\alpha(p<q)$ values requires only for us to solve a linear system determined by the entries in the transition matrix (Appendix A). Hence, if we have accurate estimates for the entries in $M$ , we can use the theory of perturbed linear systems to bound the resulting error in the estimates of the $\alpha(p<q)$ values. Thereafter, using the argument from the previous paragraph, we can obtain a performance guarantee for the competitiveness of a dominating distribution algorithm that uses these estimates.

We can turn the above informal argument into a formal learning-theoretic result. We choose to adopt the following result of [10] for our exposition:

Theorem 17 (Theorem 4 in [10]).

Suppose we unroll a Markov chain to obtain $m$ samples $X_{1},\dots,X_{m}$ , where the initial distribution of $X_{1}$ is arbitrary, but the transition matrix $M\in[0,1]^{n\times n}$ of the Markov chain satisfies $M_{i,j}\geq\delta>0$ for every $i, j$ . Then, there exists an estimator $\hat{M}=\hat{M}(X_{1},\dots,X_{m})$ that satisfies

\displaystyle\operatorname{{\mathds{E}}}_{X_{1},\dots,X_{m}}\|M(i,:)-\hat{M}(i% ,:)\|_{2}^{2}\leq O\left(\frac{1}{m\delta}\right)

for every $i\in[n]$ , where $M(i,:)$ (respectively $\hat{M}(i,:)$ ) denotes the $i^{\text{th}}$ row of $M$ (respectively $\hat{M}$ ).

Using this theorem, we can obtain the following result:

Theorem 18.

Suppose that the page requests are generated from an unknown Markov chain where every entry in the transition matrix $M$ is at least $\delta>0$ . Given a training dataset of $m=O\left(\frac{n^{2}}{\varepsilon^{2}\delta}\right)$ past page requests from $M$ , there is an algorithm $\mathcal{A}$ which is $\frac{2}{1-2\varepsilon}$ -competitive against $\mathrm{OPT}$ with probability at least $0.99$ over the $m$ samples..

The proof of this theorem is given in the full version, and follows the outline sketched above. We remark that the $O(\cdot)$ in the bound for $m$ hides a constant that depends on the conditioning of the linear systems that determine the $\alpha(p<q)$ values.

References

[1] Spyros Angelopoulos and Pascal Schweitzer. Paging and list update under bijective analysis. In Proceedings of the twentieth annual ACM-SIAM symposium on Discrete algorithms, pages 1136–1145. SIAM, 2009. doi:10.1137/1.9781611973068.123.
[2] Luca Becchetti. Modeling locality: A probabilistic analysis of lru and fwf. In Algorithms–ESA 2004: 12th Annual European Symposium, Bergen, Norway, September 14-17, 2004. Proceedings 12, pages 98–109. Springer, 2004. doi:10.1007/978-3-540-30140-0_11.
[3] Laszlo A. Belady. A study of replacement algorithms for a virtual-storage computer. IBM Systems journal, 5(2):78–101, 1966. doi:10.1147/sj.52.0078.
[4] Allan Borodin and Ran El-Yaniv. Online computation and competitive analysis. cambridge university press, 2005.
[5] Allan Borodin, Prabhakar Raghavan, Sandy Irani, and Baruch Schieber. Competitive paging with locality of reference. In Proceedings of the twenty-third annual ACM symposium on Theory of computing, pages 249–259, 1991.
[6] Peter J Denning. The working set model for program behavior. Communications of the ACM, 11(5):323–333, 1968. doi:10.1145/363095.363141.
[7] Reza Dorrigiv and Alejandro López-Ortiz. A survey of performance measures for on-line algorithms. SIGACT News, 36(3):67–81, 2005. URL: http://dl.acm.org/citation.cfm?id=1086670.
[8] Amos Fiat and Anna R Karlin. Randomized and multipointer paging with locality of reference. In Proceedings of the twenty-seventh annual ACM symposium on Theory of computing, pages 626–634, 1995. doi:10.1145/225058.225280.
[9] Amos Fiat and Manor Mendel. Truly online paging with locality of reference. In Proceedings 38th Annual Symposium on Foundations of Computer Science, pages 326–335. IEEE, 1997. doi:10.1109/SFCS.1997.646121.
[10] Yi Hao, Alon Orlitsky, and Venkatadheeraj Pichapati. On learning markov chains. Advances in Neural Information Processing Systems, 31, 2018.
[11] De Huang and Xiangyuan Li. Non-asymptotic estimates for markov transition matrices with rigorous error bounds. arXiv preprint arXiv:2408.05963, 2024.
[12] Sandy Irani. Competitive analysis of paging. Online Algorithms: The State of the Art, pages 52–73, 2005.
[13] Sandy Irani, Anna R Karlin, and Steven Phillips. Strongly competitive algorithms for paging with locality of reference. In Proceedings of the third annual ACM-SIAM symposium on Discrete algorithms, pages 228–236, 1992. URL: http://dl.acm.org/citation.cfm?id=139404.139455.
[14] AR Karlin, SJ Phillips, and P Raghavan. Markov paging. In Proceedings of the 33rd Annual Symposium on Foundations of Computer Science, pages 208–217, 1992.
[15] Elias Koutsoupias and Christos H Papadimitriou. Beyond competitive analysis. SIAM Journal on Computing, 30(1):300–317, 2000. doi:10.1137/S0097539796299540.
[16] Carsten Lund, Steven Phillips, and Nick Reingold. IP over connection-oriented networks and distributional paging. In Proceedings 35th Annual Symposium on Foundations of Computer Science, pages 424–434. IEEE, 1994. doi:10.1109/SFCS.1994.365674.
[17] Carsten Lund, Steven Phillips, and Nick Reingold. Paging against a distribution and IP networking. Journal of Computer and System Sciences, 58(1):222–231, 1999. doi:10.1006/jcss.1997.1498.
[18] Thodoris Lykouris and Sergei Vassilvitskii. Competitive caching with machine learned advice. Journal of the ACM (JACM), 68(4):1–25, 2021. doi:10.1145/3447579.
[19] Mohammad Mahdian, Hamid Nazerzadeh, and Amin Saberi. Online optimization with uncertain information. ACM Transactions on Algorithms (TALG), 8(1):1–29, 2012. doi:10.1145/2071379.2071381.
[20] Chirag Pabbaraju and Ali Vakilian. New and improved bounds for markov paging. arXiv preprint arXiv:2502.05511, 2025. doi:10.48550/arXiv.2502.05511.
[21] Tim Roughgarden. CS 369N Beyond Worst-Case Analysis, Lecture Notes 2: Models of Data in Online Paging. https://timroughgarden.org/f11/l2.pdf, 2010.
[22] Daniel D Sleator and Robert E Tarjan. Amortized efficiency of list update and paging rules. Communications of the ACM, 28(2):202–208, 1985. doi:10.1145/2786.2793.
[23] Eric Torng. A unified analysis of paging and caching. Algorithmica, 20:175–200, 1998. doi:10.1007/PL00009192.
[24] Geoffrey Wolfer and Aryeh Kontorovich. Statistical estimation of ergodic markov chain kernel over discrete state space. Bernoulli, 27(1):532–553, 2021.
[25] Neal E Young. Bounding the diffuse adversary. In Proceedings of the ninth annual ACM-SIAM symposium on Discrete algorithms, pages 420–425, 1998. URL: http://dl.acm.org/citation.cfm?id=314613.314772.
[26] Neal E Young. On-line paging against adversarially biased random inputs. Journal of Algorithms, 37(1):218–235, 2000. doi:10.1006/jagm.2000.1099.

Appendix A Linear System for Computing $\alpha(p<q|s)$

Let $M$ be the transition matrix on $n$ pages, and let $x_{s}=\alpha(p<q|s)$ . Note that $x_{p}=1$ , $x_{q}=0$ . For any other page $r\neq p,q$ , note that

\displaystyle x_{r}=M_{r,1}x_{1}+\dots+M_{r,n}x_{n}.

Thus, upon solving the linear system given by

\displaystyle\begin{bmatrix}M_{1,1}-1&M_{1,2}&\dots&M_{1,n}\\ M_{2,1}&M_{2,2}-1&\dots&M_{1,n}\\ \vdots&\vdots&\cdots&\vdots\\ \boldsymbol{e_{p}}\\ \vdots&\vdots&\cdots&\vdots\\ \boldsymbol{e_{q}}\\ \vdots&\vdots&\cdots&\vdots\\ M_{n,1}&M_{n,2}&\dots&M_{n,n}-1\end{bmatrix}\begin{bmatrix}x_{1}\\ x_{2}\\ \vdots\\ x_{p}\\ \vdots\\ x_{q}\\ \vdots\\ x_{n}\end{bmatrix}=\begin{bmatrix}0\\ 0\\ \vdots\\ 1\\ \vdots\\ 0\\ \vdots\\ 0\end{bmatrix},

(12)

where $\boldsymbol{e_{p}}$ and $\boldsymbol{e_{q}}$ are row vectors with a $1$ in the $p^{\text{th}}$ and $q^{\text{th}}$ coordinates, respectively, and $0$ elsewhere, $x_{s}$ is the desired value $\alpha(p<q|s)$ . In this way, we can solve a linear system for each of the $\leq n^{2}$ possible pairs for $q, p$ , and compute all $\alpha(p<q|s)$ values in time $O(n^{4})$ .

Appendix B Finishing the Proof of Lemma 7

Fix any $t\leq T$ . Let $\sigma_{\leq t}$ denote a fixed sequence of $t$ page requests, $\mathrm{OPT}_{\leq t}$ denote the execution of $\mathrm{OPT}$ on these $t$ page requests, and $\mathcal{A}_{<t}$ denote the execution of $\mathcal{A}$ on all but the last of these page requests, such that $\sigma_{\leq t},\mathrm{OPT}_{\leq t},\mathcal{A}_{<t}$ together result in a cache miss for $\mathcal{A}$ at time $t$ . Then, we have that

	$\displaystyle\operatorname{{\mathds{E}}}[\beta(t)]$	$\displaystyle=\operatorname{{Pr}}[\text{$\mathcal{A}$ is forced to evict at % time $t$ and the page $\boldsymbol{p}$ it evicts satisfies that $c(\boldsymbol% {p})$ is }$
		$\displaystyle\quad\text{requested no later than $r(t,\boldsymbol{p})$}]$
		$\displaystyle=\sum_{\sigma_{\leq t},\mathrm{OPT}_{\leq t},\mathcal{A}_{<t}}% \operatorname{{Pr}}[\sigma_{\leq t},\mathrm{OPT}_{\leq t},\mathcal{A}_{<t}]$
		$\displaystyle\quad\cdot\operatorname{{Pr}}\left[\text{page $\boldsymbol{p}$ % evicted by $\mathcal{A}$ at time $t$ satisfies that $c(\boldsymbol{p})$}\right.$
		$\displaystyle\qquad\qquad\left.\text{is requested no later than $r(t,% \boldsymbol{p})$}\ \big{\|}\ \sigma_{\leq t},\mathrm{OPT}_{\leq t},\mathcal{A}_% {<t}\right],$

Let us use the shorthand $\mathcal{B}:=\sigma_{\leq t},\mathrm{OPT}_{\leq t},\mathcal{A}_{<t}$ , and focus on the latter term in the summation. Note that once we have conditioned on $\mathcal{B}$ , the configuration of $\mathcal{A}$ ’s cache (before the page request at $t$ ) is determined – denote its pages by $\mathcal{A}^{-}$ . At the last page request in $\sigma_{\leq t}$ , $\mathcal{A}$ suffers a cache miss, and chooses a page to evict from $\mathcal{A}^{-}$ from a (conditional) distribution $\mathcal{P}_{t}$ satisfying the property given in the lemma statement. Namely,

	$\displaystyle\hskip-15.0pt\operatorname{{Pr}}$	$\displaystyle\left[\text{page $\boldsymbol{p}$ evicted by $\mathcal{A}$ at % time $t$ satisfies that $c(\boldsymbol{p})$ is requested no later than $r(t,% \boldsymbol{p})$}\ \big{\|}\ \mathcal{B}\right]$
		$\displaystyle=\sum_{p\in\mathcal{A}^{-}}\operatorname{{Pr}}_{\mathcal{P}_{t}}[% p]\operatorname{{Pr}}\left[\text{$c(p)$ is requested no later than $r(t,p)$}\ % \big{\|}\ \mathcal{B}\right].$

But note that conditioning on $\sigma_{\leq t}$ , $\mathrm{OPT}_{\leq t}$ determines the cache of $\mathrm{OPT}$ after time $t$ : let its contents be denoted by $\mathrm{OPT}^{+}$ . Then, according to our charging scheme, for any $p\in\mathcal{A}^{-}$ , $c(p)$ is as follows: if $p\notin\mathrm{OPT}^{+},c(p)=p$ , whereas if $p\in\mathrm{OPT}^{+}$ , $c(p)=q$ for some fixed $q\in\mathcal{A}^{-}\setminus\mathrm{OPT}^{+}$ that satisfies the condition in Item 2b. Note importantly that we make the same choice of $q$ for any $p$ in the latter case.

	$\displaystyle\sum_{p\in\mathcal{A}^{-}}\operatorname{{Pr}}_{\mathcal{P}_{t}}[p% ]\operatorname{{Pr}}\left[\text{$c(p)$ is requested no later than $r(t,p)$}\ % \big{\|}\ \mathcal{B}\right]$
	$\displaystyle=\sum_{p\in\mathcal{A}^{-},c(p)=p}\operatorname{{Pr}}_{\mathcal{P% }_{t}}[p]\underbrace{\operatorname{{Pr}}\left[\text{$p$ is requested no later % than $r(t,p)$}\ \big{\|}\ \mathcal{B}\right]}_{=1\text{ since $p$ itself is the% page requested at $r(t,p)$}}$
	$\displaystyle+\sum_{p\in\mathcal{A}^{-},c(p)=q}\operatorname{{Pr}}_{\mathcal{P% }_{t}}[p]\operatorname{{Pr}}\left[\text{$q$ is requested no later than $r(t,p)% $}\ \big{\|}\ \mathcal{B}\right]$
	$\displaystyle\geq\sum_{p\in\mathcal{A}^{-},c(p)=p}\operatorname{{Pr}}_{% \mathcal{P}_{t}}[p]\operatorname{{Pr}}\left[\text{$q$ is requested no later % than $r(t,p)$}\ \big{\|}\ \mathcal{B}\right]$
	$\displaystyle+\sum_{p\in\mathcal{A}^{-},c(p)=q}\operatorname{{Pr}}_{\mathcal{P% }_{t}}[p]\operatorname{{Pr}}\left[\text{$q$ is requested no later than $r(t,p)% $}\ \big{\|}\ \mathcal{B}\right]$
	$\displaystyle=\sum_{p\in\mathcal{A}^{-}}\operatorname{{Pr}}_{\mathcal{P}_{t}}[% p]\operatorname{{Pr}}\left[\text{$q$ is requested no later than $r(t,p)$}\ % \big{\|}\ \mathcal{B}\right]\geq\frac{1}{c},$

where in the last line, we used the property of the distribution $\mathcal{P}_{t}$ from the lemma statement. Tracing backwards, we have obtained that

	$\displaystyle\operatorname{{\mathds{E}}}[\beta(t)]$	$\displaystyle\geq\sum_{\sigma_{\leq t},\mathrm{OPT}_{\leq t},\mathcal{A}_{<t}}% \operatorname{{Pr}}[\sigma_{\leq t},\mathrm{OPT}_{\leq t},\mathcal{A}_{<t}]% \cdot\frac{1}{c}$
		$\displaystyle=\frac{1}{c}\cdot\operatorname{{Pr}}[\text{$\mathcal{A}$ is % forced to evict at time $t$}]=\frac{1}{c}\cdot\operatorname{{\mathds{E}}}[% \alpha(t)].$

Finally, we observe that the random variable $\mathcal{I}-\mathcal{O}$ is always nonnegative. This is because, any page that is in the cache of $\mathcal{A}$ after the request at time $T$ , or not in the cache of $\mathcal{A}$ after time $T$ but giving a charge, must necessarily have either been in the initial cache, or must have been requested at some time $t\leq T$ . This implies that $k+\mathcal{O}\leq k+\mathcal{I}$ , which implies that $\mathcal{I}-\mathcal{O}\geq 0$ . In total,

\displaystyle\operatorname{{\mathds{E}}}[\mathrm{Cost}(\mathrm{OPT},T)]\geq% \frac{1}{2}\sum_{t\leq T}\operatorname{{\mathds{E}}}[\beta(t)]+\operatorname{{% \mathds{E}}}\left[\mathcal{I}-\mathcal{O}\right]\geq\frac{1}{2c}\operatorname{% {\mathds{E}}}\left[\sum_{t\leq T}\alpha(t)\right]=\frac{1}{2c}\operatorname{{% \mathds{E}}}[\mathrm{Cost}(\mathcal{A},T)]

as required.

Appendix C Proof of Claim 11

Proof.

We first show that if the page $s$ requested at time $t$ satisfies the condition, then $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ decreases by 1. Since $s$ is in $\mathrm{OPT}$ ’s cache, the request to $s$ does not change $\mathcal{U}$ (see the definition in (9)). Moreover, $s$ being in $\mathrm{OPT}$ ’s cache implies it was either in the initial cache or previously requested, so $\mathcal{I}$ also remains unchanged. Similarly, because $s$ is not doubly charged, $\mathcal{D}$ remains unchanged. Thus, we only need to account for the change in $\mathcal{O}$ .

Because $s$ is neither giving nor bearing any charges, both Item 1a and Item 1b cause no change in $\mathcal{O}$ . Finally, because $s$ does not exist in $\mathcal{A}$ ’s cache and results in a cache miss, Item 2 creates a new charge, causing $\mathcal{O}$ to increase by 1. In total, $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ decreases by 1.

Next, we will show that if $s$ does not satisfy the condition, then $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ either increases or stays the same. Towards this, consider each of the following cases:

Case 1: $𝒔$ is a doubly-charged page.

In this case, $\mathcal{D}$ increases by 1. Note that one of the charges on $s$ is by $s$ itself, and the other charge is by some other page $q$ . In particular, $s$ is not giving a charge to a page other than itself. Thus, when $s$ is requested, Item 1a and Item 1b ensure that the charge by $s$ on itself as well as the charge on $s$ by $q$ are both dropped.⁹⁹9Note how Item 1b was necessary to ensure this. However, note also that $s$ is not in the cache of $\mathcal{A}$ (since it has a charge on itself, it was previously evicted by $\mathcal{A}$ ), and hence this request has caused a cache miss in $\mathcal{A}$ , resulting in the creation of a new charge in Item 2. Item 3 can only reassign a charge, and thus, the net change in $\mathcal{O}$ is $-1$ . Finally, $\mathcal{I}$ and $\mathcal{U}$ remain the same. Therefore, the overall change in $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ is 0.

Case 2: $𝒔$ is a singly-charged page.

This means that either $s$ is not in the cache of $\mathcal{A}$ and is charging itself, or $s$ is in the cache of $\mathcal{A}$ and is bearing a charge given by some other page $p$ at the time of its eviction.

In the former case, observe that none of $\mathcal{I}$ , $\mathcal{D}$ or $\mathcal{U}$ are affected. The clearing of charges in Item 1 causes $\mathcal{O}$ to decrease by 1, and the cache miss causes the creation of a new charge in Item 2. In total, $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ stays unchanged. In the latter case, observe that the charge on $s$ is cleared in Item 1b, causing $\mathcal{O}$ to decrease by 1. Furthermore, because $s$ is in the cache of $\mathcal{A}$ , there is no creation of a new charge in Item 2. Thus, $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ increases by 1.

Case 3: $𝒔$ is not in $\mathrm{OPT}$ ’s cache.

If $s$ is either singly or doubly-charged, we fall under Case 1 or 2. If $s$ has no charges on it, then:

Subcase 3a: $𝒔$ has never been requested before.

In this case, $\mathcal{I}$ increases by 1. Also, $s$ cannot be giving or bearing any charges; thus Item 1a and Item 1b cause no change to $\mathcal{O}$ . However, the request to $s$ causes a cache miss in $\mathcal{A}$ , resulting in an eviction, and the creation of a new charge. Thus, $\mathcal{O}$ increases by 1. Additionally, $\mathcal{D}$ and $\mathcal{U}$ remain the same. Thus, the net change in $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ is 0.

Subcase 3b: $𝒔$ has been requested before.

This means that $s$ was previously in $\mathrm{OPT}$ ’s cache at some time but was since evicted. Also, $s$ has no charges on it. Thus, $\mathcal{U}$ increases by 1, while $\mathcal{I}$ and $\mathcal{D}$ remain unchanged. It remains to reason about $\mathcal{O}$ . Because $s$ has no charges on it, Item 1b causes no change in $\mathcal{O}$ . Item 1a either decreases $\mathcal{O}$ by 1 or causes no change to it. While the request to $s$ can cause a cache miss to $\mathcal{A}$ , this can only result in the creation of a single new charge, and $\mathcal{O}$ can increase by at most 1 due to this. In total, $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ either increases or stays the same.

Case 4: $𝒔$ is in $\mathcal{A}$ ’s cache.

This means that $s$ is giving no charges. Then, either $s$ is singly-charged or has no charges on it. It cannot be doubly-charged because it would have to be out of $\mathcal{A}$ ’s cache for that. If it is singly-charged, we fall under Case 2. If it has no charges on it, we reason as follows: both Item 1 and Item 2 leave $\mathcal{O}$ unaffected. Moreover, $\mathcal{I}$ and $\mathcal{D}$ remain unaffected. Finally, depending on whether $s$ is or isn’t in $\mathrm{OPT}$ ’s cache, $\mathcal{U}$ either stays the same or increases. Hence, $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ either stays the same or increases.

Case 5: $𝒔$ is giving a charge.

If $s$ has any charges on it, we fall under Case 1 or 2. So we assume that $s$ has no charges on it. This means that $s$ is not in $\mathcal{A}$ ’s cache, but is still in $\mathrm{OPT}$ ’s cache. Note then that $\mathcal{I},\mathcal{D},\mathcal{U}$ remain unchanged. We reason about the change in $\mathcal{O}$ as follows: Item 1a clears the charge that $s$ is giving and decreases $\mathcal{O}$ by 1, whereas Item 2 creates a new charge and increases $\mathcal{O}$ by 1. In total, $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ remains unchanged.

Thus, in any way that the requested page $s$ might not satisfy the condition, $\mathcal{I}-\mathcal{D}-\mathcal{O}+\mathcal{U}$ either increases or stays the same, concluding the proof. $\hfill\blacktriangleleft$

[bib.bib1] [1] Spyros Angelopoulos and Pascal Schweitzer. Paging and list update under bijective analysis. In Proceedings of the twentieth annual ACM-SIAM symposium on Discrete algorithms, pages 1136–1145. SIAM, 2009. doi:10.1137/1.9781611973068.123.

[bib.bib2] [2] Luca Becchetti. Modeling locality: A probabilistic analysis of lru and fwf. In Algorithms–ESA 2004: 12th Annual European Symposium, Bergen, Norway, September 14-17, 2004. Proceedings 12, pages 98–109. Springer, 2004. doi:10.1007/978-3-540-30140-0_11.

[bib.bib3] [3] Laszlo A. Belady. A study of replacement algorithms for a virtual-storage computer. IBM Systems journal, 5(2):78–101, 1966. doi:10.1147/sj.52.0078.

[bib.bib4] [4] Allan Borodin and Ran El-Yaniv. Online computation and competitive analysis. cambridge university press, 2005.

[bib.bib5] [5] Allan Borodin, Prabhakar Raghavan, Sandy Irani, and Baruch Schieber. Competitive paging with locality of reference. In Proceedings of the twenty-third annual ACM symposium on Theory of computing, pages 249–259, 1991.

[bib.bib6] [6] Peter J Denning. The working set model for program behavior. Communications of the ACM, 11(5):323–333, 1968. doi:10.1145/363095.363141.

[bib.bib7] [7] Reza Dorrigiv and Alejandro López-Ortiz. A survey of performance measures for on-line algorithms. SIGACT News, 36(3):67–81, 2005. URL: http://dl.acm.org/citation.cfm?id=1086670.

[bib.bib8] [8] Amos Fiat and Anna R Karlin. Randomized and multipointer paging with locality of reference. In Proceedings of the twenty-seventh annual ACM symposium on Theory of computing, pages 626–634, 1995. doi:10.1145/225058.225280.

[bib.bib9] [9] Amos Fiat and Manor Mendel. Truly online paging with locality of reference. In Proceedings 38th Annual Symposium on Foundations of Computer Science, pages 326–335. IEEE, 1997. doi:10.1109/SFCS.1997.646121.

[bib.bib10] [10] Yi Hao, Alon Orlitsky, and Venkatadheeraj Pichapati. On learning markov chains. Advances in Neural Information Processing Systems, 31, 2018.

[bib.bib11] [11] De Huang and Xiangyuan Li. Non-asymptotic estimates for markov transition matrices with rigorous error bounds. arXiv preprint arXiv:2408.05963, 2024.

[bib.bib12] [12] Sandy Irani. Competitive analysis of paging. Online Algorithms: The State of the Art, pages 52–73, 2005.

[bib.bib13] [13] Sandy Irani, Anna R Karlin, and Steven Phillips. Strongly competitive algorithms for paging with locality of reference. In Proceedings of the third annual ACM-SIAM symposium on Discrete algorithms, pages 228–236, 1992. URL: http://dl.acm.org/citation.cfm?id=139404.139455.

[bib.bib14] [14] AR Karlin, SJ Phillips, and P Raghavan. Markov paging. In Proceedings of the 33rd Annual Symposium on Foundations of Computer Science, pages 208–217, 1992.

[bib.bib15] [15] Elias Koutsoupias and Christos H Papadimitriou. Beyond competitive analysis. SIAM Journal on Computing, 30(1):300–317, 2000. doi:10.1137/S0097539796299540.

[bib.bib16] [16] Carsten Lund, Steven Phillips, and Nick Reingold. IP over connection-oriented networks and distributional paging. In Proceedings 35th Annual Symposium on Foundations of Computer Science, pages 424–434. IEEE, 1994. doi:10.1109/SFCS.1994.365674.

[bib.bib17] [17] Carsten Lund, Steven Phillips, and Nick Reingold. Paging against a distribution and IP networking. Journal of Computer and System Sciences, 58(1):222–231, 1999. doi:10.1006/jcss.1997.1498.

[bib.bib18] [18] Thodoris Lykouris and Sergei Vassilvitskii. Competitive caching with machine learned advice. Journal of the ACM (JACM), 68(4):1–25, 2021. doi:10.1145/3447579.

[bib.bib19] [19] Mohammad Mahdian, Hamid Nazerzadeh, and Amin Saberi. Online optimization with uncertain information. ACM Transactions on Algorithms (TALG), 8(1):1–29, 2012. doi:10.1145/2071379.2071381.

[bib.bib20] [20] Chirag Pabbaraju and Ali Vakilian. New and improved bounds for markov paging. arXiv preprint arXiv:2502.05511, 2025. doi:10.48550/arXiv.2502.05511.

[bib.bib21] [21] Tim Roughgarden. CS 369N Beyond Worst-Case Analysis, Lecture Notes 2: Models of Data in Online Paging. https://timroughgarden.org/f11/l2.pdf, 2010.

[bib.bib22] [22] Daniel D Sleator and Robert E Tarjan. Amortized efficiency of list update and paging rules. Communications of the ACM, 28(2):202–208, 1985. doi:10.1145/2786.2793.

[bib.bib23] [23] Eric Torng. A unified analysis of paging and caching. Algorithmica, 20:175–200, 1998. doi:10.1007/PL00009192.

[bib.bib24] [24] Geoffrey Wolfer and Aryeh Kontorovich. Statistical estimation of ergodic markov chain kernel over discrete state space. Bernoulli, 27(1):532–553, 2021.

[bib.bib25] [25] Neal E Young. Bounding the diffuse adversary. In Proceedings of the ninth annual ACM-SIAM symposium on Discrete algorithms, pages 420–425, 1998. URL: http://dl.acm.org/citation.cfm?id=314613.314772.

[bib.bib26] [26] Neal E Young. On-line paging against adversarially biased random inputs. Journal of Algorithms, 37(1):218–235, 2000. doi:10.1006/jagm.2000.1099.

	$\displaystyle\sum_{p\in\mathcal{A}^{-}}\operatorname{{Pr}}_{\mathcal{P}_{t}}[p% ]\operatorname{{Pr}}\left[\text{$c(p)$ is requested no later than $r(t,p)$}\ % \big{\|}\ \mathcal{B}\right]$
	$\displaystyle=\sum_{p\in\mathcal{A}^{-},c(p)=p}\operatorname{{Pr}}_{\mathcal{P% }_{t}}[p]\underbrace{\operatorname{{Pr}}\left[\text{$p$ is requested no later % than $r(t,p)$}\ \big{\|}\ \mathcal{B}\right]}_{=1\text{ since $p$ itself is the% page requested at $r(t,p)$}}$
	$\displaystyle+\sum_{p\in\mathcal{A}^{-},c(p)=q}\operatorname{{Pr}}_{\mathcal{P% }_{t}}[p]\operatorname{{Pr}}\left[\text{$q$ is requested no later than $r(t,p)% $}\ \big{\|}\ \mathcal{B}\right]$
	$\displaystyle\geq\sum_{p\in\mathcal{A}^{-},c(p)=p}\operatorname{{Pr}}_{% \mathcal{P}_{t}}[p]\operatorname{{Pr}}\left[\text{$q$ is requested no later % than $r(t,p)$}\ \big{\|}\ \mathcal{B}\right]$
	$\displaystyle+\sum_{p\in\mathcal{A}^{-},c(p)=q}\operatorname{{Pr}}_{\mathcal{P% }_{t}}[p]\operatorname{{Pr}}\left[\text{$q$ is requested no later than $r(t,p)% $}\ \big{\|}\ \mathcal{B}\right]$
	$\displaystyle=\sum_{p\in\mathcal{A}^{-}}\operatorname{{Pr}}_{\mathcal{P}_{t}}[% p]\operatorname{{Pr}}\left[\text{$q$ is requested no later than $r(t,p)$}\ % \big{\|}\ \mathcal{B}\right]\geq\frac{1}{c},$

New and Improved Bounds for Markov Paging

Abstract

Keywords and phrases:

Category:

Funding:

Copyright and License:

2012 ACM Subject Classification:

Related Version:

Acknowledgements:

DOI:

Event:

Editors:

Series and Publisher:

1 Introduction

Theorem 1.

Theorem 2.

Theorem 3.

1.1 Other Related Work

2 Background and Setup

2.1 Markov Paging

Theorem 4 (Theorems 1, 2 in [14]).

2.2 Dominating Distribution Algorithm

Theorem 5 (Theorem 3.4 in [17]).

Claim 6.

3 4-competitive Analysis of [17]

Lemma 7 (Lemma 2.5 in [17]).

Proof.

Corollary 8.

Proof.

▶ Remark 9.

4 Sources of Looseness in the Analysis

4.1 A Conservative Approach to Handling Doubly-Charged Pages

4.2 Inexhaustive Clearing of Charges upon a Page Request

4.3 No Accounting for Uncharged, Non-first-timer Pages

5 Tightening the Analysis to 2-competitiveness

Lemma 10.

Proof.

Claim 11.

Claim 12.

Proof.

Corollary 13.

Proof.

▶ Remark 14.

▶ Remark 15.

Corollary 16.

6 Lower Bound for Dominating Distribution Algorithms

7 Learning the Markov Chain from Samples

Theorem 17 (Theorem 4 in [10]).

Theorem 18.

References

Appendix A Linear System for Computing 𝜶⁢(𝒑⁢<𝒒|⁢𝒔)

Appendix B Finishing the Proof of Lemma 7

Appendix C Proof of Claim 11

Proof.

Case 1: 𝒔 is a doubly-charged page.

Case 2: 𝒔 is a singly-charged page.

Case 3: 𝒔 is not in 𝐎𝐏𝐓’s cache.

Subcase 3a: 𝒔 has never been requested before.

Subcase 3b: 𝒔 has been requested before.

Case 4: 𝒔 is in 𝓐’s cache.

Case 5: 𝒔 is giving a charge.

$\blacktriangleright$ Remark 9.

$\blacktriangleright$ Remark 14.

$\blacktriangleright$ Remark 15.

Appendix A Linear System for Computing $\alpha(p<q|s)$

Case 1: $𝒔$ is a doubly-charged page.

Case 2: $𝒔$ is a singly-charged page.

Case 3: $𝒔$ is not in $\mathrm{OPT}$ ’s cache.

Subcase 3a: $𝒔$ has never been requested before.

Subcase 3b: $𝒔$ has been requested before.

Case 4: $𝒔$ is in $\mathcal{A}$ ’s cache.

Case 5: $𝒔$ is giving a charge.