Containment for Guarded Monotone Strict NP
Abstract
Guarded Monotone Strict NP (GMSNP) extends Monotone Monadic Strict NP (MMSNP) by guarded existentially quantified predicates of arbitrary arities. We prove that the containment problem for GMSNP is decidable, thereby settling an open question of Bienvenu, ten Cate, Lutz, and Wolter, later restated by Bourhis and Lutz. Our proof also comes with a 2NEXPTIME upper bound on the complexity of the problem, which matches the lower bound for containment of MMSNP due to Bourhis and Lutz. In order to obtain these results, we significantly improve the state of knowledge of the model-theoretic properties of GMSNP. Bodirsky, Knäuer, and Starke previously showed that every GMSNP sentence defines a finite union of CSPs of -categorical structures. We show that these structures can be used to obtain a reduction from the containment problem for GMSNP to the much simpler problem of testing the existence of a certain map called recolouring, albeit in a more general setting than GMSNP; a careful analysis of this yields said upper bound. As a secondary contribution, we refine the construction of Bodirsky, Knäuer, and Starke by adding a restricted form of homogeneity to the properties of these structures, making the logic amenable to future complexity classifications for query evaluation using techniques developed for infinite-domain CSPs.
Keywords and phrases:
guarded, monotone, SNP, forbidden patterns, query containment, recolouring, decidability, computational complexity, -categoricity, constraint satisfaction, homogeneity, amalgamation property, Ramsey property, canonical functionCategory:
Track B: Automata, Logic, Semantics, and Theory of ProgrammingCopyright and License:
2012 ACM Subject Classification:
Theory of computation Logic ; Theory of computation Computational complexity and cryptographyAcknowledgements:
The first author is thankful to Florent Madelaine for making him aware of the containment problem for GMSNP.Funding:
This research was funded in whole or in part by the Austrian Science Fund (FWF) [P 32337, I 5948]. For the purpose of Open Access, the authors have applied a CC BY public copyright licence to any Author Accepted Manuscript (AAM) version arising from this submission. This research is also funded by the European Union (ERC, POCOCOP, 101071674). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them.Editors:
Keren Censor-Hillel, Fabrizio Grandoni, Joël Ouaknine, and Gabriele PuppisSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
1.1 The logic GMSNP
Guarded Monotone Strict NP () is a syntactic fragment of existential second-order logic describing problems of the form
Is there a colouring of the relational tuples in a given finite relational structure avoiding a fixed set of finitely many forbidden colour-patterns?
The logic GMSNP was introduced in [6] as a generalisation of the logic Monotone Monadic Strict NP without inequality () of Feder and Vardi [19], which captures similar problems concerning colourings of vertices instead of relational tuples. However, its true origins actually go back to an earlier work of Madelaine [28], who was studying GMSNP under the names MMSNP2 and FPP (standing for Forbidden Pattern Problems).
Formally, a GMSNP sentence is of the form , for a CNF-formula over a finite relational signature , satisfying the following two conditions:
-
-atoms and equalities may only appear negatively in clauses of , i.e., the only positive atoms in clauses of are of the form for some ; (Monotonicity)
-
for every clause of and every positive atom in there exists a negative atom in with such that . (Guarding)
Unless stated otherwise, we will denote the set of the second-order variables in by ; we refer to as the existential symbols and as the input symbols in . We also refer to the first-order -sentence as the first-order part of . By a simple application of De Morgan’s laws, we can rewrite as a formula of the form , where each is a conjunction of -atoms and possibly negated -atoms. We refer to the conjuncts as the forbidden patterns of .
A typical example of a problem that can be defined in is whether a given undirected simple graph, say with edge relation denoted by , can be edge-2-coloured while avoiding monochromatic triangles [21]:
| (1) | ||||
See Figure 1 for illustration.

The forbidden patterns of this problem are the two monochromatic triangles, overlapping colours, and uncoloured edges. In MMSNP, we can formulate a similar problem where the task is to find a vertex-2-colouring instead of an edge-2-colouring:
| (2) | ||||
Strictly speaking, does not fully contain because the latter does not require the guarding axiom (it instead requires the monadicity axiom). However, the containment does hold up to a small syntactic transformation, modulo which GMSNP is in fact strictly more expressive than MMSNP [6]. Namely, every MMSNP sentence can be converted into a GMSNP sentence by expanding the base signature by a fresh unary “domain” symbol and adding negative atoms to each clause, for every universally quantified first-order variable appearing in that clause. Given a -structure , we have that holds in if and only if holds in , where is the -structure obtained from by including every domain element in the relation interpreting . On the other hand, given a -structure , we have that holds in if and only if holds in , where is the -structure obtained from by forgetting and removing all domain elements which were not contained in the relation interpreting . For example, the last two clauses in (1.1) do not satisfy the guarding axiom, but we can obtain a polynomial-time equivalent GMSNP sentence by padding (1.1) with the predicate :
1.2 A brief history of GMSNP
In 2014, Bienvenu, ten Cate, Lutz, and Wolter [6] discovered an interesting correspondence that allows one to translate complexity classification results for certain well-behaved fragments of the logic SNP [26, 34] to analogous statements about the complexity of ontology-mediated queries. In the special case of MMSNP, the above-mentioned result from [6] implies that there is a dichotomy between P and NP-completeness if and only if there is a dichotomy between P and coNP-completeness for the evaluation of unions of conjunctive queries mediated by ontologies specified in the description logic [1]. The significance of this equivalence lies in the fact that the computational complexity of MMSNP had already been intensively investigated within the programme initiated by Feder and Vardi in 1998 [19].
Feder and Vardi proved that every problem described by an MMSNP sentence is equivalent under polynomial-time randomised reductions to the Constraint Satisfaction Problem (CSP) of a structure with a finite domain, i.e., the problem of testing whether a given conjunctive query is satisfiable in that structure. They moreover conjectured that every finite-domain CSP is in P or NP-complete, which was eventually confirmed twenty years later by Bulatov and Zhuk [17, 39] in what can be viewed as the culmination of decades of work on connections between algorithms for CSPs and universal algebra. This implied dichotomies for MMSNP and, in turn, for the above-mentioned queries up to randomised reductions. Although the originally randomised reduction of MMSNP to CSPs by Feder and Vardi was derandomised by Kun in 2013 [27], it still relied on a probabilistic proof of the existence of expanders of large girth. The first truly constructive proof of the dichotomy was obtained in 2018 by Bodirsky, Madelaine, and Mottet [12] using methods from infinite-domain constraint satisfaction, i.e., CSPs of infinite structures. Roughly speaking, they start with the observation from [9] that every MMSNP sentence defines a finite union of CSPs of (infinite) -categorical structures. They then gradually upgrade these structures until a state is reached where they can show that their CSPs admit a polynomial-time many-one reduction to a finite-domain CSP which is polynomial-time tractable unless one of the -categorical structures can simulate the 3-colouring problem via a pp-construction [4] (in which case the sentence defines a NP-complete problem).
The question whether GMSNP also exhibits a P/NP-dichotomy was left open in [6]; a positive answer would yield a P/coNP-dichotomy for the evaluation of unions of conjunctive queries mediated by ontologies specified in guarded first-order logic. It was observed by Bodirsky, Knäuer, and Starke [11] that similarly to MMSNP, the logic GMSNP can be studied using methods from infinite-domain constraint satisfaction. Using this approach, the existence of a dichotomy has already been confirmed in some specific cases, e.g., for graph orientations with forbidden tournaments [10, 7, 20]. However, at the moment there is no clear road map for how exactly the question of the existence of a P/NP-dichotomy for GMSNP should be approached: it is apparent that the increase in the arity of the existentially quantified predicates introduces new obstacles which were not present with MMSNP. Hope is sparked by a recently announced result of Guzmán-Pro [22] who used the sparse-incomparability lemma [27] to show that the homomorphism-sandwiching method [16] for obtaining hardness reductions from finite-domain promise CSPs fails for CSPs definable in GMSNP. This is in fact a good plausibility argument for the applicability of methods from infinite-domain constraint satisfaction to GMSNP, because several NP-hardness results for finite-domain promise CSPs (Proposition 10.1 in [3] and Theorem 2.2 in [38]) are inconsistent with the algebraic dichotomy conjecture for infinite-domain CSPs [5].
1.3 The containment problem
Besides query evaluation, two other computational decision problems for ontology-mediated queries were studied in [6]: first-order/datalog rewritability and containment. As with their counterparts in automata theory, the complexity of such problems tends to be significantly higher. This raises the question of whether, in studying the complexity of these problems, one can perhaps avoid the fine-grained analysis that makes the proof of complexity dichotomies so intricate. In the case of MMSNP, the precise complexity of first-order/datalog rewritability and containment is known: both are 2NEXPTIME-complete [31, 32, 15]. While rewritability seems to be intimately linked to the reduction from MMSNP to finite-domain CSPs [31, 32], for the containment problem, the link seems to be much weaker [15, 12]. This makes the study of the containment problem for GMSNP a perfect starting point for the development of tools that will later be useful for approaching the topics of rewritability and query evaluation.
In the proof of our main result, it will be important that we formulate the containment problem in the more general setting of SNP sentences, which are obtained by leaving out the monotonicity and the guarding axioms.
For an SNP sentence , we denote the class of all finite models of by .
Formally, the containment problem can be stated as follows:
Containment for SNP
INSTANCE: A pair of SNP sentences in a common signature .
QUESTION: Is it true that ?
The containment problem for SNP is undecidable in general; in fact, it is already undecidable for the Datalog fragment [37]. The question whether it is decidable for GMSNP was left open in [6, 15]; the only known result regarding the complexity of this problem is the lower bound of Bourhis and Lutz for the containment within MMSNP. To see that this lower bound also applies for GMSNP, note that the map introduced in Section 1.1 is not only a polynomial-time reduction from MMSNP to GMSNP, but it also acts as a fully faithful covariant functor with respect to containment. More specifically, for a pair of MMSNP -sentences, we have if and only if .
Theorem 1 (Theorem 3 in [15]).
Containment for GMSNP is 2NEXPTIME-hard.
1.4 Contributions
The contributions of the present article are twofold. On the one hand, we confirm that the containment problem for GMSNP is indeed decidable. Our proof of decidability also comes with an upper bound on the complexity matching the lower bound in Theorem 1.
Theorem 2.
The containment problem for GMSNP is in 2NEXPTIME.
Corollary 3.
The containment problem for GMSNP is 2NEXPTIME-complete.
The proof of Theorem 2 is based on the recolouring method, first used implicitly by Feder and Vardi [19, Theorem 7] in their proof of decidability of containment for MMSNP.111Recolourings were first explicitly mentioned in the work of Madelaine and Stewart [30] (see also [29]). Roughly said, the strategy is to modify the input sentences by adding new clauses and existentially quantified symbols until a state is reached where the containment problem becomes equivalent to the much simpler problem of testing the existence of a mapping between the existential symbols of the two sentences satisfying a certain condition (a recolouring). In contrast to MMSNP, in order to achieve the promised 2NEXPTIME upper bound on the complexity of containment for GMSNP using the recolouring method, we have to deviate from the GMSNP framework (to SNP) and significantly generalise the notion of a recolouring.
The first preprocessing step, common across most approaches to the containment problem for MMSNP, is a reduction to the connected case [12, 15, 19, 29]. Intuitively, an MMSNP sentence is connected if its forbidden colour-patterns are connected in the graph-theoretic sense. This reduction can be generalised to GMSNP, as shown in [11]. Bodirsky, Knäuer, and Starke [11, Proposition 1] showed that every GMSNP sentence is logically equivalent to a finite disjunction of connected GMSNP sentences. An inspection of their proof reveals that if the complexity of checking containment is in 2NEXPTIME for connected GMSNP sentences, then so it is for the entire class GMSNP.
The second preprocessing step (in the approaches to the containment for MMSNP) is typically a reduction to the biconnected case [15, 12]. Intuitively, an MMSNP sentence is biconnected if no forbidden colour-pattern can be disconnected by deleting a single vertex. The reduction to biconnected MMSNP is the point where a significant amount of work can be outsourced to a general combinatorial result, e.g., a lemma of Erdős in the case of [15] or a theorem of Hubička and Nešetřil in the case of [12]. The procedure for attaining biconnectedness from [12, Lemma 4.4] transforms a given connected MMSNP sentence to a logically equivalent biconnected MMSNP sentence by iteratively selecting a forbidden colour-pattern which can be disconnected by deleting a single vertex and splitting it into two forbidden colour-patterns (corresponding to the two parts); the split is then marked using a fresh unary existential predicate. The GMSNP-analogue of this procedure does not terminate if the arities of the existentially quantified predicates are greater than , and we do not see any way how this issue could be fixed. Therefore, to progress further, we must understand how exactly the said general combinatorial results are used in the complexity analysis of the containment problem; in the present paper, we focus specifically on the approach from [12] using the mentioned theorem of Hubička and Nešetřil.
Roughly said, the theorem implies that every connected MMSNP -sentence can be assigned a highly symmetric infinite structure in a signature extending such that the -reducts of the finite substructures of are up to isomorphism precisely the finite models of the first-order part of ; this was first observed by Bodirsky and Dalmau [9]. Bodirsky, Madelaine, and Mottet [12] proved that if is biconnected, then the -reduct of retains a certain amount of the original symmetry, and this fact is crucial in their take on the recolouring method. Later on, Bodirsky, Knäuer, and Starke [11] showed that also connected GMSNP sentences can be assigned said highly symmetric infinite structures; they did not comment on whether this fact is helpful in analysing the complexity of the containment problem for GMSNP. We show that the highly symmetric infinite structures associated with GMSNP sentences can be described by SNP sentences of size doubly exponential in the size of . Subsequently, we show that the containment is equivalent to the existence of a particular mapping from to which is uniquely determined by the images of substructures whose size is bounded by the maximal arity of a symbol in or . From this fact, we extract our more general version of recolourings for SNP. By carefully analysing the total complexity of computing the SNP sentences and stemming from the theorem of Hubička and Nešetřil and of the subsequent check for the existence of a recolouring between such sentences, we conclude that the containment problem for GMSNP is in 2NEXPTIME. We remark that our methods are, in theory, applicable in a more general setting than GMSNP; a fragment of SNP which is closely related to such applicability is Amalgamation SNP introduced in [11]. We also remark that the SNP sentences and define a linear order over the domain of a given structure, which is at the core of our argument why the recolouring method works in our case. It is provably not possible to define a linear order in GMSNP [11, Example 6], which indicates that this method requires us to leave the GMSNP framework.
As our secondary contribution, we analyse to what extent it is possible to prove the decidability of the containment problem for GMSNP while staying as close as possible to the original recolouring method for MMSNP. A (vertex)-recolouring between two MMSNP sentences and is simply a mapping from the (unary) existential symbols of to those of whose application to the relations denoted by these symbols of any model of the first-order part of yields a model of the first-order part of . That is, the mapping does not introduce any vertex-colour patterns forbidden by into structures which originally did not contain any patterns forbidden by (see [12, Definition 4.25]). If and assert that the existential relations form a partition of all vertices (cf. the notion of normal form in [12]), then this is what one would intuitively understand under a recolouring of vertices – hence the name. But the true intention of this concept, which does not require any additional assumptions on and (such as the vertices being partitioned by the existential predicates) is to capture a very specific case of the containment , which is witnessed uniformly across all structures in . The natural extension of vertex-recolourings to GMSNP would be edge-recolourings, i.e., mappings
| (3) |
where and is an atomic -formula (), such that induces a mapping between models of the first-order parts of the two sentences. The notion of a recolouring for SNP we use in the proof of Theorem 2 is considerably more general and abstract. Hence, it makes sense to ask whether one can also prove decidability of containment for GMSNP by simply refining the input sentences and long enough, while staying in GMSNP, until the containment becomes equivalent to the existence of an edge-recolouring from to .
The central notion in analysing this possibility is recolouring-readiness, which is comparable to the notion of a simple program of Bourhis and Lutz [15] or the normal form of Bodirsky, Madelaine, and Mottet [12]. Instead of relying purely on syntactic preprocessing, in the definition of recolouring-readiness, we draw our inspiration from the proof of Theorem 2. Intuitively, a GMSNP -sentence is recolouring-ready if it can be assigned a highly symmetric infinite structure as in our proof of Theorem 2 such that the -reduct of retains a sufficient amount of the original symmetry for a reduction from containment to edge-recolouring to work. We show that every connected GMSNP sentence is logically equivalent to a connected recolouring-ready GMSNP sentence . However, the size of the smallest such that we are able to obtain surpasses the upper bound provided in Theorem 2. We leave it as an open question whether the precise complexity of containment for GMSNP can be determined purely from within the GMSNP framework.
Theorem 4.
For every connected GMSNP -sentence there exists a logically equivalent recolouring-ready connected GMSNP -sentence of size triple-exponential in the size of such that the maximal arity of the symbols in and in is the same. Moreover, can be computed from in nondeterministic triple-exponential time.
1.5 Outline
2 Preliminaries
We use the bar notation for tuples, and the set is denoted by . We extend the containment relation on sets to tuples by ignoring the ordering on the entries. For example, we might write for a set and a tuple .
Structures.
A (relational) signature is a set of relation symbols, each is associated with a natural number called arity. A (relational) -structure consists of a set (the domain) together with the relations for each with arity . An expansion of is a -structure with such that and for each relation symbol . Conversely, we then call a reduct of . We denote the reduct of to a subset of its signature by . A linear-order expansion of a -structure is an expansion by a single linear order denoted by (assuming ); we denote such expansion by . We often do not distinguish between the symbol and the associated linear order. Given a class of -structures , we denote by the class of all -structures which are linear-order expansions of structures from . The union of two -structures and is the -structure with domain and relations for every . A structure is connected if it is not the union of two structures with disjoint non-empty domains.
A homomorphism for -structures is a mapping that preserves each relation of , i.e., whenever for some relation symbol , then (computed componentwise) is an element of . We write if maps homomorphically into . The Constraint Satisfaction Problem (CSP) of , denoted by , is defined as the class of all finite structures which homomorphically map into . An embedding is an injective homomorphism that additionally satisfies the following condition: for every -ary relation symbol and we have only if We write if embeds into . The age of , denoted by , is the class of all finite structures which embed into . A substructure of is a structure over such that the inclusion map is an embedding. An isomorphism is a surjective embedding. A partial isomorphism on a structure is an isomorphism between two substructures of . Two structures and are isomorphic if there exists an isomorphism from to . An automorphism of is an isomorphism from to itself. The set of all automorphisms of is denoted by .
The orbit of a tuple in is the set For two structures and , a function is called canonical from to if, for every , the componentwise action of induces a well-defined function from the orbits of -tuples in to the orbits of -tuples in ; that is, if any two -tuples belonging to the same orbit, say , are mapped into the same orbit, say ; we can then write . In other words, for every , every , and every , there exists such that . A countable structure is -categorical if, for every , there are only finitely many orbits of -tuples in . The following lemma can be shown by a standard compactness argument, e.g., using Kőnig’s tree lemma.
Lemma 5 (Lemma 4.1.7 in [8]).
Let and be countable relational structures such that is -categorical. Then if and only if every finite substructure of embeds into .
Logic.
We assume that the reader is familiar with classical first-order logic as well as with basic preservation properties of first-order formulas, e.g., that every first-order formula is preserved by isomorphisms; by embeddings if is existential, and by homomorphisms if is existential positive. We assume that equality is always available when building first-order formulas. We say that a first-order formula is -ary if it has free variables; we use the notation to indicate that the free variables of are among . This does not mean that the truth value of depends on each entry in .
In the present article, atomic -formulas, or -atoms for short, over a relational signature are of the form for some and a tuple of first-order variables matching the arity of . For technical reasons, formulas of the form built using the default equality predicate are not considered atomic. For a finite conjunction of -atoms, the canonical database of is the structure whose domain consists of the variables of and such that holds if and only if contains the -atom as a conjunct. The canonical database of admits a homomorphism to a -structure if and only if is satisfiable in [18]. For a finite -structure , the canonical query of is defined as the formula . The canonical query of is satisfiable in a -structure if and only if there exists a homomorphism from to [18].
Structural Ramsey theory.
A relational structure is homogeneous if, for every , two tuples lie in the same orbit if and only if the function mapping the -th coordinate in to the -th coordinate in for all is an isomorphism between two substructures of . In other words, a structure is homogeneous if every partial isomorphism between two finite substructures extends to an automorphism of the entire structure. Every homogeneous structure over a finite relational signature is -categorical.
Homogeneous structures arise as limit objects of certain classes of finite structures. Let be a class of finite structures in a finite relational signature closed under isomorphisms and substructures. We say that has the amalgamation property (AP) if, for all whose substructures induced on are identical, there exist and embeddings , such that
Theorem 6 (Fraïssé, Theorem 6.1.2 in [23]).
For a class of finite structures in a finite relational signature , the following are equivalent:
-
is the age of a countable homogeneous -structure; this structure is necessarily unique up to isomorphism and called the Fraïssé-limit of ;
-
is closed under isomorphisms, substructures, and has the AP.
For structures and , we denote by the set of all embeddings of into . A class of structures over a common signature has the Ramsey property (RP) if, for all and , there exists such that, for every map , there exists such that is constant on the set . Following [12, Definition 5.3], in the present article, we call a (countable) -categorical structure Ramsey if the age of the expansion of by all first-order definable relations (which is always a homogeneous structure) has the Ramsey property. By the theorem of Engeler, Ryll-Nardzewski and Svenonius [23], this property only depends on the automorphism group . It is not hard to see that every homogeneous -categorical structure whose age has the RP is Ramsey, since all of its first-order definable relations are in fact definable without quantifiers.
In the proof of Theorem 2, we employ structural Ramsey theory to effectively reduce the problem of containment between two infinite classes of finite structures to the existence of a certain computable function between two infinite structures. This reduction is achieved by first representing the two classes by infinite structures via Theorem 6 above, and then ensuring the computability of the function comparing the two infinite structures (if it exists) using the following statement, an immediate consequence of Theorem 5 in [13].
3 The containment problem
To accurately measure the size of SNP sentences , we introduce the following four parameters:
-
the height denotes the number of relation symbols in ;
-
the length denotes the number of clauses in ;
-
the width denotes the the maximum number of variables per clause in ;
-
the arity denotes the maximum arity among all relation symbols in .
3.1 Connectedness
An SNP -sentence is connected in the sense of [11, 8] if, for each clause in , the following -structure is connected: the domain consists of all variables in , and if and only if is a disjunct in (). For example, the sentences in equations (1.1) and (1.1) from the introduction are connected, while the sentence
is not because the variable sets and partition the structure associated to the clause into two disjoint substructures.
The next proposition was essentially proved in [11] (Proposition 1), except that the authors did not comment on the complexity of the procedure arising from their proof.
Proposition 8 (Proposition 1 in [11]).
Every GMSNP sentence is logically equivalent to a disjunction of connected sentences over the same input and existential signatures with the following properties: for all , and are polynomial in and , respectively; is single-exponential in ; and the entire disjunction can be computed from in deterministic single-exponential time.
Proposition 8 shows that when studying the complexity of the the containment problem for GMSNP, we may without loss of generality restrict ourselves to connected GMSNP.
Corollary 9.
If the containment problem for connected GMSNP sentences is in 2NEXPTIME, then also the containment problem for general GMSNP sentences is in 2NEXPTIME.
3.2 Recolourings
We call a relational structure standard if its domain is for some . For an SNP -sentence , we denote the class of all finite models of the first-order part of (over the signature ) by . We define the -colours of , denoted , as the set of all standard structures from of size . A recolouring between two SNP -sentences and is a mapping from to , where , with the two following properties. First, the -reducts of every -colour of and of its -image are identical. Secondly, for every , there is a structure on the same domain such that for all and every embedding we have . In other words, the following extension of is a well-defined mapping from to :
For every , the structure on the same domain as is obtained by replacing for every and every embedding the substructure of by .
Note that the second formulation makes it clear that is unique, because . For the same reason, we have that . Also observe that in the second formulation the well-definedness of is a non-trivial property since the required replacements might be on overlapping substructures.
We remark that this definition of a recolouring is compatible with the definition of a recolouring for the logic MMSNP given in [29, 12]. There, the unary existential symbols were interpreted as colours, and a recolouring was simply a mapping between the existential symbols which does not introduce any forbidden patterns. It is noteworthy, however, that in that case the compatibility on overlapping structures is trivially satisfied.

Example 10.
Consider the GMSNP -sentences ( is binary)
whose forbidden colour patterns are as in Figure 2; we additionally forbid uncoloured edges and overlapping colours in order to ensure that the colours partition the edges.
Note that in GMSNP we cannot enforce that the colours partition all pairs of elements of the domain, because every clause must satisfy the guarding axiom. Now consider a map mapping the green colour of undirected edges to itself, while merging the red and the blue colours to purple. The remaining structures in , where , consist either of a single vertex or two non--related vertices, possibly related with -relations. They are mapped to in an arbitrary way consistent with the first recolouring condition, i.e., that the -reducts are identical.
To show that is a recolouring, we must show that it does not produce green or purple triangles in edge-coloured graphs that originally did not admit a homomorphism from any of the 5 forbidden colourings of pentagons. Clearly, cannot produce a green triangle: the only way to produce a green triangle would be to start with one, and a green triangle admits a homomorphism from a green pentagon, which is forbidden. We can argue similarly in the case of a purple triangle, which can only be obtained with from one of the 4 red/blue-coloured triangles at the bottom of the figure. All 4 of them admit a homomorphism from one of the forbidden coloured pentagons. Hence, is a recolouring.
Lemma 11.
The existence of a recolouring between two SNP sentences and can be tested non-deterministically in time .
3.3 The theorem of Hubička and Nešetřil
A general construction method of -categorical homogeneous Ramsey structures was provided by Hubička and Nešetřil [25]. We use a variant of their result, which can be found in the appendix of [12] (Theorem A.4 in the print version, or Theorem A.3 in the arXiv version).
Pieces of structures.
The following notion, originating from [24], is of essential importance in the present article. A piece of a structure is a pair , where is a proper substructure of (with domain ) and (called the root of ) is a tuple with pairwise distinct entries enumerating a non-empty subset of such that every tuple contained in a relation of is completely contained either in or in .
Remark 12.
To every piece , we assign a relational symbol of arity equal to the length of , which for the sake of brevity will be denoted by the piece itself. For an atomic formula using such a symbol, let be the -formula obtained from the canonical query of by substituting for in the order in which both tuples are listed; that is, the formula asserts about all atomic -formulas (with parameters) that hold for in . Finally, the primitive positive formula is obtained from by existentially quantifying over all variables which are not contained in . That is, the formula asserts the existence of a homomorphic image of the piece around , with taking the place of .
For a set of structures with a signature , we denote by the class of all finite -structures which do not admit a homomorphism from any member of . The following theorem of Hubička and Nešetřil states that every class of the form , where each member of is connected, almost has the amalgamation property, up to taking an expansion where pieces of the structures in are marked using fresh predicates ; moreover, the class of all linear-order expansions of structures from such a class has the Ramsey property.
Theorem 13 (Hubička and Nešetřil, Theorem A.4 in [12]).
Let be a finite set of finite connected structures over a common finite relational signature . Let be the signature whose elements are the pieces of structures from . Consider the class consisting of all substructures of those -expansions of structures from that satisfy
| (4) |
Then the class has the RP and the AP.
To illustrate the construction in Theorem 13, consider the two sets and consisting of the canonical databases of the forbidden patterns of and from Figure 2. It is not hard to see that already has the AP because the forbidden graphs are cliques; moreover, has the AP and the RP by a theorem of Nešetřil and Rödl [33]. Therefore, represents a trivial case where adding -predicates is not necessary. This is not true for , since does not have the AP. In Figure 3, we provide a graphical representation of the pieces of structures that need to be stored using -predicates in order to obtain a class of expansions of structures from with the AP and the RP.
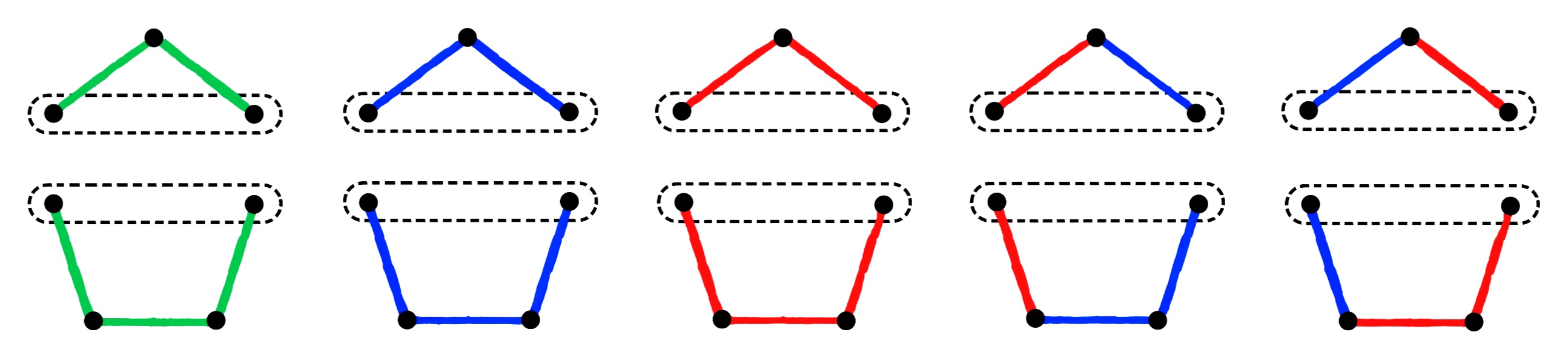
3.4 A proof of Theorem 2
Besides the reduction to the connected case, the proof of Theorem 2 is a straightforward consequence of the combination of the following three intermediate results. First, Lemma 11 from Section 3.2 gives a (non-deterministic) double-exponential upper bound on the time complexity of finding a recolouring between two SNP sentences. Second, Proposition 14 below states that every connected GMSNP sentence is equivalent to an at most double-exponentially larger SNP sentence whose class of expanded finite models enjoys the AP and the RP. Third, Proposition 15 states that, for SNP sentences with the latter property, containment is equivalent to the existence of a recolouring. Here we are in fact very lucky that the parameters on which Lemma 11 and Proposition 14 depend doubly-exponentially are different – this will become clear in the proof of Theorem 2.
Proposition 14.
From every connected GMSNP -sentence one can compute in deterministic double-exponential time an SNP -sentence such that:
-
1.
;
-
2.
;
-
3.
-
4.
;
-
5.
has the AP and the RP;
-
6.
.
The proof of Proposition 14 below builds on on the proof of [11, Theorem 5], so we omit some details that can be found in [11].
Proof sketch.
Let be an arbitrary connected GMSNP -sentence. We first obtain signatures and by introducing, for every , two new symbols and of the same arity. Next, we obtain an auxiliary GMSNP -sentence from as follows. For each forbidden pattern of , the sentence contains the forbidden pattern obtained by replacing each positive atom with and each negative atom with .
Let be the set of canonical databases for the forbidden patterns of (which are just conjunctions of positive -atoms); define from as in Theorem 13. Consider the -sentence with the additional existential symbols obtained from by adding the following new clauses:
-
i.
clauses defining the linear order using irreflexivity, transitivity, and totality:
-
ii.
every clause in the signature of the form (for ) with at most -many variables, where is a conjunction of positive atoms with the following property: replacing every atomic subformula in by yields a -formula such that there exists a homomorphism from the canonical database of to the canonical database of satisfying ;
-
iii.
every clause in the signature with at most -many variables whose forbidden pattern is a conjunction of positive atoms with the following property: replacing every atomic subformula in by yields a formula whose canonical database admits a homomorphism from a member of .
Before we proceed further, let us assess the size of in detail. The number of variables per clause remains in . The arity of the symbols from is in , because inherits all symbols from and gains additional symbols whose arity is bounded by the domain size of structures in . The number of relation symbols increases exponentially in and polynomially in the remaining parameters, more specifically it is in ; the reason is that the pieces of structures in are no more than all possible substructures of structures in . Regarding the number of clauses: Item (i) produces constant number of clauses and items (ii) and (iii) produce many clauses. The reason for the double-exponential blow-up in item (iii) is that there are as many new clauses as there are structures of size at most over the signature of . Similarly, also item (ii) yields a double-exponential blow-up; here the number from item (iii) is additionally multiplied with the number of symbols in (i.e., pieces of structures in ), which is in .
Note that all structures in are connected since is connected. By Theorem 13, the class over the signature has the AP and the RP. Theorem 6 then implies that there exists a homogeneous Ramsey structure with . By the construction of , we have that ; below we provide an intuitive explanation of why this is the case. First, item (i) ensures that interprets as a linear order in each which, for lack of additional clauses with , is independent of the remaining signature; the same is true in each . Next, consider the remaining part of the signature. If , then by definition, it does not admit a homomorphism from any member of ; moreover, its -predicates are obtained through equation (4) by definition, and hence it satisfies items (ii) and (iii). Whence, . Conversely, if a finite structure satisfies the first-order part of , then extending it by new elements so that the truth of all -predicates is witnessed as in equation (4) yields a structure in which the equivalence (4) holds (because of item (ii)) and which does not admit a homomorphism from any member from (because of item (iii)); hence .
We say that a set is correctly labelled if every tuple over matching the arity of some is contained either in or in , but not both. Consider the -expansion of where each of arity interprets as the -ary relation defined by the quantifier-free first-order formula
| (5) |
As first-order definable relations are preserved by automorphisms, is homogeneous Ramsey.
Finally, we obtain the sentence from by first adding clauses defining -relations using equation (5) and then existentially quantifying over all symbols in . The length of only increases by an additional multiplicative single exponential because we need to consider all subsets of for every relation symbol in ; its width, height, and arity remain unchanged. It follows from Theorem 13 that has the AP and the RP. Moreover, we have . It remains to show that . This follows from the fact that .
The next proposition shows that the property in item (5) of Proposition 14 attained through the transformation is sufficient for a reduction from containment to recolouring.
Proposition 15.
For SNP -sentences and such that and both have the AP and the RP the following are equivalent.
-
1.
.
-
2.
There exists a recolouring from to .
Proof.
Let .
“(1)(2)” By Theorem 6, there exist homogeneous Ramsey structures and such that and . Then, . By the -categoricity of , Lemma 5 implies that there exists an embedding from to . By Theorem 7, we may assume that is canonical as a function from to since the former is an -categorical Ramsey structure. Let be the mapping from to defined as follows. Given , consider an arbitrary embedding from to . Then, we define with domain whose relations are defined through their preimages under . Let be the restriction of to . We claim that arises from as in the definition of a recolouring.
First, the -reduct of any and its -image are identical since is obtained by pulling back relations via the -embedding . For the second part of the definition pertaining to , let , , and be arbitrary; we claim that . By definition, the relations of and of are obtained by first embedding and into , then applying , and then pulling back the relations from . This definition does not depend on the choice of the embeddings into , by the homogeneity of and the canonicity of – the claim follows.
Proof of Theorem 2.
By Corollary 9, we can restrict ourselves to connected GMSNP. Now the statement follows directly from Proposition 14 combined with Proposition 15 and Lemma 11. To see this, note that, through the application of Proposition 14, the arity and width increase polynomially, the height increases single-exponentially, and the length increases double-exponentially. According to Lemma 11, the complexity of testing the existence of a recolouring only depends single-exponentially on the height, so a single-exponential increase in height is not an issue. Moreover, the complexity only depends polynomially on the length, so a double-exponential increase in length is not an issue either. We conclude that the combined complexity is indeed 2NEXPTIME.
4 Recolouring-ready GMSNP
We first introduce the notion of recolouring-readiness. Then, we give a high-level explanation of how to obtain recolouring-ready GMSNP sentences and elaborate on our claim that recolouring-readiness can be paired with a notion of a recolouring generalising the corresponding notion for MMSNP in a fashion that is less abstract than the notion introduced in Section 3.2 and closer to the idea of edge-recolourings as in equation (3) of Section 1.4.
We will use the following weaker version of homogeneity, generalising the notion of 1-homogeneity of Bodirsky, Madelaine, and Mottet [12] from vertices to relational -tuples. A relational structure whose signature contains is -edge-homogeneous if it satisfies the homogeneity condition restricted to tuples contained in for some .
Remark 16.
The -reduct of a -edge-homogeneous structure is not necessarily homogeneous. Consider the disjoint union of the random graph with a countably infinite set marked by a unary predicate . For , the -reduct of this structure is -edge-homogeneous but not homogeneous.
A connected GMSNP -sentence is called recolouring-ready if there exists a -edge-homogeneous -categorical Ramsey structure with the following properties:
-
i.
consists of all linear-order expansions of structures from ;
-
ii.
consists of the finite models of the first-order part of ;
-
iii.
.
Theorem 17.
For every connected GMSNP -sentence there exists a logically equivalent recolouring-ready connected GMSNP -sentence such that:
-
1.
;
-
2.
;
-
3.
;
-
4.
;
-
5.
.
Moreover, can be computed from in nondeterministic triple-exponential time.
Proof sketch.
We only describe how is constructed and discuss its size. The overall strategy is similar to the proof of Proposition 14, but with several thorny technical details.
First, for every , we add a new symbol of the same arity as . Then, for every , we replace in every clause of every negated -atom with a positive -atom. Next, we make every clause correctly labelled. Intuitively, for every clause , every tuple such that there is an atom in with , and every whose arity matches the arity of , we replace with two new clauses and . The process is repeated until the canonical databases of all clauses are correctly labelled in the sense of Proposition 14. This step results in a doubly-exponential increase of the number of clauses, but is necessary because the definition of here is more involved than in Proposition 14. Denote the resulting sentence by and the family of canonical databases of the clauses of by . Now, for every and every piece of , we extend the tuple with new variables in every possible way so that the arity of the resulting tuple matches the arity of some relation . We define as the signature consisting of all such symbols associated with these pieces. Note that is at most the number of -structures on at most elements. So, is in . Finally, we obtain the sentence from by adding new clauses defining the predicates with a symbol in . We first add clauses stating that the canonical query of a piece implies the predicate ; that is, the implication in equation (4) holds. As in item (ii) from the proof of Proposition 14, we do this in a way that accounts for the fact that already present -predicates themselves encode formulas of the form . Similarly, we reproduce item (iii) from the proof of Proposition 14; for convenience of the reader, we provide an explicit set of clauses: Let be the size of the largest element of . We add to the first-order part of every clause in the signature of at most variables whose forbidden pattern is a conjunction of positive atoms with the following property: replacing every subconjunction (where holds in the piece) by yields a formula whose canonical database admits a homomorphism from a member of . By construction, the sentence is still in GMSNP; we set .
It can be verified that item (1) holds, i.e. that . Items (2) and (3) follow from the construction, item (4) follows from the upper bound on . The parameter is bounded from above by the number of -structures on at most elements, so it is in . Hence, item (5) follows as well. Let be a structure over a relational signature containing . We say that is -guarded if there exist and such that . Now, let and be GMSNP -sentences; as in Section 3.2, we set . A structure with domain over a signature containing is standardly ordered if coincides with the natural ordering . A GMSNP-recolouring from to is a mapping from standardly ordered -guarded structures in to standardly ordered -guarded structures in with the following two properties. First, the -reduct of any structure and its -image are isomorphic. Secondly, for every , there is a structure on the same domain such that and, for all standardly ordered -guarded and for every embedding , we have .
Modulo the fact that the ordering of the colours matters in this definition, it is what one would intuitively understand under a recolouring of relational -tuples. The fact that the containment between recolouring-ready GMSNP sentences can be reduced to the existence of such a recolouring can be proved almost exactly as in the proof of Proposition 15.
Proposition 18.
For connected recolouring-ready GMSNP -sentences and , the following are equivalent:
-
1.
;
-
2.
There exists a GMSNP-recolouring from to .
Now we compare the above defined GMSNP-recolourings, which depend on an external linear order, with the (linear-order-free) edge-recolourings from equation (3) in Section 1.4. We claim that, for connected recolouring-ready GMSNP sentences and over signatures and , respectively, the two notions only differ up to a minor syntactic modification : there exists a GMSNP-recolouring from to if and only if there exists an edge-recolouring from to .
We describe . For every -guarded of size , we introduce a new -ary existential symbol ; the set of all such symbols is denoted by . The atomic diagram of a structure is the conjunction extending its canonical query by listing not only all the atoms that hold in , but also their negations [23]. We replace the clauses of by all possible clauses over with at most -many variables satisfying the monotonicity and the guarding axioms such that replacing every atom in the forbidden pattern of by the atomic diagram of yields a formula that is not satisfiable together with the first-order part of . Note that a similar trick was used in the proof sketch of Proposition 14. Next, we introduce a new binary existential symbol , add all clauses forbidding cycles in of size at most , and for every we add the clause The resulting GMSNP sentence is denoted by .
Note that is logically equivalent to : any can be turned into a model of the first-order part of without changing the -relations by first equipping it with a linear order , adding the predicates according to their semantics, and then removing the -predicates; satisfies the consistency clauses by definition. In the converse direction, we obtain a model of the first-order part of from a model of by the obvious replacement and by forgetting , thanks to the consistency requirements. Note that it is also the consistency requirements that guarantee that the obvious replacement is not contradictory on overlapping -guarded -colours; to ensure this, we allowed clauses up to size .
Let be a GMSNP-recolouring from to ; we claim it naturally induces an edge-recolouring from to . Namely, for any , we replace every predicate in which holds on some tuple in by the predicate encoding the image of , ordered by the appearance of its elements in the predicate, under . The resulting structure is an element of : suppose otherwise. Then realizes a forbidden pattern of on some set ; without loss of generality, since forbids cycles of size at most , we may assume that implies for all pairs guarded in that pattern. Let be the structure induced by in , equipped with the order ; then , where is obtained from by the definition of a GMSNP-recolouring, is a model of the first-order part of which agrees with on guarded tuples, a contradiction.
Conversely, given an edge-recolouring from to , we trivially get that , which means that there exists a GMSNP-recolouring from to due to Proposition 18 because and are recolouring-ready.
5 Conclusion
We proved the decidability of the containment problem for GMSNP, thereby settling an open question posed in [6, 15]. Our decision procedure runs in non-deterministic double-exponential time, which exactly matches the lower bound on the complexity obtained in [15].
In the proof of Theorem 2, our main result, we employ structural Ramsey theory to effectively reduce from the containment problem for GMSNP to the problem of testing the existence of a recolouring between SNP sentences. As mentioned in the introduction, the use of structural Ramsey theory is only one of the possible ways to outsource combinatorics. In fact, in all works on the containment problem for MMSNP except for [12] a different tool was used, commonly known as the sparse incomparability lemma [27, Theorem 1] (Feder and Vardi originally used a weaker, randomised version of this result, which they attributed to Erdős [19, Theorem 5]). It would be interesting to know if this alternative approach can also be used to analyse the complexity of containment for GMSNP, perhaps in combination with the reduction to relativised emptiness from [15].
Regarding our approach using structural Ramsey theory, one can clearly see that our methods have the potential to work in a broader setting than GMSNP. More specifically, by Proposition 15, the 2NEXPTIME upper bound on the complexity of containment holds for all pairs of SNP sentences whose first-order part defines a class of finite structures with the AP and the RP. The issue with this statement is that the said fragment of SNP does not have any known explicit description; it might be difficult to judge Proposition 15 as a stand-alone contribution since the complexity of recognizing which SNP sentences fall within its scope might be high, potentially even undecidable. For a discussion of the complexity of related meta problems, see [35] (cf. also [36]). We would be interested in locating virtually any fragment of existential second-order logic that properly generalises GMSNP, can be embedded into SNP with AP and RP similarly as GMSNP, and whose syntax is efficiently verifiable as in the case of GMSNP.
References
- [1] F. Baader. The Description Logic Handbook: Theory, Implementation, and Applications. Cambridge University Press, 2003. doi:10.1017/CBO9780511711787.
- [2] A. Barsukov, M. Pinsker, and J. Rydval. Containment for Guarded Monotone Strict NP. CoRR, abs/2310.01254, 2023. doi:10.48550/arxiv.2310.01254.
- [3] L. Barto, J. Bulín, A. A. Krokhin, and J. Oprsal. Algebraic Approach to Promise Constraint Satisfaction. J. ACM, 68(4):28:1–28:66, 2021. doi:10.1145/3457606.
- [4] L. Barto, J. Opršal, and M. Pinsker. The wonderland of reflections. Israel Journal of Mathematics, 223(1):363–398, 2018. doi:10.1007/s11856-017-1621-9.
- [5] L. Barto and M. Pinsker. Topology Is Irrelevant (In a Dichotomy Conjecture for Infinite Domain Constraint Satisfaction Problems). SIAM J. Comput., 49(2):365–393, 2020. doi:10.1137/18M1216213.
- [6] M. Bienvenu, B. ten Cate, C. Lutz, and F. Wolter. Ontology-Based Data Access: A Study through Disjunctive Datalog, CSP, and MMSNP. ACM Trans. Database Syst., 39(4):33:1–33:44, 2014. doi:10.1145/2661643.
- [7] Z. Bitter and A. Mottet. Generalized Completion Problems with Forbidden Tournaments. In R. Královic and A. Kucera, editors, 49th International Symposium on Mathematical Foundations of Computer Science, MFCS 2024, August 26-30, 2024, Bratislava, Slovakia, volume 306 of Leibniz International Proceedings in Informatics (LIPIcs), pages 28:1–28:17, Dagstuhl, Germany, 2024. Schloss Dagstuhl – Leibniz-Zentrum für Informatik. doi:10.4230/LIPIcs.MFCS.2024.28.
- [8] M. Bodirsky. Complexity of Infinite-Domain Constraint Satisfaction. Lecture Notes in Logic. Cambridge University Press, 2021. Postprint available online: https://wwwpub.zih.tu-dresden.de/˜bodirsky/Book.pdf. doi:10.1017/9781107337534.
- [9] M. Bodirsky and V. Dalmau. Datalog and Constraint Satisfaction with Infinite Templates. J. Comput. Syst. Sci., 79(1):79–100, 2013. A preliminary version appeared in the proceedings of the Symposium on Theoretical Aspects of Computer Science (STACS’06). doi:10.1016/j.jcss.2012.05.012.
- [10] M. Bodirsky and S. Guzmán-Pro. Forbidden Tournaments and the Orientation Completion Problem. SIAM J. Discret. Math., 39(1):170–205, 2025. doi:10.1137/23m1604849.
- [11] M. Bodirsky, S. Knäuer, and F. Starke. ASNP: A tame fragment of existential second-order logic. In CiE 2020, Proceedings, volume 12098 of Lecture Notes in Computer Science, pages 149–162. Springer, 2020. doi:10.1007/978-3-030-51466-2_13.
- [12] M. Bodirsky, F. R. Madelaine, and A. Mottet. A Proof of the Algebraic Tractability Conjecture for Monotone Monadic SNP. SIAM J. Comput., 50(4):1359–1409, 2021. doi:10.1137/19M128466X.
- [13] M. Bodirsky and M. Pinsker. Canonical functions: a proof via topological dynamics. Contributions Discret. Math., 16(2):36–45, 2021. doi:10.11575/cdm.v16i2.71724.
- [14] M. Bodirsky, M. Pinsker, and T. Tsankov. Decidability of Definability. J. Symb. Log., 78(4):1036–1054, 2013. doi:10.2178/jsl.7804020.
- [15] P. Bourhis and C. Lutz. Containment in monadic disjunctive datalog, mmsnp, and expressive description logics. In C. Baral, J. P. Delgrande, and F. Wolter, editors, Principles of Knowledge Representation and Reasoning: Proceedings of the Fifteenth International Conference, KR 2016, Cape Town, South Africa, April 25-29, 2016, KR’16, pages 207–216. AAAI Press, 2016. URL: https://cdn.aaai.org/ocs/12847/12847-57546-1-PB.pdf.
- [16] J. Brakensiek and V. Guruswami. An Algorithmic Blend of LPs and Ring Equations for Promise CSPs. In Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, pages 436–455. SIAM, 2019. doi:10.1137/1.9781611975482.28.
- [17] A. A. Bulatov. A Dichotomy Theorem for Nonuniform CSPs. In C. Umans, editor, 58th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2017, Berkeley, CA, USA, October 15-17, 2017, pages 319–330. IEEE Computer Society, 2017. doi:10.1109/FOCS.2017.37.
- [18] A. K. Chandra and P. M. Merlin. Optimal implementation of conjunctive queries in relational data bases. In Proceedings of the Ninth Annual ACM Symposium on Theory of Computing, STOC ’77, pages 77–90, New York, NY, USA, 1977. Association for Computing Machinery. doi:10.1145/800105.803397.
- [19] T. Feder and M. Y. Vardi. The Computational Structure of Monotone Monadic SNP and Constraint Satisfaction: A Study through Datalog and Group Theory. SIAM J. Comput., 28(1):57–104, 1998. doi:10.1137/S0097539794266766.
- [20] R. Feller and M. Pinsker. An algebraic proof of the graph orientation problem dichotomy for forbidden tournaments. Submitted, preprint: arXiv.2405.20263, 2024. doi:10.48550/arXiv.2405.20263.
- [21] M. R. Garey and D. S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. Mathematical Sciences Series. W. H. Freeman, 1979.
- [22] S. Guzmán-Pro. GMSNP and Finite Structures. Submitted, preprint: arXiv.2406.13529, 2024. doi:10.48550/arXiv.2406.13529.
- [23] W. Hodges. A Shorter Model Theory. Cambridge University Press, USA, 1997.
- [24] J. Hubička and J. Nešetřil. Universal Structures with Forbidden Homomorphisms. In Å. Hirvonen, J. Kontinen, R. Kossak, and A. Villaveces, editors, Logic Without Borders - Essays on Set Theory, Model Theory, Philosophical Logic and Philosophy of Mathematics, volume 5 of Ontos Mathematical Logic, pages 241–264. De Gruyter, 2015. doi:10.1515/9781614516873.241.
- [25] J. Hubička and J. Nešetřil. All those Ramsey classes (Ramsey classes with closures and forbidden homomorphisms). Adv. Math., 356:106791, 2019. doi:10.1016/j.aim.2019.106791.
- [26] P. Kolaitis and M. Vardi. The decision problem for the probabilities of higher-order properties. In Proceedings of the nineteenth annual ACM Symposium on Theory of Computing, pages 425–435, 1987. doi:10.1145/28395.28441.
- [27] G. Kun. Constraints, MMSNP and expander relational structures. Combinatorica, 33(3):335–347, 2013. doi:10.1007/s00493-013-2405-4.
- [28] F. R. Madelaine. Universal Structures and the logic of Forbidden Patterns. Log. Methods Comput. Sci., 5, 2009. doi:10.2168/LMCS-5(2:13)2009.
- [29] F. R. Madelaine. On the Containment of Forbidden Patterns Problems. In D. Cohen, editor, Principles and Practice of Constraint Programming - CP 2010 - 16th International Conference, CP 2010, St. Andrews, Scotland, UK, September 6-10, 2010. Proceedings, volume 6308 of Lecture Notes in Computer Science, pages 345–359. Springer, 2010. doi:10.1007/978-3-642-15396-9_29.
- [30] F. R. Madelaine and I. A. Stewart. Constraint Satisfaction, Logic and Forbidden Patterns. SIAM J. Comput., 37(1):132–163, 2007. doi:10.1137/050634840.
- [31] A. Mottet, T. Nagy, M. Pinsker, and M. Wrona. Smooth Approximations and Relational Width Collapses. In N. Bansal, E. Merelli, and J. Worrell, editors, 48th International Colloquium on Automata, Languages, and Programming, ICALP 2021, July 12-16, 2021, Glasgow, Scotland (Virtual Conference), volume 198 of LIPIcs, pages 138:1–138:20. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2021. doi:10.4230/LIPIcs.ICALP.2021.138.
- [32] A. Mottet, T. Nagy, M. Pinsker, and M. Wrona. Collapsing the Bounded Width Hierarchy for Infinite-Domain Constraint Satisfaction Problems: When Symmetries Are Enough. SIAM J. Comput., 53(6):1709–1745, 2024. doi:10.1137/22M1538934.
- [33] J. Nešetřil and V. Rödl. Ramsey classes of set systems. J. Comb. Theory A, 34(2):183–201, 1983. doi:10.1016/0097-3165(83)90055-9.
- [34] C. Papadimitriou and M. Yannakakis. Optimization, approximation, and complexity classes. In Proceedings of the twentieth annual ACM Symposium on Theory of Computing, pages 229–234, 1988. doi:10.1145/62212.62233.
- [35] J. Rydval. Homogeneity and Homogenizability: Hard Problems for the Logic SNP. In K. Bringmann, M. Grohe, G. Puppis, and O. Svensson, editors, 51st International Colloquium on Automata, Languages, and Programming (ICALP 2024), volume 297 of Leibniz International Proceedings in Informatics (LIPIcs), pages 150:1–150:20, Dagstuhl, Germany, 2024. Schloss Dagstuhl – Leibniz-Zentrum für Informatik. doi:10.4230/LIPIcs.ICALP.2024.150.
- [36] J. Rydval. Finitely Bounded Homogeneity Turned Inside-Out. To appear in J. Math. Log., preprint: arXiv.2108.00452, 2025.
- [37] O. Shmueli. Equivalence of Datalog queries is undecidable. J. Log. Program., 15(3):231–241, 1993. doi:10.1016/0743-1066(93)90040-N.
- [38] M. Wrochna and S. Živný. Improved hardness for H-colourings of G-colourable graphs. In S. Chawla, editor, Proceedings of the 2020 ACM-SIAM Symposium on Discrete Algorithms, SODA 2020, Salt Lake City, UT, USA, January 5-8, 2020, pages 1426–1435. SIAM, 2020. doi:10.1137/1.9781611975994.86.
- [39] D. Zhuk. A Proof of the CSP Dichotomy Conjecture. J. ACM, 67(5):30:1–30:78, 2020. doi:10.1145/3402029.
