Multiparty Communication Complexity of Collision-Finding and Cutting Planes Proofs of Concise Pigeonhole Principles
Abstract
We prove several results concerning the communication complexity of a collision-finding problem, each of which has applications to the complexity of cutting-plane proofs, which make inferences based on integer linear inequalities.
In particular, we prove an lower bound on the -party number-in-hand communication complexity of collision-finding. This implies a lower bound on the size of tree-like cutting-planes refutations of the bit pigeonhole principle CNFs, which are compact and natural propositional encodings of the negation of the pigeonhole principle, improving on the best previous lower bound of . Using the method of density-restoring partitions, we also extend that previous lower bound to the full range of pigeonhole parameters.
Finally, using a refinement of a bottleneck-counting framework of Haken and Cook and Sokolov for DAG-like communication protocols, we give a lower bound on the size of fully general (not necessarily tree-like) cutting planes refutations of the same bit pigeonhole principle formulas, improving on the best previous lower bound of .
Keywords and phrases:
Proof Complexity, Communication ComplexityCategory:
Track A: Algorithms, Complexity and GamesCopyright and License:
2012 ACM Subject Classification:
Mathematics of computingFunding:
Research supported by NSF grants CCF-2006359 and CCF-2422205.Editors:
Keren Censor-Hillel, Fabrizio Grandoni, Joël Ouaknine, and Gabriele PuppisSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
The pigeonhole principle, which asserts that there is no injective function for , is a cornerstone problem in the study of proof complexity. It is typically encoded as unsatisfiable conjunctive normal form formula (CNF), henceforth denoted , on the variables , each of which is an indicator that “pigeon” is mapped to “hole” .
It is well known that any refutation of using resolution proofs requires size [12] and the same asymptotic bound holds for all that are [6]. On the other hand, if we allow our proof system to reason about linear inequalities (for example using cutting-planes proofs), then it is easy to see that refuting becomes easy – indeed, there exist polynomial size refutations of .
Despite the pigeonhole principle having short cutting-planes refutations, the related clique-coloring formulas, which state that a graph cannot have both -cliques and -colorings, requires exponential-size cutting-planes refutation [24].111Lower bounds for restricted cutting-planes refutations of these formulas were earlier shown in [17, 4] The clique-coloring formula can be viewed as a kind of indirect pigeonhole principle: The nodes of the clique correspond to the pigeons and colors correspond to the holes, but the representation of possible mappings is quite indirect.
It is natural to wonder about the extent to which indirection is required for the pigeonhole principle to be hard for cutting-planes reasoning. As part of studying techniques for cutting-planes proofs, Hrubeš and Pudlák [16] considered a very natural compact and direct way of expressing the pigeonhole principle, known as the bit or binary pigeonhole principle222This encoding of the pigeonhole principle was introduced in [1].. The bit pigeonhole principle analog of (henceforth denoted ) has variables for and the principle asserts that, when we organize these variables as an matrix, the rows of the matrix all have distinct values. is the following CNF formula: for each , include the clauses of a CNF encoding that . One can achieve this by including a clause for each expressing that . The end result is a CNF with clauses of size .
Using techniques related to those of [24], Hrubeš and Pudlák [16] showed that requires cutting-planes refutations of size for any , proving that even a very direct representation of the pigeonhole principle is hard for cutting-planes proofs. Their arguments, like those of Pudlák, also apply to any proof system that has proof lines consisting of integer linear inequalities with two antecedents per inference that are sound with respect to -valued variables; such proofs are known alternatively as semantic cutting-planes proofs or proofs [2].
Recently, Dantchev, Galesi, Ghani, and Martin [8] exhibited a lower bound on the size of any general resolution refutation of for all . In fact, they showed that requires proofs of size for a more powerful class of proof systems that extend resolution by operating on -DNFs (known as proofs) for . (Note that any sound proof system operating on DNFs requires size at least to refute [23, 20, 14].) In addition, [8] showed that has no refutations in the Sherali-Adams proof system [27] of size smaller than . Finally, just as has polynomial-size Sum-of-Squares refutations [11], Dantchev et al. showed that has polynomial-sized Sum-of-Squares refutations.
Given the large lower bounds for resolution, , and Sherali-Adams refutations of , it is natural to ask the extent to which the sub-exponential lower bounds can be improved for cutting-planes proofs; how close to a lower bound is possible?
1.1 Tree-like Proofs and Multiparty Communication
In prior work there has been progress towards this question for the restricted class of tree-like refutations. Tree-like proofs require that any time an inequality is used, it must be re-derived (i.e., the underlying graph of deductions is a tree); the polynomial-size cutting-planes refutations of can be made tree-like. In contrast, Itsykson and Riazanov [18] showed that requires tree-like cutting-planes refutations of size when .
Our first result pushes this bound almost to its limit. Specifically, we prove that any tree-like semantic cutting-planes refutation of requires size whenever .
In order to show this, we utilize a well-known connection between tree-like refutations and communication complexity. While the results of [18] for cutting planes rely on two-party communication complexity (and number-on-forehead multiparty communication for other results that we mention below), our stronger results are based on multiparty number-in-hand communication. In particular they are based on a similar natural collision-finding communication problem , in which each player in the number-in-hand model receives an input in , and their goal is to communicate and find a pair such that for all players . Such a communication problem is well-defined (in the sense that such a pair always exists) when .
This collision-finding problem is intimately related to the unsatisfiable formula via the following natural search problem associated with any unsatisfiable CNF formula: Given unsatisfiable CNF , the associated search problem takes as input a truth assignment to the variables of and requires the output of the index of a clause of that is falsified by . In particular the connection follows by considering a natural -party number-in-hand communication game that we denote by wherein the assignment to the variables of is evenly distributed among the players. and the players must communicate to find an answer for . It is not hard to see that if we have a communication protocol solving then such a protocol also solves on input .
Our first result is a lower bound on that holds even when we allow randomized protocols.
Theorem 1.1.
The randomized number-in-hand communication complexity of is whenever .
We pause here to note that this bound is nearly tight. There is a deterministic protocol wherein the first player sends a subset of coordinates of size in which their inputs are all equal. This requires bits; when , this is bits of communication. Player two then announces a subset of these coordinates on which they are equal of size . The players can continue in this manner until they have found a collision (which is guaranteed by the pigeonhole principle). Note that the amount of communication is bounded by a geometric series, and is dominated by the first term, which results in communication . This shows that up to logarithmic factors and a factor of , Theorem 1.1 is tight.
We state here a simplified corollary333When is somewhat larger, we can obtain somewhat weaker lower bounds. of Theorem 1.1 which formalizes our lower bounds for cutting-planes refutations of .
Theorem 1.2.
Any tree-like semantic cutting-planes refutation of requires size when .
We remark that Itsykson and Riazanov [18] utilized the same connection between communication and proof complexity to achieve their results. They were also interested in a -party number-on-forehead version of (in particular, in their version, the matrices are added rather than concatenated), which leads to weaker lower bounds in stronger proof systems that manipulate degree polynomial inequalities.
Itsykson and Riazanov also left as an open problem whether their bounds for could be extended to the regime of the “weak” pigeonhole principle when . Göös and Jain [10] first answered this in the affirmative, giving an lower bound on the randomized communication complexity of . Yang and Zhang [32] subsequently improved this to an bound, which is tight for randomized computation. Because of the connection between communication protocols and tree-like communication, Yang and Zhang’s bound showed that any tree-like cutting planes refutation of requires size . We extend the lower bounds of Yang and Zhang for all as follows:
Theorem 1.3.
For all and , the randomized number-in-hand communication complexity of is .
This bound, whose proof combines techniques of Yang, Zhang, and Wang [31, 32], is much weaker than that of Theorem 1.1 when is close to but it is tight, up to an factor, for randomized protocols when is . For , it also implies the following proof complexity bound which asymptotically matches the bound of [18], but applies for all .
Corollary 1.4.
For all , any tree-like semantic cutting-planes refutation of requires size .
1.2 General Proofs and DAG-like Protocols
Our second result improves on the lower bound on the size of cutting-planes refutations of (for all ) of Hrubeš and Pudlák [16], and subsumes the lower bound for tree-like proofs of Yang and Zhang [32]. Hrubeš and Pudlák used the method of interpolation involving a version of the method of approximation due to Jukna [19]. On the other hand, we use a bottleneck-counting method inspired by recent work of Sokolov [29] that refines a method introduced by Haken and Cook [13].
Theorem 1.5.
Any semantic cutting planes refutation of requires size at least , for any .
We prove Theorem 1.5 via a connection between cutting-planes refutations and certain types of DAG-like communication protocols [15, 28]. Specifically, we prove a lower bound on the size of any two party triangle-DAG protocol computing . We define such protocols formally in Section 2.3.
For now, we state the connection as the following proposition, originally due to Sokolov and Hrubeš and Pudlák [28, 15]. Its proof can be found in Section 2.3 for completeness.
Proposition 1.6 ([28, 15]).
Given a semantic cutting planes refutation for CNF formula of size and any partition of the variables of into two sets, there is a size triangle-DAG computing .
In our setting, for , there is a natural partition of the variables such that each clause has exactly half of its variables coming from and half of its variables coming from . This can be achieved, for example, by letting be the set of variables corresponding to the first columns of the matrix associated with . In light of Proposition 1.6, we derive Theorem 1.5 by proving the following.
Theorem 1.7.
For the natural partition of variables , any triangle-DAG computing requires size .
2 Preliminaries
2.1 Proof Complexity
Proof complexity studies how the size required for refutations of unsatisfiable formulas depends on the size of the formulas themselves. The size of a refutation in general depends on the allowable structure (lines, derivation rules, etc.) of a proof. In general, a proof system corresponds to a polynomial-time verifier that can check proofs of a certain format. It generally suffices to derive refutations of unsatisfiable CNF formulas; so it is usual to focus solely on inputs of this form.
For most proof systems, a sequence of deductions can be thought of as a directed graph, where two (or possibly more) lines (whether given or derived) are combined soundly to create a new line. The underlying graph then has edges pointing from the derived inequality to its antecedents.444The direction of arrows in this digraph may seem counterintuitive, but it is convenient when thinking of the graph as a search problem for a violated axiom. In this case, we can follow a path in the graph to find such a a violated axiom on one of the leaves/sources. We say that a proof is tree-like if every inequality is used as an antecedent at most once in the proof – that is, if we want to use an inequality twice, we must derive it twice.
For example, in the resolution proof system the lines are clauses, and we have the derivation rule
A more powerful proof system is the cutting planes proof system555Cutting planes proofs can simulate resolution proofs, see e.g. [19, 25]., denoted , where lines are linear inequalities. Clauses can be trivially converted into linear inequalities666For example, could be converted to the inequality . but, more generally, cutting planes can start with any system of inequalities where is a matrix with integer entries. We say that the system is unsatisfiable iff it is unsatisfiable for any . The most basic form of the cutting planes proof system consists of three rules: addition of inequalities, multiplication of inequalities by positive integers, and most crucially, the rounded division rule, also known as the Gomory-Chvátal rule. The rounded division rule is the simple but powerful observation that if are all integers with a common factor , and we have the inequality , then we can derive that .
In general, there are many more sound derivation rules for integer/linear inequalities than just rounded division (such as saturation [9] for example), and even more generally, one may allow any sound derivation rule for linear inequalities, which yields what is known as semantic cutting planes or – we use the two names interchangeably.
There is a well-known connection between communication complexity and tree-like proofs, which we will now detail. Given any unsatisfiable formula , an assignment to the variables can be distributed among players, who must then communicate in order to find a a violated clause in . This is a search problem, and is denoted . Short tree-like proofs of the unsatisfiability of can often be converted into short protocols for using standard techniques.
For example, a short tree-like proof of unsatisfiability of using the resolution rule naturally corresponds to a decision tree for finding a violated clause of in the following way. For every derivation of the form where is known to be false, we query in order see whether or is necessarily false. We can continue in this manner, from the root of the tree-like refutation, until we hit an unsatisfied clause in the original formula.
On the other hand, tree-like semantic cutting planes refutations naturally correspond to threshold decision trees, which we now define.
Definition 2.1 (Threshold Decision Tree).
A threshold decision tree is a tree whose vertices are labeled with inequalities of the form where are integers. Edges are labelled with 0 or 1, and leaves are axioms of a system of inequalities .
We traverse a threshold decision tree by computing the threshold function at the root, following the corresponding edge, and continuing in this manner until we hit a leaf. We say that a threshold decision tree computes the search problem for a formula if this process leads to a leaf corresponding to a violated clause in .
First, we have the following well-known lemma, which states that one can derive a low-depth threshold decision tree from a small refutation.777As noted in [19], there is no meaningful converse to this statement, since if there are inequalities in our unsatisfiable system, there exists a trivial depth threshold decision tree finding one that is violated.
Proposition 2.2.
Given a size tree-like refutation of an unsatisfiable system , there is a depth threshold decision tree finding a violated axiom.
Proposition 2.2 goes back to the work of Impagliazzo, Pitassi, and Urquhart [17], and can also be found for instance in [19]. We omit the proof, but the idea is a common one: find a node in the tree with roughly half (between 1/3 and 2/3) of the leaves as its descendants, make that the root of the threshold decision tree, and recurse.
2.2 Communication Complexity
We mainly focus on -party number-in-hand communication, wherein each player receives an input , and the players’ goal is to communicate as little as possible in order to compute a known function or relation involving their collective inputs. In general, players may have access to shared randomness, and we allow incorrect answers with probability .
An important function for us is the number-in-hand disjointness problem with players and input size , henceforth denoted . This is the communication problem wherein each player and input in , and they must decide if there exists a coordinate for which they all have a 1 in that coordinate. Disjointness in general is an extremely well-studied problem [7, 25], and for the specific case of the NIH model, we have the following lower bound due to Braverman and Oshman.
Theorem 2.3 ([5]).
The randomized communication complexity of is .
Our results rely on the following connection between threshold decision trees for finding violated clauses and -party NIH communication. It is closely related to previous work.
Lemma 2.4.
For , if an unsatisfiable system on has a threshold decision tree of depth finding a violated axiom, then for any partition of the input variables into parts there is a randomized protocol for using bits of communication.
Lemma 2.4 is similar for example to Lemma 5 in [17] or Lemma 19.11 in [19], but is slightly stronger so we give a brief proof. Using a well-known theorem of Muroga [21] we can assume, without loss of generality, that each of the threshold functions in the decision tree has integer coefficients of absolute value at most .
The players evaluate these threshold functions using the following efficient randomized protocol given by Viola [30] which tightens and refines a protocol first given by Nisan [22].
Proposition 2.5 ([30]).
Suppose that each player receives an input . Then there is a randomized number-in-hand protocol with error at most that determines whether and communicates bits.
Corollary 2.6.
Suppose that each player receives an input . Then they can execute a randomized number-in-hand protocol to determine whether , where each with error at most using at most bits of communication.
Proof of Lemma 2.4.
Given a threshold decision tree of depth , which has coefficients of magnitude at most without loss of generality [21], we simply traverse it from the root, evaluating the threshold functions until a root is reached. By Corollary 2.6, the players can communicate bits to compute the threshold function with error probability . Setting and continuing in this manner, by a union bound the threshold functions are all computed correctly with constant probability. Using the assumption that , this yields a protocol communicating bits.
Given a system of unsatisfiable inequalities , and a partition of an assignment between players, there is a natural (number-in-hand) communication game wherein players must communicate to a find an axiom violated by . Lemma 2.4 implies the following result connecting communication complexity and proof complexity.
Lemma 2.7.
For any partition of variables into parts, if requires bits of communication, then any tree-like refutation of requires size .
Proof.
By Proposition 2.2, given a size tree-like proof, we get a depth threshold decision tree finding a violated axiom. By Lemma 2.4, there exists a communication protocol finding a violated axiom using bits of communication. This implies that for constant , which in turn implies is , as desired.
2.3 Triangle-DAGs
Given a bipartite domain , a triangle is any set that can be written as for some labelling and .
A triangle-DAG computing a search problem is a directed acyclic graph of fan-out at most 2 where each node is associated with a triangle satisfying the following:
-
there is a distinguished root node with fan-in zero, and , and
-
for each non-sink node with children we have , and
-
each sink node is labeled with an output such that .
Given these definitions, we restate Proposition 1.6 for convenience. Proofs may be found in [28, 15] or in our full paper [3].
See 1.6
3 Multiparty Communication Lower Bounds for
In this section we prove Theorem 1.1, which we now recall. See 1.1 The idea for the proof is to exhibit a random reduction from the decision problem to the collision problem. This is analogous to the approach of Itsykson and Riazanov [18] for number-on-forehead communication complexity which used lower bounds for disjointness in that model and a randomized decision-to-search reduction paradigm introduced by Raz and Wigderson [26] to prove lower bounds on the monotone depth complexity of matching. The details and parameters of our reduction are necessarily quite different.
In our setting, we embed players’ inputs to a disjointness problem into matrices such that, when these matrices are concatenated, the resulting matrix has distinct rows if and only if the players’ inputs were disjoint. We can then add a few “fake” rows to this matrix and run our algorithm for , and see if the collisions it finds involve the fake rows or not. If so, we conclude that the inputs were disjoint and if not, we know that they were not disjoint.
The following key combinatorial lemma allows us to carry out the first step of this process.
Lemma 3.1.
For all integers there exist matrices and such that
-
1.
has unique pairs of identical rows.
-
2.
For any string , define the matrix as the matrix formed by making its -th column equal to the -th column of if , and equal to the -th column of if . Then has unique rows for all .
We defer the proof of Lemma 3.1 to Section 3.1.
Proof of Theorem 1.1 using Lemma 3.1.
As alluded to, we will reduce the NIH disjointness problem to our bit-pigeonhole problem. Namely, we will reduce to a communication game, where , and .
The players get (viewed as bit strings of length ), and need to determine whether . First, we define where the same row is repeated times.
For each , consider the matrix from Lemma 3.1. Note that each player knows the -th column of for all , but without communication the other players do not know this column. Then we can define
Observe that each player can construct their “part” of this matrix without communicating by constructing the -th column of every matrix (which only depends on ), and then taking the the -th part of each of the matrices.
Lemma 3.1 lets us connect the distinctness property of this matrix with the disjointness property of the players’ inputs.
Claim 3.2.
If are disjoint, then has distinct rows.
Proof.
The only possible collisions happen in every group of rows, since has every row different from for all . Within these groups, by Lemma 3.1, if the inputs are disjoint then there are no collisions.
Claim 3.3.
If is not disjoint, then there are at least pairs of colliding rows in .
Proof.
Any coordinate for which for all generates , which by Lemma 3.1 generates such pairs, since input was repeated times.
We cannot run any collision protocol for yet, as there are not guaranteed collisions. To address this, the players use shared randomness to put an additional rows at the bottom of . These rows will be chosen randomly with the following two properties:
-
1.
Each fake row will be distinct.
-
2.
Each player’s “part” of the matrix (which consists of columns) when restricted to these rows will repeat the unique possible bit strings an addition times.888This is important because if we bias and have a certain fake row appear more often in the input for player , then could potentially detect and use this to its advantage.
Denote this new matrix . now has “fake” collisions which involve any of the last rows.
Let denote the randomized protocol solving the problem.
Observe that if the inputs are disjoint, then the only collisions in involve fake rows. The players would like to feed their parts of this matrix into and conclude that their inputs are disjoint if the output involves a fake row, and conclude that they were not disjoint if the output involves two non-fake rows. However, this is problematic, as we have no guarantees over how behaves, and it could always find a collision involving one of the last rows (which it knows are fake), regardless of if there are other collisions. This necessitates the following random shuffling.
-
1.
Each player applies (the same) random permutation which shuffles the rows of .
-
2.
Each player applies an individual random permutation to each of their rows. Note that this preserves collisions/distinctness in the concatenation.
Denote , and call this final matrix .
Algorithm.
The algorithm for disjointness is as follows: the players use their inputs and shared randomness to compute (without communication) their respective parts of 5 independent copies of an constructed in the above manner, and run using these as inputs. The players then examine the outputs of the algorithm on these five inputs. They then exchange an additional bits to determine if each claimed collision actually was a collision. Finally, if any of the claimed collisions were actually collisions on rows that were not fake (under the appropriate permutation), then the players can conclude with certainty that their inputs were not disjoint. Otherwise, if only ever finds colliding pairs that involve a row the players know is fake (or otherwise fail to find any collisions), then players guess that were disjoint.
Analysis.
We analyze one iteration of the algorithm. Suppose has error probability at most – that is, with probability at least , it outputs two rows that are equal.
Suppose are disjoint. Then by assumption, finds a collision with probability at least , and we know this collision will always involve a fake row by ˜3.2. Therefore the players will correctly output that their inputs were distinct with probability at least , and this is only improved by the five-fold repetition.
Otherwise, suppose that the players’ inputs were not disjoint. Suppose further that successfully finds a collision – this happens with probability at least . Recall that by ˜3.3 will have at least distinct pairs of real collisions. Adding the fake rows produced additional “fake” collisions. These fake rows could have created up to additional unique pairs of fake collisions, or could have “joined” the real collisions, creating up to groups of 3 equal rows in .
If outputs a collision from one of the groups of three, then because we applied random permutations to the rows, it is equally likely to have chosen any of the 3 possible pairs. Therefore, with probability at least , it outputs a real collision, and the players successfully discover that they are not disjoint. Otherwise, if outputs one of the unique collision pairs, then (again because we have applied random permutations to the rows), any such unique collision is equally likely to be output. If of the fake rows formed a group of three with real collisions, then that leaves at most fake rows to collide with a different unique row. It also leaves untouched real collisions, so outputs a real collision with probability at least . Either way, the probability that outputs a real collision is at least .
Therefore, after repeating this 5 times independently, the probability of seeing at least one real collision is at least .
Let . We have shown that if with input size can be solved with communication, then we can solve the decision disjointness problem with which is at most , contradicting the lower bound from Theorem 2.3.
3.1 Proof of Lemma 3.1
We first recall Lemma 3.1.
See 3.1
Proof.
Let be the set of integers with an even number of 1s in their binary representation.
Define
where is the -th smallest number in .
We pause here to note that each of the columns of are actually each the truth table of a linear function. Let be the linear function , where is the first standard basis vector. Then we can describe the first column of as the truth table of . More generally, we have that for the -th column of is the truth table of , and the last column is the truth table of .
If we define to be the matrix whose column is the vector whose inner product we are taking with in , and whose rows are the binary strings written in order, then we have that
where all operations are over . has repeated rows precisely because has linearly dependent columns.
With this perspective in mind, if we can find a matrix over such that replacing any (nonzero) number of columns of with corresponding columns in produces a matrix with linearly independent columns, then we are done, as we can let .
We define to be the following lower triangular matrix:
Clearly is full rank.
We claim that replacing any set nonempty set of columns of with the corresponding columns in produces a matrix with linearly independent columns. Consider arbitrary , and arbitrary nonempty .
Case 1.
Suppose , that is, the last column of is . Then our matrix is lower triangular with 1s on the diagonal, and so has linearly independent columns.
Case 2.
Suppose , that is, the last column of is . In this case, the first columns are lower triangular with 1s on the diagonal, and therefore their span is equal to . It suffices then to show that also is in the column span. Towards this goal, take the minimal such that , and observe that summing the first columns of equals , the all 1s vector. Adding this to the last column produces , so we are done.
4 Tree-like Proof Complexity Lower Bounds
In this section, we prove the following more detailed version of Theorem 1.2.
Theorem 4.1.
When , any tree-like semantic cuttings planes refutation of must have size at least .
Proof.
The theorem follows quite readily from Lemma 2.7 and the fact that reduces to . If we translate to a system of inequalities, then there are inequalities on variables.
Lemma 2.7 then says that any tree-like semantic cutting planes proof of the unsatisfiability of must have size at least By Theorem 1.1, . Plugging this in yields that the tree-like size must be at least .
From Theorem 4.1 we achieve Theorem 1.2, which we restate now.
Corollary 4.2.
Any tree-like semantic cutting planes refutation of requires size when .
Proof.
Let . Plugging this into the bound from Theorem 4.1, we get that . In this regime, Theorem 4.1 gives the size lower bound
for appropriate constant . Using the fact that , the bound becomes
5 Triangle-DAG Lower Bounds
In this section, we prove Theorem 1.7, which we restate here for convenience.
See 1.7
Before proving Theorem 1.7, we need the following notion of triangle slices. For a triangle and a given , we define the slice to be , and define the slice analogously. Note that for any triangle defined by functions and there is a natural total pre-order on where iff and hence ; similarly, there is an total pre-order on where iff and hence . This immediately implies the following.
Proposition 5.1.
Given a triangle , if is such that is maximized, then for all we have .
We will have the following proposition.
Proposition 5.2.
For any triangle and rectangle , is a triangle.
Proof.
By definition, for some . If , simply modify for all and for all .
The proof of Theorem 1.7 uses the bottleneck counting method of Haken and Cook for cutting planes proofs [13] as adapted for direct use on triangle-DAGs by Sokolov [29].
Let denote the nodes of a triangle-DAG computing under the natural partition of variables. At a high level, to prove Theorem 1.7, we will construct a partial function such that
-
(a) (Lemma 5.5) most and are mapped by to a node of , and
-
(b) (Lemma 5.6) there is no node of with too many or assigned to it by .
It is then easy to combine these two properties and conclude that must be large999The name bottleneck counting came from its original version due to Haken [12] in which a class of full input assignments was mapped by a function to nodes in a proof DAG and each input assignment could be viewed as “flowing” from the root to a particular sink node (defined by the assignment). In that case, identified a node on such a path, a bottleneck node, that did not permit many assignments to flow through it. Since there were many assignments, only few of which could pass through any bottleneck node identified by , there must be many bottleneck nodes in the DAG. In the modified form for cutting planes/triangle-DAGs, while the full assignment is flowing through the triangle-DAG, the mapping is based on half of the input assignment, either the or portion, and the sink node is not unique; not all assignments are assigned in this way, but many are..
For any , there is an associated rectangle of inputs that violate at least one of the clauses enforcing an inequality between coordinates and given by
Observe that the set of all rectangles covers the entire space as long as . (That is, .) Note that in order for a triangle-DAG to correctly compute , it must, at the very least, have each sink be contained in a single .
Definition 5.3.
For a node , let denote the triangle associated with that node. Define the width of in triangle to be the minimal size of any subset such that .
With this definition in hand, we can define our using Algorithm 1 which depends on a parameter that we will eventually set to .
Intuitively, in using Algorithm 1 we are going backwards through our DAG , and whenever the protocol had too many options for what clause to output when the protocol was at a node for a fixed (which corresponds to large width), we assign to . Arguing that is not too large is thus arguing that a protocol cannot make huge strides in learning about which clause to output for too many suddenly in one single node .
We now make some basic observations about our definition of . First, note that no is assigned to any sink node of , since every sink node is wholly contained in an , and therefore we have that for all . The following observation will be of critical importance in our analysis.
Claim 5.4.
During the execution of Algorithm 1, for every in triangle-DAG and every , .
Proof.
By definition in a triangle-DAG, if and are children of node , then we have that . In particular, we know that if was not assigned to nodes or , then , since we can take the union of the coverings for and .
Finally, we note that at the end of Algorithm 1 at the root , for all , we have that .
Lemma 5.5.
Let . For constructed using Algorithm 1, at least elements of are assigned by or at least elements of are assigned by .
Proof.
At the end of Algorithm 1 after processing the root of , since , we have which is the rectangle of unassigned inputs. If then we are done; otherwise, let . Since , there exists a set , , such that for all , for at least one .
So, we obtain
Hence, , as desired.
This shows that a large number of elements of are assigned by . It remains to show that each node in the protocol only has a bounded number of elements of assigned by .
Lemma 5.6.
Let be defined by Algorithm 1 with . For all all , maps at most elements of to ; the analogous bound also holds for .
Proof.
We fix any and focus on the number of elements that maps to ; the bound for the number of such is identical. In particular, consider the values of and and in Algorithm 1 immediately before processing node ; any that maps to must be in .
Our strategy will be to construct a set of potential coverings for the slices by monochromatic rectangles. We will then aim to show that most have width even when restricted to this set of potential coverings, thereby limiting how many could be assigned by to .
We now describe this potential covering in detail. Intuitively, our strategy will be to construct a tree , each of whose nodes is labelled by a triangle of inputs that are not yet covered, where each edge of the tree is labelled with a pair . We say that is consistent with a node iff for all labels on the edges of the unique path to in , we have that . Furthermore, will be constructed so that if is consistent with a leaf of , then is covered by . We produce the tree of potential coverings of of for all using Algorithm 2 applied with , , and which satisfy the preconditions by ˜5.4.
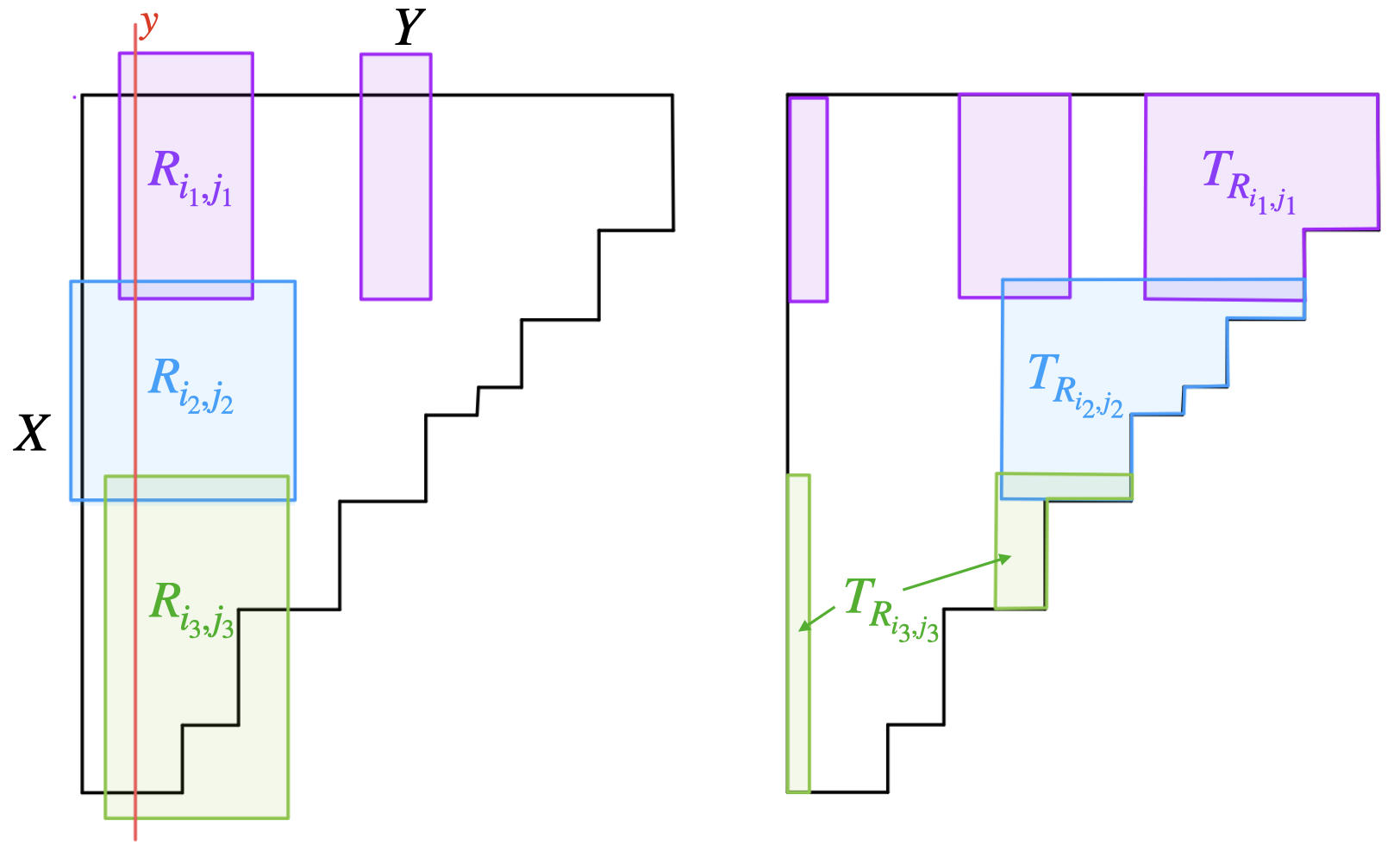
First, observe that any such that is consistent with at least one leaf in , by the choice of in Algorithm 2 along with Proposition 5.1. We define the set of equality constraints of a leaf to be the set . Observe that we have the desired property that if is consistent with a leaf of , then is covered by , thereby ensuring that .
Therefore, if maps to then must be consistent with a leaf of of depth at least . Let denote tree truncated at depth . Thus, the total number of that maps to is at most
| (1) |
Remark 5.7.
Before explaining the details of our analysis, it is useful to discuss a naive bound on (1) that does not suffice to yield our bounds: Naively, there could be leaves in at depth , and each such leaf could have the property that forms a clique on coordinates when viewed as a graph. In this case, the fraction of that could be consistent with the intersection is . If we simply take a union bound over all paths, the upper bound we would get on (1) is which, since is only , is larger than 1 unless is at most polynomial in , which requires that is .
In light of Remark 5.7, we need to be more careful about how we bound (1). For , we define its equality graph to be a graph with vertex set and edge set . We use this name because if is consistent with , then for all . We say that an edge denoting is implied by equality graph if adding it completes a cycle in .
The key observation is the following.
Claim 5.8.
Let be a node in , and its associated equality graph. If has out-degree strictly larger than 1 in , then none of the outgoing edges can be labelled by an that is implied by .
Proof.
We prove the contrapositive. Consider any consistent with the path to in (meaning for all ). Let be the triangle labelling node and consider the that we choose when processing in Algorithm 2. If there is some outgoing edge from labelled that is implied by , then and hence . Since we know that is already implied in , the single rectangle covers all of , so will have out-degree 1 in .
˜5.8 implies that every path in goes through a node that branches at least times, since edges must imply equality constraints on at least coordinates (the worst case is a clique). We simplify further by collapsing nodes of with out-degree 1. Then we are left with , which is a tree with every path of length between and . Since the input distribution on is uniform and none of the out-degree 1 edges of involve new constraints by ˜5.8, the probability that is consistent with any leaf is precisely . Then we can bound (1) as follows:
This implies that the number of that get assigned to by is at most as required. The analogous bound holds for the number of assigned to by . We now have all we need to prove our main theorem.
Proof of Theorem 1.5.
Let . By Lemma 5.5, given by Algorithm 1 maps at least of the elements of or elements of to vertices of . Choose the applicable or . By Lemma 5.6, at most a fraction of these can map to a single vertex of . Therefore has at least vertices.
Remark 5.9.
Hrubeš and Pudlák [16] proved their lower bound using the interpolation method combined with a modified form of a general monotone switching lemma of Jukna [19]. The construction of Algorithm 2 has some flavor of the monotone switching lemma arguments, but the overall argument here seems fairly different. It would not be surprising that if one could modify this method to yield a similar lower bound to the one we give here, but exactly how to do that is not clear. In any case, we find the form of the bottleneck counting argument appealing.
6 Multiparty Communication Lower Bounds for all
See 1.3
We note that this is essentially optimal in that a simple randomized protocol nearly matches our lower bound.
Proposition 6.1.
For and , there is a randomized -party number-in-hand protocol for with complexity .
Details of both proofs are in our full paper [3]. We sketch the proof of Theorem 1.3, which simplifies and generalizes ideas of Yang, Zhang, and Wang [32, 31] to the -party setting for . It is based on a method for decomposing the input space into structured rectangles on which a protocol’s output is constant.
Definition 6.2.
For a random variable supported on , we say it is -dense if the min-entropy of all its projections is nearly as large as possible; that is, for all , , where denotes marginalized to the coordinates in .
For we have for and we will choose .
Definition 6.3 (Structured rectangle).
Given a rectangle , where each , we say that is structured iff there exist and where each such that
-
is -dense on the coordinates in and
-
is fixed to on the coordinates in .
Using ideas from [31] we obtain:
Lemma 6.4.
Let be a deterministic -party number-in-hand protocol solving . There is a partition of the inputs into structured rectangles, each of which yields a fixed output of , such that the probability distribution on these structured rectangles induced by uniform inputs satisfies where are the sets associated with the structured property of .
Our proof considers rectangles in the support of of three kinds: (1) Those where is larger than its expected value of , (2) those where it is not much larger and every element of the rectangle contains some fixed collision, and (3) the rest. The fraction of inputs in rectangles of type (1) is small by Markov’s inequality and the fraction in rectangles of type (3) on which any fixed answer of can be correct, is small because they are structured. Analyzing the total measure of inputs in rectangles of type (2) relies on a subtle charging scheme that allocates the total number of such inputs to rectangles of all types using a per-rectangle fraction proportional to .
7 Discussion
We end by discussing some related problems and directions for future study. In particular, we highlight three possible directions.
-
Multiparty DAG-like communication lower bounds. In general, it would be interesting to see if the we give can be further improved, or if any nontrivial (size ) cutting planes refutation of exists. One possible way to improve the lower bound could be to study a multiparty () version of DAG-like protocols. Concretely, could one can prove DAG-like communication lower bounds for the -player analog ? We have shown that generalizing to players helps in the tree-like case, and perhaps this holds true in the DAG-like setting as well.
-
Stronger bounds for tree-like cutting-planes proof complexity of the weak bit pigeonhole principle When , we only obtain the weaker size lower bound for , rather than the size lower bound we obtain for values of closer to . Can we extend the range of our strong lower bound to all values of ? To do so we must use a technique that does not use randomized communication complexity.
-
Finally, we highlight that for close to , the loss of in the denominator of Theorem 1.1 could potentially be improved when . Indeed, we do not suspect that it should be present at all, and we conjecture that should remain hard for all the way up to . However, it seems unlikely that any reduction from -party disjointness would be able to achieve this since an additional input bit per player seems essential in implementing the reduction.
References
- [1] Albert Atserias, Moritz Müller, and Sergi Oliva. Lower bounds for DNF-refutations of a relativized weak pigeonhole principle. J. Symb. Log., 80(2):450–476, 2015. doi:10.1017/JSL.2014.56.
- [2] Paul Beame, Toniann Pitassi, and Nathan Segerlind. Lower bounds for Lovász–Schrijver systems and beyond follow from multiparty communication complexity. SIAM J. Comput., 37(3):845–869, 2007. doi:10.1137/060654645.
- [3] Paul Beame and Michael Whitmeyer. Multiparty communication complexity of collision-finding and cutting planes proofs of concise pigeonhole principles. Electron. Colloquium Comput. Complex., TR25-057, 2025. URL: https://eccc.weizmann.ac.il/report/2025/057.
- [4] Maria Luisa Bonet, Toniann Pitassi, and Ran Raz. Lower bounds for cutting planes proofs with small coefficients. In Proceedings of the Twenty-Seventh Annual ACM Symposium on Theory of Computing (STOC 1995), pages 575–584, Las Vegas, Nevada, 1995. ACM. doi:10.1145/225058.225275.
- [5] Mark Braverman and Rotem Oshman. The communication complexity of number-in-hand set disjointness with no promise. Electron. Colloquium Comput. Complex., TR15-002, 2015. URL: https://eccc.weizmann.ac.il/report/2015/002.
- [6] Samuel R. Buss and György Turán. Resolution proofs of generalized pigeonhole principles. Theor. Comput. Sci., 62(3):311–317, 1988. doi:10.1016/0304-3975(88)90072-2.
- [7] Arkadev Chattopadhyay and Toniann Pitassi. The story of set disjointness. SIGACT News, 41(3):59–85, 2010. doi:10.1145/1855118.1855133.
- [8] Stefan S. Dantchev, Nicola Galesi, Abdul Ghani, and Barnaby Martin. Proof complexity and the binary encoding of combinatorial principles. SIAM J. Comput., 53(3):764–802, 2024. doi:10.1137/20M134784X.
- [9] Stephan Gocht, Jakob Nordström, and Amir Yehudayoff. On division versus saturation in pseudo-boolean solving. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI 2019, pages 1711–1718. ijcai.org, August 2019. doi:10.24963/IJCAI.2019/237.
- [10] Mika Göös and Siddhartha Jain. Communication complexity of collision. In Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques, APPROX/RANDOM 2022, volume 245 of LIPIcs, pages 19:1–19:9. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2022. doi:10.4230/LIPICS.APPROX/RANDOM.2022.19.
- [11] Dima Grigoriev, Edward A. Hirsch, and Dmitrii V. Pasechnik. Complexity of semi-algebraic proofs. In STACS 2002, 19th Annual Symposium on Theoretical Aspects of Computer Science, Proceedings, volume 2285 of Lecture Notes in Computer Science, pages 419–430. Springer, 2002. doi:10.1007/3-540-45841-7_34.
- [12] Armin Haken. The intractability of resolution. Theor. Comput. Sci., 39:297–308, 1985. doi:10.1016/0304-3975(85)90144-6.
- [13] Armin Haken and Stephen A. Cook. An exponential lower bound for the size of monotone real circuits. J. Comput. Syst. Sci., 58(2):326–335, 1999. doi:10.1006/JCSS.1998.1617.
- [14] Johan Håstad. On small-depth Frege proofs for PHP. In 64th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2023, pages 37–49. IEEE, November 2023. doi:10.1109/FOCS57990.2023.00010.
- [15] Pavel Hrubes and Pavel Pudlák. A note on monotone real circuits. Electron. Colloquium Comput. Complex., TR17-048, 2017. URL: https://eccc.weizmann.ac.il/report/2017/048.
- [16] Pavel Hrubes and Pavel Pudlák. Random formulas, monotone circuits, and interpolation. Electron. Colloquium Comput. Complex., TR17-042, 2017. URL: https://eccc.weizmann.ac.il/report/2017/042.
- [17] Russell Impagliazzo, Toniann Pitassi, and Alasdair Urquhart. Upper and lower bounds for tree-like cutting planes proofs. In Proceedings of the Ninth Annual Symposium on Logic in Computer Science (LICS ’94), pages 220–228, Paris, France, 1994. IEEE Computer Society. doi:10.1109/LICS.1994.316069.
- [18] Dmitry Itsykson and Artur Riazanov. Proof complexity of natural formulas via communication arguments. In Proceeedings of the 36th Computational Complexity Conference, CCC 2021, volume 200 of LIPIcs, pages 3:1–3:34. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2021. doi:10.4230/LIPICS.CCC.2021.3.
- [19] Stasys Jukna. Boolean Function Complexity - Advances and Frontiers, volume 27 of Algorithms and combinatorics. Springer, 2012. doi:10.1007/978-3-642-24508-4.
- [20] Jan Krajícek, Pavel Pudlák, and Alan R. Woods. An exponential lower bound to the size of bounded depth Frege proofs of the pigeonhole principle. Random Struct. Algorithms, 7(1):15–40, 1995. doi:10.1002/RSA.3240070103.
- [21] Saburo Muroga, Iwao Toda, and Satoru Takasu. Theory of majority decision elements. Journal of the Franklin Institute, 271(5):376–418, 1961.
- [22] Noam Nisan. The communication complexity of threshold gates. Combinatorics, Paul Erdos is Eighty, 1(301-315):6, 1993.
- [23] Toniann Pitassi, Paul Beame, and Russell Impagliazzo. Exponential lower bounds for the pigeonhole principle. Comput. Complex., 3:97–140, 1993. doi:10.1007/BF01200117.
- [24] Pavel Pudlák. Lower bounds for resolution and cutting plane proofs and monotone computations. J. Symb. Log., 62(3):981–998, 1997. doi:10.2307/2275583.
- [25] Anup Rao and Amir Yehudayoff. Communication Complexity: and Applications. Cambridge University Press, 2020. doi:10.1017/9781108671644.
- [26] Ran Raz and Avi Wigderson. Monotone circuits for matching require linear depth. J. ACM, 39(3):736–744, 1992. doi:10.1145/146637.146684.
- [27] Hanif D. Sherali and Warren P. Adams. A hierarchy of relaxations between the continuous and convex hull representations for zero-one programming problems. SIAM J. Discret. Math., 3(3):411–430, 1990. doi:10.1137/0403036.
- [28] Dmitry Sokolov. Dag-like communication and its applications. In Computer Science - Theory and Applications - 12th International Computer Science Symposium in Russia, CSR 2017, Proceedings, volume 10304 of Lecture Notes in Computer Science, pages 294–307. Springer, 2017. doi:10.1007/978-3-319-58747-9_26.
- [29] Dmitry Sokolov. Random (log n)-CNF are hard for cutting planes (again). In Proceedings of the 56th Annual ACM Symposium on Theory of Computing, STOC 2024, Vancouver, BC, Canada, June 24-28, 2024, pages 2008–2015. ACM, 2024. doi:10.1145/3618260.3649636.
- [30] Emanuele Viola. The communication complexity of addition. Combinatorica, 35(6):703–747, 2015. doi:10.1007/S00493-014-3078-3.
- [31] Shuo Wang, Guangxu Yang, and Jiapeng Zhang. Communication complexity of set-intersection problems and its applications. Electron. Colloquium Comput. Complex., TR23-164, 2023. URL: https://eccc.weizmann.ac.il/report/2023/164.
- [32] Guangxu Yang and Jiapeng Zhang. Communication lower bounds for collision problems via density increment arguments. In Proceedings of the 56th Annual ACM Symposium on Theory of Computing, STOC 2024, pages 630–639. ACM, June 2024. doi:10.1145/3618260.3649607.
