Minimum+1 Steiner Cut and Dual Edge Sensitivity Oracle: Bridging Gap between Global and (s,t)-cut

Bhanja, Koustav

doi:10.4230/LIPIcs.ICALP.2025.27

Minimum+1 Steiner Cut and Dual Edge Sensitivity Oracle: Bridging Gap between Global and (s,t)-cut

Koustav Bhanja

Weizmann Institute of Science, Rehovot, Israel

Abstract

Let $G=(V,E)$ be an undirected multi-graph on $n=|V|$ vertices and $S\subseteq V$ be a Steiner set in $G$ . Steiner cut is a fundamental concept; moreover, global cut ( $|S|=n$ ), as well as $(s,t)$ -cut ( $|S|=2$ ), is just a special case of Steiner cut. We study Steiner cuts of capacity minimum+1, and as an important application, we provide a dual edge Sensitivity Oracle for Steiner mincut – a compact data structure for efficiently reporting a Steiner mincut after failure/insertion of any pair of edges.

A compact data structure for cuts of capacity minimum+1 has been designed for both global cuts [Dinitz and Nutov, STOC 1995] and $(s,t)$ -cuts [Baswana, Bhanja, and Pandey, ICALP 2022 & TALG 2023]. Moreover, both data structures are also used crucially to design a dual edge Sensitivity Oracle for their respective mincuts. Unfortunately, except for these two extreme scenarios of Steiner cuts, no generalization of these results is known. Therefore, to address this gap, we present the following first results on Steiner cuts for any $S$ satisfying $2\leq|S|\leq n$ .

1.

Data Structure for Minimum+1 Steiner Cut: There is an ${\mathcal{O}}(n(n-|S|+1))$ space data structure that, given any pair of vertices $u, v$ , can determine in ${\mathcal{O}}(1)$ time whether the Steiner cut of the least capacity separating $u$ and $v$ has capacity minimum+1. It can report such a cut, if it exists, in ${\mathcal{O}}(n)$ time, which is worst-case optimal.
2.

Dual Edge Sensitivity Oracle: We design the following pair of data structures.
(a) There is an ${\mathcal{O}}(n(n-|S|+1))$ space data structure that, after the failure or insertion of any pair of edges in $G$ , can report the capacity of Steiner mincut in ${\mathcal{O}}(1)$ time and a Steiner mincut in ${\mathcal{O}}(n)$ time, which is worst-case optimal.
(b) If we are interested in reporting only the capacity of Steiner mincut, there is a more compact data structure that occupies ${\mathcal{O}}((n-|S|)^{2}+n)$ space and can report the capacity of Steiner mincut in ${\mathcal{O}}(1)$ time after the failure or insertion of any pair of edges.
3.

Lower Bound for Sensitivity Oracle: For undirected multi-graphs, for any Steiner set $S\subseteq V$ , any data structure that, after the failure or insertion of any pair of edges, can report the capacity of Steiner mincut must occupy $\Omega((n-|S|)^{2})$ bits of space in the worst case, irrespective of the query time.

To arrive at our results, we provide several techniques, especially a generalization of the 3-Star Lemma given by Dinitz and Vainshtein [SICOMP 2000], which is of independent interest.

Our results achieve the same space and time bounds of the existing results for the two extreme scenarios of Steiner cuts – global and $(s,t)$ -cut. In addition, the space occupied by our data structures in (1) and (2) reduces as $|S|$ tends to $n$ . Also, they occupy subquadratic space if $|S|$ is close to $n$ .

Keywords and phrases:

cut, mincut, minimum+1, steiner, edge fault, sensitivity oracle, dual edges

Category:

Track A: Algorithms, Complexity and Games

Copyright and License:

2012 ACM Subject Classification:

Theory of computation

\rightarrow

Data structures design and analysis ; Theory of computation

\rightarrow

Dynamic graph algorithms ; Theory of computation

\rightarrow

Network flows

Related Version:

Full Version: https://arxiv.org/abs/2406.15129 [6]

Acknowledgements:

This research work was carried out during my doctoral studies at IIT Kanpur, India. I am grateful to my doctoral advisor, Prof. Surender Baswana, for reviewing this article, having many helpful discussions on connectivity carcass, and providing feedback on improving its readability. I am also thankful to an anonymous reviewer for carefully reviewing a preliminary version of this article and for highlighting subtle technical points that helped improve its quality.

Funding:

This project is partially funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme, grant agreement No. 949083

DOI:

10.4230/LIPIcs.ICALP.2025.27

Event:

52nd International Colloquium on Automata, Languages, and Programming (ICALP 2025)

Editors:

Keren Censor-Hillel, Fabrizio Grandoni, Joël Ouaknine, and Gabriele Puppis

Series and Publisher:

Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik

1 Introduction

In the real world, networks (or graphs) experience changes as a result of the failure/insertion of edges/vertices. They may lead to a change in the solution of various graph problems. Although these failures/insertions may occur at any point in the network at any time, they are mostly transient in nature. The aim is to quickly report the solution of the given problem once any failure/insertion has occurred in the network. This motivates us to design Sensitivity Oracles for various graph problems. A Sensitivity Oracle for a graph problem is a compact data structure that can efficiently report the solution of the given problem after the failure/insertion of a set of edges/vertices. Sensitivity Oracles have been designed for many fundamental graph problems, namely, shortest paths [3, 7], reachability [26, 11], traversals [29]. The (minimum) cut of a graph is also a fundamental concept consisting of numerous applications [1]. In this article, for undirected multi-graphs, we present (1) a compact data structure for Steiner cuts of capacity minimum+1 and, as an important application, (2) a dual edge Sensitivity Oracle for Steiner mincut – a compact data structure for handling insertion/failure of any pair of edges. The results in $(1)$ and $(2)$ provide the first generalization to the existing results for global mincut [14] and $(s,t)$ -mincut [2] while matching their bounds on both space and time. In addition, our Sensitivity Oracle in (2) is the first result on Steiner mincut for handling multiple insertions/failures of edges after the single edge Sensitivity Oracles in undirected multi-graphs [4, 16, 15, 17].

Two well-studied cuts and their generalization.

Let $G=(V,E)$ be an undirected connected multi-graph on $n=|V|$ vertices and $m=|E|$ edges ( $E$ is a multi-set). There are mainly two types of well-studied cuts in a graph – global cut and $(s,t)$ -cut. A (global) cut is defined as a nonempty proper subset of the vertex set. Let $C$ be any cut in $G$ . Cut $C$ is said to separate a pair of vertices $u, v$ if $u\in C$ and $v\in\overline{C}=V\setminus C$ or vice versa. For any pair of vertices $s$ and $t$ , cut $C$ is said to be an $(s,t)$ -cut if $C$ separates $s$ and $t$ . Let $S\subseteq V$ denote a Steiner set with $|S|\geq 2$ . A generalization of global cut and $(s,t)$ -cut is captured using Steiner cut, which is formally defined as follows.

Definition 1 (Steiner cut).

For any given Steiner set $S$ , a cut $C$ is said to be a Steiner cut if there is a pair of vertices $s_{1},s_{2}\in S$ such that $s_{1}\in C$ and $s_{2}\notin C$ .

An edge $e=(u,v)$ is a contributing edge of a cut $C$ if $C$ separates endpoints $u$ and $v$ of $e$ . The capacity of $C$ , denoted by $c(C)$ , is defined as the number of contributing edges of $C$ . A Steiner cut having the least capacity is known as a Steiner mincut of $G$ . For any given Steiner set $S$ , we denote the Steiner mincut by $S$ -mincut and its capacity by $\lambda_{S}$ . By Definition 1, the two types of well-known minimum cuts of a graph are just two special cases of $S$ -mincut, namely, global mincut when $S=V$ and $(s,t)$ -mincut when $S=\{s,t\}$ .

Data Structure for Minimum+1 Steiner Cut

There has been extensive research in designing compact data structures for minimum cuts [23, 12, 31, 27, 10], as well as cuts of capacity near minimum [14, 5, 27, 2], that can efficiently answer the following fundamental query.
cut( $u,v,\kappa$ ): For any given pair of vertices $u, v$ , determine if the least capacity cut separating $u$ and $v$ has capacity $\kappa$ . Then, report a cut $C$ of capacity $\kappa$ separating $u, v$ , if it exists.
Dinitz, Karzanov, and Lomonosov [12] designed an ${\mathcal{O}}(n)$ space cactus structure for storing all global mincuts in undirected weighted graphs. Likewise, Picard and Queyranne [31] designed an ${\mathcal{O}}(m)$ space directed acyclic graph (dag) for storing all $(s,t)$ -mincuts in directed weighted graphs. Both structures act as a data structure for answering query cut in ${\mathcal{O}}(n)$ time for their respective mincuts. It has been observed that a quite richer analysis was required to arrive at a compact structure for storing all $S$ -mincuts. In a series of remarkable results by Dinitz and Vainshtein [15, 16, 17], they showed that there is an ${\mathcal{O}}(\min\{n\lambda_{S},m\})$ space structure, known as Connectivity Carcass, for storing all $S$ -mincuts in an undirected multi-graph, which generalizes the results for $(s,t)$ -mincut [31] and global mincut [12]. They present an incremental algorithm for maintaining the structure until the capacity of $S$ -mincut increases. This structure helps in answering query cut for $S$ -mincut in ${\mathcal{O}}(m)$ time and is the first single edge Sensitivity Oracle for $S$ -mincut in undirected multi-graphs.

There also exist compact data structures for both global cut [14, 27, 5] and $(s,t)$ -cut [2] of capacity beyond the minimum, and they are applied to establish many important algorithmic results [27, 5, 14, 2, 24]. Specifically for cuts of capacity minimum+1, Dinitz and Nutov [14] gave an ${\mathcal{O}}(n)$ space $2$ -level cactus model that stores all global cuts of capacity minimum+1 in undirected multi-graphs. Their structure answers query cut in ${\mathcal{O}}(n)$ time and is used crucially for incremental maintenance of minimum+2 edge connected components [14], which generalizes the results of Galil and Italiano [21], and Dinitz and Westbrook [13, 18]. Similarly, for minimum+1 $(s,t)$ -cuts in directed multi-graphs, Baswana, Bhanja, and Pandey [2] designed an ${\mathcal{O}}(n^{2})$ space data structure that answers query cut in ${\mathcal{O}}(n)$ time. This data structure acts as the key component in the design of a dual edge Sensitivity Oracle for $(s,t)$ -mincut [2]. Unfortunately, there does not exist any nontrivial data structure for Steiner cuts of capacity beyond the minimum till date. Therefore, to bridge the gap between $(s,t)$ -cut [2] and global cut [14], it is natural to raise the following question for any given Steiner set $S$ satisfying $2\leq|S|\leq n$ .

Question 1.

For undirected multi-graphs, does there exist a compact data structure that can efficiently answer query cut for Steiner cuts of capacity minimum+1?

Dual Edge Sensitivity Oracle for Steiner Mincut

It is easy to observe that the failure of a pair of edges reduces the capacity of $S$ -mincut if and only if at least one failed edge is contributing to an $S$ -mincut or the pair of failed edges are contributing to a Steiner cut of capacity minimum+1. Therefore, the study of Steiner cuts of capacity minimum+1 has an important application to the problem of designing a dual edge Sensitivity Oracle for $S$ -mincut, which is formally defined as follows.

Definition 2 (Dual edge Sensitivity Oracle).

For any given Steiner set $S$ , a dual edge Sensitivity Oracle for $S$ -mincut is a compact data structure that can efficiently report an $S$ -mincut and its capacity after the failure or insertion of any given pair of query edges in $G$ .

For $S$ -mincuts, the existing Sensitivity Oracles can handle the insertion or failure of only a single edge, and are based on the Connectivity Carcass of Dinitz and Vainshtein [15, 16, 17], which dates back to 2000. Baswana and Pandey [4], using Connectivity Carcass as the foundation [15, 16, 17], designed an ${\mathcal{O}}(n)$ space single edge Sensitivity Oracle for $S$ -mincut in undirected multi-graphs. It can report the capacity of $S$ -mincut and an $S$ -mincut in the resulting graph in ${\mathcal{O}}(1)$ and ${\mathcal{O}}(n)$ time, respectively.

It is also important to design Sensitivity Oracles that can handle the insertions/failures of multiple edges/vertices. For undirected multi-graphs, by using single edge Sensitivity Oracle for $S$ -mincut [4], observe that the trivial data structure that can handle any $f>0$ edge failures occupies ${\mathcal{O}}(m^{f-1}n)$ space. To design a Sensitivity Oracle for handling multiple edge insertions/failures, a natural and also quite commonly taken approach is to first design a Sensitivity Oracle that can handle the insertions/failures of a pair of edges. It has been observed that a dual edge Sensitivity Oracle for several fundamental graph problems, namely, reachability [11, 9], breadth-first search [29, 25], shortest path [19], often requires a significantly richer analysis compared to the single edge Sensitivity Oracles. Moreover, it either reveals the difficulty or assists in several ways to solve the problem in its generality. Specifically, in the area of minimum cuts, the following two dual edge Sensitivity Oracles are the only existing Sensitivity Oracles that can handle multiple edge insertions/failures. For $(s,t)$ -mincut, Baswana, Bhanja, and Pandey [2] showed that there is an ${\mathcal{O}}(n^{2})$ space data structure that, after the insertion/failure of any pair of edges from a directed multi-graph, can report an $(s,t)$ -mincut and its capacity in ${\mathcal{O}}(n)$ and ${\mathcal{O}}(1)$ time, respectively. So, for $(s,t)$ -mincut in directed multi-graphs, by designing a dual edge Sensitivity Oracle, they improved the space by a factor of $\Omega(\frac{m}{n})$ over the trivial data structure for handling any $f>0$ edge insertions/failures. The ${\mathcal{O}}(n)$ space 2-level cactus model of Dinitz and Nutov [14] for minimum+1 global cuts immediately leads to an ${\mathcal{O}}(n)$ space data structure for handling dual edge failures for global mincuts as follows. It can report a global mincut and its capacity for the resulting graph after the failure of any pair of edges in ${\mathcal{O}}(n)$ and ${\mathcal{O}}(1)$ time, respectively. Therefore, the existing results or the results that can be derived from the existing results are only for the two extreme cases of $S$ -mincut. So, to provide a generalization of these results to any given Steiner set $S$ satisfying $2\leq|S|\leq n$ , the following question emerges naturally.

Question 2.

For undirected multi-graphs, does there exist a compact data structure that can efficiently report the capacity of $S$ -mincut and an $S$ -mincut after the insertion or failure of any given pair of query edges?

$\blacktriangleright$ Note 3.

The problem of handling dual edge insertions is provided in the full version [6]. Henceforth, we discuss only the results of handling the failure of a pair of edges.

1.1 Our Results

In this article, we answer both Question 1 and Question 2 in the affirmative. Moreover, the space and time bounds for our results also match with the existing best-known results for the two extreme scenarios of Steiner cuts – global cut [14] and $(s,t)$ -cut [2]. Let us denote a Steiner cut of capacity minimum+1 by $(\lambda_{S}+1)$ cut.

One of our key technical contributions is a generalization of the crucial 3-Star Lemma from the seminal work of Dinitz and Vainshtein [15, 16, 17]. We believe that this result is of independent interest. By heavily exploiting the generalized version of 3-star Lemma, we arrive at the following data structure for efficiently answering query cut for $(\lambda_{S}+1)$ cuts. This result provides an affirmative answer to Question 1.

Theorem 4 (Data Structure).

Let $G=(V,E)$ be an undirected multi-graph on $n=|V|$ vertices and $m=|E|$ edges. Let $S\subseteq V$ be any Steiner set of $G$ and $\lambda_{S}$ be the capacity of $S$ -mincut. There is an ${\mathcal{O}}(n(n-|S|+1))$ space data structure that, given any pair of vertices $u, v$ in $G$ , can determine in ${\mathcal{O}}(1)$ time whether the Steiner cut of the least capacity separating $u$ and $v$ has capacity $\lambda_{S}+1$ . Moreover, the data structure can report such a $(\lambda_{S}+1)$ cut $C$ separating $u$ and $v$ in ${\mathcal{O}}(n)$ time, if it exists.

Data structure in Theorem 4 occupies subquadratic, that is $o(n^{2})$ , space if $|S|$ is at least $n-o(n)$ . For minimum+1 global cuts ( $S=V$ ), it occupies only ${\mathcal{O}}(n)$ space, which matches with the $2$ -level cactus model of Dintz and Nutov [14]. Moreover, for $S=\{s,t\}$ (the other extreme scenario), it occupies ${\mathcal{O}}(n^{2})$ space, which also matches with the existing best-known result on minimum+1 $(s,t)$ -cut given by Baswana, Bhanja, and Pandey [2].

For dual edge Sensitivity Oracle, we design a pair of data structures. Our first data structure helps in reporting an $S$ -mincut in worst-case optimal time; however, it requires ${\mathcal{O}}(|S|)$ time to report its capacity. If the aim is to report only the capacity of $S$ -mincut, we present a more compact data structure that, interestingly, has a faster query time. These results on dual edge Sensitivity Oracle for $S$ -mincut are stated in the following theorem, which answer Question 2 in the affirmative.

Theorem 5 (Sensitivity Oracle).

Let $G=(V,E)$ be an undirected multi-graph on $n=|V|$ vertices and $m=|E|$ edges. For any Steiner set $S\subseteq V$ ,

1.

there is an ${\mathcal{O}}((n-|S|)^{2}+n)$ space data structure that can report the capacity of $S$ -mincut for the resulting graph in ${\mathcal{O}}(1)$ time and
2.

there is an ${\mathcal{O}}(n(n-|S|+1))$ space data structure that can report an $S$ -mincut for the resulting graph in ${\mathcal{O}}(n)$ time

after the insertion or failure of any pair of given query edges in $G$ .

The dual edge Sensitivity Oracle in Theorem 5 also achieves the same bound on space and query time for the existing best-known results on the two extreme scenarios of $S$ -mincuts, namely, global mincut ( $|S|=n$ ) [14] and $(s,t)$ -mincut ( $|S|=2$ ) [2].

To complement our results in Theorem 5, we provide the following lower bound for any dual edge Sensitivity Oracle. This makes data structures in Theorem 5 worst-case optimal almost for the whole range of $S$ (refer to Note 7).

Theorem 6 (Lower Bound).

Let $D$ be any data structure that can report the capacity of Steiner mincut after the insertion or failure of any pair of edges in undirected multi-graphs on $n$ vertices. For any given Steiner set $S$ , data structure $D$ must occupy $\Omega((n-|S|)^{2})$ bits of space in the worst case, irrespective of the query time.

For $S$ -mincuts, the only existing lower bound for dual edge Sensitivity Oracle is for $|S|=2$ by Baswana, Bhanja, and Pandey [2]. Moreover, it is conditioned on the Reachability Hypothesis [22, 30]. Our lower bound in Theorem 6 not only generalizes their result from $|S|=2$ to any $S\subseteq V$ , but it also does not depend on any hypothesis, hence, an unconditional lower bound.

$\blacktriangleright$ Note 7.

We present the following comparison between the upper and lower bounds.

$\blacksquare$

The upper bounds on space of Sensitivity Oracles in Theorem 5(1) and (2) match the lower bound in Theorem 6 except when $|S|$ is at least $n-o(\sqrt{n})$ and $n-o(n)$ , respectively.
$\blacksquare$

Sensitivity Oracles in Theorem 5(1) and (2) occupy space only linear in $n$ and subquadratic in $n$ when $|S|$ is at least $n-o(\sqrt{n})$ and $n-o(n)$ , respectively.

All the results of this article are compactly presented in Table 1.

Table 1: A comparison of our results with the existing results of extreme Scenarios of Steiner cut: global cut [14] and

(s,t)

-cut [2]. Sensitivity Oracles are for handling insertion or failure of up to a pair of edges. Also, we note that the result in [2] holds for directed multi-graphs.

Results	Data Structure for	Query	Sensitivity Oracle	Sensitivity Oracle
	Minimum+1 Cut (space)	cut (time)	for Reporting Capacity	for Reporting Cut
Global Cut [14]			space: ${\mathcal{O}}(n)$	space: ${\mathcal{O}}(n)$
( $\|S\|=n$ )	${\mathcal{O}}(n)$	${\mathcal{O}}(n)$	time: ${\mathcal{O}}(1)$	time: ${\mathcal{O}}(n)$
$(s,t)$ -cut [2]			space: ${\mathcal{O}}(n^{2})$	space: ${\mathcal{O}}(n^{2})$
( $\|S\|=2$ )	${\mathcal{O}}(n^{2})$	${\mathcal{O}}(n)$	time: ${\mathcal{O}}(1)$	time: ${\mathcal{O}}(n)$
Steiner Cuts			space: $\mathbf{{\mathcal{O}}((n-\|S\|)^{2}+n)}$	space: $\mathbf{{\mathcal{O}}(n(n-\|S\|+1))}$
( $2\leq\|S\|\leq n$ )	$\mathbf{{\mathcal{O}}(n(n-\|S\|+1))}$	$\mathbf{{\mathcal{O}}(n)}$	time: $\mathbf{{\mathcal{O}}(1)}$	time: $\mathbf{{\mathcal{O}}(n)}$

1.2 Organization of this article

This article is organized as follows. Section 2 contains basic preliminaries. The generalization of 3-Star-Lemma is established in Section 3. The overview of our data structure for $(\lambda_{S}+1)$ cuts is in Section 4. It is followed by an overview of the dual edge Sensitivity Oracle in Section 5. Section 6 contains the overview of our lower bound for dual edge Sensitivity Oracle. Finally, we conclude in Section 7. All the omitted proofs are provided in the full version [6].

2 Preliminaries

In this section, we define a set of notations and basic properties of cuts.

$\blacksquare$

A vertex $u$ is a Steiner vertex if $u\in S$ ; otherwise $u$ is a nonSteiner vertex.
$\blacksquare$

$G\setminus e$ denotes the graph obtained from $G$ after the removal of edge $e$ . Also, for any cut $C$ in $G\setminus e$ , without causing any ambiguity, we denote the capacity of $C$ by $c(C)$ .
$\blacksquare$

A cut $C$ is said to subdivide a set $X\subseteq V$ if both $C\cap X$ and $\overline{C}\cap X$ are nonempty.
$\blacksquare$

It follows from the definition of capacity of cuts that capacity of an empty set is zero.

Lemma 8 (Sub-modularity of cuts (Problem 48(a,b) in [28])).

For any two sets $A,B\subset V$ ,
$(1)$ $c(A)+c(B)\geq c(A\cap B)+c(A\cup B)$ and $(2)$ $c(A)+c(B)\geq c(A\setminus B)+c(B\setminus A)$ .

Dinitz and Vainshtein [15, 16, 17] defined the following concept of $(\lambda_{S}+1)$ -connectivity class, which is also referred to as a $(\lambda_{S}+1)$ $(s,t)$ -class for $S=\{s,t\}$ in [2].

Definition 9.

Let $R$ be an equivalence relation defined on the vertex set of $G$ as follows. A pair of vertices $u$ and $v$ are related by $R$ if and only if $u$ and $v$ are not separated by any $S$ -mincut. Every equivalence class of relation $R$ is called a $(\lambda_{S}+1)$ -connectivity class.

For brevity we denote a $(\lambda_{S}+1)$ -connectivity class by $(\lambda_{S}+1)$ class henceforth. A $(\lambda_{S}+1)$ class ${\mathcal{W}}$ is said to be a Singleton $(\lambda_{S}+1)$ class if ${\mathcal{W}}$ has exactly one Steiner vertex of $G$ .

Let us define the following notion of crossing cuts initially introduced by Dinitz, Karzanov, and Lomonosov [12], and the concept of nearest $(\lambda_{S}+1)$ cuts of a vertex.

Definition 10 (Crossing cuts and Corner sets).

For a pair of cuts $A, B$ in $G$ , each of the four sets, $A\cap B$ , $A\setminus B$ , $B\setminus A$ , and $\overline{A\cup B}$ , is called a corner set of $A$ and $B$ . Cuts $A$ and $B$ are said to be crossing if each corner set is nonempty.

Definition 11 (Nearest $(\lambda_{S}+1)$ cut of a vertex).

For a vertex $u$ , a $(\lambda_{S}+1)$ cut $C$ is said to be a nearest $(\lambda_{S}+1)$ cut of $u$ if $u\in C$ and there is no $(\lambda_{S}+1)$ cut $C^{\prime}$ such that $u\in C^{\prime}$ and $C^{\prime}\subset C$ . We denote the set of all nearest $(\lambda_{S}+1)$ cut of vertex $u$ by $N_{S}(u)$ .

The nearest $(\lambda_{S}+1)$ cut from a vertex $u$ to a vertex $v$ is defined as a nearest $(\lambda_{S}+1)$ cut $C$ of $u$ such that $u\in C$ and $v\in\overline{C}$ .

3 A Generalization of 3-Star Lemma

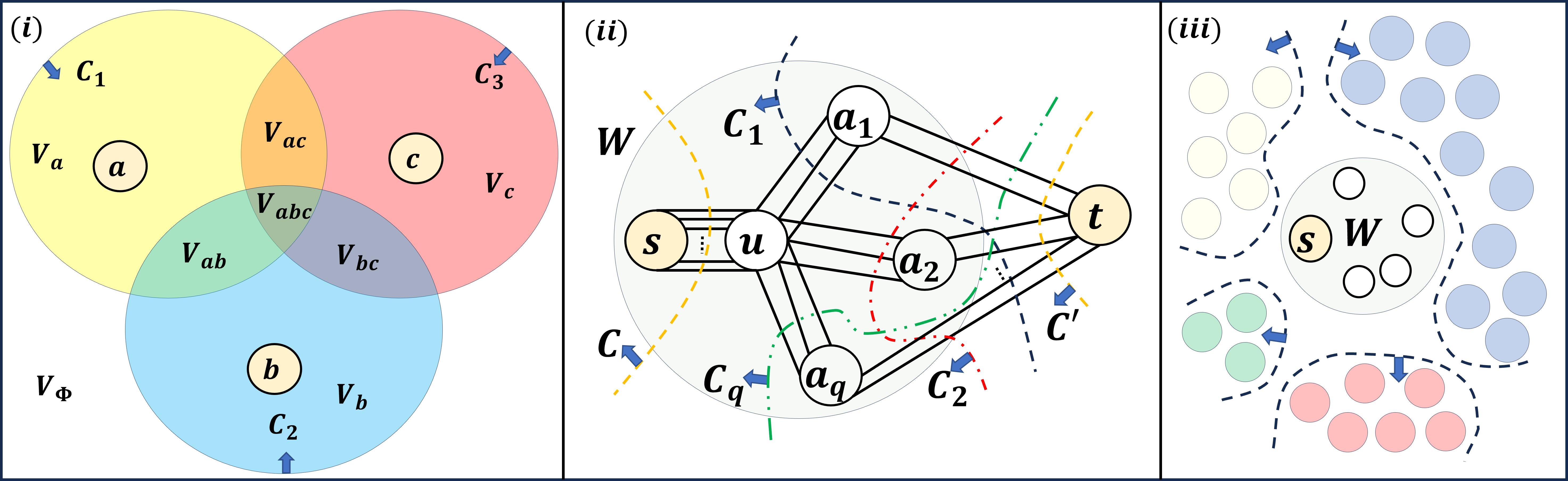
Let $C_{1},C_{2},$ and $C_{3}$ be three Steiner cuts of $G$ . Each of the three sets $C_{1}\cap\overline{C_{2}}\cap\overline{C_{3}}$ , $\overline{C_{1}}\cap C_{2}\cap\overline{C_{3}}$ , $\overline{C_{1}}\cap\overline{C_{2}}\cap C_{3}$ is called a star cut. For a pair of crossing $S$ -mincuts, at least two of the four corner sets are also $S$ -mincuts. Dinitz and Vainshtein [15, 16, 17], exploiting this property of $S$ -mincuts, established the following result for the set of $S$ -mincuts.
3-Star Lemma [15, 16, 17]: For any three $S$ -mincuts $C_{1},C_{2}$ , and $C_{3}$ , if each of the star cuts formed by $C_{1},C_{2}$ , and $C_{3}$ contains a vertex from $S$ , then $c(C_{1}\cap C_{2}\cap C_{3})=0$ .
3-Star Lemma turned out to be an essential tool for designing the Connectivity Carcass [15, 16, 17] for $S$ -mincuts. Unfortunately, for a pair of crossing $(\lambda_{S}+1)$ cuts, it is quite possible that none of the four corner sets is a $(\lambda_{S}+1)$ cut (refer to cuts $C_{1}$ and $C_{2}$ in Figure 1( $i i$ )). As a result, 3-Star Lemma no longer holds for the set of $(\lambda_{S}+1)$ cuts. Interestingly, to design a tool for addressing $(\lambda_{S}+1)$ cuts, exploiting the relation between a $(\lambda_{S}+1)$ class and $(\lambda_{S}+1)$ cuts, we generalize the 3-Star Lemma for $(\lambda_{S}+1)$ cuts as follows.

We begin by stating the following lemma, which can be seen as a generalization of the sub-modularity of cuts (Lemma 8) property.

Lemma 12 (Four Component Lemma (Problem 48(c) in [28])).

For any three sets $A,B,C\subset V$ , $c(A)+c(B)+c(C)\geq c(A\cap B\cap C)+c(\overline{A}\cap\overline{B}\cap C)+c(% \overline{A}\cap B\cap\overline{C})+c(A\cap\overline{B}\cap\overline{C})$ .

Let $C_{1},C_{2},$ and $C_{3}$ be any three $(\lambda_{S}+1)$ cuts of $G$ (refer to Figure 1( $i$ )). These three cuts define the following eight disjoint subsets of $V$ : $V_{a}=C_{1}\cap\overline{C_{2}}\cap\overline{C_{3}}$ , $V_{b}=\overline{C_{1}}\cap C_{2}\cap\overline{C_{3}}$ , $V_{c}=\overline{C_{1}}\cap\overline{C_{2}}\cap C_{3}$ , $V_{ab}=C_{1}\cap C_{2}\cap\overline{C_{3}}$ , $V_{bc}=\overline{C_{1}}\cap C_{2}\cap C_{3}$ , $V_{ac}=C_{1}\cap\overline{C_{2}}\cap C_{3}$ , $V_{abc}=C_{1}\cap C_{2}\cap C_{3}$ , and $V_{\Phi}=\overline{C_{1}\cup C_{2}\cup C_{3}}$ .

Refer to caption — Figure 1: ( $i$ ) Depicting all the eight regions formed by three $(\lambda_{S}+1)$ cuts $C_{1},C_{2},$ and $C_{3}$ of $G$ . ( $i i$ ) Let $q=\Omega(|{\mathcal{W}}|)$ . The capacity of global mincut of this graph is at least $4$ for $q\geq 2$ . $C$ and $C^{\prime}$ are Steiner cuts of capacity $2q+1$ and $2q$ respectively. The capacity of S-mincut is $2q$ . Each cut $C_{i}$ , $1\leq i\leq q$ , has capacity $2q+1$ ; and moreover, $C_{i}$ has $t$ in $\overline{C_{i}}$ . $(iii)$ Construction of $G({\mathcal{W}})$ from $G^{\prime}$ . The vertices not belonging to ${\mathcal{W}}$ having same color are contracted into a Steiner vertex in $G({\mathcal{W}})$ .

Theorem 13 (Gen-3-Star Lemma).

Suppose there are three Steiner vertices $a, b, c$ such that $a\in V_{a}$ , $b\in V_{b}$ , and $c\in V_{c}$ . Then, the following three properties hold.

1.

$c(C_{1}\cap C_{2}\cap C_{3})\leq 3$ .
2.

For a $(\lambda_{S}+1)$ class ${\mathcal{W}}$ and an integer $k\in[0,3]$ , if $(i)$ $V_{\Phi}\cap{\mathcal{W}}\neq\emptyset$ and $(ii)$ exactly $k$ of the three sets $V_{a},V_{b},$ and $V_{c}$ contains a vertex from ${\mathcal{W}}$ , then $c(C_{1}\cap C_{2}\cap C_{3})\leq 3-k$ .
3.

Let $x,y,z\in\{a,b,c\}$ and $x\neq y\neq z$ . Vertices of $V_{xy}$ are adjacent to vertices of $V_{xy},V_{x}$ and $V_{y}$ . Moreover, there are at most two edges between $V_{xy}$ and $V\setminus(V_{x}\cup V_{y}\cup V_{xy})=V_{z}\cup V_{xz}\cup V_{yz}\cup V_{xyz}% \cup V_{\Phi}$ .

Proof.

Each of the three sets $V_{a}$ , $V_{b}$ , and $V_{c}$ contains a Steiner vertex. Moreover, observe that $V_{a}$ , $V_{b}$ , and $V_{c}$ are disjoint sets. Therefore, each of the three sets $V_{a},V_{b}$ , and $V_{c}$ defines a Steiner cut. This implies that each cut of the three cuts $V_{a}$ , $V_{b}$ , and $V_{c}$ has capacity at least $\lambda_{S}$ . For cuts $C_{1},C_{2},$ and $C_{3}$ , the following equation follows from Lemma 12,

c(C_{1})+c(C_{2})+c(C_{3})\geq c(C_{1}\cap C_{2}\cap C_{3})+c(V_{a})+c(V_{b})+% c(V_{c})

(1)

Since $c(C_{i})=\lambda_{S}+1$ for each $i\in\{1,2,3\}$ , it follows from Equation 1 that $c(C_{1}\cap C_{2}\cap C_{3})\leq 3$ . This completes the proof of property (1).

Suppose, without loss of generality, cut $V_{a}$ contains a vertex from ${\mathcal{W}}$ . It is given that there is a vertex $u\in V_{\Phi}\cap{\mathcal{W}}$ . Therefore, $V_{a}$ is a Steiner cut that subdivides the $(\lambda_{S}+1)$ class ${\mathcal{W}}$ . Hence, $c(V_{a})\geq\lambda_{S}+1$ by Definition 9. So, any $k\geq 0$ sets of the three sets, $V_{a}$ , $V_{b}$ , and $V_{c}$ , containing a vertex from ${\mathcal{W}}$ has a capacity at least $\lambda_{S}+1$ . This, using Equation 1, implies that $c(C_{1}\cap C_{2}\cap C_{3})\leq 3-k$ . This completes the proof of property (2). The proof of property (3) is in the full version [6]. $\hfill\blacktriangleleft$ Gen-3-Star Lemma (Theorem 13) is used crucially throughout this article for establishing several structural results for $(\lambda_{S}+1)$ cuts. We now establish the following lemma as a corollary of Theorem 13(2).

Lemma 14.

For any three $(\lambda_{S}+1)$ cuts $C_{1},C_{2},$ and $C_{3}$ , if each of the three sets $V_{a},V_{b},$ and $V_{c}$ contains a Steiner vertex and a vertex from the same $(\lambda_{S}+1)$ class ${\mathcal{W}}$ of $G$ , then $C_{1}\cap C_{2}\cap C_{3}=\emptyset$ .

Proof.

Each of the three sets $\{V_{a},V_{b},V_{c}\}$ contains a Steiner vertex and a vertex from ${\mathcal{W}}$ . Since $V_{a},V_{b},$ and $V_{c}$ are disjoint sets, therefore, each of them defines a Steiner cut and subdivides ${\mathcal{W}}$ . Therefore, observe that for these three Steiner cuts $C_{1},C_{2},C_{3}$ , Theorem 13(2) holds even if $C_{1},C_{2},C_{3}$ do not satisfy condition $(i)$ of Theorem 13(2) (there is no vertex $u\in V_{\Phi}\cap{\mathcal{W}}$ ). Now, by assigning the value of $k=3$ in Theorem 13(2), we get $c(C_{1}\cap C_{2}\cap C_{3})=0$ . Since graph $G$ is connected, therefore, $C_{1}\cap C_{2}\cap C_{3}$ is an empty set. $\hfill\blacktriangleleft$

4 A Data Structure for Reporting Minimum+1 Steiner Cuts

We first discuss the limitations of the existing results for the extreme scenarios of Steiner cuts. It is followed by an overview of our data structure for minimum+1 Steiner cuts.

Limitations of existing results.

For any pair of crossing global cuts $A, B$ of capacity $\lambda_{V}+1$ , each of the four corner sets must have capacity at least $\lambda_{V}$ because it is also a global cut. For $\lambda_{V}\geq 3$ , using this insight, Dinitz and Nutov [14] designed the ${\mathcal{O}}(n)$ space $2$ -level cactus model as a data structure for all global cuts of capacity $\lambda_{V}+1$ . Unfortunately, this property no longer holds for $(\lambda_{S}+1)$ cuts because a corner set for a pair of crossing $(\lambda_{S}+1)$ cuts is not necessarily a Steiner cut; hence, a corner set can have capacity strictly less than $\lambda_{S}$ . As a result, it does not seem possible to extend the approach of Dinitz and Nutov [14] for designing a data structure for $(\lambda_{S}+1)$ cuts. On the other hand, for $S=\{s,t\}$ , since there are exactly two Steiner vertices, the intersection, as well as union, of a pair of $(\lambda_{\{s,t\}}+1)$ $(s,t)$ -cut is always an $(s,t)$ -cut, and has capacity at least $\lambda_{\{s,t\}}$ . Baswana, Bhanja, and Pandey [2] crucially exploit this fact and present the following result. For any $(\lambda_{\{s,t\}}+1)$ class ${\mathcal{W}}$ of $G$ , there is an ${\mathcal{O}}(|{\mathcal{W}}|^{2}+n)$ space data structure that answers query cut for any pair of vertices in ${\mathcal{W}}$ in ${\mathcal{O}}(n)$ time. For any Steiner set $S\subseteq V$ , storing their data structure for every pair of vertices in $S$ results in an ${\mathcal{O}}(n^{2}|S|^{2})$ space data structure, which can be $\Omega(n^{4})$ for any $S$ satisfying $|S|=\Omega(n)$ .

Our approach.

We now present the overview of our data structure in Theorem 4 that occupies only ${\mathcal{O}}(n(n-|S|+1))$ space and answers query cut for $(\lambda_{S}+1)$ cuts in ${\mathcal{O}}(n)$ time. Let $u$ and $v$ be any pair of vertices. By Definition 9, the cut of the least capacity that separates $u, v$ is $\lambda_{S}+1$ only if $u, v$ belong to the same $(\lambda_{S}+1)$ class of $G$ . Henceforth, to design a compact data structure for efficiently answering query cut for $(\lambda_{S}+1)$ cuts, we consider $(\lambda_{S}+1)$ classes of $G$ . It turns out that the main challenge arises in handling the Singleton $(\lambda_{S}+1)$ classes of $G$ . We first present a data structure for a Singleton $(\lambda_{S}+1)$ class. Later, to arrive at a compact data structure for any general $(\lambda_{S}+1)$ class (containing multiple or no vertex from $S$ ), we show that the Connectivity Carcass [15, 16, 17] can be suitably augmented with the data structure for Singleton $(\lambda_{S}+1)$ class. The procedure of augmentation requires establishing several new insights on $S$ -mincuts, revealing close relationships between $S$ -mincuts and $(\lambda_{S}+1)$ cuts, and extending the recent covering technique of [2] given for $(s,t)$ -cuts to Steiner cuts.

4.1 A Data Structure for a Singleton $(\lambda_{S}+1)$ class

Suppose ${\mathcal{W}}$ is a Singleton $(\lambda_{S}+1)$ class and $s$ is the only Steiner vertex belonging to ${\mathcal{W}}$ . For any cut $C$ , we assume that $s\in C$ ; otherwise, consider $\overline{C}$ . Let $C$ be a $(\lambda_{S}+1)$ cut that subdivides ${\mathcal{W}}$ . Cut $C$ can cross multiple $S$ -mincuts of $G$ and also contains vertices of $G$ that do not belong to ${\mathcal{W}}$ . This makes it harder to analyze all the $(\lambda_{S}+1)$ cuts that subdivide ${\mathcal{W}}$ . To circumvent this difficulty, we construct a smaller graph $G({\mathcal{W}})$ from $G$ as follows. We first contract every $(\lambda_{S}+1)$ class, except ${\mathcal{W}}$ , into a vertex. Let $G^{\prime}$ be the obtained graph. We construct graph $G({\mathcal{W}})$ from $G^{\prime}$ by constructing a sequence of graphs $\langle G_{1}=G^{\prime},G_{2},\ldots,G_{i}=G({\mathcal{W}})\rangle$ as follows. For any $1<j<i$ , graph $G_{j+1}$ is obtained from $G_{j}$ by contracting a pair of vertices $u, v$ if there is a Steiner mincut $C$ in $G_{j}$ such that ${\mathcal{W}}\subseteq C$ and $u,v\in\overline{C}$ . The final obtained graph is $G({\mathcal{W}})$ (refer to Figure 1 $(iii)$ ). All vertices of $G({\mathcal{W}})$ that do not belong to ${\mathcal{W}}$ , along with $s$ , define the Steiner set of $G({\mathcal{W}})$ , denoted by $S({\mathcal{W}})$ . We show that in $G({\mathcal{W}})$ , $\lambda_{S}$ is the capacity of Steiner mincut, and every Steiner mincut separates exactly one Steiner vertex from $s$ . It turns out that no $(\lambda_{S}+1)$ cut can cross a Steiner mincut in graph $G({\mathcal{W}})$ . By construction, $(\lambda_{S}+1)$ class ${\mathcal{W}}$ of $G$ also appears as a $(\lambda_{S}+1)$ class in $G({\mathcal{W}})$ . Importantly, we show that graph $G({\mathcal{W}})$ satisfies the following property.

Lemma 15.

A $(\lambda_{S}+1)$ cut subdivides ${\mathcal{W}}$ into $({\mathcal{W}}_{1}\subset{\mathcal{W}},{\mathcal{W}}\setminus{\mathcal{W}}_{1})$ in $G$ if and only if there exists a $(\lambda_{S}+1)$ cut that subdivides ${\mathcal{W}}$ into $({\mathcal{W}}_{1},{\mathcal{W}}\setminus{\mathcal{W}}_{1})$ in $G({\mathcal{W}})$ .

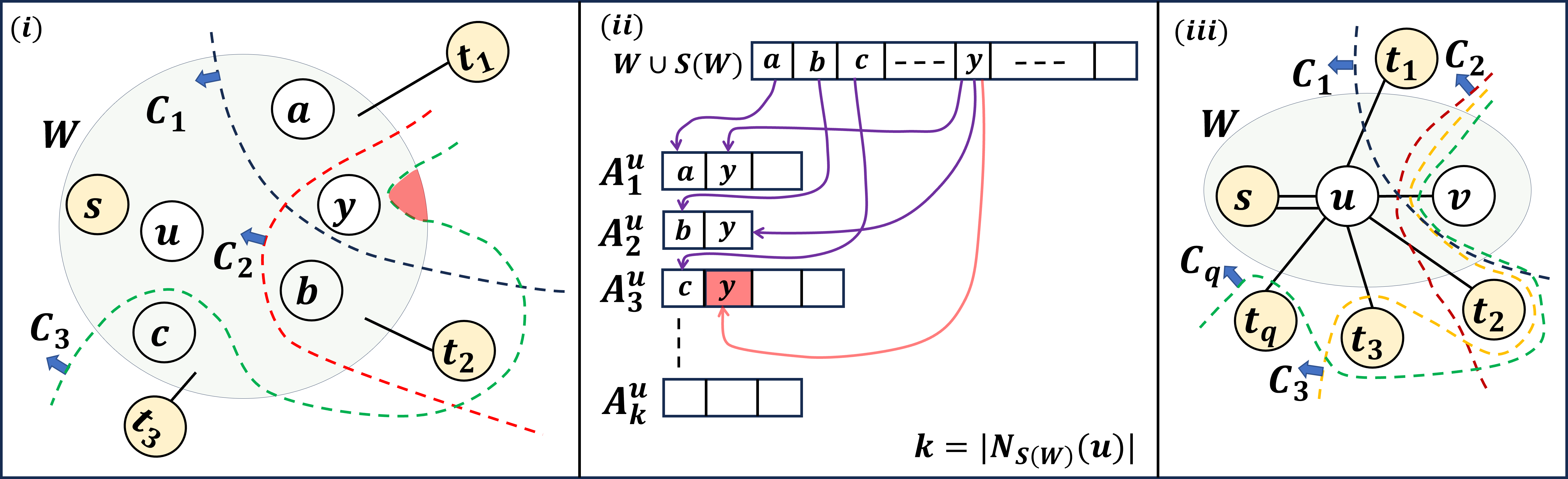
Henceforth, by Lemma 15, we work on graph $G({\mathcal{W}})$ instead of $G$ . To design a compact data structure for answering query cut for $(\lambda_{S}+1)$ cuts of $G({\mathcal{W}})$ , we pursue an approach of compactly storing all the nearest $(\lambda_{S}+1)$ cuts of vertices in ${\mathcal{W}}$ . This approach has been found to be quite useful for $S=\{s,t\}$ [2]. Let $u$ be a vertex in ${\mathcal{W}}$ . Unlike for $|S|=2$ [2], it turns out that the nearest $(\lambda_{S}+1)$ cut of $u$ to even a single vertex in ${\mathcal{W}}$ might not be unique. This is because the union of a pair of nearest $(\lambda_{S}+1)$ cuts of $u$ is not necessarily a Steiner cut (for example, cuts $C_{1},C_{2}$ in Figure 2 $(iii)$ ). To achieve our goal, we first establish the following property for $N_{S({\mathcal{W}})}(u)$ .

Lemma 16.

If the union of a pair of cuts $C_{1},C_{2}\in N_{S({\mathcal{W}})}(u)$ is a Steiner cut, then no vertex of ${\mathcal{W}}$ can belong to ${\overline{C_{1}\cup C_{2}}}$ .

For $S=\{s,t\}$ , the union of a pair of nearest $(\lambda_{S}+1)$ cuts is always a Steiner cut. Hence, every pair of nearest $(\lambda_{S}+1)$ cut satisfies the property in Lemma 16. This insight was used crucially for designing the compact data structure for minimum+1 $(s,t)$ -cuts [2]. However, as mentioned above, for any $S$ , $2<|S|\leq n$ , for any pair of cuts from $N_{S({\mathcal{W}})}(u)$ , their union might not be a Steiner cut. In fact, there can be $\Omega(|S({\mathcal{W}})|)$ number of cuts from $N_{S({\mathcal{W}})}(u)$ such that the complement of their union can contain a subset of vertices from ${\mathcal{W}}$ , which can be $\Omega(n)$ in the worst case (refer to Figure 2 $(iii)$ ). To overcome this difficulty, we address the problem in two different scenarios – firstly, when $\lambda({\mathcal{W}})\geq 4$ , and secondly, when $\lambda({\mathcal{W}})\leq 3$ , where $\lambda({\mathcal{W}})$ is the global mincut capacity of $G({\mathcal{W}})$ .

Suppose graph $G({\mathcal{W}})$ has global mincut capacity at least $4$ . Exploiting Gen-3-Star Lemma (Theorem 13) and Lemma 16, we present the following extension of the property stated in Lemma 16 for cuts from $N_{S({\mathcal{W}})}(u)$ even when their union is not a Steiner cut.

Lemma 17.

If the capacity of global mincut of $G({\mathcal{W}})$ is at least $4$ , then for any three cuts $C_{1},C_{2},C_{3}$ from $N_{S({\mathcal{W}})}(u)$ , no vertex of ${\mathcal{W}}$ can belong to $\overline{C_{1}\cup C_{2}\cup C_{3}}$ .

Proof.

Assume that for cuts $C_{1},C_{2}$ , and $C_{3}$ , the set $\overline{C_{1}}\cap\overline{C_{2}}\cap\overline{C_{3}}\cap{\mathcal{W}}$ is nonempty (refer to Figure 2 $(i)$ ). So, for any pair of cuts $C_{i},C_{j}$ , $1\leq i\neq j\leq 3$ , $\overline{C_{i}}\cap\overline{C_{j}}$ contains at least one vertex from ${\mathcal{W}}$ . By Lemma 16, there cannot exist any Steiner vertex $t\neq s$ such that $t\in\overline{C_{i}}\cap\overline{C_{j}}$ . Note that $C_{1},C_{2},$ and $C_{3}$ are Steiner cuts. This implies that each of the three sets $\overline{C_{1}}\cap C_{2}\cap C_{3}$ , $C_{1}\cap\overline{C_{2}}\cap C_{3}$ , and $C_{1}\cap C_{2}\cap\overline{C_{3}}$ must contain at least one Steiner vertex. So, each of the three sets $\overline{C_{1}}\cap C_{2}\cap C_{3}$ , $C_{1}\cap\overline{C_{2}}\cap C_{3}$ , and $C_{1}\cap C_{2}\cap\overline{C_{3}}$ defines a Steiner cut. Therefore, for three cuts $\overline{C_{1}},\overline{C_{2}},$ and $\overline{C_{3}}$ , by Theorem 13(1), we have $c(\overline{C_{1}}\cap\overline{C_{2}}\cap\overline{C_{3}})\leq 3$ , a contradiction because the capacity of global mincut in $G({\mathcal{W}})$ is at least $4$ . $\hfill\blacktriangleleft$ Lemma 17 essentially states that, for any vertex $u$ of ${\mathcal{W}}$ , there are at most two cuts $C_{1},C_{2}$ from $N_{S({\mathcal{W}})}(u)$ such that $u$ belongs to $\overline{C_{1}\cup C_{2}}$ . This shows that only ${\mathcal{O}}(|{\mathcal{W}}|)$ space is sufficient to store $\overline{C}\cap{\mathcal{W}}$ for all $C\in N_{S({\mathcal{W}})}(u)$ . Unfortunately, the problem still remains in compactly storing Steiner vertices $\overline{C}\cap S({\mathcal{W}})$ for all $C\in N_{S({\mathcal{W}})}(u)$ . Unlike the vertices from ${\mathcal{W}}$ , a Steiner vertex can appear in the complement of multiple cuts from $N_{S({\mathcal{W}})}(u)$ even if the global mincut capacity is at least $4$ (refer to Figure 1 $(ii)$ ). Therefore, storing all cuts from $N_{S({\mathcal{W}})}(u)$ would occupy ${\mathcal{O}}(|{\mathcal{W}}||S({\mathcal{W}})|)$ space. Interestingly, we now show, in two phases, that ${\mathcal{O}}(|{\mathcal{W}}|+|S({\mathcal{W}})|)$ space is sufficient to store all the cuts from $N_{S({\mathcal{W}})}(u)$ . We begin our analysis by classifying the set of all cuts from $N_{S({\mathcal{W}})}(u)$ into two sets as follows.

A classification of all cuts from $N_{S({\mathcal{W}})}(u)$ .

A cut $C\in N_{S({\mathcal{W}})}(u)$ is said to be a $l$ -cut if it has exactly one Steiner vertex in $\overline{C}$ ; otherwise, it is called a $m$ -cut.
It follows that storing $\overline{C}$ for every $l$ -cut $C$ from $N_{S({\mathcal{W}})}(u)$ occupies ${\mathcal{O}}(|{\mathcal{W}}|+|S({\mathcal{W}})|)$ space. However, the challenge arises in storing all $m$ -cuts compactly. It seems quite possible that there are many Steiner vertices that belong to the complement of multiple $m$ -cuts from $N_{S({\mathcal{W}})}(u)$ . In the first phase, exploiting the structural properties of $G({\mathcal{W}})$ , we establish the following lemma for a pair of cuts from $N_{S({\mathcal{W}})}(u)$ , which holds for pair of $m$ -cuts as well.

Lemma 18.

For any pair of cuts $C_{1},C_{2}\in N_{S({\mathcal{W}})}(u)$ , there cannot exist more than one Steiner vertex in $\overline{C_{1}\cup C_{2}}$ .

Proof.

Suppose there is a pair of Steiner vertices $t_{1},t_{2}$ such that $t_{1},t_{2}\in\overline{C_{1}}\cap\overline{C_{2}}$ . Since $s$ belongs to both $C_{1}$ and $C_{2}$ , so, both $C_{1}\cap C_{2}$ and $C_{1}\cup C_{2}$ are Steiner cuts. This implies that $c(C_{1}\cap C_{2})$ , as well as $c(C_{1}\cup C_{2})$ , is at least $\lambda_{S}$ . Since $C_{1},C_{2}\in N_{S({\mathcal{W}})}(u)$ , by Definition 11, $C_{1}$ and $C_{2}$ cannot be subsets of each other. So, we have $u\in C_{1}\cap C_{2}$ and $C_{1}\cap C_{2}$ is a proper subset of both $C_{1}$ and $C_{2}$ . It follows that $c(C_{1}\cap C_{2})\geq\lambda_{S}+2$ . By applying sub-modularity of cuts (Lemma 8(1)) on $C_{1},C_{2}$ , we arrive at $c(C_{1}\cap C_{2})+c(C_{1}\cup C_{2})\leq 2\lambda_{S}+2$ . This implies that $c(C_{1}\cup C_{2})=\lambda_{S}$ , a contradiction because, by construction of $G({\mathcal{W}})$ , there is no $S$ -mincut $C$ such that $s\in C$ and $t_{1},t_{2}\in\overline{C}$ or vice versa. $\hfill\blacktriangleleft$ To exploit the insight stated in Lemma 18, we design a bipartite graph $B$ using the set of $m$ -cuts and the nonSteiner vertices belonging to ${\mathcal{W}}$ . Exploiting the structure of $B$ and the well-known girth conjecture by [20] and [8], we show that Lemma 18 can ensure an ${\mathcal{O}}(|{\mathcal{W}}|\sqrt{|S({\mathcal{W}})|})$ bound on space for storing all $m$ -cuts.

To achieve a stricter bound on space, in the second phase, we further explore the relation of Steiner vertices with at least three $m$ -cuts from $N_{S({\mathcal{W}})}(u)$ . Interestingly, by exploiting Lemma 16, Lemma 18, Gen-3-Star Lemma, and the definition of $m$ -cuts, we are able to establish the following crucial result for $m$ -cuts, which acts as the key tool for storing all $m$ -cuts compactly.

Lemma 19.

For any three $m$ -cuts $C_{1},C_{2},$ and $C_{3}$ from $N_{S({\mathcal{W}})}(u)$ , there cannot exist any Steiner vertex $t$ in $S({\mathcal{W}})$ such that $t$ belongs to $\overline{C_{1}\cup C_{2}\cup C_{3}}$ .

Proof.

Suppose there exist three $m$ -cuts $C_{1},C_{2}$ , and $C_{3}$ such that $t\in\overline{C_{1}}\cap\overline{C_{2}}\cap\overline{C_{3}}$ . By definition, for every $m$ -cut $C\in\{C_{1},C_{2},C_{3}\}$ , there are at least two Steiner vertices $t_{1},t_{2}$ such that $t_{1},t_{2}\in\overline{C}$ . For any pair of integers $i,j\in\{1,2,3\}$ and $i\neq j$ , by Lemma 18, there cannot exist more than one Steiner vertex in $\overline{C_{i}}\cap\overline{C_{j}}$ . Therefore, for the three cuts, $C_{1},C_{2},C_{3}$ , there must exist at least three Steiner vertices $t_{1},t_{2},t_{3}$ such that $t_{1}\in\overline{C_{1}}\cap C_{2}\cap C_{3}$ , $t_{2}\in C_{1}\cap\overline{C_{2}}\cap C_{3}$ , and $t_{3}\in C_{1}\cap C_{2}\cap\overline{C_{3}}$ . Now, since $C_{1},C_{2},C_{3}$ are nearest cuts of $u$ that subdivide ${\mathcal{W}}$ , there must exist vertices $v_{1},v_{2},v_{3}\in{\mathcal{W}}$ such that $v_{1}\in\overline{C_{1}}$ , $v_{2}\in\overline{C_{2}}$ , and $v_{3}\in\overline{C_{3}}$ . It is also assumed that $t\in\overline{C_{1}}\cap\overline{C_{2}}\cap\overline{C_{3}}$ . So, for any pair of integers $i,j\in\{1,2,3\}$ and $i\neq j$ , by Lemma 16, there cannot be any vertex from ${\mathcal{W}}$ in $\overline{C_{i}}\cap\overline{C_{j}}$ . This implies that $v_{1}\in\overline{C_{1}}\cap C_{2}\cap C_{3}$ , $v_{2}\in C_{1}\cap\overline{C_{2}}\cap C_{3}$ and $v_{3}\in C_{1}\cap C_{2}\cap\overline{C_{3}}$ . So, we have ensured that each of the three cuts $\overline{C_{1}}\cap C_{2}\cap C_{3}$ , $C_{1}\cap\overline{C_{2}}\cap C_{3}$ , and $C_{1}\cap C_{2}\cap\overline{C_{3}}$ contains at least one Steiner vertex of $G({\mathcal{W}})$ and at least one vertex from the same class ${\mathcal{W}}$ . Therefore, for three cuts $\overline{C_{1}},\overline{C_{2}},$ and $\overline{C_{3}}$ , it follows from Lemma 14 that $\overline{C_{1}}\cap\overline{C_{2}}\cap\overline{C_{2}}=\emptyset$ , a contradiction. $\hfill\blacktriangleleft$ This result for $m$ -cuts ensures that every Steiner vertex of $S({\mathcal{W}})$ appears in $\overline{C_{1}\cup C_{2}}$ for at most two $m$ -cuts $C_{1},C_{2}\in N_{S({\mathcal{W}})}(u)$ . Therefore, it leads to a data structure occupying ${\mathcal{O}}(|{\mathcal{W}}|+|S({\mathcal{W}})|)$ space for answering query cut for all cuts in $N_{S({\mathcal{W}})}(u)$ . The construction of the data structure is provided in Algorithm 1 (refer to Figure 2( $i i$ )).

Algorithm 1 Construction of the Data Structure for

N_{S({\mathcal{W}})}(u)

.

Extension to general graphs.

Let us now consider graph $G({\mathcal{W}})$ with global mincut capacity at most $3$ . For this case, using Gen-3-Star Lemma and Lemma 16, we establish the following insight.

Lemma 20.

For any three cuts $C_{0},C_{1},$ and $C_{2}$ from $N_{S({\mathcal{W}})}(u)$ , if $\overline{C_{0}}\cap\overline{C_{1}}\cap\overline{C_{2}}\cap{\mathcal{W}}\neq\emptyset$ , then there exists an $i\in\{0,1,2\}$ such that the star cut $\overline{C_{i}}\cap C_{(i+1)\%3}\cap C_{(i+2)\%3}\cap{\mathcal{W}}=\emptyset$ .

Exploiting Lemma 20, we can argue that, for every vertex in ${\mathcal{W}}$ , it is sufficient to store at most two cuts from $N_{S({\mathcal{W}})}(u)$ . The remaining construction and analysis (for Steiner vertices) are the same as that of the data structure in Algorithm 1, which is independent of the global mincut capacity. Therefore, ${\mathcal{O}}(|S({\mathcal{W}})|+|{\mathcal{W}}|)$ bound on space of our data structure holds for this scenario as well.

Finally, by storing this data structure on cuts from $N_{S({\mathcal{W}})}(u)$ for every $u\in{\mathcal{W}}$ , we obtain a data structure ${\mathcal{Q}}_{S}({\mathcal{W}})$ . This data structure occupies ${\mathcal{O}}(|{\mathcal{W}}|^{2}+|{\mathcal{W}}||S({\mathcal{W}})|)$ space and efficiently answers query cut for $(\lambda_{S}+1)$ cuts of $G({\mathcal{W}})$ . Moreover, by storing an ${\mathcal{O}}(n)$ space mapping of vertices of $G$ to $G({\mathcal{W}})$ , the data structure ${\mathcal{Q}}_{S}({\mathcal{W}})$ can report a cut $C$ in $G$ separating any given pair of vertices in ${\mathcal{W}}$ in ${\mathcal{O}}(n)$ time. The results of this section are summarized in the following theorem.

Theorem 21.

Let $G=(V,E)$ be an undirected multi-graph on $n$ vertices with a Steiner set $S\subseteq V$ . Let ${\mathcal{W}}$ be a $(\lambda_{S}+1)$ class of $G$ containing exactly one Steiner vertex $s$ and let $\overline{S({\mathcal{W}})}$ be the set of nonSteiner vertices of $G$ belonging to ${\mathcal{W}}$ . Let $\lambda$ be the capacity of global mincut of $G$ . For $(\lambda_{S}+1)$ class ${\mathcal{W}}$ , there is an ${\mathcal{O}}(|\overline{S({\mathcal{W}})}|^{2}+|S||\overline{S({\mathcal{W}})% }|)$ space data structure ${\mathcal{Q}}_{S}({\mathcal{W}})$ that,

1.

given vertices $u,v_{1},\ldots,v_{k}$ from ${\mathcal{W}}$ , can determine in ${\mathcal{O}}(k)$ time whether there exists a $(\lambda_{S}+1)$ cut $C$ such that $s,u\in C$ and $v_{1},\ldots,v_{k}\in\overline{C}$ if $\lambda\geq 4$ , and
2.

given vertices $u,v\in{\mathcal{W}}$ , can determine in ${\mathcal{O}}(1)$ time whether there exists a $(\lambda_{S}+1)$ cut $C$ such that $s,u\in C$ and $v\in\overline{C}$ if $\lambda\leq 3$ .

If $C$ exists, the data structure can report $\overline{C}\cap{\mathcal{W}}$ in ${\mathcal{O}}(|\overline{C}\cap{\mathcal{W}}|)$ time, and cut $C$ in ${\mathcal{O}}(n)$ time using an auxiliary ${\mathcal{O}}(n)$ space.

4.2 A Data Structure for General $(\lambda_{S}+1)$ classes

In graph $G$ , we show that storing our data structure ${\mathcal{Q}}_{S}({\mathcal{W}})$ from Theorem 21 for every Singleton $(\lambda_{S}+1)$ class ${\mathcal{W}}$ occupies overall ${\mathcal{O}}(n(n-|S|+1))$ space. However, a $(\lambda_{S}+1)$ class can also contain either no Steiner vertex or multiple Steiner vertices of $G$ . For a $(\lambda_{S}+1)$ class ${\mathcal{W}}$ containing no Steiner vertex, we develop an extension of the Covering technique of Baswana, Bhanja, and Pandey [2] to transform ${\mathcal{W}}$ into at most three Singleton $(\lambda_{S}+1)$ classes. We then construct the data structure ${\mathcal{Q}}_{S}$ for each of them.

Suppose $(\lambda_{S}+1)$ class ${\mathcal{W}}$ contains multiple Steiner vertices. A $(\lambda_{S}+1)$ cut of $G({\mathcal{W}})$ either subdivides the Steiner set belonging to ${\mathcal{W}}$ or it does not. Using this insight, we construct the following pair of graphs $G({\mathcal{W}})_{1}$ and $G({\mathcal{W}})_{2}$ from graph $G$ . Firstly, graph $G({\mathcal{W}})_{1}$ preserves each $(\lambda_{S}+1)$ cut of $G({\mathcal{W}})$ that does not subdivide the Steiner set belonging to ${\mathcal{W}}$ . We show that the data structure ${\mathcal{Q}}_{S}$ is sufficient for graph $G({\mathcal{W}})_{1}$ . Secondly, graph $G({\mathcal{W}})_{2}$ preserves the remaining $(\lambda_{S}+1)$ cuts of $G({\mathcal{W}})$ . We ensure that, for graph $G({\mathcal{W}})_{2}$ , the capacity of Steiner mincut is $\lambda_{S}+1$ . So, we use a data structure for Steiner mincut given by Baswana and Pandey [4], based on Connectivity Carcass, for answering query cut in ${\mathcal{O}}(n)$ time for $G({\mathcal{W}})_{2}$ . We also establish that the data structure for $G({\mathcal{W}})_{2}$ for all $(\lambda_{S}+1)$ classes ${\mathcal{W}}$ containing multiple Steiner vertices of $G$ occupies ${\mathcal{O}}(n)$ space. Therefore, given a pair of vertices $u, v$ in a $(\lambda_{S}+1)$ class ${\mathcal{W}}$ , if ${\mathcal{W}}$ contains multiple Steiner vertices, we query both the data structures – one for $G({\mathcal{W}})_{1}$ and the other for $G({\mathcal{W}})_{2}$ . The final obtained data structure of this section is summarized in Theorem 4.

5 Dual Edge Sensitivity Oracle For $𝑺$ -mincut

We begin by providing a brief overview of the ${\mathcal{O}}(n)$ space single edge Sensitivity Oracle for $S$ -mincut in undirected multi-graphs [4]. An edge is said to belong to a $(\lambda_{S}+1)$ class if both endpoints of the edge belong to the $(\lambda_{S}+1)$ class. By Definition 9, upon failure of an edge $e$ , the capacity of $S$ -mincut decreases by $1$ if and only if edge $e$ does not belong to any $(\lambda_{S}+1)$ class. Therefore, the ${\mathcal{O}}(n)$ space mapping of vertices to $(\lambda_{S}+1)$ classes helps in reporting the capacity of $S$ -mincut in ${\mathcal{O}}(1)$ time after the failure of any edge. Baswana and Pandey [4] established an ordering among the $(\lambda_{S}+1)$ classes of $G$ that do not contain any Steiner vertex. They showed that this ordering, along with the Connectivity Carcass of Dinitz and Vainshtein [15, 16, 17], is sufficient to design an ${\mathcal{O}}(n)$ space single edge Sensitivity Oracle for $S$ -mincut that can report an $S$ -mincut in ${\mathcal{O}}(n)$ time.

In the case of two edge failures, both failed edges can belong to the same $(\lambda_{S}+1)$ class ${\mathcal{W}}$ and contribute to a single $(\lambda_{S}+1)$ cut that subdivides ${\mathcal{W}}$ . In this case, the capacity of $S$ -mincut definitely reduces by $1$ . Unfortunately, the existing approach of designing a single edge Sensitivity Oracle does not reveal anything about the cuts that subdivide $(\lambda_{S}+1)$ classes. In the following, we present an overview of our dual edge Sensitivity Oracle from Theorem 5, which includes the establishment of several structural properties for $(\lambda_{S}+1)$ cuts and careful utilization of the data structure for Singleton $(\lambda_{S}+1)$ class (Theorem 21).

5.1 An $O(n(n-|S|+1))$ Space Data Structure with $O(|S|)$ Query Time

Let $e=(x,y)$ and $e^{\prime}=(x^{\prime},y^{\prime})$ be the pair of failed edges in $G$ . Depending on the relation between failed edges and $(\lambda_{S}+1)$ classes, the following four cases are possible.

$\blacksquare$

Case 1: both failed edges belong to the same $(\lambda_{S}+1)$ class.
$\blacksquare$

Case 2: both failed edges belong to two different $(\lambda_{S}+1)$ classes.
$\blacksquare$

Case 3: Exactly one of the two failed edges belongs to a $(\lambda_{S}+1)$ class.
$\blacksquare$

Case 4: None of the failed edges belong to any $(\lambda_{S}+1)$ class.

An ${\mathcal{O}}(n)$ space mapping of vertices to $(\lambda_{S}+1)$ classes is sufficient to determine in ${\mathcal{O}}(1)$ time which of the four cases has occurred after the failure of edges $e,e^{\prime}$ . We now handle each of these cases.

In Case 2, we show that the capacity of $S$ -mincut never decreases after the failure of the two edges. In Case 3, by Definition 9, the failure of the edge belonging to a $(\lambda_{S}+1)$ class cannot reduce the capacity of $S$ -mincut. Therefore, this case is equivalent to handling the failure of the single edge that does not belong to any $(\lambda_{S}+1)$ class. Case 4 requires a richer analysis compared to Case 2 and Case 3. To handle this case, we establish new insights for $S$ -mincuts, which help in showing that Connectivity Carcass [15, 16, 17] is sufficient to design a data structure for handling dual edge failures. So, for all these three cases, we construct an ${\mathcal{O}}((n-|S|)^{2}+n)$ space data structure that, after the failure of any pair of edges, can report an $S$ -mincut and its capacity in ${\mathcal{O}}(n)$ and ${\mathcal{O}}(1)$ time respectively. Now, the main hurdle comes in handling Case 1.

In Case 1, both failed edges $e,e^{\prime}$ belong to a $(\lambda_{S}+1)$ class ${\mathcal{W}}$ . In this case, the capacity of $S$ -mincut decreases by $1$ if and only if both failed edges are contributing to a single $(\lambda_{S}+1)$ cut that subdivides ${\mathcal{W}}$ . We consider ${\mathcal{W}}$ to be a Singleton $(\lambda_{S}+1)$ class. In a similar way to the data structure in Theorem 4, we also extend this result to any general $(\lambda_{S}+1)$ class.

Handling Dual Edge Failures in a Singleton $(\lambda_{S}+1)$ class

Let $s$ be the only Steiner vertex in ${\mathcal{W}}$ . For every cut $C$ , without loss of generality, assume that $s\in C$ ; otherwise, consider $\overline{C}$ . It follows from Lemma 15 it is sufficient to work with graph $G({\mathcal{W}})$ for ${\mathcal{W}}$ instead of $G$ . The objective is to efficiently determine the existence of a $(\lambda_{S}+1)$ cut $C$ of $G({\mathcal{W}})$ such that both failed edges $e$ and $e^{\prime}$ are contributing to $C$ . The data structure in Theorem 4 can determine in ${\mathcal{O}}(1)$ time whether each of the failed edges is contributing to a $(\lambda_{S}+1)$ cut. Unfortunately, it fails to determine whether both $e,e^{\prime}$ contribute to a single $(\lambda_{S}+1)$ cut. Suppose $(\lambda_{S}+1)$ cut $C$ exists and we assume, without loss of generality, that $x,x^{\prime}\in C$ and $y,y^{\prime}\in\overline{C}$ . The other three possible cases can be handled in the same way.

Let $C_{1}$ and $C_{2}$ be nearest $(\lambda_{S}+1)$ cuts from $x$ to $y$ and from $x^{\prime}$ to $y^{\prime}$ , respectively. The following lemma states the necessary condition.

Lemma 22.

If both edges $e,e^{\prime}$ contribute to a single $(\lambda_{S}+1)$ cut, then $y^{\prime}\notin C_{1}$ and $y\notin C_{2}$ .

If $e^{\prime}$ contributes to $C_{1}$ or $e$ contributes to $C_{2}$ then we are done. Henceforth we consider that $x\in C_{1}\setminus C_{2}$ and $x^{\prime}\in C_{2}\setminus C_{1}$ .

Let us assume that the capacity of global mincut for $G({\mathcal{W}})$ is at least $4$ ; later, we eliminate this assumption. The data structure in Theorem 4 can verify the necessary condition in Lemma 22 in ${\mathcal{O}}(1)$ time (refer to Theorem 21). Suppose the conditions in Lemma 22 holds for edges $e,e^{\prime}$ . Observe that $C_{1}\cap C_{2}$ is a cut that subdivides ${\mathcal{W}}$ . Hence, it has capacity at least $\lambda_{S}+1$ . For $S=\{s,t\}$ , the union of cuts $C_{1},C_{2}$ is always an $(s,t)$ -cut and does not contain $y,y^{\prime}$ . Exploiting this fact, it is shown in [2] that $C_{1}\cup C_{2}$ is an $(s,t)$ -cut of capacity $\lambda_{\{s,t\}}+1$ in which both failed edges are contributing. Unfortunately, for any Steiner set $S$ , there might not exist any Steiner vertex in $\overline{C_{1}\cup C_{2}}$ . So, $C_{1}\cup C_{2}$ is not always a Steiner cut and can have capacity strictly less than $\lambda_{S}$ . Moreover, even if $C_{1}\cup C_{2}$ is not a $(\lambda_{S}+1)$ cut, there might still exist a $(\lambda_{S}+1)$ cut in which both failed edges are contributing (refer to $(\lambda_{S}+1)$ cut $C$ in Figure 3( $i i$ )). Therefore, the data structure for nearest $(\lambda_{S}+1)$ cuts does not seem to work for answering dual edge failures queries. To overcome this hurdle, we establish the following important relation between vertices of ${\mathcal{W}}$ and a pair of crossing $(\lambda_{S}+1)$ cuts to which an edge belonging to ${\mathcal{W}}$ is contributing.

Lemma 23.

Let $e_{1}$ be an edge that belongs to ${\mathcal{W}}$ and contributes to a pair of crossing $(\lambda_{S}+1)$ cuts $C,C^{\prime}$ of $G({\mathcal{W}})$ . Neither $C\setminus C^{\prime}$ nor $C^{\prime}\setminus C$ contains a vertex from ${\mathcal{W}}$ if and only if each of the two sets $C\setminus C^{\prime}$ and $C^{\prime}\setminus C$ contains a Steiner vertex from $S({\mathcal{W}})$ .

Proof.

Let edge $e_{1}=(p,q)$ belongs to ${\mathcal{W}}$ and $e_{1}$ contributes to $C,C^{\prime}$ of $G({\mathcal{W}})$ (refer to Figure 3 $(i)$ ). Suppose each of the two sets $C\setminus C^{\prime}$ and $C^{\prime}\setminus C$ contains no vertex from ${\mathcal{W}}$ . Since they are crossing, there must exist at least one vertex from $S({\mathcal{W}})$ in each of the two sets $C\setminus C^{\prime}$ and $C^{\prime}\setminus C$ .

We now prove the converse part. Suppose each of the two sets $C\setminus C^{\prime}$ and $C^{\prime}\setminus C$ contains a Steiner vertex from $S({\mathcal{W}})$ . Let $t_{1}\in C^{\prime}\setminus C$ and $t_{2}\in C\setminus C^{\prime}$ . So, both $C\setminus C^{\prime}$ and $C^{\prime}\setminus C$ are Steiner cuts. Assume to the contrary that there is a vertex $u\in{\mathcal{W}}$ such that $u\in C\setminus C^{\prime}$ (the proof is along a similar line if $u\in C^{\prime}\setminus C$ ). Let us now consider graph $G({\mathcal{W}})\setminus e_{1}$ . Since $e_{1}$ contributes to both $C$ and $C^{\prime}$ , the capacity of cut $C$ and $C^{\prime}$ in $G({\mathcal{W}})\setminus e_{1}$ is $\lambda_{S}$ . By applying sub-modularity of cuts (Lemma 8(2)) for $C,C^{\prime}$ in $G({\mathcal{W}})\setminus e_{1}$ , we arrive at $c(C\setminus C^{\prime})+c(C^{\prime}\setminus C)\leq 2\lambda_{S}$ . Observe that, in graph $G({\mathcal{W}})$ , edge $e_{1}$ contributes neither to cut $C\setminus C^{\prime}$ nor to cut $C^{\prime}\setminus C$ . Hence, the following equation holds for graph $G({\mathcal{W}})$ as well.

c(C\setminus C^{\prime})+c(C^{\prime}\setminus C)\leq 2\lambda_{S}

(2)

It is also given that $u\in(C\setminus C^{\prime})\cap{\mathcal{W}}$ . So, $C\setminus C^{\prime}$ is a Steiner cut that subdivides ${\mathcal{W}}$ because $s\notin C\setminus C^{\prime}$ . Therefore, in $G({\mathcal{W}})$ , the capacity of $C\setminus C^{\prime}$ is at least $\lambda_{S}+1$ . It follows from Equation 2 that $c(C^{\prime}\setminus C)\leq\lambda_{S}-1$ . Since $t_{1}\in C^{\prime}\setminus C$ and $s\notin C^{\prime}\setminus C$ , therefore, we have a Steiner cut $C^{\prime}\setminus C$ of capacity at most $\lambda_{S}-1$ in $G({\mathcal{W}})$ , a contradiction. $\hfill\blacktriangleleft$

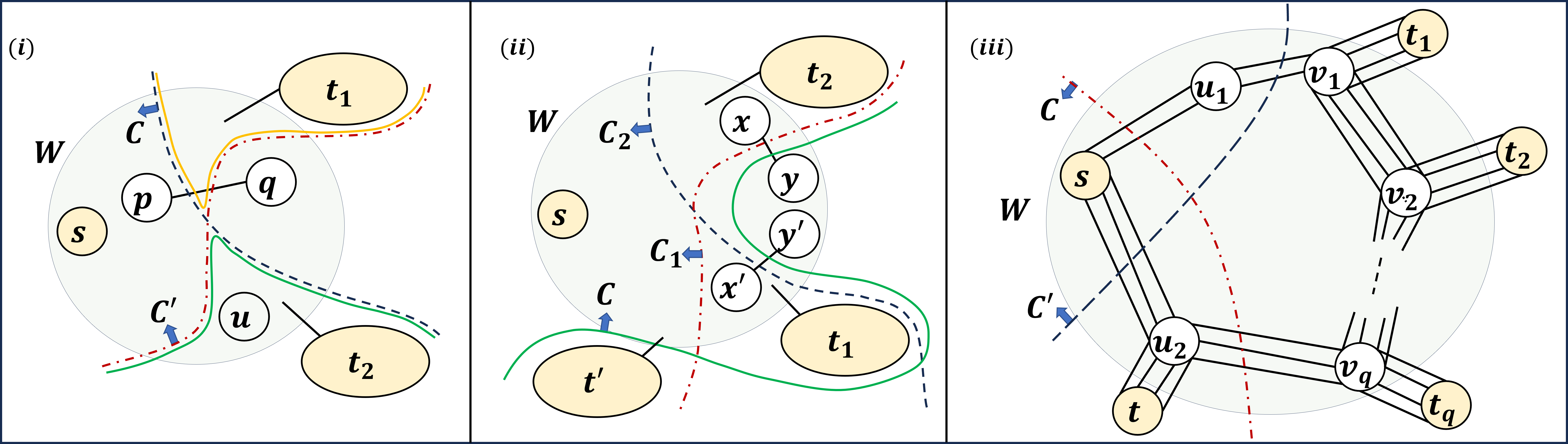
We exploit Lemma 23 crucially to arrive at the following sufficient condition.

Lemma 24.

Suppose the necessary condition holds (Lemma 22). There exists no Steiner vertex $t$ such that $t\in\overline{C_{1}\cup C_{2}}$ if and only if there is no $(\lambda_{S}+1)$ cut $C$ such that both edges $e,e^{\prime}$ contribute to $C$ .

Proof.

Suppose there exists no Steiner vertex $t$ such that $t\in\overline{C_{1}\cup C_{2}}$ . Assume to the contrary that there is a $(\lambda_{S}+1)$ cut $C$ such that both edges $e,e^{\prime}$ contribute to $C$ (refer to Figure 3 $(ii)$ ). Since $C$ is a Steiner cut, there is a Steiner vertex $t^{\prime}$ such that $t^{\prime}\in\overline{C}$ . Since $t^{\prime}$ cannot belong to $\overline{C_{1}}\cap\overline{C_{2}}$ , it follows that $t^{\prime}$ belongs to at least one of $C_{1}$ and $C_{2}$ . Without loss of generality, assume that $t^{\prime}\in C_{1}$ . So, $t^{\prime}\in C_{1}\setminus C$ , and hence, $C_{1}\setminus C$ defines a Steiner cut. Since $C_{1}$ and $C_{2}$ are Steiner cuts, there exist Steiner vertices $t_{1}$ and $t_{2}$ such that $t_{1}\notin C_{1}$ and $t_{2}\notin C_{2}$ . We now show that $t_{1}\in C\setminus C_{1}$ . Assume to the contrary that $t_{1}$ belongs to $\overline{C}$ . For cuts $C,C_{1}$ , there are vertices $s,x\in C\cap C_{1}$ and vertices $y,t_{1}\in\overline{C\cup C_{1}}$ such that $s,x,y\in{\mathcal{W}}$ . Hence, both $C\cap C_{1}$ and $C\cup C_{1}$ subdivides ${\mathcal{W}}$ and they are Steiner cuts. By Definition 9, cuts $C\cap C_{1}$ and $C\cup C_{1}$ is at least $\lambda_{S}+1$ . By sub-modularity of cuts (Lemma 8(1)), for cuts $C$ and $C_{1}$ , we have $c(C\cap C_{1})+c(C\cup C_{1})\leq 2\lambda_{S}+2$ . It follows that $C\cap C_{1}$ and $C\cup C_{1}$ both are $(\lambda_{S}+1)$ cuts. Moreover, $C\cap C_{1}$ is a proper subset of $C_{1}$ as $C\cap C_{1}$ does not contain $t^{\prime}$ . In addition, since $x\in C\cap C_{1}$ , therefore, $C_{1}$ cannot belong to $N_{S({\mathcal{W}})}(x)$ , a contradiction due to Definition 11. Therefore, we have $t_{1}\in C\setminus C_{1}$ . Observe that edge $(x,y)$ contributes to both $C_{1}$ and $C$ . Since both edges $e,e^{\prime}$ contribute to $C$ , so we have $x^{\prime}\in C$ . Moreover, it is known that $x^{\prime}\notin C_{1}$ . Therefore, $x^{\prime}\in C\setminus C_{1}$ . Finally we have an edge $(x,y)$ that contributes to a pair of crossing $(\lambda_{S}+1)$ cuts $C_{1},C$ since $s\in C\cap C_{1}$ , $t_{1}\in C\setminus C_{1}$ , $t^{\prime}\in C_{1}\setminus C$ , and $y,y^{\prime}\in\overline{C\cup C_{1}}$ . We have also shown that both $C_{1}\setminus C$ and $C\setminus C_{1}$ contain a Steiner vertex from $S({\mathcal{W}})$ . However, there is a vertex $x^{\prime}\in{\mathcal{W}}$ that belongs to $C\setminus C_{1}$ , a contradiction due to Lemma 23.

Suppose there is a Steiner vertex $t$ that belongs to $\overline{C_{1}\cup C_{2}}$ . Since $s\in(C_{1}\cap C_{2})\cap{\mathcal{W}}$ , $C_{1}\cup C_{2}$ is a Steiner cut. Since the necessary condition is satisfied, observe that $y,y^{\prime}\notin C_{1}\cup C_{2}$ and $y,y^{\prime}$ belongs to ${\mathcal{W}}$ . So, $C\cup C^{\prime}$ subdivides ${\mathcal{W}}$ . Hence, $C_{1}\cup C_{2}$ has capacity at least $\lambda_{S}+1$ . For cuts $C_{1}$ and $C_{2}$ , by sub-modularity of cuts (Lemma 8(1)), $c(C_{1}\cup C_{2})+c(C_{1}\cap C_{2})\leq\lambda_{S}+2$ . It follows that $C_{1}\cup C_{2}$ must be a $(\lambda_{S}+1)$ cut. Therefore, we have an $(\lambda_{S}+1)$ cut $C_{1}\cup C_{2}$ in which both edges $e,e^{\prime}$ are contributing. $\hfill\blacktriangleleft$ It follows from Lemma 24 that the existence of a Steiner vertex in $\overline{C_{1}\cup C_{2}}$ is indeed a sufficient condition, which leads to the following result.

Lemma 25.

Both failed edges $e=(x,y)$ and $e^{\prime}=(x^{\prime},y^{\prime})$ contribute to a single $(\lambda_{S}+1)$ cut if and only if there exist a nearest $(\lambda_{S}+1)$ cut $C_{1}$ from $x$ to $y$ and a nearest $(\lambda_{S}+1)$ cut $C_{2}$ from $x^{\prime}$ to $y^{\prime}$ such that $y^{\prime}\notin C_{1}$ , $y\notin C_{2}$ , and there exists a Steiner vertex $t\in\overline{C_{1}\cup C_{2}}$ .

It follows that if the capacity of global mincut of $G({\mathcal{W}})$ is at least $4$ , the data structure in Theorem 4 is sufficient for verifying every condition of Lemma 25. Exploiting Lemma 16, Lemma 23, and the following result, we show that data structure in Theorem 4 also works if the capacity of global mincut of $G({\mathcal{W}})$ is at most $3$ .

Lemma 26.

Let $(p,q)$ be any edge and $u$ be a vertex such that $p,q,u\in{\mathcal{W}}$ and $q\neq u\neq s$ . Let $C$ be any cut from $N_{S({\mathcal{W}})}(p)$ with $q\notin C$ . Then, $u\in C$ if and only if there is no $(\lambda_{S}+1)$ cut $C^{\prime}$ such that $s,p\in C^{\prime}$ and $q,u\in\overline{C^{\prime}}$ .

In conclusion, we have shown that for any capacity of global mincut of $G({\mathcal{W}})$ , the data structure in Theorem 4 can determine the necessary condition in Lemma 22 in ${\mathcal{O}}(1)$ time. To verify whether there is a Steiner vertex in $\overline{C_{1}\cup C_{2}}$ , it requires ${\mathcal{O}}(|S|)$ time. Moreover, data structure in Theorem 4 can report $\overline{C_{1}}$ and $\overline{C_{2}}$ in ${\mathcal{O}}(n)$ time, which ensures that $C_{1}\cup C_{2}$ can be reported in ${\mathcal{O}}(n)$ time. Therefore, we have designed an ${\mathcal{O}}(n(n-|S|+1))$ space data structure that, after the failure of any pair of edges, can report the capacity of $S$ -mincut and an $S$ -mincut in ${\mathcal{O}}(|S|)$ time and ${\mathcal{O}}(n)$ time, respectively. This leads to Theorem 5(2).

5.2 An $O((n-|S|)^{2}+n)$ Space Data Structure with $O(1)$ Query Time

After the failure of any pair of edges, the ${\mathcal{O}}(n(n-|S|+1))$ space data structure in Theorem 5(2) (designed in Section 5.1) takes ${\mathcal{O}}(|S|)$ time to report the capacity of $S$ -mincut. So, for $S=V$ , the query time is ${\mathcal{O}}(n)$ , which is significantly inferior compared to the ${\mathcal{O}}(1)$ query time for reporting the capacity of global mincut after the failure of a pair of edges using the data structure in [14]. In this section, we present a data structure that is more compact than the data structure in Theorem 5(2). In addition, it can also report the capacity of $S$ -mincut in ${\mathcal{O}}(1)$ time after the failure of a pair of edges; hence, provides a generalization to the data structure of Dinitz and Nutov [14] from $S=V$ to any $S\subseteq V$ .

Recall that, only for handling Case 1 in Section 5.1, our data structure takes ${\mathcal{O}}(|S|)$ time to report the capacity of $S$ -mincut. So, we consider the graph $G({\mathcal{W}})$ for a Singleton $(\lambda_{S}+1)$ class ${\mathcal{W}}$ . Observe that the necessary condition (Lemma 22) can be verified in ${\mathcal{O}}(1)$ time. So, our objective is to determine in ${\mathcal{O}}(1)$ time whether there exists a Steiner vertex $t\in\overline{C_{1}\cup C_{2}}$ (the sufficient condition stated in Lemma 25). For a single vertex $u\in{\mathcal{W}}$ , Lemma 18 ensures that there cannot be more than one Steiner vertex belonging to $\overline{C\cup C^{\prime}}$ , where $C,C^{\prime}\in N_{S({\mathcal{W}})}(u)$ . However, Lemma 18 cannot be extended for a pair of vertices from ${\mathcal{W}}$ . In other words, for a pair of vertices $\{u_{1},u_{2}\}\subseteq{\mathcal{W}}$ , there can be $\Omega(|S({\mathcal{W}})|)$ number of Steiner vertices that belong to $\overline{C\cup C^{\prime}}$ , where $C\in N_{S({\mathcal{W}})}(u_{1})$ and $C^{\prime}\in N_{S({\mathcal{W}})}(u_{2})$ (refer to Figure 3 $(iii)$ ). So, it may happen that the number of Steiner vertices in each set $\overline{C_{1}}$ and $\overline{C_{2}}$ is ${\Omega}(|S({\mathcal{W}})|)$ , but $|(\overline{C_{1}\cup C_{2}})\cap S({\mathcal{W}})|$ is ${\mathcal{O}}(1)$ only. Hence, $\Omega(|S({\mathcal{W}})|)$ time seems necessary to determine whether there is a Steiner vertex $t\in\overline{C_{1}\cup C_{2}}$ , which is ${\mathcal{O}}(|S|)$ in the worst case.

To achieve ${\mathcal{O}}(1)$ query time, our approach is to store a small set of Steiner vertices $SV(e_{1})$ to every edge $e_{1}$ belonging to ${\mathcal{W}}$ such that the following lemma holds.

Lemma 27.

There is a Steiner vertex $t\in\overline{C_{1}\cup C_{2}}$ if and only if $SV(e)\cap SV(e^{\prime})\neq\emptyset$ .

Observe that, for every edge $e_{1}$ , trivially storing a Steiner vertex for every other edge satisfying necessary and sufficient condition with $e_{1}$ leads to an ${\mathcal{O}}(|{\mathcal{W}}|^{4})$ space data structure. We now show that only ${\mathcal{O}}(|{\mathcal{W}}|^{2})$ space is sufficient to verify the condition in Lemma 27.

We first show that sufficient condition can be verified in constant time using ${\mathcal{O}}(|{\mathcal{W}}|^{2})$ space if at least one of the failed edges is incident on $s$ . So, let us consider any edge $e_{1}=(x_{1},y_{1})$ not incident on $s$ and let $C$ be a nearest $(\lambda_{S}+1)$ cut from $x_{1}$ to $y_{1}$ . Let $e_{2}=(x_{2},y_{2})$ and $e_{3}=(x_{3},y_{3})$ be a pair of edges in $G({\mathcal{W}})$ not incident on $s$ , and let $A$ be a nearest $(\lambda_{S}+1)$ cut from $x_{2}$ to $y_{2}$ and $B$ be a nearest $(\lambda_{S}+1)$ cut from $x_{3}$ to $y_{3}$ . Suppose both edges $e_{2}$ and $e_{3}$ with cuts $A$ and $B$ , respectively, satisfy the necessary and sufficient conditions with cut $C$ for edge $e_{1}$ . By crucially exploiting the relation among three cuts $A, B,$ and $C$ , in three different graphs $G({\mathcal{W}})$ , $G({\mathcal{W}})\setminus e_{1}$ , and $G^{\prime}$ (obtained from $G({\mathcal{W}})$ after the removal of edges $\{e_{1},e_{2}\}$ ), we establish the following interesting result.

Lemma 28.

For edge $e_{1}$ , there exists a Steiner vertex $t\in\overline{C}$ such that for any edge $e_{2}=(x_{2},y_{2})$ , if there is a nearest $(\lambda_{S}+1)$ cut $C^{\prime}$ from $x_{2}$ to $y_{2}$ that satisfies the conditions of Lemma 25 with $C$ for edge $e_{1}$ , then Steiner vertex $t$ also belongs to $\overline{C^{\prime}}$ .

Proof.

Suppose each of the two cuts $A$ and $B$ satisfies necessary and sufficient condition stated in Lemma 25 with cut $C$ for $e_{1}$ . Assume to the contrary that there is no single Steiner vertex $t\in\overline{C}$ that belongs to $\overline{A}\cap\overline{B}$ . It follows that there are at least two Steiner vertices $t_{1},t_{2}\in\overline{C}$ such that $t_{1}\in\overline{A}\cap B$ and $t_{2}\in\overline{B}\cap A$ . We have $x_{1}\in\overline{A}\cap\overline{B}$ , $x_{1}\notin\overline{C}$ , and $y_{1}\in\overline{C}\cap\overline{A}\cap\overline{B}$ . Moreover, both endpoints of $e_{2}$ and $e_{3}$ belong to $\overline{C}$ . Observe that endpoint $y_{2}$ of $e_{2}$ must belong to $\overline{A}\cap\overline{C}$ and endpoint $y_{3}$ of $e_{3}$ must belong to $\overline{B}\cap\overline{C}$ . Let us consider $(\lambda_{S}+1)$ cuts $A$ and $C$ . We have $y_{2},t_{1}\in\overline{A}\cap\overline{C}$ and $s\in A\cap C$ . Both $A\cap C$ and $A\cup C$ separate $s$ from $y_{3},t_{1}$ . Hence, the capacity of $A\cap C$ , as well as $A\cup C$ , is at least $\lambda_{S}+1$ . It follows from sub-modularity of cuts (Lemma 8(1)) that $A\cup C$ is a $(\lambda_{S}+1)$ cut. Similarly, we can show that $B\cup C$ is a $(\lambda_{S}+1)$ cut. Let $A_{1}=\overline{A}\cap\overline{C}$ and $A_{2}=\overline{B}\cap\overline{C}$ . It follows that both $A_{1}$ and $A_{2}$ are $(\lambda_{S}+1)$ cuts since graph $G({\mathcal{W}})$ is undirected. Without causing any confusion, only for cuts $A_{1}$ and $A_{2}$ here, we have $s\in\overline{A_{1}\cup A_{2}}$ . Observe that $t_{1}\in A_{1}\setminus A_{2}$ and $t_{2}\in A_{2}\setminus A_{1}$ . Moreover, $y_{1}\in A_{1}\cap A_{2}$ since $y_{1}\in\overline{C}\cap\overline{A}\cap\overline{B}$ . Also, since $x_{1}\in(\overline{A}\cap\overline{B})\setminus\overline{C}$ , it implies that edge $e_{1}$ contributes to $A_{1}\cap A_{2}$ as well as $A_{1}\cup A_{2}$ . Now, based on the position of endpoints of $e_{2}$ and $e_{3}$ with respect to cuts $A_{1}$ and $A_{2}$ , we have two cases – (1) at least one endpoint of $e_{2}$ is in $A_{1}\setminus A_{2}$ or at least one endpoint of $e_{3}$ is in $A_{2}\setminus A_{3}$ , and (2) exactly one endpoint of each of the two edges $e_{2}$ and $e_{3}$ belongs to $A_{1}\cap A_{2}$ and the other endpoints are in $(\overline{A_{1}\cup A_{2}})\cap\overline{C}$ . We now prove each case separately by contradiction.

Case 1.

Without loss of generality, assume that one endpoint of $e_{2}$ is in $A_{1}\setminus A_{2}$ . So, $c(A_{1}\setminus A_{2})$ is at least $\lambda_{S}+1$ since $A_{1}\setminus A_{2}$ separates $t_{1}$ and endpoint of $e_{2}$ from $s$ . Let us obtain graph $G({\mathcal{W}})\setminus e_{1}$ . Since $e_{1}$ contributes to both $A_{1}$ and $A_{2}$ , in graph $G({\mathcal{W}})\setminus e_{1}$ , the capacity of $A_{1}$ and $A_{2}$ is $\lambda_{S}$ . So, in graph $G({\mathcal{W}})\setminus e_{1}$ , we get $c(A_{1}\setminus A_{2})+c(A_{2}\setminus A_{2})\geq 2\lambda_{S}+1$ since $A_{2}\setminus A_{1}$ separates Steiner vertices $t_{2}$ from $s$ , and $e$ contributes to neither $A_{1}\setminus A_{2}$ nor $A_{2}\setminus A_{1}$ . However, in graph $G({\mathcal{W}})\setminus e_{1}$ , by applying sub-modularity of cuts (Lemma 8(2)) on $A_{1}$ and $A_{2}$ , we arrive at $c(A_{1}\setminus A_{2})+c(A_{2}\setminus A_{1})\leq 2\lambda_{S}$ , a contradiction.

Case 2.

In this case, both edges $e_{2}$ and $e_{3}$ contribute to $A_{1}\cap A_{2}$ ; otherwise, observe that at least one endpoint of $e_{2}$ is in $A_{1}\setminus A_{2}$ or at least one endpoint of $e_{3}$ is in $A_{2}\setminus A_{3}$ . We obtain a graph $G^{\prime}$ from $G({\mathcal{W}})$ after the removal of both edges $e_{2}$ and $e_{3}$ . For any cut $C^{\prime\prime}$ , without causing any ambiguity, let $c(C^{\prime\prime})$ denote the capacity of $C^{\prime\prime}$ in $G^{\prime}$ . In graph $G^{\prime}$ , $c(A_{1})$ , as well as $c(A_{2})$ , is $\lambda_{S}-1$ . Since both $A_{1}\setminus A_{2}$ and $A_{2}\setminus A_{1}$ are Steiner cuts in $G({\mathcal{W}})$ , $c(A_{1}\setminus A_{2})$ and $c(A_{2}\setminus A_{1})$ is at least $\lambda_{S}$ in $G({\mathcal{W}})$ . None of the edges $e_{2},e_{3}$ contribute to $A_{1}\setminus A_{2}$ and $A_{2}\setminus A_{1}$ . Hence their capacities remain intact in $G^{\prime}$ . Therefore, in graph $G^{\prime}$ , $c(A_{1}\setminus A_{2})+c(A_{2}\setminus A_{1})\geq 2\lambda_{S}$ . However, by applying sub-modularity of cuts (Lemma 8(2)) on $A_{1}$ and $A_{2}$ , we arrive at $c(A_{1}\setminus A_{2})+c(A_{2}\setminus A_{1})\leq 2\lambda_{S}-2$ , a contradiction. $\hfill\blacktriangleleft$ Lemma 28 helps us in showing that $|SV(e_{1})|\leq 4$ for any edge $e_{1}$ in ${\mathcal{W}}$ , and, we can establish Lemma 27 using Lemma 28. To verify the necessary condition in Lemma 22, we observe that the Steiner set $S({\mathcal{W}})$ is not required in the design of the data structure in Theorem 4. This leads to an ${\mathcal{O}}((n-|S|)^{2}+n)$ space data structure that can answer the necessary condition in ${\mathcal{O}}(1)$ time. Finally, we show that storing at most $4$ Steiner vertices at every edge in $G({\mathcal{W}})$ requires ${\mathcal{O}}((n-|S|)^{2}+n)$ space overall for every $(\lambda_{S}+1)$ class of $G$ . This helps in verifying the sufficient condition in ${\mathcal{O}}(1)$ time as well. Therefore, by Lemma 25 and Lemma 27, the capacity of $S$ -mincut can be reported in ${\mathcal{O}}(1)$ time using an ${\mathcal{O}}((n-|S|)^{2}+n)$ space data structure after the failure of any pair of edges. This result, along with the result of handling insertions of a pair of edges (in the full version [6]), completes the proof of Theorem 5.

6 Lower Bound for Dual Edge Sensitivity Oracle

It follows from Definition 2 that any dual edge Sensitivity Oracle for $S$ -mincut answers the following query.
cap $(e,e^{\prime})$ : Report the capacity of $S$ -mincut after the failure of a pair of edges $e,e^{\prime}$ in $G$ .
For $S=\{s,t\}$ , Baswana, Bhanja, and Pandey [2] established the following lower bound for answering query cap conditioned on Reachability Hypothesis [22, 30]. For (un)directed multi-graphs, any data structure that can answer query cap in ${\mathcal{O}}(1)$ time must occupy $\tilde{\Omega}(n^{2})$ space in the worst case ( $\tilde{\Omega}$ hides polylogarithmic factors) unless Reachability Hypothesis [22, 30] is violated.

We first show that, for any given Steiner set $S\subseteq V$ , any data structure that can answer query cap in graph $G$ can also be used to answer query cap for $(s_{1},s_{2})$ -mincut in a graph $G^{\prime}=(V^{\prime},E^{\prime})$ on $|V^{\prime}|={\mathcal{O}}(n-|S|)$ vertices, where $s_{1},s_{2}\in V^{\prime}$ are the only Steiner vertices of $G^{\prime}$ . This, along with the above-mentioned result of [2], can be used to establish the following conditional lower bound. For a (un)directed multi-graph, for any given Steiner set $S\subseteq V$ , any data structure that can answer query cap in ${\mathcal{O}}(1)$ time must occupy $\tilde{\Omega}((n-|S|)^{2})$ space in the worst case, unless Reachability Hypothesis [22, 30] is violated.

Finally, and more importantly, we show by exploiting the structure of $G^{\prime}$ that the Reachability Hypothesis [22, 30] is not required to establish an $\Omega((n-|S|)^{2})$ lower bound on space for answering query cap. Hence, our obtained lower bound is unconditional. Moreover, the lower bound is also irrespective of the time taken for answering query cap. The result is formally stated in Theorem 6.

7 Conclusion

The problem of designing a compact data structure for minimum+1 Steiner cuts and designing dual edge Sensitivity Oracle for Steiner mincut is addressed for the first time in this article. Our results provide a complete generalization of the two important existing results while matching their bounds – for global cut (Steiner set is the vertex set $V$ ) by Dinitz and Nutov [14] and for $(s,t)$ -cut (Steiner set is only a pair of vertices $\{s,t\}$ ) by Baswana, Bhanja, and Pandey [2]. The space occupied by the dual edge Sensitivity Oracle for Steiner mincut, presented in this article, is optimal almost for the whole range of $S$ . In addition, the query time for reporting Steiner mincut and its capacity is also worst-case optimal.

An immediate future work would be to design a Sensitivity Oracle for Steiner mincut that handles the insertions/failures of any $f>2$ edges. For this problem, for any Steiner set $S$ satisfying $|S|\in(2,n)$ , our result improves the space by a factor of $\Omega(\frac{m}{n-|S|})$ over the trivial result for handling any $f$ edge insertions/failures for $S$ -mincut. In conclusion, while some nontrivial insights may still be required to significantly improve this bound, we believe that our results should be quite useful for addressing this generalized version of the problem.

References

[1] Ravindra K. Ahuja, Thomas L. Magnanti, and James B. Orlin. Network flows - theory, algorithms and applications. Prentice Hall, 1993.
[2] Surender Baswana, Koustav Bhanja, and Abhyuday Pandey. Minimum+1 (s, t)-cuts and dual-edge sensitivity oracle. ACM Trans. Algorithms, 19(4):38:1–38:41, 2023. doi:10.1145/3623271.
[3] Surender Baswana, Keerti Choudhary, Moazzam Hussain, and Liam Roditty. Approximate single-source fault tolerant shortest path. ACM Trans. Algorithms, 16(4):44:1–44:22, 2020. doi:10.1145/3397532.
[4] Surender Baswana and Abhyuday Pandey. Sensitivity oracles for all-pairs mincuts. In Joseph (Seffi) Naor and Niv Buchbinder, editors, Proceedings of the 2022 ACM-SIAM Symposium on Discrete Algorithms, SODA 2022, Virtual Conference / Alexandria, VA, USA, January 9 - 12, 2022, pages 581–609. SIAM, 2022. doi:10.1137/1.9781611977073.27.
[5] András A Benczúr. A representation of cuts within 6/5 times the edge connectivity with applications. In Proceedings of IEEE 36th Annual Foundations of Computer Science, pages 92–102. IEEE, 1995. doi:10.1109/SFCS.1995.492466.
[6] Koustav Bhanja. Minimum+1 steiner cuts and dual edge sensitivity oracle: Bridging the gap between global cut and (s,t)-cut. CoRR, abs/2406.15129, 2024. doi:10.48550/arXiv.2406.15129.
[7] Davide Bilò, Shiri Chechik, Keerti Choudhary, Sarel Cohen, Tobias Friedrich, Simon Krogmann, and Martin Schirneck. Approximate distance sensitivity oracles in subquadratic space. In Proceedings of the 55th Annual ACM Symposium on Theory of Computing, pages 1396–1409, 2023. doi:10.1145/3564246.3585251.
[8] John A Bondy and Miklós Simonovits. Cycles of even length in graphs. Journal of Combinatorial Theory, Series B, 16(2):97–105, 1974.
[9] Diptarka Chakraborty, Kushagra Chatterjee, and Keerti Choudhary. Pairwise reachability oracles and preservers under failures. In 49th International Colloquium on Automata, Languages, and Programming (ICALP 2022), pages 35–1. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2022.
[10] Chung-Kuan Cheng and T. C. Hu. Ancestor tree for arbitrary multi-terminal cut functions. Ann. Oper. Res., 33(3):199–213, 1991. doi:10.1007/BF02115755.
[11] Keerti Choudhary. An optimal dual fault tolerant reachability oracle. In 43rd International Colloquium on Automata, Languages, and Programming (ICALP 2016), pages 130–1. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2016.
[12] Efim A Dinitz, Alexander V Karzanov, and Michael V Lomonosov. On the structure of the system of minimum edge cuts in a graph. Issledovaniya po Diskretnoi Optimizatsii, pages 290–306, 1976.
[13] Yefim Dinitz. Maintaining the 4-edge-connected components of a graph on-line. In Second Israel Symposium on Theory of Computing Systems, ISTCS 1993, Natanya, Israel, June 7-9, 1993, Proceedings, pages 88–97. IEEE Computer Society, 1993. doi:10.1109/ISTCS.1993.253480.
[14] Yefim Dinitz and Zeev Nutov. A 2-level cactus model for the system of minimum and minimum+1 edge-cuts in a graph and its incremental maintenance. In Frank Thomson Leighton and Allan Borodin, editors, Proceedings of the Twenty-Seventh Annual ACM Symposium on Theory of Computing, 29 May-1 June 1995, Las Vegas, Nevada, USA, pages 509–518. ACM, 1995. doi:10.1145/225058.225268.
[15] Yefim Dinitz and Alek Vainshtein. The connectivity carcass of a vertex subset in a graph and its incremental maintenance. In Frank Thomson Leighton and Michael T. Goodrich, editors, Proceedings of the Twenty-Sixth Annual ACM Symposium on Theory of Computing, 23-25 May 1994, Montréal, Québec, Canada, pages 716–725. ACM, 1994. doi:10.1145/195058.195442.
[16] Yefim Dinitz and Alek Vainshtein. Locally orientable graphs, cell structures, and a new algorithm for the incremental maintenance of connectivity carcasses. In Kenneth L. Clarkson, editor, Proceedings of the Sixth Annual ACM-SIAM Symposium on Discrete Algorithms, 22-24 January 1995. San Francisco, California, USA, pages 302–311. ACM/SIAM, 1995. URL: http://dl.acm.org/citation.cfm?id=313651.313711.
[17] Yefim Dinitz and Alek Vainshtein. The general structure of edge-connectivity of a vertex subset in a graph and its incremental maintenance. odd case. SIAM J. Comput., 30(3):753–808, 2000. doi:10.1137/S0097539797330045.
[18] Yefim Dinitz and Jeffery R. Westbrook. Maintaining the classes of 4-edge-connectivity in a graph on-line. Algorithmica, 20(3):242–276, 1998. doi:10.1007/PL00009195.
[19] Ran Duan and Seth Pettie. Dual-failure distance and connectivity oracles. In Claire Mathieu, editor, Proceedings of the Twentieth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2009, New York, NY, USA, January 4-6, 2009, pages 506–515. SIAM, 2009. doi:10.1137/1.9781611973068.56.
[20] Paul Erdös. Extremal problems in graph theory. Publ. House Cszechoslovak Acad. Sci., Prague, pages 29–36, 1964.
[21] Zvi Galil and Giuseppe F. Italiano. Maintaining the 3-edge-connected components of a graph on-line. SIAM J. Comput., 22(1):11–28, 1993. doi:10.1137/0222002.
[22] Isaac Goldstein, Tsvi Kopelowitz, Moshe Lewenstein, and Ely Porat. Conditional lower bounds for space/time tradeoffs. In Algorithms and Data Structures: 15th International Symposium, WADS 2017, St. John’s, NL, Canada, July 31–August 2, 2017, Proceedings 15, pages 421–436. Springer, 2017. doi:10.1007/978-3-319-62127-2_36.
[23] Ralph E Gomory and Tien Chung Hu. Multi-terminal network flows. Journal of the Society for Industrial and Applied Mathematics, 9(4):551–570, 1961.
[24] Gramoz Goranci, Monika Henzinger, and Mikkel Thorup. Incremental exact min-cut in polylogarithmic amortized update time. ACM Trans. Algorithms, 14(2):17:1–17:21, 2018. doi:10.1145/3174803.
[25] Manoj Gupta and Shahbaz Khan. Multiple source dual fault tolerant bfs trees. In 44th International Colloquium on Automata, Languages, and Programming (ICALP 2017), pages 127–1. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2017.
[26] Giuseppe F. Italiano, Adam Karczmarz, and Nikos Parotsidis. Planar reachability under single vertex or edge failures. In Dániel Marx, editor, Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms, SODA 2021, Virtual Conference, January 10 - 13, 2021, pages 2739–2758. SIAM, 2021. doi:10.1137/1.9781611976465.163.
[27] Ken-ichi Kawarabayashi and Mikkel Thorup. Deterministic edge connectivity in near-linear time. J. ACM, 66(1):4:1–4:50, 2019. doi:10.1145/3274663.
[28] L. Lovász. Combinatorial problems and exercises. North-Holland Publishing Co., Amsterdam-New York, 1979.
[29] Merav Parter. Dual failure resilient BFS structure. In Chryssis Georgiou and Paul G. Spirakis, editors, Proceedings of the 2015 ACM Symposium on Principles of Distributed Computing, PODC 2015, Donostia-San Sebastián, Spain, July 21 - 23, 2015, pages 481–490. ACM, 2015. doi:10.1145/2767386.2767408.
[30] Mihai Patrascu. Unifying the landscape of cell-probe lower bounds. SIAM J. Comput., 40(3):827–847, 2011. doi:10.1137/09075336X.
[31] Jean-Claude Picard and Maurice Queyranne. On the structure of all minimum cuts in a network and applications. In Rayward-Smith V.J. (eds) Combinatorial Optimization II. Mathematical Programming Studies, 13(1):8–16, 1980. doi:10.1007/BFb0120902.

[bib.bib1] [1] Ravindra K. Ahuja, Thomas L. Magnanti, and James B. Orlin. Network flows - theory, algorithms and applications. Prentice Hall, 1993.

[bib.bib2] [2] Surender Baswana, Koustav Bhanja, and Abhyuday Pandey. Minimum+1 (s, t)-cuts and dual-edge sensitivity oracle. ACM Trans. Algorithms, 19(4):38:1–38:41, 2023. doi:10.1145/3623271.

[bib.bib3] [3] Surender Baswana, Keerti Choudhary, Moazzam Hussain, and Liam Roditty. Approximate single-source fault tolerant shortest path. ACM Trans. Algorithms, 16(4):44:1–44:22, 2020. doi:10.1145/3397532.

[bib.bib4] [4] Surender Baswana and Abhyuday Pandey. Sensitivity oracles for all-pairs mincuts. In Joseph (Seffi) Naor and Niv Buchbinder, editors, Proceedings of the 2022 ACM-SIAM Symposium on Discrete Algorithms, SODA 2022, Virtual Conference / Alexandria, VA, USA, January 9 - 12, 2022, pages 581–609. SIAM, 2022. doi:10.1137/1.9781611977073.27.

[bib.bib5] [5] András A Benczúr. A representation of cuts within 6/5 times the edge connectivity with applications. In Proceedings of IEEE 36th Annual Foundations of Computer Science, pages 92–102. IEEE, 1995. doi:10.1109/SFCS.1995.492466.

[bib.bib6] [6] Koustav Bhanja. Minimum+1 steiner cuts and dual edge sensitivity oracle: Bridging the gap between global cut and (s,t)-cut. CoRR, abs/2406.15129, 2024. doi:10.48550/arXiv.2406.15129.

[bib.bib7] [7] Davide Bilò, Shiri Chechik, Keerti Choudhary, Sarel Cohen, Tobias Friedrich, Simon Krogmann, and Martin Schirneck. Approximate distance sensitivity oracles in subquadratic space. In Proceedings of the 55th Annual ACM Symposium on Theory of Computing, pages 1396–1409, 2023. doi:10.1145/3564246.3585251.

[bib.bib8] [8] John A Bondy and Miklós Simonovits. Cycles of even length in graphs. Journal of Combinatorial Theory, Series B, 16(2):97–105, 1974.

[bib.bib9] [9] Diptarka Chakraborty, Kushagra Chatterjee, and Keerti Choudhary. Pairwise reachability oracles and preservers under failures. In 49th International Colloquium on Automata, Languages, and Programming (ICALP 2022), pages 35–1. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2022.

[bib.bib10] [10] Chung-Kuan Cheng and T. C. Hu. Ancestor tree for arbitrary multi-terminal cut functions. Ann. Oper. Res., 33(3):199–213, 1991. doi:10.1007/BF02115755.

[bib.bib11] [11] Keerti Choudhary. An optimal dual fault tolerant reachability oracle. In 43rd International Colloquium on Automata, Languages, and Programming (ICALP 2016), pages 130–1. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2016.

[bib.bib12] [12] Efim A Dinitz, Alexander V Karzanov, and Michael V Lomonosov. On the structure of the system of minimum edge cuts in a graph. Issledovaniya po Diskretnoi Optimizatsii, pages 290–306, 1976.

[bib.bib13] [13] Yefim Dinitz. Maintaining the 4-edge-connected components of a graph on-line. In Second Israel Symposium on Theory of Computing Systems, ISTCS 1993, Natanya, Israel, June 7-9, 1993, Proceedings, pages 88–97. IEEE Computer Society, 1993. doi:10.1109/ISTCS.1993.253480.

[bib.bib14] [14] Yefim Dinitz and Zeev Nutov. A 2-level cactus model for the system of minimum and minimum+1 edge-cuts in a graph and its incremental maintenance. In Frank Thomson Leighton and Allan Borodin, editors, Proceedings of the Twenty-Seventh Annual ACM Symposium on Theory of Computing, 29 May-1 June 1995, Las Vegas, Nevada, USA, pages 509–518. ACM, 1995. doi:10.1145/225058.225268.

[bib.bib15] [15] Yefim Dinitz and Alek Vainshtein. The connectivity carcass of a vertex subset in a graph and its incremental maintenance. In Frank Thomson Leighton and Michael T. Goodrich, editors, Proceedings of the Twenty-Sixth Annual ACM Symposium on Theory of Computing, 23-25 May 1994, Montréal, Québec, Canada, pages 716–725. ACM, 1994. doi:10.1145/195058.195442.

[bib.bib16] [16] Yefim Dinitz and Alek Vainshtein. Locally orientable graphs, cell structures, and a new algorithm for the incremental maintenance of connectivity carcasses. In Kenneth L. Clarkson, editor, Proceedings of the Sixth Annual ACM-SIAM Symposium on Discrete Algorithms, 22-24 January 1995. San Francisco, California, USA, pages 302–311. ACM/SIAM, 1995. URL: http://dl.acm.org/citation.cfm?id=313651.313711.

[bib.bib17] [17] Yefim Dinitz and Alek Vainshtein. The general structure of edge-connectivity of a vertex subset in a graph and its incremental maintenance. odd case. SIAM J. Comput., 30(3):753–808, 2000. doi:10.1137/S0097539797330045.

[bib.bib18] [18] Yefim Dinitz and Jeffery R. Westbrook. Maintaining the classes of 4-edge-connectivity in a graph on-line. Algorithmica, 20(3):242–276, 1998. doi:10.1007/PL00009195.

[bib.bib19] [19] Ran Duan and Seth Pettie. Dual-failure distance and connectivity oracles. In Claire Mathieu, editor, Proceedings of the Twentieth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2009, New York, NY, USA, January 4-6, 2009, pages 506–515. SIAM, 2009. doi:10.1137/1.9781611973068.56.

[bib.bib20] [20] Paul Erdös. Extremal problems in graph theory. Publ. House Cszechoslovak Acad. Sci., Prague, pages 29–36, 1964.

[bib.bib21] [21] Zvi Galil and Giuseppe F. Italiano. Maintaining the 3-edge-connected components of a graph on-line. SIAM J. Comput., 22(1):11–28, 1993. doi:10.1137/0222002.

[bib.bib22] [22] Isaac Goldstein, Tsvi Kopelowitz, Moshe Lewenstein, and Ely Porat. Conditional lower bounds for space/time tradeoffs. In Algorithms and Data Structures: 15th International Symposium, WADS 2017, St. John’s, NL, Canada, July 31–August 2, 2017, Proceedings 15, pages 421–436. Springer, 2017. doi:10.1007/978-3-319-62127-2_36.

[bib.bib23] [23] Ralph E Gomory and Tien Chung Hu. Multi-terminal network flows. Journal of the Society for Industrial and Applied Mathematics, 9(4):551–570, 1961.

[bib.bib24] [24] Gramoz Goranci, Monika Henzinger, and Mikkel Thorup. Incremental exact min-cut in polylogarithmic amortized update time. ACM Trans. Algorithms, 14(2):17:1–17:21, 2018. doi:10.1145/3174803.

[bib.bib25] [25] Manoj Gupta and Shahbaz Khan. Multiple source dual fault tolerant bfs trees. In 44th International Colloquium on Automata, Languages, and Programming (ICALP 2017), pages 127–1. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2017.

[bib.bib26] [26] Giuseppe F. Italiano, Adam Karczmarz, and Nikos Parotsidis. Planar reachability under single vertex or edge failures. In Dániel Marx, editor, Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms, SODA 2021, Virtual Conference, January 10 - 13, 2021, pages 2739–2758. SIAM, 2021. doi:10.1137/1.9781611976465.163.

[bib.bib27] [27] Ken-ichi Kawarabayashi and Mikkel Thorup. Deterministic edge connectivity in near-linear time. J. ACM, 66(1):4:1–4:50, 2019. doi:10.1145/3274663.

[bib.bib28] [28] L. Lovász. Combinatorial problems and exercises. North-Holland Publishing Co., Amsterdam-New York, 1979.

[bib.bib29] [29] Merav Parter. Dual failure resilient BFS structure. In Chryssis Georgiou and Paul G. Spirakis, editors, Proceedings of the 2015 ACM Symposium on Principles of Distributed Computing, PODC 2015, Donostia-San Sebastián, Spain, July 21 - 23, 2015, pages 481–490. ACM, 2015. doi:10.1145/2767386.2767408.

[bib.bib30] [30] Mihai Patrascu. Unifying the landscape of cell-probe lower bounds. SIAM J. Comput., 40(3):827–847, 2011. doi:10.1137/09075336X.

[bib.bib31] [31] Jean-Claude Picard and Maurice Queyranne. On the structure of all minimum cuts in a network and applications. In Rayward-Smith V.J. (eds) Combinatorial Optimization II. Mathematical Programming Studies, 13(1):8–16, 1980. doi:10.1007/BFb0120902.

Minimum+1 Steiner Cut and Dual Edge Sensitivity Oracle: Bridging Gap between Global and (s,t)-cut

Abstract

Keywords and phrases:

Category:

Copyright and License:

2012 ACM Subject Classification:

Related Version:

Acknowledgements:

Funding:

DOI:

Event:

Editors:

Series and Publisher:

1 Introduction

Two well-studied cuts and their generalization.

Definition 1 (Steiner cut).

Data Structure for Minimum+1 Steiner Cut

Question 1.

Dual Edge Sensitivity Oracle for Steiner Mincut

Definition 2 (Dual edge Sensitivity Oracle).

Question 2.

▶ Note 3.

1.1 Our Results

Theorem 4 (Data Structure).

Theorem 5 (Sensitivity Oracle).

Theorem 6 (Lower Bound).

▶ Note 7.

1.2 Organization of this article

2 Preliminaries

Lemma 8 (Sub-modularity of cuts (Problem 48(a,b) in [28])).

Definition 9.

Definition 10 (Crossing cuts and Corner sets).

Definition 11 (Nearest (λS+1) cut of a vertex).

3 A Generalization of 3-Star Lemma

Lemma 12 (Four Component Lemma (Problem 48(c) in [28])).

Theorem 13 (Gen-3-Star Lemma).

Proof.

Lemma 14.

Proof.

4 A Data Structure for Reporting Minimum+1 Steiner Cuts

Limitations of existing results.

Our approach.

4.1 A Data Structure for a Singleton (𝝀𝑺+𝟏) class

Lemma 15.

Lemma 16.

Lemma 17.

Proof.

A classification of all cuts from 𝑵𝑺⁢(𝓦)⁢(𝒖).

Lemma 18.

Proof.

Lemma 19.

Proof.

Extension to general graphs.

Lemma 20.

Theorem 21.

4.2 A Data Structure for General (𝝀𝑺+𝟏) classes

5 Dual Edge Sensitivity Oracle For 𝑺-mincut

5.1 An 𝑶⁢(𝒏⁢(𝒏−|𝑺|+𝟏)) Space Data Structure with 𝑶⁢(|𝑺|) Query Time

Handling Dual Edge Failures in a Singleton (𝝀𝑺+𝟏) class

Lemma 22.

Lemma 23.

Proof.

Lemma 24.

Proof.

Lemma 25.

Lemma 26.

5.2 An 𝑶⁢((𝒏−|𝑺|)𝟐+𝒏) Space Data Structure with 𝑶⁢(𝟏) Query Time

Lemma 27.

Lemma 28.

Proof.

Case 1.

Case 2.

6 Lower Bound for Dual Edge Sensitivity Oracle

7 Conclusion

References

$\blacktriangleright$ Note 3.

$\blacktriangleright$ Note 7.

Definition 11 (Nearest $(\lambda_{S}+1)$ cut of a vertex).

4.1 A Data Structure for a Singleton $(\lambda_{S}+1)$ class

A classification of all cuts from $N_{S({\mathcal{W}})}(u)$ .

4.2 A Data Structure for General $(\lambda_{S}+1)$ classes

5 Dual Edge Sensitivity Oracle For $𝑺$ -mincut

5.1 An $O(n(n-|S|+1))$ Space Data Structure with $O(|S|)$ Query Time

Handling Dual Edge Failures in a Singleton $(\lambda_{S}+1)$ class

5.2 An $O((n-|S|)^{2}+n)$ Space Data Structure with $O(1)$ Query Time