-Leaf Powers Cannot Be Characterized by a Finite Set of Forbidden Induced Subgraphs for
Abstract
A graph is a -leaf power if there is a tree whose leaves are the vertices of , with the property that a pair of distinct leaves and share an edge in if and only if they are distance at most apart in . For , it is known that there exists a finite set of graphs such that the class of -leaf power graphs is characterized as the set of strongly chordal graphs that do not contain any graph in as an induced subgraph. We prove no such characterization holds for . That is, for any , there is no finite set of graphs such that is equivalent to the set of strongly chordal graphs that do not contain as an induced subgraph any graph in .
Keywords and phrases:
Leaf Powers, Forbidden Graph Characterizations, Strongly Chordal GraphsCategory:
Track A: Algorithms, Complexity and GamesCopyright and License:
2012 ACM Subject Classification:
Mathematics of computing Graph algorithmsAcknowledgements:
This research collaboration was instigated at the Montreal Graph Theory Workshop.Editors:
Keren Censor-Hillel, Fabrizio Grandoni, Joël Ouaknine, and Gabriele PuppisSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
A fundamental question in graph theory concerns whether or not a graph can be represented (or approximated) by a simpler graph, for instance a tree , while preserving the desired information from the original graph. The pairwise distances of often need to be summarized into sparser structures, with notable examples including graph sparsifiers [16, 1, 25] and graph spanners [11, 2, 15, 22], which ask for a subgraph of , or distance emulators [30, 9, 31] which ask for another graph that approximates the distances of . If the distance information to preserve only concerns “close together” versus “far apart” then this can take the following form: given a graph and an integer , does there exists a tree whose leaves are the vertices of , such that distinct vertices and are adjacent in if and only if the distance from to in is at most ? If the answer is affirmative then is dubbed a -leaf power of (and is dubbed a -leaf root of ).
The study of -leaf powers and roots were instigated by Nishimura, Ragde and Thilikos [28]. On the applied side, these graphs are of significant interest in the field of computational biology with respect to phylogenetic trees, which aim to explain the distance relationships observed on available data between species, genes, or other types of taxa. Indeed, -leaf powers can be used to represent and explain pairs of genes that underwent a bounded number of evolutionary events in their evolution [26, 17], or that have conserved closely related biological functions during evolution [21]. On the theory side, despite their simplicity, several fundamental graph theoretic problems concerning -leaf powers remain open. The purpose of this research is to resolve one such long-standing open problem. Specifically, we prove that the class of -leaf power graphs cannot be characterized via a finite set of forbidden induced subgraphs for . In contrast, for such finite characterizations were previously shown to exist [12, 6, 4].
1.1 Background
Let denote the class of all -leaf power graphs, for . The class of all leaf power graphs is then denoted by . The literature on leaf power graphs has primarily focused on two major themes. One, obtaining graphical characterizations for both the class and the classes , for fixed values of . Two, designing efficient algorithms to recognize graphs that belong to these classes.
Let’s begin with the former theme. Here important roles are played by chordal and strongly chordal graphs. A graph is chordal if every cycle of length four or more has a chord, an edge connecting two non-consecutive vertices of cycle. A graph is strongly chordal if it is chordal and all its even cycles of length or more have an odd chord, a chord connecting two vertices an odd distance apart along the cycle. Now, it is known that every graph in and is strongly chordal.111In particular they do not contain, as induced subgraphs, chordless cycles of length greater than three, nor sun graphs. To see this, first note that a leaf power graph is an induced subgraph of a power of a tree. Second, note that trees are strongly chordal, and taking powers and induced subgraphs both preserve this property [29]). However, the reciprocal is not true: there exist strongly chordal graphs that are not leaf powers. The first such example was discovered by Brandstädt et al. [5]. Subsequently, six additional examples were identified by Nevries and Rosenke [27] who conjectured that any strongly chordal graph not containing any of these seven graphs as an induced subgraph is a leaf power. However, a weaker version of this conjecture, that there are only a finite number (rather than seven) of obstructions was was disproved by Lafond [19]. The author constructed an infinite family of minimal strongly chordal graphs that are not leaf powers (i.e., removing any vertex results in a leaf power).
For fixed , the conjecture that may be characterized by a finite set of obstructions remained open. Indeed, for , the classes can be characterized as chordal graphs that do not contain any graph from as induced subgraphs, where is a finite set. Specifically:
-
: A graph is in if and only if it is a disjoint union of cliques. That is, is precisely the set of graphs that forbid , the chordless path with three vertices, as an induced subgraph. Thus .
-
: Brandstädt, Bang Le and Sritharan [4] proved that a graph is in if and only if it is chordal and does not contain as induced subgraph one of a finite set of graphs222Formally, they show that the set of basic 4-leaf power, where no two leaves of the leaf root share a parent, can be characterized by chordal graphs which do not have one of 8 graphs as induced subgraphs. can be deduced from this set..
Given this, the aforementioned conjecture naturally arose: for every , is the class equivalent to the set of chordal graphs that do not contain as induced subgraphs any of a finite set of graphs?
For , Brandstädt, Bang Le and Rautenbach [7] proved this is true for a special subclass of . Specifically, the distance hereditary333A graph is distance hereditary if for all pairs of vertices in all subgraphs of either the distance is the same as in or there is no path from to . -leaf power graphs are chordal graphs that do contain a set of graphs as induced subgraphs. However, for the general case, they state
“For , no characterization of -leaf powers is known despite considerable effort. Even the characterization of -leaf powers appears to be a major open problem.” [7]
The contribution of this paper is to disprove the conjecture: for all , it is impossible to characterize the set of -leaf powers as the set of chordal graphs which are -free for finite. In fact, we show that even for the more restrictive class of strongly chordal graphs it is impossible to characterize the set of -leaf powers as the set of strongly chordal graphs which are -free for finite .
Let us conclude this section by discussing the second major theme in this area, namely, efficient recognition algorithms. The computational complexity of deciding whether or not a graph is in is wide open. We remark, however, that some graphs in have a leaf rank that is exponential in the number of their vertices, where the leaf rank of a graph is the minimum such that [18]. The question of computing the leaf rank of subclasses of in polynomial time was recently initiated in [23].
For fixed values of , though, progress has been made in designing polynomial-time algorithms for the recognition problem. For and , this immediately follows from the above characterizations because and are finite. In fact, all these three recognition problems can be solved in linear time; see [6, 4]. Using a dynamic programming approach, Chang and Ko [10] described a linear-time algorithm for the recognition problem, and Ducoffe [13] proposed a polynomial-time algorithm for the recognition problem. Recently, Lafond [20] designed a polynomial-time algorithm for the recognition problem, for any constant . The algorithm is theoretically efficient albeit completely impractical: the polynomial’s exponent depends only on but is , that is, a tower of exponents of height . We remark that the algorithm does not rely on specific characterizations of -leaf power graphs aside from the fact that they are chordal. It appears difficult to significantly improve its running time without a better understanding of the graph theoretical structure of graphs in . Our work assists in this regard by improving our knowledge of -leaf powers in terms of forbidden induced subgraphs.
1.2 Overview and Results
We now present an overview of the paper and our results. In Section 2 we present our main theorem:
Theorem 1.
For , the set of -leaf powers cannot be characterized as the set of strongly chordal graphs which are -free, where is a finite set of graphs.
There we discuss the three types of gadgets we need. These gadgets can be combined to form an infinite family of pairwise incomparable graphs which are not -leaf powers. We prove the main theorem modulo three critical lemmas on the gadgets. In Section 3 we present proofs of the three critical lemmas. Finally, in Section 4 we show how to modify our proof to derive a similar theorem for linear -leaf powers:
Theorem 2.
For , the set of linear -leaf powers cannot be characterized as the set of strongly chordal graphs which are -free where is a finite set of graphs.
Here, a linear -leaf power is a graph that has a -leaf root which is the subdivision of a caterpillar. We remark that that the class of linear leaf powers can be recognised in linear time, as shown by Bergougnoux et al. [3].
2 The Proof Modulo Three Critical Lemmas
In this section we prove our main theorem, Theorem 1, assuming the validity of three critical lemmas. The proofs of these lemmas form the main technical contribution of the paper and are deferred to Section 3.
2.1 Preliminaries
Before presenting the proof of Theorem 1, we present necessary definitions and notations. Let’s start with a formal definition of -leaf powers. Let be a simple finite graph, and be an integer. Then is called a -leaf power if there exists a tree , known as a -leaf root of , with the following properties:
-
is the set of leaves of .
-
For any pair of distinct vertices , there is an edge if and only if .
Here is the distance metric induced by the tree when two adjacent vertices are a distance of apart. To simplify the notation, we will use instead of when the context is clear. We will use the notation to denote distance within the graph and thus distinguish it from the distance induced by a leaf root .
2.2 The Proof of the Main Theorem
To prove Theorem 1, for any , we will construct a collection of arbitrarily large strongly chordal graphs that are minimal non -leaf powers. Specifically, these graphs have the property that any proper induced subgraph is a -leaf power.
To accomplish this goal, we fix . We then begin by designing a graph , for all , built using three gadget graphs joined in series. First will be the top gadget and last the bottom gadget. In between will be exactly copies of the interior gadget. We denote these gadget graphs by and , respectively. These gadget graphs will satisfy a set of critical properties. To formalize these properties we require the following definition. Consider a graph and a -leaf root of . For , let . That is, is the shortest distance in the tree from the leaf to any other leaf .
The aforementioned properties of and are stated in the subsequent three critical lemmas.
Lemma 3.
For all , there exists a gadget graph Top that contains a vertex such that:
-
1.
For any -leaf root of Top, .
-
2.
There exists a -leaf root of Top.
Lemma 4.
For all , there exists a gadget graph Bot that contains a vertex such that:
-
1.
For any -leaf root of Bot, .
-
2.
There exists a -leaf root such that
Lemma 5.
For all , there exists a gadget graph that contains two distinct vertices such that:
-
1.
For all -leaf roots of , .
-
2.
There exists a -leaf root of such that and .
-
3.
There exists a -leaf root of such that and .
We will prove the existence of gadget graphs and required to verify the three lemmas in Section 3. For the rest of the section, we will assume these lemmas and use them to prove our main result.
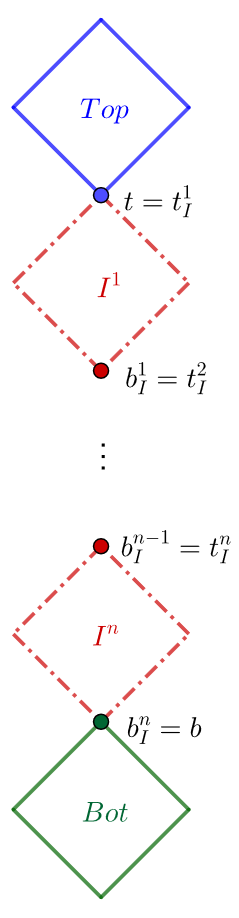
First, as alluded to above, we then combine our three gadgets to create an intermediary graph . In particular, is the graph obtained by connecting in series one copy of Top, then copies of : and finally one copy of Bot. This construction is illustrated in Figure 1(a). The vertices and , mentioned in Lemma 5, of the -th copy are denoted and , respectively. Notice that to connect the gadgets within , we identify the vertices described in Lemmas 3, 4, and 5 as follows. We identify with , for all , with , and finally, with . As a special case when , the graph is obtained by taking Top and Bot and identifying with .
In order to prove Theorem 1 we must study the structure of . We denote by (resp. ) the graph obtained from by deleting the top gadget Top (resp. the bottom gadget Bot), i.e. removing all vertices of Top (resp. Bot) except for the common vertex (resp. ). Of importance is the next lemma.
Lemma 6.
The graph has the following properties:
-
1.
.
-
2.
is strongly chordal.
-
3.
and are both -leaf powers.
-
4.
is not a -leaf power.
Proof.
In order to prove 1, the distance between and in is at least because the two vertices are distinct. Hence , because there are copies of the interior gadget .
For the proof of 2, the three gadgets are -leaf powers and, therefore, are strongly chordal. The construction of does not introduce additional cycles; thus, remains strongly chordal.
To prove 3, we combine the leaf-root properties provided by the gadgets , , , and , as illustrated in Figure 1(b).
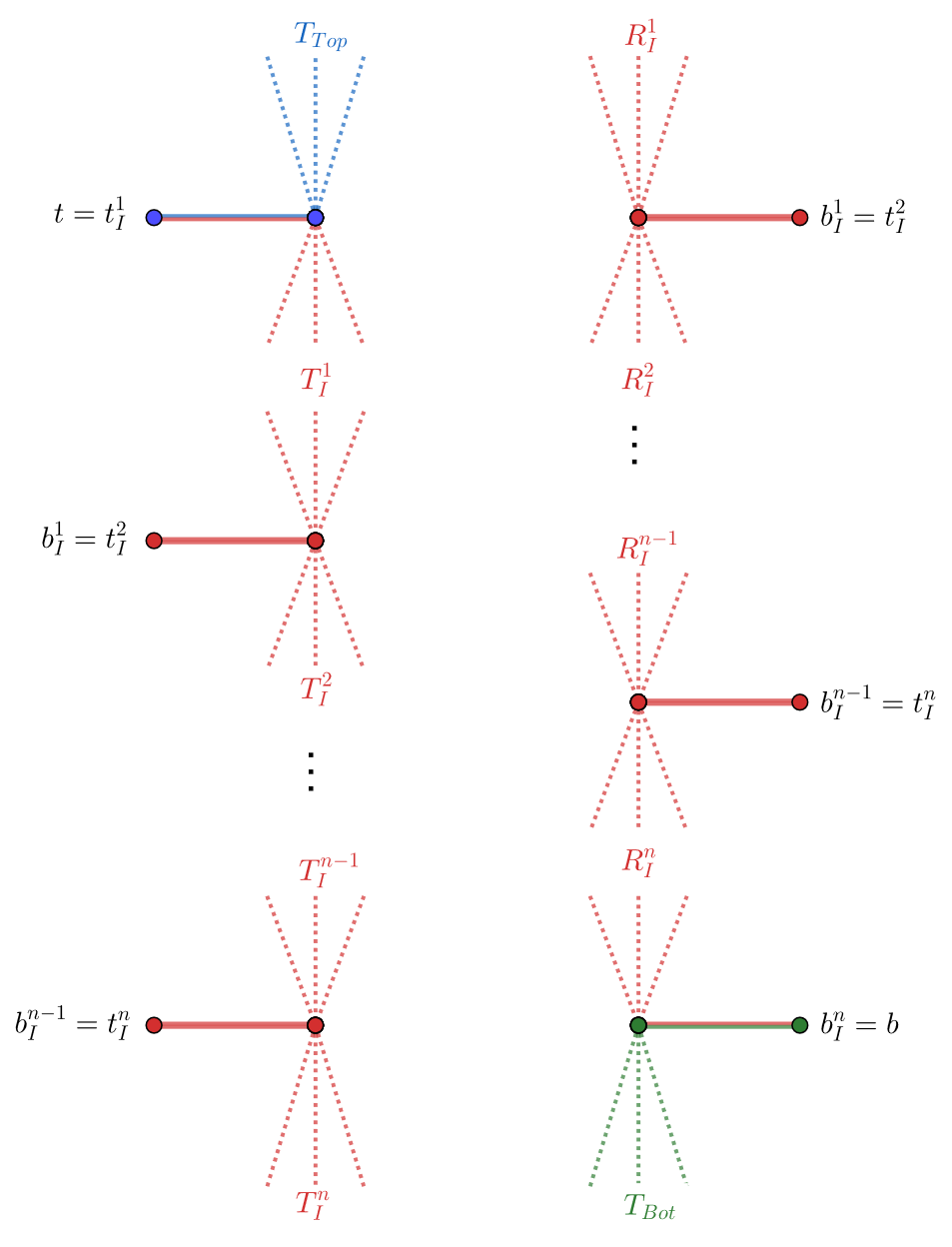
The left tree in Figure 1(b) is obtained by merging with copies of , denoted as . We identify with , and we identify the parent of in with the parent of in . Similarly, for all , we identify and its parent with and its parent, respectively. We now prove that the resulting tree is a -leaf root of . Top and each copy of the interior gadget are the -leaf power of the corresponding subtree: for Top and for the -th copy of . It remains to show that we do not introduce any additional, unwanted edges. If is a leaf of different from , and is a leaf of different from then, using Lemma 3, we conclude . Furthermore, using the second point of Lemma 5, we conclude . Therefore, , and there is no edge between and in the -th power of the tree. Similarly, if is a leaf of different from for some and is a leaf of different from , we have and . Thus, , and there is no edge between and in the -th power of the tree.
The right tree in Figure 1(b) is formed by merging copies of , denoted , with . For all , we identify with , and we identify the parent of with the parent of . Finally, we identify and its parent in with and its parent in , respectively. Similar to the left tree, we must prove that no additional, unwanted edges are created. If is a leaf of different from for some and is a leaf of different from then, using Lemma 5, we conclude and . Thus, , and there is no edge between and in the -th power of the tree. Similarly if is a leaf of different from and is a leaf of different from then we have and, using Lemma 4, . Therefore and , are not connected in the -th power of the tree. This completes the proof of 3, the third point of the lemma.
It remains to prove 4, the final point of the lemma. We start by proving by induction that for any integer , in any -leaf root of , there is a leaf at distance of in . When , there are no gadgets between Bot and Top, so and the property holds by property 1 of Lemma 3. Turning to the induction step, assume that the property holds for some and consider a -leaf root of . Since is an induced subgraph of , some induced subgraph of is a -leaf root of . By the induction hypothesis, there exists a vertex in at a distance exactly from in an induced subgraph of . Adding vertices will not alter the distance, so in . We claim that every vertex of is at distance at least from in (except itself). Assume, by contradiction, that there exists a vertex in the last copy , distinct from such that that . This assumption would imply that , meaning that and are connected in the -th power of , contradicting the fact that is a -leaf root of . Therefore, all vertices in , distinct from , are at a distance of at least from in . We can now apply property 1 of Lemma 5, which concludes the induction.
Now assume by contradiction that there exists a -leaf root of . Then induces a -leaf root of . In particular, there exists a vertex in such that . Moreover, property 1 of Lemma 4 implies that there exists a vertex in Bot, distinct from , such that . Combining these equations, we get , contradicting the fact that there is no edge between and . This proves that is not a -leaf power, as desired.
As stated is an intermediate graph in proving the main result. We will actually show the existence of an induced subgraph of that is strongly chordal and minimal non -leaf power. More precisely, we have the following lemma.
Lemma 7.
For all and , there exists a graph such that:
-
1.
is strongly chordal and contains at least vertices.
-
2.
is not a -leaf power.
-
3.
If is an induced subgraph of then is a -leaf power.
Proof.
Let be a minimal induced subgraph of that is not a -leaf power. It is strongly chordal because, by Lemma 6, is strongly chordal. By definition, is not in , but every induced subgraph of is in if . It remains to prove that . By Lemma 6, both and are in . Therefore, must contain a vertex from Top and a vertex from Bot. Moreover, is connected by its minimality, since the disjoint union of -leaf powers is a -leaf power. Hence, must contain a path from Top to Bot. By Lemma 6, , and therefore .
Our main result follows directly from Lemma 7
Proof of Theorem 1.
3 The Gadget Graphs
So we have proven the main theorem modulo the three critical lemmas. Recall to prove these lemmas we must construct the appropriate three gadget graphs, namely Top, Bot and . We present these constructions and give formal proofs of Lemmas 3, 4 and 5 in this section.
We start with a general observation. In a tree , if a pair of leaves are a distance of apart, they share the same parent. Consequently, their distances to every other leaf are identical. A consequence of this is that if two vertices are not connected by an edge, or if they have different neighborhoods in a graph, they must be at a distance of at least in any leaf root of that graph. In the gadgets we describe in this section, any two vertices connected by an edge always have distinct neighborhoods. Therefore, we assume that for any pair of vertices and and any leaf root , we have .
3.1 The Top Gadget
We begin by showing the existence of an appropriate top gadget, Top.
See 3
Proof.
Let be the path on the vertices . The top gadget Top is defined as with . Two examples of Top are shown in Figure 2, for the cases . First, note that Top is a -leaf power. In particular, a -leaf root of Top is the caterpillar , which is constructed by attaching a leaf to every vertex of . For the first property, we use Lemma from [32], which states that if is an induced subgraph of , where is a tree and , then (note that the lemma is more general, as can have length for any , and the result applies to and ; here we took ). Thus, if is any -leaf root of Top, then does contain as an induced subgraph and the property holds.
3.2 The Bottom Gadget
Next, we construct the bottom gadget, Bot. A key technical tool we require is the 4-Point Condition. This is the following classical characterization of tree metrics.
Theorem 8 (4-Point Condition).
[8] Let be a distance on a finite set , then there exists a tree whose leaves are such that , if and only if the following condition is true for all :
Our bottom gadget Bot will simply be a diamond, the complete graph on 4 vertices minus one edge. Consequently, we begin by proving the following corollary of the -Point Condition when applied to a diamond.
Corollary 9.
In any -leaf root of a diamond with vertex set where , .
Proof.
Assume for contradiction that . Then since , we get .
On the other hand, since we have a leaf root of the diamond, we must have:
This implies that and .
So, which contradicts Theorem 8
Corollary 9 allows us to prove our critical lemma for the bottom gadget.
See 4
Proof.
Let the graph Bot be the diamond with vertex set and non-edge . By Corollary 9, in any leaf root. Thus the first property holds. For the second property, there are two cases, illustrated in Figure 3, depending upon the parity of .
-
If is odd, start with and at distance . Let be the midpoint of the two at distance from both. Set and to be each at distance from . Then and will both be at distance exactly from both and , but and are at distance from each other. Thus, the only distance which is greater than is and the closest vertex to is , as desired.
-
If is even, start with and at distance . Set to be the point at distance from and the point at distance from . Add at distance from and at distance from . Then is at distance from and from , while is at distance from and from . Note that and are at distance from each other. Thus, the only distance which is greater than is and the closest vertex to is , as desired.
This lemma follows.
3.3 The Interior Gadget
Lastly, we have the most complex construction, that of the interior gadget, . Now we require the following lemma which, again, is a consequence of the 4-Point Condition.
Lemma 10.
Suppose that is the distance function between leaves of a tree . If and , then:
Proof.
Assume that . Then, by using this assumption and our bound on , we get:
Then, by combining this bound with our bound on , we get:
This contradicts Theorem 8. This implies that the assumption is wrong, that is, we must have:
Now, assume without loss of generality that . Then, by Theorem 8, we must have:
Since , this implies that . So we get that is bounded above and below by so they must be equal.
So we get:
This completes the proof.
We will also use the following simple lemma:
Lemma 11.
Suppose that is the distance function between leaves of a tree . Then for any 3 leaves of , is even.
Proof.
Since we have a tree, there is a unique vertex which is simultaneously in the path from to , the path from to and the path from to .
Hence which must be even.
We now have all the tools needed to prove our critical lemma for the interior gadget.
See 5
Before proving this lemma, let’s discuss the requirement that . First observe that no such graph can exist for because if then is an isolated vertex in . Thus its distance to other leaves does not matter as long as it’s large enough, so the lemma could not hold. Similarly, if , the existence of a -leaf root implies that is not an isolated vertex in . But the existence of a -leaf root implies that is an isolated vertex, a contradiction. Finally, for , while there is no direct simple proof that the statement does not hold for any graph, the existence of a characterization of -leaf powers implies that no such graph can exist.
Proof.
For convenience, we denote and by and , respectively. To prove the lemma, we will explicitly construct for any value of . In order to do so, we consider two cases depending, again, upon the parity of .
For odd, set . In particular, for we must have .
We construct the graph using the following sets of vertices:
-
and
-
-
The edge set is defined as follows (note that for clarity, we use ordered pairs to represent edges, with the understanding that the edges are undirected):
-
For , and are edges. That is, and are adjacent to all vertices in .
-
For , for , is an edge. That is, forms a clique.
-
For , for , is an edge.
-
is an edge.
Equivalently, it will be helpful to define the set of edges using the neighborhood of each vertex:
-
is adjacent to .
-
is adjacent to and to .
-
For , is adjacent to , to , to and to for (with having no neighbor in ).
-
For , for , is adjacent to . If , then is also adjacent to .
That is, we take to be defined by:
| (1) | ||||
This construction is illustrated in Figure 4. We remark that this construction only makes sense for because if or then is an empty set.
We will prove that this graph satisfies the lemma by proving three claims.
Proof.
Assume that , then , . Then for all distinct , by Lemma 11 with , and , must be even (and, thus, at most ).
Assume . Then . Furthermore, because is adjacent to and but not (nor ). So, by Lemma 10, we get:
But because . This is true if and only if
This implies that for every , there exists some integer such that . Moreover, as shown, the must be even. Thus . By definition, . In particular, there are only even numbers greater that and at most . Therefore, . Specifically, we have shown that , for .
Recall and , for . So, by Lemma 10, we obtain:
Consider . Recall and . So implying that . It follows that
However, we must have and . So it must be that and .
Next consider . Because , we have and so exists. Then . Therefore, because for all , we have
Finally, recall that . This implies that . In particular, . Moreover, by Lemma 11, we know is even. But is even and is odd. Hence must be odd. In particular, it must be odd and less than 5. Hence , which is what we wanted to show.
Proof.
We will prove this by explicitly constructing a leaf root. Recall is odd and .
-
1.
Take a path of length from to .
-
2.
Label the vertices along the path from to which are at distance of as for .
-
3.
Add a path of length from to for .
-
4.
Add a path of length from to .
-
5.
If , add a path of length from to for . (For we have , so these do not exist.)
This construction is shown in Figure 5. It remains to verify that this is a valid -leaf root of , that is, the leaf vertices at distance at most in the tree are exactly the edges of . The required case analysis follows.
-
The path from to has length and and are not neighbors, as desired.
-
For , the path from to goes through . That is, it is the path from to which has length followed by the path from to which has length . So, the path from to has length .
-
The path from to goes through , so it has length .
-
For , the path from to goes through and so it has length . In particular, for , the path from to has length .
-
The path from to goes through so it has length
-
For , the path from to goes through and so it has length
-
For and , the path from to goes through and (possibly the same vertex) so it has length which is at most if and only if .
-
For , the path from to goes through and so it has length which is equal to if and strictly greater than otherwise.
For the case analysis is complete. If then and so . Thus we have four more cases to verify:
-
For , the path from to goes through , so it has length .
-
For , the path from to goes through and so it has length .
-
For , the path from to goes through and , so it has length .
-
For , the path from to goes through and so it has length .
Hence the desired -leaf root exists.
It remains to prove the final property to conclude that the claim holds when is odd:
Proof.
To construct we make two minor modifications to the tree used to prove Claim 13. First we start with a path of length from to . To do this we simply place at distance from instead of . All the remaining vertices are then placed using the same process except for which is now at distance from instead of at distance . The resultant tree is shown in Figure 6.
It suffices to verify that all the vertices are still at a correct distance from and from .
-
The distance from to all other vertices except has decreased by so we need to verify that the and are still at distance at least . For , the distance from to is (since ). The distance from to is (since ).
-
The distance from to all other vertices except has increased by so we need to verify that the ’s and are still at distance at most . For , the distance from to is . The distance from to is . Moreover, all distances from to an vertex are now at least and not (including , which is at distance from ). In particular, the distance between and is exactly .
Observing that is now at distance from and is still at distance to its other neighbors, we get and . Hence the desired -leaf root exists.
We have now proven the result holds for odd. A similar but slightly more intricate proof can be used to prove the result also holds for even to complete the proof of the lemma. The proof for that case is deferred to the full version of the paper. With our three critical lemmas proven, the main theorem now holds by the method shown in Section 2.
4 Linear Leaf Powers
A caterpillar is a graph which has a central path and a set of leaves whose neighbor is on the central path. A graph is said to be a linear leaf power if it has a leaf root which is the subdivision of a caterpillar. Such a leaf root is called a linear leaf root [3]. Our results apply not only to general leaf powers but also to this variant. Indeed, even if we restrict to having a subdivision of a caterpillar as a leaf root, it is impossible to get a simple forbidden subgraph characterization of linear -leaf powers for .
Theorem 15.
For , the set of linear -leaf powers cannot be written as the set of strongly chordal graphs which are -free where is a finite set of graphs.
As in the general case, we prove this theorem using three gadgets. However, we must now add a condition to ensure that merging the gadgets preserves having a subdivision of a caterpillar as a leaf root. In particular, we will be able to use the same interior and bottom gadgets but the top gadget needs to be modified. The proof is given in the full version of the paper.
We remark that this result does not immediately imply that there is no characterization for the entire class of linear leaf powers using chordal graphs and a finite number of forbidden induced subgraphs. We have proven that such a characterization is impossible for each , but not necessarily for the union over all . It was proved by Bergougnoux et al. [3] that linear leaf powers are also co-threshold tolerance. Further work on this could include verifying whether co-threshold tolerance graphs can be characterized using a finite number of obstructions. Furthermore, it is worth noting that, despite Theorem 15, linear leaf powers are recognizable in polynomial time [3].
5 Conclusion
We have shown that -leaf powers require a deeper characterization than strong chordality with a finite set of forbidden induced subgraphs. Several directions to explore remain in order to gain a more comprehensive understanding of -leaf power graphs. First, is it possible to construct and/or characterize minimal, strongly chordal graphs that are not -leaf powers? We were able to construct graphs that contain such minimal examples as induced subgraphs; but we did not construct those examples explicitly. Following this line of reasoning, it may be possible to characterize -leaf powers as strongly chordal graphs that also forbid an additional infinite, but easy-to-describe family of forbidden subgraphs. A famous example of this are interval graphs, which are the chordal graphs containing no asteroidal triples [24].
Second, are there relevant subclasses of -leaf powers that can be characterized by strong chordality and a finite set of forbidden induced subgraphs? For example, the -leaf powers whose -leaf roots admit a subdivision of a star should be easy enough to characterize. What about subdivisions of a tree with a small number, say two or three, of non-leaf vertices? One may also consider the -leaf powers of caterpillars (not subdivided). Based on the midpoint arguments of Brandstädt et al. [5, Theorem 6], it would appear that, for even , these coincide with the unit interval graphs whose intervals have length and integer endpoints. Such (twin-free) graphs were shown to admit a finite set of forbidden induced subgraphs in [14]. If this characterization extends to caterpillar -leaf powers, this would show that taking subdivisions is necessary for our result on caterpillar graphs. It may also be interesting to characterize -leaf powers for other graph classes that are known to be contained in ; for instance, -leaf powers that are also ptolemaic graphs, interval graphs, rooted directed path graphs, and others.
References
- [1] Ittai Abraham, David Durfee, Ioannis Koutis, Sebastian Krinninger, and Richard Peng. On fully dynamic graph sparsifiers. In 2016 IEEE 57th Annual Symposium on Foundations of Computer Science (FOCS), pages 335–344, 2016. doi:10.1109/FOCS.2016.44.
- [2] R. Ahmed, G. Bodwin, F. Sahneh, K. Hamm, M. Jebelli, S. Kobourov, and R. Spence. Graph spanners: A tutorial review. Computer Science Review, 37:100253, 2020. doi:10.1016/J.COSREV.2020.100253.
- [3] B. Bergougnoux, S. Høgemo, J. Telle, and M. Vatshelle. Recognition of linear and star variants of leaf powers is in p. In Michael A. Bekos and Michael Kaufmann, editors, Graph-Theoretic Concepts in Computer Science, pages 70–83, Cham, 2022. Springer International Publishing.
- [4] A. Brandstädt, V. Le, and R. Sritharan. Structure and linear-time recognition of 4-leaf powers. ACM Trans. Algorithms, 5(1), December 2008. doi:10.1145/1435375.1435386.
- [5] A. Brandstädt, C. Hundt, F. Mancini, and P. Wagner. Rooted directed path graphs are leaf powers. Discrete Mathematics, 310(4):897–910, 2010. doi:10.1016/j.disc.2009.10.006.
- [6] A. Brandstädt and V. Le. Structure and linear time recognition of 3-leaf powers. Information Processing Letters, 98(4):133–138, 2006. doi:10.1016/j.ipl.2006.01.004.
- [7] A. Brandstädt, V. Le, and D. Rautenbach. A forbidden induced subgraph characterization of distance-hereditary 5-leaf powers. Discrete Mathematics, 309(12):3843–3852, 2009. doi:10.1016/j.disc.2008.10.025.
- [8] P. Buneman. A note on the metric properties of trees. Journal of Combinatorial Theory, Series B, 17(1):48–50, 1974. doi:10.1016/0095-8956(74)90047-1.
- [9] H-C. Chang, R. Krauthgamer, and Z. Tan. Almost-linear -emulators for planar graphs. In Proceedings of the 54th Annual ACM SIGACT Symposium on Theory of Computing, pages 1311–1324, 2022.
- [10] M-S. Chang and M-T. Ko. The 3-steiner root problem. In Andreas Brandstädt, Dieter Kratsch, and Haiko Müller, editors, Graph-Theoretic Concepts in Computer Science, pages 109–120, Berlin, Heidelberg, 2007. Springer Berlin Heidelberg.
- [11] V. Cohen-Addad, A. Filtser, P. Klein, and H. Le. On light spanners, low-treewidth embeddings and efficient traversing in minor-free graphs. In 2020 IEEE 61st Annual Symposium on Foundations of Computer Science (FOCS), pages 589–600. IEEE, 2020.
- [12] M. Dom, J. Guo, F. Hüffner, and R. Niedermeier. Error compensation in leaf root problems. In Algorithms and Computation, pages 389–401, December 2004. doi:10.1007/978-3-540-30551-4_35.
- [13] G. Ducoffe. The 4-steiner root problem. In International Workshop on Graph-Theoretic Concepts in Computer Science, pages 14–26. Springer, 2019.
- [14] G. Durán, F. Slezak, L. Grippo, F. Oliveira, and J. Szwarcfiter. On unit interval graphs with integer endpoints. Electronic Notes in Discrete Mathematics, 50:445–450, 2015. doi:10.1016/J.ENDM.2015.07.074.
- [15] A. Filtser, M. Kapralov, and N. Nouri. Graph spanners by sketching in dynamic streams and the simultaneous communication model. In Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms (SODA), pages 1894–1913. SIAM, 2021.
- [16] Wai Shing Fung, Ramesh Hariharan, Nicholas J.A. Harvey, and Debmalya Panigrahi. A general framework for graph sparsification. In Proceedings of the Forty-Third Annual ACM Symposium on Theory of Computing, STOC ’11, pages 71–80, New York, NY, USA, 2011. Association for Computing Machinery. doi:10.1145/1993636.1993647.
- [17] M. Hellmuth, C. Seemann, and P. Stadler. Generalized fitch graphs ii: Sets of binary relations that are explained by edge-labeled trees. Discrete Applied Mathematics, 283:495–511, 2020. doi:10.1016/J.DAM.2020.01.036.
- [18] S. Høgemo. Lower bounds for leaf rank of leaf powers. CoRR, abs/2402.18245, 2024. doi:10.48550/arXiv.2402.18245.
- [19] M. Lafond. On strongly chordal graphs that are not leaf powers. In H. Bodlaender and G. Woeginger, editors, Graph-Theoretic Concepts in Computer Science, pages 386–398, Cham, 2017. Springer International Publishing.
- [20] M. Lafond. Recognizing -leaf powers in polynomial time, for constant . ACM Trans. Algorithms, 19(4), September 2023. doi:10.1145/3614094.
- [21] M. Lafond and N. El-Mabrouk. Orthology and paralogy constraints: satisfiability and consistency. BMC genomics, 15:1–10, 2014.
- [22] H. Le and S. Solomon. Near-optimal spanners for general graphs in (nearly) linear time. In Proceedings of the 2022 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pages 3332–3361. SIAM, 2022.
- [23] V. Le and C. Rosenke. Computing optimal leaf roots of chordal cographs in linear time. In International Symposium on Fundamentals of Computation Theory, pages 348–362. Springer, 2023.
- [24] C. Lekkerkerker and J Boland. Representation of a finite graph by a set of intervals on the real line. Fundamenta Mathematicae, 51:45–64, 1962.
- [25] Jiayu Li, Tianyun Zhang, Hao Tian, Shengmin Jin, Makan Fardad, and Reza Zafarani. Sgcn: A graph sparsifier based on graph convolutional networks. In Hady W. Lauw, Raymond Chi-Wing Wong, Alexandros Ntoulas, Ee-Peng Lim, See-Kiong Ng, and Sinno Jialin Pan, editors, Advances in Knowledge Discovery and Data Mining, pages 275–287, Cham, 2020. Springer International Publishing. doi:10.1007/978-3-030-47426-3_22.
- [26] Y. Long and P. Stadler. Exact-2-relation graphs. Discrete Applied Mathematics, 285:212–226, 2020. doi:10.1016/J.DAM.2020.05.015.
- [27] R. Nevries and C. Rosenke. Towards a characterization of leaf powers by clique arrangements. Graphs and Combinatorics, 32:2053–2077, 2016. doi:10.1007/S00373-016-1707-X.
- [28] N. Nishimura, P Ragde, and D. Thilikos. On graph powers for leaf-labeled trees. Journal of Algorithms, 42(1):69–108, 2002. doi:10.1006/jagm.2001.1195.
- [29] A. Raychaudhuri. On powers of strongly chordal and circular arc graphs. Ars Combin., 34:147–160, 1992.
- [30] M. Thorup and U. Zwick. Spanners and emulators with sublinear distance errors. In Proceedings of the seventeenth annual ACM-SIAM symposium on Discrete algorithm, pages 802–809, 2006.
- [31] J. Van Den Brand, S. Forster, and Y. Nazari. Fast deterministic fully dynamic distance approximation. In 2022 IEEE 63rd Annual Symposium on Foundations of Computer Science (FOCS), pages 1011–1022. IEEE, 2022.
- [32] P. Wagner and A. Brandstädt. The complete inclusion structure of leaf power classes. Theoretical Computer Science, 410(52):5505–5514, 2009. Combinatorial Optimization and Applications. doi:10.1016/j.tcs.2009.06.031.
