Identifying Approximate Minimizers Under Stochastic Uncertainity

Any solution to $\mathrm{𝖲𝖬𝖰}$ involves querying r.v.s sequentially until a $\delta$-minimum value is found. In general, the sequence of queries may depend on the realizations of previously queried r.v.s. We refer to such solutions as adaptive policies. Formally, such a solution can be described as a decision tree where each node corresponds to the next r.v. to query and the branches out of a node represent the realization of the queried r.v. Non-adaptive policies are a special class of solutions where the sequence of queries is fixed upfront: the policy then performs queries in this order until a $\delta$-minimum value is found. A central notion in stochastic optimization is the adaptivity gap [7], which is the worst-case ratio between the optimal non-adaptive value and the optimal adaptive value. All our algorithms produce non-adaptive policies and hence also bound the adaptivity gap.

Even without querying any interval, we know that the minimum value is at most $R:={\min }_{i\in N}\{r_i\}$, the minimum right-endpoint. In order to simplify notation, we incorporate this information using a dummy r.v. $X_0=[R,R]$ that is queried at the start of any policy and incurs no cost. We now formally define the condition under which a policy for $\mathrm{𝖲𝖬𝖰}$ is allowed to stop. We will refer to the partial observations at any point in a policy (i.e., values of r.v.s queried so far) as the state. Consider any state, given by a subset $S\subseteq N$ of queried r.v.s along with their observations ${\{x_i\}}_{i\in S}$. The minimum observed value is ${\min }_{i\in S}{x}_i$ and the minimum possible value among the un-queried r.v.s is ${\min }_{j\in N\setminus S}{\mathrm{\ell }}_j$. The stopping criterion is:

If this criterion is met then $\mathrm{𝖵𝖠𝖫}={\min }_{i\in S}{x}_i$ is guaranteed to satisfy $\mathrm{𝖬𝖨𝖭}\le \mathrm{𝖵𝖠𝖫}\le \mathrm{𝖬𝖨𝖭}+\delta$, where $\mathrm{𝖬𝖨𝖭}={\min }_{j\in N}{X}_j$. Also, $\arg {\min }_{i\in S}{x}_i$ is a $\delta$-minimizer. On the other hand, if this criterion is not met then there is no value $v$ that guarantees $\mathrm{𝖬𝖨𝖭}\le v\le \mathrm{𝖬𝖨𝖭}+\delta$: there is a non-zero probability that the minimum value is ${\min }_{j\in N\setminus S}{\mathrm{\ell }}_j$ or ${\min }_{i\in S}{x}_i$ (and these values are more than $\delta$ apart). So,

The stopping rule for $\mathrm{𝖲𝖬𝖰𝖨}$ is described in §2.2. An $\mathrm{𝖲𝖬𝖰𝖨}$ policy can stop either due to the $\mathrm{𝖲𝖬𝖰}$ stopping rule (above) or by inferring an un-queried interval $i^{\ast }$ as a $\delta$-minimizer.

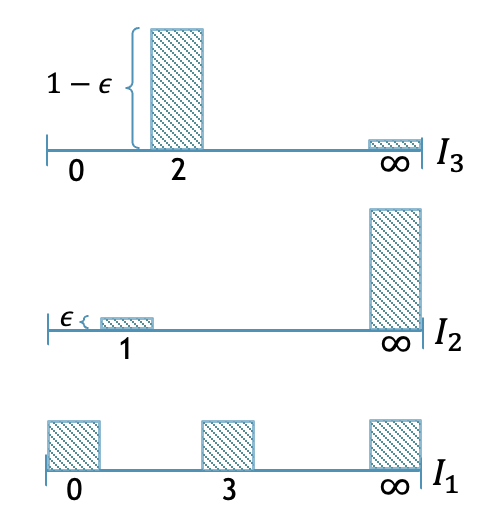
We show that the adaptivity gap for the $\mathrm{𝖲𝖬𝖰}$ problem is more than one: so adaptive policies may indeed perform better. This example also builds some intuition for the problem. Consider an instance $ℐ$ with three intervals as shown in Figure 2. In particular, $X_1\in \{0,3,\mathrm{\infty }\}$, $X_2\in \{1,\mathrm{\infty }\}$, $X_3\in \{2,\mathrm{\infty }\}$ and $\delta =1$. Let $\mathrm{Pr}(X_1=0)=\frac{1}{3},\mathrm{Pr}(X_1=3)=\frac{1}{3},\mathrm{Pr}(X_1=\mathrm{\infty })=\frac{1}{3},\mathrm{Pr}(X_2=1)=ϵ,\mathrm{Pr}(X_2=\mathrm{\infty })=1-ϵ,\mathrm{Pr}(X_3=2)=1-ϵ,\mathrm{Pr}(X_3=\mathrm{\infty })=ϵ$. An adaptive policy is shown in Figure 2, which has cost at most $1+\frac{2}{3}+\frac{ϵ}{3}=\frac{5+ϵ}{3}$. We present a case analysis in [2] and show that the best non-adaptive cost is $\min \{\frac{6-ϵ}{3},\frac{5+2ϵ}{3}\}$. Setting $ϵ=\frac{1}{3}$, we obtain an adaptivity gap of $\frac{17}{16}$. We can also modify this instance slightly to get a worse adaptivity gap of $\frac{12}{11}$.

In our analysis, we relate $\mathrm{𝖲𝖬𝖰}$ to the following simpler problem. Given $n$ r.v.s $\{X_i:i\in N\}$ with costs as before, a fixed threshold $\theta$ and budget $k$, find a policy having query-cost at most $k$ that maximizes the probability of observing a realization less than $\theta$. A useful property of this fixed threshold problem is that it has adaptivity gap one [2].

Let ${\sigma }^k$ denote the optimal policy truncated after $k$ queries: so the cost of ${\sigma }^k$ is always at most $k$. Let $L({\sigma }^k)={\min }_{i\in N\setminus {\sigma }^k}\{{\mathrm{\ell }}_i\}$ denote the smallest un-queried left-endpoint at the end of ${\sigma }^k$; this is a random value because ${\sigma }^k$ is an adaptive policy. Then,

Equality (5) is by the stopping criterion for $\mathrm{𝖲𝖬𝖰}$. The inequality in (6) uses the observation that after any $k$ queries, the smallest un-queried left-endpoint must be at most ${\mathrm{\ell }}_{k+1}$: so $L({\sigma }^k)\le {\mathrm{\ell }}_{k+1}$ always. The equality in (6) is by definition of the threshold $\theta$. Inequality (7) follows from Proposition 1.2: we view ${\sigma }^k$ is a feasible adaptive policy for the fixed-threshold problem and $T^{\ast }$ is the optimal non-adaptive policy. $◀$

Recall that each iteration $j$ of Algorithm 1 selects two intervals: $j$ in Step 3 and $b(j)$ in Step 4. Let $B=\{b(1),\mathrm{\cdots }b(2k)\}$ be the set of intervals chosen by our policy $\pi$ in Step 4 of the first $2k$ iterations. We partition $B$ into $B^{\prime }=\{b(1),\mathrm{\cdots }b(k)\}$ and $B^{\prime \prime }=\{b(k+1),\mathrm{\cdots }b(2k)\}$. Let $d^{\ast }={\text{argmin}}_{d\in T^{\ast }\setminus B}\mathrm{Pr}(X_d>{\theta }_k)={\text{argmax}}_{d\in T^{\ast }\setminus B}\mathrm{Pr}(X_d\le {\theta }_k)$.

(8) follows from the definition of $d^{\ast }$. (10) just uses that $T^{\ast }\cap B$ and $B^{\prime \prime }\setminus T^{\ast }$ are disjoint subsets of $B$. The key step above is (9), which we prove using two cases:

• $\mathrm{■}$

  Suppose that $T^{\ast }\setminus B=\mathrm{\varnothing }$. Then, using ${\theta }_k\le {\theta }_{2k}$ we obtain $\mathrm{Pr}[X_i>{\theta }_k]\ge \mathrm{Pr}[X_i>{\theta }_{2k}]$, which proves (9) for this case.

• $\mathrm{■}$

  Suppose that $T^{\ast }\setminus B\ne \mathrm{\varnothing }$. In this case, $d^{\ast }$ is well-defined. We now claim that:

  $$\text{ For each }j=k+1,\mathrm{\cdots }2k\text{, either }b(j)\in T^{\ast }\text{ or }\mathrm{Pr}[X_{b(j)}>{\theta }_{2k}]\le \mathrm{Pr}[X_{d^{\ast }}>{\theta }_k].$$

  (11)

  Indeed, consider any such $j$ and suppose that $b(j)\notin T^{\ast }$. As $d^{\ast }$ is a valid choice for $b(j)$, the greedy rule implies:

  $$\mathrm{Pr}\left[X_{d^{\ast }}>{\theta }_j\right]\ge \mathrm{Pr}\left[X_{b(j)}>{\theta }_j\right].$$

  Further, using the fact that ${\theta }_k\le {\theta }_j\le {\theta }_{2k}$, we get

  $$\mathrm{Pr}\left[X_{d^{\ast }}>{\theta }_k\right]\ge \mathrm{Pr}\left[X_{d^{\ast }}>{\theta }_j\right]\ge \mathrm{Pr}\left[X_{b(j)}>{\theta }_j\right]\ge \mathrm{Pr}\left[X_{b(j)}>{\theta }_{2k}\right],$$

  which proves (11). Let $h$ denote the number of iterations $j\in \{k+1,\mathrm{\cdots }2k\}$ where $b(j)\notin T^{\ast }$. Note that $h=|B^{\prime \prime }|-|T^{\ast }\cap B^{\prime \prime }|=k-|T^{\ast }\cap B^{\prime \prime }|\ge |T^{\ast }\setminus B|$, where we used $|T^{\ast }|=k$. Using (11), it follows that $\mathrm{Pr}[X_i>{\theta }_{2k}]\le \mathrm{Pr}[X_{d^{\ast }}>{\theta }_k]$ for all $i\in B^{\prime \prime }\setminus T^{\ast }$. Hence,

  $$\mathrm{Pr}{[X_{d^{\ast }}>{\theta }_k]}^{|T^{\ast }\setminus B|}\ge \mathrm{Pr}{[X_{d^{\ast }}>{\theta }_k]}^h\ge \prod _{i\in B^{\prime \prime }\setminus T^{\ast }}\mathrm{Pr}[X_i>{\theta }_{2k}],$$

  Combined with the fact that ${\theta }_k\le {\theta }_{2k}$ (as before), we obtain (9).

We are now ready to complete the proof. Using the $\mathrm{𝖲𝖬𝖰}$ stopping criterion and the fact that $\pi$ queries all the intervals in $B$ within $2k$ iterations,

Combined with (10),

where we use the definition $\theta ={\theta }_k$. $◀$

We note that the optimal values of $\mathrm{𝖲𝖬𝖰}$ and $\mathrm{𝖲𝖬𝖰𝖨}$ differ by at most the maximum query cost $c_{max}$. As noted above, the optimal $\mathrm{𝖲𝖬𝖰𝖨}$ value is at most that of $\mathrm{𝖲𝖬𝖰}$. On the other hand, the optimal $\mathrm{𝖲𝖬𝖰}$ value is at most the optimal $\mathrm{𝖲𝖬𝖰𝖨}$ value plus the cost to query $i^{\ast }$. In the unit-cost setting, $c_{max}=1$ and any policy has expected cost at least $1$: so the optimal values of $\mathrm{𝖲𝖬𝖰}$ and $\mathrm{𝖲𝖬𝖰𝖨}$ are within a factor two of each other. This immediately implies that Algorithm 1 is also an $8$-approximation for unit-cost $\mathrm{𝖲𝖬𝖰𝖨}$. In the rest of this subsection, we will prove a stronger result, that Algorithm 1 is a $4$-approximation for $\mathrm{𝖲𝖬𝖰𝖨}$. Apart from the improved constant factor, these ideas will also be helpful for $\mathrm{𝖲𝖬𝖰𝖨}$ with general costs. We note that under general costs, the optimal $\mathrm{𝖲𝖬𝖰}$ and $\mathrm{𝖲𝖬𝖰𝖨}$ values may differ by an arbitrarily large factor because $c_{max}$ is not a lower bound on the optimal value.

Consider any state, given by a subset $S\subseteq N$ of queried r.v.s along with their observations ${\{x_i\}}_{i\in S}$. There are two conditions under which the $\mathrm{𝖲𝖬𝖰𝖨}$ policy can stop.

• $\mathrm{■}$

  The first stopping rule is just the one for $\mathrm{𝖲𝖬𝖰}$ (1), which corresponds to the situation that interval $i^{\ast }$ is queried. We restate this rule below for easy reference:

  $$\underset{i\in S}{\min }{x}_i\le \underset{j\in N\setminus S}{\min }{\mathrm{\ell }}_j+\delta .$$

  (12)

  In this case, we return $i^{\ast }=\arg {\min }_{i\in S}{x}_i$. We refer to this as the old stopping rule.

• $\mathrm{■}$

  The second stopping rule handles the situation where an un-queried interval $i^{\ast }$ is returned. For any $i\in N$, define the “almost prefix” set . Note that either $P_i$ or $P_i\cup i$ is a prefix of $[n]$. (As before, we assume that intervals are indexed by increasing order of their left-endpoint, i.e., ${\mathrm{\ell }}_1\le {\mathrm{\ell }}_2\le \mathrm{\cdots }{\mathrm{\ell }}_n$.) The new rule is:

  $$\exists i\in N\text{ such that }{P}_i\subseteq S\text{ and }\underset{j\in P_i}{\min }{x}_j\ge r_i-\delta .$$

  (13)

  In other words, there is some interval $i$ where (1) all intervals $j\ne i$ with left-endpoint have been queried, and (2) the minimum value of these r.v.s is at least $r_i-\delta$. In this case, we return $i^{\ast }=i$ (we may not know a $\delta$-minimum value). We refer to this as the new stopping rule. See Figure 5 for an example.

Our algorithm for $\mathrm{𝖲𝖬𝖰𝖨}$ with unit costs remains the same as for $\mathrm{𝖲𝖬𝖰}$ (Algorithm 1). The only difference is in the new stopping criterion (described above). Recall that $\pi$ is the permutation used by our non-adaptive policy. When it is clear from the context, we will also use $\pi$ to denote our $\mathrm{𝖲𝖬𝖰𝖨}$ policy that performs queries in the order of $\pi$ until stopping criteria (12) or (13) applies.

We now prove this result. Let $\sigma$ denote an optimal adaptive policy for $\mathrm{𝖲𝖬𝖰𝖨}$. For any $k\ge 1$, we will show:

This would suffice to prove the $4$-approximation, exactly as in Theorem 2.2.

In order to prove (14), we fix some $k\ge 1$. As in the previous proof, let $\theta ={\theta }_k={\mathrm{\ell }}_{k+1}+\delta$ and let $T^{\ast }$ be defined as in (4). To reduce notation, define the following events.

Let $L$ denote the smallest un-queried left-endpoint at the end of iteration $2k$ in $\pi$. Note that $L$ is a deterministic value as $\pi$ is a non-adaptive policy. Moreover, $L\ge {\mathrm{\ell }}_{2k+1}$ as $\pi$ would have queried the first $2k$ r.v.s. Let $𝒢$ be the event that $X_i>L+\delta$ for all intervals $i$ queried by $\pi$ in its first $2k$ iterations. In other words, $𝒢$ is precisely the event that stopping criterion (12) does not apply at the end of iteration $2k$ in $\pi$, i.e., $𝒢=\neg {𝒜}_1$. By Lemma 2.4,

Similarly, let ${𝒢}^{\ast }$ be that event that $X_i>\theta$ for all intervals $i$ in the first $k$ queries of $\sigma$. From the proof of Lemma 2.3, we obtain ${𝒪}_1\subseteq \neg {𝒢}^{\ast }$ and

Combining the above two inequalities, we have

Let ${𝒢}_A$ be the event that $X_j>L+\delta$ for all r.v.s $j\in N$. Similarly, let ${𝒢}_A^{\ast }$ be the event that $X_j>\theta$ for all $j\in N$. Clearly,

We will now prove that

If $\sigma$ finishes due to (13) in $k$ queries then $P_{i^{\ast }}\subseteq [k+1]$: otherwise $|P_{i^{\ast }}|>k$ which contradicts with the fact that all r.v.s in $P_{i^{\ast }}$ must be queried. Let $R=\{i\in N:P_i\subseteq [k+1]\}$ be all such intervals. It now follows that the event ${𝒪}_2$ (which corresponds to policy $\sigma$) is a subset of the event

Note that $ℰ$ is independent of the policy: it only depends on the realizations of the r.v.s (and doesn’t depend on whether/not an interval has been queried).

Moreover, our policy $\pi$ queries all the r.v.s in $[2k]\supseteq [k+1]$ within $2k$ iterations. So, for all $i\in R$, the r.v.s in $P_i\subseteq [k+1]$ are queried by $\pi$ in $2k$ iterations. Hence, event ${𝒜}_2$ (which corresponds to policy $\pi$) contains event $ℰ$.

Recall that the event ${𝒢}_A$ (resp. ${𝒢}_A^{\ast }$) in policy $\pi$ (resp. $\sigma$) means that every r.v. is more than $L+\delta$ (resp. $\theta$). Also, $\theta \le L+\delta$, which means

In other words, for any $j\in N$, if $Y_j$ (resp. $Z_j$) is the r.v. $X_j$ conditioned on ${𝒢}_A$ (resp. ${𝒢}_A^{\ast }$) then $Y_j$ stochastically dominates $Z_j$.²²2We say that r.v. $Y$ stochastically dominates $Z$ if $\mathrm{Pr}[Y\ge u]\ge \mathrm{Pr}[Z\ge u]$ for all $u\in ℝ$. Note also that the r.v.s $Y_j$s (resp. $Z_j$s) are independent. Using the fact that event $ℰ$ corresponds to a monotone function, we obtain:

It suffices to prove the following.

Note that the r.v.s above only differ at position $k$. To keep notation simple, for any $j\in [n]\setminus k$ let $X_j^{\prime }=Y_j$ if and $X_j^{\prime }=Z_j$ if $j>k$. So, we need to show $\mathrm{Pr}[ℰ(X^{\prime },Y_k)]\ge \mathrm{Pr}[ℰ(X^{\prime },Z_k)]$. We condition on the realizations of the $X^{\prime }$ r.v.s. For each $j\in [n]\setminus k$ let $t_j$ denote the realization of the r.v. $X_j^{\prime }$. Having conditioned on these r.v.s, the only randomness is in $Y_k$ and $Z_k$. We will show:

Using the definition of the event $ℰ$ from (18), let $R(t)=\{i\in R:k\in P_i\text{ and }{t}_j>r_i-\delta \text{ for all }j\in P_i\setminus k\}$. In other words, $R(t)\subseteq R$ corresponds to those “clauses” in (18) that have not evaluated to true or false based on the realizations $\{X_j^{\prime }=t_j:j\in [n]\setminus k\}$. If there is some clause in (18) that already evaluates to true (based on $t$) then $ℰ$ holds regardless of $Y_k$ or $Z_k$. So, (19) holds in this case (both terms are one). Now, we assume that no clause in (18) already evaluates to true. We can write

where $f={\min }_{i\in R(t)}{r}_i-\delta$ is a deterministic value.³³3If $R(t)=\mathrm{\varnothing }$ then we set $f=\mathrm{\infty }$. Similarly, we have

Using the fact that $Y_k$ (resp. $Z_k$) is independent of $X^{\prime }$ and that $Y_k$ stochastically dominates $Z_k$,

This completes the proof of (19). De-conditioning the $X^{\prime }$ r.v.s, we obtain $\mathrm{Pr}[ℰ(X^{\prime },Y_k)]\ge \mathrm{Pr}[ℰ(X^{\prime },Z_k)]$ as desired. $◀$

Using Lemma 2.7, we obtain $\mathrm{Pr}[ℰ|{𝒢}_A]\ge \mathrm{Pr}[ℰ|{𝒢}_A^{\ast }]$, which proves (17). Combined with (16),

We have

This completes the proof of (14) and the theorem.

We handle separately the costs of intervals queried in Steps 3 and 6. The total cost incurred in Step 3 of the first $g$ iterations is $c(T_g)\le y^g$: this uses ${\cup }_{k=0}^g{T}_k=T_g$ because $T_g$ are prefixes. The total cost due to Step 6 can be bounded using a geometric series:

The inequality above is by the cost guarantee for (KP). The lemma now follows. $◀$

Recall that ${\sigma }_g$ denotes the optimal policy truncated at cost $y^g$. We let $L({\sigma }_g)={\min }_{j\in N\setminus {\sigma }_g}\{{\mathrm{\ell }}_j\}$ be the smallest un-queried left-endpoint: this is a random value as ${\sigma }_g$ is adaptive. In the algorithm, consider iteration $g$ and let $L(T_g)={\min }_{j\in N\setminus T_g}\{{\mathrm{\ell }}_j\}$; note that the threshold ${\theta }_g\ge L(T_g)+\delta$ in Step 4. Let ${\pi }^{\prime }={\pi }_{g-1}\circ T_g$ denote the list after Step 3 in iteration $g$. Note that the optimization in (KP) of iteration $g$ is over $T\subseteq N\setminus {\pi }^{\prime }$, which yields $U_g$. Also, ${\pi }_g={\pi }^{\prime }\cup U_g$.

The equality in (21) is given by the definition of $L({\sigma }_g)$ and the stopping rule. The inequality in (21) uses the fact that $L({\sigma }_g)\le L(T_g)$ always, which in turn is because ${\sigma }_g$ has cost at most $y^g$ and $T_g$ is the maximal prefix within this cost. The inequality in (22) uses ${\theta }_g\ge L(T_g)+\delta$. The inequality in (23) is by Proposition 1.2: we view ${\sigma }_g$ as a feasible adaptive policy for the fixed-threshold problem with threshold ${\theta }_g$ and budget $y^g$. The equality in (24) follows from independence of the random variables. The first equality in (25) uses the definition of $p_g^{\ast }$ from (KP) and independence. The first inequality in (26) uses the choice of $U_g$ and Theorem 3.2. The equality in (26) is by ${\pi }_g={\pi }^{\prime }\cup U_g$. To see the last inequality in (26), note that if ${\min }_{j\in {\pi }_i}\{X_j\}\le {\theta }_g$ then $\pi$ finishes by iteration $g$. $◀$