Completeness of the Decreasing Diagrams Method for Proving Confluence of Rewriting Systems of the Least Uncountable Cardinality

Ivanov, Ievgen

doi:10.4230/LIPIcs.FSCD.2025.25

Completeness of the Decreasing Diagrams Method for Proving Confluence of Rewriting Systems of the Least Uncountable Cardinality

Ievgen Ivanov Taras Shevchenko National University of Kyiv, Ukraine

Abstract

We show that every confluent abstract rewriting system (ARS) of the cardinality that does not exceed the first uncountable cardinal belongs to the class $DCR_{3}$ , i.e. the class of confluent ARS for which confluence can be proved with the the help of the decreasing diagrams method using the set of labels {0,1,2} ordered in such a way that 0<1<2 (in the general case, the decreasing diagrams method with two labels is not sufficient for proving confluence of such ARS). Under the Continuum Hypothesis this result implies that the decreasing diagrams method is sufficient for establishing confluence of ARS on many structures of interest to applied mathematics and various interdisciplinary fields (confluence of ARS on real numbers, continuous real functions, etc.).

We provide a machine-checked formal proof of a formalized version of the main result in Isabelle proof assistant using HOL logic and the HOL-Cardinals theory. An extended version of this formalization is available in the Archive of Formal Proofs.

Keywords and phrases:

confluence, decreasing diagrams method, rewriting systems, reduction, formal methods, formal proofs, formal verification, non-discrete models, nondeterministic models, interval models

Copyright and License:

2012 ACM Subject Classification:

Theory of computation

\rightarrow

Equational logic and rewriting ; Theory of computation

\rightarrow

Logic and verification

Editors:

Maribel Fernández

Series and Publisher:

Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik

1 Introduction

Van Oostrom’s decreasing diagrams method [41, 40] is one of the most versatile known approaches to proving confluence of abstract rewriting systems (ARS). An overview of the history of this method and its relation to De Bruijn’s work [6] on weak diamond properties can be found in [8, Section 1], information on modified versions of this method (e.g. conversion version) can be found in [42, 4, 45], application examples can be found in [40, 13].

To show that an ARS is confluent using the decreasing diagrams method, one has to choose a set of labels $L$ and a well-founded partial order $\prec$ on $L$ , and construct a labeled version of an ARS (that associates labels with reduction steps) that satisfies a condition reminiscent to local confluence, but with certain constraints on how labels of the reduction steps used in this condition are related by $\prec$ . A theorem [40, Theorem 3.7] by V. van Oostrom implies that when a labeled version of an ARS that satisfies the mentioned condition exists, the original ARS is confluent.

Semi-formally, the class of decreasing Church-Rosser (DCR) ARS is the collection of all confluent ARS for which confluence can be proved with the help of the decreasing diagrams method (note that here the words “can be proved“ mean that “there exists a labeled version of an ARS that satisfies the conditions of [40, Theorem 3.7]”). In the work [9] J. Endrullis, J.W. Klop, R. Overbeek introduced a representation of the class of DCR ARS as the union of ordinal-indexed classes $DCR_{\alpha}$ , where (semi-formally) for each ordinal $\alpha$ , $DCR_{\alpha}$ is the class of confluent ARS for which confluence can be proved with the help of the decreasing diagrams method using a fixed set of labels $L=\{\beta\leavevmode\nobreak\ |\leavevmode\nobreak\ \beta<\alpha\}$ (ordinals less than $\alpha$ ) and a fixed well-founded order on this set that is a restriction of the usual order on ordinals to $L$ . For these classes the following inclusions hold:

DCR_{0}\subseteq DCR_{1}\subseteq DCR_{2}\subseteq DCR_{3}\subseteq\leavevmode% \nobreak\ \cdots

The statement that “all ARS in the class $D C R$ are confluent” is usually called the statement about soundness of the decreasing diagrams method, while a statement of the form “all confluent ARS with a given property $P$ belong to the class $D C R$ ” (or belong to $DCR_{\alpha}$ for some $\alpha$ ) is called the statement about completeness of the decreasing diagrams method for proving confluence of ARS with the property $P$ (note that completeness does not mean that confluence can always be checked in practice for concrete rewriting systems).

In [45, 46] it was formally proved using a proof assistant that the decreasing diagrams method is sound. However, the works [45, 46] do not deal with completeness of this method (methods for proving soundness and completeness are different and, generally, one cannot use soundness proof to establish completeness).

In [9] it was shown that every ARS with the cofinality property [24, 9] belongs to $DCR_{2}$ . It was previously known [24, 9] that countable confluent ARS have the cofinality property, so in [9] it was established that all countable confluent ARS belong to $DCR_{2}$ , i.e. the decreasing diagrams method with 2 labels is complete for proving confluence of countable ARS. However, it is also known [9, p. 14, footnote 3] that uncountable confluent ARS can lack the cofinality property. This motivates study of the capabilities of the decreasing diagrams method for proving confluence of ARS that may lack the cofinality property.

In this paper we propose a machine-checked formal proof in Isabelle/HOL [34, 44] proof assistant that establishes that every confluent ARS $(A,\to)$ such that the cardinality of the reduction relation $\to$ does not exceed the first uncountable cardinal $\aleph_{1}$ belongs to the class $DCR_{3}$ , i.e. confluence of $(A,\to)$ can be proved with the help of the decreasing diagrams method using a fixed set of labels $L=\{0,1,2\}$ ordered in such a way that $0<1<2$ . To the best of our knowledge, this has not been proved before informally or formally, so our formal proof is not a formalization of a previously known non-formalized proof.

This result can be transferred from Higher-Order Logic (HOL) to a more widely known Zermelo-Fraenkel set theory with the Axiom of Choice (ZFC) [11]. If one additionally accepts the Continuum Hypothesis [36] (that is known to be independent of ZFC, if ZFC is consistent), from the main result of this paper it follows that the decreasing diagrams method is complete for proving confluence of ARS of the cardinality of the continuum, and thus this method covers confluence problems on many mathematical structures used in various interdisciplinary fields that involve applied mathematics and/or computer science, e.g. cyber-physical systems [1, 28]. In this case, theoretically, the decreasing diagrams method is sufficient for establishing confluence of an ARS when its elements are:

$\blacksquare$

real numbers
$\blacksquare$

finite-dimensional real vectors / matrices
$\blacksquare$

infinite graphs on a fixed countable set of vertices (because the set of all binary relations on the set of natural numbers has the same cardinality as the set of real numbers $\mathbb{R}$ )
$\blacksquare$

infinite sequences of natural or real numbers indexed by natural numbers
(alternatively, functions $f:\mathbb{N}\to\mathbb{N}$ or $f:\mathbb{N}\to\mathbb{R}$ )
$\blacksquare$

continuous or piecewise continuous functions $f:\mathbb{R}\to\mathbb{R}$
(because the set of all continuous functions $f:\mathbb{R}\to\mathbb{R}$ has the same cardinality as $\mathbb{R}$ )
$\blacksquare$

other mathematical objects that form a set of the cardinality of the continuum (or less) and model possible structures or possible behaviors of a real-world object of study.

Although the rewriting theory is often used to reason about transformations of syntactical objects like finite terms (in at most countable signature), in the above mentioned cases this does not need to be so: the decreasing diagrams method may be applied to ARS that describe transformations of semantical objects like real numbers or functions $f:\mathbb{N}\to\mathbb{N}$ . Thus, we expect, the results of this paper can become a part of theoretical foundations for potential applications of concepts and methods of the rewriting theory to analysis of mathematical models at the semantical level in interdisciplinary contexts (when emphasis on syntax is minimized). The latter might be called “model rewriting”. In more detail this can be explained as follows. Mathematical models in applied fields quite often combine non-discreteness, nondeterminism, uncertainty, e.g. in the sense of interval models of uncertainty. Often, important properties of such models can be described in terms of binary relations (e.g. reachability relation on the set of states) that are typically uncountable. Such relations can be viewed as ARS and some forms of model analysis can be performed using methods of the rewriting theory. More ideas on this topic can be found in [16, 18], information on applications of the rewriting theory in different fields can be found in [2, 5].

The rest of the paper is structured as follows. In Section 2 we give an overview of the related work. In Section 3 we clarify the notation and terminology. In Section 4 we give:

$\blacksquare$

a non-formalized (natural language) formulation of the main result based on set theory
$\blacksquare$

a formulation of a formal, machine-checked version of the main result in Isabelle using HOL logic (theorem thm_main in the file DCRN1.thy in the supplementary material [17]).

In Section 5 we describe the structure of the formal proof from [17] in natural language using set theory. Tables of correspondence between the notation used in the paper and in [17] are given in Appendix A.

To verify correctness of the main result, a reader can use Isabelle 2024 software¹¹1Note that Isabelle 2024 is not strict requirement. It is possible that later versions of Isabelle can be used for checking the file [17] that was originally prepared for Isabelle 2024. [14]. Instructions on re-checking formal proofs using Isabelle are given in Appendix B.

Also, an extended and more structured version of the formalization [17] is available as an article [21] in the Archive of Formal Proofs.

Note that previous formalizations [37, 46] of abstract rewriting and decreasing diagrams from the Archive of Formal Proofs are not very useful for proving the main result of this paper, so [17] does not reference them. However, they complement the main result of this paper and can be used together with it. Such a combination is used in [21].

2 Related Work

The works [41, 40, 8, 9, 10], mentioned in Section 1, are directly related to the topic of this paper. In particular, they establish that every ARS with the cofinality property is decreasing Church-Rosser (DCR), or, more precisely, belongs to the class $DCR_{2}$ . This implies that every countable confluent or weakly normalizing confluent ARS is DCR.

Additionally, the topic of this paper is related to the study of directed sets: for a nonempty confluent ARS $(A,\to)$ with connected underlying undirected graph, the Church-Rosser property implies that $(A,\to^{*})$ is a directed preordered set. Directed sets were studied in many works, a significant number of which were motivated by applications in topology or domain theory [23, 39, 12]. Various works concerning the structure or classification of (infinite) directed sets or more general pre-/partially ordered sets, e.g. [29, 43, 15, 31, 32, 38, 7], are, in a broad sense, related to the topic of the paper. However, the lack of the assumption about transitivity of a reduction relation $\to$ is specific to the study of confluence.

3 Preliminaries

A reader can assume that a background theory for understanding the natural language definitions and propositions given below is Von Neumann-Bernays-Gödel (NBG) set theory [30, 11] with the axiom of global choice [11, p. 133] (it allows one to directly reason about proper classes). Formal claims and proofs from Isabelle/HOL formalization [17] referenced in the paper can be transferred to the set-theoretic setting using a process similar to the one described in [25, 27]. The statement of the main result (Theorem 18) does not essentially depend on proper classes, so it and its proof can also be transferred to ZFC set theory.

3.1 General notation and terminology

We will use the following notation:

$\blacksquare$

$\neg$ , $\vee$ , $\wedge$ , $\Rightarrow$ are the logical negation, disjunction, conjunction, and implication respectively
$\blacksquare$

$(a_{i})_{i=0}^{\infty}$ is a sequence of elements indexed by non-negative integers
$\blacksquare$

$(a_{i})_{i\in I}$ is an indexed family indexed by elements of a set $I$ .

If $A$ is a set, any subset $R\subseteq A\times A$ is a (binary) relation on $A$ . Any subset $R^{\prime}\subseteq R$ is a subrelation of $R$ . If $A, B$ are any sets, $n$ is a positive integer, and $R\subseteq A\times A$ , then:

$\blacksquare$

$\mathrm{Fld}(R)=\{a\leavevmode\nobreak\ |\leavevmode\nobreak\ \exists b% \leavevmode\nobreak\ (a,b)\in R\}\cup\{b\leavevmode\nobreak\ |\leavevmode% \nobreak\ \exists a\leavevmode\nobreak\ (a,b)\in R\}$ , here $\mathrm{Fld}(R)$ is called the field of $R$
$\blacksquare$

$R^{-1}=\{(b,a)\leavevmode\nobreak\ |\leavevmode\nobreak\ (a,b)\in R\}$
$\blacksquare$

$\mathrm{Id}_{A}=\{(a,a)\leavevmode\nobreak\ |\leavevmode\nobreak\ a\in A\}$
$\blacksquare$

$R^{n}=\{(a,b)\leavevmode\nobreak\ |\leavevmode\nobreak\ \exists a_{0},a_{1},..% .,a_{n}\leavevmode\nobreak\ \leavevmode\nobreak\ a=a_{0}\wedge b=a_{n}\wedge% \forall i\in\{0,1,...,n-1\}\leavevmode\nobreak\ (a_{i},a_{i+1})\in R\}$
$\blacksquare$

$R^{+}=\bigcup_{n=1}^{\infty}R^{n}$ , i.e. $R^{+}$ is the transitive closure of $R$
$\blacksquare$

$R|_{B}=R\cap(B\times B)$ , i.e. $R|_{B}$ is the restriction of $R$ to $B$ .

$\blacktriangleright$ Remark 1.

We will usually use letters $R$ , $r$ , $s$ or special symbols (e.g. $\to$ ) for relations. Sometimes we will use the infix notation for membership of a pair in a relation, e.g $a\to b$ .

3.2 Ordinals and cardinality

In the paper we will assume that an ordinal [30] is a set $\alpha$ such that $\in$ well-orders $\alpha$ and each element of $\alpha$ is a subset of $\alpha$ .

$\blacktriangleright$ Remark 2.

In the supplementary material [17] we do not use the above mentioned definition of an ordinal. Instead, we use the HOL formalization [3] of ordinals (and cardinals) using typed well-orders that allows one to model reasoning that involves set-theoretic ordinals. Information on other related approaches to reasoning about ordinals can be found in [33].

If $\alpha$ , $\beta$ are ordinals, then $\alpha<\beta$ denotes $\alpha\in\beta$ and $\alpha\leq\beta$ denotes $(\alpha=\beta)\vee(\alpha<\beta)$ , Also, $\alpha>\beta$ and $\alpha\geq\beta$ denote $\beta<\alpha$ and $\beta\leq\alpha$ respectively.

$\blacktriangleright$ Remark 3.

For every ordinals $\alpha,\beta$ , $\alpha\leq\beta\vee\beta\leq\alpha$ , and every nonempty set $A$ of ordinals has a least element with respect to $\leq$ (i.e. an element $\alpha\in A$ such that $\forall\alpha^{\prime}\in A\leavevmode\nobreak\ \alpha\leq\alpha^{\prime}$ ).

An ordinal $\alpha$ is

$\blacksquare$

an (ordinal) successor of an ordinal $\alpha^{\prime}$ , if $\alpha$ is the least ordinal greater than $\alpha^{\prime}$
$\blacksquare$

a successor ordinal, if $\alpha$ is a successor of some ordinal
$\blacksquare$

a limit ordinal, if $\alpha$ is neither 0 (empty set), nor a successor ordinal.

For any ordinals $\alpha,\beta$ and a nonempty set of ordinals $A$ :

$\blacksquare$

$\alpha+1$ is the (unique) ordinal successor of $\alpha$
$\blacksquare$

$[\alpha,\beta]$ and $[\alpha,\beta)$ denote $\{\alpha^{\prime}\leavevmode\nobreak\ |\leavevmode\nobreak\ \alpha\leq\alpha^{% \prime}\leq\beta\}$ and $\{\alpha^{\prime}\leavevmode\nobreak\ |\leavevmode\nobreak\ \alpha\leq\alpha^{% \prime}<\beta\}$ respectively
$\blacksquare$

$[\alpha,\beta]_{0S}$ is the set of all $\alpha^{\prime}\in[\alpha,\beta]$ such that $\alpha^{\prime}$ is either 0, or is a successor ordinal
$\blacksquare$

$[\alpha,\beta]_{L}=[\alpha,\beta]\backslash[\alpha,\beta]_{0S}$ is the set of all limit ordinals in $[\alpha,\beta]$
$\blacksquare$

$\min A$ is the least element of $A$ with respect to $\leq$ .

For any set $A$ we will denote:

$\blacksquare$

$|A|$ (cardinality of $A$ ) is the least ordinal $\alpha$ (with respect to $\leq$ ) such that there exists a bijective function $f:\alpha\to A$ .

$\blacktriangleright$ Remark 4.

Since we assume the axiom of choice, $|A|$ is defined for any set $A$ [11, 30].

$\blacktriangleright$ Remark 5.

In [17] we use a formal notion of the cardinality of a set described in [3]. Comparisons of cardinalities of sets in [17] using special relations =o, <o, <=o described in [3] can be interpreted as comparisons of set-theoretic cardinalities defined above using $=,<,\leq$ .

We will denote:

$\blacksquare$

$\omega$ is the least limit ordinal
$\blacksquare$

$\omega_{1}$ is the least ordinal such that its cardinality is strictly greater than $\omega$ .

3.3 Decreasing Church-Rosser abstract rewriting systems

Semi-formally, a rewriting system is decreasing Church-Rosser (DCR), if it can be proven confluent using the decreasing diagrams method. Rigorous definitions are given below.

Definition 6.

1.

An abstract rewriting system (ARS) is a pair $(A,\to)$ of a set $A$ and a relation $\to\leavevmode\nobreak\ \subseteq A\times A$ .
2.

An ARS $(A,\to)$ is confluent, if

$\forall a,b,c\in A\leavevmode\nobreak\ (a\to^{*}b\wedge a\to^{*}c\Rightarrow(% \exists d\in A\leavevmode\nobreak\ b\to^{*}d\wedge c\to^{*}d)),$

where $\to^{*}=\mathrm{Id}_{A}\,\cup(\to)^{+}$ , i.e. $\to^{*}$ is the reflexive transitive closure of $\to$ on $A$ .

Definition 7.

A labelled rewriting system (LRS) is a triple $(A,I,(\to_{i})_{i\in I})$ , where $A$ and $I$ are sets and $(\to_{i})_{i\in I}$ is an indexed family (with the set of indices $I$ ) such that $\to_{i}\,\subseteq A\times A$ for each $i\in I$ . Elements of $I$ are called labels.

Definitions 11 and 12 given below are based on [41, Definition 2.3.7] (there is an insignificant difference between the definitions given below and in [41], because [41] uses a slightly different terminology and notation explained in Remark 8).

$\blacktriangleright$ Remark 8.

[41, Definition 2.3.7] refers to [41, Theorem 2.3.5] that applies the term “well-founded partial order” to a relation denoted as $\succ$ , and the well-foundness condition is defined in [41, Definition 1.2.3] for any transitive relation $R$ via a variant of ascending chain condition: there is no infinite sequence $a_{1},a_{2},...$ such that $(a_{i},a_{i+1})\in R\backslash(R\cap R^{-1})$ . In other literature relations that satisfy this kind of condition are called converse well-founded or Noetherian. We will not use the terminology concerning well-founded relations from [41] in this paper and instead use Definition 9 below that relies on the descending chain condition (and apply it to a relation denoted as $\prec$ that can be thought of as a strict partial order that corresponds to the inverse of $\succ$ from [41, Definition 2.3.7]).

Definition 9.

A transitive well-founded relation on a set $I$ is a binary relation $\prec\leavevmode\nobreak\ \subseteq I\times I$ such that $\forall a,b,c\in I\leavevmode\nobreak\ a\prec b\wedge b\prec c\Rightarrow a\prec c$ and there is no infinite sequence $(a_{i})_{i=1}^{\infty}$ such that $a_{i+1}\prec a_{i}$ for every positive integer $i$ .

$\blacktriangleright$ Remark 10.

A transitive well-founded relation is irreflexive and antisymmetric.

Definition 11.

An LRS $(A,I,(\to_{i})_{i\in I})$ is decreasing Church-Rosser (DCR), if there exists a transitive well-founded relation $\prec$ on $I$ and subsets $I_{h}\subseteq I$ and $I_{v}\subseteq I$ such that $\left(\bigcup_{i\in I}\to_{i}\right)=\left(\bigcup_{i\in I_{v}}\to_{i}\right)=% \left(\bigcup_{i\in I_{h}}\to_{i}\right)$ and for every $i\in I_{v}$ , $j\in I_{h}$ , and $a,b,c\in A$ such that $a\to_{i}b$ and $a\to_{j}c$ there exists elements $b^{\prime},b^{\prime\prime},c^{\prime},c^{\prime\prime},d\in A$ such that

\left(b\leavevmode\nobreak\ {\mathop{\buildrel*\over{\dashrightarrow}\;}% \limits_{(\curlyvee i)\cap I_{h}}}\leavevmode\nobreak\ b^{\prime}\leavevmode% \nobreak\ {\mathop{\buildrel=\over{\dashrightarrow}\;}\limits_{\{j\}\cap I_{h}% }}\leavevmode\nobreak\ b^{\prime\prime}\leavevmode\nobreak\ {\mathop{\buildrel% *\over{\dashrightarrow}\;}\limits_{(\curlyvee i\,\cup\curlyvee j)\cap I_{h}}}% \leavevmode\nobreak\ d\right)\wedge\left(c\leavevmode\nobreak\ {\mathop{% \buildrel*\over{\dashrightarrow}\;}\limits_{(\curlyvee j)\cap I_{v}}}% \leavevmode\nobreak\ c^{\prime}\leavevmode\nobreak\ {\mathop{\buildrel=\over{% \dashrightarrow}\;}\limits_{\{i\}\cap I_{v}}}\leavevmode\nobreak\ c^{\prime% \prime}\leavevmode\nobreak\ {\mathop{\buildrel*\over{\dashrightarrow}\;}% \limits_{(\curlyvee i\,\cup\curlyvee j)\cap I_{v}}}\leavevmode\nobreak\ d% \right),

where

$\blacksquare$

for any $i\in I$ , $\curlyvee i$ denotes the set $\{k\in I\leavevmode\nobreak\ |\leavevmode\nobreak\ k\prec i\}$
$\blacksquare$

symbols of the form ${\mathop{\buildrel*\over{\dashrightarrow}\;}\limits_{K}}$ and ${\mathop{\buildrel=\over{\dashrightarrow}\;}\limits_{K}}$ , where $K$ is an expression, mean:

${\mathop{\buildrel*\over{\dashrightarrow}\;}\limits_{K}}=\mathrm{Id}_{A}\cup% \left(\bigcup_{k\in K}\to_{k}\right)^{+}$ and ${\mathop{\buildrel=\over{\dashrightarrow}\;}\limits_{K}}=\mathrm{Id}_{A}\cup% \left(\bigcup_{k\in K}\to_{k}\right)$ .

Definition 12.

An ARS $(A,\to)$ is decreasing Church-Rosser (DCR), if there exists a set $I$ and an indexed family $(\to_{i})_{i\in I}$ (with the set of indices $I$ ) such that $\to_{i}\,\subseteq A\times A$ for each $i\in I$ , $\to\leavevmode\nobreak\ =\left(\bigcup_{i\in I}\to_{i}\right)$ , and $(A,I,(\to_{i})_{i\in I})$ is a decreasing Church-Rosser LRS.

3.4 DCR hierarchy and the class DCR₃

For any ordinal $\alpha$ denote $\curlyvee\alpha=\{\beta\leavevmode\nobreak\ |\leavevmode\nobreak\ \beta<\alpha\}$ (the set of all ordinals below $\alpha$ ).

$\blacktriangleright$ Remark 13.

In the sense of the usual set-theoretic definition of ordinals, $\curlyvee\alpha$ is the ordinal $\alpha$ itself. However, the notation $\curlyvee\alpha$ will be used to highlight that $\alpha$ is used as a set of labels.

The following definition is based on [10, Definition 4.4] and [10, Definition 4.2].

Definition 14 ([19]).

Let $\gamma$ be an ordinal. An ARS $(A,\to)$ belongs to the class $DCR_{\gamma}$ , if there exists an indexed family $(\to_{\alpha})_{\alpha\in(\curlyvee\gamma)}$ of binary relations on $A$ indexed by ordinals $\alpha<\gamma$ such that for every ordinals $\alpha,\beta\in(\curlyvee\gamma)$ and for every $a,b,c\in A$ the following holds:
if $a\to_{\alpha}b\wedge a\to_{\beta}c$ , then there exist elements $b^{\prime},b^{\prime\prime},c^{\prime},c^{\prime\prime},d\in A$ such that

\left(b\leavevmode\nobreak\ {\mathop{\buildrel*\over{\dashrightarrow}\;}% \limits_{\curlyvee\alpha}}\leavevmode\nobreak\ b^{\prime}\leavevmode\nobreak\ % {\mathop{\buildrel=\over{\dashrightarrow}\;}\limits_{\{\beta\}}}\leavevmode% \nobreak\ b^{\prime\prime}\leavevmode\nobreak\ {\mathop{\buildrel*\over{% \dashrightarrow}\;}\limits_{\curlyvee\alpha\,\cup\curlyvee\beta}}\leavevmode% \nobreak\ d\right)\wedge\left(c\leavevmode\nobreak\ {\mathop{\buildrel*\over{% \dashrightarrow}\;}\limits_{\curlyvee\beta}}\leavevmode\nobreak\ c^{\prime}% \leavevmode\nobreak\ {\mathop{\buildrel=\over{\dashrightarrow}\;}\limits_{\{% \alpha\}}}\leavevmode\nobreak\ c^{\prime\prime}\leavevmode\nobreak\ {\mathop{% \buildrel*\over{\dashrightarrow}\;}\limits_{\curlyvee\beta\,\cup\curlyvee% \alpha}}\leavevmode\nobreak\ d\right),

where symbols of the form ${\mathop{\buildrel=\over{\dashrightarrow}\;}\limits_{K}}$ and ${\mathop{\buildrel*\over{\dashrightarrow}\;}\limits_{K}}$ , where $K$ is an expression, mean:

{\mathop{\buildrel=\over{\dashrightarrow}\;}\limits_{K}}=\{(a,a)\,|\,a\in A\}% \cup\bigcup_{\kappa\in K}\to_{\kappa}\text{ \leavevmode\nobreak\ and% \leavevmode\nobreak\ }{\mathop{\buildrel*\over{\dashrightarrow}\;}\limits_{K}% }=\{(a,a)\,|\,a\in A\}\cup\left(\bigcup_{\kappa\in K}\to_{\kappa}\right)^{+}.

(1)

$\blacktriangleright$ Remark 15.

For a finite ordinal $\gamma$ (that corresponds to a natural number), semi-formally, the class $DCR_{\gamma}$ consists of ARS which can be proved confluent with help of the decreasing diagrams method using labels $0,1,...,\gamma-1$ ordered in the usual way ( $0<1<...<\gamma-1$ ).

Proposition 16.

If $\gamma$ is an ordinal and $(A,\to)$ is an ARS in the class $DCR_{\gamma}$ , then $(A,\to)$ is decreasing Church-Rosser in the sense of Definition 12.

Proof.

Follows from Definitions 12, 11 by assuming that $I=I_{h}=I_{v}=(\curlyvee\gamma)$ and that a (transitive well-founded) relation $\prec$ is the restriction of the usual order on ordinals to $I$ . $\hfill\blacktriangleleft$

The next proposition makes the definition of the class $DCR_{3}$ explicit.

Proposition 17 ([19]).

An ARS $(A,\to)$ belongs to the class $DCR_{3}$ if and only if there exist binary relations $\to_{0},\to_{1},\to_{2}\,\subseteq A\times A$ such that $\to\,=(\to_{0}\cup\to_{1}\cup\to_{2})$ and the following conditions 1–6 hold, where

$\blacksquare$

for $i=0,1,2$ the symbol $\to_{i}^{=}$ denotes the reflexive closure of $\to_{i}$ on $A$
$\blacksquare$

for $i=0,1,2$ the symbol $\to_{i}^{*}$ denotes the reflexive-transitive closure of $\to_{i}$ on $A$
$\blacksquare$
the symbol $\to_{01}^{*}$ denotes the reflexive-transitive closure of $\to_{0}\cup\to_{1}$ on A:
1. 1.
  
  $\forall a,b,c\in A\leavevmode\nobreak\ ((a\to_{0}b\wedge a\to_{0}c)\Rightarrow% \exists d\in A\leavevmode\nobreak\ (b\to_{0}^{=}d\wedge c\to_{0}^{=}d))$
2. 2.
  
  $\forall a,b,c\in A\leavevmode\nobreak\ ((a\to_{0}b\wedge a\to_{1}c)\Rightarrow% \exists b^{\prime},d\in A\leavevmode\nobreak\ (b\to_{1}^{=}b^{\prime}\wedge b^% {\prime}\to_{0}^{*}d\wedge c\to_{0}^{*}d))$
3. 3.
  
  $\forall a,b,c\in A\leavevmode\nobreak\ ((a\to_{1}b\wedge a\to_{1}c)\Rightarrow$
  
  $\exists b^{\prime},b^{\prime\prime},c^{\prime},c^{\prime\prime},d\in A% \leavevmode\nobreak\ (b\to_{0}^{*}b^{\prime}\wedge b^{\prime}\to_{1}^{=}b^{% \prime\prime}\wedge b^{\prime\prime}\to_{0}^{*}d\wedge c\to_{0}^{*}c^{\prime}% \wedge c^{\prime}\to_{1}^{=}c^{\prime\prime}\wedge c^{\prime\prime}\to_{0}^{*}% d))$
4. 4.
  
  $\forall a,b,c\in A\leavevmode\nobreak\ ((a\to_{0}b\wedge a\to_{2}c)\Rightarrow% \exists b^{\prime},d\in A\leavevmode\nobreak\ (b\to_{2}^{=}b^{\prime}\wedge b^% {\prime}\to_{01}^{*}d\wedge c\to_{01}^{*}d))$
5. 5.
  
  $\forall a,b,c\in A\leavevmode\nobreak\ ((a\to_{1}b\wedge a\to_{2}c)\Rightarrow% \exists b^{\prime},b^{\prime\prime},d\in A\leavevmode\nobreak\ (b\to_{0}^{*}b^% {\prime}\wedge b^{\prime}\to_{2}^{=}b^{\prime\prime}\wedge b^{\prime\prime}\to% _{01}^{*}d\wedge c\to_{01}^{*}d))$
6. 6.
  
  $\forall a,b,c\in A\leavevmode\nobreak\ ((a\to_{2}b\wedge a\to_{2}c)\Rightarrow$
  
  $\exists b^{\prime},b^{\prime\prime},c^{\prime},c^{\prime\prime},d\in A% \leavevmode\nobreak\ (b\to_{01}^{*}b^{\prime}\wedge b^{\prime}\to_{2}^{=}b^{% \prime\prime}\wedge b^{\prime\prime}\to_{01}^{*}d\wedge c\to_{01}^{*}c^{\prime% }\wedge c^{\prime}\to_{2}^{=}c^{\prime\prime}\wedge c^{\prime\prime}\to_{01}^{% *}d)).$

Proof.

Follows directly from Definition 14 by assuming that $\gamma=3$ and using symmetry of the cases $(\alpha,\beta)\in\{(0,1),(1,0)\}$ , $(\alpha,\beta)\in\{(0,2),(2,0)\}$ , $(\alpha,\beta)\in\{(1,2),(2,1)\}$ . $\hfill\blacktriangleleft$

4 Main Result

Let $U$ be a nonempty set.

Theorem 18 (Completeness of the decreasing diagrams method with 3 labels for proving confluence of ARS of the least uncountable cardinality).

If $(U,r)$ is a confluent ARS and $|r|\leq\omega_{1}$ , then $(U,r)$ belongs to the class $DCR_{3}$ .

The proof of Theorem 18 will be described in Section 5 below.

The statement of a formalized version of Theorem 18 (called thm_main) in the formal language of Isabelle/HOL [34] can be found in the supplementary material [17, lines 11760-11790]. It has the following form:

Main parts of the statement of thm_main can be understood as follows:

$\blacksquare$

fixes r::"(’U $\times$ ’U) set"

– means that $r$ is a binary relation on elements of an arbitrary (nonempty) type $U$
$\blacksquare$

assumes " $\forall\,$ a b c . (a,b) $\in$ rˆ* $\wedge$ (a,c) $\in$ rˆ* $\longrightarrow$ ( $\exists\,$ d. (b,d) $\in$ rˆ* $\wedge$ (c,d) $\in$ rˆ*)"

– means that $(U,r)$ is assumed to be a confluent ARS (here and below $r$ ˆ* denotes the reflexive transitive closure of $r$ on $U$ , and $r$ ˆ= denotes the reflexive closure of $r$ )
$\blacksquare$

and "|r| $\leq$ o cardSuc |{n::nat . True}|"

– means that the cardinality of $r$ does not exceed the cardinal successor of the cardinality of the set of natural numbers, or, equivalently, $|r|\leq\omega_{1}$ . A rigorous description of the notations |.| (cardinality), cardSuc (cardinal successor), and <=o (left well-order can be embedded into the right one) defined in the theory HOL-Cardinals included in Isabelle software can be found in [3, subsections 3.2 and 4.4].
$\blacksquare$

shows " $\exists\,$ r0 r1 r2 . (

( r = (r0 $\cup$ r1 $\cup$ r2) )

$\wedge$ $\dots$

– means a conclusion that $r$ can be represented as a union of 3 relations $r_{0}$ , $r_{1}$ , $r_{2}$ that satisfy the conditions 1–6 of Proposition 17, where $\to_{i}$ is replaced with $r_{i}$ for $i=0,1,2$ .

Equivalently, by Proposition 17, $(U,r)$ is an ARS in the class $DCR_{3}$ .

To simplify interpretation of the assumptions of thm_main by readers not familiar with the formalization [3] of cardinality in Isabelle/HOL, in [17, lines 11746–11752] we provide a formal proof of the equivalence between the 2nd assumption of thm_main:

"|r| $\leq$ o cardSuc |{n::nat . True}|"

and the following formula that does not reference any notions and notations defined in [3]:

$\forall\,$ s $\subseteq$ r. ( ( $\forall\,$ t $\subseteq$ s . (( $\exists\,$ t^′ f. t^′ $\subset$ t $\wedge$ t $\subseteq$ f $\,\,\grave{\,}{}$ t^′) $\longrightarrow$ ( $\exists\,$ f. s $\subseteq$ f $\,\,\grave{\,}{}$ t )) )

$\vee$ ( $\exists\,$ g . r $\subseteq$ g $\,\,\grave{\,}{}$ s ) ) .

Here $s,r,t,t^{\prime}$ range over binary relations, $f$ , $g$ range over functions, the notation $f{\,\,\grave{\,}{}}x$ means the image of a set $x$ under a function $f$ . This formula can be interpreted as follows: every subrelation $s$ of $r$ is either at most countable (the left argument of the disjunction $\vee$ ), or is not smaller than $r$ in cardinality (the right argument of $\vee$ ), where

$\blacksquare$

“ $s$ is at most countable” is expressed as follows: for every $t\subseteq s$ , if $t$ has a proper subset $t^{\prime}$ that is not smaller than $t$ in cardinality ( $t$ is a subset of the image of $t^{\prime}$ under some function), then $t$ is not smaller than $s$ is cardinality ( $s$ is a subset of the image of $t$ )
$\blacksquare$

“ $s$ is not smaller than $r$ in cardinality“ is expressed as follows: $r$ is a subset of the image of $s$ under some function $g$ .

Note that in the general case, the conclusion “ $(U,r)$ belongs to the class $DCR_{3}$ ” in the statement of Theorem 18 cannot be strengthened to “ $(U,r)$ belongs to the class $DCR_{2}$ ”. This follows from the next theorem that extends the results of [19]:

Theorem 19 (Optimality of the index 3 of a DCR class in the conclusion of Theorem 18).

If $\omega_{1}\leq|U|$ (i.e. $U$ is uncountable), then there exists $r\subseteq U\times U$ such that $(U,r)$ is a confluent ARS, $|r|\leq\omega_{1}$ , and $(U,r)$ does not belong to the class $DCR_{2}$ .

Proof.

A machine-checked formal proof of a formalized version of this theorem can be found in [22, file DCR_Example_N1.thy, lines 1503–1529]. The idea of construction of a confluent ARS outside of $DCR_{2}$ is similar to the one proposed by the author of this paper in [19]. $\hfill\blacktriangleleft$

5 Structure of the Formal Proof of the Main Result

The formal proof of Theorem 18 uses slightly more than 80 formal definitions and 260 formal lemmas located in one file in [17] (DCRN1.thy, file length is over 11000 lines). This file depends only on standard theories included in Isabelle software (Main and HOL-Cardinals).

In subsection 5.1 we describe in a semi-formal way a high-level idea of the proof. In subsequent subsections we describe the way in which the most important definitions and lemmas are formulated in [17] (correspondence between the notation used in the paper and in [17] is described in Appendix A). Auxiliary technical lemmas used in the formal proof of the main result are not described in the paper, but are given in [17].

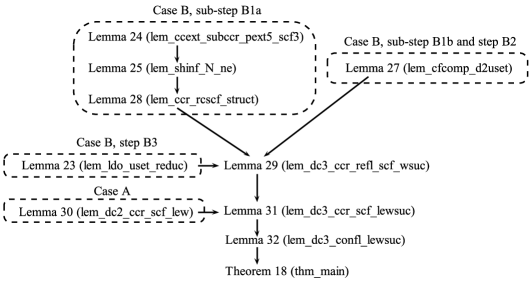
An approximate correspondence between the content of subsection 5.1 and the rest of Section 5 is illustrated in Figure 2.

5.1 General idea of the proof of Theorem 18

Consider a confluent ARS $(U,r)$ with $|r|\leq\omega_{1}$ as a directed graph.

Consider a connected component $C$ of $(U,r)$ .

Case A.

If $C$ (viewed as an ARS) has the cofinality property (defined in [9, Definition 7]), then it belongs to the class $DCR_{2}$ by [9, Theorem 19], so it also belongs to $DCR_{3}$ .

Case B.

If $C$ does not have the cofinality property, then perform the following steps.

Step B1.

Extract a subgraph $S$ from $C$ such that

$\blacksquare$

$S$ has a shape illustrated in Figure 1
$\blacksquare$

nodes of $S$ form a cofinal subset in (the preordered set induced by) $C$ .

Step B2.

Show that $S$ (viewed as an ARS) belongs to $DCR_{2}$ . In Figure 1:

$\blacksquare$

label red arcs (that start at nodes with unique successor) with 0
$\blacksquare$

label green arcs (that start at nodes with non-unique successor) with 1.

Step B3.

Use the cofinality of $S$ in $C$ to conclude that $C$ belongs to $DCR_{3}$ .

Then $(U,r)$ belongs to $DCR_{3}$ , because all its connected components belong to $DCR_{3}$ .

In more detail, the main step “B1” will involve the following sub-steps.

Sub-step B1a.: Extraction of a preliminary cofinal subgraph generally analogous to the one shown in Figure 1, but where red arcs may not form trees and there may be extra green arcs. It will be described using the relation $r_{1}$ in the proof of Lemma 29. This sub-step will be performed using an analog of Iwamura’s lemma for connected Church-Rosser (CCR) relations that will be described in subsection 5.4. The latter allows one to represent a CCR ARS as a union of a (well-ordered) chain of CCR ARS of smaller cardinality (so, e.g., a CCR ARS of the cardinality $\aleph_{1}$ can be represented as a union of a chain of at most countable CCR ARS that have the cofinality property).
Sub-step B1b.: Refinement of a subgraph mentioned above to a connected cofinal subgraph that belongs to $DCR_{2}$ . This sub-step will be described in the proof of Lemma 27.

Refer to caption — Figure 1: Structure of a connected cofinal subgraph of a connected component of a confluent ARS of the least uncountable cardinality, assuming this component lacks the cofinality property.

5.2 Formalization of finite levels of the DCR hierarchy

In this subsection we describe the way in which finite levels of the DCR hierarchy, i.e. classes $DCR_{\alpha}$ for ordinals $\alpha<\omega$ , are formalized in [17].

For any relation $s\subseteq U\times U$ we will denote as $s^{=}$ and $s^{*}$ the reflexive, and, respectively, reflexive transitive closure of $s$ on the set $U$ .

For any function $g:[0,\omega)\to 2^{U\times U}$ and any ordinals $\alpha,\beta\in[0,\omega)$ let us denote:

$\blacksquare$

$\mathfrak{L}_{1}(g,\alpha)=\bigcup_{\alpha^{\prime}\in[0,\alpha)}g(\alpha^{% \prime})$
$\blacksquare$

$\mathfrak{L}_{\vee}(g,\alpha,\beta)=\bigcup_{\alpha^{\prime}\in[0,\alpha)\cup[% 0,\beta)}g(\alpha^{\prime})$
$\blacksquare$

$\mathfrak{D}(g,\alpha,\beta)$ is the set of all tuples $(b,b^{\prime},b^{\prime\prime},d)\in U\times U\times U\times U$ such that

$(b,b^{\prime})\in(\mathfrak{L}_{1}(g,\alpha))^{*}\leavevmode\nobreak\ \wedge% \leavevmode\nobreak\ (b^{\prime},b^{\prime\prime})\in(g(\beta))^{=}\leavevmode% \nobreak\ \wedge\leavevmode\nobreak\ (b^{\prime\prime},d)\in(\mathfrak{L}_{% \vee}(g,\alpha,\beta))^{*}.$

Definition 20.

A function $g:[0,\omega)\to 2^{U\times U}$ is called DCR-generating, if
for every $\alpha,\beta\in[0,\omega)$ and every $a,b,c\in U$ the following implication holds:
if $(a,b)\in g(\alpha)\wedge(a,c)\in g(\beta)$ , then there exist $b^{\prime},b^{\prime\prime},c^{\prime},c^{\prime\prime},d\in U$ such that

(b,b^{\prime},b^{\prime\prime},d)\in\mathfrak{D}(g,\alpha,\beta)\wedge(c,c^{% \prime},c^{\prime\prime},d)\in\mathfrak{D}(g,\beta,\alpha).

Let us denote:

$\blacksquare$

$DCR_{n}(U)$ , where $n\in[0,\omega)$ , is the set of all relations $r\subseteq U\times U$ such that there exists a DCR-generating function $g$ such that $r=\bigcup_{\alpha\in[0,n)}g(\alpha)$ .

$\blacktriangleright$ Remark 21.

It is straightforward to check that for every $n\in[0,\omega)$ , a relation $r$ belongs to $DCR_{n}(U)$ if and only if the ARS $(U,r)$ belongs to the class $DCR_{n}$ .

Definition 22.

A binary relation $r\subseteq U\times U$ is called

1.

connected Church-Rosser (CCR), if $\forall a,b\in\mathrm{Fld}(r)\leavevmode\nobreak\ \exists c\in\mathrm{Fld}(r)% \leavevmode\nobreak\ (a,c)\in r^{*}\wedge(b,c)\in r^{*}$
2.

cone-like, if $r=\emptyset\vee(\exists m\in\mathrm{Fld}(r)\leavevmode\nobreak\ \forall a\in% \mathrm{Fld}(r)\leavevmode\nobreak\ (a,m)\in r^{*})$ .

We will denote:

$\blacksquare$

$CCR(U)$ is the set of all CCR relations $r\subseteq U\times U$
$\blacksquare$

$Conelike(U)$ is the set of all cone-like relations $r\subseteq U\times U$ .

For any $r\subseteq U\times U$ let us denote:

$\blacksquare$

$\mathfrak{U}(r)=\{s\in CCR(U)\leavevmode\nobreak\ |\leavevmode\nobreak\ s% \subseteq r\leavevmode\nobreak\ \wedge\leavevmode\nobreak\ \forall a\in\mathrm% {Fld}(r)\leavevmode\nobreak\ \exists b\in\mathrm{Fld}(s)\leavevmode\nobreak\ (% a,b)\in r^{*}\}$ .
We will call any element of $\mathfrak{U}(r)$ a CCR residue of $r$ .

Note that a CCR residue of $r$ is a CCR subrelation $s\subseteq r$ such that the field of $s$ is a cofinal subset in the preordered set $(\mathrm{Fld}(r),r^{*}|_{\mathrm{Fld}(r)})$ .

The next lemma will be used to implement the step “B3” from subsection 5.1 (it can be considered as a restricted version of a theorem about DCR hierarchy presented in [20]).

Lemma 23 (DCR property inference using CCR residue argument).

If $n_{0}\in[1,\omega)$ , $r\subseteq U\times U$ , $s\in\mathfrak{U}(r)$ , and $s\in DCR_{n_{0}}(U)$ , then $r\in DCR_{n_{0}+1}(U)$ .

Proof.

A formal proof is available in [17, lines 7275–7598]. The proof involves extraction of an auxiliary spanning subrelation of $r$ entitled r1 [17, line 7458, 7590], labeling r1 to show that $\texttt{r1}\in DCR_{n_{0}}(U)$ as described in [17, lines 7450–7453, 7588, 7591], and extension of a labeling of r1 to a labeling of $r$ that ensures that $r\in DCR_{n_{0}+1}(U)$ [17, line 7597]. $\hfill\blacktriangleleft$

5.3 CCR relation subfield extension lemma

For any $r\subseteq U\times U$ , $A\subseteq U$ , and $x\in U$ let us denote:

$\blacksquare$

$r\left[A\right]=\{b\leavevmode\nobreak\ |\leavevmode\nobreak\ \exists a\in A% \leavevmode\nobreak\ (a,b)\in r\}$ , i.e. $r\left[A\right]$ is the image of $A$ under $r$
$\blacksquare$

$r\{x\}=\{y\leavevmode\nobreak\ |\leavevmode\nobreak\ (x,y)\in r\}$ , i.e. $r\{x\}$ is the set of successors of $x$ w.r.t. $r$
$\blacksquare$

$\mathrm{dncl}(r,A)=((r^{*})^{-1})[A]$ , i.e. $\mathrm{dncl}(r,A)$ is the downward closure of $A$ in $(U,r^{*})$
$\blacksquare$

$Inv(r)=\{A\subseteq U\leavevmode\nobreak\ |\leavevmode\nobreak\ r\left[A\right% ]\subseteq A\leavevmode\nobreak\ \}$ , elements of $Inv(r)$ are called invariant sets of $r$
$\blacksquare$

$Span(r)=\{s\subseteq r\leavevmode\nobreak\ |\leavevmode\nobreak\ \mathrm{Fld}(% s)=\mathrm{Fld}(r)\}$ ,
elements of $Span(r)$ are called spanning subrelations of $r$
$\blacksquare$

$SF(r)=\{A\subseteq U\leavevmode\nobreak\ |\leavevmode\nobreak\ \mathrm{Fld}(r|% _{A})=A\leavevmode\nobreak\ \}$ , elements of $SF(r)$ are called subfields of $r$
(note that $A$ is a subfield of $r$ if and only if $A$ is the field of some subrelation $s\subseteq r$ )
$\blacksquare$

$SCF(r)=\{\,B\subseteq\mathrm{Fld}(r)\leavevmode\nobreak\ |\leavevmode\nobreak% \ \forall a\in\mathrm{Fld}(r)\leavevmode\nobreak\ \exists b\in B\leavevmode% \nobreak\ (a,b)\in r^{*}\}$ ,
i.e. $SCF(r)$ is the set of all cofinal sets in the preordered set $(\mathrm{Fld}(r),r^{*}|_{\mathrm{Fld}(r)})$
$\blacksquare$

$\mathrm{scf}(r)=\min\{\leavevmode\nobreak\ |B|\leavevmode\nobreak\ |% \leavevmode\nobreak\ B\in SCF(r)\leavevmode\nobreak\ \}$ , here $\mathrm{scf}(r)$ is called the sequential cofinality of $r$ .

For any set $X$ denote as $\mathcal{P}(X)$ the set of all subsets of $X$ .

Let us fix a (choice) function $\mathrm{ch}:\mathcal{P}(\mathcal{P}(U))\backslash\{\emptyset\}\to\mathcal{P}(U)$ such that $\mathrm{ch}(A)\in A$ for every nonempty set $A\subseteq\mathcal{P}(U)$ .

For any $r,s^{\prime}\subseteq U\times U$ , $A,B\subseteq U$ , and $a,b\in U$ let us denote:

$\blacksquare$

$\mathcal{F}(r,a,b)$ is the set of all (finite) subsets $F\subseteq U$ such that there exists a non-negative integer $n$ and a finite sequence $(a_{i})_{i=0}^{n}$ of elements of $U$ such that $F=\{a_{0},a_{1},...,a_{n}\}$ , $a_{0}=a$ , $a_{n}=b$ , and $(a_{i},a_{i+1})\in r$ for all $i=0,1,...,n-1$
$\blacksquare$

$\mathrm{wdncl}(r,A)=\{a\in\mathrm{dncl}(r,A)\leavevmode\nobreak\ |\leavevmode% \nobreak\ \forall b\in U\leavevmode\nobreak\ \forall F\in\mathcal{F}(r,a,b)% \leavevmode\nobreak\ (b\notin\mathrm{dncl}(r,A)\Rightarrow F\cap A\neq% \emptyset)\}$
$\blacksquare$

$\mathrm{wrank}(r,A)=\min\{\leavevmode\nobreak\ |B|\leavevmode\nobreak\ |% \leavevmode\nobreak\ A\subseteq\mathrm{wdncl}(r,B)\leavevmode\nobreak\ \}$
$\blacksquare$

$\mathrm{dn_{Esc}}(r,A,a)=\{\leavevmode\nobreak\ F\in\mathcal{P}(U)\leavevmode% \nobreak\ |\leavevmode\nobreak\ \exists b\in U\backslash\mathrm{dncl}(r,A)% \leavevmode\nobreak\ F\in\mathcal{F}(r,a,b)\wedge(F\cap A=\emptyset)% \leavevmode\nobreak\ \}$
$\blacksquare$

$\mathrm{dn_{esc}}(r,A,a)=\begin{cases}\mathrm{ch}(\mathrm{dn_{Esc}}(r,A,a)),&% \text{ if }\mathrm{dn_{Esc}}(r,A,a)\neq\emptyset\\ \{a\},&\text{ if }\mathrm{dn_{Esc}}(r,A,a)=\emptyset\\ \end{cases}$
$\blacksquare$

$\mathrm{escl}(r,A,B)=\bigcup_{b\in B}\mathrm{dn_{esc}}(r,A,b)$
$\blacksquare$

$\mathrm{clterm}(s^{\prime},r)=(s^{\prime}\in Conelike(U)\Rightarrow r\in Conelike% (U))$ .

Lemma 24.

Let $r\in CCR(U)$ , $A\in SF(r)$ , $B,B^{\prime}\subseteq U$ , $x\in U$ , and $Ps\subseteq SCF(r)$ .

Then there exists a set $A^{\prime}\subseteq U$ that satisfies of the following 9 conditions:

1.

$x\in\mathrm{Fld}(r)\Rightarrow x\in A^{\prime}$
2.

$A\subseteq A^{\prime}$
3.

$A^{\prime}\in SF(r)$
4.

$\forall a\in A\leavevmode\nobreak\ ((r\{a\}\subseteq B)\leavevmode\nobreak\ % \vee\leavevmode\nobreak\ (r\{a\}\cap(A^{\prime}\backslash B)\neq\emptyset))$
5.

$(\exists y\in U\leavevmode\nobreak\ A^{\prime}-B^{\prime}\subseteq\{y\})% \Rightarrow(\mathrm{Fld}(r)\subseteq A^{\prime}\cup B^{\prime})$
6.

$r|_{A^{\prime}}\in CCR(U)$
7.

$(|A|<\omega\Rightarrow|A^{\prime}|<\omega)\wedge(|A|\geq\omega\Rightarrow|A^{% \prime}|=|A|)$
8.

$((\exists P\leavevmode\nobreak\ Ps=\{P\})\,\vee\leavevmode\nobreak\ |Ps|\in[% \omega,|A|\,])\Rightarrow(\forall P\in Ps\leavevmode\nobreak\ (A^{\prime}\cap P% )\in SCF(r|_{A^{\prime}}))$
9.

$|A|\geq\omega\Rightarrow\mathrm{escl}(r,A,A^{\prime})\subseteq A^{\prime}% \wedge\mathrm{clterm}(r|_{A^{\prime}},r)$ .

Proof.

A formal proof is available in [17, lines 4498–4538]. It depends on several auxiliary formal lemmas that have close formulations, but provide weaker/different guarantees (lem_Ccext_finsubccr_pext5_scf3 and lem_Ccext_infsubccr_pext5_scf3 in [17] and their dependencies). The idea of the proof of the current lemma and its dependencies is related to Löwenheim-Skolem theorem.

When $A$ is infinite, the proof aims to define a required set $A^{\prime}$ as

\psi\left(\bigcup_{n=0}^{\infty}H^{(n)}(\phi(A))\right),

(2)

for some suitable increasing set function $H$ and set functions $\phi$ , $\psi$ , where $H^{(n)}$ denotes the $n$ -times composition of $H$ with itself, such that $H$ , $\phi$ , $\psi$ ensure closure properties of $A^{\prime}$ required by the lemma’s conditions (e.g. $r|_{A^{\prime}}\in CCR(U)$ ), but keep the cardinalities of sets defined by subexpressions of (2) bounded, so that the condition 7, i.e. $(|A|<\omega\Rightarrow|A^{\prime}|<\omega)\wedge(|A|\geq\omega\Rightarrow|A^{% \prime}|=|A|)$ , holds. An explicit expression for $\phi(A)$ can be obtained by unfolding the notation on the right hand side of the definition in [17, line 3972], taking into account substitutions of values in place of parameters of the auxiliary lemma lem_Ccext_infsubccr_set_ext_scf3 specified in [17, line 4280]. Similarly, $H$ can be expressed by unfolding the notation used in [17, lines 3964–3966], and as $\psi$ one can take the identity function.

If $A$ is a finite set, the proof is based on induction on the size of an auxiliary finite relation associated with $A$ . Details can be found in [17, lines 4372–4496, 3332–3414, 2485–2680]. $\hfill\blacktriangleleft$

5.4 Analog of Iwamura’s lemma on directed sets for CCR relations

In this subsection we describe a lemma that allows one to represent an infinite CCR relation $r$ as a union of a chain of CCR relations of cardinalities smaller than the cardinality of $r$ in a way reminiscent to Iwamura’s lemma on directed sets [29, Theorem 1]. Unlike Iwamura’s lemma, our lemma is applicable to a not-necessarily-transitive CCR relation $r$ and guarantees that fields of elements of the resulting chain satisfy additional constraints described below using the sets $\mathcal{N}_{i}$ that are used in the proof of the main result.

Let $\mathcal{U}$ be the set of all ordinals of the cardinality at most $|U|$ .

For any $f:\mathcal{U}\to 2^{U}$ and ordinal $\alpha\in\mathcal{U}$ let us denote:

$\blacksquare$

$\mathfrak{L}(f,\alpha)=\bigcup_{\alpha^{\prime}\in[0,\alpha)}f(\alpha^{\prime})$
$\blacksquare$

$\nabla(f,\alpha)=f(\alpha)\backslash\mathfrak{L}(f,\alpha)$
$\blacksquare$

$\mathcal{Q}(r,f,\alpha)=f(\alpha)\backslash\mathrm{dncl}(r,\mathfrak{L}(f,% \alpha))$
$\blacksquare$

$\mathcal{W}(r,f,\alpha)=f(\alpha)\backslash\mathrm{wdncl}(r,\mathfrak{L}(f,% \alpha))$ .

For any $r\subseteq U\times U$ , $Ps\subseteq 2^{U}$ , and ordinal $\alpha_{0}\in\mathcal{U}$ let us denote:

$\blacksquare$

$\mathcal{N}_{1}(r,\alpha_{0})=\{\leavevmode\nobreak\ f:\mathcal{U}\to 2^{U}% \leavevmode\nobreak\ |\leavevmode\nobreak\ \forall\alpha\in[0,\alpha_{0}]% \leavevmode\nobreak\ \forall\alpha^{\prime}\in[0,\alpha]\leavevmode\nobreak\ f% (\alpha^{\prime})\subseteq f(\alpha)\leavevmode\nobreak\ \}$
$\blacksquare$

$\mathcal{N}_{2}(r,\alpha_{0})=\{\leavevmode\nobreak\ f:\mathcal{U}\to 2^{U}% \leavevmode\nobreak\ |\leavevmode\nobreak\ \forall\alpha\in[0,\alpha_{0}]_{L}% \leavevmode\nobreak\ \nabla(f,\alpha)=\emptyset\leavevmode\nobreak\ \}$
$\blacksquare$

$\mathcal{N}_{3}(r,\alpha_{0})=\{\leavevmode\nobreak\ f:\mathcal{U}\to 2^{U}% \leavevmode\nobreak\ |\leavevmode\nobreak\ \forall\alpha\in[0,\alpha_{0}]_{0S}% \leavevmode\nobreak\ \leavevmode\nobreak\ |\mathfrak{L}(f,\alpha)|\geq\omega\Rightarrow$

$\leavevmode\nobreak\ (\leavevmode\nobreak\ \mathrm{escl}(r,\mathfrak{L}(f,% \alpha),f(\alpha))\subseteq f(\alpha)\leavevmode\nobreak\ \wedge\leavevmode% \nobreak\ \mathrm{clterm}(r|_{f(\alpha)},r)\leavevmode\nobreak\ )\leavevmode% \nobreak\ \}$
$\blacksquare$

$\mathcal{N}_{4}(r,\alpha_{0})=\{\leavevmode\nobreak\ f:\mathcal{U}\to 2^{U}% \leavevmode\nobreak\ |\leavevmode\nobreak\ \forall\alpha\in[0,\alpha_{0}]_{0S}% \leavevmode\nobreak\$
$\forall a\in\mathfrak{L}(f,\alpha)\leavevmode\nobreak\ (\leavevmode\nobreak\ r% \{a\}\subseteq\mathrm{wdncl}(r,\mathfrak{L}(f,\alpha))\leavevmode\nobreak\ % \vee\leavevmode\nobreak\ (r\{a\}\cap\mathcal{W}(r,f,\alpha)\neq\emptyset)% \leavevmode\nobreak\ )\leavevmode\nobreak\ \}$
$\blacksquare$

$\mathcal{N}_{5}(r,\alpha_{0})=\{\leavevmode\nobreak\ f:\mathcal{U}\to 2^{U}% \leavevmode\nobreak\ |\leavevmode\nobreak\ \forall\alpha\in[0,\alpha_{0}]% \leavevmode\nobreak\ f(\alpha)\in SF(r)\,\leavevmode\nobreak\ \}$
$\blacksquare$

$\mathcal{N}_{6}(r,\alpha_{0})=\{\leavevmode\nobreak\ f:\mathcal{U}\to 2^{U}% \leavevmode\nobreak\ |\leavevmode\nobreak\ \forall\alpha\in[0,\alpha_{0}]% \leavevmode\nobreak\ r|_{f(\alpha)}\in CCR(U)\leavevmode\nobreak\ \}$
$\blacksquare$

$\mathcal{N}_{7}(r,\alpha_{0})=\{\leavevmode\nobreak\ f:\mathcal{U}\to 2^{U}% \leavevmode\nobreak\ |\leavevmode\nobreak\ \forall\alpha\in[0,\alpha_{0}]% \leavevmode\nobreak\$
$(\leavevmode\nobreak\ (\alpha<\omega\Rightarrow|f(\alpha)|<\omega)\wedge(% \alpha\geq\omega\Rightarrow|f(\alpha)|\leq\alpha)\leavevmode\nobreak\ )% \leavevmode\nobreak\ \}$
$\blacksquare$

$\mathcal{N}_{8}(r,Ps,\alpha_{0})=\{\leavevmode\nobreak\ f:\mathcal{U}\to 2^{U}% \leavevmode\nobreak\ |\leavevmode\nobreak\ \forall\alpha\in[0,\alpha_{0}]_{0S}% \leavevmode\nobreak\$
$(\leavevmode\nobreak\ (|Ps|=1\leavevmode\nobreak\ \vee\leavevmode\nobreak\ |Ps% |\in[\omega,|f(\alpha)|\,])\Rightarrow(\forall P\in Ps\leavevmode\nobreak\ (f(% \alpha)\cap P)\in SCF(r|_{f(\alpha)}))\leavevmode\nobreak\ )\leavevmode% \nobreak\ \}$
$\blacksquare$

$\mathcal{N}_{9}(r,\alpha_{0})=\{\leavevmode\nobreak\ f:\mathcal{U}\to 2^{U}% \leavevmode\nobreak\ |\leavevmode\nobreak\ \alpha_{0}\geq\omega\Rightarrow\,% \mathrm{Fld}(r)\subseteq f(\alpha_{0})\leavevmode\nobreak\ \}$
$\blacksquare$

$\mathcal{N}_{10}(r,\alpha_{0})=\{\leavevmode\nobreak\ f:\mathcal{U}\to 2^{U}% \leavevmode\nobreak\ |\leavevmode\nobreak\ \forall\alpha\in[0,\alpha_{0}]$
$((\,\exists y\in U\leavevmode\nobreak\ \mathcal{Q}(r,f,\alpha)=\{y\}\,)% \Rightarrow\,\mathrm{Fld}(r)\subseteq\mathrm{dncl}(r,f(\alpha))\,)\leavevmode% \nobreak\ \}$
$\blacksquare$

$\mathcal{N}_{11}(r,\alpha_{0})=\{\leavevmode\nobreak\ f:\mathcal{U}\to 2^{U}% \leavevmode\nobreak\ |\leavevmode\nobreak\ \forall\alpha\in[0,\alpha_{0}]_{0S}% \backslash\{0\}$
$(\mathcal{Q}(r,f,\alpha)=\emptyset\,\Rightarrow\,\mathrm{Fld}(r)\subseteq% \mathrm{dncl}(r,f(\alpha))\,)\leavevmode\nobreak\ \}$
$\blacksquare$

$\mathcal{N}_{12}(r,\alpha_{0})=\{\leavevmode\nobreak\ f:\mathcal{U}\to 2^{U}% \leavevmode\nobreak\ |\leavevmode\nobreak\ \forall\alpha\in[\omega,\alpha_{0}]% \leavevmode\nobreak\ |\mathfrak{L}(f,\alpha)|\geq\omega\leavevmode\nobreak\ \}$ .

For every $r\subseteq U\times U$ and $Ps\subseteq 2^{U}$ let us denote:

\mathcal{N}(r,Ps)=\left(\bigcap_{i=1}^{7}\mathcal{N}_{i}(r,|\mathrm{Fld}(r)|)% \right)\cap\mathcal{N}_{8}(r,Ps,|\mathrm{Fld}(r)|)\cap\left(\bigcap_{i=9}^{12}% \mathcal{N}_{i}(r,|\mathrm{Fld}(r)|)\right).

(3)

Note that $|\mathrm{Fld}(r)|\in[0,|U|\,]\subseteq\mathcal{U}$ , because $\mathrm{Fld}(r)\subseteq U$ .

Lemma 25 (Analog of Iwamura’s lemma).

If $r\in CCR(U)$ and $Ps\subseteq SCF(r)$ , then $\mathcal{N}(r,Ps)\neq\emptyset$ .

Proof.

A formal proof is available in [17, lines 9533–9616]. The idea of the proof is to use Lemma 24 to define recursively a transfinite sequence of subsets of $\mathrm{Fld}(r)$ that gives values $f(\alpha)$ , $\alpha\in[0,|\mathrm{Fld}(r)|]$ for some $f\in\mathcal{N}(r,Ps)$ . $\hfill\blacktriangleleft$

$\blacktriangleright$ Remark 26.

If $f\in\mathcal{N}(r,Ps)$ for an infinite CCR relation $r$ , then the relations $r|_{f(\alpha)}$ , $\alpha\in[0,|\mathrm{Fld}(r)|)$ are smaller than $r$ in cardinality and form a chain of CCR relations, the union of which is $r$ (one can check this by unfolding the notations $\mathcal{N}_{i}(r,|\mathrm{Fld}(r)|)$ for $i=1,2,5,6,7,9$ and $\nabla(f,\alpha)$ and noting that if $r$ is infinite, then $|\mathrm{Fld}(r)|$ is a limit ordinal).

5.5 Generation of a CCR residue in the class DCR₂

Let us denote:

$\blacksquare$

$T(U)$ is the set of all nonempty relations $t\in CCR(U)$ such that $t$ is single-valued (i.e. $(a,b)\in t\wedge(a,c)\in t\Rightarrow b=c$ ), acyclic (i.e. $t^{+}$ is irreflexive), and total on its field (i.e. $\forall x\in\mathrm{Fld}(t)\leavevmode\nobreak\ t\{x\}\neq\emptyset$ ).

Lemma 27.

Let $r\subseteq U\times U$ be a relation that is reflexive on $\mathrm{Fld}(r)$ . Let $S$ be a set of ordinals and $(W_{\alpha})_{\alpha\in S}$ , $(R_{\alpha})_{\alpha\in S}$ be indexed families of subsets of $U$ such that

1.

$S\subseteq[0,\omega_{1})$ , $|[0,\omega_{1})|\leq|S|$ , and $\forall\alpha\in S\leavevmode\nobreak\ \exists\beta\in S\leavevmode\nobreak\ % \alpha<\beta$
2.

$\mathrm{Fld}(r)=\bigcup_{\alpha\in S}W_{\alpha}$ and $\forall\alpha,\beta\in S\leavevmode\nobreak\ (\alpha\neq\beta\Rightarrow W_{% \alpha}\cap W_{\beta}=\emptyset)$
3.

$\forall\alpha\in S\leavevmode\nobreak\ R_{\alpha}\in T(U)\wedge R_{\alpha}% \subseteq r\wedge|W_{\alpha}|\leq\omega\wedge\mathrm{Fld}(R_{\alpha})=W_{% \alpha}\wedge\neg Conelike(r|_{W_{\alpha}})$
4.

$\forall\alpha\in S\leavevmode\nobreak\ \forall x\in W_{\alpha}\leavevmode% \nobreak\ \exists a\in U\,\left(\leavevmode\nobreak\ (x,a)\in(r|_{W_{\alpha}})% ^{*}\wedge(\forall\beta\in S\leavevmode\nobreak\ \alpha<\beta\Rightarrow r\{a% \}\cap W_{\beta}\neq\emptyset)\leavevmode\nobreak\ \right)$ .

Then there exists $r^{\prime}\in\mathfrak{U}(r)$ such that $r^{\prime}\in DCR_{2}(U)$ .

Proof.

A formal proof is available in [17, lines 4935–5746] (note that in the formulation of the lemma in [17] the assumptions are not numbered as above and the notation $\mathfrak{U}(r)$ in the conclusion is unfolded).

The idea of the proof is to define a relation $r^{\prime}\in\mathfrak{U}(r)$ (a subrelation of $r$ ) such that, semi-formally, the graph $(\mathrm{Fld}(r^{\prime}),r^{\prime})$ has a shape similar to the one illustrated in Figure 1, and show that $r^{\prime}\in DCR_{2}(U)$ . The trees illustrated in Figure 1 are extracted from (at most countable) graphs $(W_{\alpha},r|_{W_{\alpha}})$ for ordinals $\alpha\in S$ .

In more detail this construction is described below (the relations $R^{\prime}_{\alpha}$ correspond to sets of arcs of the trees extracted from $(W_{\alpha},r|_{W_{\alpha}})$ , the relation $r_{e}^{\prime}$ corresponds to the set of arcs that connect trees, and $r^{\prime}$ is the union of $r^{\prime}_{e}$ and $R^{\prime}_{\alpha}$ for all $\alpha\in S$ ).

For every $\alpha\in S$ let us denote:

$\blacksquare$

$EP_{\alpha}=\{a\in W_{\alpha}\leavevmode\nobreak\ |\leavevmode\nobreak\ % \forall\beta\in S\leavevmode\nobreak\ (\alpha<\beta\Rightarrow r\{\alpha\}\cap W% _{\beta}\neq\emptyset)\}$ ,
the elements of $EP_{\alpha}$ are called exit points from the ARS $(W_{\alpha},r|_{W_{\alpha}})$
$\blacksquare$

$h:\mathcal{U}\to\mathcal{U}$ is a function such that for every $\alpha,\beta\in S$ and $a\in EP_{\alpha}$ , $b\in EP_{\beta}$ there exists $\gamma\in S$ and $a^{\prime},b^{\prime}\in W_{\gamma}$ such that $\alpha<\gamma$ , $\beta<\gamma$ , and $(a,a^{\prime})\in r$ , $(a^{\prime},h(\gamma))\in R_{\gamma}^{*}$ , $(b,b^{\prime})\in r$ , and $(b^{\prime},h(\gamma))\in R_{\gamma}^{*}$
$\blacksquare$

$(s_{\alpha,k})_{k=0}^{\infty}$ is some infinite cofinal reduction sequence in the (countable, CCR) ARS $(\mathrm{Fld}(R_{\alpha}),R_{\alpha})$
$\blacksquare$

$E_{\alpha}=\{(s_{\alpha,k+1},s_{\alpha,k})\notin(r|_{W_{\alpha}})^{*}\}$
$\blacksquare$

$F_{\alpha}=\{s_{\alpha,k}\leavevmode\nobreak\ |\leavevmode\nobreak\ k\in E_{% \alpha}\}\cap\{a\in W_{\alpha}\leavevmode\nobreak\ |\leavevmode\nobreak\ (h(% \alpha)\in W_{\alpha}\Rightarrow(h(\alpha),a)\in R_{\alpha}^{*})\wedge(a,h(% \alpha))\notin R_{\alpha}^{*}\}$
$\blacksquare$

$re_{0,\alpha}$ and $re_{1,\alpha}$ is some pair of consecutive elements in the sequence $(s_{\alpha,k})_{k=0}^{\infty}$ such that $re_{0,\alpha}$ is located at some index $k\in E_{\alpha}$ in $(s_{\alpha,k})_{k=0}^{\infty}$ and $re_{0,\alpha}\in F_{\alpha}$
$\blacksquare$

$ep_{\alpha}$ is some element of $EP_{\alpha}$ such that $(re_{1,\alpha},ep_{\alpha})\in(r|_{W_{\alpha}})^{*}$
$\blacksquare$

${spl}_{\alpha}$ is the length of a shortest reduction sequence in the ARS $(W_{\alpha},r|_{W_{\alpha}})$ that starts at the element ${re}_{1,\alpha}$ and ends at the element ${ep}_{\alpha}$
$\blacksquare$

${sp}_{\alpha,k}$ for $k=0,1,...,({spl}_{\alpha}-1)$ is some reduction sequence that starts at the element ${re}_{1,\alpha}$ , ends at the element ${ep}_{\alpha}$ , and has the length $spl_{\alpha}$
$\blacksquare$

$R^{\prime}_{\alpha}=\{(a,b)\in R_{\alpha}\leavevmode\nobreak\ |\leavevmode% \nobreak\ (b,{re}_{0,\alpha})\in R_{\alpha}^{*}\}\cup\{({re}_{0,\alpha},re_{1,% \alpha})\}\cup\{(sp_{\alpha,k},sp_{\alpha,k+1})\leavevmode\nobreak\ |% \leavevmode\nobreak\ k<spl_{\alpha}\}$
$\blacksquare$

$r_{e}^{\prime}=\{(a,b)\in r\leavevmode\nobreak\ |\leavevmode\nobreak\ \exists% \alpha,\beta\in S\leavevmode\nobreak\ \alpha<\beta\wedge a=ep_{\alpha}\wedge b% \in W_{\beta}\wedge(b,h(\beta))\in R_{\beta}^{*}\}$
$\blacksquare$

$r^{\prime}=r_{e}^{\prime}\cup\bigcup_{\alpha\in S}R^{\prime}_{\alpha}$
$\blacksquare$

$g:[0,\omega)\to 2^{U\times U}$ is a function such that for every $n\in[0,\omega)$ :

$g(n)=\begin{cases}\{(u,v)\in r^{\prime}\leavevmode\nobreak\ |\leavevmode% \nobreak\ r^{\prime}\{u\}=\{v\}\},&\text{ if }n=0\\ \{(u,v)\in r^{\prime}\leavevmode\nobreak\ |\leavevmode\nobreak\ r^{\prime}\{u% \}\neq\{v\}\},&\text{ if }n=1\\ \emptyset,&\text{ if }n\notin\{0,1\}.\\ \end{cases}$

Then it is shown that $g$ is DCR-generating [17, lines 5659–5720] and $r^{\prime}\in\mathfrak{U}(r)$ . Then $r^{\prime}\in\mathfrak{U}(r)\cap DCR_{2}(U)$ , because $r^{\prime}=\bigcup_{n<2}g(n)$ . $\hfill\blacktriangleleft$

5.6 Completion of the proof of the main theorem

Below we give an important lemma (Lemma 28) that can be used to describe a structure of a confluent relation $r$ when $\mathrm{scf}(r)$ is a regular cardinal. We will use it together with several other lemmas to complete the proof of Theorem 18.

Lemma 28.

Let $r\in CCR(U)$ be a relation such that $r$ reflexive on $\mathrm{Fld}(r)$ .
Assume that $\mathrm{scf}(r)$ is a regular cardinal [3] such that $\omega<\mathrm{scf}(r)=|\mathrm{Fld}(r)|$ .

Then there exists a set $P s$ and a function $f\in\mathcal{N}(r,Ps)$ such that for every successor ordinal $\alpha\in[0,|\mathrm{Fld}(r)|)$ such that $|\mathcal{L}(f,\alpha)|\geq\omega$ the following conditions 1–3 hold:

1.

$r|_{\mathcal{W}(r,f,\alpha)}\in CCR(U)$
2.

$|r|_{\mathcal{W}(r,f,\alpha)}|<|\mathrm{Fld}(r)|$
3.

for every $a\in\mathcal{W}(r,f,\alpha)$ there exists $b\in U$ (denoted in [17] as “wesc r f $\alpha$ a“) such that $b\in\mathcal{W}(r,f,\alpha)$ , $(a,b)\in(r|_{\mathcal{W}(r,f,\alpha)})^{*}$ , and $r\{b\}\cap\mathcal{W}(r,f,\beta)\neq\emptyset$ for every successor ordinal $\beta$ such that $\alpha<\beta<|\mathrm{Fld}(r)|$ .

Proof.

A formal proof is available in [17, lines 10415–10460].

The idea of the proof is to define $Ps=\{P\}$ , where

P=\{\leavevmode\nobreak\ a\in\mathrm{Fld}(r)\leavevmode\nobreak\ |\leavevmode% \nobreak\ \mathrm{scf}(r)\leq\mathrm{wrank}(r,r\{a\})\leavevmode\nobreak\ \},

then obtain $f\in\mathcal{N}(r,Ps)$ using Lemma 25, and show that $f$ satisfies the conditions 1–3. $\hfill\blacktriangleleft$

Lemma 29.

Let $r\subseteq U\times U$ be a relation that is reflexive on $\mathrm{Fld}(r)$ .

Assume that $r\in CCR(U)$ and $\mathrm{scf}(r)=|\mathrm{Fld}(r)|=\omega_{1}$ . Then $r\in DCR_{3}(U)$ .

Proof.

A formal proof is available in [17, lines 10733–11021].

The proof proceeds as follows. Let $P s$ and $f\in\mathcal{N}(r,Ps)$ be a set and a function obtained from Lemma 28 applied to $r$ . Let us denote:

$\blacksquare$

$S$ is the set of all successor ordinals in $[\omega,\omega_{1})$
$\blacksquare$

$(W_{\alpha})_{\alpha\in S}$ is an indexed family of subsets of $U$ such that $W_{\alpha}=\mathcal{W}(r,f,\alpha)$ for $\alpha\in S$
$\blacksquare$

$(R_{\alpha})_{\alpha\in S}$ is an indexed family of relations on $U$ such that

$R_{\alpha}\in{Span}(r|_{\mathcal{W}(r,f,\alpha)})\cap T(U)\text{ for }\alpha\in S$
$\blacksquare$

$r_{1}=r|_{\bigcup_{\alpha\in S}W_{\alpha}}$ .

Let $r^{\prime}$ be a relation in $DCR_{2}(U)$ obtained using Lemma 27 applied to $r_{1}$ , $S$ , $(W_{\alpha})_{\alpha\in S}$ , $(R_{\alpha})_{\alpha\in S}$ . One can show that $r^{\prime}\in\mathfrak{U}(r)$ , so $r\in DCR_{3}(U)$ by Lemma 23. $\hfill\blacktriangleleft$

Lemma 30.

If $r\in CCR(U)$ and $\mathrm{scf}(r)\leq\omega$ , then $r\in DCR_{2}(U)$ .

Proof.

A formal proof is available in [17, lines 10687–10731]. The idea of the proof is similar to the idea of [9, Theorem 19]. $\hfill\blacktriangleleft$

Lemma 31.

If $r\in CCR(U)$ and $|\mathrm{Fld}(r)|\leq\omega_{1}$ , then $r\in DCR_{3}(U)$ .

Proof.

A formal proof is available in [17, lines 11023–11072].

The proof proceeds as follows. Consider two cases.

1.

If $\mathrm{scf}(r)\leq\omega$ , then $r\in DCR_{2}(U)$ by Lemma 30, whence $r\in DCR_{3}(U)$ .
2.

Assume $\mathrm{scf}(r)=\omega_{1}$ . Let $r_{1}=r\cup\{(x,x)\leavevmode\nobreak\ |\leavevmode\nobreak\ x\in\mathrm{Fld}(% r)\}$ . Then either $\mathrm{scf}(r_{1})\leq\omega$ , or $\mathrm{scf}(r_{1})=|\mathrm{Fld}(r_{1})|$ . If $\mathrm{scf}(r_{1})\leq\omega$ , then $r_{1}\in DCR_{2}(U)$ by Lemma 30. If $\mathrm{scf}(r_{1})=|\mathrm{Fld}(r_{1})|$ , then $r_{1}\in DCR_{3}(U)$ by Lemma 29. Thus in any case, $r_{1}\in DCR_{3}(U)$ . This is used to conclude that $r\in DCR_{3}(U)$ .

$\hfill\blacktriangleleft$

Lemma 32.

If $r\subseteq U\times U$ is a confluent relation and $|\mathrm{Fld}(r)|\leq\omega_{1}$ , then $r\in DCR_{3}(U)$ .

Proof.

A formal proof is available in [17, lines 11634–11652].

The idea of the proof is as follows. Consider $(U,r)$ as a directed graph. For each connected component $(C,s)$ of $(U,r)$ , the relation $s$ satisfies the assumptions of Lemma 31, so $s\in DCR_{3}(U)$ . This is used to conclude that $r\in DCR_{3}(U)$ . $\hfill\blacktriangleleft$

Proof of Theorem 18 (i.e. if $(U,r)$ is confluent and $|r|\leq\omega_{1}$ , then $(U,r)$ is in $DCR_{3}$ ).

A formal proof of Theorem 18 is available in [17, lines 11760–11807]. It follows from Lemma 32 by observing that $|r|\leq\omega_{1}$ implies $|\mathrm{Fld}(r)|\leq\omega_{1}$ . $\hfill\blacktriangleleft$

6 Conclusion

We have shown that every confluent ARS $(A,\to)$ such that the cardinality of the reduction relation $\to$ does not exceed the first uncountable cardinal $\aleph_{1}$ belongs to the class $DCR_{3}$ , i.e. confluence of $(A,\to)$ can be proved with the help of the decreasing diagrams method using labels 0, 1, 2 ordered in such a way that $0<1<2$ .

Under the Continuum Hypothesis this result implies that, theoretically, the decreasing diagrams method is sufficient for establishing confluence of ARS on many structures of interest to applied mathematics and various interdisciplinary fields.

Investigation of potential applications of this and other methods of the rewriting theory in interdisciplinary contexts is a subject of further research.

References

[1] Radhakisan Baheti and Helen Gill. Cyber-physical systems. The impact of control technology, 12(1):161–166, 2011.
[2] Nicolas Behr and Jean Krivine. Rewriting theory for the life sciences. In International Conference on Graph Transformation, pages 185–202, 2020.
[3] Jasmin Christian Blanchette, Andrei Popescu, and Dmitriy Traytel. Cardinals in Isabelle/HOL. In Lecture Notes in Computer Science, volume 8558, pages 111–127, 2014. doi:10.1007/978-3-319-08970-6_8.
[4] Mirna Bognar. A point version of decreasing diagrams. In Proceedings Accolade 1996. Dutch Graduate School in Logic, pages 1–14, 1997.
[5] F. Bonchi, F. Gadducci, A. Kissinger, P. Sobociński, and F. Zanasi. String diagram rewrite theory I: Rewriting with Frobenius structure. Journal of the ACM, 69(2):14:1–14:58, 2022. doi:10.1145/3502719.
[6] N.G. de Bruijn. A note on weak diamond properties. Memorandum 78–08, Eindhoven Uninversity of Technology, 1978.
[7] R. Diestel and O. Pikhurko. On the cofinality of infinite partially ordered sets: Factoring a poset into lean essential subsets. Order, 20:53–66, 2003. doi:10.1023/A:1024449306316.
[8] Jörg Endrullis and Jan Willem Klop. De Bruijn’s weak diamond property revisited. Indagationes Mathematicae, 24:1050–1072, 2013.
[9] Jörg Endrullis, Jan Willem Klop, and Roy Overbeek. Decreasing diagrams with two labels are complete for confluence of countable systems. In 3rd International Conference on Formal Structures for Computation and Deduction (FSCD 2018), pages 14:1–14:15. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2018. doi:10.4230/LIPICS.FSCD.2018.14.
[10] Jörg Endrullis, Jan Willem Klop, and Roy Overbeek. Decreasing diagrams for confluence and commutation. Logical Methods in Computer Science, 16:23:1–23:25, 2020. doi:10.23638/LMCS-16(1:23)2020.
[11] A.A. Fraenkel, Y. Bar-Hillel, and A. Levy. Foundations of Set Theory. Elsevier, 1973.
[12] Jean Goubault-Larrecq. Non-Hausdorff topology and domain theory: Selected topics in point-set topology. Cambridge University Press, 2013.
[13] N. Hirokawa, A. Middeldorp, C. Sternagel, and S. Winkler. Abstract completion, formalized. Logical Methods in Computer Science, 15(3):19:1–19:42, 2019. doi:10.23638/LMCS-15(3:19)2019.
[14] Isabelle proof assistant. http://isabelle.in.tum.de. [Online].
[15] J.R. Isbell. The category of cofinal types. II. Trans. Amer. Math. Soc., 116:394–416, 1965.
[16] Ievgen Ivanov. Generalized Newman’s lemma for discrete and continuous systems. In Leibniz International Proceedings in Informatics, volume 260, pages 9:1–9:17, 2023. doi:10.4230/LIPICS.FSCD.2023.9.
[17] Ievgen Ivanov. Formal proof of completeness of the decreasing diagrams method for proving confluence of relations of the least uncountable cardinality (supplementary material for this paper). https://doi.org/10.5281/zenodo.14254256, 2024. [Online].
[18] Ievgen Ivanov. On Newman’s lemma and non-termination. In CEUR-WS.org, volume 3624, pages 14–24, 2024. URL: https://ceur-ws.org/Vol-3624/Paper_2.pdf.
[19] Ievgen Ivanov. On non-triviality of the hierarchy of decreasing Church-Rosser abstract rewriting systems. In Proceedings of the 13th International Workshop on Confluence, pages 30–35, 2024.
[20] Ievgen Ivanov. On the cofinality property in the context of the hierarchy of decreasing Church-Rosser abstract rewriting systems. In Information Technology and Implementation, November 20–21, 2024, Kyiv, Ukraine, 2024.
[21] Ievgen Ivanov. Completeness of decreasing diagrams for the least uncountable cardinality. Archive of Formal Proofs, April 2025.
https://isa-afp.org/entries/Completeness_Decreasing_Diagrams_for_N1.html, Formal proof development.
[22] Ievgen Ivanov. Formalization of a confluent abstract rewriting system of the least uncountable cardinality outside of the class DCR2. https://doi.org/10.5281/zenodo.14740062, 2025. [Online].
[23] John L. Kelley. General topology. Van Nostrand, 1955.
[24] Jan Willem Klop. Combinatory Reduction Systems. PhD thesis, Rijks-universiteit Utrecht, 1980.
[25] Alexander Krauss and Andreas Schropp. A mechanized translation from Higher-Order Logic to set theory. In Lecture Notes in Computer Science, volume 6172, pages 323–338. Springer, 2010. doi:10.1007/978-3-642-14052-5_23.
[26] Ondřej Kunčar and Andrei Popescu. Comprehending Isabelle/HOL’s consistency. In Lecture Notes in Computer Science, volume 10201, pages 724–749. Springer, 2017. doi:10.1007/978-3-662-54434-1_27.
[27] Ondřej Kunčar and Andrei Popescu. A consistent foundation for Isabelle/HOL. Journal of Automated Reasoning, 62:531–555, 2019. doi:10.1007/S10817-018-9454-8.
[28] Edward A. Lee. Fundamental limits of cyber-physical systems modeling. ACM Transactions on Cyber-Physical Systems, 1(1):1–26, 2016. doi:10.1145/2912149.
[29] George Markowsky. Chain-complete posets and directed sets with applications. Algebra universalis, 6(1):53–68, 1976.
[30] Elliott Mendelson. Introduction to Mathematical Logic. CRC Press, 2015.
[31] Eric C. Milner and Maurice Pouzet. On the cofinality of partially ordered sets. Ordered sets, pages 279–298, 1982.
[32] Eric C. Milner and Karel Prikry. The cofinality of a partially ordered set. Proc. London Math. Soc., 46:454–470, 1983.
[33] Chuangjie Xu Nicolai Kraus, Fredrik Nordvall Forsberg. Type-theoretic approaches to ordinals. Theoretical computer science, 957, 2023. doi:10.1016/J.TCS.2023.113843.
[34] Tobias Nipkow, Markus Wenzel, and Lawrence C Paulson. Isabelle/HOL: a proof assistant for higher-order logic. Springer, 2002. doi:10.1007/3-540-45949-9.
[35] Andrew Pitts. The HOL logic. In Introduction to HOL: A Theorem Proving Environment for Higher Order Logic, pages 191–232. Cambridge University Press, 1993.
[36] Raymond Smullyan. Set theory and the continuum problem. Clarendon Press, 1996.
[37] Christian Sternagel and Rene Thiemann. Abstract rewriting. Archive of Formal Proofs, June 2010.
[38] Stevo Todorcevic. Directed sets and cofinal types. Trans. Amer. Math. Soc., 290:711–723, 1985.
[39] John W. Tukey. Convergence and uniformity in topology. Princeton University Press, 1940.
[40] Vincent Van Oostrom. Confluence by decreasing diagrams. Theoretical computer science, 126(2):259–280, 1994. doi:10.1016/0304-3975(92)00023-K.
[41] Vincent Van Oostrom. Confluence for Abstract and Higher-Order Rewriting. PhD thesis, Vrije Universiteit Amsterdam, 1994.
[42] Vincent Van Oostrom. Confluence by decreasing diagrams – converted. In Lecture Notes in Computer Science, volume 5117, pages 306–320, 2008.
[43] Shang-Zhi Wang and Bo Yu Li. On the minimal cofinal subsets of a directed quasi-ordered set. Discrete Mathematics, 48:289–306, 1984. doi:10.1016/0012-365X(84)90189-4.
[44] Freek Wiedijk. The seventeen provers of the world: Foreword by Dana S. Scott, volume 3600. Springer, 2006. doi:10.1007/11542384.
[45] Harald Zankl. Confluence by decreasing diagrams – formalized. In 24th International Conference on Rewriting Techniques and Applications, pages 352–367. Leibniz International Proceedings in Informatics, 2013. doi:10.4230/LIPICS.RTA.2013.352.
[46] Harald Zankl. Decreasing diagrams. Archive of Formal Proofs, 2013.

Appendix A Correspondence Between the Notions/Notation Used in the Paper and in the Supplementary Material

Below we give tables of correspondence between the formal notions used in the supplementary material [17] (Isabelle/HOL formalization) and their intended interpretations in terms of the notions based on set theory used in natural language text in this paper.

Syntax of the formal language that is used to express Isabelle/HOL theories is described in the documentation included in Isabelle software [14]. Information on semantic aspects of Isabelle language can be found in [35, 27, 26, 25].

A.1 General notation

Notation in [17]	Notation in the paper
$\neg$ , $\vee$ , $\wedge$ , $\longrightarrow$	$\neg$ , $\vee$ , $\wedge$ , $\Rightarrow$
$=$ , $\in$ , $\subseteq$	$=$ , $\in$ , $\subseteq$
$\cup$ , $\cap$ , $-$ , $\times$	$\cup$ , $\cap$ , $\backslash$ , $\times$
{}	$\emptyset$
f::’A $\,\Rightarrow\,$ ’B	$f:A\to B$ $(A,B\neq\emptyset)$
f x	$f(x)$
{x. P x}	$\{x\leavevmode\nobreak\ \|\leavevmode\nobreak\ P(x)\}$
nat	$\{0,1,2,...\}$
UNIV::’U	$U$ ( $U\neq\emptyset$ )
x::’U	$x\in U$
A::’U set	$A\subseteq U$ ( $U\neq\emptyset$ )
r::’U rel	$r\subseteq U\times U$ ( $U\neq\emptyset$ )
Field r	$\mathrm{Fld}(r)$
Restr r B	$r\|_{B}$
r^-1, r^∧∧n, r^∧+, r^∧=, r^∧∗	$r^{-1}$ , $r^{n}$ , $r^{+}$ , $r^{=}$ , $r^{*}$
$\|$ A $\|$ =o $\|$ B $\|$	$\|A\|=\|B\|$
$\|$ A $\|$ <o $\|$ B $\|$	$\|A\|<\|B\|$
$\|$ A $\|$ <=o $\|$ B $\|$	$\|A\|\leq\|B\|$
$\omega\_$ ord	$\|\mathbb{N}\|$

A.2 Notation related to subsection 5.2

Lines in [17]	Notation in [17]	Notation in the paper
78–80	$\mathfrak{L}_{1}$ g $\alpha$	$\mathfrak{L}_{1}(g,\alpha)$
82–84	$\mathfrak{L}$ v g $\alpha$ $\beta$	$\mathfrak{L}_{\vee}(g,\alpha,\beta)$
86–88	$\mathfrak{D}$ g $\alpha$ $\beta$	$\mathfrak{D}(g,\alpha,\beta)$
116–118	CCR r	$r\in CCR(U)$
120–122	Conelike r	$r\in Conelike(U)$
90–93	DCR_generating g	$g$ is DCR-generating
95–97	DCR n r	$r\in DCR_{n}(U)$
177–178	$\mathfrak{U}$ r	$\mathfrak{U}(r)$

A.3 Notation related to subsection 5.3 (part 1)

Lines in [17]	Notation in [17]	Notation in the paper
N/A	r $\,{}^{\backprime\,\backprime}\,$ A	$r\left[A\right]$
N/A	r $\,{}^{\backprime\,\backprime}\,$ {x}	$r\{x\}$
124–126	dncl r A	$\mathrm{dncl}(r,A)$
128–130	Inv r	$Inv(r)$
189–190	Span r	$Span(r)$
132–134	SF r	$SF(r)$
136–137	SCF r	$SCF(r)$
195–196	scf r	$\mathrm{scf}(r)$

A.4 Notation related to subsection 5.3 (part 2)

Lines in [17]	Notation in [17]	Notation in the paper
147–149	$\mathcal{F}$ r a b	$\mathcal{F}(r,a,b)$
198–200	w_dncl r A	$\mathrm{wdncl}(r,A)$
307–308	wrank r A	$\mathrm{wrank}(r,A)$
155–157	dnEsc r A a	$\mathrm{dn_{Esc}}(r,A,a)$
159–161	dnesc r A a	$\mathrm{dn_{esc}}(r,A,a)$
163–165	escl r A B	$\mathrm{escl}(r,A,B)$
167	clterm s^′ r	$\mathrm{clterm}(s^{\prime},r)$

A.5 Notation related to subsection 5.4

Lines in [17]	Notation in [17]	Notation in the paper
202–204	$\mathfrak{L}$ f $\alpha$	$\mathfrak{L}(f,\alpha)$
206–208	$\nabla$ f $\alpha$	$\nabla(f,\alpha)$
210–212	$\mathcal{Q}$ r f $\alpha$	$\mathcal{Q}(r,f,\alpha)$
214–216	$\mathcal{W}$ r f $\alpha$	$\mathcal{W}(r,f,\alpha)$
218–267	$\mathcal{N}i$ r $\alpha 0$	$\mathcal{N}_{i}(r,\alpha_{0})$ , $i$ is an integer
269–274	$\mathcal{N}$ r Ps	$\mathcal{N}(r,Ps)$

Appendix B Instructions on Re-checking Formal Proofs

1.

Install Isabelle 2024 software using the instructions at:

https://isabelle.in.tum.de/website-Isabelle2024/installation.html
2.

Launch the installed Isabelle 2024 software.
3.

Obtain the file DCRN1.thy from

https://doi.org/10.5281/zenodo.14254256
4.

Choose File $\to$ Open from the main menu in Isabelle window and select DCRN1.thy.
5.

Scroll to the end of the loaded text in Isabelle and wait until all red marks on the right scroll bar disappear (this may take several minutes).
6.

At this point formal proofs have been checked.
7.

The main result (called thm_main) is located at the line 11760.

[bib.bib1] [1] Radhakisan Baheti and Helen Gill. Cyber-physical systems. The impact of control technology, 12(1):161–166, 2011.

[bib.bib2] [2] Nicolas Behr and Jean Krivine. Rewriting theory for the life sciences. In International Conference on Graph Transformation, pages 185–202, 2020.

[bib.bib3] [3] Jasmin Christian Blanchette, Andrei Popescu, and Dmitriy Traytel. Cardinals in Isabelle/HOL. In Lecture Notes in Computer Science, volume 8558, pages 111–127, 2014. doi:10.1007/978-3-319-08970-6_8.

[bib.bib4] [4] Mirna Bognar. A point version of decreasing diagrams. In Proceedings Accolade 1996. Dutch Graduate School in Logic, pages 1–14, 1997.

[bib.bib5] [5] F. Bonchi, F. Gadducci, A. Kissinger, P. Sobociński, and F. Zanasi. String diagram rewrite theory I: Rewriting with Frobenius structure. Journal of the ACM, 69(2):14:1–14:58, 2022. doi:10.1145/3502719.

[bib.bib6] [6] N.G. de Bruijn. A note on weak diamond properties. Memorandum 78–08, Eindhoven Uninversity of Technology, 1978.

[bib.bib7] [7] R. Diestel and O. Pikhurko. On the cofinality of infinite partially ordered sets: Factoring a poset into lean essential subsets. Order, 20:53–66, 2003. doi:10.1023/A:1024449306316.

[bib.bib8] [8] Jörg Endrullis and Jan Willem Klop. De Bruijn’s weak diamond property revisited. Indagationes Mathematicae, 24:1050–1072, 2013.

[bib.bib9] [9] Jörg Endrullis, Jan Willem Klop, and Roy Overbeek. Decreasing diagrams with two labels are complete for confluence of countable systems. In 3rd International Conference on Formal Structures for Computation and Deduction (FSCD 2018), pages 14:1–14:15. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2018. doi:10.4230/LIPICS.FSCD.2018.14.

[bib.bib10] [10] Jörg Endrullis, Jan Willem Klop, and Roy Overbeek. Decreasing diagrams for confluence and commutation. Logical Methods in Computer Science, 16:23:1–23:25, 2020. doi:10.23638/LMCS-16(1:23)2020.

[bib.bib11] [11] A.A. Fraenkel, Y. Bar-Hillel, and A. Levy. Foundations of Set Theory. Elsevier, 1973.

[bib.bib12] [12] Jean Goubault-Larrecq. Non-Hausdorff topology and domain theory: Selected topics in point-set topology. Cambridge University Press, 2013.

[bib.bib13] [13] N. Hirokawa, A. Middeldorp, C. Sternagel, and S. Winkler. Abstract completion, formalized. Logical Methods in Computer Science, 15(3):19:1–19:42, 2019. doi:10.23638/LMCS-15(3:19)2019.

[bib.bib14] [14] Isabelle proof assistant. http://isabelle.in.tum.de. [Online].

[bib.bib15] [15] J.R. Isbell. The category of cofinal types. II. Trans. Amer. Math. Soc., 116:394–416, 1965.

[bib.bib16] [16] Ievgen Ivanov. Generalized Newman’s lemma for discrete and continuous systems. In Leibniz International Proceedings in Informatics, volume 260, pages 9:1–9:17, 2023. doi:10.4230/LIPICS.FSCD.2023.9.

[bib.bib17] [17] Ievgen Ivanov. Formal proof of completeness of the decreasing diagrams method for proving confluence of relations of the least uncountable cardinality (supplementary material for this paper). https://doi.org/10.5281/zenodo.14254256, 2024. [Online].

[bib.bib18] [18] Ievgen Ivanov. On Newman’s lemma and non-termination. In CEUR-WS.org, volume 3624, pages 14–24, 2024. URL: https://ceur-ws.org/Vol-3624/Paper_2.pdf.

[bib.bib19] [19] Ievgen Ivanov. On non-triviality of the hierarchy of decreasing Church-Rosser abstract rewriting systems. In Proceedings of the 13th International Workshop on Confluence, pages 30–35, 2024.

[bib.bib20] [20] Ievgen Ivanov. On the cofinality property in the context of the hierarchy of decreasing Church-Rosser abstract rewriting systems. In Information Technology and Implementation, November 20–21, 2024, Kyiv, Ukraine, 2024.

[bib.bib21] [21] Ievgen Ivanov. Completeness of decreasing diagrams for the least uncountable cardinality. Archive of Formal Proofs, April 2025.
https://isa-afp.org/entries/Completeness_Decreasing_Diagrams_for_N1.html, Formal proof development.

[bib.bib22] [22] Ievgen Ivanov. Formalization of a confluent abstract rewriting system of the least uncountable cardinality outside of the class DCR2. https://doi.org/10.5281/zenodo.14740062, 2025. [Online].

[bib.bib23] [23] John L. Kelley. General topology. Van Nostrand, 1955.

[bib.bib24] [24] Jan Willem Klop. Combinatory Reduction Systems. PhD thesis, Rijks-universiteit Utrecht, 1980.

[bib.bib25] [25] Alexander Krauss and Andreas Schropp. A mechanized translation from Higher-Order Logic to set theory. In Lecture Notes in Computer Science, volume 6172, pages 323–338. Springer, 2010. doi:10.1007/978-3-642-14052-5_23.

[bib.bib26] [26] Ondřej Kunčar and Andrei Popescu. Comprehending Isabelle/HOL’s consistency. In Lecture Notes in Computer Science, volume 10201, pages 724–749. Springer, 2017. doi:10.1007/978-3-662-54434-1_27.

[bib.bib27] [27] Ondřej Kunčar and Andrei Popescu. A consistent foundation for Isabelle/HOL. Journal of Automated Reasoning, 62:531–555, 2019. doi:10.1007/S10817-018-9454-8.

[bib.bib28] [28] Edward A. Lee. Fundamental limits of cyber-physical systems modeling. ACM Transactions on Cyber-Physical Systems, 1(1):1–26, 2016. doi:10.1145/2912149.

[bib.bib29] [29] George Markowsky. Chain-complete posets and directed sets with applications. Algebra universalis, 6(1):53–68, 1976.

[bib.bib30] [30] Elliott Mendelson. Introduction to Mathematical Logic. CRC Press, 2015.

[bib.bib31] [31] Eric C. Milner and Maurice Pouzet. On the cofinality of partially ordered sets. Ordered sets, pages 279–298, 1982.

[bib.bib32] [32] Eric C. Milner and Karel Prikry. The cofinality of a partially ordered set. Proc. London Math. Soc., 46:454–470, 1983.

[bib.bib33] [33] Chuangjie Xu Nicolai Kraus, Fredrik Nordvall Forsberg. Type-theoretic approaches to ordinals. Theoretical computer science, 957, 2023. doi:10.1016/J.TCS.2023.113843.

[bib.bib34] [34] Tobias Nipkow, Markus Wenzel, and Lawrence C Paulson. Isabelle/HOL: a proof assistant for higher-order logic. Springer, 2002. doi:10.1007/3-540-45949-9.

[bib.bib35] [35] Andrew Pitts. The HOL logic. In Introduction to HOL: A Theorem Proving Environment for Higher Order Logic, pages 191–232. Cambridge University Press, 1993.

[bib.bib36] [36] Raymond Smullyan. Set theory and the continuum problem. Clarendon Press, 1996.

[bib.bib37] [37] Christian Sternagel and Rene Thiemann. Abstract rewriting. Archive of Formal Proofs, June 2010.

[bib.bib38] [38] Stevo Todorcevic. Directed sets and cofinal types. Trans. Amer. Math. Soc., 290:711–723, 1985.

[bib.bib39] [39] John W. Tukey. Convergence and uniformity in topology. Princeton University Press, 1940.

[bib.bib40] [40] Vincent Van Oostrom. Confluence by decreasing diagrams. Theoretical computer science, 126(2):259–280, 1994. doi:10.1016/0304-3975(92)00023-K.

[bib.bib41] [41] Vincent Van Oostrom. Confluence for Abstract and Higher-Order Rewriting. PhD thesis, Vrije Universiteit Amsterdam, 1994.

[bib.bib42] [42] Vincent Van Oostrom. Confluence by decreasing diagrams – converted. In Lecture Notes in Computer Science, volume 5117, pages 306–320, 2008.

[bib.bib43] [43] Shang-Zhi Wang and Bo Yu Li. On the minimal cofinal subsets of a directed quasi-ordered set. Discrete Mathematics, 48:289–306, 1984. doi:10.1016/0012-365X(84)90189-4.

[bib.bib44] [44] Freek Wiedijk. The seventeen provers of the world: Foreword by Dana S. Scott, volume 3600. Springer, 2006. doi:10.1007/11542384.

[bib.bib45] [45] Harald Zankl. Confluence by decreasing diagrams – formalized. In 24th International Conference on Rewriting Techniques and Applications, pages 352–367. Leibniz International Proceedings in Informatics, 2013. doi:10.4230/LIPICS.RTA.2013.352.

[bib.bib46] [46] Harald Zankl. Decreasing diagrams. Archive of Formal Proofs, 2013.

Completeness of the Decreasing Diagrams Method for Proving Confluence of Rewriting Systems of the Least Uncountable Cardinality

Abstract

Keywords and phrases:

Copyright and License:

2012 ACM Subject Classification:

Supplementary Material:

Related Version:

DOI:

Event:

Editors:

Series and Publisher:

1 Introduction

2 Related Work

3 Preliminaries

3.1 General notation and terminology

▶ Remark 1.

3.2 Ordinals and cardinality

▶ Remark 2.

▶ Remark 3.

▶ Remark 4.

▶ Remark 5.

3.3 Decreasing Church-Rosser abstract rewriting systems

Definition 6.

Definition 7.

▶ Remark 8.

Definition 9.

▶ Remark 10.

Definition 11.

Definition 12.

3.4 DCR hierarchy and the class DCR3

▶ Remark 13.

Definition 14 ([19]).

▶ Remark 15.

Proposition 16.

Proof.

Proposition 17 ([19]).

Proof.

4 Main Result

Theorem 18 (Completeness of the decreasing diagrams method with 3 labels for proving confluence of ARS of the least uncountable cardinality).

Theorem 19 (Optimality of the index 3 of a DCR class in the conclusion of Theorem 18).

Proof.

5 Structure of the Formal Proof of the Main Result

5.1 General idea of the proof of Theorem 18

5.2 Formalization of finite levels of the DCR hierarchy

Definition 20.

▶ Remark 21.

Definition 22.

Lemma 23 (DCR property inference using CCR residue argument).

Proof.

5.3 CCR relation subfield extension lemma

Lemma 24.

Proof.

5.4 Analog of Iwamura’s lemma on directed sets for CCR relations

Lemma 25 (Analog of Iwamura’s lemma).

Proof.

▶ Remark 26.

5.5 Generation of a CCR residue in the class DCR2

Lemma 27.

Proof.

5.6 Completion of the proof of the main theorem

Lemma 28.

Proof.

Lemma 29.

Proof.

Lemma 30.

Proof.

Lemma 31.

Proof.

Lemma 32.

Proof.

Proof of Theorem 18 (i.e. if (U,r) is confluent and |r|≤ω1, then (U,r) is in D⁢C⁢R3).

6 Conclusion

References

Appendix A Correspondence Between the Notions/Notation Used in the Paper and in the Supplementary Material

A.1 General notation

A.2 Notation related to subsection 5.2

A.3 Notation related to subsection 5.3 (part 1)

A.4 Notation related to subsection 5.3 (part 2)

A.5 Notation related to subsection 5.4

Appendix B Instructions on Re-checking Formal Proofs

$\blacktriangleright$ Remark 1.

$\blacktriangleright$ Remark 2.

$\blacktriangleright$ Remark 3.

$\blacktriangleright$ Remark 4.

$\blacktriangleright$ Remark 5.

$\blacktriangleright$ Remark 8.

$\blacktriangleright$ Remark 10.

3.4 DCR hierarchy and the class DCR₃

$\blacktriangleright$ Remark 13.

$\blacktriangleright$ Remark 15.

$\blacktriangleright$ Remark 21.

$\blacktriangleright$ Remark 26.

5.5 Generation of a CCR residue in the class DCR₂

Proof of Theorem 18 (i.e. if $(U,r)$ is confluent and $|r|\leq\omega_{1}$ , then $(U,r)$ is in $DCR_{3}$ ).