Polymorphic Cycle Basis in a Sequence of Graphs to Analyze the Structural Evolution of a Molecular Dynamic Trajectory

Aboulfath, Ylène; Barth, Dominique; Mautor, Thierry; Watel, Dimitri; Weisser, Marc-Antoine

doi:10.4230/LIPIcs.SEA.2025.1

Polymorphic Cycle Basis in a Sequence of Graphs to Analyze the Structural Evolution of a Molecular Dynamic Trajectory

Ylène Aboulfath

DAVID lab, Université de Versailles Saint-Quentin/Université Paris-Saclay, France Dominique Barth DAVID lab, Université de Versailles Saint-Quentin/Université Paris-Saclay, France Thierry Mautor DAVID lab, Université de Versailles Saint-Quentin/Université Paris-Saclay, France Dimitri Watel

SAMOVAR lab, Evry, France
Ecole Nationale Superieur d’Informatique pour l’Industrie et l’Entreprise, Evry, France Marc-Antoine Weisser

LISN, CentraleSupélec, Université Paris-Saclay, France

Abstract

Molecular dynamics analysis is a fundamental topic in chemistry, in particular the study of the formation and dissolution of hydrogen bonds over time. The dynamics of these bonds create and break cycles which are crucial to the structure of the molecules. The challenge in cycle analysis is twofold: there is an exponential number of cycles, and some cycles are very close.

We introduce a graph-based approach using minimum cycle bases to assist in molecular dynamics analysis. Given a set of graphs representing a molecule trajectory, we determine, for each graph, a minimum cycle basis and construct a graph of cycles which represents the cycles of minimum bases and their interactions. Then, we aggregate all information from these graphs of cycles into a polygraph. Each vertex of the polygraph represents a class of cycles appearing in different minimum bases and playing equivalent roles in the trajectory.

This paper introduces our approach, establishes the complexity of associated problems, and suggests an implementation. Simulations are conducted on both real and generated data to evaluate the performance of our approach.

Keywords and phrases:

Graph theory, Cycle basis, Molecular analysis

Copyright and License:

2012 ACM Subject Classification:

Theory of computation

\rightarrow

Graph algorithms analysis ; Applied computing

\rightarrow

Chemistry ; Theory of computation

\rightarrow

Theory and algorithms for application domains

DOI:

10.4230/LIPIcs.SEA.2025.1

Event:

23rd International Symposium on Experimental Algorithms (SEA 2025)

Editors:

Petra Mutzel and Nicola Prezza

Series and Publisher:

Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik

Introduction

This article proposes a new graph-based approach for analyzing the structural dynamics of molecular trajectories. Such a trajectory represents the temporal evolution of the three-dimensional positions of a set of atoms, discretely sampled over time [9]. From the resulting series of $3$ D images, a sequence of molecular graphs is derived, referred to as conformers. These conformers share identical vertices and are characterized by chemical bonds induced by the distances in three-dimensional space. A chemical bond denotes an attractive interaction between two atoms, classified into covalent bonds, representing strong bonds formed by electron sharing, and hydrogen bonds, weaker electrostatic interactions compared to covalent bonds. Covalent bonds persist across all conformers within a trajectory, while hydrogen bonds may appear or disappear over time.

A molecular dynamics (MD) trajectory is a sequence of conformers that share identical vertices and a common subset of edges that represent covalent bonds. Analyzing such a trajectory consists in examining the structural evolution of the molecule, which manifests itself as alterations in the topologies of these conformers. Previous studies [11, 15] have suggested the interest in representing the molecular structure based on interactions among elementary cycles within the molecular graph, particularly for the classification and characterization of sets of molecules.

Given the potentially extensive number of cycles in a graph, a practical representation of the structure of a molecule often involves minimum cycle bases [5] of the molecular graphs [6, 19]. Such minimum cycle bases are already used in chemistry to represent the molecular structure [12, 20]. Cycle bases can be used to study the similarity between molecular graphs [9, 19]. However, to the best of our knowledge, no study has yet addressed the analysis of a set of conformers or focused on searching for similar cycle bases.

In this study, the hypothesis is that, between consecutive conformers in a trajectory, each cycle contributing to the structure can either appear, disappear, or evolve (a partial change of its set of edges based on the evolution of hydrogen bonds). Consequently, we consider a specific minimum cycle basis for each conformer. In [2, 7], it is experimentally shown that two distinct cycles from the bases of two different conformers may assume an identical structural role in them. Thus, we can define the property that two cycles are pairwise polymorphic if they play the same role in the structure of the conformers in which they appear, i.e. if they interact in the same way with all the other such cycles in their respective conformers.

This main property, along with two additional practical ones, are precisely defined in Section 1. These properties lead to the partition of the subset of the union of cycle bases, restricted to those containing at least one hydrogen bond, into equivalence classes called polymorphic cycles. These equivalence classes are represented as the vertices in a graph, denoted as the polygraph. An edge exists between two classes if at least one cycle from each class appears in the same conformer and their intersection is nonempty. Subsequently, each conformer is characterized by a subgraph of this polygraph, induced by polymorphic cycles that are active in that particular conformer. It is the resulting sequence of sub-polygraphs along the trajectory that facilitates the analysis of molecular structure evolution [2]. Therefore, the primary objective is, given a trajectory, to determine a minimum cycle basis for each of its conformers, providing a specific representation of the structure of each conformer. Following this, we aim to determine the smallest number of equivalent classes. The main issues are to compute a polygraph with the smallest number of vertices easily and to select the cycles in each minimum cycle basis to facilitate the computation of such a polygraph.

Section 1 provides a formal definition of the set of cycles for each conformer, along with the graph modeling of polymorphic cycles and polygraphs. Section 2 demonstrates that the problem of obtaining a polygraph with minimum number of polymorphic cycles is NP-complete even for planar graphs, and not approximable. Section 3 proposes an approach to compute the polygraph. In Section 3.1, the selection of cycle bases for each conformer is discussed. Section 4 presents a performance evaluation of the approach on various trajectories.

1 Definition of polymorphic cycles and polygraphs

(a) Graph

G_{1}

.

(b) Graph

G_{2}

.

(c) Graph

G_{3}

.

(d) Graph of cycles for

G_{1}

.

(e) Graph of cycles for

G_{2}

.

(f) Graph of cycles for

G_{1}

.

Figure 1: Figures 1(a), 1(b) and 1(c) represent three conformers within the same trajectory (dotted arrows represent hydrogen bonds), each with a minimum cycle basis. Figures 1(d), 1(e) and 1(f) are the corresponding graphs of cycles in which vertices are cycles of the basis and two cycles are linked by an edge iff they share at least one edge in the conformer.

A MD trajectory consists of an ordered sequence of conformers induced by the movement of atoms in 3D space. Figure 1 shows three conformers of the same trajectory. Each conformer is represented with the cycles containing at least one hydrogen bond (illustrated with dashed arrows) of a minimum cycle basis. For each conformer, the associated graph of cycles, with vertices representing cycles and edges connecting cycles sharing at least one edge in the conformer, is illustrated. The graph of cycles reflects the structure of molecular conformer. Note that the cycles without hydrogen bonds may also contribute to the structure but, as they are present in all conformers, they are not involved in the dynamic of the structure.

Although they are not identical, it is natural to consider that the orange cycles in the conformers of Figures 1(a) and 1(b) play the same structural role as the red cycle of conformer in Figure 1(c). Indeed, they both are in the same position in the molecule, they both have the same interactions with the other cycles of their bases, and they share several vertices including a red vertex involved in an hydrogen bond. Therefore, these two cycles are in fact the same molecular cycle whose form evolves based on the appearance and disappearance of hydrogen bonds in the trajectory. One may consider the possibility that the orange cycles could be polymorphic with the brown cycle rather than the red one. However, their neighborhood in the graphs of cycles are different. Even if we can only conclude about the cycles that simultaneously appear, the brown cycle appears with the green cycle, the purple cycle and the blue cycle but does not share an edge with them, while the orange cycles actually share an edge with each of them. Thus, their neighborhood are conflicting.

The objective of the problem addressed in this article is to determine sets of polymorphic cycles during the trajectory to analyze the evolution of the molecular structure over time. Such modeling allows the recognition of equivalence between sets of conformers even if they are represented by different cycle sets. For example, when considering the three conformers of Figure 1, the goal is to identify them as representative of the same structure. This result deviates significantly from the classic straightforward conclusion that each conformer represents a distinct structure within the molecular system [2].

1.1 Modeling a molecular dynamics trajectory with graph theory

As defined in [9, 8], each conformer is modeled as a graph. In these graphs, vertices are atoms and edges are both covalent and hydrogen bonds. A MD trajectory is described by a sequence of graphs $T_{\cal G}=\{G_{1},G_{2},\ldots,G_{n_{c}}\}$ where each graph corresponds to a conformer ( $n_{c}$ : number of conformers). All these graphs share the same set of vertices and the same set of covalent edges, forming a backbone that is common to all conformers. The granularity level of the trajectory ensures that consecutive conformers differ by one, or occasionally, two hydrogen bonds. The same conformer may appear several times in the sequence. The set of distinct graphs is ${\cal G}=\{G_{1},G_{2},\ldots,G_{n_{g}}\}$ ( $n_{g}$ : number of distinct graphs, $n_{g}\leq n_{c}$ ).

Given a set of graphs ${\cal G}$ , let $E$ be the union of edge sets of all these graphs. Additionally, let $E^{H}$ be the subset of $E$ representing the edges corresponding to hydrogen bonds.

As stated in the introduction, we use a minimum cycle basis $B_{i}$ to represent the molecular structure of a graph $G_{i}$ . Recall that a cycle in a graph $G$ is defined as a subgraph in which each vertex has an even degree. The sum of two cycles is the subgraph that contains the edges present in one of these two cycles but not in both. This definition leads to a vector space known as the cycle space of a graph $G$ denoted here as ${\cal C}_{G}$ . The dimension of the cycle space is given by $\mu(G)=|E|-|V|+x$ , where $|E|$ is the number of edges, $|V|$ is the number of vertices, and $x$ is the number of connected components in $G$ . A cycle basis of a graph $G$ is a set of cycles that spans the cycle space of $G$ , meaning that any cycle in $G$ can be expressed as a linear combination of cycles in the basis (initially proposed in [5]).

Each cycle $c$ has a weight, denoted by $\omega(c)$ , which is the number of its edges (i.e. the length of the cycle). The weight of a cycle basis is the sum of the weights of the cycles that constitute it. Consequently, a minimum cycle basis is a cycle basis within the cycle space ${\cal C}_{G}$ that minimizes its weight. The cardinality of a minimum cycle basis is equal to the dimension of the cycle space. Note that for a given graph, there may exist multiple minimum cycle bases. We denote by $\mathcal{MCB}(G)$ the set of minimum cycle bases of a graph $G$ .

Various polynomial-time algorithms have been proposed to find a minimum cycle basis [3, 14]. Given a graph $G_{i}$ and one of its minimum cycle bases $B_{i}\in\mathcal{MCB}(G_{i})$ , the set of selected cycles $C_{i}\subseteq B_{i}$ that contains at least one edge in $E^{H}$ defines the molecular structure of the conformer. This selection ensures that the dynamic aspect of the molecular structure is captured. The cycles drawn on top of Figures 1(a), 1(b) and 1(c), actually, represent these selected cycle sets. Due to the multiplicity of minimum cycle bases available for each graph, the algorithm for computing $B_{i}\in\mathcal{MCB}(G_{i})$ from $G_{i}$ is discussed in Section 3.1.

It should be noted that cycles within $C_{i}$ may interact with each other by sharing edges in $E$ (including both covalent and hydrogen bonds). The set of edges for a cycle $c$ is denoted by $E(c)\subset E$ . For two cycles $c$ and $c^{\prime}$ in $C_{i}$ , if $E(c)\cap E(c^{\prime})\neq\emptyset$ , then $c$ interacts with $c^{\prime}$ and vice versa. Furthermore, considering $T_{\cal G}$ , the set of cycles of the trajectory, denoted by ${\cal C}$ , is the union of the selected cycles from all graphs: ${\cal C}=\bigcup_{1\leq i\leq n_{g}}C_{i}$ .

The selected cycles and their interactions are represented in a graph to illustrate the modeling of the molecular structure of a conformer. Given a conformer, a graph of cycles, ${GC}_{i}=(C_{i},E_{i})$ is built where $\forall c,c^{\prime}\in C_{i},\leavevmode\nobreak\ [c,c^{\prime}]\in E_{i}$ if $E(c)\cap E(c^{\prime})\neq\emptyset$ . Examples of such graphs of cycles are given in Figures 1(d), 1(e) and 1(f). In these graphs, the label of a vertex (i.e., a cycle) corresponds to the list of its hydrogen bonds.

Please note that the graph of cycles $GC_{i}$ exclusively represents the 2-connected components of $G_{i}$ . Consequently, it does not provide any information about the edges connecting these 2-connected subgraphs. Hence, several graphs may correspond to the same graph of cycles. That’s why the cycle polymorphism partition introduced in the subsequent section takes ${\cal G}$ and ${\cal C}$ as arguments instead of ${\cal GC}$ (the set of graphs of cycles $GC_{1\leq i\leq n_{g}}$ ).

1.2 Cycle polymorphism and polygraph

Given a trajectory $T_{\cal G}$ , a cycle polymorphism partition is denoted by $\Pi<{\cal G},{\cal C},E^{H}>$ , and is defined as a partition $\Pi=\{\pi_{1},\ldots,\pi_{m}\}$ of ${\cal C}=\bigcup_{1\leq i\leq n_{g}}C_{i}$ in which each part $\pi_{j}$ (with $1\leq j\leq m)$ corresponds to a polymorphic cycle.

Definition 1.

A polymorphic cycle (or polycycle) is a set of cycles that satisfies the following properties.

1.

No simultaneous occurrences. Two cycles of a polymorphic cycle never appear simultaneously in a minimum cycle basis of a graph, i.e., for every $\pi_{j}\in\Pi$ and every $i,1\leq i\leq n_{g}$ , $|\pi_{j}\cap C_{i}|\leq 1$ .
2.

Common hydrogen bond extremity. All the cycles of a polymorphic cycle share at least one same vertex connected to an edge of $E^{H}$ , i.e., for every $1\leq i\leq m$ , every cycle $c\in\pi_{i}$ contains a same vertex $v\in V$ that is the extremity of an edge in $E^{H}$ .
3.

Same interactions. The interactions between polymorphic cycles must always be the same. Cycles of a polymorphic cycle interact similarly with cycles from each other parts (i.e., other polymorphic cycles). In other words, given two cycles of two different polymorphic cycles, either they always interact or they never do it. Thus, for every $1\leq i\neq j\leq m$ , the cycles of any pair of graphs of cycles $GC_{a}$ and $GC_{b}$ satisfy the following condition: if there exist $c,d\in C_{a}$ and $c^{\prime},d^{\prime}\in C_{b}$ such that $c,c^{\prime}\in\pi_{i}$ and $d,d^{\prime}\in\pi_{j}$ , then $E_{a}(c)\cap E_{a}(d)=\emptyset$ if and only if $E_{b}(c^{\prime})\cap E_{b}(d^{\prime})=\emptyset$ .

In Figure 1, the orange cycle (in graph $G_{1}$ and $G_{2}$ ) and the red cycle (in $G_{3}$ ) are polymorphic. Indeed, they are different but are in the center of the graphs of cycles and neighbors with all the other cycles present.

For a more visual and comprehensive representation, we introduce the cycle polymorphism graph, or polygraph for short. The polygraph has vertices corresponding to the polymorphic cycles in $\Pi<{\cal G},{\cal C},E^{H}>$ and has an edge between two vertices if and only if their corresponding polymorphic cycles interact. The label of a polymorphic cycle is the list of its atoms involved in its hydrogen bonds.

Given $T_{\cal G}$ , its polygraph is denoted by $Pol_{\cal G}$ . For each graph $G_{i}\in{\cal G}$ and its set of selected cycles $C_{i}$ , we denote by $GP_{i}$ the subgraph of $Pol_{\cal G}$ induced by $\Pi_{i}\subseteq\Pi$ such that for each $\pi_{j}\in\Pi_{i}$ , there is $\pi_{j}\cap{C}_{i}\neq\emptyset$ . Note that $GP_{i}$ is isomorphic to the graph of cycles ${GC}_{i}$ .

Figure 5(a) illustrates the polymorphic cycles graph in the context of a MD trajectory composed of conformers of the same molecular system than the ones drawn in Figure 1.

The polygraph $Pol_{\cal G}$ offers a potential characterization of the MD trajectory $T_{\cal G}$ . However, the efficiency of such a characterization depends on the selected cycles in each conformer and on the ability to obtain a reduced number of polymorphic cycles. These two points will be discussed in the following sections.

2 Complexity of finding a cycle polymorphism from sets of cycles

This section formally defines the decision problem considered and proves its complexity.

Problem 1 (Cycle Polymorphism Partition, CPP).

Given a set of graphs ${\cal G}$ with the same set of vertices, a subset of its cycles ${\cal C}$ , a subset of its edges $E^{H}$ and $m\in\mathbb{N}$ , does there exist a cycle polymorphism partition $\Pi<{\cal G},{\cal C},E^{H}>$ composed of at most $m$ components?

The associated minimization problem is named min-Cycle Polymorphism Partition (min-CPP). This problem consists in searching the cycle polymorphism partition with the smallest number of components.

We focus on the complexity of problem CPP restricted to the subset of instances modeling as possible real molecular graphs (whose properties are not formally defined). Therefore, we consider here only planar graphs since molecular graphs are generally planar [13, 10]. Since a trajectory represents the evolution of a same molecule over time, the graphs must have the same set of vertices.

Theorem 2.

Problem Cycle Polymorphism Partition is NP-complete even if each graph $G_{i}$ in ${\cal G}$ is planar and if each edge of $E^{H}$ in a graph $G_{i}$ in ${\cal G}$ belongs to at least one cycle in $C_{i}\in{\cal C}$ .

We give now the proof of this theorem. First, Problem CPP is in NP. Checking if a partition $\Pi<{\cal G},{\cal C},E^{H}>$ is a cycle polymorphism partition can be done in polynomial time.

Consider now the problem Induced Subgraph Isomorphism, denoted here as ISI. Given two graphs, $H_{1}$ and $H_{2}$ , the problem ISI determines if $H_{1}$ is isomorphic to an induced subgraph of $H_{2}$ . It has been proven that ISI is NP-complete, even if $H_{1}$ and $H_{2}$ are outerplanar graphs (i.e., a planar graph in which every vertex belongs to the outer face) [21]. Let $(H_{1},H_{2})$ be two outerplanar graphs forming an instance of the problem ISI. The number of vertices in $H_{1}$ is denoted by $n_{1}$ and the number of vertices in $H_{2}$ is denoted by $n_{2}$ , with $n_{1}\leq n_{2}$ . The transformation of such any instance $(H_{1},H_{2})$ of Problem ISI into an instance of Problem CPP consisting in two graphs $G_{1},G_{2}$ with their set of cycles $C_{i}$ , a set $E^{H}$ , and $m\in\mathbb{N}$ , is made of $7$ consecutive steps giving a graph $G_{1}$ from $H_{1}$ and a graph $G_{2}$ from $H_{2}$ . Figure 2 illustrates this transformation step by step.

(a) Graphs

H_{1}

and

H_{2}

.

(b) Graph

G_{1}

after step 1.

(c) Graph

G_{1}

after step 3.

(d) Graph

G_{1}

after step 5.

(e) Final graph

G_{1}

with in dashed blue lines the edges added during step 7.

Figure 2: Illustration of the polynomial transformation of an outer-planar graph

H_{1}

into

G_{1}

.

1.

A graph $G_{1}$ with $n_{1}$ cycles is defined from $H_{1}$ such that : (a) for each vertex $u$ of $H_{1}$ , there is a cycle $c_{u}$ composed of $\delta_{H_{1}}(v)+3$ edges where $\delta_{H_{1}}(v)$ is the degree of $v$ in $H_{1}$ ; (b) for each edge $[u,v]$ of $H_{1}$ , there is an edge $e$ in $G_{1}$ such that $e\in c_{u}$ and $e\in c_{v}$ ; and (c) for each cycle $c_{u}$ , there must be one edge that is not connected to any other cycle (not even by one of its ends) on the outer face. These edges are said, “free” (they are drawn in dashed red lines in Figure 2(b)).
2.

A construction similar to 1 is applied from $H_{2}$ to initialize $G_{2}$ with $n_{2}$ cycles.
3.

Independent vertices are added to $G_{1}$ in such a way that the sets of vertices of $G_{1}$ and $G_{2}$ is the same.

Any edge created in those firsts steps belongs to the set $E_{1}^{H}$ (respectively $E_{2}^{H}$ ). Unless specified, the edges defined from now belong only to the set $\{E_{1}-E_{1}^{H}\}$ (respectively $\{E_{2}-E_{2}^{H}\}$ ).

4.

A same $3$ -cycle $x, y, z$ is added to $G_{1}$ and $G_{2}$ , with edge $[x,y]$ in $E_{1}^{H}$ and edge $[x,y]\in E_{2}^{H}$ .
5.

For each cycle $c_{u}$ in $G_{1}$ , replace a free edge $[a,b]$ of $E_{1}^{H}$ by a chain $a, x, b$ in $\{E_{1}-E_{1}^{H}\}$ .
6.

Step 5 is applied to each cycle $c_{u}$ in $G_{2}$ , by replacing edges of $E_{2}^{H}$ by chains in $\{E_{2}-E_{2}^{H}\}$ . Each cycle $c_{u}$ such obtained belongs to the cycles of $G_{1}$ (resp. $G_{2}$ ) denoted by $C_{1}$ (resp. $C_{2}$ ). The cycle formed by the vertices $x, y$ , and $z$ also belongs to $C_{1}$ (resp. $C_{2}$ ) and is denoted by $c_{1}^{+}$ (resp. $c_{2}^{+}$ ).
7.

For each vertex $v$ in $G_{1}$ , an edge $[v,x]$ is added if it doesn’t exist yet. Similarly, for each vertex $w$ in $G_{2}$ , add an edge $[w,x]$ if necessary. The edges newly defined do not belong to any cycle of $C_{1}$ (resp. $C_{2}$ ).

The edges of $\{E_{1}-E_{1}^{H}\}$ (respectively $\{E_{2}-E_{2}^{H}\}$ ) form a backbone, common to both graphs and are all connected to $x$ . This backbone corresponds to the blue edges in Figure 2. Every edge of $E_{1}^{H}$ (respectively $E_{2}^{H}$ ) in $G_{1}$ (respectively $G_{2}$ ) belong to at least one cycle of $C_{1}$ (respectively $C_{2}$ ). These edges of $E_{1}^{H}$ are the dark ones in Figure 2(e).

Lemma 3.

The graph $G_{1}$ (or $G_{2}$ ) obtained from $H_{1}$ (resp. $H_{2}$ ) by the proposed transformation is planar.

Proof.

Let us verify the planarity of the graph after each step of the transformation.

1.

The graph $G_{1}$ is initialized from a planar representation of $H_{1}$ (see Figure 2(a) and 2(c)). Each cycle is defined from a vertex of the external face in $H_{1}$ . Also, when two cycles share an edge in $G_{1}$ , their corresponding vertices are extremities of the same edge in $H_{1}$ . In such a construction, no edges can cross in $G_{1}$ .
2.

For each cycle $c_{u}$ , its free edge is located on the external face of $G_{1}$ . Hence, replacing a free edge $[a,b]$ by a chain $a, x, b$ cannot induce an edge crossing.
3.

According to the embedded plan of the draw of $G_{1}$ , the edges added in the last step can be drawn from the inside of a cycle $c_{u}$ . See Figure 2(e) for an example of this third step.

To conclude, the graph obtained by the proposed transformation is planar. $\hfill\blacktriangleleft$

Note that by construction, each edge in the set $\{E_{1}-E_{1}^{H}\}$ in $G_{1}$ is incident to $x$ . Any pair of cycles $c\in C_{1}$ and $c^{\prime}\in C_{2}$ checks the two firsts properties of Definition 1 since $x$ is a vertex connected to an edge in $E^{H}$ contained by all the cycles in $C_{1}\cup C_{2}$ . It is obvious that the construction of $G_{1}$ , $G_{2}$ , $C_{1}$ and $C_{2}$ from $H_{1}$ and $H_{2}$ is polynomial.

Consider the polynomial transformation given above from an instance $(H_{1},H_{2})$ of the problem ISI to an instance $(\{G_{1},G_{2}\},C_{1}\cup C_{2},E^{H},m=n_{2}+1)$ of Problem CPP. As explained in Lemma 3, each graph in ${\cal G}=\{G_{1},G_{2}\}$ is planar. The vertices of $G_{1}$ and $G_{2}$ are the same and, by construction, every edge of $E^{H}$ belongs to at least one cycle in ${\cal C}=C_{1}\cup C_{2}$ .

Consider $H_{1}$ isomorphic to $H^{\prime}_{2}$ , an induced subgraph of $H_{2}$ . There exists an edge $[u,u^{\prime}]\in H_{2}^{\prime}$ isomorphic to an edge $[v,v^{\prime}]\in H_{1}$ . By construction, the cycles $c_{u}$ and $c_{u^{\prime}}$ in $G_{2}$ (resp., $c_{v}$ and $c_{v^{\prime}}$ in $G_{1}$ ) verifies $c_{u}\cap c_{u^{\prime}}\neq\emptyset$ (resp. $c_{v}\cap c_{v^{\prime}}\neq\emptyset$ ). By construction, $c_{u}$ and $c_{v}$ in $C_{1}$ (resp. $c_{u^{\prime}}$ and $c_{v^{\prime}}$ in $C_{2}$ ) share an edge in $G_{1}$ (resp. $G_{2}$ ). Let us consider a partition of ${\cal C}=C_{1}\cup C_{2}$ in which for each such pair of edges $[u,v],[u^{\prime},v^{\prime}]$ , there are two parts $\{c_{u},c_{u^{\prime}}\}$ and $\{c_{v},c_{v^{\prime}}\}$ . For any vertex $w$ of $H_{2}$ not in $H^{\prime}_{2}$ , we consider singleton $\{c_{w}\}$ . Thus, the so obtained partition contains $k=n_{2}$ parts, plus part $\{c^{+}_{1},c^{+}_{2}\}$ and checks Definition 1.

Let now be $\Pi$ a cycle polymorphism of $\{C_{1}\cup C_{2}\}$ of size $k=n_{2}+1$ . As this partition is obtained from two graphs, each part is of size $1$ or $2$ . Since $n_{2}$ is the number of vertices of $H_{2}$ , the number of parts of size $2$ is $n_{1}$ . Let $\{c^{+}_{1},c^{+}_{2}\}$ be a part. Consider a pair of parts $\{c_{u},c_{v}\}$ and $\{c_{u^{\prime}},c_{v^{\prime}}\}$ of size $2$ in $\Pi$ , with $u$ and $u^{\prime}$ vertices in $H_{2}$ and $v$ and $v^{\prime}$ vertices in $H_{1}$ . Since $\Pi$ checks Definition 1, $[u,u^{\prime}]$ is an edge in $H_{2}$ (i.e., $c_{u}$ and $c_{u^{\prime}}$ share an edge in $G_{2}$ ) iff $[v,v^{\prime}]$ is an edge in $H_{1}$ (i.e., $c_{v}$ and $c_{v^{\prime}}$ share an edge in $G_{1}$ ), as a consequence of property “Same interactions” in Definition 1.

Consider sets $V_{S2}=\bigcup\limits_{\{c_{u},c_{v}\}\in\Pi\atop u\leavevmode\nobreak\ vertex% \leavevmode\nobreak\ in\leavevmode\nobreak\ H_{2}}\{u\}$ and $V_{S1}=\bigcup\limits_{\{c_{u},c_{v}\}\in\Pi\atop v\leavevmode\nobreak\ vertex% \leavevmode\nobreak\ in\leavevmode\nobreak\ H_{1}}\{v\}$ , i.e., the vertex set of $H_{1}$ . The induced subgraphs $H_{2}[V_{S2}]$ of $H_{2}$ is isomorphic to $H_{1}$ , by considering $u$ isomorphic to $v$ for any $\{c_{u},c_{v}\}\in\Pi$ . Then there is an induced subgraph of $H_{2}$ isomorphic to $H_{1}$ .

Thus, Problem Cycle Polymorphism Partition is NP-complete, even if each graph $G$ in ${\cal G}$ is planar and if each edge of $E^{H}$ in a graph $G_{i}$ in ${\cal G}$ belongs to a cycle in $C_{i}\in{\cal C}$ . This ends the proof of Theorem 2. We show now that Problem min-CPP cannot be approximated.

Theorem 4.

Problem min-Cycle Polymorphism Partition cannot be approximated with a factor of $|{\cal C}|^{1/7-\epsilon}$ for any $\epsilon$ .

Proof.

Given a graph $G$ , the Minimum Chromatic Number (MCG) problem consists of determining its chromatic number $\chi(G)$ . The associated decision problem is NP-complete [16]. From $(G=(V_{G},E_{G}),m)$ an instance of MCG, an instance of min-CPP is built as follows.

A graph $P_{G}$ is built from $G$ with a set of edges $E^{H}$ , according to the following steps : (1) For each vertex $v\in V_{G}$ , build a cycle $c_{v}$ of length $4$ defined by $v_{1},v_{2},v_{3},v_{4}$ with $[v_{1},v_{4}]$ the only edge in $E^{H}$ on it; (2) Add a chain of edges in $E-E^{H}$ with three new vertices $x, y, z$ , and then add an edge $[x,z]\in E^{H}$ ; (3) In each cycle $c_{v}$ , replace $[v_{2},v_{3}]$ by $[v_{2},x]$ and $[v_{3},z]$ both belonging to $E-E^{H}$ ; the cycle thus modified $v_{1},v_{2},x,z,v_{3},v_{4}$ , is still denoted by $c_{v}$ . Figure 3 illustrates the built of $P_{G}$ from $G$ on an example.

(a) A graph

G

with

3

colors.

(b) The graph

P_{G}

built.

Figure 3: Example of a graph

P_{G}

built from a graph

G

with the proposed procedure. In Figure 3(b), edges of

E

are in solid black lines while edges of

E^{H}

are in dashed blue lines.

Define, now, a set of graphs ${\cal G}=\{P_{1},\ldots,P_{|E_{G}|}\}$ from the graph $P_{G}$ as follows. For each edge $e_{i}=[u,v]\in E_{G}$ , a graph $P_{i}$ is a subgraph of $P_{G}$ in which for each vertex $w\in V_{G}-\{u,v\}$ the edge $[w_{1},w_{4}]$ of $c_{w}$ has been removed.
A set of cycles $C_{i}=\{c_{u},c_{v}\}$ is associated to $P_{i}$ . Note then that $|{\cal C}|=|V_{G}|$ where ${\cal C}=\bigcup_{i}^{|E_{G}|}C_{i}$ . Figure 3 illustrates three of the five graphs built from $P_{G}$ drawn in Figure 3.

(a) The graph

P_{1}

.

(b) The graph

P_{2}

.

(c) The graph

P_{3}

.

Figure 4: Example of three graphs from the set

{\cal G}=\{P_{1},\ldots,P_{|E_{G}|}\}

.

This transformation of an instance $(G=(V_{G},E_{G}),m)$ of the MCG problem into an instance $({\cal G},{\cal C},E^{H},m)$ of CPP is polynomial. All cycles in ${\cal C}$ share the same vertex $x$ connected to an edge of $E^{H}$ . Therefore, considering the property of no simultaneous occurrence of the polycycles, a polymorphism partition $<{\cal G},{\cal C},E^{H}>$ of size $m$ corresponds to a partition of size $m$ of $V_{G}$ into stable subsets (i.e., a $m$ -coloring of $G$ ).
As indicated in [4], the MCG problem cannot be approximated with a factor of $|V_{G}|^{1/7-\epsilon}$ and this for any $\epsilon$ . Therefore, due to the polynomial transformation proposed here, one can conclude that the same is true for the min-CPP problem. $\hfill\blacktriangleleft$

3 Computing a polygraph from a trajectory

3.1 Computing the set of selected cycles for each conformer

Given a trajectory, each conformer will correspond to a subgraph of the obtained polygraph. The evolution of the molecular structure during the trajectory corresponds to the modification of these subgraphs between each pair of consecutive conformers. It is therefore a question of obtaining the polygraph which minimizes these modifications as much as possible. This is directly impacted by the cycle bases chosen for each conformer graph. Indeed, given a target trajectory, the choice of minimum cycle basis of the conformers can have a significant impact on the quality of the computed polygraph, in terms of the number of vertices (i.e., polycycles). A first natural assumption is that the more cycles the cycle basis chosen for ${\cal G}$ graphs have in common, the fewer vertices the polygraph will have. The problem of determining a minimum cycle basis for each graph maximizing the overall intersection of these bases is NP-complete [1]. Furthermore, experimentally the correlation between the size of the intersection and the number of vertices of the polygraph was not very convincing.

Consider a set of graphs ${\cal G}=\{G_{1},G_{2},\ldots,G_{ng}\}$ of an input trajectory. We examine two possible algorithms for generating a cycle basis for each conformer graph $G_{i}$ . These algorithms may be further enhanced with local optimization.

The first approach involves generating a minimum cycle basis $B_{i}$ of $G_{i}$ using the Horton algorithm [14]. Briefly, this algorithm identifies a set of fundamental cycles and then incrementally selects a cycle base. The cycles are chosen from the set of fundamental cycles in order of increasing size, provided they cannot be derived by combining the cycles already present in the base under construction.

The second approach involves using an amended Horton algorithm. The cycles are ordered by size, with a priority given to those with a larger number of hydrogen bonds. As the cycles are ordered by size, this algorithm also generates a minimal cycle base.

Let $S C$ be the set of all fundamental cycles generated from all the graphs $G_{i}$ by the execution of the first or second algorithm. It may exist cycles in $S C$ which do not appear in the union of all bases $B_{i}$ . We define the following local optimization: A pair $c,c^{\prime}\in SC^{2}$ is called swappable iff (i) they do not appear in a same cycle basis $B_{i}$ , and (ii) $c^{\prime}$ can replace $c$ in all cycle bases $B_{i}$ in which $c$ appears (i.e., such that the resulting sets remain valid minimum cycle bases for their corresponding graphs).

Knowing if two cycles are swappable can be computed in polynomial time. For any cycle $c$ we also define $Cost(c)$ as the ratio between the number of cycle bases in the current set in which $c$ appears and the number of graphs in ${\cal G}$ containing $c$ . At each step of the local optimization we apply the swap maximizing the strict increasing of $\sum\nolimits_{c\in SC^{+}}Cost(c)$ , where $SC^{+}$ is the subset of cycles of $S C$ appearing in at most one cycle base of the obtained set of cycle bases after swapping. Thus algorithm ends when no such strictly increasing swapping exists. In the following, we called Swapped bases the final obtained set of cycle bases.

3.2 Computing the polygraph

Finally, given a set of cycles for each graph of the trajectory obtained as described in the previous section, due to the NP-completeness of Problem min-Cycle Polymorphism Partition and that even for planar graphs, to minimize as possible the number of polycycles we propose the following greedy algorithm. Let us start from the cycle polymorphism partition $\Pi<{\cal G},{\cal C},E^{H}>$ where each part is a singleton. At each step, two parts $\pi_{i},\pi_{j}$ such that $\pi_{i}\cup\pi_{j}$ is a polymorphic cycle are selected and merged to create a new partition with one less part. This selection supposes the use of an objective function to evaluate each potential couple of parts. Therefore, if the union of two polymorphic cycles remains a polymorphic cycle, we propose the following scoring : $S(\pi_{i},\pi_{j})=|\pi_{i}\cup\pi_{j}|\times|V^{H}(\pi_{i})\cap V^{H}(\pi_{j})|$ where $V^{H}(\pi_{i})$ is the set of vertices in the union of cycles of $\pi_{i}$ being an extremity of an edge in $E^{H}$ . Using this scoring consists in choosing the fusion on one hand with a large resulting size and on the other hand the one giving the less constraints on next possible fusions considering second proposition of Definition 1.

Starting from the cycle polymorphism partition composed of singletons and performing successive merges, the result is a cycle polymorphism partition. The proposed objective function can be modified and improved independently of the rest of the algorithm if necessary.

4 Performance evaluation of the whole approach

Effectiveness of the polygraph.

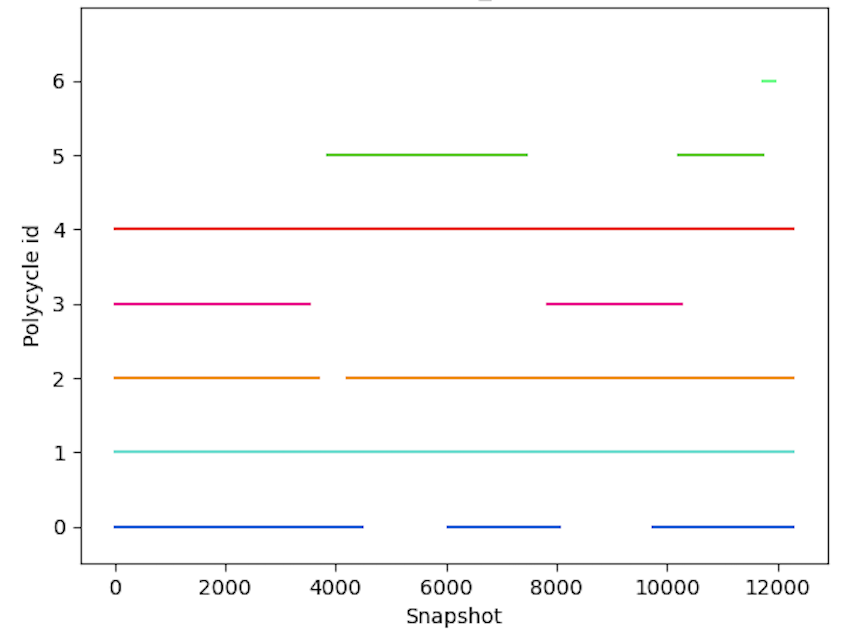
The relevance of the polygraph for MD trajectory analysis has already been demonstrated [2]. Figure 5 illustrates the expected results of the method. Given a MD trajectory, Figure 5(a) is the polygraph obtained using Horton’s algorithm to compute the basis. The polygraph represents the polymorphic cycles and their interactions, which constitute the structure of the molecule throughout the dynamics. Figure 5(b) is a representation of the occurrences of polycycles in conformers over time along the trajectory; one dot in column $i$ indicates that one cycle of the corresponding polycycle occurs in the $i^{th}$ snapshots of the trajectory. Some polycycles are almost always present, such as P1, P2 or P4. Others only appear under certain conditions, such as P3 and P5, which never appear together. Finally, $P6$ only appears at the very end of the trajectory. Such an event can be considered a significant structural change, since it implies a new polycycle. This analysis is only possible using the polygraph, which has previously grouped together equivalent cycles. Furthermore, examining Figure 5(b), several lines are full, indicating that a cycle from the set is always present. This also implies that polymorphic cycles exist at the same time and cannot be merged. This shows that the obtained polygraph is already highly condensed and it is challenging to further reduce the number of polycycles.

Refer to caption — (a) The polygraph obtained.

Performances of the approach.

To evaluate our approach, we carried out tests on a few trajectories measured by chemists. Given a trajectory, we systematically compute the polygraph from cycles obtained by the Horton algorithm and its variant, with or without the local optimization. Table 1 presents our results. The number of graphs in each trajectory varies from 60 to 500. In these molecules, the difference between the number of atoms and the number of covalent bonds indicates that they contain few cycles composed solely of covalent bonds. For each trajectory, we compute the polygraphs based on the cycles provided by the Horton algorithm and its variant without and the local optimization. The most crucial metric is the number of polycycles in the polygraph. A smaller value indicates a better result. Although the results are close, we observe that using Horton’s algorithm without local descent may yield a slightly higher number of polycycles. Due to the difficulty of generating trajectories for chemists, we currently do not have any additional trajectories that would allow for further exploration of these results.

Table 1: On the right-hand columns, the number of polycycles in polygraphs obtained for different trajectories (Chondroitin Disulfate, Zala6 and Gramicidine) according to the four different cycle base generation methods. Information on the trajectories is shown in the left-hand columns.

Trajectory	Trajectory parameters			Number of polycycles
				Horton	A. Horton	Horton	A. Horton
	$\|V\|$	$\|E\|$	$\|E^{H}\|$	With local opt.		Without local opt.
Chond. D.	35	37	13	18	16	16	16
Zala6	41	41	9	6	6	6	6
Gram.	136	143	13	42	41	41	41

To extend our study, we generate random trajectories similar to those provided by chemists. Initially, we create a backbone graph and a set of hydrogen bonds, which serve for generating each trajectory graph. For a graph with $n$ nodes, we initiate the process by randomly generating a connected $4$ -regular graph $G=(V,E)$ with $n$ vertices. From $G$ , we extract a random spanning tree $A=(V,E^{\prime})$ . Subsequently, we select a set $B$ of $b$ edges uniformly at random from $E\backslash E^{\prime}$ . These edges, combined with those from the spanning tree, constitute the backbone, representing the covalent links present in all graphs within the trajectory. Next, we select a set $H$ of $h$ edges from $E\backslash(E^{\prime}\cup B)$ to represent potential hydrogen bonds. The edges in $H$ are chosen randomly, subject to the following criterion: each time an edge is selected, the two end vertices are assigned “hydrogen” or “oxygen” labels. If these labels do not conform to those previously assigned to the end vertices, the edge is rejected, and a new edge is randomly chosen.

Using the backbone graph $(V,E\cup B)$ and the set of hydrogen bonds, we generate a trajectory by producing a sequence of graphs such that no two consecutive graphs differ by more or less than one hydrogen bond, and each graph contains no more than $k$ hydrogen bonds. For the initial graph in the sequence, a set of $\lfloor\frac{k}{2}\rfloor$ edges are randomly selected.

The algorithms used to generate the $d$ -regular graph and the spanning tree are those provided by the Networkx libraries, which implement the algorithms described in [17] and [18]. The trajectories obtained are close to those provided by chemists, in several aspects. The maximum degree of the vertices is limited to 4, as in molecules. The graphs are planar or very close to being planar. The number of cycles without hydrogen bonds is small and controlled by the $b$ parameter. Hydrogen bonds appear among a set of bonds of size $h$ . Successive graphs in a trajectory differ by no more than one edge.

For our analysis, we generated 500 random trajectories, each consisting of 500 graphs. These graphs contain of 25 nodes, 3 backbone cycles, and 15 hydrogen bonds. Figure 6 illustrates the distribution of the number of polycycles in the polygraphs depending on the algorithm used to generate the cycle bases. Among the 4 available algorithms, Horton without descent appears to be statistically the least favorable option. On relatively small graphs with relatively few cycles, switching to the Amended Horton with descent reduces the number of polycycles from 34 to 30. However, this distribution alone does not allow us to draw definitive conclusions. It’s possible that there are rare trajectories for which Horton performs better.

Figure 6: Number of polycycles in polygraphs of 500 trajectories. On the left, the polygraph is based on the cycles generated from Horton algorithm, on the right with Amended Horton with local descent. Graphs in the trajectories have 3 cycles in backbones and 15 hydrogen bonds.

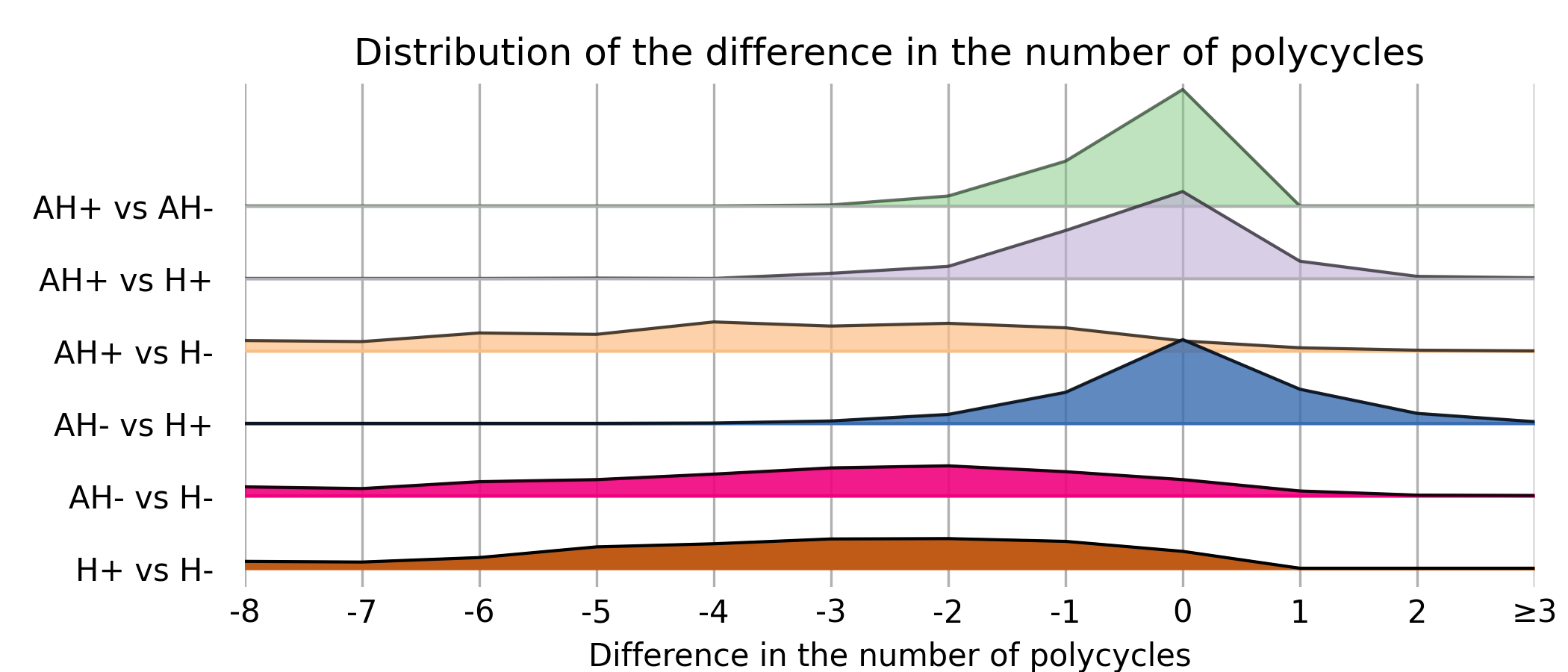
For each trajectory, we compare the results obtained for the four algorithms. Figure 7 illustrates the distribution of the difference in polycycle size for a given pair of algorithms. The first and last curves confirm that the descent algorithm consistently reduces the size of the polycycle, i.e. difference in polycycle size is always negative or zero. The descent algorithm can significantly reduce the polycycle size when starting from Horton’s algorithm. However, the reduction is more marginal when using the amended Horton algorithm.

The first three curves indicate that, with the exception of a small number of trajectories, Horton modified with local optimization is always preferable. Conversely, Horton without local optimization does not give satisfactory results (lines AH+ vs H-, AH- vs H- and H+ vs H-). Amended Horton and Horton with descent can be considered relatively similar (AH- vs. H+ line). It seems that forcing Horton to select hydrogen bonds is a good strategy that the local optimization manages to compensate for. This compensation comes with a cost in terms of runtime. On average, the Horton algorithm and its variant each run in about 3 seconds on a commercial laptop. However, the descent algorithm adds an additional 25 seconds when starting with cycles generated by Horton, and an extra 21 seconds when starting with cycles generated by Amended Horton. Statistically, Amended Horton’s solutions not only yield better results but also require fewer optimization steps to reach a local optimum. We have generated trajectories containing larger graphs (up to 50 vertices) with more cycles, and so far the results seem identical, even if the computation time increases.

Conclusion

In this article, in order to deal with a real problem in chemoinformatics, the analysis of molecular dynamics trajectories, we introduce the min-Cycle Polymorphism Partition problem. We prove its NP-completeness and establish that it does not admit a $|{\cal C}|^{1/7-\epsilon}$ -approximation for any $\epsilon$ .

However, the heuristic approach that we propose has proven to be effective in practice and realistic from the point of view of execution time and quality of results. Results on large sets of random graphs show that using our amended version of Horton algorihtm is highly effective for initial base selection. The improvement of the bases obtained by the greedy cycle swapping approach that we propose makes it possible to consider the use of neighborhood metaheuristics whose performance is to be studied.

References

[1] Ylène Aboulfath, Dimitri Watel, Marc-Antoine Weisser, Thierry Mautor, and Dominique Barth. Maximizing minimum cycle bases intersection. In Combinatorial Algorithms: 35th International Workshop, IWOCA 2024, Ischia, Italy, July 1–3, 2024, Proceedings, pages 55–68, Berlin, Heidelberg, 2024. Springer-Verlag. doi:10.1007/978-3-031-63021-7_5.
[2] Ylène Aboulfath, Sana Bougueroua, Alvaro Cimas, Dominique Barth, and Marie-Pierre Gaigeot. Time-resolved graphs of polymorphic cycles for h-bonded network identification in flexible biomolecules. Journal of Chemical Theory and Computation, 20(3):1019–1035, 2024. doi:10.1021/acs.jctc.3c01031.
[3] Edoardo Amaldi, Claudio Iuliano, Tomasz Jurkiewicz, Kurt Mehlhorn, and Romeo Rizzi. Breaking the $O(m^{2}n)$ barrier for minimum cycle bases. In Amos Fiat and Peter Sanders, editors, Algorithms – ESA 2009, pages 301–312, Berlin, Heidelberg, 2009. Springer Berlin Heidelberg. doi:10.1007/978-3-642-04128-0_28.
[4] Mihir Bellare, Oded Goldreich, and Madhu Sudan. Free bits, pcps, and nonapproximability—towards tight results. SIAM Journal on Computing, 27(3):804–915, 1998. doi:10.1137/S0097539796302531.
[5] Claude Berge. Graphs and Hypergraphs. Graphs and Hypergraphs. North-Holland Publishing Company, 1973.
[6] Franziska Berger, Peter Gritzmann, and Sven de Vries. Computing cyclic invariants for molecular graphs. Networks, 70(2):116–131, 2017. doi:10.1002/net.21757.
[7] Sana Bougueroua, Marie Bricage, Ylène Aboulfath, Dominique Barth, and Marie-Pierre Gaigeot. Algorithmic graph theory, reinforcement learning and game theory in md simulations: From 3d structures to topological 2d-molecular graphs (2d-molgraphs) and vice versa. Molecules, 28(7), 2023. doi:10.3390/molecules28072892.
[8] Sana Bougueroua, Franck Quessette, Dominique Barth, and Marie-Pierre Gaigeot. Gateway : Graph theory based software for an automatic analyses of molecular conformers generated over time. ChemRxiv, 2022. doi:10.26434/chemrxiv-2022-1d5x8-v2.
[9] Sana Bougueroua, Riccardo Spezia, S. Pezzotti, Sandrine Vial, Franck Quessette, Dominique Barth, and Marie-Pierre Gaigeot. Graph theory for automatic structural recognition in molecular dynamics simulations. The Journal of Chemical Physics, 149(18):184102, November 2018. doi:10.1063/1.5045818.
[10] Radoslav Dimitrov, Zeyang Zhao, Ralph Abboud, and İsmail İlkan Ceylan. PlanE: representation learning over planar graphs. In Proceedings of the 37th International Conference on Neural Information Processing Systems, NIPS ’23, Red Hook, NY, USA, 2023. Curran Associates Inc. doi:10.48550/arXiv.2307.01180.
[11] Benoît Gaüzère, Luc Brun, and Didier Villemin. Relevant cycle hypergraph representation for molecules. In Graph-Based Representations in Pattern Recognition, pages 111–120, Berlin, Heidelberg, 2013. Springer Berlin Heidelberg. doi:10.1007/978-3-642-38221-5_12.
[12] Kurt De Grave and Fabrizio Costa. Molecular graph augmentation with rings and functional groups. Journal of Chemical Information and Modeling, 50(9):1660–1668, 2010. doi:10.1021/ci9005035.
[13] Janna Hastings, Oliver Kutz, and Till Mossakowski. How to model the shapes of molecules? combining topology and ontology using heterogeneous specifications. In Deep Knowledge Representation Challenge Workshop. International Conference on Knowledge Capture (K-Cap-11), 6th, befindet sich co-located with K-CAP 2011, June 25-29, Banff, Alberta, Canada, 2011.
[14] Joseph Horton. A polynomial-time algorithm to find the shortest cycle basis of a graph. SIAM Journal on Computing, 16:358–366, April 1987. doi:10.1137/0216026.
[15] Tamás Horváth, Thomas Gärtner, and Stefan Wrobel. Cyclic pattern kernels for predictive graph mining. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’04, pages 158–167, New York, NY, USA, 2004. Association for Computing Machinery. doi:10.1145/1014052.1014072.
[16] Richard M. Karp. Reducibility among Combinatorial Problems, pages 85–103. Springer US, Boston, MA, 1972. doi:10.1007/978-1-4684-2001-2_9.
[17] Jeong Han Kim and Van Hanh Vu. Generating random regular graphs. Combinatorica, 26:683–708, December 2006. doi:10.1007/s00493-006-0037-7.
[18] Vidyadhar G. Kulkarni. Generating random combinatorial objects. Journal of Algorithms, 11(2):185–207, 1990. doi:10.1016/0196-6774(90)90002-V.
[19] Stefi Nouleho Ilemo, Dominique Barth, Olivier David, Franck Quessette, Marc-Antoine Weisser, and Dimitri Watel. Improving graphs of cycles approach to structural similarity of molecules. PLOS ONE, 14(12):1–25, December 2019. doi:10.1371/journal.pone.0226680.
[20] Vismara P. Union of all the minimum cycle bases of a graph. The Electronic Journal of Combinatorics, 4(1), January 1997. doi:10.37236/1294.
[21] Maciej M. SysŁ;o. The subgraph isomorphism problem for outerplanar graphs. Theoretical Computer Science, 17(1):91–97, 1982. doi:10.1016/0304-3975(82)90133-5.

[bib.bib1] [1] Ylène Aboulfath, Dimitri Watel, Marc-Antoine Weisser, Thierry Mautor, and Dominique Barth. Maximizing minimum cycle bases intersection. In Combinatorial Algorithms: 35th International Workshop, IWOCA 2024, Ischia, Italy, July 1–3, 2024, Proceedings, pages 55–68, Berlin, Heidelberg, 2024. Springer-Verlag. doi:10.1007/978-3-031-63021-7_5.

[bib.bib2] [2] Ylène Aboulfath, Sana Bougueroua, Alvaro Cimas, Dominique Barth, and Marie-Pierre Gaigeot. Time-resolved graphs of polymorphic cycles for h-bonded network identification in flexible biomolecules. Journal of Chemical Theory and Computation, 20(3):1019–1035, 2024. doi:10.1021/acs.jctc.3c01031.

[bib.bib3] [3] Edoardo Amaldi, Claudio Iuliano, Tomasz Jurkiewicz, Kurt Mehlhorn, and Romeo Rizzi. Breaking the $O(m^{2}n)$ barrier for minimum cycle bases. In Amos Fiat and Peter Sanders, editors, Algorithms – ESA 2009, pages 301–312, Berlin, Heidelberg, 2009. Springer Berlin Heidelberg. doi:10.1007/978-3-642-04128-0_28.

[bib.bib4] [4] Mihir Bellare, Oded Goldreich, and Madhu Sudan. Free bits, pcps, and nonapproximability—towards tight results. SIAM Journal on Computing, 27(3):804–915, 1998. doi:10.1137/S0097539796302531.

[bib.bib5] [5] Claude Berge. Graphs and Hypergraphs. Graphs and Hypergraphs. North-Holland Publishing Company, 1973.

[bib.bib6] [6] Franziska Berger, Peter Gritzmann, and Sven de Vries. Computing cyclic invariants for molecular graphs. Networks, 70(2):116–131, 2017. doi:10.1002/net.21757.

[bib.bib7] [7] Sana Bougueroua, Marie Bricage, Ylène Aboulfath, Dominique Barth, and Marie-Pierre Gaigeot. Algorithmic graph theory, reinforcement learning and game theory in md simulations: From 3d structures to topological 2d-molecular graphs (2d-molgraphs) and vice versa. Molecules, 28(7), 2023. doi:10.3390/molecules28072892.

[bib.bib8] [8] Sana Bougueroua, Franck Quessette, Dominique Barth, and Marie-Pierre Gaigeot. Gateway : Graph theory based software for an automatic analyses of molecular conformers generated over time. ChemRxiv, 2022. doi:10.26434/chemrxiv-2022-1d5x8-v2.

[bib.bib9] [9] Sana Bougueroua, Riccardo Spezia, S. Pezzotti, Sandrine Vial, Franck Quessette, Dominique Barth, and Marie-Pierre Gaigeot. Graph theory for automatic structural recognition in molecular dynamics simulations. The Journal of Chemical Physics, 149(18):184102, November 2018. doi:10.1063/1.5045818.

[bib.bib10] [10] Radoslav Dimitrov, Zeyang Zhao, Ralph Abboud, and İsmail İlkan Ceylan. PlanE: representation learning over planar graphs. In Proceedings of the 37th International Conference on Neural Information Processing Systems, NIPS ’23, Red Hook, NY, USA, 2023. Curran Associates Inc. doi:10.48550/arXiv.2307.01180.

[bib.bib11] [11] Benoît Gaüzère, Luc Brun, and Didier Villemin. Relevant cycle hypergraph representation for molecules. In Graph-Based Representations in Pattern Recognition, pages 111–120, Berlin, Heidelberg, 2013. Springer Berlin Heidelberg. doi:10.1007/978-3-642-38221-5_12.

[bib.bib12] [12] Kurt De Grave and Fabrizio Costa. Molecular graph augmentation with rings and functional groups. Journal of Chemical Information and Modeling, 50(9):1660–1668, 2010. doi:10.1021/ci9005035.

[bib.bib13] [13] Janna Hastings, Oliver Kutz, and Till Mossakowski. How to model the shapes of molecules? combining topology and ontology using heterogeneous specifications. In Deep Knowledge Representation Challenge Workshop. International Conference on Knowledge Capture (K-Cap-11), 6th, befindet sich co-located with K-CAP 2011, June 25-29, Banff, Alberta, Canada, 2011.

[bib.bib14] [14] Joseph Horton. A polynomial-time algorithm to find the shortest cycle basis of a graph. SIAM Journal on Computing, 16:358–366, April 1987. doi:10.1137/0216026.

[bib.bib15] [15] Tamás Horváth, Thomas Gärtner, and Stefan Wrobel. Cyclic pattern kernels for predictive graph mining. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’04, pages 158–167, New York, NY, USA, 2004. Association for Computing Machinery. doi:10.1145/1014052.1014072.

[bib.bib16] [16] Richard M. Karp. Reducibility among Combinatorial Problems, pages 85–103. Springer US, Boston, MA, 1972. doi:10.1007/978-1-4684-2001-2_9.

[bib.bib17] [17] Jeong Han Kim and Van Hanh Vu. Generating random regular graphs. Combinatorica, 26:683–708, December 2006. doi:10.1007/s00493-006-0037-7.

[bib.bib18] [18] Vidyadhar G. Kulkarni. Generating random combinatorial objects. Journal of Algorithms, 11(2):185–207, 1990. doi:10.1016/0196-6774(90)90002-V.

[bib.bib19] [19] Stefi Nouleho Ilemo, Dominique Barth, Olivier David, Franck Quessette, Marc-Antoine Weisser, and Dimitri Watel. Improving graphs of cycles approach to structural similarity of molecules. PLOS ONE, 14(12):1–25, December 2019. doi:10.1371/journal.pone.0226680.

[bib.bib20] [20] Vismara P. Union of all the minimum cycle bases of a graph. The Electronic Journal of Combinatorics, 4(1), January 1997. doi:10.37236/1294.

[bib.bib21] [21] Maciej M. SysŁ;o. The subgraph isomorphism problem for outerplanar graphs. Theoretical Computer Science, 17(1):91–97, 1982. doi:10.1016/0304-3975(82)90133-5.