Bit Packed Encodings for Grammar-Compressed Strings Supporting Fast Random Access
Abstract
Grammar-based compression is a powerful compression technique that allows for computation over the compressed data. While there has been extensive theoretical work on grammar and encoding size, there has been little work on practical grammar encodings. In this work, we consider the canonical array-of-arrays grammar representation and present a general bit packing approach for reducing its space requirements in practice. We then present three bit packing strategies based on this approach – one online and two offline – with different space-time trade-offs. This technique can be used to encode any grammar-compressed string while preserving the virtues of the array-of-arrays representation. We show that our encodings are away from the information-theoretic bound, where is the number of symbols in the grammar, and that they are much smaller than methods that meet the information-theoretic bound in practice. Moreover, our experiments show that by using bit packed encodings we can achieve state-of-the-art performance both in grammar encoding size and run-time performance of random-access queries.
Keywords and phrases:
String algorithms, data compression, random access, grammar-based compressionFunding:
Shunsuke Inenaga: The work of Shunsuke Inenaga was supported by JSPS KAKENHI grant numbers JP23K24808 and JP23K18466.Copyright and License:
2012 ACM Subject Classification:
Theory of computation Data compressionSupplementary Material:
Software (Source Code): https://github.com/alancleary/FRASarchived at
 swh:1:dir:b44d80347961d131d08c1d6de7842e82b466a594
swh:1:dir:b44d80347961d131d08c1d6de7842e82b466a594
Acknowledgements:
We thank the authors of [7] for providing the c1000 data set.Funding:
The work of Alan M. Cleary, Joseph Winjum, and Jordan Dood was supported by NSF award number 2105391.Editors:
Petra Mutzel and Nicola PrezzaSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
Grammar-based compression is the process of compressing a string by computing a context-free grammar that generates the string (and no others) such that the encoded grammar is smaller than the original string. Consequently, determining bounds for the size of such grammars and their encodings has received much attention in the literature. Notably, in [17] the authors provide an information-theoretic lower bound for representing grammars in Chomsky normal form using bits, where is the number of symbols in the grammar. The authors also describe a grammar representation that is asymptotically equivalent to this lower bound that requires bits of space, where is the size of the string alphabet. In [15] the authors show that the length of the binary code output by RePair [11] and all irreducible grammars is upper bounded by for any , where is the -order empirical entropy of the string that the grammar generates. This bound was shown to be tight in [9]. And recently in [18] the authors presented a representation for grammars in Chomsky normal form that approaches the information-theoretic lower bound taking bits of space and supports random access queries in -time, where is the number of symmetric centroid paths in the DAG representation of the grammar and is the length of the substring accessed.
While there has been much theoretical work on the space required to encode grammar-compressed strings, there exists very few practical algorithms. In [13] the authors present FOLCA – a grammar representation that supports online encoding that achieves the information-theoretic lower bound of Tabei et al. [17] and supports random access. And in [7] the authors present ShapedSLP – an encoding specifically for random access to grammar-compressed strings. Both FOLCA and ShapedSLP only work on RePair style grammars, making them incompatible with recent grammar-based compression algorithms [14, 6]. Moreover, excluding the canonical array-of-arrays representation, we are not aware of a general purpose encoding that will work on any grammar-compressed string.
In this work, we consider the array-of-arrays representation of grammar-compressed strings and present a general bit packing approach for reducing the space required by grammars represented in this way. We then present three novel bit packing algorithms – one online and two offline – that provide space-time trade-offs both as a function of the bit packing algorithm and the type of grammar being encoded. We show that our bit packing approach is away from the information-theoretic bound, and our experiments show that this bit packing approach achieves state-of-the-art performance both in grammar encoding size and run-time performance of random-access queries.
2 Preliminaries
In this section, we define terminology and syntax and briefly review relevant background information. Note that in this work indexes start at 1.
2.1 Binary Numbers and Model of Computation
In this work, all numbers are integers represented using two’s complement. The bit width of an integer is the number of bits used in the integer’s binary representation. We denote an integer with a specific bit width as , where , e.g. the binary representation of is . The most significant bit (MSB) of an integer is the position of the left-most bit set to , e.g. . In addition to arithmetic operators, we use the bitwise AND () and OR () operators. For brevity, these operators may be combined with the assignment () operator for a compound assignment, e.g. is equivalent to . The left shift () operator shifts the bits of a number left, e.g. . Similarly, the right shift () operator shifts the bits of a number right, e.g. .
Our theoretical model of computation is the word RAM with machine word size , in which bitwise operations can be performed in -time. In theory, the MSB of a given integer in range can be computed in -time on the word RAM [5]. In practice, typical implementations of MSBs, or equivalently of counting leading zeros (CLZ), require -time. We hereby make a reasonable assumption that MSBs take -time in practice as well, as the machine word size is typically in modern computers.
2.2 Grammar-Based Compression
A context-free grammar is a set of recursive rules that describe how to form strings from a language’s alphabet. A context-free grammar is called an admissible grammar if the language it generates consists only of a single string. Grammar-based compression is a compression technique that computes an admissible grammar for a given string such that the encoded grammar uses less space than the original string. In this work, we refer to admissible grammars simply as grammars.
Let be a string over alphabet , where denotes the length of . is a grammar that generates , where is a set of non-terminal characters, is the alphabet of (i.e. terminal characters) and is disjoint from , is a finite relation in , and is the symbol in that should be used as the start rule when using to generate . defines the rules of as a set of productions such that each is a non-terminal in and is a non-empty sequence from . Note that there is a total ordering of the (non-)terminal characters of a grammar: . The size of grammar is the total length of the right-hand sides of the productions and is denoted . We say that a non-terminal represents a string if is the (unique) string that derives. We only consider grammars with no useless rules and symbols.
There are three main types of grammars in the literature: straight-line programs (SLPs), Chomsky normal form (CNF) grammars, and RePair grammars. An SLP is simply an admissible grammar. A CNF grammar is an SLP in Chomsky normal form, i.e. every rule (including start rule ) is of the form () or (). A RePair grammar is a CNF grammar in which the start rule can have arbitrarily many symbols in its right-hand side, i.e. with [11]. In this work, all grammars are assumed to be SLPs, unless stated otherwise.
Let be a grammar that represents a string of length . A random access query on grammar is, given a query position (), return the th character in the uncompressed string . In practice, random access queries can be for entire substrings , where . Our experiments include results for both single character and substring queries.
The canonical representation of a grammar-compressed string is an array-of-arrays, where each subarray represents a rule in the grammar [17]. Generally speaking, such an array is a jagged array, meaning subarrays can have different lengths. In this representation each non-terminal character is represented as its rule’s index in the array, with the first values reserved for the alphabet. Subsequently, the subarrays are integer arrays, where the integer bit width is typically 32 or 64 bits. Moreover, this encoding requires bits, where . Although not optimal in size, the array-of-arrays is a versatile representation of grammar-compressed strings due to its simplicity, direct access to grammar rules and characters, algorithmic flexibility, and memory locality.
3 Algorithms
In this section, we present a general bit packing approach for grammars represented as an array-of-arrays. We then present three novel bit packing strategies that implement this approach. Note that each strategy can be computed in -time.
3.1 Bit Packing Approach
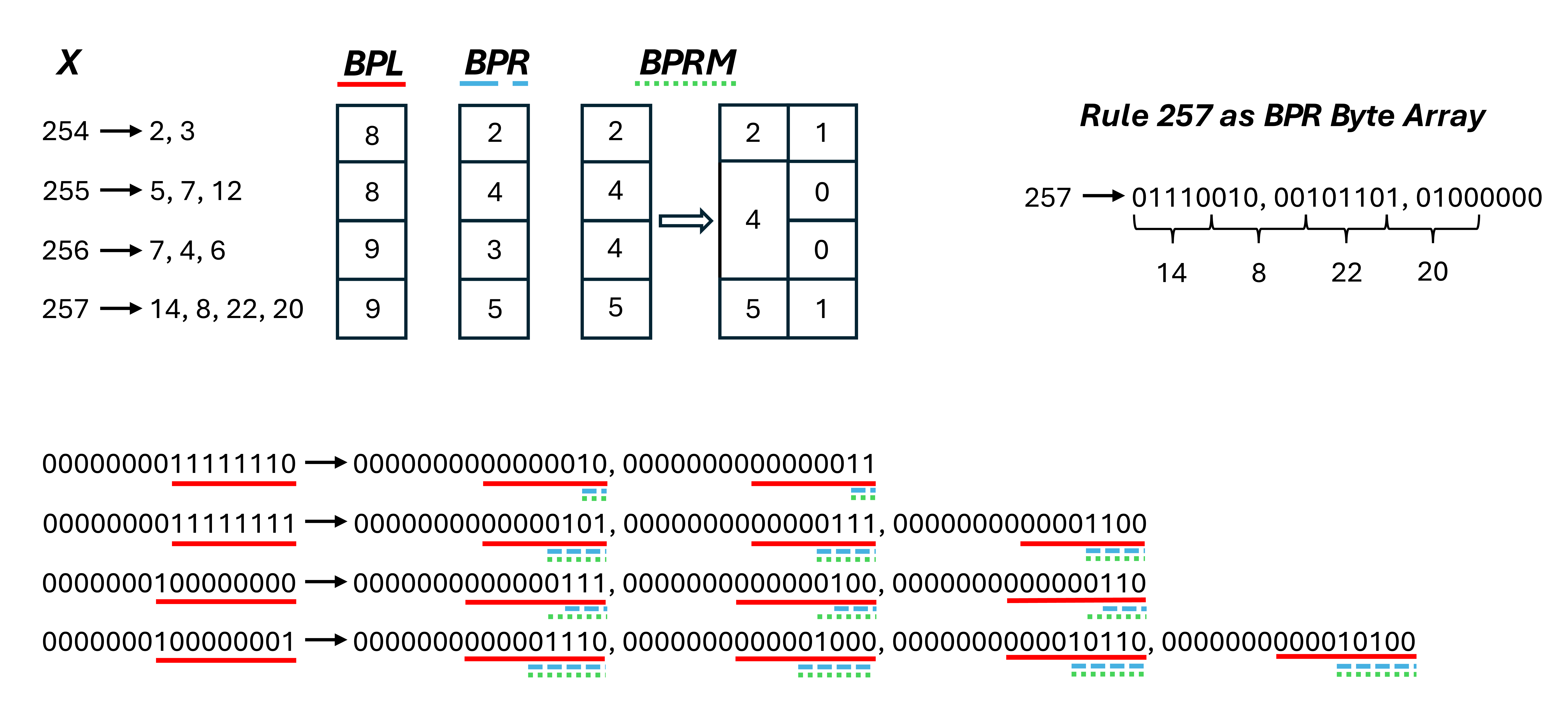
In the array-of-arrays representation of a grammar-compressed string each rule is a subarray and every non-terminal character is the index of its subarray in the array. Since every rule has the constraint (i.e. no character in a rule can be larger than the rule’s index), we observe that the smaller a rule’s index is, the fewer bits its characters can use in its subarray. Furthermore, it is possible for the largest number of bits required by any single character in a subarray to be much smaller than the subarray’s index. See Figure 1 for an example.
Bit packing is the technique of encoding multiple pieces of data using as few bits as possible by packing the raw bits into contiguous blocks of memory [16]. Given the observations above, we propose encoding grammar-compressed strings represented as an array-of-arrays using bit packing. Specifically, each rule (i.e. subarray) can be encoded using a different bit width, where each character in the rule is encoded using the same number of bits. This bit width can be smaller than the typical 64 bit integer size but still large enough to represent all the bits of each character in the rule. By using the same bit width for an entire rule, a subarray’s characters can be set and accessed just like the typical 64 bit integer arrays. We refer to the bit width for a subarray as its packing width.
In this work, we pack rules into byte arrays since a byte is typically the smallest unit of addressable memory, although our algorithms may be easily extended to other integer widths or raw memory. Given a rule as a 64 bit integer array, Algorithm 1 shows how to pack the rule into a byte array in -time and Algorithm 2 shows how to access a single value from the packed byte array in -time. The function used in both algorithms provides the rule’s packing width, allowing different strategies for determining a subarray’s packing width to be used. It is assumed that can determine a rule’s packing width in -time, either through direct computation or preprocessing and memoization. We discuss how to compute in -time in Section 4. The remaining subsections describe three different strategies for determining the packing width for a rule.
3.2 Left-Side Strategy
Given a rule , the simplest strategy for determining the rule’s packing width is to use by computing the MSB for . Due to the rule constraint , this guarantees that every character in will fit in the packing width. This strategy is also advantageous because it can be computed directly for a given index, meaning grammars can be encoded online, i.e. as the grammar itself is being computed. We refer to this strategy as Bit Pack Left (BPL). It takes -time and is shown in Algorithm 3.
3.3 Right-Side Strategy
A strategy that requires preprocessing each rule is to compute the MSB for each character in the rule and use the largest value as the rule’s packing width. Although this requires storing each rule’s packing width for decoding, we observe that these widths can be stored in a byte array because no width will exceed 64. We refer to this strategy as Bit Pack Right (BPR). It takes -time and is shown in Algorithm 3. Technically this is an offline strategy but it can be applied whenever an entire rule is added to the grammar, making it pseudo-online.
3.4 Right-Side Monotonic Strategy
The last strategy is a variation of the BPR strategy. In this strategy, the MSB is computed for every character in a rule . The largest MSB computed is then compared to the packing width of the previous rule’s subarray and the larger of the two is used as the rule’s packing width. As with BPR, each rule’s packing width needs to be stored for decoding. However, the packing widths of this strategy form a monotonic sequence, meaning the packing width byte array can be replaced by a unique packing width byte array that contains at most 64 values. A bit vector is then used to lookup each rule’s packing width in the unique packing width array using -time rank queries [19]. We refer to this strategy as Bit Pack Right Mono (BPRM). It takes -time and is shown in Algorithm 3. Like BPR, this strategy is technically offline but can be used pseudo-online by applying it whenever an entire rule is added to the grammar. Note that the effectiveness of this strategy is determined by the ordering of the rules in the grammar.
4 Bounds
In this section we, determine space bounds for all three bit packing strategies on both CNF and RePair grammars. SLPs, however, remain unbounded as the structures of these grammars are less deterministic.
4.1 Interface versus Implementation
To begin, we observe that for CNF and RePair grammars the implementation underlying the array-of-arrays interface need not be an array-of-arrays. Specifically, the array-of-arrays interface can be implemented using a single contiguous byte array with no gaps between the bits of consecutive rules. The byte a rule starts at in this array and the specific bit the rule starts at in that byte can then be computed for each packing width strategy using only the information that strategy already requires, as described in Section 3.
Given a rule , the left-side strategy determines a rule’s packing width by computing the MSB for . This is equivalent to using as the packing width for each rule . Recall that a CNF grammar has at most 2 characters per rule. This means that, when packing a grammar into a single contiguous byte array, the specific bit position at which a given rule starts is equal to
| (1) |
where denotes the number of terminal symbols. It is known (c.f. [1]) that
| (2) |
holds. Notice that the binary representation of is obtained by setting the -th bit to 1 and all the other bits to 0, and thus takes -time by computing the MSB of . Thus the starting bit position for can be retrieved in -time using Equations 1 and 2. The byte position and local bit position in the single byte array can then be obtained by computing and , respectively, where is the byte size.
A RePair grammar can be packed into a single contiguous byte array the same way. This is because only the start rule is variable in size and it is the last rule to be packed into the array, meaning each rule’s position in the array can be computed in the same way as for a CNF grammar.
Observe that using Equations 1 and 2 to compute the bit position for each rule is equivalent to computing the partial sums of the packing widths for the grammar. This can be computed directly for the left-side strategy using the closed form of the sum because the packing widths are derived directly from the non-terminal character , i.e. the sums are a well-defined series. However, for the right-side and right-side monotonic strategies these partial sums must be precomputed and memoized. Fortunately, this can be done without asymptotically increasing the space requirements of these strategies.
For the right-side strategy, this can be done by replacing the packing width array with an array storing the partial sums of the packing widths . The packing width for a rule can then be computed as
| (3) |
And the bit position at which starts can be computed as
| (4) |
Similarly, for the right-side monotonic strategy, the unique packing width array can be replaced by a partial sum array such that, for all ,
| (5) |
where and are and , respectively, and is the original lookup bit vector for . The packing width of a rule can then be computed as
| (6) |
where and and are and , respectively. The bit position at which starts can then be computed as
| (7) |
In total, we have shown that the array-of-arrays interface can be implemented using a single contiguous byte array for CNF and RePair grammars while preserving the asymptotic run-time and space complexities of all three bit packing strategies.
4.2 CNF and RePair Bounds
We observe that Equation 1 can be used to compute the number of bits in a CNF grammar when using the left-side strategy. Specifically, given a CNF grammar with total symbols, where is the number of non-terminals and is the number of terminals, the number of bits is
| (8) |
Consider the following summation and the derivation of its closed-form
| (9) |
Using the closed form of Equation 9, we can define an upper bound on Equation 8 as
| (10) |
Thus, using the left-side strategy, a CNF grammar requires no more than bits of space. Similarly, a RePair grammar with total symbols and start rule requires at most bits of space. Since the packing widths of the left-side strategy are the worst possible packing widths that may be used by the right-side and right-side monotonic strategies, these bounds can be extended to the right-side and right-side monotonic strategies by simply adding an additional term to account for the memoized packing width data [17].
4.3 Optimality
For simplicity, here we only consider the bounds for the left-side strategy on CNF grammars. Using Stirling’s approximation, our CNF bound can be expressed as
Again, using Stirling’s approximation, we observe that this is bigger than the information-theoretic bound of Tabei et al. [17], which is
By ignoring minor terms, our bound is bits away from Tabei et al.’s method. However, in practice, our method can be both faster and smaller than Tabei et al.’s method, as will be seen in the next section.
5 Results
In this section, we describe our implementation, experiments, and discuss results.
5.1 Implementation
In [3] Cleary et al. presented a modified version of the folklore algorithm for random access to grammar-compressed strings. Excluding the original folklore algorithm, which only works on CNF grammars, the implementation from [3], called Folklore Random Access for SLPs (FRAS), is currently the fastest random access algorithm in the literature. However, FRAS uses the array-of-arrays grammar representation and is subsequently not the smallest in practice. In this work we extend the FRAS implementation to include all three bit packing strategies described in the Algorithms section. FRAS is implemented in C++. Bitvectors and their respective rank and select data structures are implemented using the Succinct Data Structure Library (SDSL) [10]. The source code is available at https://github.com/alancleary/FRAS.
5.2 Experiments
Reducing the encoding size of grammar-compressed strings in practice is the primary goal of this work. However, we also want to understand how our bit packed encodings affect decoding and random access run-time. For this reason, we compare FRAS to FOLCA [13] and ShapedSLP [7] – two grammar encodings that support random access. Notably, FOLCA achieves the information-theoretic bound of Tabei et al. [17]. Due to its use of the array-of-arrays grammar representation, when randomly accessing a substring FRAS only performs one random access operation to determine where the first character of the substring is located in the grammar. The rest of the substring is then acquired by decoding the grammar from that position. For this reason, comparing FRAS to FOLCA and ShapedSLP on multiple substring lengths across a variety of data sets should elucidate how our bit packed encodings affect both decoding and random access run-times.
We performed experiments on two corpora of data: the Pizza&Chili corpus222https://pizzachili.dcc.uchile.cl/ and a collection of pangenomes containing 12 yeast assemblies from the Yeast Population Reference Panel (YPRP) [20] and 1000 copies of Human chromosome 19 (c1000) [7]. For each corpus, we generated grammars and benchmarked FRAS against FOLCA and ShapedSLP, measuring encoding size and random access run-time. For the Pizza&Chili corpus, grammars were generated using Gonzalo Navarro’s implementation333https://users.dcc.uchile.cl/~gnavarro/software/repair.tgz of RePair [11] and Isamu Furuya’s implementation444https://github.com/izflare/MR-RePair of MR-RePair [6]. Detailed depth and size metrics for the grammars derived from each dataset can be found in Table 1. For the collection of pangenomes, grammars were generated using BigRePair [8]. Note that RePair and BigRePair generate RePair style grammars, whereas MR-RePair generates SLPs. The original array-of-arrays representation of FRAS is used as a baseline of comparison for the bit packed encodings; we will simply call it Array. For each grammar generated, we accessed substrings of length 1, 10, 100, and 1,000 at pseudo-random positions.555Pseudo-random numbers were generated on a uniform distribution using the xoroshiro128+ generator [2]. The generator was seeded so that the same numbers were used by every algorithm. We performed this procedure 10,000 times for each substring length and computed the average run-time. Experiments were run on a server with two AMD EPYC 7543 32-Core 2.8GHz (3.7GHz max boost) processors and 2TB of 8-channel DDR4 3200MHz memory running CentOS Stream release 9. Note that this server is excessively overpowered for these experiments and was used for the purpose of stability and accuracy of measurement. Similar results can be achieved on a consumer laptop.
5.3 Discussion
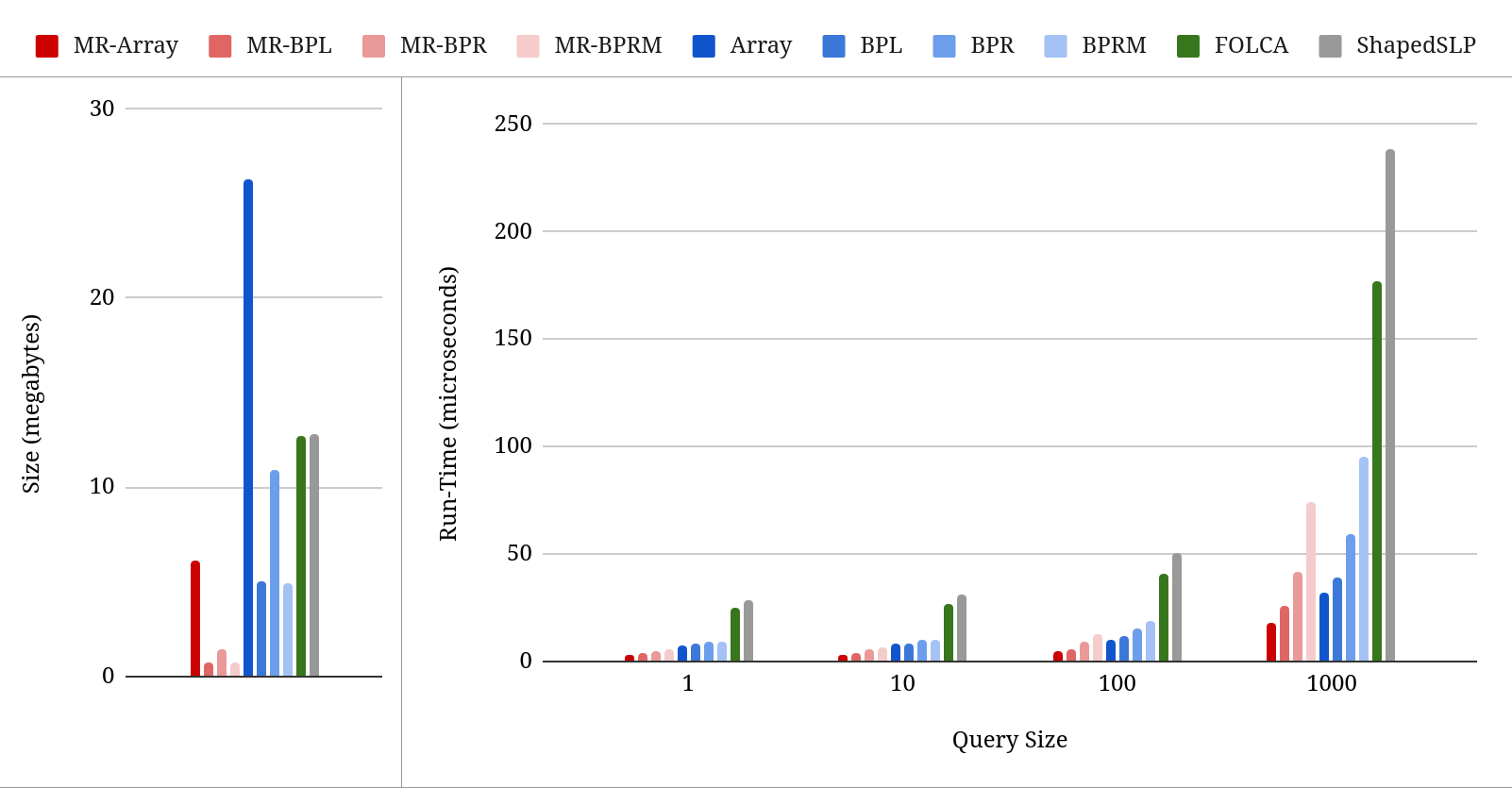
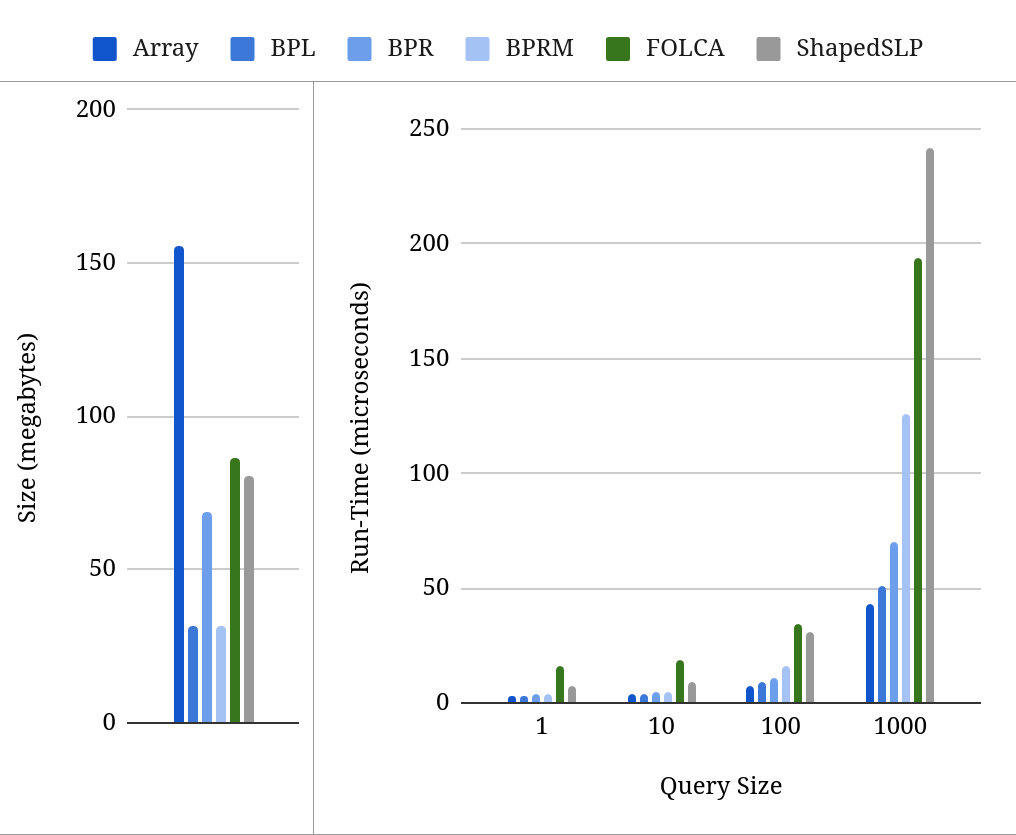
Results are given in Table 2. The graphs in Figure 2 summarize the average encoding size and run-times for every algorithm, and the graphs in Figure 3 summarize the encoding sizes and run-times for all of the RePair algorithms on only the c1000 data set. We chose to highlight the c1000 results because it has the largest encodings and some of the slowest run-times across all algorithms, which we will use to emphasize the trade-offs and advantages of our encodings.
Generally, we found that all the bit packing strategies use significantly less space than the original array-of-arrays implementation (Array). Interestingly, BPL and BPRM achieved nearly identical sizes, each consistently about 50% smaller than BPR, although BPRM was slower than BPL across the board. In comparison, BPL and BPRM used significantly less space than FOLCA and ShapedSLP on every grammar. Although every bit packing strategy was slower than the original Array encoding, each one was much faster than FOLCA and ShapedSLP, with BPL being the fastest and BPRM being the slowest. While BPL is only slightly slower than Array, it uses considerably less space, as depicted in Figures 2 and 3. Moreover, BPL provided the best space-time trade-off of the three bit packing strategies. This, coupled with the fact that BPL can be computed online, makes it the most practical of the bit packing strategies. Furthermore, we observed that all FRAS bit packed encodings were both smaller and faster on MR-RePair grammars than on RePair grammars. This suggests that SLP grammars may be generally advantageous in practice and that designing encodings and algorithms that support these types of grammars is a worthwhile endeavor.
To expand on these finding, we first consider specific size differences. Note, however, that here we omit the Pizza&Chili artificial data sets due to the low precision of Table 2. For RePair grammars, we found that BPL is 1.58-4.69 smaller than FOLCA/ShapedSLP, and is 2.53 smaller on average. Similarly, BPR is 0.81-2.1 smaller than FOLCA/ShapedSLP, and is 1.22 smaller on average. And BPRM is 1.58-4.69 smaller than FOLCA/ShapedSLP, and is 2.54 smaller on average. For MR-RePair grammars, we found that MR-BPL is 2-10.33 smaller than FOLCA/ShapedSLP, and is 6.91x smaller on average. Similarly, MR-BPR is 2-4.89 smaller than FOLCA/ShapedSLP, and is 3.45 smaller on average. And MR-BPRM is 2-10.33 smaller than FOLCA/ShapedSLP, and is 6.91 smaller on average. These results are especially significant because the FOLCA grammar encoding achieves the information-theoretic bound, as described in Section 4, suggesting that our bit packed encodings can be implemented using minimal additional factors to those described in the bound.
To further expand on our finding, we consider specific run-time differences. For RePair grammars, we found that BPL is 2.23-17.83 faster than FOLCA/ShapedSLP, and is 4.87 faster on average. Similarly, BPR is 1.81-10.25 faster than FOLCA/ShapedSLP, and is 3.63 faster on average. And BPRM is 1.55-11.89 faster than FOLCA/ShapedSLP, and is 2.91 faster on average. For MR-RePair grammars, we found that MR-BPL is 5.17-26.75 faster than FOLCA/ShapedSLP, and is 8.96 faster on average. Similarly, MR-BPR is 3.77-17.83 faster than FOLCA/ShapedSLP, and is 6.28 faster on average. And MR-BPRM is 1.93-15.29 faster than FOLCA/ShapedSLP, and is 4.61 faster on average. Furthermore, every bit packed algorithm achieved submicrosecond run-times on at least one experiment, whereas FOLCA and ShapedSLP did not.
A property of all the algorithms that we observed is that their run-times scale linearly relative to the size of the query string, as illustrated in Figures 2 and 3. This suggests that the disparity in run-time between the bit packed encodings and FOLCA/ShapedSLP will also continue to grow with query size. Figures 2 and 3 also illustrate how our bit packed encodings affect decoding and random access run-time. When computing a random access query, FRAS only performs one random access operation to determine where the first character of the substring is located in the grammar. The rest of the substring is then acquired by traversing the grammar’s parse tree from that position. This means when querying the bit packed encodings, the first character in the substring will likely require many more bits to be unpacked than subsequent characters. However, this additional overhead is not perceptible for the BPL strategy and is barely present for the BPR and BPRM strategies, as illustrated by the size 1 queries in Figures 2 and 3. This shows that the overhead of the bit packed encodings is so negligible that it must be compounded over many character unpackings to make a discernible difference, i.e. query size 1000 in Figures 2 and 3. This makes the use of the bit packed encodings well worth the space savings they provide over the array-of-arrays representation.
5.4 Conclusion and Future Work
In this work, we presented a general bit packing approach for reducing the space required to represent grammars in the canonical array-of-arrays representation. We then presented three bit packing strategies based on this approach and showed that our encodings are away from the information-theoretic bound. Through our experiments, we demonstrated that in practice these bit packing strategies are much smaller than methods that meet the information-theoretic bound, achieving state-of-the-art performance both in grammar encoding size and run-time performance of random-access queries.
Our approach exploits the total ordering of the non-terminal characters in grammar-compressed strings. It is a simple and natural approach for encoding grammars and in this work we endeavored to characterize it. In future work, we would like to explore other methods for compactly encoding the array-of-arrays representation of grammar-compressed strings, such Elias- and - codes or, more generally, variable bit-length arrays [4], as well as optimizations that could further improve the run-time performance of our approach, such as utilizing SIMD algorithms for bit packed encodings [12].
| Data Set | Size | RePair | MR-RePair | |||||
|---|---|---|---|---|---|---|---|---|
| Rules | Depth | Size | Rules | Depth | Size | |||
| real | Escherichia_Coli | 112,689,515 | 2,012,087 | 3,279 | 5,625,656 | 712,228 | 23 | 5,028,691 |
| cere | 461,286,644 | 2,561,292 | 1,359 | 5,777,882 | 836,956 | 29 | 4,878,322 | |
| coreutils | 205,281,778 | 1,821,734 | 43,728 | 3,796,814 | 437,054 | 30 | 2,423,962 | |
| einstein.de.txt | 92,758,441 | 49,949 | 269 | 112,563 | 21,787 | 42 | 84,392 | |
| einstein.en.txt | 467,626,544 | 100,611 | 1,355 | 263,695 | 49,565 | 48 | 212,824 | |
| influenza | 154,808,555 | 643,587 | 366 | 2,174,010 | 429,027 | 28 | 1,986,529 | |
| kernel | 257,961,616 | 1,057,914 | 5,822 | 2,185,255 | 246,596 | 34 | 1,373,880 | |
| para | 429,265,758 | 3,093,873 | 487 | 7,335,396 | 1,079,287 | 30 | 6,370,815 | |
| world_leaders | 46,968,181 | 206,508 | 463 | 507,343 | 100,293 | 30 | 407,619 | |
| art. | fib41 | 267,914,296 | 38 | 40 | 79 | 38 | 40 | 79 |
| rs.13 | 216,747,218 | 66 | 47 | 156 | 55 | 45 | 147 | |
| tm29 | 268,435,456 | 75 | 45 | 156 | 51 | 29 | 132 | |
| Data Set | Size | BigRePair | ||||||
| Rules | Depth | Size | ||||||
| pan. | YPRP | 143,169,461 | 3,755,345 | 2,435 | 9,905,715 | |||
| c1000 | 59,125,115,010 | 12,898,128 | 45 | 30,291,616 | ||||
| Data Set | MR-Array | MR-BPL | MR-BPR | MR-BPRM | FOLCA | |||||||||||||||||||||
| size | 1 | 10 | 100 | 1,000 | size | 1 | 10 | 100 | 1,000 | size | 1 | 10 | 100 | 1,000 | size | 1 | 10 | 100 | 1,000 | size | 1 | 10 | 100 | 1,000 | ||
| real | E.coli | 13.1 | 1.9 | 2.1 | 3.7 | 19.0 | 1.4 | 2.3 | 2.5 | 4.7 | 26.7 | 3.0 | 3.0 | 3.4 | 7.2 | 45.3 | 1.4 | 3.6 | 4.3 | 11.3 | 82.3 | 13.8 | 25.0 | 26.3 | 42.0 | 191.5 |
| cere | 16.4 | 1.4 | 1.6 | 3.0 | 17.0 | 1.7 | 1.6 | 2.0 | 4.0 | 24.7 | 3.6 | 2.1 | 2.5 | 6.2 | 43.1 | 1.7 | 2.4 | 3.2 | 10.6 | 84.2 | 13.1 | 17.7 | 19.4 | 34.7 | 182.2 | |
| coreutils | 8.8 | 19.5 | 19.8 | 24.7 | 38.4 | 0.9 | 25.2 | 25.6 | 28.1 | 51.3 | 1.9 | 33.5 | 34.0 | 38.3 | 77.4 | 0.9 | 41.4 | 42.1 | 48.1 | 105.4 | 7.9 | 155.9 | 158.5 | 180.8 | 354.7 | |
| einstein.de.txt | 0.4 | 0.9 | 1.1 | 2.7 | 16.9 | 0.1 | 1.1 | 1.3 | 3.5 | 24.4 | 0.1 | 1.3 | 1.7 | 5.4 | 39.9 | 0.1 | 1.6 | 2.2 | 7.5 | 59.6 | 0.2 | 10.6 | 12.3 | 28.5 | 176.7 | |
| einstein.en.txt | 0.9 | 1.1 | 1.3 | 3.1 | 18.6 | 0.2 | 1.2 | 1.5 | 3.9 | 26.3 | 0.3 | 1.4 | 1.9 | 5.3 | 37.4 | 0.2 | 1.7 | 2.3 | 7.9 | 63.8 | 0.7 | 11.8 | 13.7 | 30.2 | 184.6 | |
| influenza | 6.1 | 0.3 | 0.6 | 2.3 | 18.2 | 0.9 | 0.4 | 0.8 | 3.1 | 26.1 | 1.8 | 0.6 | 1.1 | 5.2 | 45.7 | 0.9 | 0.7 | 1.4 | 9.5 | 88.6 | 6.1 | 10.7 | 12.3 | 27.3 | 172.4 | |
| kernel | 5.6 | 5.6 | 5.9 | 7.8 | 23.8 | 0.5 | 6.8 | 7.1 | 9.6 | 31.5 | 1.1 | 8.8 | 9.3 | 13.3 | 49.4 | 0.5 | 10.8 | 11.6 | 17.6 | 75.7 | 4.5 | 51.4 | 54.5 | 72.3 | 241.7 | |
| para | 20.7 | 0.9 | 1.1 | 2.8 | 18.5 | 2.2 | 0.9 | 1.2 | 3.6 | 25.7 | 4.8 | 1.2 | 1.6 | 5.9 | 46.3 | 2.2 | 1.4 | 2.2 | 10.7 | 94.4 | 17.4 | 13.2 | 15.0 | 30.7 | 182.3 | |
| world_leaders | 1.7 | 0.6 | 0.8 | 2.1 | 14.3 | 0.2 | 0.7 | 1.0 | 3.1 | 23.4 | 0.4 | 1.0 | 1.4 | 4.8 | 37.5 | 0.2 | 1.2 | 1.8 | 7.7 | 66.7 | 1.1 | 11.8 | 13.4 | 28.1 | 166.4 | |
| art. | fib41 | 1.0 | 1.1 | 1.4 | 8.4 | 1.1 | 1.1 | 2.2 | 15.3 | 1.1 | 1.2 | 3.9 | 27.4 | 1.4 | 2.1 | 7.1 | 57.0 | 2.6 | 3.3 | 10.3 | 81.2 | |||||
| rs.13 | 1.0 | 1.0 | 1.6 | 8.7 | 1.1 | 1.1 | 2.6 | 15.4 | 1.2 | 1.5 | 4.0 | 28.4 | 1.7 | 2.1 | 7.2 | 57.4 | 3.0 | 3.8 | 11.2 | 85.4 | ||||||
| tm29 | 0.9 | 1.0 | 1.4 | 7.8 | 1.0 | 1.1 | 2.1 | 13.2 | 1.2 | 1.4 | 3.4 | 23.7 | 1.6 | 2.1 | 6.5 | 51.8 | 2.8 | 3.5 | 10.6 | 80.8 | ||||||
| pan. | YPRP | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 25.9 | 11.6 | 13.3 | 29.7 | 187.8 |
| c1000 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 86.5 | 16.5 | 18.3 | 34.7 | 194.0 | |
| Data Set | Array | BPL | BPR | BPRM | ShapedSLP | |||||||||||||||||||||
| size | 1 | 10 | 100 | 1,000 | size | 1 | 10 | 100 | 1,000 | size | 1 | 10 | 100 | 1,000 | size | 1 | 10 | 100 | 1,000 | size | 1 | 10 | 100 | 1,000 | ||
| real | E.coli | 24.4 | 7.3 | 7.6 | 10.6 | 36.9 | 4.4 | 7.7 | 7.9 | 11.7 | 45.2 | 9.3 | 8.8 | 9.4 | 15.3 | 69.2 | 4.3 | 8.7 | 9.7 | 18.8 | 108.1 | 14.0 | 21.2 | 22.6 | 42.7 | 239.8 |
| cere | 31.2 | 6.0 | 6.2 | 9.6 | 39.0 | 5.7 | 6.2 | 6.5 | 10.5 | 46.0 | 12.4 | 7.1 | 7.7 | 13.9 | 70.7 | 5.6 | 6.8 | 7.8 | 18.3 | 117.8 | 13.7 | 14.0 | 22.6 | 42.7 | 236.4 | |
| coreutils | 23.2 | 55.4 | 56.3 | 61.8 | 92.7 | 5.0 | 58.7 | 60.5 | 66.3 | 102.1 | 9.7 | 69.9 | 71.2 | 80.3 | 138.2 | 5.0 | 71.5 | 72.8 | 83.4 | 159.5 | 9.3 | 245.1 | 249.5 | 278.7 | 493.0 | |
| einstein.de.txt | 0.7 | 1.6 | 1.8 | 3.9 | 22.2 | 0.1 | 1.7 | 2.0 | 4.7 | 29.5 | 0.2 | 2.0 | 2.5 | 6.2 | 42.0 | 0.1 | 2.3 | 2.9 | 9.5 | 73.9 | 0.2 | 6.5 | 8.6 | 27.8 | 219.5 | |
| einstein.en.txt | 1.4 | 1.4 | 1.7 | 3.8 | 22.0 | 0.3 | 1.6 | 1.9 | 4.6 | 29.7 | 0.5 | 1.9 | 2.4 | 6.6 | 46.0 | 0.3 | 2.0 | 2.8 | 9.4 | 73.6 | 0.6 | 6.2 | 8.3 | 27.7 | 218.1 | |
| influenza | 7.8 | 0.5 | 0.8 | 2.5 | 18.7 | 1.3 | 0.6 | 0.9 | 3.2 | 25.8 | 2.9 | 0.8 | 1.2 | 5.4 | 45.9 | 1.3 | 0.9 | 1.7 | 9.9 | 91.1 | 5.5 | 3.1 | 5.0 | 24.1 | 213.1 | |
| kernel | 13.1 | 19.3 | 20.2 | 23.2 | 47.6 | 2.5 | 20.4 | 21.3 | 24.9 | 55.0 | 5.3 | 23.7 | 25.0 | 30.7 | 81.1 | 2.5 | 23.6 | 25.1 | 33.9 | 112.7 | 5.0 | 60.7 | 64.6 | 84.7 | 290.3 | |
| para | 37.1 | 2.5 | 3.0 | 6.2 | 34.6 | 6.3 | 2.6 | 3.1 | 7.1 | 42.6 | 14.4 | 3.2 | 3.9 | 10.1 | 67.1 | 6.3 | 2.9 | 4.0 | 14.4 | 113.1 | 18.2 | 5.8 | 7.8 | 27.3 | 218.9 | |
| world_leaders | 2.6 | 1.3 | 1.5 | 3.0 | 16.5 | 0.5 | 1.4 | 1.7 | 4.0 | 24.9 | 0.9 | 1.8 | 2.2 | 5.8 | 40.5 | 0.5 | 1.9 | 2.5 | 8.9 | 70.3 | 1.1 | 5.7 | 7.7 | 27.0 | 213.3 | |
| art. | fib41 | 1.0 | 1.1 | 1.4 | 8.8 | 1.1 | 1.1 | 2.2 | 15.3 | 1.1 | 1.2 | 3.9 | 27.4 | 1.4 | 2.1 | 7.1 | 56.8 | 4.2 | 5.7 | 20.8 | 171.9 | |||||
| rs.13 | 1.0 | 1.0 | 1.4 | 8.4 | 1.1 | 1.1 | 2.2 | 14.8 | 1.1 | 1.3 | 3.8 | 27.1 | 1.5 | 2.1 | 7.1 | 57.3 | 4.6 | 6.2 | 22.0 | 180.0 | ||||||
| tm29 | 0.9 | 1.0 | 1.4 | 8.5 | 1.0 | 1.1 | 2.2 | 14.9 | 1.2 | 1.4 | 3.8 | 26.5 | 1.7 | 2.2 | 7.3 | 57.0 | 4.7 | 6.3 | 22.5 | 183.8 | ||||||
| pan. | YPRP | 70.8 | 2.0 | 2.3 | 6.0 | 40.6 | 11.9 | 1.9 | 2.6 | 6.9 | 47.7 | 28.1 | 2.2 | 2.8 | 9.3 | 71.9 | 11.9 | 2.0 | 3.1 | 13.9 | 119.1 | 31.4 | 3.0 | 5.0 | 24.8 | 221.3 |
| c1000 | 155.3 | 3.3 | 3.8 | 7.7 | 43.2 | 31.4 | 3.4 | 4.0 | 8.7 | 51.0 | 68.8 | 3.9 | 4.8 | 11.0 | 70.3 | 31.4 | 3.8 | 4.9 | 16.3 | 126.0 | 80.6 | 7.0 | 9.3 | 30.9 | 241.6 | |
References
- [1] A061168 (partial sums of ). The On-Line Encyclopedia of Integer Sequences. URL: https://oeis.org/A061168.
- [2] David Blackman and Sebastiano Vigna. Scrambled linear pseudorandom number generators. ACM Trans. Math. Softw., 47(4), September 2021. doi:10.1145/3460772.
- [3] Alan M. Cleary, Joseph Winjum, Jordan Dood, and Shunsuke Inenaga. Revisiting the folklore algorithm for random access to grammar-compressed strings. In Zsuzsanna Lipták, Edleno Moura, Karina Figueroa, and Ricardo Baeza-Yates, editors, String Processing and Information Retrieval, pages 88–101, Cham, 2024. Springer Nature Switzerland. doi:10.1007/978-3-031-72200-4_7.
- [4] P. Elias. Universal codeword sets and representations of the integers. IEEE Transactions on Information Theory, 21(2):194–203, 1975. doi:10.1109/TIT.1975.1055349.
- [5] Michael L. Fredman and Dan E. Willard. Surpassing the information theoretic bound with fusion trees. J. Comput. Syst. Sci., 47(3):424–436, 1993. doi:10.1016/0022-0000(93)90040-4.
- [6] Isamu Furuya, Takuya Takagi, Yuto Nakashima, Shunsuke Inenaga, Hideo Bannai, and Takuya Kida. Practical grammar compression based on maximal repeats. Algorithms, 13(4):103, 2020. doi:10.3390/A13040103.
- [7] Travis Gagie, Tomohiro I, Giovanni Manzini, Gonzalo Navarro, Hiroshi Sakamoto, Louisa Seelbach Benkner, and Yoshimasa Takabatake. Practical random access to SLP-compressed texts. In SPIRE 2020, volume 12303 of Lecture Notes in Computer Science, pages 221–231, 2020. doi:10.1007/978-3-030-59212-7_16.
- [8] Travis Gagie, Tomohiro I, Giovanni Manzini, Gonzalo Navarro, Hiroshi Sakamoto, and Yoshimasa Takabatake. Rpair: Rescaling RePair with rsync. In String Processing and Information Retrieval (SPIRE 2019), pages 35–44. Springer, 2019. doi:10.1007/978-3-030-32686-9_3.
- [9] Michał Gańczorz. Entropy Lower Bounds for Dictionary Compression. In Nadia Pisanti and Solon P. Pissis, editors, 30th Annual Symposium on Combinatorial Pattern Matching (CPM 2019), volume 128 of Leibniz International Proceedings in Informatics (LIPIcs), pages 11:1–11:18, Dagstuhl, Germany, 2019. Schloss Dagstuhl – Leibniz-Zentrum für Informatik. doi:10.4230/LIPIcs.CPM.2019.11.
- [10] Simon Gog, Timo Beller, Alistair Moffat, and Matthias Petri. From theory to practice: Plug and play with succinct data structures. In Joachim Gudmundsson and Jyrki Katajainen, editors, Experimental Algorithms, pages 326–337, Cham, 2014. Springer International Publishing. doi:10.1007/978-3-319-07959-2_28.
- [11] N.J. Larsson and A. Moffat. Off-line dictionary-based compression. Proceedings of the IEEE, 88(11):1722–1732, 2000. doi:10.1109/5.892708.
- [12] D. Lemire and L. Boytsov. Decoding billions of integers per second through vectorization. Software: Practice and Experience, 45(1):1–29, 2015. doi:10.1002/spe.2203.
- [13] Shirou Maruyama, Yasuo Tabei, Hiroshi Sakamoto, and Kunihiko Sadakane. Fully-online grammar compression. In Oren Kurland, Moshe Lewenstein, and Ely Porat, editors, String Processing and Information Retrieval, pages 218–229, Cham, 2013. Springer International Publishing. doi:10.1007/978-3-319-02432-5_25.
- [14] Daniel Saad Nogueira Nunes, Felipe A. Louza, Simon Gog, Mauricio Ayala-Rincón, and Gonzalo Navarro. A grammar compression algorithm based on induced suffix sorting. In Ali Bilgin, Michael W. Marcellin, Joan Serra-Sagristà, and James A. Storer, editors, DCC 2018, pages 42–51. IEEE, 2018. doi:10.1109/DCC.2018.00012.
- [15] Carlos Ochoa and Gonzalo Navarro. Repair and all irreducible grammars are upper bounded by high-order empirical entropy. IEEE Transactions on Information Theory, 65(5):3160–3164, 2019. doi:10.1109/TIT.2018.2871452.
- [16] David Salomon. Data Compression: The Complete Reference. Springer London, 2007. doi:10.1007/978-1-84628-603-2.
- [17] Yasuo Tabei, Yoshimasa Takabatake, and Hiroshi Sakamoto. A succinct grammar compression. In Johannes Fischer and Peter Sanders, editors, Combinatorial Pattern Matching, pages 235–246, Berlin, Heidelberg, 2013. Springer Berlin Heidelberg. doi:10.1007/978-3-642-38905-4_23.
- [18] Akito Takasaka and Tomohiro I. Space-efficient SLP encoding for -time random access. In String Processing and Information Retrieval (SPIRE 2024), volume 14899 of Lecture Notes in Computer Science, pages 336–347. Springer, 2024. doi:10.1007/978-3-031-72200-4_25.
- [19] Sebastiano Vigna. Broadword implementation of rank/select queries. In Catherine C. McGeoch, editor, WEA 2008, pages 154–168, Berlin, Heidelberg, 2008. Springer Berlin Heidelberg. doi:10.1007/978-3-540-68552-4_12.
- [20] Jia-Xing Yue, Jing Li, Louise Aigrain, Johan Hallin, Karl Persson, Karen Oliver, Anders Bergström, Paul Coupland, Jonas Warringer, Marco Cosentino Lagomarsino, Gilles Fischer, Richard Durbin, and Gianni Liti. Contrasting evolutionary genome dynamics between domesticated and wild yeasts. Nature Genetics, 49(6):913–924, April 2017.
