Abstract 1 Introduction 2 The Work Task Variation Problem 3 A MiniZinc Model 4 RosterLogic Variation: A Local Search Solver for WTV 5 Experiments 6 Conclusion References Appendix A Detailed results Appendix B Large plots for CP-SAT 9.12 10 threads Appendix C Pattern Swap Patterns

The Work Task Variation Problem

Mikael Z. Lagerkvist111Current affiliation is SambaNova Systems; work carried out while at Optischedule. ORCID SambaNova Systems, Stockholm, Sweden
Optischedule, Stockholm, Sweden Magnus Rattfeldt222Current affiliation is Jeppesen; work carried out while at Optischedule. ORCID Jeppesen, Gothenburg, Sweden
Optischedule, Stockholm, Sweden
Abstract

This paper introduces the Work Task Variation (WTV) problem, a novel scheduling post-processing challenge focused on improving worker shift quality by rearranging tasks within their assigned time slots. The objective is to avoid excessively short or long durations of specific task types, creating smoother and more ergonomic work patterns.

We present RosterLogic Variation, a constraint-based local search (CBLS) inspired solver originally developed at Optischedule and successfully deployed in real-world retail settings. This solver rapidly improves existing schedules using tailored invariants and heuristics. We also provide a complete MiniZinc model and a set of generated realistic publicly available benchmark instances.

We compare our solver’s performance with that of modern CP solvers using the MiniZinc model. Contemporary state-of-the-art CP solvers are approaching the interactive performance of our CBLS solver for coarse planning, representing a significant advancement since the original design and implementation of our solver.

Keywords and phrases:
Constraint-Based Local Search, Constraint Programming, Metaheuristics, Scheduling
Copyright and License:
[Uncaptioned image] © Mikael Z. Lagerkvist and Magnus Rattfeldt; licensed under Creative Commons License CC-BY 4.0
2012 ACM Subject Classification:
Theory of computation → Constraint and logic programming ; Computing methodologies → Planning and scheduling
Supplementary Material:
Software  (Source Code): https://github.com/optischedule/work-task-variation-instances/tree/cp2025
  archived at Software Heritage Logo swh:1:dir:42f8c7d521bea4ed7fffcd5463d2b2c89353a236
Acknowledgements:
We thank the anonymous reviewers for their helpful comments, Linnea Stjerna, and all those with whom we discussed the WTV problem.
DOI:
10.4230/LIPIcs.CP.2025.24
Event:
31st International Conference on Principles and Practice of Constraint Programming (CP 2025)
Editors:
Maria Garcia de la Banda
Series and Publisher:
LIPIcs Logo Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik

1 Introduction

Employee scheduling is a common and significant challenge across various industries, with many studies focusing on generating feasible schedules while minimizing global metrics (e.g., [27, 23]). However, the quality of individual worker shifts – particularly concerning task variation and ergonomic factors – often remains a secondary consideration. This oversight can lead to worker fatigue, reduced productivity, regulation violations, and even potential safety risks.

This paper introduces the Work Task Variation (WTV) problem, addressing this gap by focusing on post-processing existing schedules. Given a schedule with fixed worker time slots and task assignments, the core challenge of the WTV problem lies in rearranging tasks between workers while preserving the original time slot allocations to improve flow and ergonomics. The cost function penalizes both excessively short and long spans of a single task, aiming for a balanced variety minimizing repetitive strain and promotes engagement.

The WTV problem is particularly relevant when work-safety regulations limit continuous time on specific tasks, for example hand-intensive tasks common in retail. WTV provides an effective mechanism to ensure compliance by varying tasks within predefined schedules. It is especially useful when an initial schedule is generated automatically, but requires refinement to meet operational and regulatory needs.

Our approach, motivated by the need for fast and interactive schedule improvement, is a custom solver called RosterLogic Variation that is inspired by Constraint-Based Local Search (CBLS) [15, 10, 19]. Developed at Optischedule, this solver utilizes carefully chosen invariants for feasibility and efficient neighborhood exploration, combined with metaheuristics to guide the search process effectively. Importantly, this solver has been successfully deployed in practice, improving work schedules in multiple retail locations.

To facilitate further research and benchmarking within the constraint programming community, we have also developed a complete MiniZinc [18] model for the WTV problem. This model serves as a precise description of the problem and can, together with a set of generated publicly available problem instances, be used as a benchmarking problem for constraint programming tools and other solution approaches.

Contributions.

This paper contributes: (i) defining the Work Task Variation (WTV) problem, a novel scheduling problem with practical implications for worker well-being; (ii) a description of RosterLogic Variation, a CBLS-inspired solver (developed at Optischedule and proven in practice) for the WTV problem, focused on rapid improvement of existing schedules; (iii) a complete MiniZinc model of the WTV problem for research and exploration with standard CP tools; and (iv) introducing a set of realistic, publicly available benchmark instances for evaluating solution approaches. Benchmarks of RosterLogic Variation against the MiniZinc model with different CP backend solvers shows that the custom solver performs well.

Structure.

The remainder of the paper is structured as follows: Section 2 describes the WTV problem. In Section 3 the MiniZinc model is described to formally define the problem, and in Section 4 the custom CBLS-inspired solver is described. Section 5 describes the generated benchmark instances and presents the results comparing the custom solver with CP backend solvers. Finally, Section 6 concludes and summarizes the findings.

2 The Work Task Variation Problem

The Work Task Variation (WTV) problem is a scheduling optimization problem designed as a post-processing step to enhance pre-existing work schedules. Unlike traditional scheduling, which often focuses on creating shifts based on requirements (such as in Minimum Shift Design [6]) and then assigning workers to shifts and tasks [4], WTV assumes fixed worker-to-time-slot allocations and task quantities per time slot. The challenge is to rearrange task assignments within these time slots, optimizing task variation and distribution for each worker. For an example schedule with four shifts, see Figure 1 with one bad set of shifts (1(a)) with lots of task-switching, and a corresponding good set of shifts (1(b)) with reasonable task lengths.

(a) Fragmented Task Assignments.
(b) Good Task Assignments.
Figure 1: Comparison of two different sets of shifts for the same work. The tasks are till (T), store (S), warehouse (W), other (O), and lunch (L). In (1(a)) the work is very fragmented with frequent switching between shorter tasks. In (1(b)) the tasks are longer and less fragmented.

The primary motivation is to improve worker well-being, reduce fatigue, and ensure compliance with work-safety regulations, especially in industries with repetitive or physically demanding tasks. Previous research has explored similar concerns, highlighting the need for ergonomic considerations in workforce scheduling [27, 23]. Key application areas for WTV include:

Retail

Working at the till/cash register in a retail store is repetitive both physically and mentally.

Warehouses/Logistics

Picking, packing, loading, and unloading in a warehouse is often repetitive and lead to physical stress.

Manufacturing

Rotating workers between assembly line stations can reduce repetitive strain injuries.

In these scenarios, using a WTV solver that improves the ergonomic concerns and creates smooth operational schedules is beneficial for creating good schedules. On a process level, it is a refinement step, not a complete rescheduling.

The WTV optimization seeks an assignment of tasks to workers within each time slot that minimizes a cost function reflecting two complementary objectives directly derived from customer requirements: good lengths for task runs, and limiting the number of task initiations within each shift. This naturally relates to broader discussions of fairness and balancing in scheduling [2, 3, 11], as we aim to create a smooth task flow while respecting ergonomic principles. It is common to use WTV in cyclical schedules [1, 17], where fairness between shifts is less important as all workers will eventually work all types of shifts. For task run lengths, the cost function typically penalizes both excessively short and excessively long runs of a single task.

The ideal solution balances these, creating a smooth task flow with appropriate durations – neither too long nor too short. What is appropriate is defined by costs for duration ranges, with an ideal range incurring zero cost. In addition, any solution to the WTV problem must respect the following hard constraints from the initial schedules:

Fixed Time Slots

Worker shift times and the schedule’s time slot structure remain fixed.

Fixed Resource Requirements

The number of workers required for each task in each time slot is predetermined. WTV rearranges task assignments among workers but preserves the total number of workers assigned to each task per slot.

Optional Fixed Assignments

Specific task assignments for certain workers and time slots can be predefined and must be respected.

Single work periods

Each resource only has a single work period (no split shifts).

It is important to note that WTV is designed as a post-processing step in a scheduling workflow. Some existing system or process is responsible for the initial schedule generation (using either automatic or manual scheduling), creating a schedule considering factors such as staffing levels, demand, competencies, rules and regulations, and availability. This initial schedule may not fully address ergonomics. Given the initial schedule, the WTV solver rearranges task assignments within time slots, optimizing for suitable variation by minimizing the associated cost. The improved schedule can be presented to a human scheduler for manual adjustments after which the WTV solver can be re-run iteratively.

This approach integrates WTV seamlessly into existing processes, improving schedule quality without a system overhaul. It offers a targeted solution for worker well-being and efficiency.

As a simplification, we do not consider competencies for workers for the WTV problem in this paper. While in full generality competencies might be needed, in most cases we have seen the sets of tasks that are involved in a single WTV optimization instance typically require a uniform competency level among all involved workers.

3 A MiniZinc Model

The problem definition of Work Task Variation has a natural encoding into a MiniZinc model. The fact that schedules are typically defined in blocks that are synchronized across all shifts makes for a model that operates on an abstract set of discretized slots (a grid), without regard to real time spans. This model formally defines the problem’s constraints and objective function, enabling experimentation with different constraint solvers and providing a means to validate solutions obtained via other methods.

Listing 1: Data Definitions.
⬇
1enum Resources;
2enum Activities;
3
4enum ActivitiesOrNone = A(Activities) ++ { None };
5
6int: slots;
7set of int: Slots = 1..slots;
8set of int: SlotsAndZero = 0..slots;
9
10array[Activities, Slots] of 0..card(Resources): requirements;
11
12array[Resources, Slots] of opt ActivitiesOrNone: fixed;
13
14array[Activities, SlotsAndZero] of int: activity_run_cost;
15array[Activities, SlotsAndZero] of int: activity_frequency_cost;
16
17array[ActivitiesOrNone, SlotsAndZero] of int: extended_activity_run_cost =
18 array2d(ActivitiesOrNone, SlotsAndZero,
19 array1d(activity_run_cost) ++
20 % Cost for None, which is 0 for all lengths
21 [0 | r in SlotsAndZero]
22);
23
24array[ActivitiesOrNone, Slots] of 0..card(Resources): extended_requirements =
25 array2d(ActivitiesOrNone, Slots,
26 % Base requirements for all activities
27 array1d(requirements) ++
28 % The complement of the sum of requirements with respect to total resources
29 [card(Resources) - sum(requirements[.., s]) | s in Slots]
30);

The data-definitions are shown in Listing 1. Each schedule is defined over the Resources (the workers), the Activities (the tasks) with None representing time outside a shift, and finally the Slots to schedule in. For each slot there is a set of requirements for the number of activities of that type needed for that slot. There are also a set of fixed activities for each resource. The cost is defined as the cost associated with each possible run length and frequency count for every activity.

The run costs and the requirements are extended using MiniZinc to work over activities and the None value, as that enables simpler expressions for calculating costs and enforcing requirements.

Listing 2: Variable Definitions.
⬇
1% The schedule: what activities are done when for each resource
2array[Resources, Slots] of var ActivitiesOrNone: schedule;
3
4% Markers for when runs end
5array[Resources, Slots] of var bool: run_end;
6
7% Length for each run at the current slot from the currents runs start
8array[Resources, Slots] of var SlotsAndZero: run_length;
9
10% Cost for each run at the end of a run with zero cost in the middle of runs
11array[Resources, Slots] of var int: run_cost;
12
13% Cost for number of runs of each activity per resource
14array[Resources, Activities] of var int: frequency_cost;
15
16% The total cost of runs
17var int: cost = sum(run_cost) + sum(frequency_cost);

In Listing 2 the variables for the problem are defined. The main variable is the schedule matrix that contains the actual schedule. The remaining variables are all for computing the cost of the schedule. The costs are defined over maximal runs of adjacent slots in the schedule with the same activity. We use the end of a run in run_end as the marker for when a run is finished. The run_length is the length of each run up to that point. The run_cost are the costs for each run based on their length, and is only non-zero at the end of runs. The frequency_cost is based on the number of occurrences of runs for each activity type for each resource. Finally, the cost is simply the sum of the run costs and the frequency costs.

Listing 3: Constraints for Structure.
⬇
30% All shifts are only Activities (that is, not None) and surrounded with None
31constraint forall (r in Resources) (
32 regular(schedule[r, ..], "None* [^None]* None*")
33);
34
35% Always respect the requirements for each slot (column in the schedule)
36constraint forall (s in Slots) (
37 global_cardinality(schedule[.., s], ActivitiesOrNone, extended_requirements[.., s])
38);
39
40% Always respect the fixed requirements
41constraint forall (r in Resources, s in Slots where occurs(fixed[r, s])) (
42 schedule[r, s] = deopt(fixed[r, s])
43);
44
45% Mark when runs end
46constraint forall (r in Resources, s in Slots) (
47 if s = slots then
48 run_end[r, s] = true
49 else
50 run_end[r, s] = (schedule[r, s] != schedule[r, s+1])
51 endif
52);
53
54% Count length of runs
55constraint forall (r in Resources, s in Slots) (
56 if s = 1 \/ run_end[r, s-1] then
57 run_length[r, s] = 1
58 else
59 run_length[r, s] = run_length[r, s-1] + 1
60 endif
61);

Listing 3 contains the main constraints for the problem. First, regular constraints are used to make sure that each shift has the expected format (None at start and end, and Activities between). The global_cardinality constraints ensure that for each time slot, the required number of activities (and no more) is allocated. After that, all fixed requirements in the instance are set using simple assignments. The run_end variables are connected to the schedule using simple reified not equal constraints. Relatedly, the run_length is a simple increasing sequence that is reset to 1 after a run ends.

Listing 4: Constraints for Calculating Costs.
⬇
17% Count run costs
18constraint forall (r in Resources, s in Slots) (
19 if run_end[r, s] then
20 run_cost[r, s] = extended_activity_run_cost[schedule[r, s], run_length[r, s]]
21 else
22 run_cost[r, s] = 0
23 endif
24);
25
26%Count frequency costs
27constraint forall (r in Resources, a in Activities) (
28 let {
29 var int: activity_run_count = count(s in Slots) (
30 run_end[r, s] /\ schedule[r, s] = A(a)
31 )
32 } in
33 frequency_cost[r, a] = activity_frequency_cost[a, activity_run_count]
34);

Finally, in Listing 4, the actual cost of the schedule is computed. The run costs are fetched at the end of a run using the corresponding run length. The frequency costs are computed by counting the number of runs of each activity type.

Putting it all together.

Listings 1 to 4 collectively define all the required parts to solve the WTV problem. The only missing parts are inclusion of the globals.mzn library and a solve minimize cost. Output statements can be added as needed. For the benchmarks experiments reported in Section 5, no specific MiniZinc search strategy was specified, and the output was limited to the objective cost value.

4 RosterLogic Variation: A Local Search Solver for WTV

To address the Work Task Variation (WTV) problem, we have developed a constraint-based local search (CBLS) [16] solver designed for interactive use within a real-world scheduling process called RosterLogic Variation [20]. Local search [12] is a natural fit for problems that involve improving an existing solution. Our approach prioritizes rapid solution improvement over finding provably optimal solutions, making it well-suited for integration with a user-facing scheduling tool, where quick feedback and iterative refinement are paramount. The solver has been successfully applied in operational retail scheduling environments.

The core of our approach lies in a carefully designed combination of: a compact and efficiently manipulated state representation, a flexible and extensible neighborhood exploration strategy, a configurable cost model, and a portfolio of local search algorithms including metaheuristics. These components are interconnected to find high-quality WTV solutions in limited time.

When we set out to solve the WTV problem in 2018, our experiments with using traditional CP directly did not indicate that we would get suitable solutions quickly enough. In addition, given that we had usable initial solutions, a local search approach was a natural fit. Our prototype for the RosterLogic Variation solver quickly showed us that the custom CBLS style solver approach was feasible.

4.1 State Representation and Invariants

The key design principle for the state of a local search solver is to enable efficient incremental evaluation of solution quality and move feasibility. To achieve this, we maintain a set of invariants [15, 25] that are dynamically updated during search in addition to the core schedule. We also use simulation [19] when possible to speed up move evaluation further.

Our solver represents a complete schedule (a solution) as an assignment of activity types to each worker (resource) for each time slot within a given planning horizon.

The primary state representation is a matrix where rows represent workers and columns represent time slots. Each cell in this matrix contains an activity assignment.

Run-length encoding.

A crucial optimization is the use of an auxiliary run-length encoding state to represent consecutive assignments of the same activity. At the start of each run of activities (a sequence of consecutive identical activities) the length of the run is maintained. At each interior position the number of steps to go backwards to find the start of the run instead. This structure allows for O(1) access to run lengths and boundaries from each activity position, significantly accelerating cost calculations related to activity durations.

Consider the example illustrated in Table 1. The table shows a sample schedule using 0 for no work and 1 and 2 for two different task types, alongside the corresponding run-lengths. Positive values in the “Run Lengths” rows indicate the start of a run and the length of that run. Negative values indicate positions within a run, showing the offset to the run’s start.

Table 1: Example of a schedule and the corresponding run-length encoding.
Slot 1 2 3 4 5 6
Shift 1 1 1 1 2 2 0
Run Lengths 3 −1 −2 2 −1 1
Shift 2 0 0 2 2 2 2
Run Lengths 2 −1 4 −1 −2 −3

Activity counts.

We maintain aggregate counts of the number of occurrences of each activity type within each time slot; this allows for efficient verification of constraints related to the overall distribution of activities across the work force at any given time.

We maintain counts of the number of times each activity is assigned to each worker; this is essential for evaluating costs and constraints related to the frequency of activities for individual workers.

4.2 Cost Model and Constraints

The objective function, or cost, of a schedule is defined by a configurable cost model. The cost model for the WTV includes both duration costs and frequency costs for runs of tasks in each shift. The run-length encodings and the activity counts described in the previous subsection are the core invariants used to calculate these costs.

The cost model is designed to be extensible. We support both a hard-coded cost model with predefined rules and a configurable model that loads parameters from a JSON configuration file. This allows users to tailor the cost function to their specific needs without modifying the solver’s core logic. The JSON-based configuration provides a high degree of flexibility, enabling users to define costs for different activity durations using range mappings.

4.3 Neighborhood Structure and Move Generation

The search space is explored through a neighborhood structure defined by a set of move generators. These generators produce moves that transform one schedule into a neighboring schedule while maintaining the invariants for the run lengths and activity counts. We have designed several move generators, each capturing different types of schedule modifications relevant to the WTV problem:

Local swaps

The most basic move generator produces swaps between workers for the same time slot. Swaps can have configurable durations, allowing the exchange of sequences of activities. This generator can target specific activity types, e.g., a swap generator that swaps a till and store activity in the same slot.

Pattern-based moves

A more sophisticated generator searches for predefined patterns of activities that can be exchanged to improve the schedule’s structure. This allows for larger, non-local changes to the schedule. See below for more details.

Constrained move generation

Move generators can be configured with checks for valid moves. This is achieved through a filtering mechanism that takes a base move generator and a predicate defining allowed moves. For instance, we can enforce constraints that prevent assigning certain activities to workers who are not qualified for those tasks, or that limit the number of times a particular activity can be assigned within a certain time window. This flexible constraint integration allows for incorporating domain-specific knowledge and hard constraints directly into the search process.

The move generators produce instances of a generic interface for a set of moves, which provides methods for applying the move to a schedule, computing the resulting cost difference (without applying the move first), and querying the move’s properties. This abstraction allows different move types to be handled uniformly by the search algorithms. The base moves collection for local swaps uses a compact representation using a single array of integers in order to use fewer allocations and keep memory locality high.

Pattern-based move generation.

This is a move generator (which turned out to be crucial for achieving good performance) where swaps are defined by high-level activity patterns, in order to achieve larger and non-local changes to the schedule. A pattern is defined as a sequence of activity types – such as SSSTT for three store activities followed by two till activities – representing a desirable target activity sequence. Note that these patterns are strongly connected to the duration cost part of the used cost model.

The pattern-based move generation identifies local sequences of activities in the schedule that can be transformed into one of the desired patterns, by performing a set of vertical swaps between shifts at the same time slots. The following is a sketch of the pattern-based move generation process.

Candidate matching

For each pattern (and its reverse if it is different), the schedule is scanned to identify sequences of matching lengths that consist only of store or till shifts. These sequences do not have to (and should not) match the pattern exactly but must be transformable into it.

Mismatch analysis

For each such candidate (mis)match, the schedule is scanned vertically – that is, within the same time slots across other shifts – for sequences in other shifts that match the required activity sequence. This step ensures that each non-matching element has a possible replacement available.

Swap generation

Once all required replacements are identified, all viable combinations of vertical swaps that could realize the pattern are generated. These combinations are then ranked according to (i) highest cost decrease and (ii) the lowest total vertical distance traveled by the swaps (tiebreaker). The most promising combinations are selected to generate actual swap candidates.

Patterns are extended with respect to the block size, and grouped by length for efficient parallel processing. To reduce redundancy, only one direction of each symmetric pattern (e.g., SSSTT and TTTSS) is stored, and its flipped version is automatically included. See Appendix C for a list of all patterns defined in RosterLogic Variation.

Example.

Consider the desired pattern SSSTT. Figure 2 illustrates the process using a segment of a roster. The initial state is shown in Figure 2(a).

The algorithm identifies the sequence STSTS in Shift 0 (Figure 2(a)), starting at slot 1, as a candidate. It determines that slots 2 and 5 must be replaced to match the desired pattern. Matching activities S and T are located vertically in shifts 2 and 3, respectively. Swapping these values results in the updated roster in Figure 2(b). This introduces the desired pattern SSSTT in Shift 0, while also strengthening the contiguous blocks of till shifts in Shift 2 and store shifts in Shift 3.

Slot 1 2 3 4 5 6 7 8
Shift 0 S T S T S O O O
Shift 1 S S T S T T T T
Shift 2 T S S S S O O O
Shift 3 T T T S T S S S
(a) Initial Schedule.
Slot 1 2 3 4 5 6 7 8
Shift 0 S S S T T O O O
Shift 1 S S T S T T T T
Shift 2 T T S S S O O O
Shift 3 T T T S S S S S
(b) Schedule After Pattern Swaps.
Figure 2: Example SSSTT pattern swap operation. In (2(a)) the initial schedule is shown, and in (2(b)) the resulting schedule after the pattern swap operation is shown (cells whose values changed are printed in bold to indicate the modification.).

4.4 Search Algorithms

Our solver implements a portfolio of local search algorithms, enabling experimentation and selection of the most effective approach for a given problem family.

Steepest descent

A greedy algorithm that always selects the best improving move in the neighborhood.

Tabu search

A metaheuristic that maintains a “tabu list” of recently visited states to avoid cycling and encourage exploration of the search space [8, 9].

Simulated annealing

A probabilistic metaheuristic that accepts worsening moves with a probability that decreases over time, inspired by the physical process of annealing [13].

Restart

A restarting metaheuristic that runs a base algorithm multiple times on scrambled states returning the best solution found.

Portfolio

A metaheuristic that wraps several different algorithms or configurations of the same algorithm. All algorithms are called, and the best result is returned.

Parallel restart and portfolio

To leverage multi-core processors, we implement parallel variants of both the restart and portfolio metaheuristics.

Scramble

A randomized algorithm that makes a set of random moves. This is useful in combination with restart and parallel portfolio in order to explore new neighborhoods.

These algorithms can be combined and configured. For instance, a typical configuration might involve a parallel portfolio of steepest descent, tabu search, and simulated annealing. This allows for a highly adaptable and robust system.

4.5 Algorithm Configuration

RosterLogic Variation has a default configuration of the algorithm components that is optimized for the retail interactive use cases. The system builds on a core search algorithm configuration that has a parallel portfolio consisting of a greedy steepest descent asset, three different tabu search assets, a simulated annealing asset, and a scrambling asset. The parallel portfolio is furthermore wrapped in a restart algorithm with four restarts. Building on this base algorithm, the final algorithm has the following 5 stages.

  1. 1.

    Apply base algorithm with moves for swapping till and store activities.

  2. 2.

    Apply base algorithm with moves for swapping warehouse activities with till and store activities.

  3. 3.

    Apply a greedy steepest descent algorithm for swapping till and store activities.

  4. 4.

    Apply a greedy steepest descent algorithm with a pattern moves generator with 10 common patterns for improving till and store layouts.

  5. 5.

    Repeat the greedy algorithms in 3 and 4 again.

As is obvious from this description, the specific configuration is heavily geared towards a problem instance space where the till activities are a significantly limiting factor. However, this is quite a common problem setting for the WTV problem, with a specific activity that is the most important to focus on,

Similarly, the fact that only a single step (of a composite algorithm) actually includes warehouse tasks is because these are often quite forgiving and easy to parcel out, especially after an initial pass has been made that gives a decent set of till and store activities.

4.6 Development and Pragmatics

The RosterLogic Variation solver has been developed over the course of several years starting in 2018 with most of the development in 2019. The system has been used in practice by expert planners, mainly for retail planning.

Development environment.

The RosterLogic Variation solver is implemented in Java and Kotlin for the JVM platform. The state is maintained as a set of compact arrays with suitably chosen types to minimize the memory usage, with most arrays either using bytes or shorts. This type of state management makes the total memory footprint low, ensuring good cache behavior even though the code is written in a pointer-based, garbage collected language like Java.

Development of the solver has been on Linux and Mac, and the application has been packaged as a self-contained executable for the Windows platform as that is the platform used by most planners. For the expert planners that we have worked with there is a willingness to use command-line applications with structured input and output formats. Thus, we could focus on the core algorithmic challenges and avoid too much focus on user interface challenges.

Repeatability and feedback.

All algorithms use a controlled stable source of randomness for repeatability. Newer parts of the framework at Optischedule use the xorshift* [26], which has better properties for maintaining and modifying the state and to create parallel streams of randomness.

All algorithms use a structured progress reporting system to indicate how far along in the search they are. A progress reporter instance can be split with adjustable amounts for each part. For example, a Portfolio algorithm with 5 different sub-algorithms would split it’s progress reporter into 5 equal parts. A base algorithm can report either a percentage done, or the number of steps out of a configurable step count. All together, the progress reporter is a best-effort approximation, but it is very useful for user to see a rough estimate of how far along the system is.

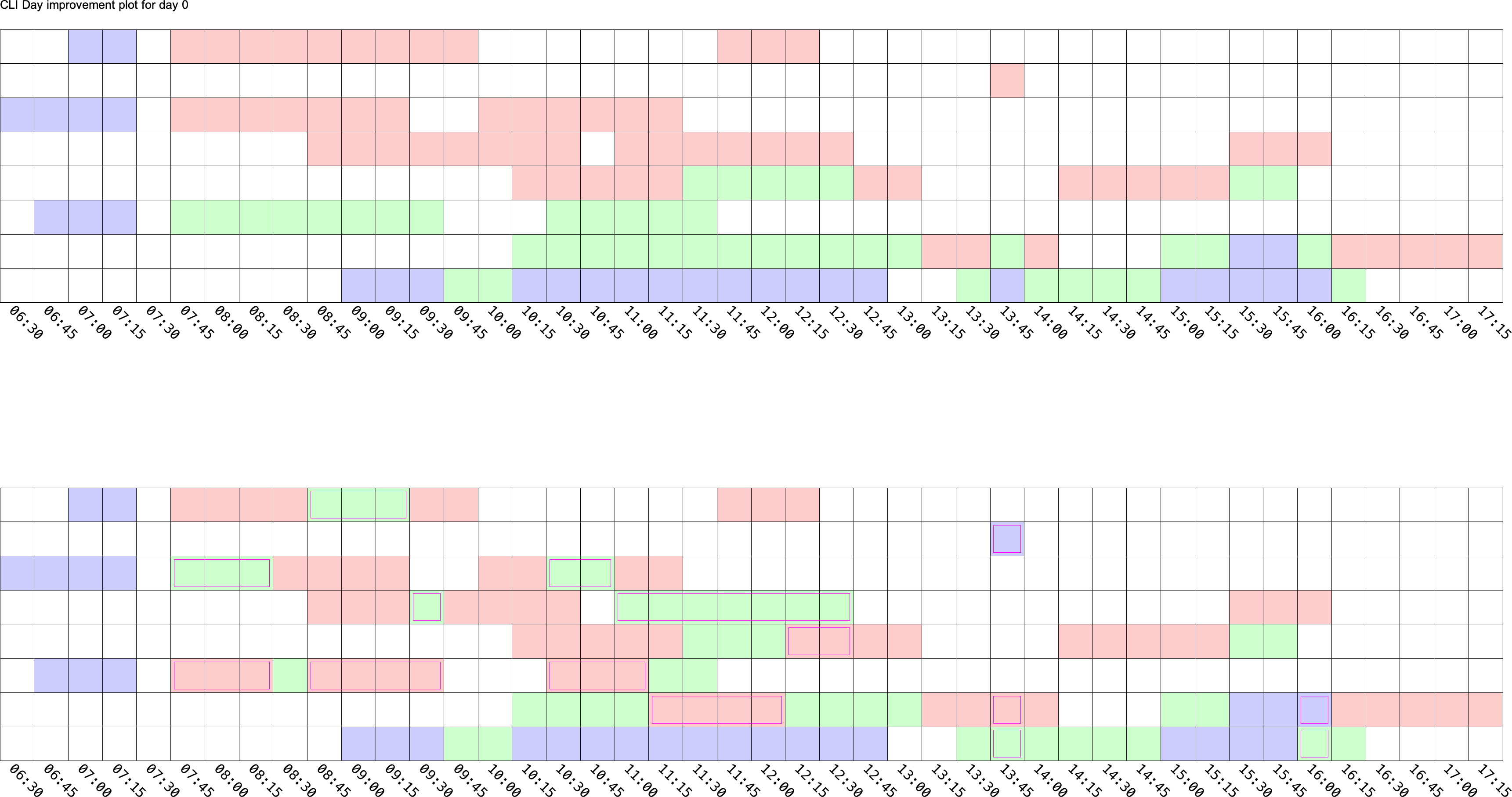
Refer to caption
Figure 3: The RosterLogic Variation debug plot output when solving the length 12, workers 8, blocks size 15, seed 3 instance. The plot shows only the blocks with till, store, and warehouse activities.

A simple plotting system gives visual feedback for both planners and developers. Having a clear visualization of how changes are made to the schedule is critical for effective development. An example of the plot is shown in Figure 3.

5 Experiments

To evaluate the RosterLogic Variation solver and compare and contrast it with the results for the MiniZinc model, a set of benchmark instances is needed. Since the data from our customers is confidential, we have created a set of artificial problems with similar characteristics. Below we will describe the generated instances, the different solvers we benchmark against, and finally discuss the actual results.

5.1 Generated Instances

We have written an instance generator for WTV that mimics real-world instances that we have worked with, without disclosing any sensitive customer data. The domain for the instances is the retail case, where WTV is applied to till, store, and warehouse tasks. In particular, working at the till is the limiting factor, with stricter costs for the right task lengths and a significant cost for each worker that works too long or too often at the till.

The set of instances are generated with a fixed block length of either 15 or 5 minutes, which are both common planning resolutions in real-world settings. Naturally, using a 5 minute block size gives larger and harder instances than 15 minute block sizes for the same length of the schedule. The schedule has a length of 10 to 16 hours in steps of 2 hours. Within these times, 8 to 14 hours are designated as the store opening time, within which all the till and store tasks are allocated. The warehouse task (and other tasks) may extend outside this time.

The number of worker shifts varies between 8 and 16. Workers shifts are randomized over and around the start time of the store, and the three main tasks are interspersed with other work (that is fixed in time and place) and breaks. Workers have lunch breaks between 30 and 60 minutes long, and sometimes a morning and/or afternoon coffee break of 15 minutes, for long enough shifts.

For each combination, 10 different instances have been generated to give a good variety of instances, for a total of 2∗4∗5∗10=400 instances. The generated instances are available at https://github.com/optischedule/work-task-variation-instances including the full MiniZinc model. For brevity of exposition, only 4 instances per size are tested (so 160 different instances in 40 different sizes).

The generated instances represent typical sizes for normal workloads. For larger sites, it is common to schedule personnel in groups (often divided based on competencies), leading to smaller groups of workers to exchange tasks between.

5.2 Solvers and System

We benchmark our RosterLogic Variation solver against 8 different variants of OR-Tools CP-SAT [22] and Gecode [7], using the MiniZinc formulation. In total we ran 1+8 different variations of the following solvers:

RosterLogic Variation

RosterLogic Variation is run in its default configuration described in Section 4.5.

OR-Tools CP-SAT 9.12

The current release of CP-SAT and available in MiniZinc 2.9.2.

OR-Tools CP-SAT 9.3

A release of CP-SAT from 3 years ago (March 2022).

Gecode 6.3.0

The standard Gecode solver supplied with MiniZinc 2.9.2.

Gecode 6.3.0, with restarts

The standard Gecode solver supplied with MiniZinc 2.9.2, with settings to enable restarts (--restart luby, restarts using the Luby sequence [14]), no-good recording (--nogoods), and an increased copying distance (--c-d 50, peak depth is over 100, and with restarts early copies are wasteful).

All tests are limited to a maximum of 60 seconds run-time. The common use-case for solving the WTV problem is in an interactive setting, where the planner expects answers in a short timeframe. We consider 60 seconds to be on the outside of what would be accepted in the intended context.

All tests are run on a MacBook Pro M1 Max (10 cores) with 64 GiB of memory. RosterLogic Variation is naturally parallelized, and uses up to 5 cores at a time in its default configuration. Worth noting is that the default configuration was set in 2019, and that the common use-case was to use it on computers with 4-6 cores. The framework supports using more parallelism, but we have not tested this. All CP solvers are tested both single-threaded (1t) and multi-threaded with 10 threads (10t). Using a multi-threaded configuration is the intended usage of CP-SAT. The single-threaded runs for CP-SAT 9.12 are mostly shown for completeness and the ones for CP-SAT 9.3 are skipped as it did not show any interesting differences across versions. Full results are available on request from the authors.

For timing of RosterLogic Variation, note that the system is written in Java, and while it can be used as a stand-alone tool, the intended deployment scenario is as a long-running server. To make the stand-alone tool for short-running processes faster, static compilation of the system with, for example, GraalVM [21] could be applied.

5.3 Results

In this section the results of the experiments are shown, more detailed results are given in Appendix A.

No solution.

In many cases, CP-SAT fails to find any solution at all. In Table 2 the number of cases of no solution is shown for all the configurations tested. Note that all variations of Gecode found a solution, although generally not a good one. Since the problem is not inherently hard to solve if the right variables are branched on (the schedule variables in Listing 2), we believe that CP-SAT tries to focus on the extra variables used for cost calculations instead. Adding an explicit search annotation did not help in our experiments.

Table 2: Number of instances where the no solution is found out of 80 tested instances for each block size.
Slot length CP-SAT 9.12 1t CP-SAT 9.12 10t CP-SAT 9.3 10t
5 40 36 40
15 40 13 35

Plots.

All costs in the plots are given normalized to the cost produced by RosterLogic Variation. This is because the objective cost values are not meaningful in themselves and vary widely in scale between different instances. As RosterLogic Variation has been used effectively in production, we can view it as a base-line level of “good enough”. A value lower than 1 for the cost (below the vertical line at 1) means that a better solution than RosterLogic Variation was found (e.g., 0.5 means a solution twice as good was found), while a value higher than one means a worse solution was found (e.g., 2.5 means the solution found was two and a half times worse than RosterLogic Variation’s solution).

Similarly, the time is given as a normalized multiple compared with RosterLogic Variation, as that gives an indication of the complexity of the problem and is suitable for comparison in collected plots. For block size 15, run times for RosterLogic Variation in its default configuration is around 1.8 to 7.4 seconds, and for block size 5 it is between 3.7 and 16.2 seconds. A value below 1 (to the left of the vertical line at 1) means that solution was found faster than RosterLogic Variation, while conversely a value to the right of the line means the solution was found after RosterLogic Variation was done.

The plots use a base 2 logarithmic scale, and are intended to show the typical behavior of the solvers. We include all intermediate solutions reported through MiniZinc in the plots, as the any-time behavior of the solvers is of general interest for an interactive tool. RosterLogic Variation is not configured to give intermediate solutions currently, but could be retrofitted to do that. We omit the plot for Gecode-R with 1 thread for space reasons, as it showed no significant difference in behavior compare with Gecode-R with 10 threads.

Figure 4: Normalized Quality vs. Time (vs RosterLogic Variation) for block size 15. Lower values are better. Dashed lines at 1.0 mark CBLS performance. Shapes denote number of workers W8 , W10 , W12 , W14 , and W16 as . Colors denote length of schedule: L10 , L12 , L14 , and L16 as .

Block size 15.

In Figure 4 results for instances with block size 15 are reported. As can be seen there are very few markers that are both faster and have better results than RosterLogic Variation. CP-SAT in the multi-threaded configuration often reaches better results than RosterLogic Variation, although it takes more time to do so.

CP-SAT in the single-threaded configuration gets significantly worse results than in the multi-threaded configuration. This is not surprising, as the single-threaded configuration does not include the portfolio assets that use LNS [24] and local search [5] that find improved solutions.

From the difference in the tables for CP-SAT 9.12 and 9.3 for 10 threads, it is obvious that CP-SAT is much faster at finding good solutions now than it was three years ago, as the collected point cloud has shifted to the left in the plot.

Gecode with the normal settings does not gain much from multiple threads (except a few cases where a solution was found very quickly), as it is used to help a search that is mostly weighted towards DFS exploration. Gecode with restarts produces a lot better solutions, and here the multi-threading quite often helps, although not always (results for the single-threaded Gecode-R is shown in Appendix A).

Figure 5: Normalized Quality vs. Time (vs RosterLogic Variation) for block size 5. Lower values are better. Dashed lines at 1.0 mark CBLS performance. Shapes denote number of workers W8 , W10 , W12 , W14 , and W16 as . Colors denote length of schedule: L10 , L12 , L14 , and L16 as .

Block size 5.

In Figure 5 results for instances with block size 5 are reported. With block size 5, the same length of schedule has three times as many variables. This naturally means that the run-times are also longer, although the limits for what is an acceptable wait time for an interactive use-case is still the same. Note that this means that the scale on run-time has changed compared with the plot for block size 15.

The big difference in results for block size 5 is that RosterLogic Variation also wins most cases on cost, except for a few of the ones with a lower number of workers that CP-SAT 9.12 with 10 threads finds better solutions for.

5.4 Solver Choice for the WTV Problem

It is quite clear in the previous results that with a modern solver (Google OR-Tools CP-SAT 9.12) using multiple threads, investing the resources into creating a custom solver like RosterLogic Variation is likely not justified, if the end goal is to solve instances with 15 minute blocks. This assumes that the issue with sometimes not finding solutions can be solved. However, for the common case of scheduling in 5 minute blocks, RosterLogic Variation still outperforms modern CP variants. The cases where no solution is produced in 60 seconds is also concerning, but something that we believe is not a fundamental problem as shown by the Gecode solver always finding solutions.

It is also clear from the difference between CP-SAT versions 9.12 and 9.3 that development of automatic heuristics for solvers has progressed a lot in just a few years, and the recommendations may be very different in just a few years from now.

6 Conclusion

We have introduced the Work Task Variation (WTV) problem as a post-processing optimization challenge, particularly useful in personnel scheduling. Our work relates to existing research in ergonomic workforce scheduling [27, 23] and fairness trade-offs in resource allocation [2, 3, 11]. Although the WTV problem is understudied and lacks system support in many scheduling domains, it is often very important for creating ergonomic work shifts.

We presented a custom CBLS-inspired solver, RosterLogic Variation, designed for fast, interactive schedule improvement. RosterLogic Variation provides rapid feedback suitable for iterative refinement in practical settings. We hope that our description of the solver can be used as inspiration for others that wish to develop a custom CBLS inspired solver. The complete MiniZinc model developed for the problem enables comparison using standard CP solvers and facilitates further research. Together with the provided benchmark instances, these contributions allow researchers to investigate the WTV problem and develop more efficient solution methods.

Our experiments show that the custom solver, RosterLogic Variation, provides excellent performance for interactive use cases, rapidly finding good quality solutions. Furthermore, it demonstrates superior solution quality compared to current standard solvers on instances with finer-grained time resolutions (5-minute blocks).

References

  • [1] Kenneth R. Baker. Workforce allocation in cyclical scheduling problems: A survey. Journal of the Operational Research Society, 27(1):155–167, 1976. doi:10.1057/jors.1976.30.
  • [2] Dimitris Bertsimas, Vivek F. Farias, and Nikolaos Trichakis. The price of fairness. Operations Research, 59(1):17–31, 2011. doi:10.1287/opre.1100.0869.
  • [3] Dimitris Bertsimas, Vivek F. Farias, and Nikolaos Trichakis. On the efficiency-fairness trade-off. Management Science, 58(12):2234–2250, 2012. doi:10.1287/mnsc.1120.1554.
  • [4] Edmund Burke, Patrick De Causmaecker, Greet Vanden Berghe, and Hendrik Van Landeghem. The state of the art of nurse rostering. J. Scheduling, 7:441–499, November 2004. doi:10.1023/B:JOSH.0000046076.75950.0b.
  • [5] Toby O. Davies, Frédéric Didier, and Laurent Perron. Violationls: Constraint-based local search in cp-sat. In Proceedings of the 30th International Conference on Principles and Practice of Constraint Programming (CP 2024), volume 13958 of Lecture Notes in Computer Science, pages 417–431. Springer, 2024. doi:10.1007/978-3-031-60597-0_16.
  • [6] Luca Di Gaspero, Johannes Gaertner, Guy Kortsarz, Nysret Musliu, Andrea Schaerf, and Wolfgang Slany. The minimum shift design problem. Annals of Operations Research, 155:79–105, August 2007. doi:10.1007/s10479-007-0221-1.
  • [7] Gecode Team. Gecode: Generic Constraint Development Environment. URL: https://www.gecode.org/.
  • [8] Fred Glover. Tabu search – Part I. ORSA Journal on Computing, 1(3), 1989. doi:10.1287/IJOC.1.3.190.
  • [9] Fred Glover. Tabu search – Part II. ORSA Journal on Computing, 2(1), 1990. doi:10.1287/IJOC.2.1.4.
  • [10] Pascal Van Hentenryck and Laurent Michel. Constraint-Based Local Search. The MIT Press, 2009.
  • [11] John N. Hooker and H. Paul Williams. Combining equity and utilitarianism in a mathematical programming model. Management Science, 58(9):1682–1693, 2012. doi:10.1287/mnsc.1110.1510.
  • [12] Holger H. Hoos and Thomas Stützle. Stochastic Local Search: Foundations and Applications. Elsevier, Amsterdam, The Netherlands, 2004.
  • [13] Scott Kirkpatrick, C. Daniel Gelatt, Jr., and Mario P. Vecchi. Optimization by simulated annealing. Science, 220(4598):671–680, May 1983. doi:10.1126/SCIENCE.220.4598.671.
  • [14] Michael Luby, Alistair Sinclair, and David Zuckerman. Optimal speedup of las vegas algorithms. Information Processing Letters, 47(4):173–180, 1993. doi:10.1016/0020-0190(93)90029-9.
  • [15] Laurent Michel and Pascal Van Hentenryck. Localizer. Constraints, 5(1):43–84, 2000. doi:10.1023/A:1009990419456.
  • [16] Laurent Michel and Pascal Van Hentenryck. Constraint-based local search. In Francesca Rossi, Peter van Beek, and Toby Walsh, editors, Handbook of Constraint Programming, pages 223–260. Elsevier, Amsterdam, The Netherlands, 2018. doi:10.1016/B978-0-444-52726-4.50010-6.
  • [17] Nysret Musliu, Andreas Schutt, and Peter J. Stuckey. Solver independent rotating workforce scheduling. In Willem-Jan van Hoeve, editor, Integration of Constraint Programming, Artificial Intelligence, and Operations Research, pages 429–445, Cham, 2018. Springer International Publishing. doi:10.1007/978-3-319-93031-2_31.
  • [18] Nicholas Nethercote, Peter J. Stuckey, Ralph Becket, Sebastian Brand, Gregory J. Duck, and Guido Tack. MiniZinc: Towards a standard cp modelling language. In Christian Bessière, editor, Principles and Practice of Constraint Programming – CP 2007, pages 529–543, Berlin, Heidelberg, 2007. Springer Berlin Heidelberg. doi:10.1007/978-3-540-74970-7_38.
  • [19] M. A. Hakim Newton, Duc Nghia Pham, Abdul Sattar, and Michael Maher. Kangaroo: An efficient constraint-based local search system using lazy propagation. In Principles and Practice of Constraint Programming, volume 6876 of Lecture Notes in Computer Science, pages 645–659, Perugia, Italy, 2011. Springer. doi:10.1007/978-3-642-23786-7_48.
  • [20] Optischedule AB. RosterLogic Variation, 2019.
  • [21] Oracle Labs. GraalVM: Run Programs Faster Anywhere. https://www.graalvm.org/. Accessed: 21st July 2025.
  • [22] Laurent Perron and Frédéric Didier. CP-SAT. URL: https://developers.google.com/optimization/cp/cp_solver/.
  • [23] S. S. Sana, H. Ospina-Mateus, F. G. Arrieta, and J. A. Chedid. Application of genetic algorithm to job scheduling under ergonomic constraints in manufacturing industry. Journal of Ambient Intelligence and Humanized Computing, 10:2063–2090, 2019. doi:10.1007/S12652-018-0814-3.
  • [24] Paul Shaw. Using constraint programming and local search methods to solve vehicle routing problems. In Michael Maher and Jean-François Puget, editors, Principles and Practice of Constraint Programming – CP98, volume 1520 of Lecture Notes in Computer Science, pages 417–431. Springer, 1998. doi:10.1007/3-540-49481-2_30.
  • [25] Pascal Van Hentenryck and Laurent Michel. Differentiable invariants. In Frédéric Benhamou, editor, Proceedings of CP’06, volume 4204 of LNCS, pages 604–619. Springer-Verlag, 2006. doi:10.1007/11889205_43.
  • [26] Sebastiano Vigna. Further scramblings of Marsaglia’s xorshift generators. Journal of Computational and Applied Mathematics, 315:175–181, 2017. doi:10.1016/j.cam.2016.11.006.
  • [27] Thitinan Wongwien and Suebsak Nanthavanij. Priority-based ergonomic workforce scheduling for industrial workers performing hazardous jobs. Journal of Industrial and Production Engineering, 34(1):52–60, 2017.

Appendix A Detailed results

This appendix gives more detailed results compared with the plots in Section 5.3. Similar to the plots, the costs are shown normalized to the cost produced by RosterLogic Variation. The tables show the best solution found, and if no solution was found within 60 seconds then a “-” is shown. In contrast to the plots the timings are shown in seconds. If the time is less than 60, the solver has proven the solution to be optimal.

The Time To Improvement (TTI) column indicates how long it took for the solver to find a solution that was equal to or better than the solution from RosterLogic Variation in relation to the time RosterLogic Variation took. For example, when there is a TTI value of 2.73x and RosterLogic Variation took 4.5 seconds, it means that the solver found a solution of equal or better value than RosterLogic Variation after 12.3 seconds. Note that the solver may have continued running until the 60-second time limit and found solutions even better than those merely on par with RosterLogic Variation. If no improvement over RosterLogic Variation was found, then a “-” is shown.

For each row, the best cost found is marked with dark blue, and values within five percent are marked with blue, and values within ten percent of the best are marked with light blue. The same is done independently for the timings.

Block size 15.

In Table 3 results for instances with block size 15 are reported. RosterLogic Variation run times are between 2 and 7 seconds, and are for the most part dominating in speed. CP-SAT 9.12 with 10 threads dominates in solution quality, although the TTI is almost never below 1x (just three times), indicating the RosterLogic Variation still produces decent results faster.

CP-SAT 9.12 with 10 threads proves the optimal solution for 52 of the 80 instances, finds a solution but does not prove it optimal in 15 cases, and fails to solve 13 instances. This can be compared with CP-SAT 9.3 with 10 threads that proves the optimal solution in just 12 of the instances and fails to solve 36, with 32 solved but not proven optimal.

Gecode always finds solutions, but quite often very bad solutions. Gecode with the normal settings does not gain much from multiple threads, as it is used to help a search that is mostly weighted towards DFS exploration. Gecode with restarts produces a lot better solutions, and here the multi-threading quite often helps, although not always.

Block size 5.

In Table 4 results for instances with block size 5 are reported. Using 5 minute blocks makes the problem a lot harder for all solvers. RosterLogic Variation increases its run-time to up to around 15 seconds here.

The big difference is that RosterLogic Variation also wins most cases on cost, except for a few of the ones with fewer workers that CP-SAT 9.12 with 10 threads can solve better, although there are also a lot of cases that CP-SAT does not solve at all. With 5-minute blocks, CP-SAT 9.12 with 10 threads proves optimality for only 9 instances, and CP-SAT 9.3 with 10 threads does not do it for any instance.

Gecode still finds solutions to all instances (and Gecode with restarts even find the best solution for one case), but the quality of the solutions found is quite bad in general.

Table 3: Benchmark results for block duration 15 minutes. Time (s), Cost (obj), TTI (Time To Improvement factor vs CBLS).
Instance RosterLogic CP-SAT 9.12 1t CP-SAT 9.12 10t CP-SAT 9.3 10t Gecode 1t Gecode 10t Gecode-R 1t Gecode-R 10t
Time Cost Time Cost TTI Time Cost TTI Time Cost TTI Time Cost TTI Time Cost TTI Time Cost TTI Time Cost TTI
L10 W8 - 1 2.1 1.00 60 18.25 - 2.7 0.92 1.21x 16.1 0.92 3.92x 60 15.32 - 60 14.83 - 60 4.57 - 60 3.13 -
L10 W8 - 2 2.1 1.00 60 9.23 - 29.4 0.99 2.43x 60 1.00 12.28x 60 5.01 - 60 4.99 - 60 2.32 - 60 2.51 -
L10 W8 - 3 1.8 1.00 60 - - 2.3 0.96 1.25x 4.9 0.96 2.71x 60 9.84 - 60 9.93 - 60 6.50 - 60 4.08 -
L10 W8 - 4 2.3 1.00 60 - - 3.5 0.77 1.54x 34.9 0.77 15.29x 60 11.80 - 60 10.62 - 60 2.37 - 60 3.28 -
L10 W10 - 1 2.5 1.00 60 20.70 - 3.4 0.92 1.31x 60 0.92 6.85x 60 19.32 - 60 18.94 - 60 11.09 - 60 10.71 -
L10 W10 - 2 2.5 1.00 60 8.91 - 21.7 0.90 2.38x 60 0.93 4.19x 60 10.29 - 60 10.08 - 60 3.86 - 60 3.82 -
L10 W10 - 3 3.0 1.00 60 - - 60 - - 60 - - 60 6.74 - 60 5.66 - 60 5.36 - 60 4.19 -
L10 W10 - 4 3.6 1.00 60 - - 60 - - 60 - - 60 21.35 - 60 18.33 - 60 3.27 - 60 8.04 -
L10 W12 - 1 3.2 1.00 60 12.33 - 4.2 0.84 1.31x 60 0.85 5.05x 60 13.93 - 60 13.48 - 60 3.44 - 60 3.75 -
L10 W12 - 2 3.6 1.00 60 4.97 - 60 0.94 6.87x 60 0.97 14.25x 60 6.60 - 60 6.26 - 60 3.28 - 60 2.87 -
L10 W12 - 3 3.0 1.00 60 - - 56.0 0.69 18.36x 60 - - 60 12.49 - 60 11.51 - 60 4.20 - 60 4.01 -
L10 W12 - 4 4.0 1.00 60 - - 12.7 0.84 3.15x 60 - - 60 25.74 - 60 21.62 - 60 5.44 - 60 6.26 -
L10 W14 - 1 4.2 1.00 60 13.07 - 60 0.89 2.62x 60 0.91 6.85x 60 7.10 - 60 6.20 - 60 3.18 - 60 2.49 -
L10 W14 - 2 4.7 1.00 60 18.69 - 60 1.02 - 60 1.66 - 60 17.61 - 60 17.63 - 60 5.86 - 60 5.40 -
L10 W14 - 3 4.2 1.00 60 - - 19.7 0.85 4.64x 60 - - 60 16.06 - 60 15.31 - 60 3.35 - 60 3.65 -
L10 W14 - 4 6.0 1.00 60 - - 60 - - 60 - - 60 27.09 - 60 23.90 - 60 9.78 - 60 11.05 -
L10 W16 - 1 6.1 1.00 60 15.32 - 60 0.82 1.50x 60 0.95 7.44x 60 21.95 - 60 21.94 - 60 10.72 - 60 8.83 -
L10 W16 - 2 6.2 1.00 60 15.36 - 60 0.92 3.34x 60 1.01 - 60 12.19 - 60 11.79 - 60 2.52 - 60 2.64 -
L10 W16 - 3 5.5 1.00 60 - - 60 - - 60 - - 60 12.80 - 60 12.83 - 60 6.13 - 60 6.04 -
L10 W16 - 4 6.2 1.00 60 - - 60 - - 60 - - 60 10.09 - 60 8.46 - 60 3.63 - 60 4.10 -
L12 W8 - 1 2.5 1.00 60 22.94 - 9.0 0.70 1.87x 39.5 0.70 6.15x 60 26.01 - 60 25.50 - 60 9.22 - 60 10.03 -
L12 W8 - 2 2.5 1.00 60 19.97 - 3.7 0.88 1.44x 60 0.88 5.03x 60 13.63 - 60 13.24 - 60 5.69 - 60 5.50 -
L12 W8 - 3 1.9 1.00 60 - - 9.2 0.90 4.90x 60 - - 60 24.17 - 60 23.61 - 60 5.56 - 60 6.80 -
L12 W8 - 4 2.9 1.00 60 - - 6.9 0.76 2.33x 60 - - 60 10.87 - 60 10.25 - 60 2.28 - 60 3.14 -
L12 W10 - 1 2.9 1.00 60 17.38 - 8.8 0.97 2.40x 60 0.99 14.19x 60 15.05 - 60 14.67 - 60 4.62 - 60 4.42 -
L12 W10 - 2 2.9 1.00 60 9.07 - 8.4 0.89 1.46x 60 0.93 4.73x 60 13.80 - 60 12.69 - 60 4.99 - 60 3.68 -
L12 W10 - 3 2.6 1.00 60 - - 41.3 0.72 16.00x 60 - - 60 25.62 - 60 24.21 - 60 5.51 - 60 3.70 -
L12 W10 - 4 3.5 1.00 60 - - 60 - - 60 - - 60 28.97 - 60 25.18 - 60 7.47 - 60 7.33 -
L12 W12 - 1 4.1 1.00 60 31.29 - 7.6 0.96 1.82x 60 1.06 - 60 24.26 - 60 24.09 - 60 7.73 - 60 7.86 -
L12 W12 - 2 4.1 1.00 60 13.82 - 60 0.98 2.99x 60 1.00 12.73x 60 19.40 - 60 18.64 - 60 4.58 - 60 3.58 -
L12 W12 - 3 3.4 1.00 60 - - 5.2 0.88 1.53x 60 - - 60 29.41 - 60 24.46 - 60 15.51 - 60 15.67 -
L12 W12 - 4 4.0 1.00 60 - - 60 - - 60 - - 60 19.15 - 60 17.90 - 60 4.69 - 60 3.65 -
L12 W14 - 1 4.5 1.00 60 25.19 - 60 0.72 2.73x 60 1.60 - 60 28.84 - 60 28.42 - 60 17.07 - 60 10.36 -
L12 W14 - 2 5.1 1.00 60 14.24 - 60 1.02 - 60 1.47 - 60 16.59 - 60 16.42 - 60 5.70 - 60 5.73 -
L12 W14 - 3 3.9 1.00 60 - - 27.2 0.78 6.88x 60 - - 60 21.96 - 60 19.29 - 60 12.52 - 60 7.79 -
L12 W14 - 4 5.9 1.00 60 - - 12.3 0.86 2.09x 60 - - 60 26.09 - 60 23.81 - 60 8.17 - 60 6.37 -
L12 W16 - 1 6.0 1.00 60 14.72 - 60 0.57 2.12x 60 1.06 - 60 27.43 - 60 21.18 - 60 11.95 - 60 10.49 -
L12 W16 - 2 7.4 1.00 60 14.50 - 60 0.96 2.46x 60 1.05 - 60 18.11 - 60 17.79 - 60 5.24 - 60 6.28 -
L12 W16 - 3 4.7 1.00 60 - - 12.1 0.44 2.56x 60 - - 60 19.05 - 60 17.39 - 60 11.93 - 60 8.46 -
L12 W16 - 4 6.0 1.00 60 - - 60 - - 60 - - 60 20.28 - 60 14.53 - 60 5.80 - 60 5.78 -
L14 W8 - 1 2.4 1.00 60 12.45 - 6.7 0.88 1.68x 60 0.89 5.57x 60 9.97 - 60 9.83 - 60 3.88 - 60 4.59 -
L14 W8 - 2 2.2 1.00 60 21.72 - 4.4 0.86 1.73x 51.9 0.86 3.91x 60 9.42 - 60 9.48 - 60 4.87 - 60 3.75 -
L14 W8 - 3 1.5 1.00 60 - - 2.3 0.57 1.46x 3.1 0.57 2.00x 60 9.80 - 60 9.78 - 60 2.71 - 60 1.98 -
L14 W8 - 4 3.4 1.00 60 - - 9.0 0.76 2.64x 60 - - 60 17.46 - 60 16.67 - 60 3.17 - 60 3.19 -
L14 W10 - 1 2.7 1.00 60 41.24 - 7.0 0.66 1.71x 60 0.66 6.22x 60 53.93 - 60 52.95 - 60 7.56 - 60 13.71 -
L14 W10 - 2 3.4 1.00 60 11.65 - 7.1 0.89 1.90x 60 0.90 4.96x 60 11.96 - 60 11.85 - 60 3.40 - 60 2.69 -
L14 W10 - 3 2.6 1.00 60 - - 3.9 0.94 1.50x 57.9 0.94 22.50x 60 23.20 - 60 20.87 - 60 6.34 - 60 3.99 -
L14 W10 - 4 4.3 1.00 60 - - 6.9 0.39 1.59x 60 - - 60 33.45 - 60 32.52 - 60 15.91 - 60 9.11 -
L14 W12 - 1 3.9 1.00 60 32.66 - 60 0.82 3.65x 60 1.10 - 60 42.25 - 60 41.51 - 60 9.08 - 60 6.76 -
L14 W12 - 2 3.5 1.00 60 17.96 - 60 0.91 5.38x 60 1.09 - 60 25.45 - 60 25.45 - 60 7.54 - 60 3.53 -
L14 W12 - 3 3.0 1.00 60 - - 9.7 0.88 3.21x 60 - - 60 39.57 - 60 38.52 - 60 13.89 - 60 13.98 -
L14 W12 - 4 4.2 1.00 60 - - 25.7 0.67 6.14x 60 - - 60 31.83 - 60 28.47 - 60 8.05 - 60 12.92 -
L14 W14 - 1 5.6 1.00 60 40.53 - 9.1 0.59 1.59x 60 0.86 9.19x 60 74.99 - 60 71.76 - 60 25.43 - 60 24.57 -
L14 W14 - 2 5.5 1.00 60 39.44 - 16.8 0.78 3.02x 60 1.26 - 60 42.42 - 60 41.71 - 60 16.31 - 60 17.33 -
L14 W14 - 3 4.3 1.00 60 - - 42.3 0.43 9.91x 60 - - 60 11.83 - 60 11.36 - 60 6.38 - 60 5.82 -
L14 W14 - 4 6.0 1.00 60 - - 17.6 0.86 2.91x 60 - - 60 37.25 - 60 35.86 - 60 10.78 - 60 9.30 -
L14 W16 - 1 6.4 1.00 60 46.03 - 5.7 0.51 0.87x 60 1.77 - 60 55.44 - 60 48.57 - 60 12.84 - 60 14.05 -
L14 W16 - 2 7.2 1.00 60 29.76 - 23.7 0.82 2.48x 60 1.23 - 60 34.35 - 60 31.23 - 60 10.47 - 60 13.00 -
L14 W16 - 3 5.1 1.00 60 - - 60 - - 60 - - 60 20.80 - 60 20.77 - 60 8.71 - 60 6.80 -
L14 W16 - 4 6.9 1.00 60 - - 60 - - 60 - - 60 22.92 - 60 18.25 - 60 6.79 - 60 9.39 -
L16 W8 - 1 2.4 1.00 60 21.55 - 4.3 0.43 1.47x 7.7 0.43 2.25x 60 31.02 - 60 28.71 - 60 16.08 - 60 9.24 -
L16 W8 - 2 2.0 1.00 60 31.99 - 3.3 0.87 1.59x 13.2 0.87 4.32x 60 36.22 - 60 34.11 - 60 5.95 - 60 5.74 -
L16 W8 - 3 1.7 1.00 60 - - 3.9 0.93 2.33x 14.9 0.93 8.92x 60 10.05 - 60 7.96 - 60 3.09 - 60 3.14 -
L16 W8 - 4 2.9 1.00 60 - - 9.6 0.92 3.32x 60 - - 60 28.85 - 60 28.82 - 60 7.16 - 60 6.32 -
L16 W10 - 1 2.9 1.00 60 28.52 - 4.0 0.60 1.13x 32.9 0.60 3.05x 60 35.48 - 60 33.19 - 60 12.26 - 60 9.14 -
L16 W10 - 2 3.0 1.00 60 9.89 - 60 0.92 13.40x 60 1.01 - 60 12.25 - 60 12.03 - 60 3.08 - 60 3.10 -
L16 W10 - 3 2.4 1.00 60 - - 5.7 0.72 2.34x 60 - - 60 46.83 - 60 45.35 - 60 20.38 - 60 10.11 -
L16 W10 - 4 3.7 1.00 60 - - 11.2 0.75 2.99x 60 - - 60 28.59 - 60 27.88 - 60 10.67 - 60 11.06 -
L16 W12 - 1 4.3 1.00 60 30.46 - 5.3 0.69 0.97x 60 0.75 6.03x 60 50.89 - 60 50.28 - 60 10.31 - 60 10.14 -
L16 W12 - 2 3.7 1.00 60 19.01 - 60 0.98 3.58x 60 1.00 16.08x 60 19.77 - 60 19.59 - 60 3.91 - 60 3.49 -
L16 W12 - 3 3.1 1.00 60 - - 8.3 0.91 2.68x 60 - - 60 27.99 - 60 27.99 - 60 10.32 - 60 7.12 -
L16 W12 - 4 4.5 1.00 60 - - 60 - - 60 - - 60 45.27 - 60 40.02 - 60 15.63 - 60 12.91 -
L16 W14 - 1 4.7 1.00 60 31.25 - 47.6 0.44 2.75x 60 1.17 - 60 49.41 - 60 47.04 - 60 15.92 - 60 14.14 -
L16 W14 - 2 5.5 1.00 60 15.67 - 7.5 0.88 1.35x 60 1.01 - 60 10.90 - 60 11.30 - 60 4.18 - 60 3.62 -
L16 W14 - 3 4.5 1.00 60 - - 48.6 0.72 10.89x 60 - - 60 35.10 - 60 35.71 - 60 9.85 - 60 8.48 -
L16 W14 - 4 5.7 1.00 60 - - 60 - - 60 - - 60 15.37 - 60 12.76 - 60 7.91 - 60 7.13 -
L16 W16 - 1 5.7 1.00 60 46.80 - 60 1.17 - 60 1.69 - 60 51.67 - 60 47.37 - 60 11.80 - 60 14.91 -
L16 W16 - 2 7.2 1.00 60 73.40 - 6.9 0.55 0.94x 43.0 0.55 5.33x 60 65.55 - 60 64.76 - 60 31.07 - 60 33.96 -
L16 W16 - 3 5.4 1.00 60 - - 7.2 0.49 1.33x 60 - - 60 95.42 - 60 89.10 - 60 27.90 - 60 28.22 -
L16 W16 - 4 6.3 1.00 60 - - 60 - - 60 - - 60 41.74 - 60 37.15 - 60 23.02 - 60 21.41 -
Table 4: Benchmark results for block duration 5 minutes. Time (s), Cost (obj), TTI (Time To Improvement factor vs CBLS).
Instance RosterLogic CP-SAT 9.12 1t CP-SAT 9.12 10t CP-SAT 9.3 10t Gecode 1t Gecode 10t Gecode-R 1t Gecode-R 10t
Time Cost Time Cost TTI Time Cost TTI Time Cost TTI Time Cost TTI Time Cost TTI Time Cost TTI Time Cost TTI
L10 W8 - 1 3.7 1.00 60 11.01 - 34.0 0.31 6.32x 60 1.16 - 60 9.44 - 60 9.35 - 60 4.16 - 60 1.85 -
L10 W8 - 2 3.8 1.00 60 10.65 - 58.8 0.47 5.11x 60 0.91 10.31x 60 14.91 - 60 14.91 - 60 4.97 - 60 2.59 -
L10 W8 - 3 3.0 1.00 60 - - 60 - - 60 - - 60 11.18 - 60 11.15 - 60 3.42 - 60 3.73 -
L10 W8 - 4 4.0 1.00 60 - - 28.8 0.39 7.14x 60 - - 60 14.34 - 60 13.50 - 60 7.62 - 60 14.17 -
L10 W10 - 1 5.1 1.00 60 14.09 - 60 0.86 7.22x 60 3.08 - 60 18.36 - 60 18.45 - 60 13.48 - 60 7.55 -
L10 W10 - 2 5.4 1.00 60 8.04 - 60 0.47 5.67x 60 3.18 - 60 12.00 - 60 11.27 - 60 3.70 - 60 3.87 -
L10 W10 - 3 5.4 1.00 60 - - 60 - - 60 - - 60 14.44 - 60 14.24 - 60 7.75 - 60 13.12 -
L10 W10 - 4 5.3 1.00 60 - - 60 - - 60 - - 60 14.86 - 60 14.99 - 60 5.42 - 60 3.45 -
L10 W12 - 1 5.6 1.00 60 25.88 - 33.2 0.33 5.90x 60 7.52 - 60 18.04 - 60 18.06 - 60 7.90 - 60 5.16 -
L10 W12 - 2 7.3 1.00 60 13.34 - 60 2.32 - 60 7.23 - 60 19.83 - 60 20.10 - 60 5.82 - 60 6.04 -
L10 W12 - 3 6.8 1.00 60 - - 60 - - 60 - - 60 13.31 - 60 13.95 - 60 8.58 - 60 7.60 -
L10 W12 - 4 7.4 1.00 60 - - 52.1 0.37 6.99x 60 - - 60 14.45 - 60 14.76 - 60 5.37 - 60 5.44 -
L10 W14 - 1 8.1 1.00 60 15.75 - 60 1.33 - 60 8.55 - 60 11.74 - 60 11.38 - 60 8.57 - 60 7.40 -
L10 W14 - 2 9.3 1.00 60 10.86 - 60 4.48 - 60 21.03 - 60 16.99 - 60 16.40 - 60 6.32 - 60 5.81 -
L10 W14 - 3 8.9 1.00 60 - - 60 - - 60 - - 60 9.69 - 60 10.11 - 60 2.37 - 60 2.20 -
L10 W14 - 4 9.1 1.00 60 - - 60 - - 60 - - 60 13.42 - 60 13.05 - 60 8.47 - 60 6.28 -
L10 W16 - 1 10.5 1.00 60 18.93 - 60 5.17 - 60 10.92 - 60 13.69 - 60 13.82 - 60 11.86 - 60 8.83 -
L10 W16 - 2 12.9 1.00 60 17.22 - 60 7.00 - 60 11.58 - 60 15.33 - 60 15.21 - 60 8.01 - 60 7.17 -
L10 W16 - 3 10.2 1.00 60 - - 60 - - 60 - - 60 18.79 - 60 17.89 - 60 9.48 - 60 9.93 -
L10 W16 - 4 11.8 1.00 60 - - 60 - - 60 - - 60 17.10 - 60 17.44 - 60 10.52 - 60 9.67 -
L12 W8 - 1 5.1 1.00 60 10.47 - 60 0.61 7.92x 60 1.78 - 60 12.73 - 60 11.78 - 60 6.41 - 60 7.36 -
L12 W8 - 2 4.1 1.00 60 32.82 - 60 0.73 11.89x 60 3.14 - 60 25.43 - 60 28.70 - 60 19.33 - 60 13.30 -
L12 W8 - 3 3.5 1.00 60 - - 60 - - 60 - - 60 16.69 - 60 16.21 - 60 3.51 - 60 3.01 -
L12 W8 - 4 5.4 1.00 60 - - 60 - - 60 - - 60 20.05 - 60 19.51 - 60 11.98 - 60 7.50 -
L12 W10 - 1 5.7 1.00 60 21.35 - 60 1.62 - 60 4.60 - 60 31.18 - 60 29.92 - 60 15.11 - 60 13.03 -
L12 W10 - 2 5.8 1.00 60 18.93 - 60 1.26 - 60 2.29 - 60 18.08 - 60 16.80 - 60 4.89 - 60 4.13 -
L12 W10 - 3 5.2 1.00 60 - - 28.0 0.40 5.40x 60 - - 60 21.60 - 60 21.34 - 60 7.18 - 60 4.29 -
L12 W10 - 4 7.7 1.00 60 - - 60 - - 60 - - 60 16.19 - 60 15.92 - 60 4.43 - 60 4.54 -
L12 W12 - 1 7.7 1.00 60 12.71 - 60 1.26 - 60 7.48 - 60 13.95 - 60 13.84 - 60 11.12 - 60 7.49 -
L12 W12 - 2 7.8 1.00 60 22.00 - 60 2.02 - 60 14.14 - 60 25.26 - 60 22.92 - 60 11.55 - 60 8.61 -
L12 W12 - 3 6.7 1.00 60 - - 60 - - 60 - - 60 25.75 - 60 24.76 - 60 10.64 - 60 11.23 -
L12 W12 - 4 9.5 1.00 60 - - 60 - - 60 - - 60 12.89 - 60 12.54 - 60 6.27 - 60 12.69 -
L12 W14 - 1 10.7 1.00 60 18.99 - 60 7.66 - 60 7.27 - 60 27.38 - 60 27.45 - 60 15.21 - 60 14.51 -
L12 W14 - 2 11.3 1.00 60 31.38 - 60 7.18 - 60 13.65 - 60 29.28 - 60 26.76 - 60 15.71 - 60 17.68 -
L12 W14 - 3 8.9 1.00 60 - - 60 - - 60 - - 60 16.83 - 60 16.72 - 60 6.88 - 60 6.74 -
L12 W14 - 4 12.7 1.00 60 - - 60 - - 60 - - 60 27.52 - 60 26.34 - 60 8.23 - 60 7.75 -
L12 W16 - 1 15.4 1.00 60 33.05 - 60 14.88 - 60 18.93 - 60 31.58 - 60 31.66 - 60 20.33 - 60 22.42 -
L12 W16 - 2 13.8 1.00 60 19.88 - 60 15.31 - 60 73.68 - 60 25.58 - 60 22.86 - 60 15.77 - 60 12.87 -
L12 W16 - 3 11.6 1.00 60 - - 60 - - 60 - - 60 43.82 - 60 41.61 - 60 15.72 - 60 16.51 -
L12 W16 - 4 15.1 1.00 60 - - 60 - - 60 - - 60 32.77 - 60 32.59 - 60 18.53 - 60 17.01 -
L14 W8 - 1 4.8 1.00 60 20.76 - 60 1.63 - 60 4.18 - 60 28.56 - 60 28.35 - 60 8.72 - 60 9.79 -
L14 W8 - 2 4.0 1.00 60 17.14 - 60 0.78 7.11x 60 1.27 - 60 12.29 - 60 12.59 - 60 2.67 - 60 4.30 -
L14 W8 - 3 3.3 1.00 60 - - 60 - - 60 - - 60 10.32 - 60 10.31 - 60 3.96 - 60 5.35 -
L14 W8 - 4 6.0 1.00 60 - - 60 - - 60 - - 60 15.97 - 60 16.13 - 60 7.24 - 60 7.11 -
L14 W10 - 1 6.0 1.00 60 30.10 - 60 2.90 - 60 2.86 - 60 34.19 - 60 31.50 - 60 10.52 - 60 9.24 -
L14 W10 - 2 6.9 1.00 60 20.78 - 60 1.47 - 60 4.55 - 60 23.89 - 60 22.10 - 60 5.94 - 60 3.92 -
L14 W10 - 3 4.7 1.00 60 - - 60 - - 60 - - 60 20.01 - 60 18.47 - 60 5.51 - 60 7.49 -
L14 W10 - 4 8.2 1.00 60 - - 60 - - 60 - - 60 15.26 - 60 15.81 - 60 9.02 - 60 7.90 -
L14 W12 - 1 8.2 1.00 60 28.86 - 60 3.29 - 60 10.85 - 60 31.69 - 60 31.06 - 60 17.41 - 60 13.01 -
L14 W12 - 2 7.2 1.00 60 15.81 - 60 2.17 - 60 8.93 - 60 21.98 - 60 21.98 - 60 7.14 - 60 7.91 -
L14 W12 - 3 6.9 1.00 60 - - 60 - - 60 - - 60 35.29 - 60 35.33 - 60 17.73 - 60 16.67 -
L14 W12 - 4 11.3 1.00 60 - - 60 - - 60 - - 60 35.79 - 60 31.72 - 60 17.81 - 60 18.93 -
L14 W14 - 1 11.1 1.00 60 56.10 - 60 13.08 - 60 31.00 - 60 95.87 - 60 100.07 - 60 44.16 - 60 47.80 -
L14 W14 - 2 11.4 1.00 60 251.84 - 56.4 1.04 - 60 124.31 - 60 298.87 - 60 279.27 - 60 105.18 - 60 63.73 -
L14 W14 - 3 9.6 1.00 60 - - 60 - - 60 - - 60 30.05 - 60 31.09 - 60 20.99 - 60 21.33 -
L14 W14 - 4 12.4 1.00 60 - - 60 - - 60 - - 60 22.69 - 60 22.81 - 60 10.83 - 60 10.94 -
L14 W16 - 1 14.5 1.00 60 13.85 - 60 5.62 - 60 12.47 - 60 25.19 - 60 24.45 - 60 10.53 - 60 8.94 -
L14 W16 - 2 15.2 1.00 60 31.58 - 60 31.85 - 60 119.49 - 60 30.60 - 60 30.72 - 60 15.34 - 60 18.60 -
L14 W16 - 3 11.7 1.00 60 - - 60 - - 60 - - 60 23.80 - 60 24.45 - 60 12.61 - 60 12.25 -
L14 W16 - 4 14.6 1.00 60 - - 60 - - 60 - - 60 35.06 - 60 36.46 - 60 19.70 - 60 20.05 -
L16 W8 - 1 4.6 1.00 60 44.53 - 43.2 0.50 6.24x 60 1.38 - 60 46.55 - 60 41.41 - 60 10.43 - 60 9.38 -
L16 W8 - 2 4.4 1.00 60 8.83 - 60 0.43 5.94x 60 0.89 11.61x 60 10.61 - 60 9.69 - 60 7.06 - 60 5.73 -
L16 W8 - 3 3.5 1.00 60 - - 60 - - 60 - - 60 2.76 - 60 2.61 - 60 0.28 17.26x 60 0.69 17.26x
L16 W8 - 4 5.7 1.00 60 - - 60 - - 60 - - 60 19.38 - 60 16.51 - 60 8.88 - 60 5.00 -
L16 W10 - 1 6.2 1.00 60 21.09 - 60 2.18 - 60 5.77 - 60 40.03 - 60 38.22 - 60 14.40 - 60 13.91 -
L16 W10 - 2 7.4 1.00 60 20.71 - 60 1.28 - 60 4.94 - 60 22.13 - 60 21.69 - 60 5.81 - 60 5.22 -
L16 W10 - 3 5.1 1.00 60 - - 46.8 0.35 9.09x 60 - - 60 36.41 - 60 34.80 - 60 16.33 - 60 11.65 -
L16 W10 - 4 7.9 1.00 60 - - 60 - - 60 - - 60 29.91 - 60 29.80 - 60 13.12 - 60 12.58 -
L16 W12 - 1 8.9 1.00 60 41.72 - 60 3.19 - 60 19.23 - 60 48.93 - 60 45.33 - 60 10.23 - 60 11.44 -
L16 W12 - 2 8.2 1.00 60 6.20 - 60 2.51 - 60 4.77 - 60 11.51 - 60 11.29 - 60 3.15 - 60 3.28 -
L16 W12 - 3 7.3 1.00 60 - - 60 - - 60 - - 60 33.30 - 60 33.30 - 60 18.58 - 60 17.54 -
L16 W12 - 4 10.4 1.00 60 - - 60 - - 60 - - 60 24.91 - 60 23.92 - 60 14.65 - 60 14.36 -
L16 W14 - 1 10.9 1.00 60 39.54 - 60 9.48 - 60 13.69 - 60 47.65 - 60 47.66 - 60 15.34 - 60 12.26 -
L16 W14 - 2 12.9 1.00 60 28.62 - 60 15.41 - 60 18.53 - 60 36.33 - 60 36.39 - 60 17.28 - 60 18.49 -
L16 W14 - 3 10.1 1.00 60 - - 60 - - 60 - - 60 27.60 - 60 26.76 - 60 10.44 - 60 7.00 -
L16 W14 - 4 13.0 1.00 60 - - 60 - - 60 - - 60 28.35 - 60 27.92 - 60 9.68 - 60 8.82 -
L16 W16 - 1 16.2 1.00 60 12.75 - 60 5.99 - 60 6.93 - 60 19.68 - 60 19.78 - 60 8.88 - 60 9.62 -
L16 W16 - 2 15.7 1.00 60 82.95 - 60 38.01 - 60 55.44 - 60 99.29 - 60 102.26 - 60 42.53 - 60 35.53 -
L16 W16 - 3 11.6 1.00 60 - - 60 - - 60 - - 60 35.34 - 60 35.56 - 60 16.06 - 60 15.59 -
L16 W16 - 4 15.9 1.00 60 - - 60 - - 60 - - 60 26.90 - 60 25.05 - 60 11.47 - 60 9.24 -

Appendix B Large plots for CP-SAT 9.12 10 threads

In Figure 6 the plot for the results of CP-SAT 9.12 with 10 threads is given in a larger format for more detailed inspeaction compared with in Section 5.3. Similarly, in Figure 7 the results for CP-SAT 9.12 with 10 threads is shown.

Figure 6: Normalized Quality vs. Time CP-SAT 9.12 10 threads vs RosterLogic Variation for block size 15. Lower values are better. Dashed lines at 1.0 mark CBLS performance. Shapes denote number of workers W8 , W10 , W12 , W14 , and W16 as . Colors denote length of schedule: L10 , L12 , L14 , and L16 as .
Figure 7: Normalized Quality vs. Time CP-SAT 9.12 10 threads vs RosterLogic Variation for block size 5. Lower values are better. Dashed lines at 1.0 mark CBLS performance. Shapes denote number of workers W8 , W10 , W12 , W14 , and W16 as . Colors denote length of schedule: L10 , L12 , L14 , and L16 as .

Appendix C Pattern Swap Patterns

In Table 5 all the patterns defined for the Pattern Swap moves described in Section 4.3 for swapping till and store tasks. Note that these patterns are the ones that were found to be useful for the types of instances of WTV that we worked with in practice, for the common style of cost functions. These patterns are shown for 15-minute block sizes, for 5-minute block sizes the patterns are adjusted accordingly to account for the same durations (e.g., a pattern SST would become SSSSSSTTT). Out of the 10 defined patterns, 4 are symmetric which gives a total of 16 unique patterns.

Table 5: The 10 common patterns used for the pattern swap move generator are shown to the left. For each pattern, the reversed version is also shown to the right.