Modeling and Solving a Composite Structure Design Problem with Constraint Programming (Short Paper)

Antoons, Miguel; Delecluse, Augustin; Zein, Samih; Schaus, Pierre

doi:10.4230/LIPIcs.CP.2025.41

Modeling and Solving a Composite Structure Design Problem with Constraint Programming

Miguel Antoons

UCLouvain, Belgium Augustin Delecluse

TRAIL, ICTEAM, UCLouvain, Belgium Samih Zein

High Performance Composite team, Cenaero, Gosselies, Belgium Pierre Schaus

ICTEAM, UCLouvain, Belgium

Abstract

Composite structures are composed of plies (layers) of carbon fibers. For each ply, one must decide its orientation from the set of possible angles: -45°, 0°, 45°, and 90°. The stack of plies must follow strict constraints on the chosen orientations to achieve mechanical properties of the composite, such as sufficient buckling load. The design problem becomes more complex when determining the stack of plies for a complete surface material, that does not require the same number of plies in every region of the surface. Not only must the orientations be selected in each region, but it is also necessary to decide which plies are discontinued between adjacent regions. Thanks to its declarative nature, Constraint Programming (CP) offers an elegant modeling of the constraints, making it easy for designers to activate or deactivate them as needed. We propose a CP model, implemented in MiniZinc. The performance of this model on synthetic yet realistic instances when solved by different exact solvers, including Mixed Integer Programming (MIP) solvers, demonstrates the superiority of CP over MIP on our MiniZinc model, and over a commercial solution implemented by an industrial partner. It opens up the adoption of CP as an efficient building block of Computer-Aided Design tools for composite structures. By making the model and instances publicly available, we also hope to facilitate the inclusion of this problem in CP solver competitions and stimulate further research in this area.

Keywords and phrases:

Constraint Programming, Composite Structures, Design Rules, MiniZinc

Category:

Short Paper

Funding:

Augustin Delecluse: This work was supported by Service Public de Wallonie Recherche under grant n°2010235 – ARIAC by DIGITALWALLONIA4.A.

Copyright and License:

2012 ACM Subject Classification:

Theory of computation

\rightarrow

Constraint and logic programming ; Theory of computation

\rightarrow

Backtracking ; Mathematics of computing

\rightarrow

Combinatoric problems ; Computing methodologies

\rightarrow

Combinatorial algorithms ; Computing methodologies

\rightarrow

Model development and analysis ; Applied computing

\rightarrow

Aerospace

Editors:

Maria Garcia de la Banda

Series and Publisher:

Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik

1 Introduction

Composite structures are widely used in the industry to design components such as aeronautical or automotive pieces, due to their high strength-to-weight ratio. A composite structure is typically subdivided into several panels, and each panel is made up of multiple thin layers, or plies, arranged in a specific stacking sequence. The fibers in each ply are commonly oriented at one of four discrete angles in $\{0\degree,\pm 45\degree,90\degree\}$ . An example of a composite structure is a plane wing, as shown in Figure 1, where we can see the stacking sequence of a panel on the right. Due to manufacturing limitations, as well as to ensure consistent load transfer and meet required stiffness and strength, design constraints restrict how a ply may be oriented, depending on its neighbors and on adjacent panels.

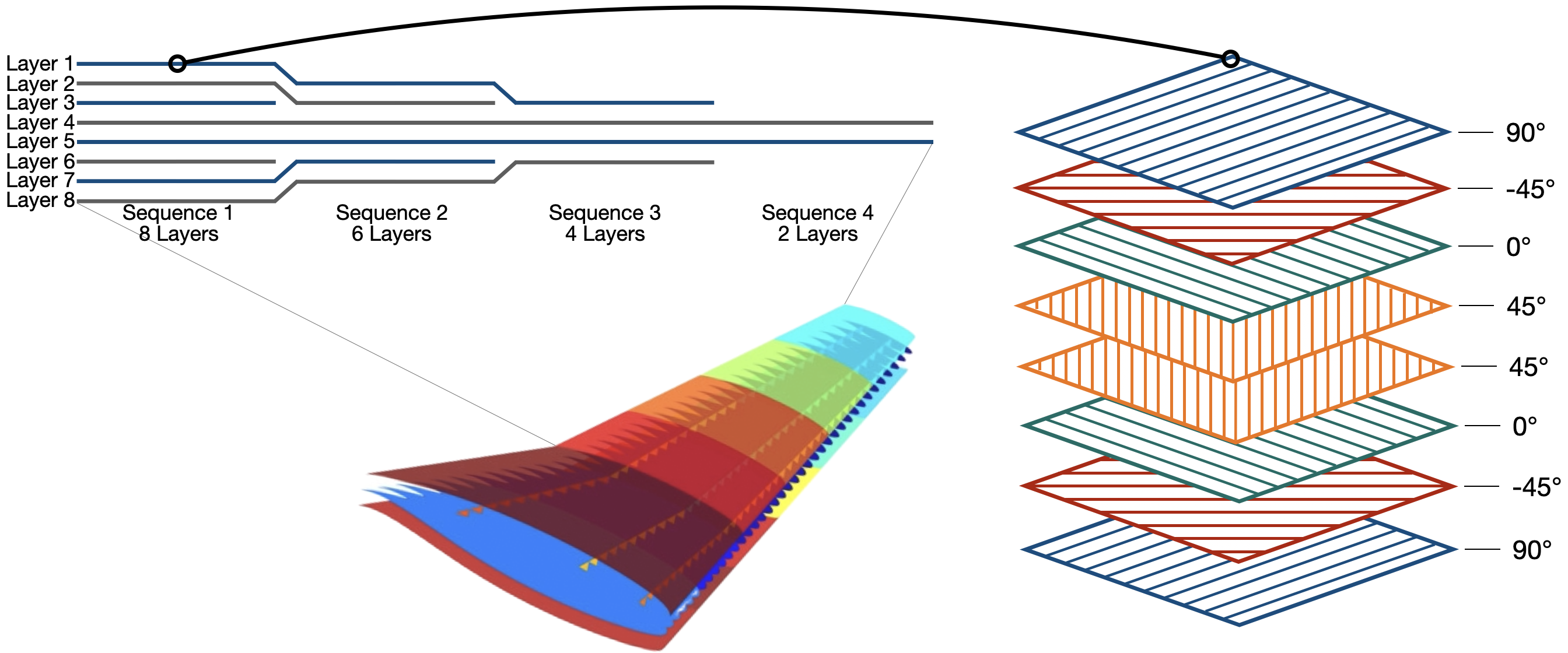
Refer to caption — Figure 1: Example of the use of composite structures, here with a plane wing.

As can be seen in a review on the optimization of composite structures [15], this type of problem has so far been mainly addressed using genetic algorithms. A notable exception is the exact algorithm proposed in [21], implemented in the commercial tool of our industrial partner, and which we compare with. Our contributions are as follows:

1.

The introduction of a pure declarative constraint programming model that can be used to generate a consistent composite structure.
2.

An empirical validation of the model through Minizinc, improving the generation of admissible sequences proposed in [21].

The paper is organized as follows. Section 2 first presents the problem definition for deriving stacking sequences of a composite structure. A Constraint Programming (CP) model is introduced in Section 3. Section 4 is dedicated to the related work and mostly explains the main ideas of the exact custom algorithm of [21]. The CP model, implemented in MiniZinc, is experimentally validated in Section 5 and compared with the approach of [21]. Finally, Section 6 concludes and highlights possible future research directions.

2 Design Constraints for Composite Structures

The problem is to decide the orientation for each ply in each stacking sequence while satisfying rules specific to each stacking sequence and connecting those rules between adjacent sequences.

A first set of rules are the structural ones for each individual stacking sequence $S_{i}$ .

$\blacksquare$

D1: The number of plies for each orientation is imposed and denoted by $n_{i}^{-45},n_{i}^{0},n_{i}^{45},n_{i}^{90}$ . We also define $n_{i}$ as the sum of these: $n_{i}=n_{i}^{-45}+n_{i}^{0}+n_{i}^{45}+n_{i}^{90}$ .
$\blacksquare$

D2: The angle difference between two consecutive plies cannot be equal to 90°. This means that a -45° ply cannot be followed by a 45° ply, a 0° ply cannot be followed by a 90° ply and the inverse of those two cases is also prohibited.
$\blacksquare$

D3: A succession of four or more plies having the same angle is disallowed.
$\blacksquare$

D4: The sequence must be symmetric vertically (e.g. $(0\degree,45\degree,45\degree,0\degree),...$ ). However, some exceptions are accepted at the center of the sequence in addition to symmetrical patterns, namely $(-45\degree,45\degree)$ , $(-45\degree,0\degree,45\degree)$ , $(-45\degree,90\degree,45\degree)$ and their inverses.
$\blacksquare$

D5: The top and bottom plies are only allowed to take values in $\{-45\degree,45\degree\}$ .

A second set of constraints consists of the blending rules, which restrict how neighboring stacking sequences relate to each other. For every pair of neighboring stacking sequences $S_{i},S_{j}$ , an implicit directed edge points from the sequence with the larger number of plies toward the one with fewer plies ( $n_{i}>n_{j}$ ). We call $i$ a parent of $j$ . A directed graph represents the neighboring relationships. This graph must be acyclic for the structure to be feasible. This set of edges is denoted $E$ .

$\blacksquare$

B1: The subsequence $S_{j}$ (the thinner one) must be a subsequence of $S_{i}$ (the thicker one). In the event $S_{j}$ has multiple parents, its plies must be contained in all of them.
$\blacksquare$

B2: A ply can either be shared between two neighboring stacking sequences or be discontinued, but two continuous plies cannot cross each other. This can be seen as having the same ordering for the common plies between neighboring sequences: given a parent sequence $S_{i}=(A,B,C)$ , a child sequence could be $S_{j}=(A,C)$ but cannot be $S_{j}=(C,A)$ as the ordering is not preserved.
$\blacksquare$

B3: The top ply of $S_{i}$ must be the same as the top ply of $S_{j}$ , and the same applies to their bottom plies. This ensures the continuity of the top and bottom surface plies throughout the entire structure.
$\blacksquare$

B4: A maximum of three consecutive layers can be dropped at once from $S_{i}$ to $S_{j}$ .

Depending on the structure requirements in practical applications, some rules may be ignored. The blending rules B1-B4 are always present, to ensure a global coherence between adjacent sequences. In the same manner, the design rule D1 is always enforced to generate sequences of required size. However, the design rules D2-D5 may be absent in some settings. This further motivates the use of declarative paradigms such as CP to tackle this problem.

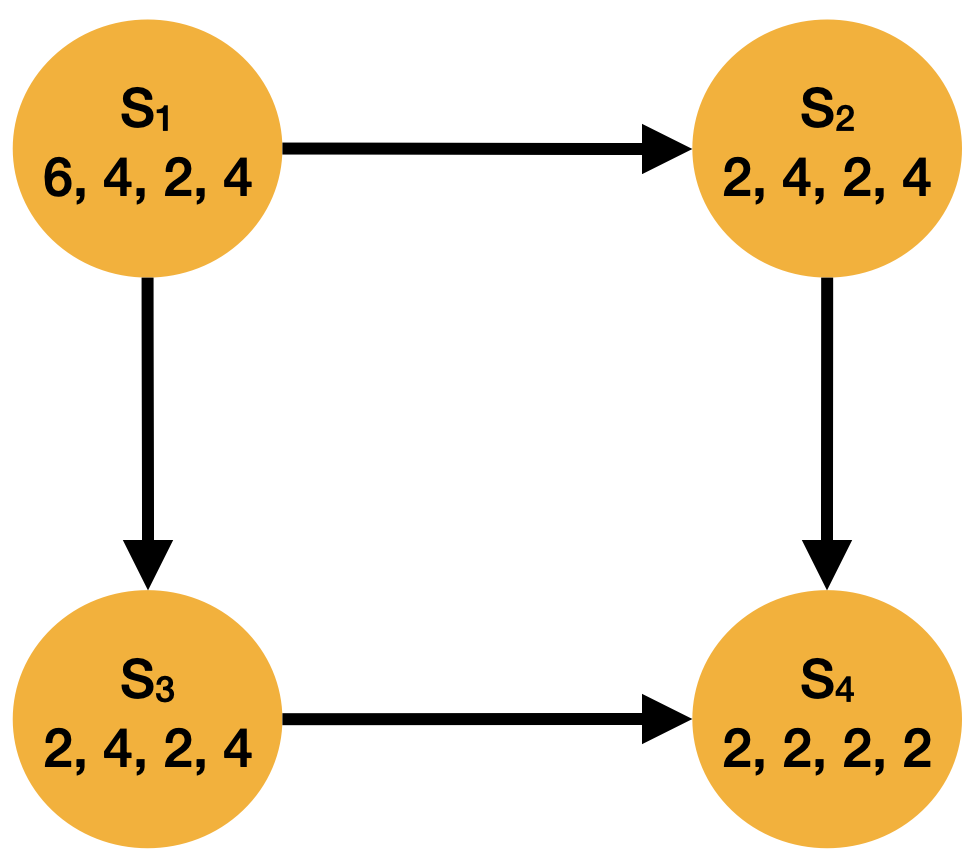
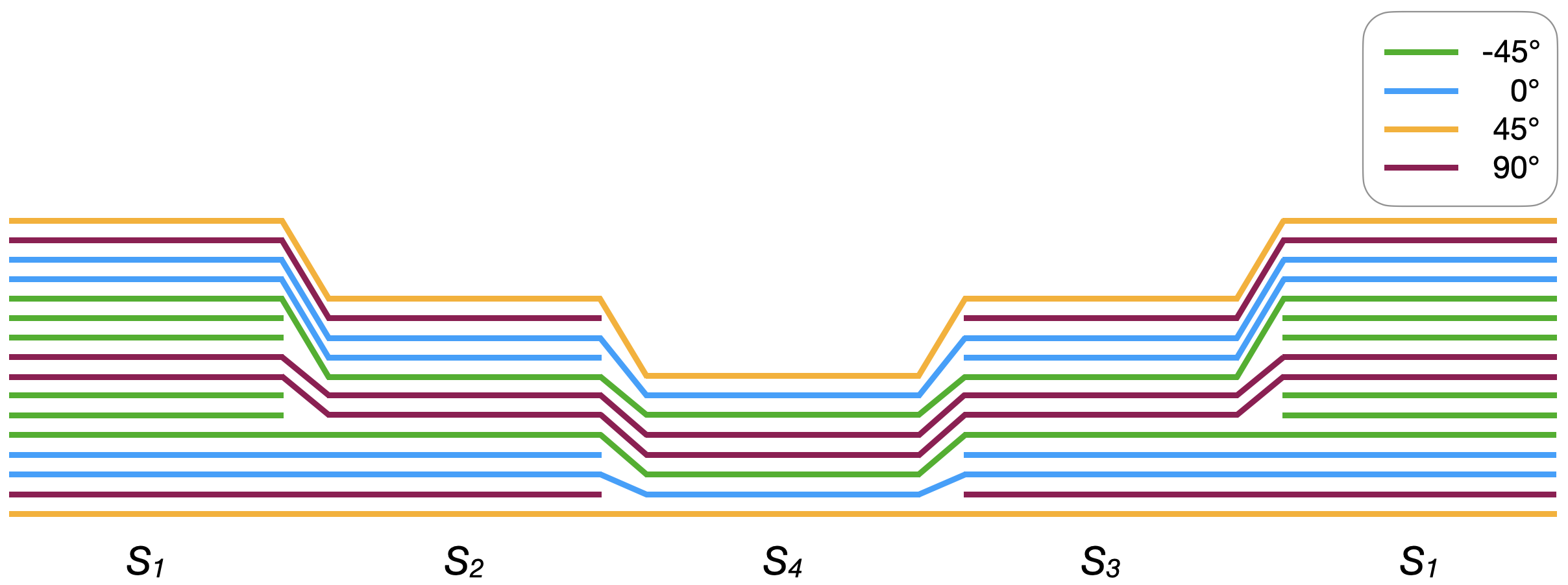
Example 1.

Given the input graph from Figure 3, a solution satisfying most of the constraints is shown in Figure 3. In this solution, the constraints satisfied are B1, B2, B3, B4 and D1, which are always activated as well as the optional constraints D3, D4 and D5. There are some places where an angle difference of 90° is present, which is prohibited by constraint D2. This is for instance the case for $S_{1}[2]=90\degree$ and $S_{1}[3]=0\degree$ .

3 CP Model

3.1 Decision Variables

The main decision variables of our problem are the orientations that each layer $k$ can take in every stacking sequence $i$ :

S_{i}[k]\in\{Id_{-45},\ Id_{0},\ Id_{45},\ Id_{90}\}\qquad\forall\ 1\leq k\leq n% _{i}\qquad\forall i\in\mathcal{I}

(1)

Where $Id_{o},o\in\{0\degree,\pm 45\degree,90\degree\}$ denotes the plies orientation and $\mathcal{I}=\{1\dots|S|\}$ is the set of indices for all stacking sequences $S$ . A second set of variables $Y_{i,j}[k]\in\{1,\ldots,n_{i}\},\forall 1\leq k\leq n_{j}$ , for all $(i,j)\in E$ is used to ensure the continuity of layers between adjacent regions. More precisely $Y_{i,j}[k]$ indicates that the ply $k$ of the stacking sequence $j$ is the continuation of the ply $Y_{i,j}[k]$ in the neighboring stacking sequence $i$ . For example, referring to Figure 3 and 3, $Y_{1,2}[6]=8$ since the sixth ply from $S_{2}$ is the same as the eighth ply from $S_{1}$ .

3.2 Constraints

To ease the constraint notations, we first define some set of indices and constants. $\mathcal{I}_{\textit{even}}=\{i\in\mathcal{I}\mid n_{i}\text{ is even}\}$ , $\mathcal{I}_{\textit{odd}}=\{i\in\mathcal{I}\mid n_{i}\text{ is odd}\}$ are the sets of indices for sequences of even and odd length, respectively. Moreover, $m_{i}:=\lfloor n_{i}/2\rfloor$ denotes the midpoint of a sequence $S_{i}\in S$ .

The structural constraints D1-D5 on each stacking sequence are expressed on $S_{i}[k]$ variables while the blending constraints B1-B4 are expressed on $y_{i,j}$ variables. The formal definition of the constraints is given next.

$\displaystyle\text{cardinality}(S_{i},[Id_{-45},Id_{0},Id_{45},Id_{90}],[n_{i}% ^{-45},n_{i}^{0},n_{i}^{45},n_{i}^{90}])$	$\displaystyle\forall i\in\mathcal{I}$	(2)
$\displaystyle(S_{i}[k],S_{i}[k+1],S_{i}[k+2],S_{i}[k+3])\in\text{allowed\_tuples}$	$\displaystyle\forall 1\leq k\leq n_{i}-3,\forall i\in\mathcal{I}$	(3)
$\displaystyle S_{i}[k]=S_{i}[n_{i}-k+1]$	$\displaystyle\forall 1\leq k<\lfloor n_{i}/2\rfloor,\forall i\in\mathcal{I}$	(4)
$\displaystyle(S_{i}[m_{i}],S_{i}[m_{i}+1])\in\text{allowed\_even}$	$\displaystyle\forall i\in\mathcal{I}_{\textit{even}}$	(5)
$\displaystyle(S_{i}[m_{i}],S_{i}[m_{i}+1],S_{i}[m_{i}+2])\in\text{allowed\_odd}$	$\displaystyle\forall i\in\mathcal{I}_{\textit{odd}}$	(6)
$\displaystyle S_{i}[1]\in\{Id_{-45},Id_{45}\}$	$\displaystyle\forall i\in\mathcal{I}$	(7)
$\displaystyle S_{i}[n_{i}]\in\{Id_{-45},Id_{45}\}$	$\displaystyle\forall i\in\mathcal{I}$	(8)
$\displaystyle S_{j}[k]=S_{i}[Y_{i,j}[k]]$	$\displaystyle\forall 1\leq k\leq n_{j},\forall(i,j)\in E$	(9)
$\displaystyle Y_{i,j}[k]<Y_{i,j}[k+1]$	$\displaystyle\forall 1\leq k<n_{j},\forall(i,j)\in E$	(10)
$\displaystyle Y_{i,j}[1]=1$	$\displaystyle\forall(i,j)\in E$	(11)
$\displaystyle Y_{i,j}[n_{j}]=n_{i}$	$\displaystyle\forall(i,j)\in E$	(12)
$\displaystyle Y_{i,j}[k+1]-Y_{i,j}[k]\leq 4$	$\displaystyle\forall 1\leq k<n_{j},\forall(i,j)\in E$	(13)

The design rules D1-D5 correspond to constraints (2)-(8). The D1 constraint is enforced in (2) with a global cardinality constraint [10]. It ensures that the requested plies of every angle, requested by the user, are present in every sequence. This constraint is applied on every stacking sequence $S_{i}$ and takes three arguments:

1.

The sequence of variables forming the stacking sequence.
2.

The possible values, one for each angle,
3.

The cardinalities, one for every possible angle.

Then, the D2 and D3 rules are implemented in (3) by a single table constraint [2, 16, 5, 11] that covers both prohibiting 90° angles and disallowing four or more consecutive plies that have the same angle. It does so by applying a table on every set of four consecutive plies. This table, represented by allowed_tuples, contains all tuples that have at least one different ply from the three others and that does not contain a 90° gap anywhere. This constraint is also enforced on all stacking sequences. In cases where only one constraint between D2 and D3 is activated, the tuples are adapted.

Next is the D4 rule. The equality constraint (4) enforces every ply to be the same as their opposite ply, resulting in the symmetry required by the D4 rule. So, for instance, the first ply must be the same as the last, the second must be the same as the penultimate and so on. This goes on until the middle two plies in case of an even thickness sequence, or until the middle three plies in case of an odd thickness sequence. Indeed, this allows for the exception to the D4 rule, allowing a dissymmetry in the middle to mitigate the problem of odd cardinalities since the symmetry constraint only works when all cardinalities are even. This exception is formulated in (5) in the case of an even thickness and in (6) in the case of an odd thickness. We can see that a table constraint is applied on the middle two or three plies of every stacking sequence. In addition to allowing for a symmetric suite of plies (in case all cardinalities are even), it also allows for the $(-45,45)$ , $(-45,0,45)$ , $(-45,90,45)$ suites and their inverses. For this constraint to work properly, 90° gaps must be possible in the middle and thus the constraint implemented in (3) is relaxed in the middle only. Moreover, we expect CP solvers to represent constraint (4) by reusing the same variables for $S_{i}[k]$ and $S_{i}[n_{i}-k+1]$ instead of using equality constraints, which reduces the number of variables¹¹1Using the same variables for (4) instead of equality constraints is performed by MiniZinc[14], used in our experiments.

The last design rule, D5, is implemented by (7) and (8) by redefining the domain of the top and bottom plies of every stacking sequence (i.e. $S_{i}[1]$ and $S_{i}[n_{i}]$ , respectively), so that only values representing the -45° angle or the 45° angle are allowed.

The blending rules are enforced by (9)-(13), and are mandatory in every variant of the problem. The B1 rule is implemented in (9) using element constraints [8]. It ensures that every ply of a subsequence $S_{j}$ must be present in all its parents denoted by $S_{i}$ . In our model, this is enforced using an element constraint between $S_{i}$ and $S_{j}$ . This means that every ply from a thinner sequence must come from its thicker neighbors. This constraint is applied on every edge of the input graph.

The B2 rule is then implemented in (10). This rule prohibits plies from crossing each other when going from one sequence to another, which is ensured by forcing each index variable ( $Y_{i,j}[k]$ ) to be strictly lower than the next ( $Y_{i,j}[k+1]$ ).

The B3 rule is implemented in (11) and (12) by fixing the domains of the $Y_{i,j}[1]$ and $Y_{i,j}[n_{j}]$ to $1$ and $n_{i}$ respectively. Fixing these values will cause the top and bottom plies of every subsequence to be the same as their neighboring subsequences, and thus cause the top and bottom plies to be continuous across the whole structure.

Finally, the B4 rule is implemented in (13). In order to prevent drop-offs of four or more consecutive plies in between sequences, we can define a constraint that forces the absolute difference of two consecutive index variables (i.e. $Y_{i,j}[k]$ and $Y_{i,j}[k+1]$ ) to be less than or equal to four. In other words, this constraint allows a maximum of three consecutive plies to stop at once between two sequences, satisfying the B4 rule.

4 Related Works

A first exact approach was proposed in [22]. It iteratively generates a set of admissible structures (i.e., stacking sequences that meet all coherence constraints), performs numerical simulations, and selects the sequence(s) yielding the highest buckling load. However, it does not include the blending constraints. The approach of Zein et al. (2014) [21] solves the same problem as ours. Despite the title, the problem is not formalized as a declarative CSP. Instead, the authors introduce a custom depth-first search algorithm. During the search, stacking sequences are considered one by one in decreasing order of their number of layers. For each stacking sequence, branching decisions related to blending constraints are made before those related to design constraints. The approach does not rely on a solver with variables, domains, and a fixed-point computation of generic constraints. The algorithm verifies the consistency of the current layer in the stacking sequence with respect to the prefix of already fixed stacking sequences from previous decisions. If an infeasibility is detected for a layer, the search backtracks. The rules are thus enforced as checkers that verify the validity of a prefix, rather than through a filtering algorithm acting on all the variables in its scope as in a standard CP approach. This means that in a stack $S$ of $n$ plies, the ply orientation $S[k]$ is only deemed invalid if it conflicts with plies $S[1..k-1]$ but no inference is made regarding subsequent plies $S[k+1..n]$ . This algorithm shares similarities with Generative Constraint Programming [17], which lazily prunes only the domain of the next variable to instantiate taking into account the prefix of already fixed variables. Our approach, on the other hand, relies on a pure declarative model where the search is decoupled from the model. While it is understandable that the custom approach uses a search algorithm that makes decisions in the order of stacking sequences to facilitate the verification of blending constraints, it is unclear whether this is the best search strategy, given that all layers are interconnected through blending constraints. Our approach can utilize efficient black-box searches that could detect or learn that, for instance, branching on the thinnest stack first might be more effective.

5 Experimental results

To assess the performance of our model, we generated in agreement with our industrial partner a set of instances representative of the ones that are generally processed by their software. Four datasets were generated using grid sizes of 3x3, 4x4, 5x5 and 6x6²²2Figure 3 corresponds to a grid size of 2x2, stacking sequences, each containing 40 instances. Each node in the grid is connected to a minimum of two and up to four of its neighbors (top, left, bottom, right) in the grid by a directed edge, whose direction is chosen randomly. The cardinality constraints on the number of plies per orientation in each layer were selected uniformly with up to 60 plies per stacking layer. The retained instances are such that none is trivially detected as infeasible by the industrial solver when adding all constraints (B1-B4, D1-D5).

The model was implemented using MiniZinc [14], allowing us to easily experiment with the solving of our problem using different solvers. In particular, three different CP and Lazy Clause Generation solvers are compared: Gecode [18], OR-Tools [4] and Chuffed [3]. We also tried two Mixed Integer Linear Programming (MILP) [20] solvers using their MiniZinc backend: Gurobi [7], HiGHS [9]. Lastly, the performance of the solution deployed by our industrial partner that implements the approach of [21] with all constraints activated is also reported. Instances and models are available at https://github.com/augustindelecluse/composite_structure.

Figure 4 reports the number of instances solved over time with the 3 tested models, using a timeout of 15 minutes. Each model includes constraints B1-B4 and D1. Depending on the application, not all optional constraints must be considered, which was also the case in [21]. The first model (top) does not include any optional constraints, the second (middle) adds constraints D3 and D4, and the third (bottom) includes all constraints.

OR-Tools appears as the most stable solver, and consistently solves more than 80% of the instances within 15 minutes in all datasets and all models. Additionally, its performance does not degrade much when the size of the instances increases, which is not the case with Gecode, Chuffed and the industrial solver. Although not visible in this aggregated plot, Gecode is generally faster on feasible instances, while OR-Tools performs better at proving infeasibility. MILP solvers are behind CP solvers, and Gurobi performs better than Highs. The industrial solver achieves performance competitive with Gecode but is outperformed by the lazy-clause generation solvers OR-Tools and Chuffed. This indicates that clause learning significantly enhances the ability to solve this problem robustly.

Figure 4: Solver performances with different sets of design constraints (rows). Each column denotes a given dataset.

6 Conclusion and Future Work

We have introduced a CP model for the Composite Structure Design Problem, including the blending constraints between neighboring stacking sequences. This model was implemented in MiniZinc and tested with various CP-based solvers and MIP solvers. The results clearly show that CP outperforms MIP on the MiniZinc models, with lazy clause generation solvers enabling the solution of even more instances. This approach also outperforms a state-of-the-art industrial solver that employs a dedicated algorithm for this problem.

In future work, we plan to improve the filtering and search. For filtering, the standard MiniZinc library does not include the AtMostSeqCard constraint from [19]. This constraint limits the number of consecutive variables that can take a specific value $v$ and restricts the total number of variables instantiated to $v$ . We believe that this constraint could help reduce the solving time by acting as a redundant constraint. In addition, our goal is to experiment with different search strategies to further accelerate the solving process. More specifically, one could try to use custom search strategies, possibly combined with conflict-based searches [6] and restart-based strategies with no-good learning [12]. Finally, we would like to include some possible objective functions or hybridize the model with a finite element simulator that would allow for a more fine-grained estimation of the mechanical properties. An interesting approach we could try in that direction is the so-called Empirical Decision Model Learning framework [13].

References

[1] Miguel Antoons, Augustin Delecluse, Samih Zein, and Pierre Schaus. composite_structure. Software, swhId: swh:1:dir:6a1da259835bc6788634d1ba52bda3a11d8b03b1 (visited on 2025-07-23). URL: https://github.com/augustindelecluse/composite_structure, doi:10.4230/artifacts.24098.
[2] Kenil CK Cheng and Roland HC Yap. An MDD-based generalized arc consistency algorithm for positive and negative table constraints and some global constraints. Constraints, 15(2):265–304, 2010. doi:10.1007/S10601-009-9087-Y.
[3] Geoffrey Chu, Peter J. Stuckey, Andreas Schutt, Thorsten Ehlers, Graeme Gange, and Kathryn Francis. Chuffed - a lazy clause solver, 2016. URL: https://github.com/chuffed/chuffed.
[4] Thibaut Cuvelier, Frederic Didier, Vincent Furnon, Steven Gay, Sarah Mohajeri, and Laurent Perron. OR-Tools’ vehicle routing solver: a generic constraint-programming solver with heuristic search for routing problems. In 24e congrès annuel de la société française de recherche opérationnelle et d’aide à la décision, 2023.
[5] Jordan Demeulenaere, Renaud Hartert, Christophe Lecoutre, Guillaume Perez, Laurent Perron, Jean-Charles Régin, and Pierre Schaus. Compact-table: efficiently filtering table constraints with reversible sparse bit-sets. In Principles and Practice of Constraint Programming: 22nd International Conference, CP 2016, Toulouse, France, September 5-9, 2016, Proceedings 22, pages 207–223. Springer, 2016. doi:10.1007/978-3-319-44953-1_14.
[6] Steven Gay, Renaud Hartert, Christophe Lecoutre, and Pierre Schaus. Conflict ordering search for scheduling problems. In Principles and Practice of Constraint Programming: 21st International Conference, CP 2015, Cork, Ireland, August 31–September 4, 2015, Proceedings 21, pages 140–148. Springer, 2015. doi:10.1007/978-3-319-23219-5_10.
[7] Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual, 2024. URL: https://www.gurobi.com.
[8] Pascal Van Hentenryck and Jean-Philippe Carillon. Generality versus specificity: An experience with AI and OR techniques. In Proceedings of the Seventh AAAI National Conference on Artificial Intelligence, pages 660–664, 1988. URL: http://www.aaai.org/Library/AAAI/1988/aaai88-117.php.
[9] Qi Huangfu and JA Julian Hall. Parallelizing the dual revised simplex method. Mathematical Programming Computation, 10(1):119–142, 2018. doi:10.1007/S12532-017-0130-5.
[10] Régin Jean-Charles. Generalized arc consistency for global cardinality constraint. American Association for Artificial Intelligence (AAAI 1996), pages 209–215, 1996. URL: http://www.aaai.org/Library/AAAI/1996/aaai96-031.php.
[11] Christophe Lecoutre. STR2: optimized simple tabular reduction for table constraints. Constraints, 16:341–371, 2011. doi:10.1007/S10601-011-9107-6.
[12] Christophe Lecoutre, Lakhdar Saïs, Sébastien Tabary, and Vincent Vidal. Reasoning from last conflict(s) in constraint programming. Artificial Intelligence, 173(18):1592–1614, 2009. doi:10.1016/J.ARTINT.2009.09.002.
[13] Michele Lombardi, Michela Milano, and Andrea Bartolini. Empirical decision model learning. Artificial Intelligence, 244:343–367, 2017. doi:10.1016/J.ARTINT.2016.01.005.
[14] Nicholas Nethercote, Peter J Stuckey, Ralph Becket, Sebastian Brand, Gregory J Duck, and Guido Tack. MiniZinc: Towards a standard CP modelling language. In International Conference on Principles and Practice of Constraint Programming, pages 529–543. Springer, 2007. doi:10.1007/978-3-540-74970-7_38.
[15] SKMSS Nikbakt, Saeed Kamarian, and Mahdieh Shakeri. A review on optimization of composite structures part i: Laminated composites. Composite Structures, 195:158–185, 2018.
[16] Guillaume Perez and Jean-Charles Régin. Improving GAC-4 for table and MDD constraints. In International Conference on Principles and Practice of Constraint Programming, pages 606–621. Springer, 2014. doi:10.1007/978-3-319-10428-7_44.
[17] Florian Régin and Elisabetta De Maria. Generative constraint programming revisited. In 2024 IEEE 36th International Conference on Tools with Artificial Intelligence (ICTAI), pages 18–26. IEEE, 2024. doi:10.1109/ICTAI62512.2024.00012.
[18] Christian Schulte, Guido Tack, and Mikael Z Lagerkvist. Modeling and programming with gecode. Schulte, Christian and Tack, Guido and Lagerkvist, Mikael, 1, 2010.
[19] Mohamed Siala, Emmanuel Hebrard, and Marie-José Huguet. An optimal arc consistency algorithm for a particular case of sequence constraint. Constraints, 19:30–56, 2014. doi:10.1007/S10601-013-9150-6.
[20] Juan Pablo Vielma. Mixed integer linear programming formulation techniques. Siam Review, 57(1):3–57, 2015. doi:10.1137/130915303.
[21] S Zein, P Basso, and S Grihon. A constraint satisfaction programming approach for computing manufacturable stacking sequences. Computers & Structures, 136:56–63, 2014.
[22] Samih Zein, Benoît Colson, and Stéphane Grihon. A primal-dual backtracking optimization method for blended composite structures. Structural and Multidisciplinary Optimization, 45(5):669–680, 2012.

[bib.bib1] [1] Miguel Antoons, Augustin Delecluse, Samih Zein, and Pierre Schaus. composite_structure. Software, swhId: swh:1:dir:6a1da259835bc6788634d1ba52bda3a11d8b03b1 (visited on 2025-07-23). URL: https://github.com/augustindelecluse/composite_structure, doi:10.4230/artifacts.24098.

[bib.bib2] [2] Kenil CK Cheng and Roland HC Yap. An MDD-based generalized arc consistency algorithm for positive and negative table constraints and some global constraints. Constraints, 15(2):265–304, 2010. doi:10.1007/S10601-009-9087-Y.

[bib.bib3] [3] Geoffrey Chu, Peter J. Stuckey, Andreas Schutt, Thorsten Ehlers, Graeme Gange, and Kathryn Francis. Chuffed - a lazy clause solver, 2016. URL: https://github.com/chuffed/chuffed.

[bib.bib4] [4] Thibaut Cuvelier, Frederic Didier, Vincent Furnon, Steven Gay, Sarah Mohajeri, and Laurent Perron. OR-Tools’ vehicle routing solver: a generic constraint-programming solver with heuristic search for routing problems. In 24e congrès annuel de la société française de recherche opérationnelle et d’aide à la décision, 2023.

[bib.bib5] [5] Jordan Demeulenaere, Renaud Hartert, Christophe Lecoutre, Guillaume Perez, Laurent Perron, Jean-Charles Régin, and Pierre Schaus. Compact-table: efficiently filtering table constraints with reversible sparse bit-sets. In Principles and Practice of Constraint Programming: 22nd International Conference, CP 2016, Toulouse, France, September 5-9, 2016, Proceedings 22, pages 207–223. Springer, 2016. doi:10.1007/978-3-319-44953-1_14.

[bib.bib6] [6] Steven Gay, Renaud Hartert, Christophe Lecoutre, and Pierre Schaus. Conflict ordering search for scheduling problems. In Principles and Practice of Constraint Programming: 21st International Conference, CP 2015, Cork, Ireland, August 31–September 4, 2015, Proceedings 21, pages 140–148. Springer, 2015. doi:10.1007/978-3-319-23219-5_10.

[bib.bib7] [7] Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual, 2024. URL: https://www.gurobi.com.

[bib.bib8] [8] Pascal Van Hentenryck and Jean-Philippe Carillon. Generality versus specificity: An experience with AI and OR techniques. In Proceedings of the Seventh AAAI National Conference on Artificial Intelligence, pages 660–664, 1988. URL: http://www.aaai.org/Library/AAAI/1988/aaai88-117.php.

[bib.bib9] [9] Qi Huangfu and JA Julian Hall. Parallelizing the dual revised simplex method. Mathematical Programming Computation, 10(1):119–142, 2018. doi:10.1007/S12532-017-0130-5.

[bib.bib10] [10] Régin Jean-Charles. Generalized arc consistency for global cardinality constraint. American Association for Artificial Intelligence (AAAI 1996), pages 209–215, 1996. URL: http://www.aaai.org/Library/AAAI/1996/aaai96-031.php.

[bib.bib11] [11] Christophe Lecoutre. STR2: optimized simple tabular reduction for table constraints. Constraints, 16:341–371, 2011. doi:10.1007/S10601-011-9107-6.

[bib.bib12] [12] Christophe Lecoutre, Lakhdar Saïs, Sébastien Tabary, and Vincent Vidal. Reasoning from last conflict(s) in constraint programming. Artificial Intelligence, 173(18):1592–1614, 2009. doi:10.1016/J.ARTINT.2009.09.002.

[bib.bib13] [13] Michele Lombardi, Michela Milano, and Andrea Bartolini. Empirical decision model learning. Artificial Intelligence, 244:343–367, 2017. doi:10.1016/J.ARTINT.2016.01.005.

[bib.bib14] [14] Nicholas Nethercote, Peter J Stuckey, Ralph Becket, Sebastian Brand, Gregory J Duck, and Guido Tack. MiniZinc: Towards a standard CP modelling language. In International Conference on Principles and Practice of Constraint Programming, pages 529–543. Springer, 2007. doi:10.1007/978-3-540-74970-7_38.

[bib.bib15] [15] SKMSS Nikbakt, Saeed Kamarian, and Mahdieh Shakeri. A review on optimization of composite structures part i: Laminated composites. Composite Structures, 195:158–185, 2018.

[bib.bib16] [16] Guillaume Perez and Jean-Charles Régin. Improving GAC-4 for table and MDD constraints. In International Conference on Principles and Practice of Constraint Programming, pages 606–621. Springer, 2014. doi:10.1007/978-3-319-10428-7_44.

[bib.bib17] [17] Florian Régin and Elisabetta De Maria. Generative constraint programming revisited. In 2024 IEEE 36th International Conference on Tools with Artificial Intelligence (ICTAI), pages 18–26. IEEE, 2024. doi:10.1109/ICTAI62512.2024.00012.

[bib.bib18] [18] Christian Schulte, Guido Tack, and Mikael Z Lagerkvist. Modeling and programming with gecode. Schulte, Christian and Tack, Guido and Lagerkvist, Mikael, 1, 2010.

[bib.bib19] [19] Mohamed Siala, Emmanuel Hebrard, and Marie-José Huguet. An optimal arc consistency algorithm for a particular case of sequence constraint. Constraints, 19:30–56, 2014. doi:10.1007/S10601-013-9150-6.

[bib.bib20] [20] Juan Pablo Vielma. Mixed integer linear programming formulation techniques. Siam Review, 57(1):3–57, 2015. doi:10.1137/130915303.

[bib.bib21] [21] S Zein, P Basso, and S Grihon. A constraint satisfaction programming approach for computing manufacturable stacking sequences. Computers & Structures, 136:56–63, 2014.

[bib.bib22] [22] Samih Zein, Benoît Colson, and Stéphane Grihon. A primal-dual backtracking optimization method for blended composite structures. Structural and Multidisciplinary Optimization, 45(5):669–680, 2012.