Extension of Partial Atom-To-Atom Maps: Uniqueness and Algorithms
Abstract
Chemical reaction databases typically report the molecular structures of reactant and product compounds, as well as their stoichiometry, but lack information, in particular, on the correspondence of reactant and product atoms. These atom-to-atom maps (AAM), however, are crucial for applications including chemical synthesis planning in organic chemistry and the analysis of isotope labeling experiments in modern metabolomics. AAMs therefore need to be reconstructed computationally. This situation is aggravated, furthermore, by the fact that chemically correct AAMs are, fundamentally, determined by quantum-mechanical phenomena and thus cannot be reliably computed by solving graph-theoretical optimization problems defined by the reactant and product structures. A viable solution for this problem is to shift the focus into first identifying a partial AAM containing the reaction center, i.e., covering the atoms incident with all bonds that change during a reaction. This then leads to the problem of extending the partial map to the full reaction. The AAM of a reaction is faithfully represented by the Imaginary Transition State (ITS) graph, providing a convenient graph-theoretic framework to address the questions of when and how a partial AAM can be extended. We show that an unique extension exists whenever, and only if, these partial AAMs cover the reaction center. In this case their extension can be computed by solving a constrained graph-isomorphism search between specific subgraphs of ITS graphs. We close by benchmarking different tools for this task.
Keywords and phrases:
atom-to-atom maps, imaginary transition state (ITS) graphs, condensed graph of the reaction (CGR), chemical reaction mechanisms, molecular graphs, metabolic networks, chemical synthesis planning, constrained graph isomorphismFunding:
Marcos E. González Laffitte: Acknowledges financial support from the Federal Ministry of Education and Research of Germany (BMBF) and the Sächsische Staatsministerium für Wissenschaft Kultur und Tourismus in the program Center of Excellence for AI-research “Center for Scalable Data Analytics and Artificial Intelligence Dresden/Leipzig”, project identification number: ScaDS.AI.Copyright and License:
2012 ACM Subject Classification:
Theory of computation Graph algorithms analysis ; Theory of computation Discrete optimizationAcknowledgements:
We want to thank Annachiara Korchmaros for the interesting graph-theoretical questions and conversations on the topic.Editors:
Broňa Brejová and Rob PatroSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction and Motivation
A large part of chemical knowledge is encoded in chemical reactions and formalized as transformations of structural formulae, i.e., of labeled graphs that explicitly represent atoms as vertices and chemical bonds as edges. Large-scale data bases, such as Reaxys® [16] or the United States Patent and Trademark Office (USPTO) database [30], collect this knowledge in the form of some model for a reaction , where and are the disjoint unions of the structural formulae of reactants and products, respectively. The same representation is used for metabolic reactions in the KEGG and EcoCyc databases.
For a wide variety of practical applications, ranging from chemical synthesis planning to the analysis of isotope labeling experiments in metabolic networks, the knowledge of and is insufficient, however. In addition, the exact correspondence of reactant and product atoms is required. This atom-to-atom map (AAM) is usually represented as a bijection between vertex sets of the reactants-graph and the products-graph modeling . The AAM, moreover, preserves atom types and determines the bonds that are formed, broken and conserved in the course of the reaction [25]. Thus, AAMs can also be understood as a summary of the mechanism of a reaction, at least at the level of abstraction defined specified by structure formulas.
The databases introduced above, for example, typically do not provide AAMs together with the reactions, which therefore need to be constructed by computational means. This has turned out to be a non-trivial problem that still remains an area of active research. The main difficulty is that the chemically correct AAM is determined by the ground-truth mechanism of the reaction (or reactions in the case of multi-step transformations which are of particular relevance in enzyme-catalyzed biochemical reactions), which is inherently a quantum-mechanical phenomenon whose outcome is, at best, approximated by heuristic rules such as the Principle of Minimal Chemical Distance [23], geometric rules such as the Principle of Least Nuclear Motion [21], or maximum common subgraph approaches [10]. More recently, machine-learning methods have been devised to complement the shortcomings of the combinatorial methods, see [28] for are recent comparative benchmarking effort.
An alternative for seeking to infer an AAM in a single step, is to divide this task into three potentially easier subproblems: (a) determine the most likely type of the reaction, (b) identify the reaction center(s), i.e., the atoms incident with all bonds that change, and (c) construct the AAMs using the results of (a) and (b) as constraints.
The rationale for this approach is that, fundamentally, reactions are not arbitrary changes of bonds. On the contrary, chemical reactions usually follow specific localized patterns of bond changes and are restricted to particular classes of reactants. In the chemistry literature, such reaction types are often referred to as “name(d) reactions” such as Grignard reaction, Claisen condensation or Friedel–Crafts acylation [27].
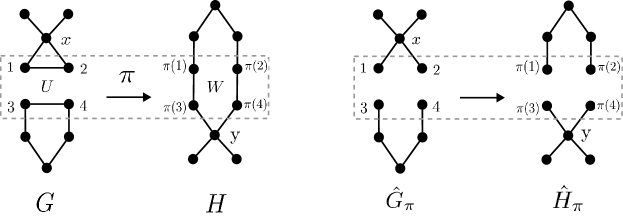
Reaction types can be specified, moreover, by reaction templates describing the parts of the involved molecules that are actually affected and/or necessary for the reaction to take place. A reaction template thus is a pair of pattern graphs, one, in the reactants-graph and the other, , in the products-graph , together with a bijection that establishes the AAM at the level of the patterns. A reaction template is said to explain the reaction if (i) and appear as (are isomorphic to) subgraphs of and , respectively, (ii) the bijection can be extended to an AAM for and , and (iii) all bonds that change during are covered by . Reaction templates therefore contain and typically extend beyond the reaction center. Formally, they can be interpreted as a special case of double pushout graph rewriting rules, see e.g. [8, 2, 3]. Preservation of mass and atom types, i.e., of the number of vertices and their labels, makes it possible to express the necessary theory in terms of graph isomorphisms and induced subgraphs. We therefore forego a description of the category-theoretic formalism of graph transformations for the purposes of this contribution.
Definition 1.
Consider two reactions and , where the latter is endowed with an AAM . Then is a pattern for , if there are subgraph isomorphisms and of the patterns into reactants and products, such that the induced partial atom-to-atom map given by for all , can be extended to an AAM that coincides with on , i.e., for all .
Throughout this contribution we will assume that a reaction and a partial AAM with and are given. In practice, such partial AAMs can be produced, e.g., by learning-based reaction mapping tools [6, 35]. Another source of partial AAM data are the RCLASS data provided by the KEGG database, although in this case extensive processing is required to obtain the partial AAMs explicitly [5]. We therefore do not need to concern ourselves with pattern graphs and and their embeddings and into the graphs and . The mathematical structure of full and partial AAMs has been studied in some details in [25, 26]. A key observation is that AAMs over balanced reactions can be represented equivalently by means of Imaginary Transition State (ITS) graph and its subgraphs. ITS graphs were introduced by Shinsaku Fujita [13] and Wilcox and Levinson [37] for storage and processing of reactions in chemical databases, and later utilized under the name Condensed Graph of the Reaction (CGR) in machine learning applications [22]. The one-to-one correspondence between AAMs and ITS graphs is, therefore, the basis for the graph-theoretical approach to AAMs that we pursue in this contribution.
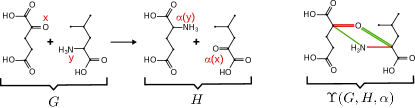
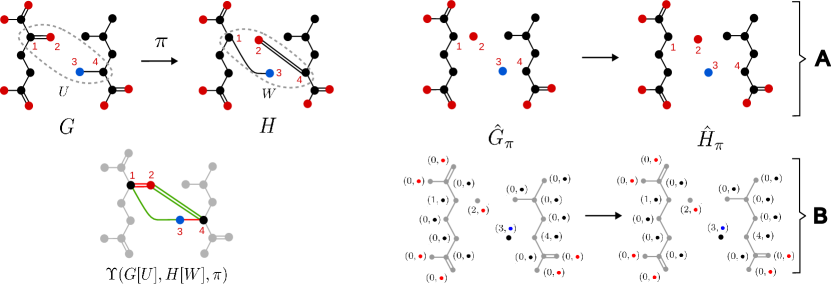
Applications to Bioinformatics of our algorithms, therefore, are strongly dependent on their applications to Organic Chemistry. Figure 1, for example, exhibits the biochemical exchange mechanism, and the corresponding ITS graph, that allows E. coli to recycle and route nitrogen in an efficient way [33]. Studying domain-specific mechanisms such as this one is the focus of separate intended future contributions. In order to elucidate the mechanisms of such reactions, nonetheless, one requires in the first place to address the problem of comparing and extending the associated AAMs in a mathematically-correct fashion. Here we will focus on answering two research questions: (1) when does such extensions of a partial AAM exist? and (2) how can such an extension be computed efficiently?
In the following section we provide the necessary theoretical framework, establishing the equivalence of AAMs and ITS graphs and introducing the remainder graphs. It is shown, moreover, that certain isomorphisms of these remainder graphs are a sufficient condition for the construction of equivalent of AAMs. We then consider reaction centers and their associated partial AAMs. The main result of this section establishes that good partial AAMs are characterized by the existence of a unique stable extension, i.e., extensions preserving the reaction mechanism, that are in turn isomorphisms between remainder graphs, providing, therefore, the basis for our algorithms for the completion of good partial AAMs.
2 Reactions, AAMs and ITS graphs
2.1 Basic Notation
Molecules are modeled as connected, labeled simple graphs with vertices representing atoms and edges corresponding to bonds. We write and for the vertex and edge set of a graph . Atom types and bond types are specified by labeling functions and , respectively, for non-empty and disjoint label sets and . We reserve a special symbol for our construction (Definition 6 below). Charges can be associated as labels to loops. We will not, however, consider this issue explicitly here, hence examples will be simple graphs throughout. For standard terminology on Graph Theory, e.g. adjacency and connectedness, we refer to [19]. Two labeled graphs and are isomorphic if there is a bijection that preserves adjacency as well as vertex and edge labels. A map thus is an isomorphism if: it is bijective, if and only if , for all and for all . We write for the set of all isomorphisms from to , and whenever and are isomorphic. Isomorphisms of to itself are called automorphisms and form an algebraic group denoted when endowed the usual composition of functions. We express the composition of functions and as .
Reactions, denoted as , are pairs of graphs whose connected components represent the reactant and product molecules, respectively. Note that both and may contain multiple copies of isomorphic connected components depending on the stoichiometry of the the reaction. A reaction is balanced if there is an AAM for it, that is, there exists a bijection preserving atom-labels, i.e., for all . Equivalently, is balanced if for each atom type we have , i.e., reactants and products contain the same number of atoms of each type. Consider an AAM for a balanced reaction and . We say that is a reaction edge of induced by , if either , or if whenever . Equally we say that is a reaction edge of induced by if , or provided . A vertex is a reacting vertex (for ) if is incident with a reaction edge in or is incident with a reaction edge in . Analogously, is a reacting vertex (for ) if is incident with a reaction edge in or is incident with a reaction edge in . In particular, therefore, both ends of a reaction edge are reacting vertices.
Definition 2.
Let be an AAM for the balanced reaction . The remainder graph of under , denoted , is the subgraph of obtained by removing all reaction edges of , and preserving all vertex labels and all remaining edge labels. The remainder graph of under is defined analogously.
All non-reaction edges are by construction preserved between and . That is, if is not a reaction edge then and, vice versa, if is not a reaction edge in , then . As an immediate consequence we obtain,
Lemma 3 ([26], Lemma 1).
Every AAM for a balanced reaction is an isomorphism from the remainder graph to the remainder graph .
2.2 Equivalent AAMs and Isomorphic ITS graphs
The problem of determining whether two AAMs and for the same reaction are actually “the same” arises, for example, when comparing the results of different reaction mapping tools, because each tools uses its own graph representation. As a consequence, for a formal treatment of this problem it becomes necessary to compare and given that and , as well as and , respectively, are isomorphic,
Definition 4 ([25]).
Let and be AAMs for, respectively, the balanced reactions and with and . We say that and are equivalent, denoted as , if there exist isomorphisms and such that .
There is a close connection between the AAM and isomorphisms on the remainder graphs that plays a central role, in particular, for Theorem 20, which is the main result supporting the methods of our contribution,
Proposition 5.
Let be an AAM for the balanced reaction and let be an isomorphism from the remainder graph to the remainder graph . If holds for all reacting vertices of , then and are equivalent AAMs for .
Proof.
Included in Appendix A.
The information contained in a balanced reaction and its AAM can be compiled into the Imaginary Transition State (ITS) graph of the reaction by identifying atoms that correspond to each other via . The ITS graphs thus contains the edges of both the product and the educt graph. Both vertices and edges are associated with label pairs that derive from the labels in and . Formally this is,
Definition 6.
Let be a balanced reaction with AAM . An ITS graph of is a graph with vertex set , edge set , vertex-labeling function and edge-labeling function , obtained from by means of a bijection such that
-
(i)
we have if and only if or ;
-
(ii)
each vertex is labeled by the ordered pair ,
-
(iii)
each edge is labeled by the ordered pair determined as follows:
Figure 2 below showcases the construction of an ITS graph. We will use, moreover, the notation and to address the two components of the vertex and edge labels of an arbitrary ITS graphs.
For every balanced reaction with AAM there exists an ITS graph. The construction is not unique, however, because of the arbitrary bijection between the vertices of and the vertices of . We note that the vertices of the ITS graph also bijectively map to since for every there is a unique and , from where . Now we confirm, nonetheless, our intuition that ITS graphs are unique up to isomorphism,
Lemma 7.
Let be the (non-empty) collection of all ITS graphs built for a balanced reaction with AAM and consider a graph . Then if and only if .
Proof.
Included in Appendix A.
Thus it suffices to consider an arbitrary representative ITS from , which we will denote by . In earlier work, moreover, the ITS graph is defined by setting and using the identity map on for , see e.g. [25]. We will denote this (unique) particular representative, that we call canonical ITS graph, by , see Figure 2. The uniqueness of follows immediately from Definition 6. To see this suppose that there exist two such ITS graphs and . Substituting with the identity map on we get from that if and only if for all , and from and it follows, respectively, and .
In [25], we proved the statement of the following Corollary for . With Lemma 7, on the other hand, we can now restate this result for arbitrary representatives,
Corollary 8 ([25], Cor. 1).
Let and be balanced reactions with AAMs and and assume and . Then if and only if holds for any pair of ITS graphs for the two reactions.
Corollary 8 shows that each equivalence class of AAMs for a reaction produces a unique equivalence class of isomorphic ITS graph representations, provided that the AAMs being compared are defined over reactions with isomorphic reactants and products . It is natural to ask whether there exist isomorphic ITS graphs and for reactions with non-isomorphic graphs or . The following result shows that this is indeed not possible,
Proposition 9.
Let and be AAMs for, respectively, two balanced reactions and , and let and be their corresponding ITS representations. Then if and only if , , and .
Proof.
Included in Appendix A.
2.3 Reaction Centers
In Section 2.1 we defined reaction edges and reacting vertices for a reaction with a given AAM . Since , , and are uniquely defined up to graph isomorphisms and equivalence of AAMs by any representative ITS graph , these definitions carry over ITS graphs, i.e., they also have (a version of) reaction edges and reacting vertices. ITS graphs contain, moreover, an isomorphic copy of the remainder graphs and ,
Lemma 10.
Let be an ITS representation of the balanced reaction with AAM and let and be the corresponding bijections that embed and into , i.e., where for as required by Definition 6. Then the following hold,
-
(i)
is a reaction edge in if and only if , and is a reaction edge in if and only if .
-
(ii)
, and thus also , if and only if, and .
Proof.
Included in Appendix A.
We then refer to the edges with unequal labels, i.e., with , simply as reaction edges. Reacting vertices of are thus represented in the ITS graph as the vertices incident with edges that have unequal labels. The reaction center of a reaction comprises all the bonds modified by the electron exchange occurring during the reaction. This notion appeared already in [14, 15, 32] and was used in [20] to classify reaction types. Its formal properties were studied in more detail in [26] and [11].
Definition 11.
Let be an ITS representation of the balanced reaction with AAM . The reaction center is the subgraph of comprising all the reaction edges and reacting vertices.
It follows immediately from Prop. 9 that whenever , , and . The converse statement, however, is not true in general. We show examples about this in [26], of graphs with isomorphic reaction centers, and with but (Fig. 8 in [26]), and with and but (Fig. 10 in [26]). We will write, moreover, for the reaction center of the canonical representation of the triple . It is worth mentioning that in [26] we considered the connectedness of these graphs. Though in general the connectedness of an ITS graph does not guarantee the connectedness of its reaction center or vice versa (see Figure 2 of [26]), we will, in practice, restrict ourselves to single-step reactions, which have connected reaction centers, i.e., a disconnected reaction center models two independent reactions. The following result, therefore, will also be of relevance for our algorithmic approach:
Lemma 12 ([26], Lemma 2).
Let be an AAM for a balanced reaction . If is a connected graph, then every connected component of and contains at least one reacting vertex.
2.4 Partial AAMs and their Partial ITS graphs
Theoretically speaking, both matches and of a reaction template, as in Definition 1, generally provide only a partial AAM. This is also the case, in practice, of computational mapping tools such as LocalMapper [6], which can focus on only determining a most plausible reaction center and necessary adjacent context.
Definition 13.
Let be a reaction. A partial AAM is a bijection , for two subsets and , which preserves vertex labels, i.e., such that for all .
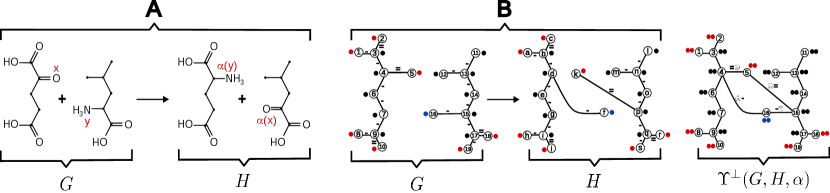
Given a reaction and a partial AAM , it is immediate that the ITS graph , together, in particular, with the canonical graphs and , are all well-defined, see Figure 3 for an example.
Definition 14.
Let be a balanced reaction and let with and be a partial AAM. Then an AAM is said to be an extension of , or to extend , if for all .
As noted in [26, Obs. 3], every partial AAM for has an extension . Moreover, it follows directly from the definition that the partial ITS graph representing is isomorphic to the subgraph of the canonical ITS graph of induced by , i.e., . This isomorphism, furthermore, becomes the identity for the respective canonical ITS graphs, while for the canonical reaction centers we get . In general, therefore, will not contain all reaction edges. For many application scenarios, in particular the ones mentioned in the introduction, we do expect this to be the case. It is of interest, therefore, to determine whether a partial AAM, and thus its corresponding partial ITS graphs, already contains all reaction edges.
Definition 15.
A partial AAM with and for a balanced reaction is said to be a good partial AAM, if there is an extension of such that .
In other words, is a good partial reaction map for a balanced reaction if and only if there is an extension of , such that the induced subgraph of the canonical ITS graph, contains all reaction edges of . In this case we call a stable extension of . Recall that and denote the remainder graphs obtained from and with respect to a full AAM (see Definition 2). In order to better understand stable extensions we need to consider, additionally, the remainder graphs and induced by , preserving vertex and edge labels of and , but obtained by removing from them, respectively, those reaction edges induced by for and , i.e., edges such that , or but with , and edges with , or such that but with . Consider an arbitrary extension of . Clearly and . Moreover, we have
Observation 16.
Let be an arbitrary extension of a partial AAM for a balanced reaction . Then, and .
Based on this simple observation, the following two results strengthen the connection between the remainder graphs induced by full and partial AAMs:
Lemma 17.
Let be a balanced reaction and with and be a partial AAM. Consider an extension of . Then, is a good partial AAM with stable extension , if and only if, and .
Proof.
Included in Appendix A.
Lemma 18.
Let be a balanced reaction and with and be a partial AAM. Consider an extension of . Then, is an isomorphism from to , if and only if, is a good partial AAM with stable extension .
Proof.
Included in Appendix A.
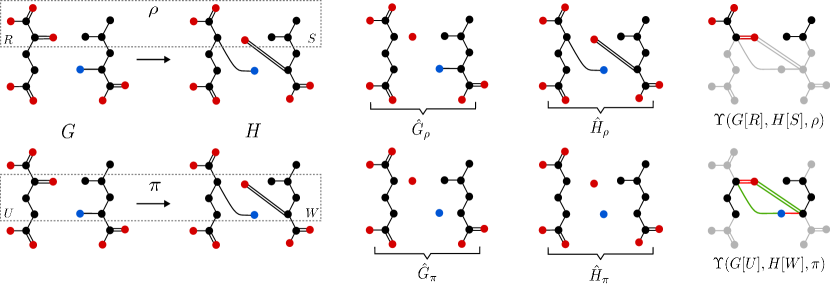
The hypothesis of Lemma 18 requires the isomorphism between the remainder graphs and to be an extension of . The existence of an arbitrary isomorphism between and indeed is not sufficient for the existence of a stable extension for , see Figure 7 in Appendix B. With Lemmas 17 and 18, moreover, we recover the following results that we originally stated in [26, Prop. 1]:
Proposition 19.
Let be a partial AAM for a balanced reaction and an extension of . The following statements are equivalent,
-
(i)
is a good partial AAM and is a stable extension of ,
-
(ii)
and ,
-
(iii)
.
2.5 Uniqueness of Stable Extensions
Good partial AAMs can have multiple non-identical stable extensions. Prop. 19, on the other hand, implies that all of them are isomorphisms between the remainder graphs and .
Theorem 20.
Let be a good partial AAM for a balanced reaction and let and be two stable extensions of . Then .
Proof.
Included in Appendix A.
Since all stable extensions of are equivalent, their ITS representations are isomorphic,
Corollary 21.
Let be a good partial AAM for a balanced reaction and let and be two stable extensions of . Then .
A good partial atom map for a balanced reaction, therefore, uniquely determines the ITS graph of the full AAM for the reaction, up to graph isomorphism.
3 Algorithms for Completing Good AAMs over Balanced Reactions
Conceptually, Definition 15 implies that the existence of a stable extension for a partial map over a reaction ensures that already provides all necessary information about the reaction mechanism of . A bad partial AAM , in contrast, fails to faithfully disclose the electron bookkeeping fundamental for understanding . The characterization of stable extensions as isomorphisms of the reminder graphs and in Proposition 19, on the other hand, suggests to employ modified versions of algorithms for isomorphism search in order to test the existence of a stable extension, and thus the goodness of , and to retrieve such extensions whenever they exist.
From a theoretical point of view, this stable extension problem can be solved efficiently for chemical graphs. To see this, we note that the bounded valency of atoms implies that graphs that represent molecules must have bounded degree. As an immediate consequence ITS graphs also have bounded degree. A classical result establishes that isomorphisms of graphs with bounded degree can be computed in polynomial time [31], although algorithms following this approach are not competitive in practice. For recent progress we refer to [17]. No implementations of these polynomial-time algorithms seem to have become available, however. Hence we have to resort to general purpose algorithms for graph isomorphism. This situation conveys, furthermore, the relevance of the uniqueness of stable extensions of good partial AAMs in Theorem 20, given that these depend, therefore, on the existence of one and only one of such constrained isomorphisms and are unambiguously determined by it.
We address the stable extension problem through three algorithmic approaches: (1) an anchored isomorphism search, (2) a relabeling-and-isomorphism strategy, and (3) an ILP approach. In [26] we devised said ILP formulation based on Lemma 3, and here we recapitulate it in order to benchmark it against the other methods. As shown later, the graph-based isomorphism searches perform better than the ILP in practice. Nonetheless, Theorem 20 implies that our methodologies are all mathematically equivalent, i.e., they return the same stable extension (up to equivalence of AAMs), whenever it exists.
Anchored isomorphism tests.
Conceptually these constitute a variant within the VF2-family of algorithms designed for the (sub-)graph isomorphism problem. A detailed formulation of the VF2 algorithm can be found in [7]. This class of algorithms operates by progressively extending a candidate map for an isomorphism for arbitrary input graphs and . In each step, an ordered pair called a match, with and , is added to a collection portraying the vertex , therefore, as the image of under a prototype for . Later, if is added to , further candidate pairs to extend the map are then selected, either from the sets of unmatched neighbors of and , called terminal sets, or arbitrarily selected from the remaining unmatched vertices. This last case is specifically designed to process disconnected graphs, since it allows the selection of vertices from distinct components once the terminal sets are exhausted.
Though such progressive procedure was originally designed as a recursive traversal, more recent variations construct the match set in an iterative manner [1].
The extension of depends on evaluating the syntactic feasibility i.e., a one-to-one correspondence of the edges connecting and respectively, to the vertices already included in , as well as the semantic feasibility. The latter evaluates that and have the same vertex-labels, and that corresponding edges incident with them have compatible edge-labels. In this way, whenever the VF2 finds that all available candidate pairs are unfeasible for extending a current set of matches , the algorithm backtracks by removing from the last added match, and then testing other alternative candidate pairs.
This progressive exploration behavior of available matches is ideal for our anchored isomorphism search, of which we include a high-level description in Algorithm 1. Given a partial map , moreover, for a balanced reaction , the collection of pairs with , actually constitutes an initial state for the set described before. In other words, since an isomorphism between the reminder graphs and , necessarily coincides with on all reacting vertices if it is a (stable) extension of , the set , prepared in lines 8 to 10 of Algorithm 1, therefore acts as an anchor for seed the VF2 routine. This seed is then expanded by passing it to a further call to a regular VF2 routine in line 12.
By definition the reaction center of is composed of unmatchable edges, that is, the reaction edges in cannot be matched by the VF2 with edges in , and similarly, reaction edges in will have no matching edge in , i.e., these edges cannot satisfy either one or both feasibility tests of the VF2. Consequently, we remove the reaction edges in a preprocessing step in line 6 of our algorithm. We remove, moreover, all edges whose ends are both reacting vertices, simplifying the search even further whenever possible.
The remainder graphs and obtained after removing all reaction edges edges may be disconnected. As mentioned in Subsection 2.3, we are interested in applying Algorithm 1 only over balanced single-step reactions producing connected ITS graphs. Thus Lemma 12 implies that, even under such conditions, every connected component of and contains at least one reacting vertex. Hence all non-reacting vertices in and remain, in general, reachable during the progressive expansion with the VF2 through the terminal sets. This implies a reduction in complexity of the search space, in particular, when processing molecular graphs, by avoiding the exhaustive evaluation of trivial or non-informative matches.
Publicly available implementations of the VF2 algorithm, such as the one from the Python package NetworkX [18], do not provide default options to handle the initialization of a search state with an anchor map, as required by line 9 of Algorithm 1. We opted, therefore, to develop a custom implementation of this anchored search. For this we made use, in particular, of the Cython language [4], which allows the implementation of C and C++ data structures through a Python-like syntax, and facilitates the back-and-ford conversion of these data containers and data types, respectively, with Python native objects and types.
Our implementation is available as the routine search_stable_extension, inside the Python package GranMapache (GRAphs-and-Networks MAPping Applications with Cython and HEuristics), in the repository: https://github.com/MarcosLaffitte/GranMapache, where we provide diverse functionalities to address problems related to mappings between graphs.
Relabeling-and-isomorphism strategy.
Throughout this contribution, except for a few cases, e.g. for the definition of ITS graphs, we have considered vertex labels to represent atom types. Formally speaking, nonetheless, these labels embody the broader notion of comparability classes of vertices, i.e., two vertices are comparable with each other if and only if they have the same label.
Here we device a relabeling strategy, condensed in Algorithm 2, that offers an equivalent, but simpler alternative, to the anchored isomorphism approach described earlier. To illustrate this, consider a balanced reaction with a partial AAM with and , and four vertices and . Suppose that and , but and . Assume, moreover, that there exists a stable extension of such that . Thus, any algorithm capable of retrieving as an isomorphism between the remainder graphs and , has to match again and without admitting for them any other matches and must be able to recognize and as comparable vertices. Clearly Algorithm 1 satisfies these conditions.
The same result, however, can be achieved by creating copies of and with new labeling functions, enforcing comparability constrains with these new labels. By slight abuse of notation we write for the labeling function on the copy of , and for the copy of . This labels are described formally in lines 6 and 7 of Algorithm 2. With them, for the example above, the vertices matched by are now labeled by ordered pairs for a unique integer , while remaining vertices are assigned a label , thus satisfying as well conditions and from before.
Once the new labeling functions are built, we only need to create the copies of and as stated in line 11 of Algorithm 2, and finally run for these graphs an arbitrary isomorphism routine handling labeled graphs, as in line 13, in order to recover the stable extension . An example of the application of this algorithm is shown in Figure 8 in Appendix B.
We implemented this method in Python, making use of the
NetworkX [18] package for the handling of
graphs and their labeling functions. This implementation is also
available in the repository GranMapache, in a directory
dedicated to examples of usage of our functionalities:
https://github.com/MarcosLaffitte/GranMapache/tree/main/examples/Stable_Extensions.
Integer Linerar Programming formulation.
Finally, Algorithm 3 describes, as a pipeline, the
formulation of the Integer Linear Programming (ILP) search for stable
extensions, that we originally proposed in
[26]. For this we made use of the
CBC solver 2.10.3 [29], made in C++
and callable from Python.
4 Benchmarking, Empirical Results and Discussion
We evaluate the methodologies discussed in the previous section over two sets of empirical data, one of real chemical reactions with partial AAMs covering exactly the ground-truth reacting vertices, and another set consisting of random graphs with AAMs inducing connected ITS graphs with connected reaction centers and an increasing number of nodes and edges.
Four different implementations are evaluated: (GM) our custom anchored isomorphism search from our package GranMapache [24] implementing Algorithm 1, two relabeling-and-isomorphism variants implementing Algorithm 2 from which one (RB1) uses the VF2 isomorphism function [9] from NetworkX and another (RB2) uses a custom isomorphism function from GranMapache, and lastly (ILP) implementing the ILP formulation in Algorithm 3 from the package AAMutils introduced in previous work [26].
Stable extensions over real chemical reactions
The reactions were retrieved from USPTO_50K corpus of 50,016 reactions [36]. Each reaction was rebalanced with the tool SynRBL [34] and preprocessed with the SynTemp pipeline [35], which enforces ensemble consistency, resolves hydrogen ambiguity and validates that the partial maps are good. The preprocessing stage yield 39,732 rebalanced and consistent reactions with full AAMs, good partial AAMs derived from the full ones, and the corresponding ITS graphs. We process the mapped reactions in SMILES format, via another custom tool SynKit for the methods GM, RB1 and RB2, and with the AAMutils API [26] for the ILP.
The 39,732 reactions were processed five times with each of the four methods. Here we report the average running time of these procedures over this data set. From Theorem 20 and Corollary 21, moreover, it follows that all possible full AAMs recovered by our algorithms are to be equivalent and thus produce isomorphic ITS graphs. As a back-up test for our implementations, therefore, we corroborate the successful recovery of the full AAMs by means of the isomorphism of the initial and recovered ITS graphs. The graph-based methods GM, RB1 and RB2 were able to recover 100% of the ground AAMs of the 39,732 reactions, while the ILP retrieved the AAMs successfully in 99.48% of the reactions. The few ILP mismatches are attributable to discrepancies in the canonicalization SMILES during the conversion of the output of reaction-mapping tools to the graph representations used here.
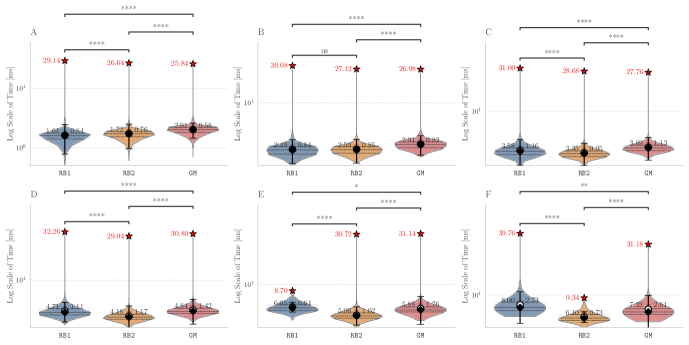
Figure 4 below shows the distributions of the average running time per reaction for each method, and with respect to each of the five repetitions. The numerical values of the average running times per trial are summarized in Table 1 in Appendix B. All benchmarks were run under Python 3.11 on a 12-core Intel Core i7-8700 @ 3.20 GHz, Fedora 37. The programs made for this analysis can be found in https://github.com/TieuLongPhan/PartialAAMs.
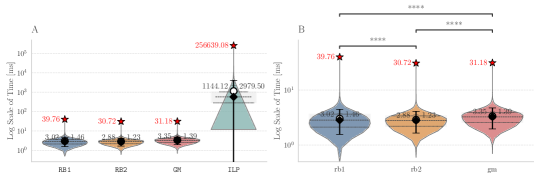
While the ILP average running time exceeds second, all graph-based methods take only a few milliseconds (). Among these, RB2 is the fastest on average for processing the molecular graphs ( ms), followed by RB1 ( ms) and GM ( ms). The small differences of to ms attained on this set of real molecular graphs, and disclosed by Figure 4, are attributable to the time required by the custom implementations RB2 and GM to convert native Python objects into C++ containers and vice versa, carried by the Cython functions on run time when called by other external Python scripts.
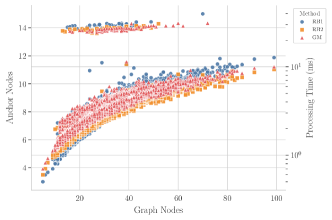
Tests for scalability were carried by analyzing the obtained running times while varying the number of vertices in the input molecular graphs. The distribution of the reactions with each number of vertices is shown in Figure 9A in Appendix B. On the other hand, Figure 10 shows that for small graphs (less than 30 vertices), RB1 is faster than RB2 and GM, while beyond the 30-vertices threshold RB2 scales more favorably. Moreover, GM surpasses RB1 on larger graphs, suggesting that the custom implementations RB2 and GM offer an scalability advantage with respect to the amount of vertices in the input graphs. The small discrepancies in the running time of RB2 and GM is further explained by the implementation of different heuristics for building the total order required by VF2-like approaches. The trial and evaluation of such heuristics is out of the scope of this contribution.
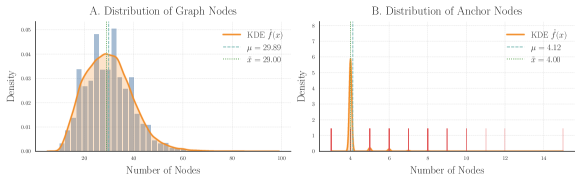
Another scalability analysis was carried with respect to the proportion of reacting vertices vs total vertices in the ITS graph of each reaction. See the distribution of such proportions in Figure 9B. The scatter plot in Figure 5 below, together with Figures 11 and 12 in Appendix B, suggest that all graph-based methods perform best for reactions with bigger proportions of reacting vertices from the total amount of vertices. This is expected since smaller proportions of reacting vertices lead to a bigger search space for the VF2-based approaches.
Stable extensions over random graphs
We implemented the generation and analysis of random ITS graphs in Cython making use, in particular, of NetworkX [18]. All scripts for this analysis can be found in the GranMapache repository [24], and were run under Python 3.11 on an 8-core 11th Gen Intel Core i7-1165G7 @ 2.80GHz, Lenovo ThinkPad E15 Gen 2 with 16GB and Ubuntu 22.04.
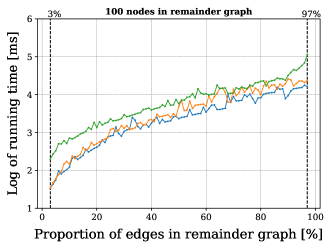
For this analysis we produced connected ITS graphs with connected reaction centers. These graphs were built with an increasing amounts of edges outside the reaction center so as to test the performance of our methods over (simple) labeled graphs with varying density, i.e., with an increasing proportion of existing edges in the graph with respect to the theoretical maximum. Based on this we built 5 data sets of such graphs having each a different number of non-reacting vertices, specifically for 100, 125, 150, 175 and 200 nodes.
Within each data set we built 10 ITS graphs per each percentage-point for the percentage of edges outside the reaction center, starting at 3% and up to 97%. This leads to a total of 4,750 randomly generated ITS graphs conforming 1.6 GB of labeled graphs serialized and stored with the package Pickle [12] from Python. The interval 3 - 97 % was chosen under theoretical reasons for the graphs to be connected and for them to have the exact specified density. All the graphs were produced with a (randomly generated) connected reaction center of 15 vertices and 20 edges, in addition to the specified number of non-reacting vertices.
The pairs of labels needed for vertices and edges of these ITS graphs were chosen uniformly at random from a set of 6 integer labels for the vertices, and 3 labels for the edges. The labels in the reaction center, moreover, were produced by selecting the source of the (reaction) edge uniformly at random from the reactants graph, the products graph, or both of them. Finally, we tested the extension of the partial map covering exactly the reaction center.
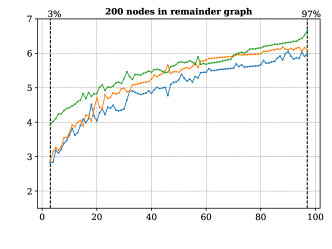
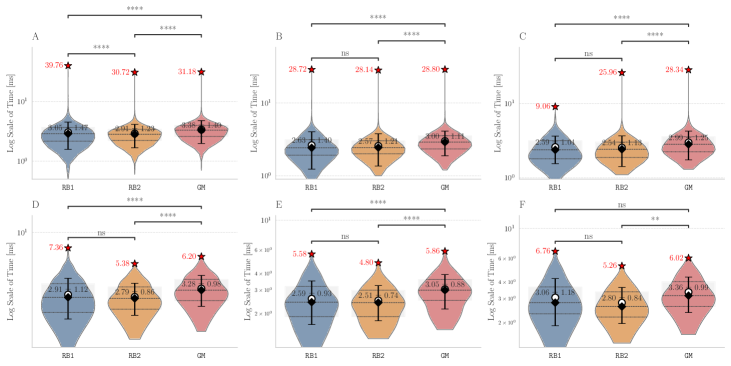
For this we made use of the graph-based methods RB1, RB2 and GM, but omitted the ILP approach due to its comparably slower performance. All methods successfully extended the reaction center in all cases. The average running times for the analysis over the graphs with 100 non-reacting vertices are summarized in Figure 6, while the results for graphs with 125-200 vertices are included in Figure 13 in Appendix B. These show a consistent hierarchical performance, where GM completes the analysis faster, followed by RB2, and then RB1. This is consistent with the observations over real reactions, where molecules have at most 98 vertices and 108 edges and thus density . This suggests again that the custom methods GM and RB2 are appropriate for dealing with bigger graphs, while RB1 proves to be comparably efficient for processing smaller and more sparse graphs.
5 Concluding Remarks
In this contribution we first gave a comprehensive mathematical description of the relationships between good partial AAMs and full descriptions of the underlying reaction. In particular, we showed that good partial AAMs, i.e., those that cover the reaction center, are exactly the partial AAMs that have unique extensions constituting isomorphisms of the remainder graphs of the reactant and product sides. These results extend our work in [26] by establishing equivalent characterizations of good AAMs. This shows that the practical problem of determining whether a partial AAM is good and, if so, retrieving its unique stable extension, is equivalent to a restricted graph isomorphism problem. Based on these theoretical insights we benchmark different implementations of graph isomorphism tests. Not all such methods lend themselves to incorporate additional constraints implied by the partial AAM. In VF2-like methods, these constitute an immutable set of initial matches. Canonization-based methods can be used after modifying the vertex labels, such that the two vertices of the corresponding pairs are assigned unique matching labels. For comparison we also consider an ILP formulation. Benchmarking simulations show that the completion is feasible for graphs relevant to applications in chemistry. Moreover, we observe that dedicated graph isomorphism algorithms are much more efficient than the ILP.
In contrast to graph-based methods, however, the ILP can potentially be used for bad partial AAMs, for which the plausible extensions are, of course, no longer isomorphisms between and , and are determined by minimizing the number of necessary reaction edges in an AAM extending [26]. This is of practical importance since most reaction mapping tools do not predict correspondences between hydrogen atoms, though these often take part in the reactions and hence are reactive vertices. A further extension to the – usually bad – partial AAMs on unbalanced reactions remains an open problem for future research.
References
- [1] Alpár Alpár Jüttner and Péter Madarasi. VF2++ – An improved subgraph isomorphism algorithm. Discr. Appl. Math., 242:69–81, 2018. doi:10.1016/j.dam.2018.02.018.
- [2] Jakob L Andersen, Christoph Flamm, Daniel Merkle, and Peter F. Stadler. Inferring chemical reaction patterns using graph grammar rule composition. J. Syst. Chem., 4:4, 2013. doi:10.1186/1759-2208-4-4.
- [3] Jakob Lykke Andersen, Christoph Flamm, Daniel Merkle, and Peter F. Stadler. A software package for chemically inspired graph transformation. In Rachid Echahed and Mark Minas, editors, Graph Transformation, ICGT 2016, volume 9761 of Lecture Notes Comp. Sci., pages 73–88, Berlin, Heidelberg, D, 2016. Springer Verlag. doi:10.1007/978-3-319-40530-8_5.
- [4] Stefan Behnel, Robert Bradshaw, Craig Citro, Lisandro Dalcin, Dag Sverre Seljebotn, and Kurt Smith. Cython: The best of both worlds. Computing in Science Engineering, 13(2):31–39, March 2011. doi:10.1109/MCSE.2010.118.
- [5] Nora Beier, Thomas Gatter, Jakob Lykke Andersen, and Peter F. Stadler. Computing double-pushout graph transformation rules and atom-to-atom maps from KEGG RCLASS data, 2025. submitted to Alg. Mol. Biol. doi:10.21203/rs.3.rs-6765982/v1.
- [6] Shuan Chen, Sunggi An, Ramil Babazade, and Yousung Jung. Precise atom-to-atom mapping for organic reactions via human-in-the-loop machine learning. Nature Communications, 15:2250, 2024. doi:10.1038/s41467-024-46364-y.
- [7] Luigi P. Cordella, Pasquale Foggia, Carlo Sansone, and Mario Vento. A (sub)graph isomorphism algorithm for matching large graphs. IEEE Trans. Pattern Analysis Machine Intelligence, 26:1367–1372, 2004. doi:10.1109/TPAMI.2004.75.
- [8] Andrea Corradini, Ugo Montanari, Francesca Rossi, Hartmut Ehrig, Reiko Heckel, and Michael Löwe. Algebraic approaches to graph transformation–part i: Basic concepts and double pushout approach. In Handbook Of Graph Grammars And Computing By Graph Transformation: Volume 1: Foundations, pages 163–245. World Scientific, 1997.
- [9] NetworkX Documentation. NetworkX 3.4.2: VF2 Algorithm. https://networkx.org/documentation/stable/reference/algorithms/isomorphism.vf2.html.
- [10] Hans-Christian Ehrlich and Matthias Rarey. Maximum common subgraph isomorphism algorithms and their applications in molecular science: a review. Wiley Interdisciplinary Reviews: Computational Molecular Science, 1(1):68–79, 2011.
- [11] Christoph Flamm, Stefan Müller, and Peter F. Stadler. Every atom-atom map for neutral molecules can be explained by electron pair pushing diagrams. Discr. Math. Chem., 2024. in press; arxiv doi:. doi:10.48550/arXiv.2311.13492.
- [12] Python Software Foundation. Pickle package for serialization of Python objects., 2025. Accessed: 2025-06-22. URL: https://docs.python.org/3/library/pickle.html.
- [13] Shinsaku Fujita. Description of organic reactions based on imaginary transition structures. 1. Introduction of new concepts. J. Chem. Inf. Comput. Sci., 26:205–212, 1986. doi:10.1021/ci00052a009.
- [14] Shinsaku Fujita. Imaginary transition structures. a novel approach to computer oriented representation of organic reactions. J. Synth. Org. Chem. Japan, 47(5):396–412, 1989. doi:10.5059/yukigoseikyokaishi.47.396.
- [15] Kimito Funatsu, Tomoaki Endo, Norio Kotera, and Shin-Ichi Sasaki. Automatic recognition of reaction site in organic chemical reactions. Tetrahedron Comput Methodology, 1(1):53–69, 1988. doi:10.1016/0898-5529(88)90008-5.
- [16] Jonathan Goodman. Computer software review: Reaxys. J. Chem. Inf. Model., 49(12):2897–2898, 2009. doi:10.1021/ci900437n.
- [17] Martin Grohe, Daniel Neuen, and Pascal Schweitzer. A faster isomorphism test for graphs of small degree. SIAM J. Computing, 52, 2023. doi:10.1137/19M1245293.
- [18] Aric A. Hagberg, Daniel A. Schult, and Pieter J. Swart. Exploring network structure, dynamics, and function using NetworkX. In Gaël Varoquaux, Travis Vaught, and Jarrod Millman, editors, Proceedings of the 7th Python in Science Conference, pages 11–15, Pasadena, CA USA, 2008.
- [19] Frank Harary. Graph theory. CRC Press, FL, USA, 2018.
- [20] James B. Hendrickson. Comprehensive system for classification and nomenclature of organic reactions. J. Chem. Inf. Comput. Sci., 37(5):852–860, 1997. doi:10.1021/ci970040v.
- [21] J. Hine. The principle of least nuclear motion. Advances in Physical Organic Chemistry, 15:1–61, 1977. doi:10.1016/S0065-3160(08)60117-3.
- [22] Frank Hoonakker, Nicolas Lachiche, Alexandre Varnek, and Alain Wagner. A representation to apply usual data mining techniques to chemical reactions – illustration on the rate constant of reactions in water. Int. J. Artif. Intelligence Tools, 20:253–270, 2011. doi:10.1142/S0218213011000140.
- [23] Clemens Jochum, Johann Gasteiger, and Ivar Ugi. The principle of minimum chemical distance (PMCD). Ang. Chem. Intl. Ed., 19(7):495–505, 1980. doi:10.1002/anie.198004953.
- [24] Marcos E. González Laffitte. GranMapache: GRAphs-and-Networks MAPping Applications with Cython and HEuristics). https://github.com/MarcosLaffitte/GranMapache.
- [25] Marcos E. González Laffitte, Nora Beier, Nico Domschke, and Peter F. Stadler. Comparison of Atom Maps. MATCH Commun. Math. Comput. Chem., 90:75–102, 2023. doi:10.46793/match.90-1.075G.
- [26] Marcos E. González Laffitte, Klaus Weinbauer, Tieu-Long Phan, Nora Beier, Nico Domschke, Christoph Flamm, Thomas Gatter, Daniel Merkle, and Peter F. Stadler. Partial imaginary transition state (ITS) graphs: A formal framework for research and analysis of atom-to-atom maps of unbalanced chemical reactions and their completions. MDPI Symmetry, 16(9), 2024. doi:10.3390/sym16091217.
- [27] Jie Jack Li. Name Reactions: A Collection of Detailed Reaction Mechanisms and Synthetic Applications. Springer, 2025.
- [28] Arkadii Lin, Natalia Dyubankova, Timur I Madzhidov, Ramil I Nugmanov, Jonas Verhoeven, Timur R Gimadiev, Valentina A Afonina, Zarina Ibragimova, Assima Rakhimbekova, Pavel Sidorov, et al. Atom-to-atom mapping: a benchmarking study of popular mapping algorithms and consensus strategies. Molecular Informatics, 41(4):2100138, 2022.
- [29] Jeffrey T. Linderoth and Ted K. Ralphs. Noncommercial software for mixed-integer linear programming. In John Karlof, editor, Integer programming: theory and practice, pages 253–303. CRC Press, 2005.
- [30] Daniel Mark Lowe. Extraction of chemical structures and reactions from the literature. Technical report, Apollo – University of Cambridge Repository, 2012. doi:10.17863/CAM.16293.
- [31] Eugene M. Luks. Isomorphism of graphs of bounded valence can be tested in polynomial time. J. Comp. Syst. Sci., 25:42–65, 1982. doi:10.1016/0022-0000(82)90009-5.
- [32] Michael F. Lynch and Peter Willett. The automatic detection of chemical reaction sites. J Chem Inf Comput Sci, 18:154–159, 1978. doi:10.1021/ci60015a009.
- [33] Alfred J. Meijer, Wouter H. Lamers, and Robert A. F. M. Chamuleau. Nitrogen metabolism and ornithine cycle function. Physiological Reviews, 70(3):701–748, 1990. PMID: 2194222. doi:10.1152/physrev.1990.70.3.701.
- [34] Tieu-Long Phan, Klaus Weinbauer, Thomas Gärtner, Daniel Merkle, Jakob L Andersen, Rolf Fagerberg, and Peter F Stadler. Reaction rebalancing: a novel approach to curating reaction databases. Journal of Cheminformatics, 16(1):82, 2024. doi:10.1186/S13321-024-00875-4.
- [35] Tieu-Long Phan, Klaus Weinbauer, Marcos E. González Laffitte, Yingjie Pan, Daniel Merkle, Jakob L. Andersen, Rolf Fagerberg, Christoph Flamm, and Peter F. Stadler. SynTemp: Efficient Extraction of Graph-Based Reaction Rules from Large-Scale Reaction Databases. Journal of Chemical Information and Modeling, 65(6):1549–9596, 2025. doi:10.1021/acs.jcim.4c01795.
- [36] Nadine Schneider, Nikolaus Stiefl, and Gregory A Landrum. What’s what: The (nearly) definitive guide to reaction role assignment. Journal of chemical information and modeling, 56(12):2336–2346, 2016. doi:10.1021/ACS.JCIM.6B00564.
- [37] Craig S. Wilcox and Robert A. Levinson. A self-organized knowledge base for recall, design, and discovery in organic chemistry. In T. H. Pierce and B. A. Hohne, editors, Artificial Intelligence Applications in Chemistry, volume 306 of Am. Chem. Soc. symposium series, chapter 18, pages 209–230. American Chemical Society, Washington, DC, 1986. doi:10.1021/bk-1986-0306.ch018.
Appendix A Appendix: Mathematical Results and Proofs
Proposition 5.
[Restated, see original statement.]
Let be an AAM for the balanced reaction and let be an isomorphism from the remainder graph to the remainder graph . If holds for all reacting vertices of , then and are equivalent AAMs for .
Proof.
To prove the equivalence of and it suffices to show that . To see this note first that by Lemma 3 we have . Thus by inverses and composition of isomorphisms it follows and therefore, by definition, we get for all . Consider now . Then either or is a reaction edge of . In the first case, from follows that (A1) if and only if , and again . Suppose, on the other hand, that is a reaction edge, i.e., . Then, both and are reacting vertices, and by hypothesis and , or equivalently and . Thus formally we also have (A2) if and only if and similarly . In this way, from (A1) and (A2) we get if and only if , i.e., preserves adjacency in , and since it also preserves vertex and edge labels we have . Therefore, by setting and for the identity automorphism , we get and thus , proving the proposition.
Lemma 7.
[Restated, see original statement.]
Let be the (non-empty) collection of all ITS graphs built for a balanced reaction with AAM and consider a graph . Then if and only if .
Proof.
Suppose first that . Let and be the bijections required by Definition 6 for and , respectively.
Consider two arbitrary vertices and in and their preimages and in . Condition in the definition can be restated for and as , if and only if, or . At the same time, for two vertices it holds , if and only if, or . From these statements it follows that if and only if , i.e., the bijection preserves adjacency between and . We see, moreover, that , thus the map preserves vertex labels. Similarly, and without loss of generality, we have
that is, also preserves edge labels and is, therefore, an isomorphism from to , i.e., proving the forward direction.
Suppose, on the other hand, that there exist an isomorphism from to . Given that preserves adjacency, vertex-labels and edge-labels, it follows that: (i) , if and only if, , and equivalently, or , also (ii) , and lastly (iii) . Thus satisfies all the conditions required by Definition 6 for and therefore , which proves the converse statement.
Proposition 9.
[Restated, see original statement.]
Let and be AAMs for, respectively, two balanced reactions and , and let and be their corresponding ITS representations. Then if and only if , , and .
Proof.
Note that by Lemma 7 and by the transitivity of the isomorphism relation , from , it follows that holds for the canonical ITS representations of and of , having and , and for which the identity maps over and over satisfy Definition 6, respectively. Consider an isomorphism , and note that this is also a bijection . Thus when applying condition in Definition 6 and given that preserves adjacency between and it follows that, or , if and only if, or . This suggests that the bijections and are the required isomorphisms and . To actually prove this, note first that under all labels are preserved component-wise, i.e., for any vertices we have, (P1) and (P2) . For and , (P1) implies , while from (P2) we get , which by condition in the definition can only happen if preserves adjacency, i.e., if and only if , also yielding when the edges are present in these graphs. Thus preserves adjacency, vertex labels and edge labels, and therefore . Similarly for and , (P1) implies , which we can rewrite as for , thus preserves vertex labels. Since from (P2) it holds , we have , and equivalently for and in , whenever the respective edges are present, while in general, from this together with condition in Definition 6, we get again if and only if , or equivalently, if and only if . This shows that preserves adjacency, and vertex and edge labels, and thus . Lastly, since and hold, the hypothesis , together with Corollary 8, now implies also that . The converse statement follows from Corollary 8.
Lemma 10.
[Restated, see original statement.]
Let be an ITS representation of the balanced reaction with AAM and let and be the corresponding bijections that embed and into , i.e., where for as required by Definition 6. Then the following hold,
-
(i)
is a reaction edge in if and only if , and is a reaction edge in if and only if .
-
(ii)
, and thus also , if and only if, and .
Proof.
Set for as in Definition 6. This implies that if and only if or . The definition of the edge labels and the bijection now yield . Recall that is a reaction edge in if either, in which case , or and thus . In either case Definition 6 yields . The same argument can be made for edges . The second statement now follows directly from Definition 2 since the remainder graph contains exactly the edges with and hence .
Lemma 17.
[Restated, see original statement.]
Let be a balanced reaction and with and be a partial AAM. Consider an extension of . Then, is a good partial AAM with stable extension , if and only if, and .
Proof.
Suppose first that is a good partial AAM with stable extension . Thus, by definition we have . Consider then a reaction edge of induced by . By taking, in Lemma 10, the bijection (resp. ) to be the identity mapping on , it follows that is an edge in with , and therefore .
Then is also a reaction edge of , and by another application of Lemma 10 we conclude that is also a reaction edge of . By contraposition, moreover, this implies that if , then , proving the contention , which together with Observation 16, yields and thus . By similar arguments, for a reaction edge of induced by it follows that is an edge in with . Then is also an edge in , implying that . But and coincide for all vertices , and so and , that is, is an edge in with and thus, applying Lemma 10, we see that is also a reaction edge of induced by . By contraposition this also proves the inclusion . Observation 16 implies , proving the forward direction.
For the proof of the converse statement note that the hypotheses and , imply that and induce the same reaction edges for each and , that is, (R1) is a reaction edge of w.r.t if and only if is a reaction edge of w.r.t and similarly (R2) is a reaction edge of w.r.t if and only if is a reaction edge of w.r.t .
This implies, by definition of the remainder graphs, that the vertices are all in , and thus and coincide for each of the two ends of every reaction edge of and/or . Thus, denoting and , through Lemma 10 condition (R1) implies (R1’) given , is a reaction edge of if and only if is a reaction edge of , i.e., is labeled by an ordered pair with different entries and, moreover, since . Similarly, (R2) implies (R2’) given , is a reaction edge of if and only if is a reaction edge of , and again since . But every reaction edge of , and , is labeled by a pair with , that is: is only a reaction edge of , is only a reaction edge of , or both edges are respective reaction edges of and . Thus (R1’) and (R2’) are exhaustive cases, and since the edge labels are the same in both and , we have if and only if with . Thus . Therefore is good and has as stable extension.
Lemma 18.
[Restated, see original statement.]
Let be a balanced reaction and with and be a partial AAM. Consider an extension of . Then, is an isomorphism from to , if and only if, is a good partial AAM with stable extension .
Proof.
Suppose first that . Consider any edge . Since by assumption preserves adjacency, vertex labels and edge labels, we obtain . Since and take their edge labels from and , respectively, we also have , i.e., is not a reaction edge of w.r.t and thus . Similarly, for , we get and , from where . This shows and . Then, Observation 16 implies that and , and from Lemma 17 it follows, therefore, that is good and is a stable extension for .
To prove the converse, suppose is a stable extension for . Then, by definition, is also a full AAM for , and by Lemma 3 we see that is also an isomorphism from to . But from Lemma 17 we should have and , and therefore .
Theorem 20.
[Restated, see original statement.]
Let be a good partial AAM for a balanced reaction and let and be two stable extensions of . Then .
Proof.
Suppose is the map for subsets to . Since and are extensions of , by definition we have and for all . Moreover contains all reacting vertices induced by . In symbols we have and thus holds in particular for all . By definition we get , since and are stable extensions of . Therefore contains all reacting vertices of and . Lemma 10 implies that and coincide for all reacting vertices induced, in particular, by for , i.e., understood as reacting vertices and . In addition, statement (iii) of Proposition 19 yields , while statement (ii) ensures that and . Thus is an isomorphism from the remainder graph to the remainder graph . Proposition 5 therefore applies to and , and implies .
Appendix B Appendix: Additional Figures and Tables
| Trial | GM (ms) | (ms) | (ms) | ILP (ms) |
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| Average |
(a)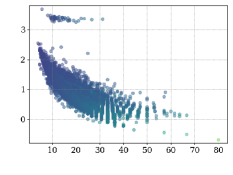 (b)
(b)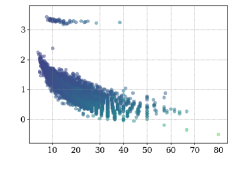 (c)
(c)
(a)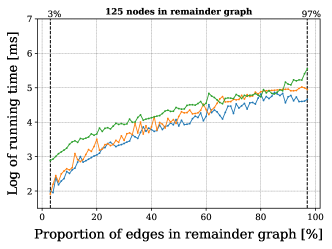 (b)
(b)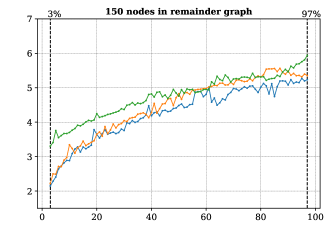
(c) (d)
(d)