Positional-Player Games
Abstract
In reactive synthesis, we transform a specification to a system that satisfies the specification in all environments. For specifications in linear-temporal logic, research on bounded synthesis, where the sizes of the system and the environment are bounded, captures realistic settings and has lead to algorithms of improved complexity and implementability. In the game-based approach to synthesis, the system and its environment are modeled by strategies in a two-player game with an -regular objective, induced by the specification. There, bounded synthesis corresponds to bounding the memory of the strategies of the players. The memory requirement for various objectives has been extensively studied. In particular, researchers have identified positional objectives, where the winning player can follow a memoryless strategy – one that needs no memory.
In this work we study bounded synthesis in the game setting. Specifically, we define and study positional-player games, in which one or both players are restricted to memoryless strategies, which correspond to non-intrusive control in various applications. We study positional-player games with Rabin, Streett, and Muller objectives, as well as with weighted multiple Büchi and reachability objectives. Our contribution covers their theoretical properties as well as a complete picture of the complexity of deciding the game in the various settings.
Keywords and phrases:
Games, -Regular Objectives, Memory, ComplexityCopyright and License:
2012 ACM Subject Classification:
Theory of computation Formal languages and automata theory ; Theory of computation Semantics and reasoningEditors:
Paweł Gawrychowski, Filip Mazowiecki, and Michał SkrzypczakSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
Synthesis is the automated construction of a system from its specification [46]. A reactive system interacts with its environment and has to satisfy its specification in all environments [28]. A useful way to approach synthesis of reactive systems is to consider the situation as a game between the system and its environment. In each round of the game, the environment provides an assignment to the input signals and the system responds with an assignment to the output signals. The system wins if the generated computation satisfies the specification. The system and the environment are modeled by transducers, which direct them how to assign values to the signals given the history of the interaction so far.
Aiming to study realistic settings, researchers have studied bounded synthesis [50]. There, the input to the problem also contains bounds on the sizes of the transducers. Beyond modeling the setting more accurately, bounded synthesis has turned out to have practical advantages. Indeed, bounding the system enables a reduction of synthesis to SAT [19, 22]. Bounding both the system and the environment, a naive algorithm, which essentially checks all systems and environments, was shown to be optimal [38]. In richer settings, for example ones with concurrency, partial visibility, or probability, restricting the available memory is sometimes the key to decidability or to significantly improved complexity [9, 42, 16].
Algorithms for synthesis reduce the problem to deciding a two-player graph game. The arena of the game is a graph induced from the specification. The vertices are partitioned between the two players, namely the system and the environment. Starting from an initial vertex, the players jointly generate a play, namely a path in the graph, with each player deciding the successor vertex when the play reaches a vertex she owns. The objectives of the players refer to the infinite play that they generate. Each objective defines a subset of [41], where is the set of vertices of the game graph.111As we elaborate in Section 2, all our results apply also for edge-based objectives, namely when defines a subset of , for the set of edges of the graph. For example, in games with Büchi objectives, is a subset of , and a play satisfies if it visits vertices in infinitely often.
In the graph-game setting, a strategy for a player directs her how to proceed in vertices she owns, and it is winning if it guarantees the satisfaction of the player’s objective. Winning strategies may need to choose different successors of a vertex in different visits to the vertex. Indeed, choices may depend on the history of the play so far. The number of histories is unbounded, and extensive research has concerned the memory requirements for strategies in games with -regular objectives, namely the minimal number of equivalence classes to which the histories can be partitioned [51, 18, 8, 10]. For example, it is well known that a winning strategy for a conjunction of Büchi objectives requires memory [18]. In practice, the strategies of the system and the environment are implemented by controllers whose state spaces correspond to the different memories that the strategies require. Clearly, we seek winning strategies whose controllers are of minimal size. Of special interest are memoryless strategies (also called positional strategies), which depend only on the current vertex. For them, all histories are in one equivalence class, leading to trivial controllers.
The need to design efficient controllers has led to extensive research on memoryless strategies. Researchers identified positional objectives, namely ones in which both players can use memoryless strategies (formally, an objective is positional if in all games with objective , the winner of the game has a memoryless winning strategy), and half-positional objectives, namely ones in which one of the players can use a memoryless strategy (formally, an objective is -positional (-positional) if in all games with objective , if the system (environment, respectively) wins the game, then it has a memoryless winning strategy). For example, it is well known that parity (and hence, also Büchi) objectives are positional [21, 55, 26]. Then, Rabin objectives are -positional, and their dual Streett objectives are -positional [21, 35]. On the other hand, Muller objectives are not even half-positional. In addition, researchers study positional [25, 14, 45] and -positional [36, 44, 7] fragments of objectives that are in general not positional. For example, [11] identifies a class of parity automata that recognize general -regular positional objectives.
In this work we take a different view on the topic. Rather than studying the memory required for different types of objectives, we take the approach of bounded synthesis and study games in which the memory of the players is bounded, possibly to a level that prevents them from winning. We focus on controllers of size . Note that while transducers of size are not of much interest, controllers of size in the game setting correspond to memoryless strategies, and are thus of great interest. Indeed, in applications like program repair [33, 27], supervisory control [17] and regret minimization [31], researchers have studied non-intrusive control, which is modeled by memoryless strategies. Although controllers of size do not always exist, due to the obvious implementation advantages, one can first try to find a controller of size , and extend the search if one does not exist. Since memoryless strategies amount to consistent behavior, restricting the memory of the environment models setting in which the system may learn an unknown yet static environment [47, 48].
We define and study positional-player games (PPGs, for short), in which both players are restricted to memoryless strategies, and half-positional-player games (HPPGs, for short), in which only one player is restricted to memoryless strategies. We distinguish between positional-Player 1 games (PP1Gs, for short), in which only the system is restricted to memoryless strategies, and positional-Player 2 games (PP2Gs, for short), in which only the environment is restricted.
We study PPGs and HPPGs with Rabin, Streett, and Muller objectives, as well as with weighted multiple objectives [40]. Such objectives are of the form , where , is a set of objectives that are all Büchi, co-Büchi, reachability, or avoid objectives, is a non-decreasing, non-negative weight function that maps each subset of to a reward earned when exactly all the objectives in are satisfied, and is a threshold. An objective can be viewed as a maximization objective, in which case the goal is to maximize the earned reward (and serves as a lower bound) or a minimization objective, in which case the goal is to minimize the earned reward (and serves as an upper bound). Weighted multiple objectives can express generalized objectives, namely when contains several objectives, all of which have to be satisfied. A weight function allows for a much richer reference to the underlying objectives: prioritizing them, referring to desired and less desired combinations, and addressing settings where we cannot expect all sub-specifications to be satisfied together.
Studying the theoretical properties of PPGs and HPPGs, we start with some easy observations on how the positionality of the objective type causes different variants of PPGs to coincide. We then study determinacy for PPGs and HPPGs; that is, whether there always exists a player that has a winning strategy. Clearly, if a player wins in a game but needs memory in order to win, she no longer wins when restricted to memoryless strategies. Can the other player always win in this case? We prove that the answer is positive for prefix-independent objectives (and only for them). On the other hand, when the other player is restricted too, the answer may be negative; thus PPGs of all objective types that are not -positional or not -positional need not be determined. Also, interestingly, even for objectives that are -positional, Player 1 may need memory in order to win against a positional Player 2. Indeed in games in which Player 2 wins when her memory is not bounded, Player 1 can win only by learning and remembering the memoryless strategy of Player 2.
We continue and study the complexity of deciding whether Player 1 or Player 2 win in a given PPG or HPPG. Our results are summarized in Tables 1 and 2. Since memoryless strategies are polynomial in the game graph, the problems for PPGs are clearly in , namely they can be solved in NP using a co-NP oracle. Indeed, one can guess a strategy for the system, then guess a strategy for the environment, and finally check their outcome. Our main technical contribution here is to identify cases in which this naive algorithm is tight and cases where it can be improved. Moving to HPPGs, deciding the winner involves reasoning about the graph induced by a given strategy, and again, the complexity picture is diverse and depends on the half-positionality of the objective, the determinacy of HPPGs, and the succinctness of the objective type. In particular, handling Muller objectives, we have to cope with their complementation (a naive dualization may be exponential) and to introduce and study the alternating vertex-disjoint paths problem, which adds alternation to the graph.
2 Preliminaries
2.1 Two-player games
A two-player game graph is a tuple , where , are finite disjoint sets of vertices, controlled by Player 1 and Player 2, respectively, and we let . Then, is an initial vertex, and is a total edge relation, thus for every , there is such that . The size of , denoted , is , namely the number of edges in it.
In the beginning of a play in the game, a token is placed on . Then, in each turn, the player that owns the vertex that hosts the token chooses a successor vertex and moves the token to it. Together, the players generate a play in , namely an infinite path that starts in and respects : for all , we have that .
For , a strategy for Player is a function that maps prefixes of plays that end in a vertex that belongs to Player to possible extensions in a way that respects . That is, for every and , we have that . Intuitively, a strategy for Player directs her how to move the token, and the direction may depend on the history of the game so far. The strategy is finite-memory if it is possible to replace the unbounded histories in by a finite number of memories. The strategy is memoryless if it depends only on the current vertex,222Memoryless strategies are sometimes termed positional strategies. We are going to use “positional” in order to describe objectives and games in which the players use memoryless strategies, and prefer to leave the adjective used for describing strategies different from the one used for describing objectives and games. thus for all and , we have that . Accordingly, a memoryless strategy is given by a function .
A profile is a tuple of strategies, one for each player. The outcome of a profile is the play obtained when the players follow their strategies in . Formally, is such that for all , we have that , where is such that .
A two-player game is a pair , where is a two-player game graph, and is a winning condition for Player 1, specifying a subset of , namely the set of plays in which Player 1 wins. The game is zero-sum, thus Player 2 wins when the play does not satisfy . A strategy is a winning strategy for Player 1 if for every strategy for Player 2, Player 1 wins in the profile , thus satisfies . Dually, a strategy for Player 2 is a winning strategy for Player 2 if for every strategy for Player 1, we have that Player 2 wins in . We say that Player wins in if she has a winning strategy. A game is determined if Player 1 or Player 2 wins in it.
2.2 Boolean objectives
For a play , we denote by the set of vertices that are visited at least once along , and we denote by the set of vertices that are visited infinitely often along . That is, , and . For a set of vertices , a play satisfies the reachability objective iff , and satisfies the Büchi objective iff . The objectives dual to reachability and Büchi are avoid (also known as safety) and co-Büchi, respectively. Formally, a play satisfies an avoid objective iff , and satisfies a co-Büchi objective iff .
A Rabin objective is a set of pairs of sets of vertices. A play satisfies iff there exists such that visits infinitely often and visits only finitely often. That is, and , for some . The objective dual to Rabin is Streett. Formally, a play satisfies a Streett objective iff or , for every .
Finally, a Muller objective over a set of colors is a pair , where specifies desired subsets of colors and colors the vertices in . A play satisfies iff the set of colors visited infinitely often along is in . That is, . The objective dual to is the Muller objective .
We define the size of an objective as the size of the sets in it. For Muller objectives, we also add the number of colors. That is, the size of is .
Remark 1.
Objectives in two-player games can also be defined with respect to the edges (rather than vertices) traversed during plays. For some problems, the change is significant. For example, minimization of some types of automata is NP-complete in the state-based setting and can be solved in polynomial time in the edge-based setting [49, 1]. For our study here, all the results also apply for edge-based objectives. For example, for Muller objectives, by adding a new color, we can allow uncolored vertices, which enable a translation of games with colored-edges objectives to games with colored-vertices objectives in a way that preserves winning and memoryless winning strategies. Similar translations can be applied for other types of objectives. ∎
For two types of objectives and , we use to indicate that every set of plays that satisfy an objective of type can be specified also as an objective of type . For example, Büchi Rabin, as every Büchi objective is equivalent to the Rabin objective .
An objective type is prefix-independent if the satisfaction of any objective in a play depends only on the infinite suffix of the play. That is, for every play , we have that satisfies iff every infinite suffix of satisfies . An objective that is not prefix-independent is prefix-dependent. Note that objectives defined with respect to only are prefix-independent, whereas objectives defined with respect to are prefix-dependent.
2.3 Weighted multiple objectives
A weighted objective is a pair , where is a set of objectives, all of the same type, and is a weight function that maps subsets of objectives in to natural numbers. We assume that is non-decreasing: for every sets , if , then . In the context of game theory, non-decreasing functions are very useful, as they correspond to settings with free disposal, namely when satisfaction of additional objectives does not decrease the utility [43]. We also assume that . A non-decreasing weight function is additive if for every set , the weight of equals to the sum of weights of the singleton subsets that constitute . That is, . An additive weight function is thus given by , and is extended to sets of objectives in the expected way, thus , for every .
For a play , let be the set of objectives in that are satisfied in . The satisfaction value of in , denoted , is then the weight of the set of objectives in that are satisfied in . That is, .
Weighted objectives can be viewed as either maximization or minimization objectives. That is, the goal is to maximize or minimize the weight of the set of objectives satisfied. 333Note that adding a threshold to the objective makes satisfaction binary, and the corresponding optimization problem can be solved using a binary search. Note that when is uniform, thus when for all , the goal is to maximize or minimize the number of satisfied objectives. A special case of the latter, known in the literature as generalized conditions, is when we aim to satisfy all or at least one objective. We denote different classes of weighted objectives by acronyms in , describing the way we refer to the satisfaction value and the objectives type: reachability (R), avoid (A), Büchi (B), or co-Büchi (C). Formally, for a play , an objective type , a set of objectives, a weight function , and a threshold , we have the following winning conditions.
-
satisfies a MaxW- objective if .
-
satisfies a MinW- objective if .
-
satisfies an All- objective if .
-
satisfies an Exists- objective if .
For All- and Exists- objectives, we omit the weight function from the specification of the objective. Note that for all objective types , we have that All- MaxW- and Exists- MaxW-. Also, by [40], MaxWB Muller. Indeed, it is easy to specify in a Muller objective all sets such that . Since we assume non-decreasing weight functions, the other direction does not hold, thus Muller MaxWB. In Section 8, we study dualities in weighted objectives and extend the above observations to minimization games and to underlying co-Büchi and avoid objectives. Finally, note that MaxW- and MinW- objectives are prefix-independent iff is prefix-independent.
3 Positional Objectives and PPGs
For , an objective type is -positional if for every -game , Player wins in iff she has a memoryless winning strategy in . Then, is positional iff it is both -positional and -positional, thus the winner of every -game has a memoryless winning strategy. If is neither -positional nor -positional, we say that it is non-positional.444In the literature, -positional and -positional objectives are sometimes termed positional, and positional objectives are sometimes termed bipositional [11]. It is known that the objective types reachability, Büchi, and parity (and thus also avoid and co-Büchi) are positional [21], Rabin is -positional (and thus Streett is -positional) [35], and Muller is non-positional [18]. As for weighted multiple objectives, MaxWB and MinWB are - and -positional, respectively, whereas MaxWR and MinWR are non-positional [40].
We lift the notion of positionality to games, studying settings in which one or both players are restricted to memoryless strategies. For , a game is a positional-Player game if Player is restricted to memoryless strategies, and is a positional-player game (PPG, for short) if both players are restricted to memoryless strategies. Positional-Player 1 and positional-Player 2 games are also called half-positional-player games (HPPG, for short).555An automaton is determinizable by pruning if it embodies an equivalent deterministic automaton, thus if nondeterminism can be resolved in a memoryless manner [3]. This may hint on a relation to PP1Gs. However, the labels on the transitions of automata make the setting different, and reasoning about determinization by pruning is different from reasoning about PP1Gs [37, 2].
For a game , we use Pos-, 1Pos-, and 2Pos- to denote the positional-player and half-positional-player variants of , respectively. Formally, for a game , we have the following.
-
Player 1 wins Pos- iff she has a memoryless strategy such that for every memoryless strategy for Player 2, we have that satisfies .
-
Player 1 wins 1Pos- iff she has a memoryless strategy such that for every strategy for Player 2, we have that satisfies .
-
Player 1 wins 2Pos- iff she has a strategy such that for every memoryless strategy for Player 2, we have that satisfies .
Example 2.
Consider the AllB game , for that appears in Fig. 1, and . Since the objective of Player 1 is to satisfy both Büchi objectives in , she wins iff for infinitely many traversals of , the choices of the players from the vertices and as to whether they go up or down do not match.
It is easy to see that Player 1 wins in . Indeed, a winning strategy for Player 1 can move the token up to after visits of the token in , and move the token down to after visits of the token in . Since 2Pos- only restricts the strategies that Player 2 may use, the strategy is a winning strategy for Player 1 also in 2Pos-.
On the other hand, Player 1 does not win in 1Pos-. Indeed, for every memoryless strategy for Player 1, Player 2 has a strategy , in fact a memoryless one, that matches the choice Player 1 makes in . That is, if , then , and if , then . Since is memoryless, Player 1 does not win in Pos- either.
As for Player 2, she clearly does not win in and 2Pos-. In 1Pos-, a winning strategy for Player 2 can move the token up to after visits in , and move the token down to after visits in . The strategy requires memory, and Player 2 does not have a winning strategy in Pos-. Indeed, for every memoryless strategy for Player 2, Player 1 has a memoryless strategy in which the choice in does not match the choice Player 2 makes in , causing both Büchi objectives to be satisfied. Thus, interestingly, even though AllB objectives are -positional, Player 2 needs memory in order to win in 1Pos-. ∎
We conclude with some easy observations about PPGs and HPPGs and positional and half-positional objectives. The first follows immediately from the fact that the restriction to memoryless strategies only reduces the set of possible strategies. For a player , we use to denote the other player; thus, if , then , and if , then .
Theorem 3.
For every game and , all the following hold.
-
If Player wins Pos-, then she also wins and Pos-.
-
If Player wins Pos-, then she also wins Pos-.
We continue with observations that use the positionality of the objective type in order to relate different variants of PPGs. The proof of Theorem 4 follows immediately from the definitions and the proof of Theorem 5 can be found in the full version.
Theorem 4.
Consider and an -positional objective type . For every -game , Player wins iff Player wins Pos-. In particular, if is positional, then Player wins iff Player wins Pos-, 1Pos-, and 2Pos-.
Theorem 5.
Consider , and an -positional objective type . For every -game , Player wins Pos- iff Player wins Pos-.
4 Determinacy of PPGs and HPPGs
Games with -regular objectives enjoy determinacy: in every game, one player wins [41]. In this section we study the determinacy of PPGs and HPPGs. As expected, restricting the strategies of both players makes some games undetermined. Surprisingly, we are able to prove that for every prefix-independent objective that is not positional, there is an undetermined PPG with the objective . On the other hand, all HPPGs with prefix-independent objectives are determined. Thus, if a player needs memory in order to win a game with a prefix-independent objective, then restricting her to use only memoryless strategies without restricting her opponent, not only prevents her from winning, but also makes the opponent winning.
Theorem 6.
For every objective that is prefix-independent, not positional, and requires finite memory, there is an undetermined PPG with objective . In particular, AllB and ExistsC PPGs need not be determined.
Proof.
Since is not positional, then it is not -positional or not -positional. We consider the case is not -positional. The case is not -positional follows, as Player 2 has an objective that is not -positional. In the full version, we prove that for every objective as above, there is a set of vertices, a finite graph over consisting of a vertex and two simple and vertex-disjoint paths , such that and are cycles, and either satisfies , and and do not satisfy , or does not satisfy , and and satisfy . We then take two copies of in order to construct a PPG with the same objective in which no player wins.
We continue to HPPGs. Note that for in Example 2, allowing a single player to use memory makes this player win. Indeed, as the other player uses a memoryless strategy, she commits on her strategy in vertices visited along the play. As we formalize in Theorem 7 below, the player that uses memory can then learn these commitments, and follow a strategy that is tailored for them. Since learning is performed during a traversal of a prefix of the play, this works only for objectives that are prefix-independent.
Theorem 7.
Consider a prefix-independent objective type . For every -game and , we have that Pos- is determined.
Proof.
Consider a -game . Let . We show that Player 1 wins in 1Pos- iff Player 2 does not win 1Pos-. The proof for 2Pos- is similar.
Clearly, if Player 1 wins 1Pos-, then Player 2 does not win 1Pos-. For the second direction, assume that Player 1 does not win 1Pos-. We show that then, Player 2 has a strategy that wins against all memoryless strategies of Player 1. Let be the set of vertices from which Player 1 does not have a memoryless winning strategy in , and let be the sub-graph of that contains only vertices in . That is, . Note that indeed since Player 1 does not win 1Pos-.
Let be all the memoryless strategies for Player 1 in . Since all of them are not winning strategies, there exist strategies for Player 2 in such that does not satisfy , from every vertex in , for every . Note that for every , such a strategy exists only because is restricted to vertices in . We construct from a winning strategy for Player 2 in 1Pos-.
Intuitively, starting with , the strategy follows , and whenever Player 1 takes a transition from a vertex to a vertex , it checks that the transition is consistent with ; that is, whether . If this is not the case, the strategy updates to the minimal such that . In the full version, we define formally and prove that an index as above always exists, and that the process eventually stabilizes, simulating a game in which Player 1 uses some memoryless strategy , and Player 2 uses a strategy that wins against , making a winning strategy for Player 2.
As for prefix-dependent objective types, here the vertices traversed while the unrestricted player learns the memoryless strategy of the restricted player may play a role in the satisfaction of the objective, and the picture is different (see detailed proof in the full version):
Theorem 8.
For every objective type such that or , both -PPGs and -HPPGs need not be determined.
5 The Complexity of PPGs and HPPGs
Given a game , we would like to decide whether Player 1 wins in 1Pos-, 2Pos-, and Pos-. The complexity of the problem depends on the type of objective in . In this section we present general complexity results for the problem. Then, in Sections 6, 7, and 8, we provide an analysis for the different objective types. Note that since not all PPGs and HPPGs are determined, the results for Player 2 do not follow immediately from the results for Player 1. They do, however, follow from results about the dual objective.
5.1 General upper bound results
We start with upper bounds. We say that an objective type is path-efficient if given a lasso shape path , for and , checking whether satisfies a objective can be done in time polynomial in , and . We say that an objective type is all-path-efficient if given a graph , checking whether all the infinite paths in satisfy a objective can be done in time polynomial in and .
The complexity class contains all the problems that can be solved in polynomial time by a nondeterministic Turing machine augmented by a co-NP oracle. Since memoryless strategies are of polynomial size, the complexity class is a natural class in the context of PPGs. Formally, we have the following (see proof in the full version).
Theorem 9.
Consider a path-efficient objective type . For every -game , deciding whether Player 1 wins in Pos- can be done in .
For HPPGs, once a memoryless strategy for Player 1 is guessed, one has to check all the paths in the graph that are consistent with it. Formally, consider a -game and a memoryless strategy for Player 1. Let be the graph obtained from by removing edges that leave vertices in that do not agree with . Clearly, is a winning strategy iff all the paths in satisfy . Hence, we have the following (see proof in the full version).
Theorem 10.
Consider an all-path-efficient objective type . For every -game , deciding whether Player 1 wins 1Pos- can be done in NP.
5.2 General lower bound constructions
For our lower bounds, we use reductions from two well-known problems: QBF (Quantified Boolean Formulas) and its special case 2QBF, which are standard problems for proving hardness in PSPACE and , respectively. Here, we define these problems and set some infrastructure for the reductions. Consider a set of variables. Let . A QBF formula is of the form , where are existential and universal quantifiers, and is a propositional formula over . The QBF problem is to decide whether is valid.
A QBF formula is in 2QBF if there is only one alternation between existential and universal quantification in , and the external quantification is existential. In 2QBF, we can assume that is given in 3DNF. For nicer presentation, we use and for the sets of existentially and universally quantified variables, respectively. That is, a 2QBF formula is of the form , where , for some , and for every , we have , with .
Below we describe two game graphs that are used in our reductions.
Consider a set of variables , and a QBF formula , where . The two-player game graph lets Player 1 choose assignments to the existentially-quantified variables and Player 2 choose assignments to the universally-quantified variables. The idea is that when the players use memoryless strategies, they repeat the same choices. For the special case of 2QBF (see Figure 2), the order of the quantifiers on the variables corresponds to the way the strategies of the players are quantified. For QBF, the quantification on the variables is arbitrary, and is used in the context of HPPGs. In the full version, we define formally.
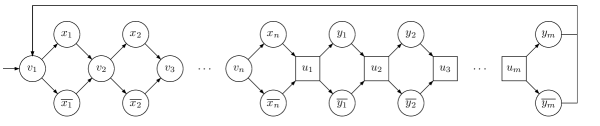
In , the vertices that correspond to the assignment to the last variable go back to the initial vertex. We use to denote the game graph obtained from by replacing these edges by self-loops. Note that and are independent of and only depend on the partition of in to existentially and universally quantified variables.
Next, we define a game graph , induced by a QBF formula , for in 3DNF. The game proceeds in two phases that are repeated infinitely often and are described as follows (see the full version for the full details, and Figure 3 below for an example). In the assignment phase, the players choose an assignment to the variables in . This is done as in . Then, the game continues to a checking phase, in which Player 2 tries to refute the chosen assignment by showing that every clause has a literal that is evaluated to . For this, the game sequentially traverses, for every clause , a vertex from which Player 2 can visit refute-literal vertices, associated with , , and , and continues to the next clause. Thus, for every clause, Player 2 chooses a vertex that corresponds to the negation of one of its literals.
Intuitively, when the players use memoryless strategies, the assignment phase induces an assignment to the variables. An assignment satisfies iff there exists a clause all whose literals are evaluated to , which holds iff Player 2 is forced to choose a refute-literal vertex that corresponds to a literal evaluated to . Then, is valid iff there exists a memoryless strategy for Player 1 such that for every memoryless strategy for Player 2, there exists a literal such that both and a refute-literal vertex that corresponds to are visited infinitely often.
We use to denote the game graph obtained from by replacing the edges from the rightmost refute-literal vertices to the initial vertex by self-loops.
6 Rabin and Streett PPGs and HPPGs
In this section we study Rabin and Streett (and their respective special cases ExistsC and AllB) PPGs and HPPGs. Our results are summarized in Table 1 below.
| Type | Positionality | P1 wins | P1 wins Pos- | P1 wins 1Pos- | P1 wins 2Pos- | ||||||||
| ExistsC | -positional |
|
|
|
|
||||||||
| Rabin | -positional |
|
|
||||||||||
| AllB | -positional |
|
|
|
|
||||||||
| Streett | -positional |
|
|
||||||||||
| Muller | non-positional |
|
|
|
|
We start with HPPGs (see proof in the full version).
Theorem 11.
Deciding whether Player 1 wins:
-
an ExistsC PP1G or a AllB PP2G can be done in polynomial time.
-
a -PP1G is NP-complete, for .
-
a -PP2G is co-NP-complete, for .
Theorem 12.
Deciding whether Player 1 wins a Rabin PPG is -complete. Hardness in applies already for ExistsC PPGs.
Proof.
The upper bound follows from Theorem 9. For the lower bound, we describe a reduction from 2QBF. That is, given a 2QBF formula , we construct an ExistsC game such that iff Player 1 wins Pos-.
Consider a 2QBF formula such that and . Recall the game graph defined in Section 5.2, and recall that memoryless strategies for the players induce assignments to the variables in and in a way that corresponds to their quantification in . Thus, we only need to define an objective that captures the satisfaction of some clause in . For this, we define the ExistsC objective . Thus, each clause of contributes to a set with the negations of the literals in . Since for each variable , a play visits exactly one of the literal vertices and infinitely often, the play satisfies a co-Büchi objective in iff the chosen assignment satisfies , and so iff Player 1 wins in Pos- (see proof in the full version).
Theorem 12 shows that Rabin PPGs are strictly more complex than general Rabin games. For the dual Streett objective, the -positionality of Rabin objectives does make the problem easier. Formally, we have the following (see proof in the full version).
Theorem 13.
Deciding whether Player 1 wins a Streett PPG is NP-complete. Hardness in NP applies already for AllB PPGs.
7 Muller PPGs and HPPGs
In this section, we study the complexity of Muller PPGs and HPPGs. Our results are summarized in Table 1. We start with PPGs. It is not hard to see that Muller is path-efficient, and so Theorem 9 implies that the problem of deciding whether Player 1 wins a Muller PPG is in . In Theorem 12, we proved that the problem is -hard for Rabin and even ExistsC PPGs, and as ExistsC Muller, it may seem that a similar lower bound would be easy to obtain. The translation from an ExistsC objective to a Muller objective may, however, be exponential [6], which is in particular the case for the objective used in the lower bound proof in Theorem 12. Note that the AllB objective used in the lower bound proof in Theorem 13 can be translated with no blow-up to a Muller objective, but deciding whether Player 1 wins an AllB PPG is NP-complete.
Accordingly, our first heavy technical result in the context of Muller PPGs is a proof of their -hardness. For this, we add an alternation to the problem of vertex-disjoint paths, used in [33] in order to prove NP-hardness for AllB PPGs. We show that a Muller objective can capture the alternation, which lifts the complexity from NP to .
We first need some definitions and notations. Consider a directed graph . A path in is simple if each vertex appears in at most once. Two simple paths and in are vertex-disjoint iff they do not have vertices in common, except maybe their first and last vertices. The vertex-disjoint-paths (VDP, for short) problem is to decide, given and two vertices , whether there exist two vertex-disjoint paths from to and from to in . The complementing problem, termed NVDP, is to decide whether there do not exist two vertex-disjoint paths from to and from to in .
Now, the alternating NVDP problem (ANVDP, for short) is to decide, given a two-player game graph and two vertices , whether there exists a memoryless strategy for Player 1 in such that the is in NVDP. That is, there do not exist two vertex-disjoint paths from to and from to in .
Lemma 14.
ANVDP is -complete.
Proof.
VDP is known to be NP-complete [24, 33], making NVDP co-NP-complete, and inducing a upper bound. NP-hardness is shown in [24] by a reduction from SAT (see full version for details): given a CNF formula over variables in , a graph with vertices and is constructed such that paths from to correspond to choosing an assignment to the variables in , and then choosing one literal in every clause in . Then, a path from to has a path from to that is vertex-disjoint from iff all the chosen literals are evaluated to in the chosen assignment. Accordingly, is in VDP iff is satisfiable.
For ANVDP, we use a similar reduction, but from QBF. Given a QBF formula where is in DNF, we construct a game graph similar to for the CNF formula with vertices and , where memoryless strategies for Player 1 correspond to assignments to the variables in . Every such assignment defines a sub-graph that is in VDP iff there exists an assignment to the variables in that, together with the assignment Player 1 chose, satisfies . Accordingly, there exists a memoryless strategy for Player 1 such that the corresponding sub-graph, together with and , is in NVDP iff .
Theorem 15.
Deciding whether Player 1 wins a Muller PPG is -complete.
Proof.
The upper bound follows from Theorem 9. For the lower bound, we describe a reduction from ANVDP, which, by Lemma 14, is -hard. Consider a two-player game graph , and a vertex . We define a Muller game such that Player 1 wins Pos- iff is in ANVDP.
Consider the set of colors . We define , where , , and for every . Then, . Thus, Player 1 wins in a play iff it does not visit both and infinitely often. For the correctness of the construction, note that for every memoryless strategy for Player 1 in , we have that is winning in Pos- iff Player 2 does not have a memoryless winning strategy in , which she has iff there exists a simple cycle in that visits both and . Such a simple cycle exists iff there exist two vertex-disjoint paths from to and from to in . That is, if is in VDP. Accordingly, Player 1 wins Pos- iff is in ANVDP.
We continue to Muller HPPGs. Note that beyond implying membership in NP for the problem of deciding whether Player 1 wins a Muller PP1G, establishing the all-path efficiency of the Muller objective also implies that the universality problem for universal Muller word automata can be solved in polynomial time.666An alternative proof to Theorem 16 can use the known polynomial translation of Muller objectives to Zielonka DAGs [30] and the fact Zielonka-DAG automata can be complemented in polynomial time [29]. In the full version, we describe this approach in detail. We find our direct proof useful, as it shows that translating full CNF formulas to equivalent DNF formulas can be done in polynomial time.
Theorem 16.
Muller objectives are all-path-efficient.
Proof.
Consider a graph , and a Muller objective defined over a set of colors . Deciding whether every infinite path in satisfies can be reduced to deciding whether there is an infinite path in that satisfies the dual Muller objective . Since the size of need not be polynomial in , a naive algorithm that checks the existence of a path that satisfies does not run in polynomial time.
The key point in our algorithm is to complement a given Muller objective not to another Muller objective, but rather to view as a DNF formula over , dualize it to a CNF formula , and then convert to an equivalent DNF formula. Specifically, , with the semantics that a literal (, respectively) requires vertices with the color to be visited infinitely (finitely, respectively) often [4]. The dual Muller objective then corresponds to the complementing CNF formula; thus it corresponds to the Emerson-Lei objective [30] .
Note that deciding whether a graph has a path that satisfies a DNF formula can be done in polynomial time (for example by checking whether there exists a path in that respects the requirements induced by one clause in the formula). On the other hand, deciding whether a graph has a path that satisfies a CNF formula is hard, which is why we convert to an equivalent DNF formula. Converting CNF to DNF is in general exponential. The CNF formula , however, is full: for every variable , every conjunct contains the literal or the literal . In the full version, we show that full CNF formulas can be converted to DNF in polynomial time. The conversion is based on the equality , recursively applied to and . The blow-up is kept polynomial by minimizing to include only clauses of that contain , after removing from them, and similarly for .
We can now conclude with the complexity of Muller HPPGs (see proof in the full version).
Theorem 17.
Deciding whether Player 1 wins a Muller PP1G is NP-complete, and deciding whether Player 1 wins a Muller PP2G is co-NP-complete.
8 Weighted Multiple Objectives PPGs and HPPGs
In this section we study PPGs and HPPGs with weighted multiple objectives. We focus on games with underlying Büchi or reachability objectives. In the full version, we prove that the results for underlying co-Büchi or avoid objectives follow. Essentially, this follows from the fact that weighted objectives may be dualized by complementing either the type of the objective or the way we refer to the satisfaction value. Specifically, for an objective type , let be the dual objective, thus and . Then, as shown in [40], for every , every MaxW- objective has an equivalent MinW- objective of polynomial size, and vise versa. Our results are summarized in Table 2 below.
| Type | Positionality | P1 wins | P1 wins Pos- | P1 wins 1Pos- | P1 wins 2Pos- | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
We start with PPGs with underlying Büchi and reachability objectives.
Theorem 18.
Deciding whether Player 1 wins a MinWB or MaxWB PPG is -complete. Hardness in applies already for games with uniform weight functions.
Proof.
Both upper bounds follow from Theorem 9. Since the ExistsC objective used in the lower bound in the proof of Theorem 12 can be specified as a MinWB objective with a uniform weight function, a matching lower bound for MinWB PPGs is easy.
A lower bound for MaxWB PPGs is less easy. Consider a 2QBF formula such that is in 3DNF. We construct a MaxWB game over the game graph defined in Section 5.2 such that iff Player 1 wins Pos-.
For every literal in , we define a Büchi objective as the set of vertices associated with . That is, the literal vertex from the assignment phase of the game, and refute-literal vertices in the checking phase that originate from appearing in some clause. The objective of Player 1 is to satisfy at least different Büchi objectives, which can be expressed with a uniform weight function. Formally, , where , with , for every .
Intuitively (see proof in the full version), the literal vertices that a play visits infinitely often are exactly those that correspond to literals evaluated to in the chosen assignment, and thus the play satisfies Büchi objectives during the assignment phase – one for every literal evaluated to . Then, the game satisfies an additional Büchi objective in the checking phase iff Player 2 chooses a refute-literal vertex that corresponds to a literal evaluated to . Since Player 2 is forced to choose such a refute-literal vertex iff there exists a clause all whose literals are evaluated to , Player 2 is forced to satisfy an additional Büchi objective iff the chosen assignment satisfies . Therefore, iff Player 1 can force the satisfaction of at least Büchi objectives.
Theorem 19.
Deciding whether Player 1 wins a MinWR or MaxWR PPG is -complete. Hardness in applies already for uniform weight functions.
Proof.
The upper bounds follow from Theorem 9. The reductions from 2QBF to MinWB and MaxWB PPGs in the proof of Theorem 18 are also valid for MinWR and MaxWR PPGs. Indeed, when the players are restricted to memoryless strategies in and , every vertex is visited infinitely often iff it is reached. Thus, a Büchi (co-Büchi) objective is satisfied iff the reachability (avoid, respectively) objective is satisfied.
Moving to HPPGs, we start with underlying Büchi objectives, where things are easy (see proof in the full version):
Theorem 20.
Deciding whether Player 1 wins:
-
a MinWB PP1G is NP-complete.
-
a MaxWB PP1G is -complete.
-
a MaxWB PP2G is co-NP-complete.
-
a MinWB PP2G is -complete.
In all cases, hardness holds already for games with a uniform weight function.
For HPPGs with underlying reachability objectives, things are more complicated. First, recall that MinWR and MaxWR HPPGs are undetermined, thus the results for PP2Gs cannot be inferred from the results for PP1Gs. In addition, since MinWR and MaxWR objectives are not half-positional, the memory requirements for the unrestricted player adds to the complexity.
Theorem 21.
Deciding whether Player 1 wins:
-
a MinWR or MaxWR PP1G is -complete.
-
a MinWR or MaxWR PP2G is PSPACE-complete.
In all cases, hardness holds already for games with a uniform weight function.
Proof.
(sketch, see full details in the full version). We start with PP1Gs. For the upper bounds, consider a MinWR or MaxWR game . A memoryless strategy for Player 1 in is winning iff the objectives that are satisfied in are reached within polynomially many rounds of the game. Hence, an NP algorithm that uses a co-NP oracle guesses a memoryless strategy for Player 1, and checks that is satisfied in every guessed path of the appropriate length in .
For the lower bounds, we argue that the reductions from 2QBF to MinWR and MaxWR PPGs in the proof of Theorem 19 are valid also for MinWR and MaxWR PP1Gs when replacing the game graphs and by and , respectively. Essentially, this follows from the fact that in these games each vertex is visited at most once.
We continue to the PP2Gs. Proving a PSPACE upper bound, we describe an ATM that runs in polynomial time and accepts a MinWR or a MaxWR game iff Player 1 wins 2Pos-. The alternation of is used in order to simulate the game, and we show that, for MaxWR, we can require the reachability objectives to be satisfied within , and for MinWR, we can require the reachability objectives to not be satisfied while traversing a cycle. Accordingly, we can bound the number of rounds in the simulation, with maintaining on the tape the set of reachability objectives satisfied so far, and information required to detect when it may terminate and to ensure that Player 2 uses a memoryless strategy.
For the lower bounds, we describe reductions from QBF. That is, given a QBF formula , we construct a MinWR and a MaxWR game such that iff Player 1 wins 2Pos-. For MinWR, we assume that is in DNF and the winning objective is similar to the ExistsC objective in Theorem 12. For MaxWR, we assume that is in CNF, and define an AllR objective in which each clause induces the set of its literals. It is easy to see that the reduction is valid when the strategies of the players are not restricted. We argue that since each vertex in is visited in each outcome at most ones, Player 1 wins iff Player 1 wins 2Pos-, and so we are done.
9 Discussion
We introduced and studied positional-player games, where one or both players are restricted to memoryless strategies. Below we discuss two directions for future research.
The focus on memoryless strategies corresponds to non-intrusiveness in applications like program repair [33, 27], supervisory control [17], regret minimization [31], and more. More intrusive approaches involve executing controllers of bounded size in parallel with the system or environment, leading to bounded-player games. There, the input to the problem contains, in addition to the game , also bounds and to the sizes of the system and the environment. Player 1 wins - iff she has a strategy with memory of size at most that wins against all strategies of size at most of Player 2.
Note that the games -, -, and - coincide with Pos-, 1Pos-, and 2Pos-, respectively, and so our complexity lower bounds here apply also to the bounded setting. Moreover, if we assume, as in work about bounded synthesis [38], that and are given in unary, then many of our upper bounds here extend easily to the bounded setting. Indeed, upper bounds that guess memoryless strategies for a player can now guess memory structures of the given size, and reason about the game obtained by taking the product with the structures. Some of our results, however, are not extended easily. For example, the NP upper bound for Streett PPGs relies on the fact that for every memoryless strategy for Player 1, we have that Player 2 has a winning strategy in iff she has a memoryless winning strategy in . When , the latter is not helpful for Player 2, and we conjecture that the problem in the bounded setting is more complex.
The second direction concerns positional-player non-zero-sum games, namely multi-player games in which the objectives of the players may overlap [13, 52]. There, typical questions concern the stability of the game and equilibria the players may reach [54]. In particular, in rational synthesis, we seek an equilibrium in which the objective of the system is satisfied [23, 15]. The study of positional strategies in the non-zero-sum setting is of particular interest, as it also restricts the type of deviations that players may perform, and our ability to incentivize or block such deviations [39].
References
- [1] B. Abu Radi and O. Kupferman. Minimization and canonization of GFG transition-based automata. Log. Methods Comput. Sci., 18(3), 2022. doi:10.46298/LMCS-18(3:16)2022.
- [2] B. Abu Radi, O. Kupferman, and O. Leshkowitz. A hierarchy of nondeterminism. In 46th Int. Symp. on Mathematical Foundations of Computer Science, volume 202 of LIPIcs, pages 85:1–85:21, 2021. doi:10.4230/LIPICS.MFCS.2021.85.
- [3] B. Aminof, O. Kupferman, and R. Lampert. Formal analysis of online algorithms. In 9th Int. Symp. on Automated Technology for Verification and Analysis, volume 6996 of Lecture Notes in Computer Science, pages 213–227. Springer, 2011. doi:10.1007/978-3-642-24372-1_16.
- [4] T. Babiak, F. Blahoudek, A. Duret-Lutz, J. Klein, J. Kretínský, D. Müller, D. Parker, and J. Strejcek. The hanoi omega-automata format. In Proc. 27th Int. Conf. on Computer Aided Verification, volume 9206 of Lecture Notes in Computer Science, pages 479–486. Springer, 2015. doi:10.1007/978-3-319-21690-4_31.
- [5] C. Beeri. On the membership problem for functional and multivalued dependencies in relational databases. ACM Trans. on Database Systems, 5:241–259, 1980. doi:10.1145/320613.320614.
- [6] U. Boker. On the (in)succinctness of muller automata. In Proc. 26th Annual Conf. of the European Association for Computer Science Logic, volume 82 of LIPIcs, pages 12:1–12:16. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2017. doi:10.4230/LIPICS.CSL.2017.12.
- [7] P. Bouyer, A. Casares, M Randour, and P. Vandenhove. Half-Positional Objectives Recognized by Deterministic Büchi Automata. In Proc. 33rd Int. Conf. on Concurrency Theory, volume 243 of Leibniz International Proceedings in Informatics (LIPIcs), pages 20:1–20:18. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2022. doi:10.4230/LIPICS.CONCUR.2022.20.
- [8] P. Bouyer, Fijalkow N, M. Randour, and P. Vandenhove. How to play optimally for regular objectives?, 2023. doi:10.4230/LIPICS.ICALP.2023.118.
- [9] N. Bulling and V. Goranko. Combining quantitative and qualitative reasoning in concurrent multi-player games. In Proceedings of the 21st International Conference on Autonomous Agents and Multiagent Systems, page 1926?1928. International Foundation for Autonomous Agents and Multiagent Systems, 2022.
- [10] A. Casares. On the minimisation of transition-based rabin automata and the chromatic memory requirements of muller conditions. In Proc. 30th Annual Conf. of the European Association for Computer Science Logic, volume 216 of LIPIcs, pages 12:1–12:17. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2022. doi:10.4230/LIPICS.CSL.2022.12.
- [11] A. Casares and P. Ohlmann. Positional -regular languages. In Proc. 39th ACM/IEEE Symp. on Logic in Computer Science. Association for Computing Machinery, 2024.
- [12] K. Chatterjee, W. Dvorak, M. Henzinger, and V. Loitzenbauer. Conditionally optimal algorithms for generalized büchi games. In 41st Int. Symp. on Mathematical Foundations of Computer Science, volume 58 of LIPIcs, pages 25:1–25:15. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2016. doi:10.4230/LIPICS.MFCS.2016.25.
- [13] K. Chatterjee, R. Majumdar, and M. Jurdzinski. On Nash equilibria in stochastic games. In Proc. 13th Annual Conf. of the European Association for Computer Science Logic, volume 3210 of Lecture Notes in Computer Science, pages 26–40. Springer, 2004. doi:10.1007/978-3-540-30124-0_6.
- [14] T. Colcombet and D. Niwiński. On the positional determinacy of edge-labeled games. Theoretical Computer Science, 352(1):190–196, 2006. doi:10.1016/J.TCS.2005.10.046.
- [15] R. Condurache, E. Filiot, R. Gentilini, and J.-F. Raskin. The complexity of rational synthesis. In Proc. 43th Int. Colloq. on Automata, Languages, and Programming, volume 55 of LIPIcs, pages 121:1–121:15. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2016. doi:10.4230/LIPICS.ICALP.2016.121.
- [16] F. Delgrange, J.P. Katoen, T. Quatmann, and M. Randour. Simple strategies in multi-objective mdps. In Proc. 26th Int. Conf. on Tools and Algorithms for the Construction and Analysis of Systems, pages 346–364. Springer International Publishing, 2020.
- [17] J. Dubreil, Ph. Darondeau, and H. Marchand. Supervisory control for opacity. IEEE Transactions on Automatic Control, 55(5):1089–1100, 2010. doi:10.1109/TAC.2010.2042008.
- [18] S. Dziembowski, M. Jurdzinski, and I. Walukiewicz. How much memory is needed to win infinite games. In Proc. 12th ACM/IEEE Symp. on Logic in Computer Science, pages 99–110, 1997.
- [19] R. Ehlers. Symbolic bounded synthesis. In Proc. 22nd Int. Conf. on Computer Aided Verification, volume 6174 of Lecture Notes in Computer Science, pages 365–379. Springer, 2010. doi:10.1007/978-3-642-14295-6_33.
- [20] E.A. Emerson and C. Jutla. The complexity of tree automata and logics of programs. In Proc. 29th IEEE Symp. on Foundations of Computer Science, pages 328–337, 1988.
- [21] E.A. Emerson and C. Jutla. Tree automata, -calculus and determinacy. In Proc. 32nd IEEE Symp. on Foundations of Computer Science, pages 368–377, 1991.
- [22] E. Filiot, N. Jin, and J.-F. Raskin. An antichain algorithm for LTL realizability. In Proc. 21st Int. Conf. on Computer Aided Verification, volume 5643, pages 263–277, 2009. doi:10.1007/978-3-642-02658-4_22.
- [23] D. Fisman, O. Kupferman, and Y. Lustig. Rational synthesis. In Proc. 16th Int. Conf. on Tools and Algorithms for the Construction and Analysis of Systems, volume 6015 of Lecture Notes in Computer Science, pages 190–204. Springer, 2010. doi:10.1007/978-3-642-12002-2_16.
- [24] S. Fortune, J. Hopcroft, and J. Wyllie. The directed subgraph homeomorphism problem. Theoretical Computer Science, 10(2):111–121, 1980. doi:10.1016/0304-3975(80)90009-2.
- [25] H. Gimbert and W. Zielonka. Games where you can play optimally without any memory. In Proc. 16th Int. Conf. on Concurrency Theory, volume 3653 of Lecture Notes in Computer Science, pages 428–442, 2005. doi:10.1007/11539452_33.
- [26] E. Grädel. Positional determinacy of infinite games. In Proc. 21st Symp. on Theoretical Aspects of Computer Science, volume 2996 of Lecture Notes in Computer Science, pages 4–18, 2004. doi:10.1007/978-3-540-24749-4_2.
- [27] D. Harel, G. Katz, A. Marron, and G. Weiss. Non-intrusive repair of reactive programs. In 17th IEEE International Conference on Engineering of Complex Computer Systems, ICECCS 2012, Paris, France, July 18-20, 2012, pages 3–12. IEEE Computer Society, 2012. doi:10.1109/ICECCS.2012.25.
- [28] D. Harel and A. Pnueli. On the development of reactive systems. In K. Apt, editor, Logics and Models of Concurrent Systems, volume F-13 of NATO Advanced Summer Institutes, pages 477–498. Springer, 1985.
- [29] C. Hugenroth. Zielonka dag acceptance and regular languages over infinite words. In Developments in Language Theory, pages 143–155. Springer Nature Switzerland, 2023.
- [30] P. Hunter and A. Dawar. Complexity bounds for regular games. In 30th Int. Symp. on Mathematical Foundations of Computer Science, volume 3618, pages 495–506. Springer, 2005. doi:10.1007/11549345_43.
- [31] P. Hunter, G.A. Pérez, and J.F. Raskin. Reactive synthesis without regret. In Proc. 26th Int. Conf. on Concurrency Theory, volume 42 of Leibniz International Proceedings in Informatics (LIPIcs), pages 114–127. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2015. doi:10.4230/LIPICS.CONCUR.2015.114.
- [32] N. Immerman. Number of quantifiers is better than number of tape cells. Journal of Computer and Systems Science, 22(3):384–406, 1981. doi:10.1016/0022-0000(81)90039-8.
- [33] B. Jobstmann, A. Griesmayer, and R. Bloem. Program repair as a game. In Proc. 17th Int. Conf. on Computer Aided Verification, volume 3576 of Lecture Notes in Computer Science, pages 226–238, 2005. doi:10.1007/11513988_23.
- [34] M. Jurdzinski. Deciding the winner in parity games is in UP co-UP. Information Processing Letters, 68(3):119–124, 1998.
- [35] N. Klarlund. Progress measures, immediate determinacy, and a subset construction for tree automata. Annals of Pure and Applied Logic, 69(2):243–268, 1994. doi:10.1016/0168-0072(94)90086-8.
- [36] E. Kopczyński. Half-positional determinacy of infinite games. In Proc. 33rd Int. Colloq. on Automata, Languages, and Programming, volume 4052 of Lecture Notes in Computer Science, pages 336–347. Springer, 2006. doi:10.1007/11787006_29.
- [37] D. Kuperberg and A. Majumdar. Width of non-deterministic automata. In Proc. 35th Symp. on Theoretical Aspects of Computer Science, volume 96 of LIPIcs, pages 47:1–47:14. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2018. doi:10.4230/LIPICS.STACS.2018.47.
- [38] O. Kupferman, Y. Lustig, M.Y. Vardi, and M. Yannakakis. Temporal synthesis for bounded systems and environments. In Proc. 28th Symp. on Theoretical Aspects of Computer Science, pages 615–626, 2011.
- [39] O. Kupferman and N. Shenwald. Games with trading of control. In Proc. 34th Int. Conf. on Concurrency Theory, volume 279 of Leibniz International Proceedings in Informatics (LIPIcs), pages 19:1–19:17. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2023. doi:10.4230/LIPICS.CONCUR.2023.19.
- [40] O. Kupferman and N. Shenwald. Games with weighted multiple objectives. In 22nd Int. Symp. on Automated Technology for Verification and Analysis, Lecture Notes in Computer Science. Springer, 2024.
- [41] D.A. Martin. Borel determinacy. Annals of Mathematics, 65:363–371, 1975.
- [42] S. Nain and M.Y. Vardi. Solving partial-information stochastic parity games. In Proc. 28th ACM/IEEE Symp. on Logic in Computer Science, pages 341–348. IEEE Computer Society, 2013. doi:10.1109/LICS.2013.40.
- [43] N. Nisan, T. Roughgarden, E. Tardos, and V.V. Vazirani. Algorithmic Game Theory. Cambridge University Press, 2007.
- [44] P. Ohlmann. Characterizing positionality in games of infinite duration over infinite graphs. In Proc. 37th ACM/IEEE Symp. on Logic in Computer Science. Association for Computing Machinery, 2022.
- [45] P. Ohlmann and M. Skrzypczak. Positionality in and a completeness result, 2024. arXiv:2309.17022.
- [46] A. Pnueli and R. Rosner. On the synthesis of a reactive module. In Proc. 16th ACM Symp. on Principles of Programming Languages, pages 179–190, 1989.
- [47] D. Raju, R. Ehlers, and U. Topcu. Playing against opponents with limited memory. CoRR, abs/2002.07274, 2020. arXiv:2002.07274.
- [48] D. Raju, R. Ehlers, and U. Topcu. Adapting to the behavior of environments with bounded memory. In Proc. 12th International Symposium on Games, Automata, Logics and Formal Verification, 2021.
- [49] S. Schewe. Minimising good-for-games automata is NP-complete. In Proc. 40th Conf. on Foundations of Software Technology and Theoretical Computer Science, volume 182 of LIPIcs, pages 56:1–56:13. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2020. doi:10.4230/LIPICS.FSTTCS.2020.56.
- [50] S. Schewe and B. Finkbeiner. Bounded synthesis. In 5th Int. Symp. on Automated Technology for Verification and Analysis, volume 4762 of Lecture Notes in Computer Science, pages 474–488. Springer, 2007. doi:10.1007/978-3-540-75596-8_33.
- [51] W. Thomas. On the synthesis of strategies in infinite games. In Proc. 12th Symp. on Theoretical Aspects of Computer Science, volume 900 of Lecture Notes in Computer Science, pages 1–13. Springer, 1995. doi:10.1007/3-540-59042-0_57.
- [52] M. Ummels. The complexity of Nash equilibria in infinite multiplayer games. In Proc. 11th Int. Conf. on Foundations of Software Science and Computation Structures, pages 20–34, 2008.
- [53] M.Y. Vardi and P. Wolper. Automata-theoretic techniques for modal logics of programs. Journal of Computer and Systems Science, 32(2):182–221, 1986. doi:10.1016/0022-0000(86)90026-7.
- [54] J. von Neumann and O. Morgenstern. Theory of games and economic behavior. Princeton University Press, 1953.
- [55] W. Zielonka. Infinite games on finitely coloured graphs with applications to automata on infinite trees. Theoretical Computer Science, 200(1-2):135–183, 1998. doi:10.1016/S0304-3975(98)00009-7.
