An Axiomatic Study of Leveraging Blockers to Self-Assemble Arbitrary Shapes via Temperature Programming
Abstract
In this paper we present a theoretical design for tile-based self-assembling systems where individual tile sets that are universal for various tasks (e.g. building shapes or encoding arbitrary data for algorithmic systems) can be provided their input solely using sequences of variations in temperatures. Although there is prior theoretical work in so-called “temperature programming,” the results presented here are based upon recent experimental work with “blocked tiles” that provides plausible evidence for their practical implementation. We develop and present an abstract mathematical model, the BlockTAM, for such systems that is based upon the experimental work, and provide constructions within it for universal number encoding systems and a universal shape building construction. These results mirror previous results in temperature programming, covering the two ends of the spectrum that seek to balance the scale factors of assemblies with the number of temperature phases required, while leveraging the features of the BlockTAM that we hope provide a pathway for future experimental implementations.
Keywords and phrases:
DNA tiles, self-assembly, temperature programmingFunding:
Matthew J. Patitz: This author’s work was supported in part by NSF grant 2329908.Copyright and License:
2012 ACM Subject Classification:
Theory of computation Models of computationSupplementary Material:
Software: http://self-assembly.net/software/BlockTAM_examples/BlockTAM_examples-source-2025-04-23-14-42-34.zipEditors:
Josie Schaeffer and Fei ZhangSeries and Publisher:
 Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
One of the central themes of technological advancement is mastering the manipulation of matter. In particular, humans have been fascinated with the construction of arbitrary structures since the beginning of human history. At times, this fascination has been due to the fact that survival has depended on a sufficient mastery of crafting structures while at other times this fascination has had more recreational roots. Over the millennia, humans have mastered building macroscale structures, but the idea of constructing nanoscale structures was unfathomable until relatively recently. Even though the manufacture of arbitrary nanoscale shapes may be a new endeavor for humanity, we are already seeing it begin to take a central role in the development of our future. Nanoscale structures are already proving to be useful both in terms of aiding in humanity’s survival and recreational pursuits as nanoscale structures have seen a wide range of uses including molecular computers [24], drug delivery [22], and lithographically-patterned electronic/photonic devices [6].
Observing and influencing matter at the nanoscale presents a seemingly insurmountable challenge since the structures at this scale are smaller than the wavelengths of visible light. How can we build a structure that we cannot see using components whose location we cannot control? As opposed to the traditional macroscopic approach, self-assembly uses a bottom up approach: instead of attempting to mechanically manipulate components to place them in certain relative locations, chemically manipulate components so that they are prone to stick together in specific locations relative to one another. Unfortunately, this general approach is still quite abstract and difficult to leverage, with successful physical realizations remaining elusive. In 1981, Ned Seeman proposed leveraging the programmability and specificity of deoxyribonucleic acid (DNA) to implement such self-assembling systems, and he constructed the first intentionally designed DNA nanostructure[3, 19].
Building on the work of Ned Seeman, Erik Winfree introduced and physically realized a framework to make the design of DNA nanostructures more tractable (and hence, less error prone) [23]. This framework uses designed DNA strands to assemble molecules that behave like square “tiles” with programmable “glues” that allow a tile to bind to other particular tiles. This approach is known as tile-based DNA self-assembly. Peng Yin et al. [9] leveraged this approach to develop a technology capable of assembling arbitrary nanoscale structures (where the resolution is limited by the size of the molecule that acts as a tile). William Shih et al. [12] further refined this approach (albeit with non-planar, non-square tiles) to eliminate technical hurdles which resulted in less than desirable error rates.
In 2006, Paul Rothemund introduced a new paradigm for the assembly of arbitrary nanostructures from DNA [17]. Like Winfree’s framework, Rothemund’s framework constrains the problem of designing DNA nanostructures by placing it into a logical framework to make the problem more tractable. This framework is known as DNA origami. The idea is to create the target structure by folding a very long DNA strand, called the scaffold strand, into the target shape through the use of small staple strands which bind to multiple positions along the scaffold. These staple strands pinch, or collocate, certain parts of the scaffold strand together and the net effect of this is to fold the scaffold strand into the target structure.
Regardless of which ubiquitous method listed above is used, each significantly different target structure requires a unique set of DNA strands to assemble it. Designing, synthesizing, ordering, and preparing these DNA strands for experiments is costly in terms of time, money and labor. This process also introduces the possibility of human errors and unintended sequence interactions. One way to reduce this burden of requiring new DNA strands is to reduce the number of new strands needed by as much as possible. Soleveichik and Winfree showed that in an axiomatic model of tile-based self-assembly, a target structure can be assembled using (nearly) information theoretic optimal number of strands [20]. While the result of Soleveichik and Winfree greatly reduces (theoretically) the number of strands that needed to assemble a new target structure, it does not completely eliminate it.
Is it possible to design a fixed set of DNA strands that can assemble any arbitrary shape without the need for pipetting or any other manual intervention steps? In the standard axiomatic model of tile-based self-assembly, it is not possible to eliminate the need for new DNA strands for assembling new target structures (since this is how input is passed into the system specifying what structure it should assemble). But, in [21], Summers showed (theoretically) that a fixed set of tiles could assemble any arbitrary 2D shape by controlling the growth of the assembly using controlled temperature fluctuations. This was shown in the multiple temperature model originally introduced in [1]. Unfortunately, this model makes a couple of assumptions which have yet to be demonstrated in the laboratory setting, namely that temperature fluctuations do not lead to tiles aggregating off of the seed assembly and that the binding of one tile to an assembly can prevent the binding of another tile to the assembly. Fortunately, recent experimental work has shown temperature programming may be feasible in the laboratory setting through the use of blockers. This is discussed in the next section.
Experimental Motivation
As mentioned above, previous theoretical results on temperature programming relied on two yet to be demonstrated mechanisms: 1) suppressing interactions of sticky glues off-seed at lower temperatures and 2) using the existence of a tile in the assembly to prevent the binding of another tile.
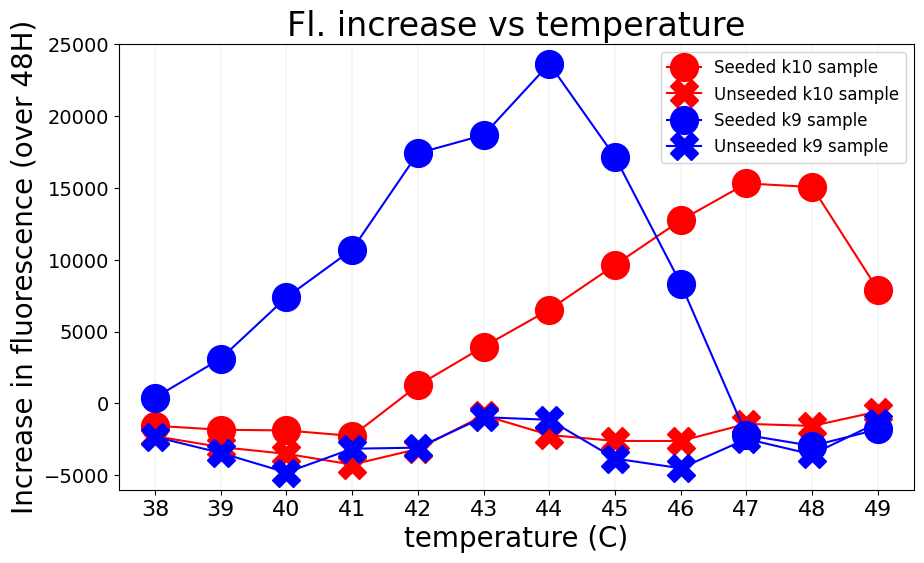
Recent experimental work [16] has shown that by “poisoning” systems with single glue domain length strands, called blockers, which are complementary to “input” glues, that one can not only “turn off” high strength (that is, very sticky) glues at lower temperatures, but also suppress spurious nucleation (that is, off-lattice interactions that lead to structures not grown from a seed) across all temperatures. This is thought to be due to the binding penalty induced by blockers being multiplicative for pathways that lead to spurious nucleation (which leads to an exponential impact on the spurious nucleation rate) while having a less significant impact on the growth rate of seeded assemblies since the penalty will result in linear slowdown [5]. Figure 1(a), constructed from data in [15], shows this effect in practice. In the presence of a seed, growth may be slowed, but still proceeds at a reasonable rate (as indicated by the increase in fluorescence in samples with seeds), while spurious nucleation is suppressed to undetectable levels across all temperatures (as indicated by the relatively flat fluorescence trace of unseeded samples). Also, shown in this plot is the deactivation effect blockers have on stickier (that is, high-strength) glues at lower temperatures. It shows the growth rate of tiles consisting of length 10 glues becomes suppressed to undetectable levels at lower temperatures (evidenced by the insignificant increase in the seeded sample containing tiles with length 10 glues at temperatures and below) where the growth rate of tiles consisting of length 9 glues is still significant (evidenced by the significant increase in the seeded samples at these temperatures).
The Blocked Tile Assembly Model is inspired by the glue deactivation and spurious nucleation suppression afforded by blockers. But, it still remains in the realm of theory since attempting to implement such system in the laboratory could face technical hurdles such as spurious nucleation due to the oscillation of temperature or strain at the interfaces of tiles with different glue lengths preventing further growth. In [15], temperature programming was physically realized. The authors showed that the key mechanisms required to physically realize temperature programming are attainable, and they used these features to program nanotube length using temperature oscillations. When interpreted through the lens of the Blocked Tile Assembly Model, the construction in [15] is simple. Two sets of tiles which assemble a cross-section of a nanotube were designed: one having length 10 glues (which are the high strength glues) and the other having length 9 glues (which are the low strength glues). These tile sets were designed to form alternating cross-sections of the nanotube. Blockers were added to the input side of the length 10 glues preventing those tiles from attaching at a lower temperature where the length 9 glues are active. On the other hand, the tiles with length 9 glues are unable to attach at warmer temperatures were the length 10 glues are active. The authors leverage the exclusivity of growth temperatures to design a system which requires the temperature to be oscillated in order to grow the next segment of the tube. In this manner, the number of oscillations dictates the length of the nanotube. (See Figure 2 for an example system which illustrates this idea.)
Figure 1(b) presents atomic force microscopy (AFM) data from [15]) which shows a nanotube grown using the temperature programming technique described above. The segments composed of tiles with length 9 glues were marked with a special molecule so that they appear with bright dots on the image. The temperature was oscillated 4 times (that is, it was held a high temperature and then a low temperature and this process was repeated 4 times) so that we would expect to see 8 cross-section segments alternating between being unmarked and marked. Note that this is indeed what we see in the image. We see the seed, the bright tube in the bottom right-hand corner of the image, followed by eight alternating unmarked and marked segments. This provides evidence that the system is working as intended.
Our contributions
We first formally define the Blocked Tile Assembly Model that presents a formalization of the intuitive model used to design the system presented in [15], which is capable of using temperature to program tube length. A natural extension of the work presented in [15] is to examine whether we can leverage the mechanisms used in that paper to use temperature to program not just length, but the shape of the structure. This is akin to the idea of a 3D printer (although we work in 2 dimensions) which uses a universal ink to construct arbitrary structures. That is, can we assemble a target nanostructure purely through temperature fluctuations without the need to design, order, or add new strands?
We answer this question affirmatively through our two main results. The constructions we present rely on the same mechanisms already demonstrated in [15] with two exceptions. Our constructions rely on having three or more tile sets which have disjoint growth temperatures. In other words, our constructions would require something like length 8 glues in addition to length 9 and length 10 glues. Another yet to be experimentally demonstrated mechanism is having mismatches in the glues between neighboring tiles. However, this mechanism has been demonstrated experimentally, albeit unintentionally, with other DNA tile motifs through the occurrence of errors in algorithmic self-assembly [24]. Neither of these technical challenges appear insurmountable which provides us hope that these constructions, or at least somewhat simplified versions of them, may be experimentally feasible.
Our first main result provides a way for a single BlockTAM tile and blocker set, always beginning from the same seed tile, to receive, and then encode, an arbitrary input value into the glues of a row of tiles solely via a sequence of temperature changes. We call this a universal number encoder, and such a system could be combined with an aTAM system designed to perform any algorithmic self-assembly task by first reading that information as its input and then carrying out its algorithmic growth. Dozens of powerful examples of algorithmic self-assembling systems have been theoretically demonstrated, e.g. [18, 20, 2, 10, 14, 11], and one in particular worth mentioning is that of [20] in which such an input sequence could be the information-theoretically optimal encoding of the definition of an arbitrary shape so that the assembly then proceeds to grow into a scaled version of that shape.
This leads naturally to our second main result, which we call a universal shape builder, and is a fixed tile and blocker set such that, given any arbitrary shape , a system that always begins from the same seed tile can be controlled by a temperature sequence taken from the set of temperatures that is specific to so that the resulting terminal assembly is in the shape of at a constant scale factor of .
As an input module to the construction of [20], our universal number encoder is also a version of a universal shape builder, and although it is optimal in terms of the number of temperature phases required to build an arbitrary shape, the scale factor of the shape is extremely large.111The scale factor would depend on the particular shape, but would likely be on the order of at least tens of thousands. However, while our second construction requires a number of temperature phases that is linear in the number of points in the target shape, its scale factor is a mere . In combination, these results provide evidence of the broad powers and potential of the BlockTAM and inspiration for both further theoretical and experimental implementations.
Both results have been fully designed, implemented, and simulated. Python code that can be used to generate example systems for both results (along with pre-existing examples) [13] and a web-based simulator [8] can be accessed from: http://self-assembly.net/wiki/index.php/Blocked_Tile_Assembly_Model_(BlockTAM).
2 Preliminary Definitions and Models
2.1 The Blocked Tile Assembly Model Intuition
We begin by providing a high-level overview of the aTAM and BlockTAM so that readers familiar with the aTAM may skip the formal definitions section.
The abstract Tile Assembly Model is a tile-based model of self-assembly where growth proceeds from an initial assembly called the seed and proceeds asynchronously and nondeterministically via single-tile attachments. The systems which make up the abstract Tile Assembly Model (aTAM) are called tile assembly systems (TAS) and they are triples where is the set of tile types, is the seed assembly, and is the temperature, or minimum binding threshold, of the system. Growth of the system begins from the seed and grows via single tile attachments (where the tiles come from the tile set ) provided that each tile binds to the assembly with at least a combined strength of .
The Blocked Tile Assembly Model (BlockTAM) is an adaptation of the Multiple Temperature Model introduced in [4]. To formally define this model, we first define a 1 Phase Blocked Tile Assembly Model (1BlockTAM). The BlockTAM can be thought of as consisting of a sequence of 1BlockTAM systems where the resulting terminal assembly of the system is fed into the system as a seed.
A system in the 1 Phase Blocked Tile Assembly Model (1BlockTAM) is a 4-tuple where , and are defined as in the aTAM, and is defined to be a set of “blockers”. A blocker is defined as a triple where is a tile, is a direction on the tile, and is a strength. Growth of the system proceeds as in the aTAM with the exception that any glue which has a blocker whose strength is is treated as a strength 0 glue (to reflect the fact that the glue is “blocked”). We formalize this by constructing an aTAM system from the 1BlockTAM system where any glues that are “blocked” in the system have their strength set to 0 and defining the behavior of the 1BlockTAM system to be the same as the derived aTAM system.
2.2 Abstract Tile Assembly Model
The definitions below are an adaptation of the abstract Tile Assembly Model (aTAM) definition presented in [7]. We note that [18] and [11] are good introductions to the model for unfamiliar readers.
Let be the set of nonnegative integers, and for , let . Similarly, for , let .
Fix to be some alphabet with its finite strings. A glue consists of a finite string label and non-negative integer strength. A tile type is a tuple , thought of as a unit square with a glue on each side. A tile set is a finite set of tile types. We always assume a finite set of tile types, but allow an infinite number of copies of each tile type to occupy locations in the lattice, each called a tile.
Given a tile set , a configuration is an arrangement (possibly empty) of tiles in the lattice , i.e. a partial function . Two adjacent tiles in a configuration interact, or are bound or attached, if the glues on their abutting sides are equal (in both label and strength) and have positive strength. Each configuration induces a binding graph whose vertices are those points occupied by tiles, with an edge of weight between two vertices if the corresponding tiles interact with strength . An assembly is a configuration whose domain (as a graph) is connected and non-empty. The shape of assembly is the domain of . For some , an assembly is -stable if every cut of has weight at least , i.e. a -stable assembly cannot be split into two pieces without separating bound tiles whose shared glues have cumulative strength . Given two assemblies , we say is a subassembly of (denoted ) if and for all , (i.e., they have tiles of the same types in all locations of ).
A tile-assembly system (TAS) is a triple , where is a tile set, is a finite -stable assembly called the seed assembly, and is called the binding threshold (a.k.a. temperature). If the seed consists of a single tile, i.e. , we say is singly-seeded. Given a TAS and two -stable assemblies and , we say that -produces in one step (written ) if and . That is, if differs from by the addition of a single tile. The -frontier is the set of locations in which a tile could -stably attach to . When is clear from context we simply refer to these as the frontier locations.
We use to denote the set of all assemblies of tiles in tile set . Given a TAS , a sequence of assemblies over is called a -assembly sequence if, for all , . The result of an assembly sequence is the unique limiting assembly of the sequence. For finite assembly sequences, this is the final assembly; whereas for infinite assembly sequences, this is the assembly consisting of all tiles from any assembly in the sequence. We say that -produces (denoted ) if there is a -assembly sequence starting with whose result is . We say is -producible if and write to denote the set of -producible assemblies. We say is -terminal if is -stable and there exists no assembly that is -producible from . We denote the set of -producible and -terminal assemblies by . If , i.e., there is exactly one terminal assembly, we say that is directed. When is clear from context, we may omit from notation.
2.3 The 1-Phase Blocked Tile Assembly Model
Assembly in the BlockTAM proceeds through a series of temperature phases, each of which consists of a hold at a specified temperature during which growth proceeds until all assemblies are terminal. Once all assemblies are terminal, the temperature of the system is set to the next temperature in a specified series and remains there until all growth is again terminal. This process continues until all growth is terminal during the last temperature phase. Note that a temperature sequence must be finite and that infinite growth (in the limit) during a phase is only allowed during the final phase.
Although the BlockTAM shares similarities with other tile-assembly models that allow for temperature variations (e.g. [1, 21]), additional complexity arises from the fact that, at different temperatures, different subsets of the blockers in a system may be actively blocking glues. Therefore, to ease explanation of the BlockTAM, here we first define its dynamics during a single phase, then in Section 2.4 define the full model in terms of phases.
In order to easily translate between a tile and its blocked version, we assume all distinct glues have distinct labels. That is, there are not two glues with the same labels, but different strengths. This is a simple transformation that can be obtained by relabeling each glue so that the new label is a concatenation of the glue’s original label along with its strength.
A blocker is defined as a triple where is a tile, is a direction on the tile, and is a strength. We say that a blocker binds to tile on its edge with strength . Let be a tile, be a set of blockers, and be a temperature, then we define the tile blocked at temperature by blocker set , denoted to be the tile with the same glues as unless there is a blocker which binds at the location of the glue on the tile with strength greater than or equal to . Note that when and are obvious from context, we simply write . Also, since we define an assembly to map points to tiles we can compose this function with an assembly to obtain a function which maps each point to a blocked version of the tile. We define the function unblocked to be the inverse of the blocked function. That is, . The function blocked is invertible due to our assumption distinct glues have distinct labels.
A 1-Phase BlockTAM system (1BlockTAS) is a 4-tuple where is a tile set, is a blocker set, is the seed assembly, and is the temperature. We define the equivalent TAS of , denoted , to be the aTAM system where consists of a modified version of such that any glue whose blocker binds with strength is set to have strength . That is . Given a 1BlockTAS and two -stable assemblies and formed from tiles in , we say that -produces in one step, written , if . The -frontier is the set .
Given a 1BlockTAS , a sequence of assemblies over is called a assembly sequence if is a -assembly sequence. We say that -produces denoted if . We say that is -producible if and write to denote the set of -producible assemblies. We is -terminal if is -terminal. We denote the set of -producible and -terminal assemblies by . We say that is directed provided that is directed.
2.4 The Blocked Tile Assembly Model
The following formal definitions are an adaptation of those used to define the Multiple Temperature Model in [21].
A BlockTAM system (BlockTAS) is a 4-tuple where is a tile set, is a blocker set, is the seed assembly, and is a sequence of non-negative binding thresholds. The number is the temperature complexity.
We define an assembly sequence for the temperature phase, for , of as follows. For , an assembly sequence is an assembly sequence of the 1BlockTAS . For , an assembly sequence for temperature phase of is a sequence of assemblies satisfying the following conditions.
-
1.
There exists such that is -stable , and is an assembly sequence for temperature phase of ; and
-
2.
for all , either or is obtained from by deleting the portion of which does not contain the seed across a cut having strength less than .
Intuitively, an assembly sequence for the temperature phase is defined recursively. That is, we say that is an assembly sequence for the temperature phase provided that (1) if , then is an assembly sequence of the 1BlockTAS and (2) if , then two conditions must be met. The first condition says that there exists such that the sequence can be broken up at so that the sequence up to index is an assembly sequence for the temperature phase. Condition 2 says that the sequence after index is a sequence of assemblies such that can be obtained from by either (1) a single tile addition (with combined binding strength of at least ) or (2) by “melting off” a subassembly from with a cut of strength .
An assembly sequence in is an assembly sequence for the temperature phase of for some . We say that an assembly sequence in finishes every temperature phase of if is a finite assembly sequence for temperature stage of and its final assembly, denoted , is -stable and . In this case, we call a terminal assembly and write . If , then we say that is directed. Given system , let (i.e. the maximum value of any stage). We say that is -robust if every terminal assembly of every temperature phase is -stable. In a -robust system, no temperature change causes any portions of any assemblies to dissociate and thus growth is monotone. All constructions in this paper are -robust.
If for every , , then we say that self-assembles the shape . Given , a connected set of points in , we define a version of scaled by factor , and denote it by , as . If for every , there exists such that , then we say that self-assembles the shape at scale factor . Note that the Blocked Tile Assembly Model is defined so that a “blocked glue” on a tile which binds into the assembly immediately binds to any neighboring glue.
2.5 BlockTAM System Example
We now provide a simple example of a BlockTAM system to familiarize the reader with key ideas and notation regarding the model. This example is inspired by the system designed in [15]. Part (a) of Figure 2 shows a BlockTAS . In this example, we assume that all blockers bind with the same strength as the glue. If a temperature TAS was defined to have the same tile set and seed as , the assembly shown in part (b) of Figure 2 would be an element of (that is, the assembly is producible by ). Parts (c) and (d) Figure 2 shows the equivalent blocked tile assembly systems for each temperature phase of and the terminal assembly for each. Note that in part (c), the shown producible assembly of is terminal since the blue tile lacks the strength required to attach. In part (d), the shown assembly is terminal in the context of since the red tile is blocked (meaning it has strength ) and is consequently unable to attach.
3 Encoding Input Values via Temperature Sequences
In this section we present a construction that works in two parts. In the first, the input is a set of temperatures (i.e. positive integers), which we’ll denote as . Using this set of temperatures, the first part of the construction returns a tile set, set of blockers, and seed tile that compose a universal number encoder that is specific for that set of temperatures.
The input to the second part is an arbitrary value , and the output is a sequence of temperatures over such that a BlockTAM system made using that sequence and the universal number encoder previously produced results in a terminal assembly that is a rectangle with an encoding of the value (in a base to be discussed) represented by its northern glues. The design is such that, as previously mentioned, a standard temperature-2 aTAM tile set could then attach to read that encoding as its input and carry out arbitrary algorithmic self-assembly.
A notable feature of our construction it is that is generalized so that it works for any set consisting of at least temperatures, creating a universal number encoder specific to that . This allows for maximal design flexibility in terms of optimizing between tile complexity (i.e. the number of unique tile types required), glue diversity (in terms of numbers of unique sequences and unique strengths), and the temperature complexity (i.e. the number of distinct temperature phases required). In general, the greater the variety of temperatures allowed (i.e. larger ) the greater the tile and glue complexity but the lower the temperature complexity.
3.1 Generation of a universal number encoder
As mentioned, the input is a set of temperatures, . The construction requires at least three distinct allowable temperature values since having only two possible temperatures in a BlockTAM system does not allow any way to create series of temperature sequences that are distinct from each other for different values to encode without using unary encoding, which is infeasible for all but the very smallest values.
Let be the number of temperatures, and let be sorted from lowest to highest. For clarity, we will often use to refer to . The tile set that we are creating will be specific to the values of , but will be able to build assemblies representing arbitrary values of . Each such will be encoded in some base , which is determined as follows: if then , otherwise . Let be an arbitrary number to eventually be encoded. In general, encoding in base requires values. However, if it will be necessary to represent each bit of the base representation of using bits (for reasons to be explained later). Therefore, let represent the number of values needed to represent the encoding of a given value in base .
The target assembly will consist of columns. The glue exposed on the north of the top tile of the first column will be a special “start” glue, and the northern glue of each of the following columns will encode subsequent values of the encoding of . The north-south glues binding the tiles of a column will all be of strength equal to so that each column is -stable across all temperatures of the system. However, the glues that bind each column to another will consist of varying strengths from . Therefore, when glues of any strength are used, it will be necessary for multiple glues of that strength to bind the columns together to ensure stability if/when the system temperature is set to .

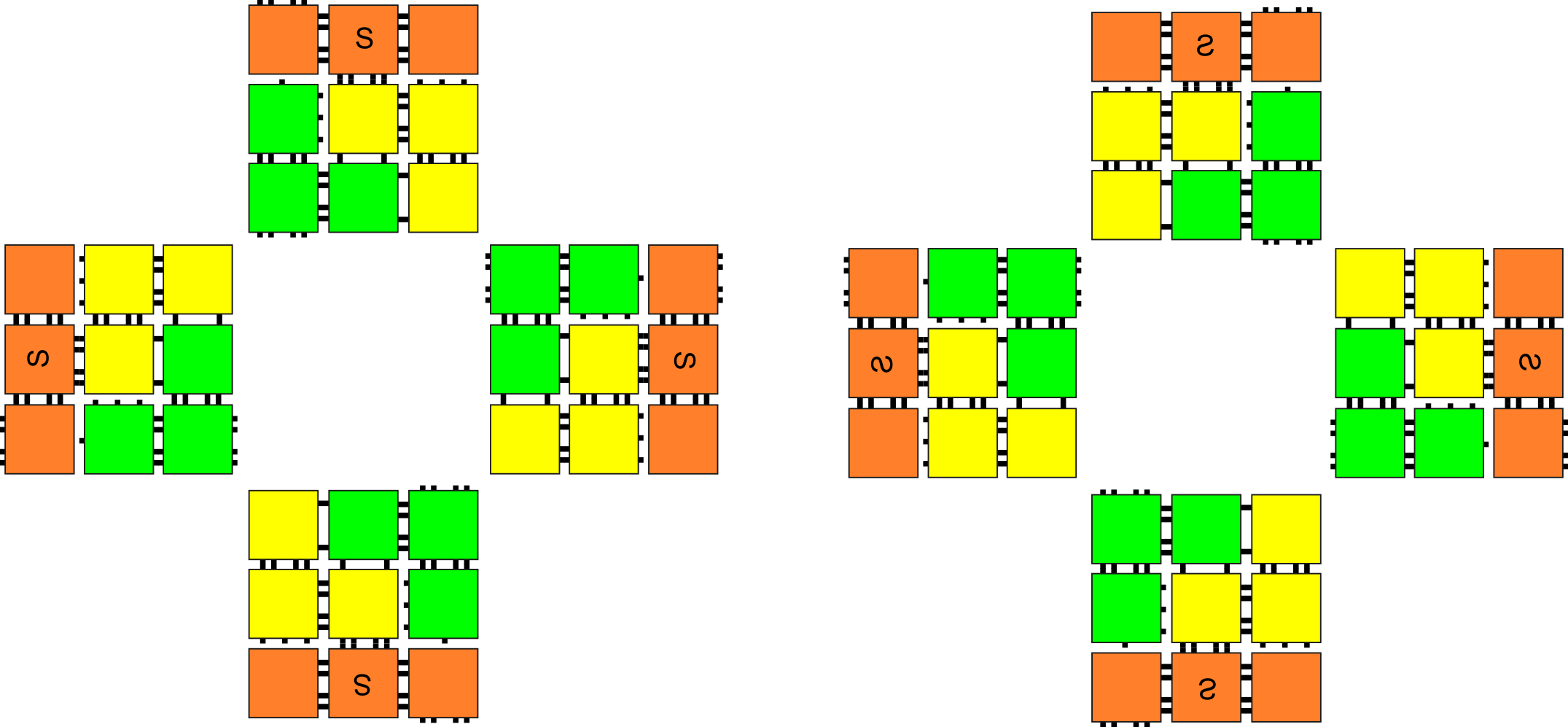
Let be the height of a column (with the determination of the value to be explained later). We refer to the bottom location of a column as and the one above that as , continuing up to the topmost at . Across all columns, the row at each location for is dedicated to tiles whose east/west glues are of the same strength, which we’ll refer to as . Furthermore, the binding of any pair of columns to each other will be via one or more glues all of the same strength. To compute we first determine how many instances of each temperature in are required to sum to the smallest value . We then take the sum of that sum to be . For example, if the set of possible temperatures is , since it takes glues of strength to sum to , each of strength and , and of course only of strength . Thus, every column in a system using those temperature values would be of height . (See Figures 3 and 4 for examples.)
With the value as the necessary height of each column, we then compute the assignment of each , that is, which east/west strengths are assigned to each row . Since these are the glues that bind neighboring columns to each other, we try to assign them to maximize stability. Therefore, we assign the center location to the strongest glue, . Then, since each weaker glue requires two or more locations (so that the multiple copies of each can sum to ), we assign them moving outward from the center, alternating up and down for each subsequently weaker glue until all positions are assigned. Examples can be seen in Figures 3 and 4. For instance, Figure 3 shows how the strengths and are assigned, with the ordering from bottom to top being .
Since the north/south glues between the tiles of each column are of strength , and now we know the strengths of the east/west glues for the tiles at each height, we can determine how to create the columns necessary to represent the values of the numbers to be encoded. Note that a seemingly straightforward method would be to create one unique column for each value that needs to be represented to the north. However, then it is not possible for the encoding to contain the same symbol in two consecutive positions (e.g. the binary representation of , which has two pairs of consecutive s) since then the same column would have to be able to connect to a copy of itself, which would result in “pumping” into an infinite sequence of s. A relatively simple fix to that problem would be to have a column that doesn’t represent any value that could then be located between each value-encoding column. However, this would double the number of temperature phases needed, and that is the primary metric that we are trying to minimize. Therefore, we use the following scheme which compresses the temperature sequence at the expense of requiring slightly more unique tile types (approximately double).
Our method of creating columns for encoded values works by permuting over all pairs of (non-identical) temperatures from . Let be the number of unique temperatures. For each , there are temperatures such that . For each such pair we create exactly one unique column and we assign a value for that column to encode from the set . (Note that, in the case where , no “” character is explicitly used but instead the ending condition is encoded using a special sequence of bits, to be discussed in Section 3.2.) This mapping from each pair of temperatures to an encoded value is referred to as the column_transition_map (and the code used to generate it can be seen in Listing 1 in the Appendix). The resulting map ensures that any encoded symbol can follow any other, except for the “” symbol which is the final symbol to be encoded by the last temperature phase. (Again, when , there is no “” symbol, just s and s, which will each be able to follow each symbol.) Note that the column that contains the seed tile is unique, composed of tiles that only appear in that column, and its northernmost glue encodes the start value “”. The glue encoding “” is of strength 2, and all other value encoding glues are of strength 1. Once the number encoding assembly is terminal, the system temperature can be set to 2, allowing for a standard aTAM tile set to attach and grow across from left to right, reading the encoded value then proceeding with arbitrary algorithmic behavior.
To generate the tile type for each location of each column, we use the previously computed glue strengths for each side of each location and the information in the column_transition_map. For each temperature pair , again where , we generate a set of distinct tile types to create a unique column. The purpose of the column is to (1) encode the value column_transition_map in the north glue of its northernmost tile, (2) to have its growth initiated by a temperature phase of temperature , and (3) to grow immediately to the right of a column whose growth was initiated by a temperature phase of temperature . To effect this, each north/south glue label between two tiles of a column are specific to the column type, i.e. , and location , e.g. for the glue pair between the th and th tile in the column for . On the east, output side of the tile in location is a glue of strength (which is the strength value assigned to that row) for all locations except that for which , which has no east-facing glue. As previously mentioned, this is to prevent the column from being able to initiate growth of another column to its right at the same temperature at which it grew. The label of each such glue will be , so that it can bind to a tile in the th location of the column for temperature sequence (assuming that the next phase is at temperature ). Figure 4 shows an example of these glues.
In this way, the full tile set is constructed. Next, the blocker set is created. This simply consists of a blocker for every west-facing glue that is strength if the glue’s strength is . This ensures that those “input” glues, which initiate the growth of each new column, are only active during phases of the temperatures for which their columns were designed, and growth proceeds with a single column forming for each phase.
With the designated seed tile being a tile of the type designed for the middle of the leftmost column, the resulting tile set, blocker set, and seed is a universal number encoder for . We next describe how to, given a specific value of to encode, compute the temperature sequence necessary for a BlockTAS to assemble an assembly encoding .
3.2 Temperature sequence generation
The input to this portion of the construction is a number and a universal number encoder from the previous portion. From that encoder, we can determine the base in which to encode . Additionally, we can know which of two paths to take to compute the encoding of : If the number of temperatures, , is , then will consist of a “doubled” base encoding, otherwise will simply be the encoding of in base (which is set to ), with the character “” appended to the end. Note that in either case, the encoding will begin with the “” symbol which is encoded by the column with the seed tile.
To compute the doubled encoding for the case of , we note that with only three temperatures to select from, once a given phase of assembly completes, which is necessarily at some , then there are only two choices for some other such that . Because of this, we can’t directly encode a symbol to mark the end of sequence, which makes it difficult or impossible for an algorithmic (aTAM-style) tile set to then read the encoded value and effectively use it as input that controls its algorithmic behavior. (It would either have to pause at the end of the assembly “waiting” for a stop symbol, or instead be able to grow on its own past the last symbol without cooperating with the assembly which means that at other points of growth it could “ignore” the assembly and grow without cooperation, yielding an invalid input. This is a well-known problem in the domain of tile-based self-assembly.) Therefore, we utilize the method of representing each bit of the binary encoding of as follows. We represent each by , and each by a . We build our encoding in this way, and to indicate the end of the sequence, after all bits have been encoded this way, we append two consecutive s. In this way, a tile set growing over the north of the terminal assembly and reading the encoding will be able to detect when it has read the final position.
Now with the encoded string , we convert that into a series of temperatures over . Because there are no blockers for tiles in the column containing the seed, that column grows at any temperature in , as all north/south glues are of strength . This means that no separate temperature phase is necessary to account for the placement of the “” symbol and the first temperature phase is used to grow the column of the first encoded value of . Additionally, the east-facing, output glues of the seed column use the same labels as a column that grew at the second highest temperature so that new glues do not need to be designed for tiles to attach to that column. Thus, for the first, and then each subsequent, encoded value we simply iterate over the values and examine the column_transition_map keeping track of which temperature was used to grow the previous column (pretending it was the second largest temperature if that was the seed column). For each , We find the unique such that column_transition_map. We then append that as the next temperature in the sequence. Iterating through the full encoded string, the resulting temperature sequence is the exact sequence that will cause the universal number encoder to build an assembly of columns expressing the encoded value of in its northern glues. (For details of a few examples of systems, please see Section A.1 of the Appendix.)
4 Using Temperature Changes to Steer Assembly Through Shapes
The most common goal in the design of a self-assembling system is for the resulting system to deterministically form into assemblies of a single, target shape. However, the goal of accurate shape-building must usually be balanced with competing factors such as minimizing the number of unique tile types required and the scale factor at which the shape is formed. In this section, we present a universal shape builder consisting of a fixed tile set, blocker set, seed tile, and temperature set that is capable of being utilized to build any arbitrary, finite (and necessarily connected) shape. That is, given an arbitrary shape , a temperature sequence exists that causes the BlockTAM system composed of these components to self-assemble a scaled version of , i.e. . If has a Hamiltonian path, our construction assembles at scale factor 3. If not, our construction assembles it at scale factor 6. It has valid temperature set , consists of 145 tile types with glues of strengths 1, 2, 3, and 4, and has 16 strength-3 and 16 strength-4 blockers. There is a single designated tile type for the seed.
We first explain the algorithm that takes as input an arbitrary shape and outputs a path through it. We then explain the tile set and how it is capable of following such a path. Finally, we demonstrate how that path can be converted into a series of temperatures to drive the universal shape constructor along it.
4.1 Finding a “turtle graphics” path
In [21] it was shown how, beginning with an arbitrary input shape , can be scaled by a factor of two to , and then a Hamiltonian path through can be created that visits each point in exactly once. (Note that any shape that already has a Hamiltonian path through it does not require the scaling by two, but we’ll assume that, in the worst case for an arbitrary , the scaling is required.) Using the technique of [21] we can convert that path into a series of “turtle graphics” instructions. That is, starting on the first point of the path, we simply follow a series of instructions taken from the set (which we’ll abbreviate as ) to visit every point on the path (and thus in ) exactly once. Let be the number of locations, or pixels, in the original shape . The output of this step is an ordered list , that is, a list of directions that allow one to begin at one point in and visit every other (since each pixel in is composed of 4 in , and we don’t need an instruction to get to the pixel from which the path begins).
4.2 The universal tile set
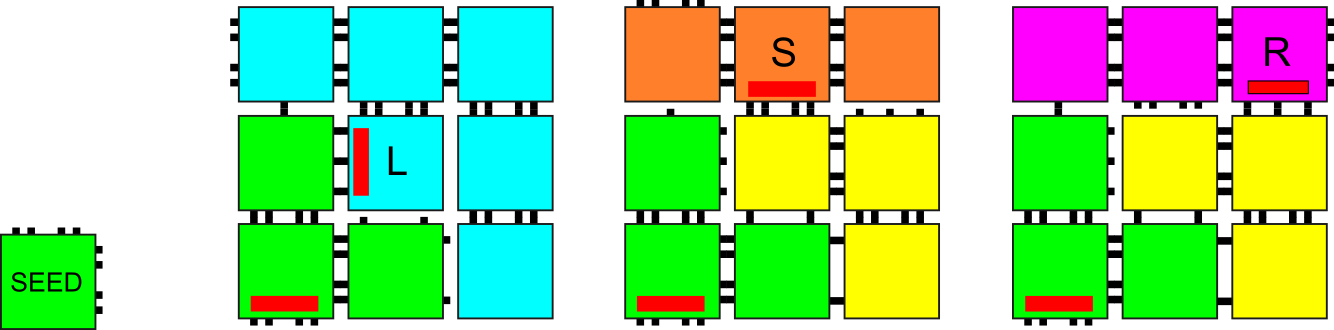
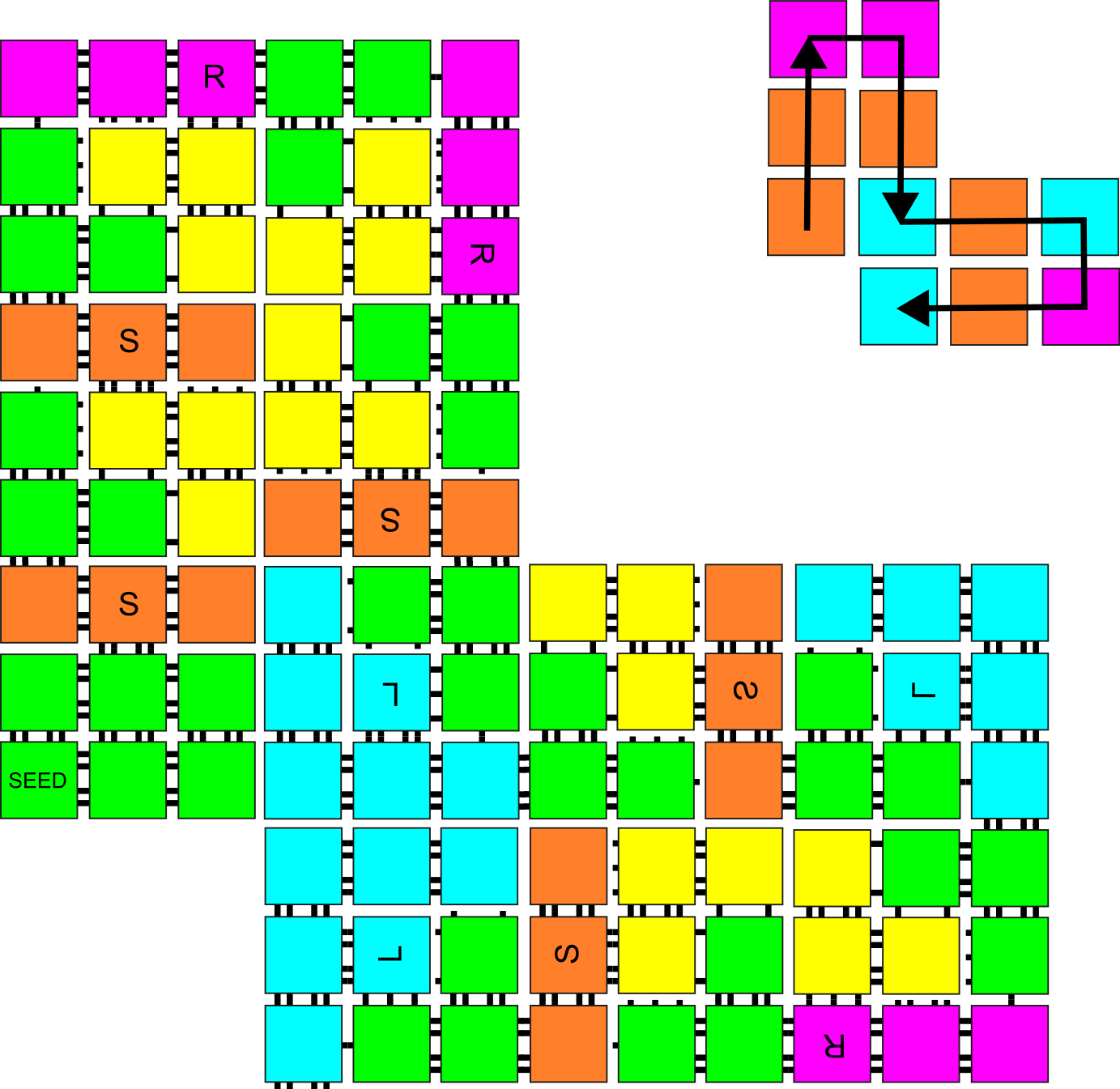
We now describe the tile set and blockers of the universal shape builder by explaining how they are able to follow such a path. The assembly that follows is composed of macrotiles that are squares of tiles. That is, each pixel of is represented by a square of tiles (yielding an overall scale factor of from ). Starting from the seed tile and with a temperature phase of , the first macrotile grows the base portion of a macrotile, which is composed of 3 tiles (that can be seen as green in the macrotiles in Figure 5). The macrotile then becomes terminal, until the next temperature phase begins. A phase of 3 causes the blue tiles to become unblocked and attach, finishing the macrotile and orienting the output glue toward the left. A phase of 2 causes the blue and pink tiles to be blocked but allows the yellow tiles to attach, after which the macrotile becomes terminal. Then, a next temperature phase of allows the orange tiles to become unblocked and attach, exposing the macrotile’s output glue straight ahead. A phase of would instead cause the orange tiles to be blocked and the pink tiles to be unblocked and thus attach. They expose a right-facing output glue for the macrotile. Refer to Figure 5 to see that all portions of macrotile growth are fully stabilized before the temperature can increase.
The result of the temperature phases described are that the macrotile completes, is fully stable at all temperatures (at the end of each intermediate temperature phase and the final), and exposes exactly one output glue of strength 4 that can initiate the growth of the next macrotile. While growth of the next macrotile begins with a temperature phase of , note that in the case of the direction being , the final phase of growth of the current macrotile is also at . In this case, the base portion of the next macrotile forms during the same phase that the current macrotile completes. This is not a problem and is easily accounted for when designing our temperature sequence.
The final, and relatively straightforward, aspect of the construction is necessary to handle growth of macrotiles following one or more or turns. For each clockwise rotation of and degrees, we simply create a new copy of each tile making up any of the three versions of the macrotile. We give each copy new glue labels that are specific for that rotation, with the only glue labels that are shared between tiles intended for different rotations being the four glues on the exteriors. These glue labels are designed so that each macrotile output glue is specific to the input glue (i.e. the glue exposed by the green tile) of the correctly oriented version. Since the output locations for and turns are not symmetrically located on the macrotile exterior, it is also necessary to make a reflected version of the basic macrotile, and copies of that for each of the rotations. (An example of the full set of rotations and reflections can be seen in Figure 7 in the Appendix.) We use an additional glue prefix of “” for all of the labels of glues on tiles of the reflected copies so that tiles intended for a macrotile of one rotation and/or reflection are not able to bind inside of macrotiles with different rotations and/or reflections, but again we make sure that each rotated and/or reflected macrotile’s output glue labels correctly match those of the properly rotated and/or reflected macrotile input glues to match their output directions (relative to their orientations). (A complete simple example can be seen in Figure 8 of the Appendix.)
4.3 Generating the temperature sequence
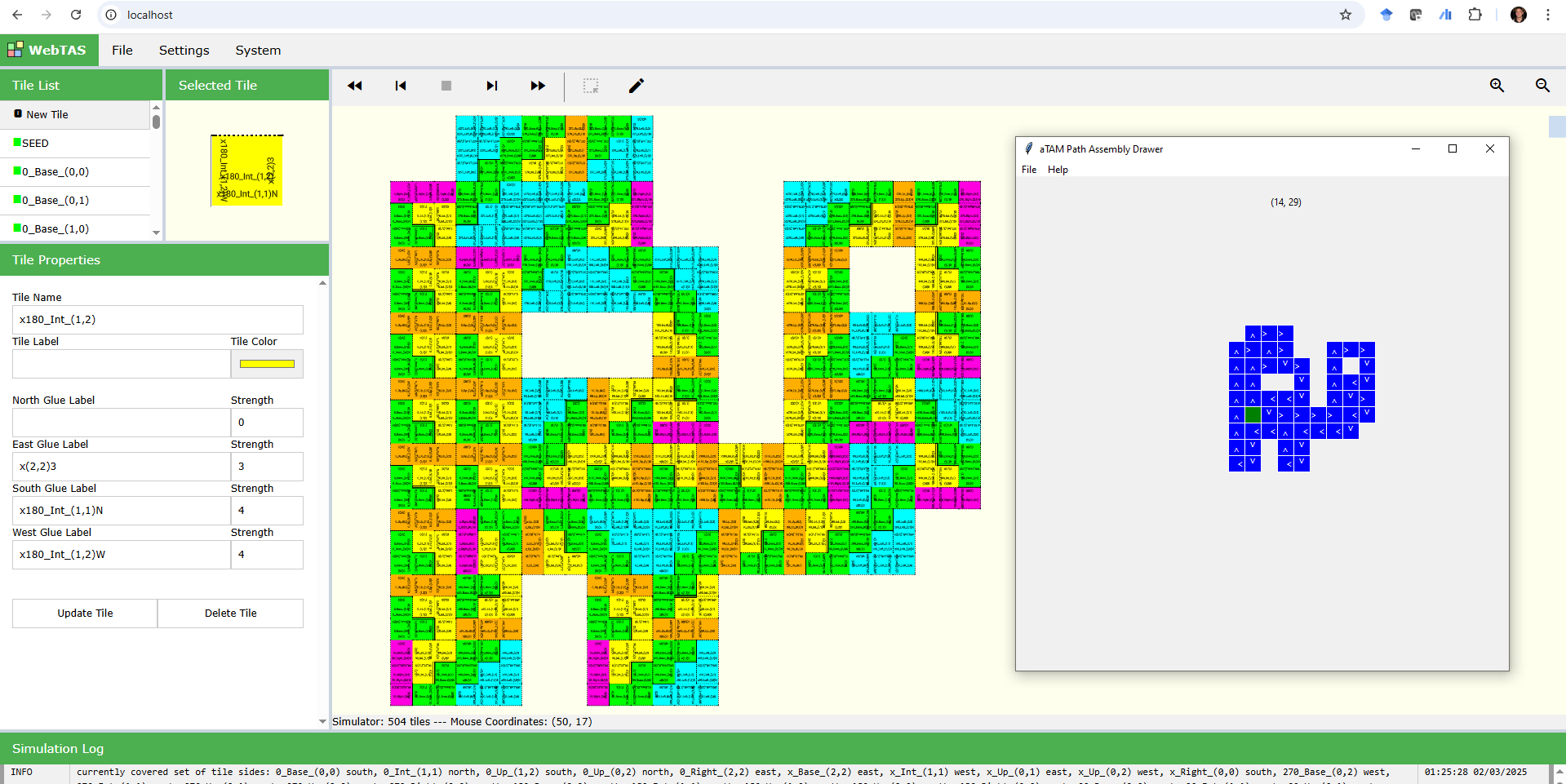
From the above description, it is clear that the universal shape builder can correctly follow an arbitrary turtle graphics path. Thus, all that remains is to show how a shape’s path can be turned into a proper temperature sequence. This is also quite trivial, as we have already seen which temperature sequences are necessary for each movement of or . Since we require that every step is either , or , if the path through starts with a backward step we simply rotate the shape so that the first step is , or , which doesn’t change the shape since shapes are invariant up to rotation. The first temperature is , allowing the base of the first macrotile to grow. Then, for a is appended; for , a and are appended; and for R and . To initiate the next macrotile, if the last direction was or , we append , but if it was we don’t need to do that. The final main consideration is for handling reflected macrotiles. We keep track of each turn that uses the version of the macrotile, as that causes a flip between reflected and non-reflected versions, and note that, when in a reflected macrotile it is an turn that uses the blue tiles and flips the reflection status. Finally, to make sure that the final macrotile is complete, after a phase to grow its base, we include a phase to cause it to complete. (The code used to compute the temperature sequence can be seen in Listing 2 in the Appendix.) We’ve made software freely available that allows one to draw a path, save it as a BlockTAM system [13], then simulate it in a web-based simulator [8]. (Figure 9 of the Appendix shows a screenshot.)
Thus, we have demonstrated a universal shape builder. While only requiring 145 tile types and 32 blockers, it requires an average of just over 2 temperature phases per pixel of (or if scaling isn’t required). While infeasible for experimental implementations of large shapes, the design techniques may provide tools useful for other and improved constructions.
References
- [1] Gagan Aggarwal, Michael H. Goldwasser, Ming-Yang Kao, and Robert T. Schweller. Complexities for generalized models of self-assembly. In Proceedings of ACM-SIAM Symposium on Discrete Algorithms, 2004.
- [2] Florent Becker, Daniel Hader, and Matthew J Patitz. Strict self-assembly of discrete self-similar fractals in the abstract tile assembly model. In Proceedings of the 2025 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA’25), New Orleans, USA, pages 2387–2466. SIAM, 2025. doi:10.1137/1.9781611978322.80.
- [3] Junghuei Chen and Nadrian C Seeman. Synthesis from dna of a molecule with the connectivity of a cube. Nature, 350(6319):631–633, 1991.
- [4] Qi Cheng, Gagan Aggarwal, Michael H. Goldwasser, Ming-Yang Kao, Robert T. Schweller, and Pablo Moisset de Espanés. Complexities for generalized models of self-assembly. SIAM Journal on Computing, 34:1493–1515, 2005. doi:10.1137/S0097539704445202.
- [5] Constantine Evans, Angel Cervera Roldan, Trent Rogers, and Damien Woods. Tile blockers as a simple motif to control self-assembly: kinetics and thermodynamics. Unpublished.
- [6] Ashwin Gopinath, Evan Miyazono, Andrei Faraon, and Paul WK Rothemund. Engineering and mapping nanocavity emission via precision placement of DNA origami. Nature, 2016.
- [7] Daniel Hader, Aaron Koch, Matthew J. Patitz, and Michael Sharp. The impacts of dimensionality, diffusion, and directedness on intrinsic universality in the abstract tile assembly model. In Shuchi Chawla, editor, Proceedings of the 2020 ACM-SIAM Symposium on Discrete Algorithms, SODA 2020, Salt Lake City, UT, USA, January 5-8, 2020, pages 2607–2624. SIAM, 2020. doi:10.1137/1.9781611975994.159.
- [8] Daniel Hader and Matthew J. Patitz. WebTAS (beta): A browser-based simulator for tile-assembly models, 2025. URL: http://self-assembly.net/software/WebTAS_beta/WebTAS_beta-latest/.
- [9] Yonggang Ke, Luvena L Ong, William M Shih, and Peng Yin. Three-dimensional structures self-assembled from DNA bricks. Science, 338(6111):1177–1183, 2012.
- [10] James I. Lathrop, Jack H. Lutz, Matthew J. Patitz, and Scott M. Summers. Computability and complexity in self-assembly. Theory Comput. Syst., 48(3):617–647, 2011. doi:10.1007/s00224-010-9252-0.
- [11] James I. Lathrop, Jack H. Lutz, and Scott M. Summers. Strict self-assembly of discrete Sierpinski triangles. Theoretical Computer Science, 410:384–405, 2009. doi:10.1016/J.TCS.2008.09.062.
- [12] Dionis Minev, Christopher M Wintersinger, Anastasia Ershova, and William M Shih. Robust nucleation control via crisscross polymerization of highly coordinated DNA slats. Nature Communications, 12(1):1–9, 2021.
- [13] Matthew J. Patitz and Trent Rogers. Blocked TAM wiki page and software downloads, 2025. URL: http://self-assembly.net/wiki/index.php/Blocked_Tile_Assembly_Model_(BlockTAM).
- [14] Matthew J. Patitz and Scott M. Summers. Self-assembly of decidable sets. Natural Computing, 10(2):853–877, 2011. doi:10.1007/s11047-010-9218-9.
- [15] Trent Rogers, Constantine Evans, and Damien Woods. Controlling self-assembly with blockers: programming nanostructure size with temperature. Unpublished.
- [16] Trent Rogers, Constantine Evans, and Damien Woods. Controlling self-assembly with blockers: tunable nucleation in growth conditions. Unpublished.
- [17] Paul W. K. Rothemund. Folding DNA to create nanoscale shapes and patterns. Nature, 440(7082):297–302, March 2006. doi:10.1038/nature04586.
- [18] Paul W. K. Rothemund and Erik Winfree. The program-size complexity of self-assembled squares (extended abstract). In STOC ’00: Proceedings of the thirty-second annual ACM Symposium on Theory of Computing, pages 459–468, Portland, Oregon, United States, 2000. ACM. doi:10.1145/335305.335358.
- [19] Nadrian C Seeman. Nucleic acid junctions and lattices. Journal of theoretical biology, 99(2):237–247, 1982.
- [20] David Soloveichik and Erik Winfree. Complexity of self-assembled shapes. SIAM Journal on Computing, 36(6):1544–1569, 2007. doi:10.1137/S0097539704446712.
- [21] Scott M. Summers. Reducing tile complexity for the self-assembly of scaled shapes through temperature programming. Algorithmica, 63(1-2):117–136, June 2012. doi:10.1007/s00453-011-9522-5.
- [22] Ning Wang, Chang Yu, Tingting Xu, Dan Yao, Lingye Zhu, Zhifa Shen, and Xiaoying Huang. Self-assembly of dna nanostructure containing cell-specific aptamer as a precise drug delivery system for cancer therapy in non-small cell lung cancer. Journal of Nanobiotechnology, 20(1):1–19, 2022.
- [23] Erik Winfree. Algorithmic Self-Assembly of DNA. PhD thesis, California Institute of Technology, June 1998.
- [24] Damien Woods, David Doty, Cameron Myhrvold, Joy Hui, Felix Zhou, Peng Yin, and Erik Winfree. Diverse and robust molecular algorithms using reprogrammable dna self-assembly. Nature, 567(7748):366–372, 2019. doi:10.1038/S41586-019-1014-9.
Appendix A Technical Appendix
This Technical Appendix contains additional technical details related to the results in the main body of the paper.
A.1 Number encoder examples
We now provide examples with a few details about universal number encoders for two different sets of temperatures and how they each encode a pair of numbers.
Let and be two sets of temperatures. Using the construction, the universal number encoders produced have the characteristics listed in the first two rows of Table 1. Additionally, Figure 6 demonstrates how the first three columns of the first encoder would grow for the encoded value of , and Figures 3 and 4 show their terminal assemblies.
| Temperatures | Number Tile Types | Column Height | Base | Temps(100) | Temps(10000) |
|---|---|---|---|---|---|
| 2,3,4 | 35 | 5 | 2 | 16 | 30 |
| 2,3,4,5 | 80 | 8 | 2 | 8 | 15 |
| 2,3,4,5,6 | 170 | 10 | 3 | 6 | 10 |
| 2,3,4,5,6,7 | 364 | 14 | 4 | 5 | 8 |
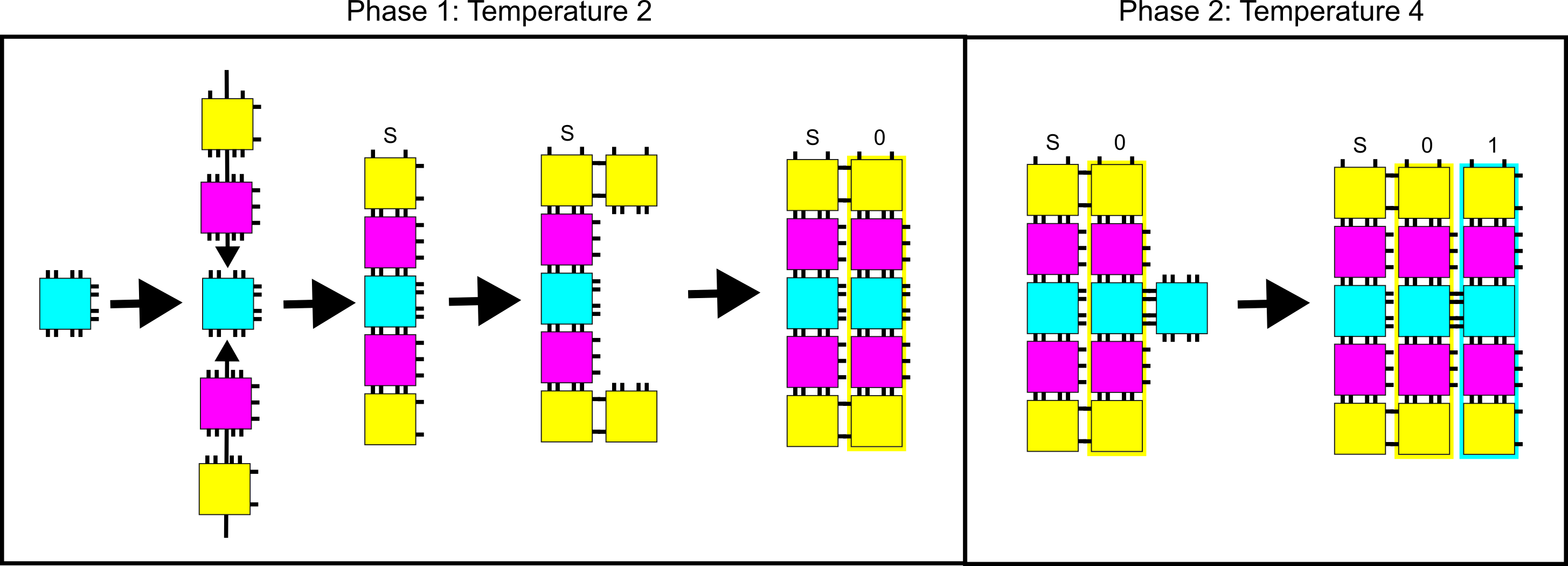
A.2 Additional details of the universal shape builder
Here we provide a few supplementary figures for the universal shape builder construction.