Beeping Deterministic CONGEST Algorithms in Graphs

Garncarek, Pawel; Kowalski, Dariusz R.; Kutten, Shay; Mosteiro, Miguel A.

doi:10.4230/LIPIcs.ESA.2025.20

Beeping Deterministic CONGEST Algorithms in Graphs

Pawel Garncarek

Institute of Computer Science, University of Wroclaw, Poland Dariusz R. Kowalski

School of Computer & Cyber Sciences, Augusta University, GA, USA Shay Kutten

Department of Data and Decision Sciences, Technion, Haifa, Israel
The Grand Technion Energy Program, Haifa, Israel Miguel A. Mosteiro

Pace University, Computer Science Department, New York, NY, USA

Abstract

Beeping Network (BN) is a popular graph-based model of wireless computation, which applies the OR operation to one-bit messages sent simultaneously by neighbors. It admits fast (polylogarithmic in the number of nodes $n$ ) randomized solutions to many graph problems, but all known deterministic algorithms for non-trivial graph problems are at least polynomial in the maximum node degree $\Delta$ .

We improve known results for deterministic algorithms by showing that this polynomial can be as low as $\widetilde{O}(\Delta^{2})$ . More precisely, we show how to simulate a single round of any CONGEST algorithm in any network in $O(\Delta^{2}\text{\em\ polylog }n)$ beeping rounds, each accommodating at most one beep per node, even if the nodes intend to send different messages to different neighbors. This upper bound reduces polynomially the time for a deterministic simulation of CONGEST in a Beeping Network, comparing to the best known algorithms, and nearly matches the time obtained recently using randomization (up to a poly-logarithmic factor) as well as the lower bound. Specifically, any algorithm designed for the CONGEST networks can be run in BNs with $O(\Delta^{2}\text{\em\ polylog }n)$ multiplicative overhead, e.g., we can now deterministically compute an MIS in any BN in $O(\Delta^{2}\text{\em\ polylog }n)$ beeping rounds, improving the previous best $\Theta(\Delta^{3})$ -round solution. For $h$ -hop simulations, we prove a lower bound $\Omega(\Delta^{h+1})$ , and we design a nearly matching algorithm that is able to “pipeline” the node-to-node information in a faster way than beeping layer-by-layer.

Keywords and phrases:

Beeping Networks, CONGEST Networks, deterministic simulations, graph algorithms

Funding:

Pawel Garncarek: Supported by the National Science Center, Poland (NCN), grant 2020/39/B/ST6/03288.

Shay Kutten: The work of this author was funded in part by grant 1346/22 from the Israeli Science Foundation. His research was carried out within the framework of the Grand Technion Energy Program (GTEP). A part of this work was done while with Fraunhofer SIT Darmstadt.

Miguel A. Mosteiro: Partially supported by Pace SRC grant and Kenan Fund.

Copyright and License:

2012 ACM Subject Classification:

Theory of computation

\rightarrow

Distributed algorithms

Editors:

Anne Benoit, Haim Kaplan, Sebastian Wild, and Grzegorz Herman

Series and Publisher:

Leibniz International Proceedings in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik

1 Introduction

The study of the Beeping Networks (BN) model [10] is simultaneously interesting, challenging, and useful in several respects. Even some less-restrictive ad-hoc networks (e.g., wireless) are frequently the algorithmist delight: a seemingly simple computational problem that becomes challenging under harsh yet realistic conditions. In terms of communication, BN may be the harshest model: network nodes can only beep (emit a signal) or listen (detect if a signal is emitted in its vicinity). A listening node may distinguish between silence (no beeps) and noise (at least one beep), but it cannot distinguish between single and multiple beeps. Theoretically, the BN model is important since it enables one to study whether distributed tasks can be performed efficiently under minimal conditions. It is a fundamental model to study communication complexity on channels where signals are superimposed (by applying the OR operator), which makes it more challenging than the basic model in which transmissions on links are independent. Moreover, in a one-hop network,¹¹1For any given path of links connecting two nodes, the number of hops is the number of links in such path. non-adaptive communication schedules in the BN model are equivalent to superimposed codes, which have been widely applied not only to communication problems, but also to text alignments, bio-computing, data pooling, dimensionality reduction, and other areas.

In addition to its theoretical importance, this model is recognized as useful for studying natural communication in biological networks [30, 2] (e.g., cells). A better understanding of the power of biological communication processes may lead to better nature-inspired algorithms [28]. It has been argued that the model is also a practical tool because algorithms designed for BNs can be implemented on non-expensive devices with low energy consumption. For example, nodes deployed (in ad-hoc topologies) for monitoring in Internet of Things (IoT) applications such as Sensor Networks. It should be noted that a mechanism similar in properties to beeping, called “busy tone,” has been in wide use in wireless networks but for very limited purposes in channel access algorithms (as opposed to the Beeping model that is intended for general-purpose distributed algorithms). See e.g., [32, 22].

A wealth of successful research on computational problems in Beeping Networks has appeared in the literature (see, for instance [5, 15] and the references therein). Nevertheless, fundamental distributed computing questions remain open in the context of Beeping Networks, especially for deterministic algorithms. On the other hand, the CONGEST [31] model has been profusely studied. A natural question that follows is how to efficiently transform CONGEST Network algorithms into Beepping Network algorithms.

1.1 Our Contributions

The main results are detailed and compared to previous work in Table 1. Our main contributions are the near optimal²²2Optimal up to a polylogarithmic factor. deterministic implementations of two simulators.

The main simulator, see Section 3 and Theorem 8, efficiently translates any CONGEST algorithms (deterministic or randomized) to the Beeping model. Each CONGEST round is simulated using $O(\Delta^{2}\text{\em\ polylog }n)$ rounds, improving the previous result of $O(\Delta^{4}\log n)$ of [5] and recent $O(\Delta^{3}\log n)$ of [12] ³³3The latter result was not explicitly stated in [12], but one could use its randomized $O(\Delta^{2}\log n)$ -round solution designed for broadcasting $O(\Delta\log n)$ input bits stored in each node (this is the number of bits in our case, as messages to individual $\Delta$ neighbors could be different), and then derandomize it by using the suggested superimposed codes (with additional factor $O(\Delta)$ , hence $O(\Delta^{3}\log n)$ in total). (for $\Delta\in\omega(\text{\em\ polylog }n)$ ), and matches the lower bound $\Omega(\Delta^{2}\log n)$ in [12] (that lower bound holds even for randomized simulations, hence combined with our algorithm they imply that the randomization can not help more than, possibly, a polylogarithmic factor).

Our approach differs substantially from previous ones based on superimposed codes. Our algorithm is adaptive, but using a family of codes, called avoiding selectors, that are parts of nodes’ beeping schedules. These codes combined assure that, gradually, more and more links will “successfully beep” the information between their two end nodes, by “avoiding” interfering beeps from other nodes. The main challenge is that each node may have some incident links already successful and other links that are not – hence, it has to beep anyways and may interfere with other neighbors but, thanks to our avoiding selectors, not all the time. In this process, once a node recognizes that a neighbor is a unique beeper (so called “announcer”), it decodes its ID and message, and then it competes with other nodes to respond in subsequent rounds, and after that – it gets confirmation from the announcer.

Simulations of some CONGEST algorithms, relying on sending the same message to all neighbors in a round such as Network Decomposition in [20], could be further improved by a polylogarithmic factor by applying a deterministic version of local broadcast algorithm (i.e., same message to all neighbors) proposed in [12] (see the full version of this work [19]).

Table 1: Summary of our main results and related work for Beeping Networks with

n

nodes and maximum degree

\Delta

. All protocols are distributed. Highlighted pairs of cells show direct comparison of our main results with previous work.

B

denotes the maximum number of input bits at a node.

problem	protocol type	beeping rounds	ref
simulation of one CONGEST round	randomized	$O(\Delta\min(n,\Delta^{2})\log n)$ whp	[3]
	randomized	$O(\Delta^{2}\log n)$ whp	[12]
	deterministic	$O(\Delta^{4}\log n)$	[5]
		$O(\Delta^{3}\log n)$	[12]
		$O(\Delta^{2}\text{\em\ polylog }n)$	Thm. 8
	rand./det.	$\Omega(\Delta^{2}\log n)$	[12]
$B$ -bit $h$ -hop simulation	deterministic	$O(h\cdot B\Delta^{h+2}\text{\em\ polylog }n)$	Thm. 11
	rand./det.	$\Omega(B\Delta^{h+1})$	Thm. 10
Learning Neighborhood	deterministic	$O(\Delta^{2}\log^{2}n)$	in full version of this work [19]
Cluster Gathering		$O(\Delta^{2}\log^{4}n)$	in full version of this work [19]
$(\log n,\log^{2}n)$ -Network Decomposition		$O(\Delta^{2}\log^{8}n)$	in full version of this work [19]
MIS		$O(\Delta^{3}+\Delta^{2}\log n)$	[5]
		$O(\Delta^{2}\text{\em\ polylog }n)$	Cor. 9

Our second main result is an extension of the notion of neighborhood to $h\geq 1$ hops and pipelining of the one-hop simulation. We call this problem a $B$ -bit $h$ -hop simulation, and show bounds $O(h\cdot B\Delta^{h+2}\text{\em\ polylog }n)$ and $\Omega(B\Delta^{h+1})$ , where the lower bound holds also for randomized solutions. See Section 4, and Theorems 11 and 10, respectively. Our algorithm efficiently “pipelines” point-to-point messages, and achieves substantially better complexity (for $h>3$ ) than a straightforward application of 1-hop simulator $h$ times (which would need $O(\Delta^{2h}\text{\em\ polylog }n)$ time). For the simpler problem when each node has to deliver the same message to all nodes in its $h$ -hop neighborhood, which we call $B$ -bit $h$ -hop Local Broadcast, we show a lower bound of $\Omega(B\Delta^{h})$ even with randomization (see the full version of this work [19]).

1.2 Related Work

The Beeping Network model was defined by Cornejo and Kuhn in [10] in 2010, inspired by continuous beeping studied by Degesys et al. [13] and Motskin et al. [29], and by the implementation of coordination by carrier sensing given by Flury and Wattenhofer in [17]. Since then, the literature has included studies on MIS and Coloring [2, 1, 27, 23, 5, 7], Naming [8], Leader Election [21, 18, 14], Broadcast [21, 25, 26, 11, 4], and Shortest Paths [15].

Techniques to implement CONGEST algorithms in BNs were studied. In [5], the approach is to schedule transmissions according to a 2-hop $c$ -coloring to avoid collisions. The multiplicative overhead introduced by the simulation is $O(c^{2}\log n)$ . A constant $c$ is enough for the simulation, but the only coloring algorithm provided in the same paper takes time $O(a^{2}\Delta^{2}\log^{2}n+a^{3}\Delta^{3}\log n)$ for a $(\Delta^{2}+1)$ -coloring. Thus, the multiplicative overhead is $O(\Delta^{4}\log n)$ , which our simulation improves by a factor of $\Delta^{2}/\text{\em\ polylog }n$ .

On the side of randomized protocols, in a recent work by Davies [12], a protocol that simulates a CONGEST round in a Beeping Network with $O(\Delta^{2}\log n)$ overhead is presented. The protocol works even in the presence of random noise in the communication channel. Still, it is correct only with high probability (whp),⁴⁴4An event $E$ occurs with high probability if $Prob(E)\geq 1-1/n^{c}$ for some $c>0$ . and requires a polynomial number of CONGEST rounds in the simulated algorithm. More relevant for comparison with our work, in the same paper, a lower bound of $\Omega(\Delta^{2}\log n)$ on the overhead to simulate a CONGEST round is shown. The lower bound applies even in a noiseless environment and regardless of randomization. Thus, our simulation is optimal modulo some poly-logarithmic factor. [12] also proposed using superimposed codes instead of randomness, resulting in $\Theta(\Delta)$ multiplicative overhead, i.e., $O(\Delta^{3}\log n)$ rounds in total. Another randomized simulation was previously presented in [3] with overhead of $O(\Delta\min(n,\Delta^{2})\log n)$ whp.

Regarding the MIS problem, the closest work is the deterministic protocol in [5], which runs in $O(\Delta^{2}\log n+\Delta^{3})$ . Thus, our results improve by a factor of $\Delta/\text{\em\ polylog }n$ for any $\Delta\in\omega(\log n)$ , and match the running time (modulo poly-logarithmic factor) for $\Delta\in O(\log n)$ .

On the side of randomized MIS protocols, an upper bound of $O(\log^{3}n)$ has been shown in [1] for the same beeping model, and faster with some additional assumptions.

Our network decomposition algorithm for BNs is based on the protocol for the CONGEST model [20] that shows a $(\log n,\log^{2}n)$ network decomposition in $O(\log^{5}n)$ CONGEST rounds. We get the same network decomposition in $O(\Delta^{2}\log^{7}n)$ beeping rounds. Other graph problems and (restricted) local broadcast of same message are discussed in the full version of this work [19].

Non-synchronized BNs pose even more challenges to graph algorithms, cf. [1, 18, 14, 24].

2 Model, Notation, and Problems

We specify first the communication network notation used throughout, and we define the communication models studied in the section that follows. We consider a communication network formed by $n$ devices with communication and computation capabilities, called nodes. Each node has a unique ID from the range $[1,n^{c}]$ for some constant $c\geq 1$ .⁵⁵5The availability of identifiers is essential in order to break symmetry in deterministic protocols, as pointed out in previous works on deterministic protocols in the Beeping model [5, 14]. Nodes communicate by sending messages among them. A message is composed of a binary sequence containing the source node ID, the destination node ID (if applicable), and the specific information to be sent. If the destination node receives the message from the source node, we say that the message was delivered. Each pair of nodes that are able to communicate directly (i.e., without relaying communication through other nodes) are said to be connected by a communication link and are called neighbors. We assume that links are symmetric, i.e., messages can be sent in both directions (delivery is restricted to the communication models specified below). The network topology defined by the communication links is modeled with an undirected graph $G=(V,E)$ where $V$ is the set of nodes and $E$ is the set of links. If $E$ is such that for every pair of nodes $u,v\in V$ there is a path of links connecting $u$ and $v$ we say that the network is connected. For each node $v\in V$ , the set of neighbors of $v$ is called its neighborhood, denoted as $N(v)$ . We assume that time is slotted in rounds of communication. All nodes start running protocols simultaneously, i.e., the network is synchronous. We assume that computations take negligible time with respect to communication. Thus, we measure algorithm performance in rounds.

2.1 Communication Models

Beeping Networks (BNs) [10].

In this model, in each round each node can either beep (send a signal) or listen (do not send any signal). By doing so, nodes obtain the following communication channel feedback. In any given round, a listening node hears either silence (no neighbor beeps) or noise (one or more neighbors beep). A listening node that hears noise cannot distinguish between a single beep and multiple beeps.

Network protocols may use the channel feedback (i.e. the temporal sequence of strings from {“silence”,“noise”}) to make decisions adaptively. However, delivering messages is not straightforward because it requires sending (and receiving) the whole binary sequence of the message (according to some beeping schedule, possibly changing adaptively during the communication), somehow encoded with beeps. In that sense, protocols for Beeping Networks can be seen as radio network coding to cope with the communication restrictions (as in [16] to cope with noise).

Refer to caption — (a) All nodes listen. All nodes hear silence.

CONGEST Networks [31].

In this model, in each round each node can send a (possibly different) message of $O(\log n)$ bits to each neighbor independently. All nodes receive the messages sent by their neighbors. That is, there are no collisions. In the CONGEST Broadcast version of this model, each node can only broadcast the same message to all its neighbors in each round.

2.2 Problems Studied

Our main research question in this work is how to efficiently simulate a round of communication of a CONGEST Network protocol in a Beeping Network, and how to improve MIS in BNs.

CONGEST Simulation.

Given a Beeping Network with topology graph $G=(V,E)$ , where each node $u\in V$ may hold a message $m_{u,v}$ of $O(\log n)$ bits that must be delivered to node $v\in N(u)$ , the CONGEST simulation problem is solved once for every $u\in V$ and $v\in N(u)$ , $m_{u,v}$ and the ID of $u$ has been delivered to $v$ .

Maximal Independent Set (MIS).

Given a Beeping Network with topology graph $G=(V,E)$ , The Maximal Independent Set problem is solved when, for some such set, $S\subseteq V$ , every node $v\in S$ , $v$ knows that it is in $S$ .

Our second main problem – generalized $h$ -hop simulations – are defined and studied in Section 4 and in the full version of this work [19]. We also study several distributed computing problems of independent interest (see their definition in the full version of this work [19]) in the context of Beeping Networks and applications of our simulator that improve efficiency with respect to known solutions for BNs.

3 Simulation of a CONGEST Round in Beeping Networks

We present a deterministic distributed algorithm that efficiently simulates a round of any algorithm designed for the CONGEST model in the Beeping Networks model, even if the algorithm sends different messages to neighbors. It is only somewhat (polylogarithmically) slower than the existing more restricted local broadcast algorithms, which require a node to send the same message to all its neighbors), e.g., the local broadcast solution mentioned in [12] (see also more details in the full version of this work [19]) and faster nearly by factor $\Delta$ than the full deterministic simulation also mentioned in [12]. Unlike the superimposed-codes-based deterministic algorithms in [12], our simulator is adaptive and uses heavier machinery. It is built hierarchically using the known family of codes called “avoiding selectors”. The codes, intuitively, say “when to beep”. However, it is still possible that when two neighbors of some node $v$ send their messages (by beeping in subsequent rounds), node $v$ will receive a “message” that is a logical OR of the two. Our simulator resolves such collision problems and assures fast progress by:

$\blacksquare$

coding messages (cf. extended-IDs) such that OR of more than one message is identified;
$\blacksquare$

beeping according to specific avoiding selectors, assuring that a fraction of links that have not yet “delivered” the beeped messages will now succeed in one direction (i.e., one end node of such link “announces” itself to the other one through successful beeping of its ID);
$\blacksquare$

allowing those who received such announcements, the responders, to compete in successful delivery of their IDs to the corresponding announcers; this competition sets up bi-directional matching between the announcers and the corresponding responders, which allows bi-directional message exchange via beeping (3-stage parallel handshaking); this competition also uses avoiding selectors, but differently parameterized than the ones used for announcing (as announcing and responding are different processes).

The announcing, followed by responders’ competition, continues until all links end up in some of the successfully realized matchings (as described in the above bullet points).

Avoiding selectors for $n$ nodes use two parameters, $k,\ell$ , corresponding to the number of competing neighbors/responders versus the other (potentially interrupting) neighbors:

Definition 1 (Avoiding selectors).

A family $\mathcal{F}$ of subsets of $[n]$ is called an $(n,k,\ell)$ -avoiding selector, where $1\leq\ell<k\leq n$ , if for every non-empty subset $S\subseteq[n]$ such that $|S|\leq k$ and for any subset $R\subseteq S$ of size at most $\ell$ , there is an element $a\in S\setminus R$ for which there exists a set $F\in\mathcal{F}$ such that $|F\cap S|=\{a\}$ .

The following fact follows directly from Definition 1, see also [6, 9].

Fact 1.

Suppose we are given an $(n,k,\ell)$ -avoiding selector $\mathcal{F}$ and a set $S$ of size at most $k$ . Then, the number of elements in $S$ not “selected” by selector $\mathcal{F}$ (i.e., for which there is no set in the selector that intersects $S$ on such singleton element) is smaller than $k-\ell$ .

Theorem 2 ([6, 9]).

There exists an $(n,k,\ell)$ -avoiding selector of size $O\left(\frac{k^{2}}{k-\ell}\log n\right)$ , and moreover, an $(n,k,\ell)$ -avoiding selector of size $O\left(\frac{k^{2}}{k-\ell}\text{\em\ polylog }n\right)$ can be efficiently deterministically constructed (in polynomial time of $n$ ) for some polylogarithmic function $\text{\em polylog }n$ , locally by each node.

3.1 The c2b Algorithm

The pseudocode of our main c2b algorithm is in Algorithm 1, and its subroutines in Algorithms 2 and 3. The algorithm proceeds in epochs $i=1,\ldots\log\Delta$ . In the beginning, each node has all its links not successfully realized – here by a link $\{v,w\}$ being realized we understand that up to the current round, an input message/ID sent by $v$ has been successfully encoded by $w$ (using a sequence of beeps) and vice versa (note that these are two different messages and were sent/encoded each in different rounds); the formal definition of link realization will be given later. The goal of the algorithm is to preserve the following invariant for epoch $i\geq 1$ :

At the end of epoch $i=1,\ldots,\log\Delta$ , each vertex has less than $\kappa_{i}=\Delta/2^{i}$ incident links not realized.

We set an auxiliary value $\kappa_{0}=\Delta$ , which corresponds to the maximum number of adjacent links per node at the beginning of the computation. For ease of presentation, we assume that node IDs come from the range $[1,n]$ . Note that in all the formulas, the number of possible IDs appears only under logarithms, so the algorithm and analysis for range $[1,n^{c}]$ are the same.

Algorithm 1 c2b algorithm for each node

u

.

E(u)

is a global variable.

Algorithm for epoch $𝒊$ : Preliminaries and main concepts

Epoch $i$ proceeds in subsequent batches of $2\log n$ rounds, each batch is called a super-round. In a single super-round, a node can constantly listen or keep beeping according to some 0-1 sequence of length $2\log n$ , where 1 corresponds to beeping in the related round and 0 means staying silent. The sequences that the nodes use during the algorithm are extended-IDs, defined as follows: the first $\log n$ positions contain an ID of some node in $\{1,\ldots,n\}$ , while the next $\log n$ positions contain the same ID with the bits flipped, that is, with ones swapped to zeros and vice versa. Note that extended-IDs are pairwise different, and each of them contains exactly $\log n$ ones and $\log n$ zeros. We say that a node $v$ beeps an extended-ID of node $w$ in a super-round $s$ if, within super-round $s$ , node $v$ beeps only in rounds corresponding to positions with $1$ ’s in the extended ID of $w$ ( $w$ could be a different node id than $v$ ). We say that a node $w$ receives an extended-ID of a node $v$ in a super-round $s$ if:

$\blacksquare$

$w$ does not beep in super-round $s$ ,
$\blacksquare$

the sequence of noise/silence heard by $w$ in super-round $s$ form an extended-ID of $v$ .

From the perspective of receiving information in a super-round, all other cases not falling under the above definition of receiving an extended-ID, i.e., when a node is not silent in the super-round or receives a sequence of beeps that does not form any extended-ID, are ignored by the algorithm, in the sense that it could be treated as meaningless information noise.

Analogously to extended-ID’s, nodes create an extended-message by taking the binary representation of the message of logarithmic length and transforming it to a $2\log n$ binary sequence in the same way as an extended-ID is created from the binary ID of a node. An extended-message, as well as an extended-ID, is easily decodable after being received without interruptions from other neighbors.

Algorithm 2 c2b algorithm for announcer node

v

.

A specification of the conditions to achieve one-to-one communication, which is given “for free” in the CONGEST model, is crucial. An illustration of the following handshake communication procedure is shown in the full version of this work [19]. We say that our algorithm realizes link $\{v,w\}$ if the following are satisfied:

(a)

there are three consecutive super-rounds (called “responding”) in which $v$ beeps an extended-ID of itself followed by an extended-ID of $w$ and then by extended-message of $v$ addressed to $w$ , and $w$ receives them in these super-rounds; intuitively, it corresponds to the situation when $v$ “tells” $w$ that it dedicates these three super-rounds for communication from itself to $w$ , and $w$ receives this information;
(b)

there are three consecutive super-rounds (called “confirming”) in which $w$ beeps an extended-ID of itself followed by an extended-ID of $v$ and by its extended-message addressed to $v$ , and $v$ receives them in these super-rounds; intuitively, it corresponds to the situation when $w$ “tells” $v$ that it dedicates these three super-rounds for communication from itself to $v$ , and $v$ receives this information;
(c)

there is a super-round, not earlier than the one specified in point (a), at the end of which node $w$ locally marks link $\{v,w\}$ as realized, and analogously, there is a super-round, not earlier than the one specified in point (b), at the end of which node $v$ locally marks link $\{v,w\}$ as realized.

It is straightforward to see that in super-rounds specified in points (a) and (b), a multi-directional communication between $v$ and $w$ takes place – by sending and receiving both “directed pairs” of extended-IDs of these two nodes, each of them commits that the super-rounds specified in points (a) and (b) are dedicated for sending a message dedicated to the other node, and vice versa. Additionally, in some super-round(s) both nodes commit that it has happened (c.f., point (c) above).

Algorithm for epoch $𝒊$ : Structure

An epoch $i$ is split into $|\mathcal{F}_{\Delta,k_{i}}|$ phases, for a given $(n,\Delta,\Delta-k_{i})$ -avoiding selector $\mathcal{F}_{\Delta,k_{i}}$ and parameter $k_{i}=\Delta/2^{i}$ , parameterized by a variable $j$ . Each phase starts with one announcing super-round, in which nodes in set $\mathcal{F}_{\Delta,k_{i}}(j)$ beep in pursuit to be received by some of their neighbors. This super-round is followed by $\log k_{i}$ sub-phases, parameterized by $a=1,\ldots,\log k_{i}$ . A sub-phase $a$ uses sets from an $(n,k_{i}/2^{a-2},k_{i}/2^{a-1})$ -avoiding selector $\mathcal{F}_{k_{i}/2^{a-2},k_{i}/2^{a-1}}$ to determine who beeps in which super-round (together with additional rules to decide what extended-ID and extended-message to beep and how to confirm receiving them), and consists of $|\mathcal{F}_{k_{i}/2^{a-2},k_{i}/2^{a-1}}|$ $6$ -tuples of super-rounds ( $3$ responding super-rounds and $3$ confirming super-rounds). The goal of a phase is to realize links that were successfully received (“announced”) in the first (announcing) super-round of this phase. This is particularly challenging in a distributed setting since many neighbors could receive such an announcement, but the links between them and the announcing node must be confirmed so that one-to-one communication between the announcer and responders could take place in different super-rounds (in one super-round, a node can receive only logarithmic-size information).

Algorithm 3 c2b algorithm for responder node

w

.

Definitions and notation.

$\mathcal{F}_{\Delta,k_{i}}$ is a locally computed $(n,\Delta,\Delta-k_{i})$ -avoiding selector, and for any $a=1,\ldots,\log k_{i}$ , $\mathcal{F}_{k_{i}/2^{a-2},k_{i}/2^{a-1}}$ is a (locally computed) $(n,k_{i}/2^{a-2},k_{i}/2^{a-1})$ -avoiding selector, as in Theorem 2. We denote the extended-ID of node $x$ as $\langle x\rangle$ , and the extended-message of node $x$ for node $y$ as $\langle m_{x,y}\rangle$ , both given as a sequence of bits. For any sequence of bits $s$ , $s(i)$ is the $i^{th}$ bit of $s$ .

3.2 Analysis of the c2b Algorithm

Recall that the algorithm proceeds in synchronized super-rounds, each containing a subsequent $2\log n$ rounds. Therefore, our analysis assumes that the computation is partitioned into consecutive super-rounds and, unless stated otherwise, it focuses on correctness and progress in super-rounds. Recall also that each node either stays silent (no beeping at all) or beeps an extended ID of some node or an extended message of one node addressed to one of its neighbors in a super-round. The missing proofs are deferred to the full version of this work [19].

In the next two technical results, we state and prove the facts that receiving an extended-ID by a node $w$ in a super-round can happen if and only if there is exactly one neighbor of $w$ has been beeping the same extended-ID during the considered super-round.

Fact 2 (Single beeping).

If during a super-round, exactly one neighbor of a node $w$ beeps an extended-ID of some $z$ , then $w$ receives this extended-ID in this super-round.

Proof.

Directly from the definition of receiving an extended-ID. $\hfill\blacktriangleleft$

Lemma 3 (Correct receiving).

During the algorithm, if a node $w$ receives some extended-ID of $z$ in a super-round, then some unique neighbor $v$ of $w$ has been beeping an extended-ID of $z$ in this super-round while all other neighbors of $w$ have been silent. The above holds except, possibly, some second responding super-rounds, in which a node can receive an extended-ID of $z$ that has been beeped by more than one neighbor.

We now prove that link realization implemented by our algorithm is consistent with the definition – it allocates in a distributed way super-rounds for bi-directional communication of distinct messages.

Lemma 4 (Correct realization).

If a node $v$ (locally) marks some link $\{v,w\}$ as realized, which may happen only at the end of a second confirming super-round, the link has been realized by then.

As mentioned earlier in the description of the phase, the goal of a phase $j$ (of epoch $i$ ) is to assure that any node $v$ that was received by some other nodes $w$ in the announcing super-round, gets all such links $\{v,w\}$ realized by the end of the phase (and vice versa, because the condition on the realization by this algorithm is symmetric). The next step is conditional progress in a sub-phase $a$ of a phase $j$ .

Lemma 5 (Sub-phase progress).

Consider any node $v$ and suppose that in the beginning of sub-phase $a$ of phase $j$ , there are at most $\Delta/2^{i+a-2}$ nodes $w$ such that $w$ is $(j,v)$ -responsive and it does not mark link $\{v,w\}$ as realized. Then, by the end of the sub-phase, the number of such nodes is reduced to less than $\Delta/2^{i+a-1}$ .

Lemma 6 (Phase progress).

Consider a phase $j$ of epoch $i$ and assume that in the beginning, there are at most $2k_{i}$ non-realized incident links to any node. Every node $w$ that becomes $(j,v)$ -responsive in the first (announcing) super-round of the phase, for some $v$ , mark locally the link $\{v,w\}$ as realized during this phase. And vice versa, also node $v$ marks locally that link as realized.

The next lemma proves the invariant for epoch $i$ , assuming that it holds in the previous epochs.

Lemma 7 (Epoch invariant).

The invariant for epoch $i\geq 1$ holds.

Theorem 8.

The c2b algorithm deterministically and distributedly simulates any round of any algorithm designed for the CONGEST networks in $O(\Delta^{2}\text{\em\ polylog }n\log\Delta)$ beeping rounds, where the $\text{\em\ polylog }n$ is the square of the (poly-)logarithm in the construction of avoiding-selectors in Theorem 2 multiplied by $\log n$ .

Proof.

By Lemma 7, each epoch $i$ reduces by at least half the number of non-realized incident links. We next count the number of rounds in each epoch by counting the number of super-rounds and multiplying the result by the $O(\log n)$ length of each super-round. Recall that link realization means that some triples of responding and confirming super rounds were not interrupted by other neighbors of both end nodes of that link; therefore, the attached extended messages (in the third super-rounds in a row) were correctly received. Thus, the local exchange of messages addressed to specific neighbors took place successfully.

Each sub-phase $a$ has $O(\Delta^{2}\text{\em\ polylog }n)$ super-rounds, because for each set in of the $(n,k_{i}/2^{a-1},k_{i}/2^{a})$ -avoiding selector $\mathcal{F}_{k_{i}/2^{a-1},k_{i}/2^{a}}$ , there are four super-rounds and the selector itself has $O((k_{i}/2^{a})\text{\em\ polylog }n)$ set, by Theorem 2.

Therefore, the total number of super-rounds in all sub-phases executed within the loops in Line 3 of Algorithm 2 and Line 5 of Algorithm 3 is

O(\sum_{a=1}^{\log k_{i}}(k_{i}/2^{a})\text{\em\ polylog }n)\leq O(k_{i}\text{% \em\ polylog }n)\ .

Within one phase, they are executed as many times as the number of announcing super-rounds. The number of such super-rounds in a phase is $|\mathcal{F}_{\Delta,k_{i}}|$ , which is $O((\Delta^{2}/k_{i})\text{\em\ polylog }n)$ by Thm. 2. Thus, the total number of super-rounds in a phase is $O((\Delta^{2}/k_{i})\text{\em\ polylog }n\cdot k_{i}\text{\em\ polylog }n)\leq O% (\Delta^{2}\text{\em\ polylog }n)$ , where the final $\text{\em\ polylog }n$ is a square of the (poly-)log in Thm. 2.

Since there are $\log\Delta$ epochs, the total number of super-rounds is $O(\Delta^{2}\text{\em\ polylog }n\log\Delta)$ , which is additionally multiplied by $O(\log n)$ – the length of each super-round – if we want to refer the total number of beeping rounds. $\hfill\blacktriangleleft$

Maximal Independent Set (MIS).

To demonstrate that the above efficient simulator can yield efficient results for many graph problems, we apply it to the $O(\log^{5}n)$ MIS algorithm in [20] to improve polynomially (with respect to $\Delta$ ) the best-known solutions for MIS (c.f. [5]):

Corollary 9.

MIS can be solved deterministically on any network of maximum node-degree $\Delta$ in $O(\Delta^{2}\text{\em\ polylog }n)$ beeping rounds.

4 Multi-hop Simulation

We generalize the simulation at distance $1$ to the following $B$ -bit $h$ -hop simulation problem: each node has messages, potentially different, of size at most $B$ bits addressed to any other node, and it needs to deliver them to all destination nodes within distance at most $h$ hops. If each node has only a single message of size at most $B$ bits to be delivered to all nodes within distance at most $h$ hops, then we call this restricted version $B$ -bit $h$ -hop Local Broadcast. Note also that we do not require messages addressed to nodes of distance larger than $h$ to be delivered. Below we generalize the lower bound for single-hop simulation in [12] to multi-hop simulation and multi-hop local broadcast.

Theorem 10.

There is an adversarial network of size $\Theta(\Delta^{h})$ such that any $B$ -bit $h$ -hop simulation algorithm requires $\Omega(B\Delta^{h+1})$ beeping rounds to succeed with probability more than $2^{-\frac{1}{2}\cdot B(\Delta-1)^{h-2}(\Delta/2)^{3}}=2^{-\Theta\left(B\Delta^% {h+1}\right)}$ .

Proof.

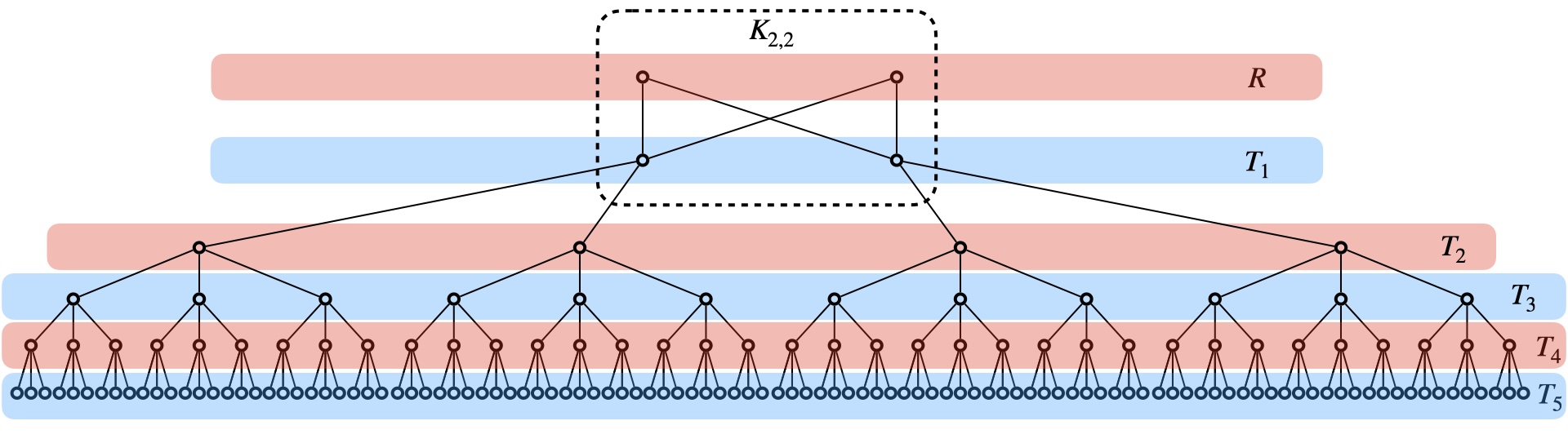
Problem instance. We describe the construction of the adversarial network and input set of messages used to prove our lower bound as follows (refer to Figures 2 and 3). Consider a full bipartite graph $K_{\Delta/2,\Delta/2}$ , with one part called $T$ and the other $R$ . We focus on transmissions going towards nodes in $R$ , hence nodes in $R$ will be called receivers, while nodes in $T=T_{1}$ will be called the first of $h$ layers of transmitters.

Each node in $T_{1}$ will be a root of an $(h-1)$ -depth tree of transmitters. We create a second layer of transmitters $T_{2}$ composed of $(\Delta/2)^{2}$ nodes. Each node in $T_{1}$ (already connected to each node in $R$ ) will also be connected to different $\Delta/2$ nodes in $T_{2}$ . For subsequent layers of transmitters, that is each layer $T_{i}$ , for $3\leq i\leq h$ , will be composed of $(\Delta/2)^{2}(\Delta-1)^{i-2}$ nodes. Each node in layer $T_{i-1}$ , for $3\leq i\leq h$ , will be connected to different $\Delta-1$ nodes in layer $T_{i}$ .

Figure 2: An illustration of the structure of the graph. The graph is partitioned into vertical layers

T_{h}

, …,

T_{1}

,

R

. The graph is branching out heavily, so we show only a path from an arbitrary node in

T_{1}

layer to an arbitrary node in

T_{h}

layer, with all the edges incident to the path. The numbers between the layers denote the number of edges between the layers that are incident to the path or on the path. Recall that layers

T_{1}

and

R

have

\Delta/2

nodes each, while the other layers have significantly more nodes, but we only show nodes that are adjacent to the considered path.

Note that each node in the defined network has at most $\Delta$ neighbors.

We define now the input set of messages as follows. Let each node $v\in T_{h}$ have a $B$ -bit message $m_{v\rightarrow u}$ to each node $u\in R$ . We choose those messages uniformly at random. We will show that just these messages cannot be relayed efficiently and we do not need any other messages in our problem instance.⁶⁶6Alternatively we can make all other messages known to the optimal algorithm, e.g., by setting them to $0^{B}$ .

Multihop Simulation. Here we analyze the multihop simulation algorithms.

There are $(\Delta/2)^{2}(\Delta-1)^{h-2}$ nodes in $T_{h}$ , and each of them has $\Delta/2$ (possibly different) messages, one for each node in $R$ . Therefore, there are $(\Delta/2)^{3}(\Delta-1)^{h-2}=\Theta(\Delta^{h+1})$ messages to nodes in $R$ that are passing through nodes in $T_{1}$ .

Let $\mathcal{R}$ be the concatenated string of local randomness in all the nodes in $R$ . The output of any receiver $u\in R$ must depend only on $\mathcal{R}$ , node IDs and the pattern of beeps and silences of nodes in $T_{1}$ .

There are $2^{t}$ possible patterns of beeps and silences in $t$ rounds. Therefore, the output of nodes in $R$ must be one of the $2^{t}$ possible distributions, where a distribution is over the randomness of $\mathcal{R}$ . The correct output of nodes in $R$ is a string $\{0,1\}^{B(\Delta-1)^{h-2}(\Delta/2)^{3}}=\{0,1\}^{\Theta(B\Delta^{h+1})}$ chosen uniformly at random (since the input messages of nodes in $T_{h}$ were chosen uniformly at random). Therefore, the probability of picking the correct result is at most $2^{t-B(\Delta-1)^{h-2}(\Delta/2)^{3}}$ , and any algorithm that finishes within $t\leq\frac{1}{2}\cdot B(\Delta-1)^{h-2}(\Delta/2)^{3}$ rounds has at most $2^{-\frac{1}{2}\cdot B(\Delta-1)^{h-2}(\Delta/2)^{3}}$ probability of outputting the correct answer. $\hfill\blacktriangleleft$

Algorithm

A simple algorithm would repeatedly use a 1-hop Local Broadcast routine to flood the network with the messages until nodes at a distance $h$ received the messages. This, however, can take $\Omega(\Delta^{2h})$ rounds. Instead, we limit the flooding by only sending messages along the shortest paths to their destinations using a 1-hop simulation algorithm. The details of the algorithm as well as its analysis are presented next.

In the beginning, nodes use a standard protocol to disseminate their IDs up to distance $h$ . They do it in $h$ subsequent epochs, each epoch $i$ of $t_{i}$ rounds sufficient to run our Local Broadcast (see full version of this work [19]) for messages of size $\Delta^{i}\log n$ . These messages contain different IDs learned by the node at the beginning of the current epoch. A direct inductive argument, also using the property that there are at most $\Delta^{i}$ nodes at a distance at most $i$ , shows that at the end of epoch $i$ , each node knows the IDs of all nodes at a distance at most $i$ from it. Additionally, each node records in which epoch $i$ it learned each known ID $v$ for the first time and from which of its neighbors $w$ – and stores this information as a triple $(v,w,i)$ . The invariant for $i=h$ proves that at the end of epoch $h$ , each node knows IDs of all nodes of distance at most $h$ from it. The round complexity is $\sum_{i=1}^{h}\Delta^{i}\log n\cdot\Delta^{2}\log n=O(\Delta^{h+2}\log^{2}n)$ , and as will be seen later, it is subsumed by the round complexity of the second part of our algorithm (as the $\text{\em\ polylog }n$ function in Theorem 8 is asymptotically bigger than $\log^{2}n$ ).

Note that a sequence of triples $(v,w_{1}=v,1),\ldots,(v,w_{\ell},\ell)$ , stored at nodes $w_{2},w_{3},\dots,w_{\ell},w_{\ell+1}=u$ respectively, represents a shortest path to node $v$ starting from the node $u$ ; the length of that path is $\ell$ .

In the second part, nodes also proceed in epochs, but this time each epoch $i$ takes $t^{*}_{i}$ rounds sufficient to execute $1$ -hop simulation algorithm from Section 3 (see Theorem 8) for point-to-point messages of size $(B+\log n)\Delta^{h}$ . Here $B$ denotes the known upper bound on the size of any input message. In epoch $i$ , every node $u$ transmits a (possibly different) message of size $(B+\log n)\Delta^{h}$ to each neighbor $w$ . Such a message contains all the input messages of nodes within $i-1$ distance and the recipients of these messages such that $w$ is the next node on the saved shortest path to the recipient. The messages have already traveled $i-1$ hops, so their destination is at most $h-(i-1)$ hops away. More specifically, the message from node $u$ addressed to a neighbor $w$ in epoch $i$ contains pairs $(v,m_{z\rightarrow v})$ , where $v$ is such that $(v,w,i^{\prime})$ is stored at the node for some $i^{\prime}\leq h-(i-1)$ and $m_{z\rightarrow v}$ is a message received by the node $u$ in epoch $i-1$ (in case of $i-1=0$ , it is the original message of the node addressed to $v$ ). A direct inductive argument shows that at the end of each epoch $i$ a node knows at most $\Delta^{i}$ messages addressed to any node $v$ of distance $\ell\leq h-i$ from the node. This invariant is based on the following arguments:

$\blacksquare$

Because there is a unique neighbor $w$ of the node $u$ such that a triple $(v,w,\ell)$ is stored at the node, the number of such nodes $v$ of distance at most $h-i+1$ from the node $u$ is at most $\Delta^{h-i+1}$ ,
$\blacksquare$

by the end of epoch $i-1$ , node $u$ could receive messages to be relayed to $v$ from $\Delta^{i-1}$ different nodes at distance $i-1$ ,
$\blacksquare$

each message contains up to $B$ -bit long original message and an ID of length $\log n$ ,
$\blacksquare$

hence, messages of size at most $(B+\log n)\Delta^{i-1}\cdot\Delta^{h-i+1}=(B+\log n)\Delta^{h}$ are being sent to each neighbor in epoch $i$ , and by definition – epoch $i$ has sufficient number of rounds to deliver them.

The invariant for $i=h$ proves the desired property of $B$ -bit $h$ -hop simulation. The total number of rounds is $O(h\cdot(B+\log n)\Delta^{h}\cdot\Delta^{2}\text{\em\ polylog }n)\subseteq O(h% \cdot B\Delta^{h+2}\text{\em\ polylog }n)$ , where factor $h$ comes from the number of epochs, each sending at most $\Delta$ point-to-point messages of size at most $(B+\log n)\Delta^{h}$ to neighbors (by the invariant) using the $1$ -hop simulation protocol with overhead $O(\Delta^{2}\text{\em\ polylog }n)$ (by Theorem 8). Hence we proved the following.

Theorem 11.

There is a distributed deterministic algorithm solving the $B$ -bit $h$ -hop simulation problem in a beeping network in $O(h\cdot B\Delta^{h+2}\text{\em\ polylog }n)$ rounds.

5 Conclusions

We provided deterministic distributed algorithms to efficiently simulate a round of algorithms designed for the CONGEST model on the Beeping Networks. This allowed us to improve polynomially the time complexity of several (also graph) problems on Beeping Networks. The first simulation by the Local Broadcast algorithm is shorter by a polylogarithmic factor than the other, more general one – yet still powerful enough to implement some algorithms, including the prominent solution to Network Decomposition [20]. The more general one could be used for solving problems such as MIS. We also considered efficient pipelining of messages via several layers of BN. Two important lines of research arise from our work. First, whether some (graph) problems do not need local broadcast to be solved deterministically, and whether their time complexity could be asymptotically below $\Delta^{2}$ . Second, could a lower bound on any deterministic local broadcast algorithm, better than $\Omega(\Delta\log n)$ , be proved?

References

[1] Yehuda Afek, Noga Alon, Ziv Bar-Joseph, Alejandro Cornejo, Bernhard Haeupler, and Fabian Kuhn. Beeping a maximal independent set. Distributed Computing, 26(4):195–208, 2013. doi:10.1007/S00446-012-0175-7.
[2] Yehuda Afek, Noga Alon, Omer Barad, Eran Hornstein, Naama Barkai, and Ziv Bar-Joseph. A biological solution to a fundamental distributed computing problem. Science, 331(6014):183–185, 2011.
[3] Yagel Ashkenazi, Ran Gelles, and Amir Leshem. Brief announcement: Noisy beeping networks. In Proceedings of the 39th Symposium on Principles of Distributed Computing, PODC 2020, pages 458–460, 2020. doi:10.1145/3382734.3405705.
[4] Joffroy Beauquier, Janna Burman, Peter Davies, and Fabien Dufoulon. Optimal multi-broadcast with beeps using group testing. In Structural Information and Communication Complexity: 26th International Colloquium, SIROCCO 2019, L’Aquila, Italy, July 1–4, 2019, Proceedings 26, pages 66–80. Springer, 2019. doi:10.1007/978-3-030-24922-9_5.
[5] Joffroy Beauquier, Janna Burman, Fabien Dufoulon, and Shay Kutten. Fast beeping protocols for deterministic mis and ( $\delta$ + 1)-coloring in sparse graphs. In IEEE INFOCOM 2018-IEEE Conference on Computer Communications, pages 1754–1762. IEEE, 2018. doi:10.1109/INFOCOM.2018.8486015.
[6] Annalisa De Bonis, Leszek Gasieniec, and Ugo Vaccaro. Optimal two-stage algorithms for group testing problems. SIAM J. Comput., 34(5):1253–1270, 2005. doi:10.1137/S0097539703428002.
[7] Arnaud Casteigts, Yves Métivier, John Michael Robson, and Akka Zemmari. Design patterns in beeping algorithms: Examples, emulation, and analysis. Information and Computation, 264:32–51, 2019. doi:10.1016/J.IC.2018.10.001.
[8] Bogdan S Chlebus, Gianluca De Marco, and Muhammed Talo. Naming a channel with beeps. Fundamenta Informaticae, 153(3):199–219, 2017. doi:10.3233/FI-2017-1537.
[9] Bogdan S. Chlebus and Dariusz R. Kowalski. Almost optimal explicit selectors. In Maciej Liskiewicz and Rüdiger Reischuk, editors, Fundamentals of Computation Theory, 15th International Symposium, FCT 2005, Lübeck, Germany, August 17-20, 2005, Proceedings, volume 3623, pages 270–280, 2005. doi:10.1007/11537311_24.
[10] Alejandro Cornejo and Fabian Kuhn. Deploying wireless networks with beeps. In Distributed Computing: 24th International Symposium, DISC 2010, Cambridge, MA, USA, September 13-15, 2010. Proceedings 24, pages 148–162. Springer, 2010. doi:10.1007/978-3-642-15763-9_15.
[11] Artur Czumaj and Peter Davies. Communicating with beeps. Journal of Parallel and Distributed Computing, 130:98–109, 2019. doi:10.1016/J.JPDC.2019.03.020.
[12] Peter Davies. Optimal message-passing with noisy beeps. In Proceedings of the 2023 ACM Symposium on Principles of Distributed Computing, PODC 2023, pages 300–309, 2023. doi:10.1145/3583668.3594594.
[13] Julius Degesys, Ian Rose, Ankit Patel, and Radhika Nagpal. Desync: Self-organizing desynchronization and tdma on wireless sensor networks. In Proceedings of the 6th international conference on Information processing in sensor networks, pages 11–20, 2007. doi:10.1145/1236360.1236363.
[14] Fabien Dufoulon, Janna Burman, and Joffroy Beauquier. Beeping a deterministic time-optimal leader election. In 32nd International Symposium on Distributed Computing, DISC 2018. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2018.
[15] Fabien Dufoulon, Yuval Emek, and Ran Gelles. Beeping shortest paths via hypergraph bipartite decomposition. arXiv preprint arXiv:2210.06882, 2022. doi:10.48550/arXiv.2210.06882.
[16] Klim Efremenko, Gillat Kol, and Raghuvansh Saxena. Interactive coding over the noisy broadcast channel. In Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing, STOC 2018, pages 507–520, 2018. doi:10.1145/3188745.3188884.
[17] Roland Flury and Roger Wattenhofer. Slotted programming for sensor networks. In Proceedings of the 9th ACM/IEEE International Conference on Information Processing in Sensor Networks, pages 24–34, 2010. doi:10.1145/1791212.1791216.
[18] Klaus-Tycho Förster, Jochen Seidel, and Roger Wattenhofer. Deterministic leader election in multi-hop beeping networks. In Distributed Computing: 28th International Symposium, DISC 2014, Austin, TX, USA, October 12-15, 2014. Proceedings 28, pages 212–226. Springer, 2014.
[19] Pawel Garncarek, Dariusz R. Kowalski, Shay Kutten, and Miguel A. Mosteiro. Beeping deterministic congest algorithms in graphs, 2025. doi:10.48550/arXiv.2502.13424.
[20] Mohsen Ghaffari, Christoph Grunau, and Vaclav Rozhoň. Improved deterministic network decomposition. In Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms, SODA 2021, pages 2904–2923. SIAM, 2021. doi:10.1137/1.9781611976465.173.
[21] Mohsen Ghaffari and Bernhard Haeupler. Near optimal leader election in multi-hop radio networks. In Proceedings of the twenty-fourth annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2013, pages 748–766. SIAM, 2013. doi:10.1137/1.9781611973105.54.
[22] Zygmunt J Haas and Jing Deng. Dual busy tone multiple access (dbtma)-a multiple access control scheme for ad hoc networks. IEEE Transactions on Communications, 50(6):975–985, 2002. doi:10.1109/TCOMM.2002.1010617.
[23] Stephan Holzer and Nancy Lynch. Brief announcement: beeping a maximal independent set fast. In 30th International Symposium on Distributed Computing, DISC 2016, 2016.
[24] Kokouvi Hounkanli, Avery Miller, and Andrzej Pelc. Global synchronization and consensus using beeps in a fault-prone multiple access channel. Theoretical Computer Science, 806:567–576, 2020. doi:10.1016/J.TCS.2019.09.020.
[25] Kokouvi Hounkanli and Andrzej Pelc. Deterministic broadcasting and gossiping with beeps. arXiv preprint arXiv:1508.06460, 2015. arXiv:1508.06460.
[26] Kokouvi Hounkanli and Andrzej Pelc. Asynchronous broadcasting with bivalent beeps. In Structural Information and Communication Complexity: 23rd International Colloquium, SIROCCO 2016, Helsinki, Finland, July 19-21, 2016, Revised Selected Papers 23, pages 291–306. Springer, 2016. doi:10.1007/978-3-319-48314-6_19.
[27] Peter Jeavons, Alex Scott, and Lei Xu. Feedback from nature: simple randomised distributed algorithms for maximal independent set selection and greedy colouring. Distributed Computing, 29:377–393, 2016. doi:10.1007/S00446-016-0269-8.
[28] Jason J. Moore, Alexander Genkin, Magnus Tournoy, Joshua L. Pughe-Sanford, Rob R. de Ruyter van Steveninck, and Dmitri B. Chklovskii. The neuron as a direct data-driven controller. Proceedings of the National Academy of Sciences, 121(27):e2311893121, 2024. doi:10.1073/pnas.2311893121.
[29] Arik Motskin, Tim Roughgarden, Primoz Skraba, and Leonidas Guibas. Lightweight coloring and desynchronization for networks. In IEEE INFOCOM 2009, pages 2383–2391. IEEE, 2009. doi:10.1109/INFCOM.2009.5062165.
[30] Saket Navlakha and Ziv Bar-Joseph. Distributed information processing in biological and computational systems. Communications of the ACM, 58(1):94–102, 2014. doi:10.1145/2678280.
[31] David Peleg. Distributed computing: a locality-sensitive approach. SIAM, Philadelphia, PA, USA, 2000.
[32] Fouad Tobagi and Leonard Kleinrock. Packet switching in radio channels: Part ii-the hidden terminal problem in carrier sense multiple-access and the busy-tone solution. IEEE Transactions on Communications, 23(12):1417–1433, 1975. doi:10.1109/TCOM.1975.1092767.

[bib.bib1] [1] Yehuda Afek, Noga Alon, Ziv Bar-Joseph, Alejandro Cornejo, Bernhard Haeupler, and Fabian Kuhn. Beeping a maximal independent set. Distributed Computing, 26(4):195–208, 2013. doi:10.1007/S00446-012-0175-7.

[bib.bib2] [2] Yehuda Afek, Noga Alon, Omer Barad, Eran Hornstein, Naama Barkai, and Ziv Bar-Joseph. A biological solution to a fundamental distributed computing problem. Science, 331(6014):183–185, 2011.

[bib.bib3] [3] Yagel Ashkenazi, Ran Gelles, and Amir Leshem. Brief announcement: Noisy beeping networks. In Proceedings of the 39th Symposium on Principles of Distributed Computing, PODC 2020, pages 458–460, 2020. doi:10.1145/3382734.3405705.

[bib.bib4] [4] Joffroy Beauquier, Janna Burman, Peter Davies, and Fabien Dufoulon. Optimal multi-broadcast with beeps using group testing. In Structural Information and Communication Complexity: 26th International Colloquium, SIROCCO 2019, L’Aquila, Italy, July 1–4, 2019, Proceedings 26, pages 66–80. Springer, 2019. doi:10.1007/978-3-030-24922-9_5.

[bib.bib5] [5] Joffroy Beauquier, Janna Burman, Fabien Dufoulon, and Shay Kutten. Fast beeping protocols for deterministic mis and ( $\delta$ + 1)-coloring in sparse graphs. In IEEE INFOCOM 2018-IEEE Conference on Computer Communications, pages 1754–1762. IEEE, 2018. doi:10.1109/INFOCOM.2018.8486015.

[bib.bib6] [6] Annalisa De Bonis, Leszek Gasieniec, and Ugo Vaccaro. Optimal two-stage algorithms for group testing problems. SIAM J. Comput., 34(5):1253–1270, 2005. doi:10.1137/S0097539703428002.

[bib.bib7] [7] Arnaud Casteigts, Yves Métivier, John Michael Robson, and Akka Zemmari. Design patterns in beeping algorithms: Examples, emulation, and analysis. Information and Computation, 264:32–51, 2019. doi:10.1016/J.IC.2018.10.001.

[bib.bib8] [8] Bogdan S Chlebus, Gianluca De Marco, and Muhammed Talo. Naming a channel with beeps. Fundamenta Informaticae, 153(3):199–219, 2017. doi:10.3233/FI-2017-1537.

[bib.bib9] [9] Bogdan S. Chlebus and Dariusz R. Kowalski. Almost optimal explicit selectors. In Maciej Liskiewicz and Rüdiger Reischuk, editors, Fundamentals of Computation Theory, 15th International Symposium, FCT 2005, Lübeck, Germany, August 17-20, 2005, Proceedings, volume 3623, pages 270–280, 2005. doi:10.1007/11537311_24.

[bib.bib10] [10] Alejandro Cornejo and Fabian Kuhn. Deploying wireless networks with beeps. In Distributed Computing: 24th International Symposium, DISC 2010, Cambridge, MA, USA, September 13-15, 2010. Proceedings 24, pages 148–162. Springer, 2010. doi:10.1007/978-3-642-15763-9_15.

[bib.bib11] [11] Artur Czumaj and Peter Davies. Communicating with beeps. Journal of Parallel and Distributed Computing, 130:98–109, 2019. doi:10.1016/J.JPDC.2019.03.020.

[bib.bib12] [12] Peter Davies. Optimal message-passing with noisy beeps. In Proceedings of the 2023 ACM Symposium on Principles of Distributed Computing, PODC 2023, pages 300–309, 2023. doi:10.1145/3583668.3594594.

[bib.bib13] [13] Julius Degesys, Ian Rose, Ankit Patel, and Radhika Nagpal. Desync: Self-organizing desynchronization and tdma on wireless sensor networks. In Proceedings of the 6th international conference on Information processing in sensor networks, pages 11–20, 2007. doi:10.1145/1236360.1236363.

[bib.bib14] [14] Fabien Dufoulon, Janna Burman, and Joffroy Beauquier. Beeping a deterministic time-optimal leader election. In 32nd International Symposium on Distributed Computing, DISC 2018. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2018.

[bib.bib15] [15] Fabien Dufoulon, Yuval Emek, and Ran Gelles. Beeping shortest paths via hypergraph bipartite decomposition. arXiv preprint arXiv:2210.06882, 2022. doi:10.48550/arXiv.2210.06882.

[bib.bib16] [16] Klim Efremenko, Gillat Kol, and Raghuvansh Saxena. Interactive coding over the noisy broadcast channel. In Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing, STOC 2018, pages 507–520, 2018. doi:10.1145/3188745.3188884.

[bib.bib17] [17] Roland Flury and Roger Wattenhofer. Slotted programming for sensor networks. In Proceedings of the 9th ACM/IEEE International Conference on Information Processing in Sensor Networks, pages 24–34, 2010. doi:10.1145/1791212.1791216.

[bib.bib18] [18] Klaus-Tycho Förster, Jochen Seidel, and Roger Wattenhofer. Deterministic leader election in multi-hop beeping networks. In Distributed Computing: 28th International Symposium, DISC 2014, Austin, TX, USA, October 12-15, 2014. Proceedings 28, pages 212–226. Springer, 2014.

[bib.bib19] [19] Pawel Garncarek, Dariusz R. Kowalski, Shay Kutten, and Miguel A. Mosteiro. Beeping deterministic congest algorithms in graphs, 2025. doi:10.48550/arXiv.2502.13424.

[bib.bib20] [20] Mohsen Ghaffari, Christoph Grunau, and Vaclav Rozhoň. Improved deterministic network decomposition. In Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms, SODA 2021, pages 2904–2923. SIAM, 2021. doi:10.1137/1.9781611976465.173.

[bib.bib21] [21] Mohsen Ghaffari and Bernhard Haeupler. Near optimal leader election in multi-hop radio networks. In Proceedings of the twenty-fourth annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2013, pages 748–766. SIAM, 2013. doi:10.1137/1.9781611973105.54.

[bib.bib22] [22] Zygmunt J Haas and Jing Deng. Dual busy tone multiple access (dbtma)-a multiple access control scheme for ad hoc networks. IEEE Transactions on Communications, 50(6):975–985, 2002. doi:10.1109/TCOMM.2002.1010617.

[bib.bib23] [23] Stephan Holzer and Nancy Lynch. Brief announcement: beeping a maximal independent set fast. In 30th International Symposium on Distributed Computing, DISC 2016, 2016.

[bib.bib24] [24] Kokouvi Hounkanli, Avery Miller, and Andrzej Pelc. Global synchronization and consensus using beeps in a fault-prone multiple access channel. Theoretical Computer Science, 806:567–576, 2020. doi:10.1016/J.TCS.2019.09.020.

[bib.bib25] [25] Kokouvi Hounkanli and Andrzej Pelc. Deterministic broadcasting and gossiping with beeps. arXiv preprint arXiv:1508.06460, 2015. arXiv:1508.06460.

[bib.bib26] [26] Kokouvi Hounkanli and Andrzej Pelc. Asynchronous broadcasting with bivalent beeps. In Structural Information and Communication Complexity: 23rd International Colloquium, SIROCCO 2016, Helsinki, Finland, July 19-21, 2016, Revised Selected Papers 23, pages 291–306. Springer, 2016. doi:10.1007/978-3-319-48314-6_19.

[bib.bib27] [27] Peter Jeavons, Alex Scott, and Lei Xu. Feedback from nature: simple randomised distributed algorithms for maximal independent set selection and greedy colouring. Distributed Computing, 29:377–393, 2016. doi:10.1007/S00446-016-0269-8.

[bib.bib28] [28] Jason J. Moore, Alexander Genkin, Magnus Tournoy, Joshua L. Pughe-Sanford, Rob R. de Ruyter van Steveninck, and Dmitri B. Chklovskii. The neuron as a direct data-driven controller. Proceedings of the National Academy of Sciences, 121(27):e2311893121, 2024. doi:10.1073/pnas.2311893121.

[bib.bib29] [29] Arik Motskin, Tim Roughgarden, Primoz Skraba, and Leonidas Guibas. Lightweight coloring and desynchronization for networks. In IEEE INFOCOM 2009, pages 2383–2391. IEEE, 2009. doi:10.1109/INFCOM.2009.5062165.

[bib.bib30] [30] Saket Navlakha and Ziv Bar-Joseph. Distributed information processing in biological and computational systems. Communications of the ACM, 58(1):94–102, 2014. doi:10.1145/2678280.

[bib.bib31] [31] David Peleg. Distributed computing: a locality-sensitive approach. SIAM, Philadelphia, PA, USA, 2000.

[bib.bib32] [32] Fouad Tobagi and Leonard Kleinrock. Packet switching in radio channels: Part ii-the hidden terminal problem in carrier sense multiple-access and the busy-tone solution. IEEE Transactions on Communications, 23(12):1417–1433, 1975. doi:10.1109/TCOM.1975.1092767.

Beeping Deterministic CONGEST Algorithms in Graphs

Abstract

Keywords and phrases:

Funding:

Copyright and License:

2012 ACM Subject Classification:

Related Version:

DOI:

Event:

Editors:

Series and Publisher:

1 Introduction

1.1 Our Contributions

1.2 Related Work

2 Model, Notation, and Problems

2.1 Communication Models

Beeping Networks (BNs) [10].

CONGEST Networks [31].

2.2 Problems Studied

CONGEST Simulation.

Maximal Independent Set (MIS).

3 Simulation of a CONGEST Round in Beeping Networks

Definition 1 (Avoiding selectors).

Fact 1.

Theorem 2 ([6, 9]).

3.1 The c2b Algorithm

Algorithm for epoch 𝒊: Preliminaries and main concepts

Algorithm for epoch 𝒊: Structure

Definitions and notation.

3.2 Analysis of the c2b Algorithm

Fact 2 (Single beeping).

Proof.

Lemma 3 (Correct receiving).

Lemma 4 (Correct realization).

Lemma 5 (Sub-phase progress).

Lemma 6 (Phase progress).

Lemma 7 (Epoch invariant).

Theorem 8.

Proof.

Maximal Independent Set (MIS).

Corollary 9.

4 Multi-hop Simulation

Theorem 10.

Proof.

Algorithm

Theorem 11.

5 Conclusions

References

Algorithm for epoch $𝒊$ : Preliminaries and main concepts

Algorithm for epoch $𝒊$ : Structure