Improved Approximation Guarantees for Advertisement Placement

In Section 2 we provide a formal definition of the problem and some useful notation. Then, in Section 3 we present our $(2+\epsilon )$-approximation for the problem, and in Section 4 we present our $(1+\epsilon )$-approximation with resource augmentation.

Suppose we place all the tasks in $\text{OPT}(\mathrm{I})$ one next to the other, sorted non-increasingly by height. Since there is a feasible schedule for them and their height is at least $\delta C$, the total width of tasks in $\text{OPT}(\mathrm{I})$, say $W$, is at most $T/\delta$. Starting from the tallest slice in the pile, we partition the slices of the tasks into groups $G_1,\mathrm{\dots },G_g$ of total width exactly $(\epsilon \delta /2)W$ each, except possibly for the last one, which can have a smaller width. We have at most $2/(\epsilon \delta )$ groups.

Our tentative set of rounding tasks from the rounding procedure will initially be defined by taking the task of smallest height from each group $G_i$, for each $i\in \{1,\mathrm{\dots },g-1\}$ (this set may contain less than $g-1$ tasks due to repetitions), and our set of shifted tasks will initially be empty. At this point, the set of rounding tasks and guessed tasks is the same, and tasks with smaller index than the rounding task with smallest index are not part of $OPT(I)$, so they can be discarded.

Consider the feasible schedule for $\text{OPT}(\mathrm{I})$. Since the first group on the left (i.e., $G_1$) is discarded, we will use the empty space due to this removal to place the slices from $G_2$ in the following way: we iteratively place the slices from $G_2$ into the leftmost time slot that had a slice from $G_1$ and does not have any slice from the same corresponding task; if some slice cannot be placed, we skip and continue. We claim that the number of tasks whose slices were not placed entirely by this procedure is at most $1/\delta -1$. Indeed, if there were more, since there must be some time slot that had some slice from $G_1$ that did not get replaced by a slice from $G_2$, this means that slices that could not get assigned into that space already have another slice from the same job there. However, since all the heights are at least $\delta C$, there can be at most $1/\delta -1$ other slices in that time slot, meaning that some task could have used that space in our procedure. This leads to a contradiction.

The set of tasks that could not get assigned by this procedure will be added to the set of shifted tasks. Now that the slices from $G_2$ were either reassigned or removed, we can use that space to place the slices from $G_3$ via the same procedure, and continue until placing the slices from $G_g$. We obtain a set of at most $2/(\epsilon {\delta }^2)$ shifted tasks that were discarded.

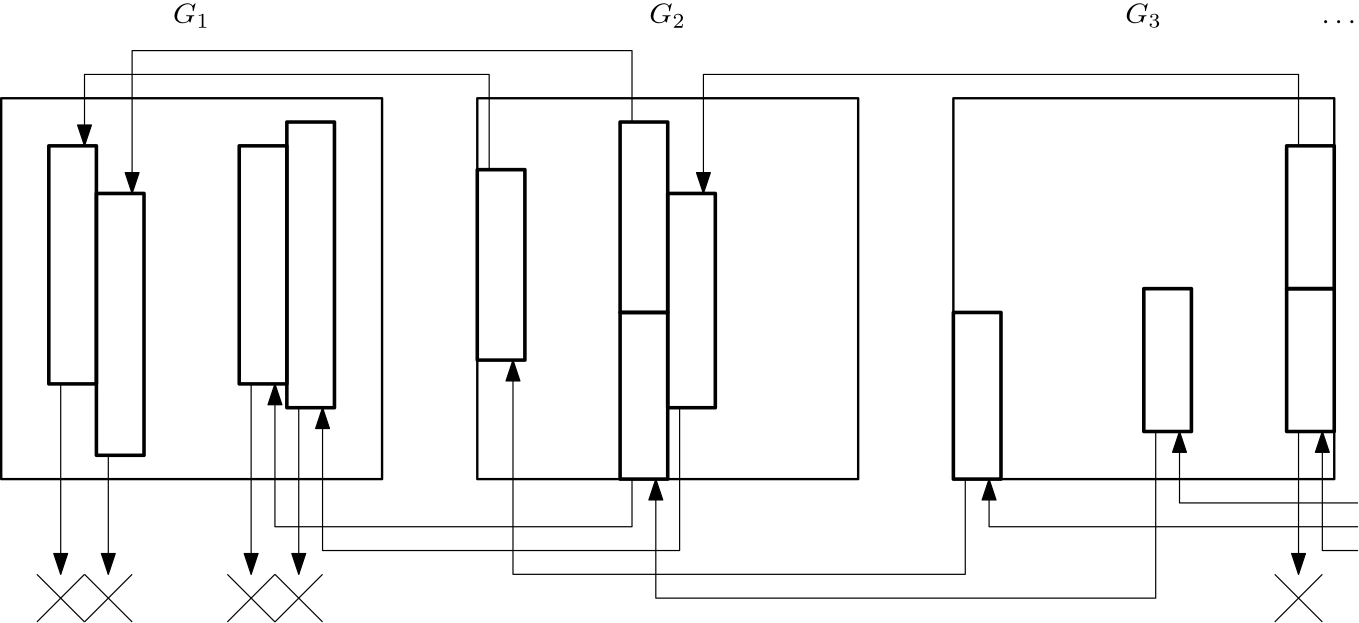
If these sets of rounding and shifted tasks have total area at most $(\epsilon /2)\text{area}(\text{OPT}(\mathrm{I}))$, we end here as all the requirements from the lemma would be fulfilled; otherwise, we remove the sets of rounding and shifted tasks from the initial pile (still considering them as guessed tasks, which will later be scheduled just as they originally were), and redo the procedure with the remaining tasks with respect to the width of the surviving tasks, until finding a set of rounding tasks of total area at most $(\epsilon /2)\text{area}(\text{OPT}(\mathrm{I}))$. Since the sets of rounding and shifted tasks from each iteration are disjoint, the procedure must end after at most $2/\epsilon$ iterations as the total area of the tasks is at most $\text{area}(\text{OPT}(\mathrm{I}))$; consequently, the number of guessed tasks at the end of this procedure is at most $\frac{2}{\epsilon }\left(\frac{2}{\epsilon \delta }+\frac{2}{\epsilon {\delta }^2}\right)\le \frac{8}{{\epsilon }^2{\delta }^2}$.

Let $\tilde{I}$ be the outcome of the aforementioned procedure. By construction, the number of possible heights in $\tilde{I}$ is at most $8/({\epsilon }^2{\delta }^2)$, corresponding to the number of guessed tasks. We can also observe that the total area of $G_1$ is at most $(\epsilon /2)\text{area}(\text{OPT}(\mathrm{I}))$; to see this, observe that, since every height is at least $\delta C$, it holds that $\text{area}({\mathrm{G}}_1)\le (1/\delta )\text{area}({\mathrm{G}}_{\mathrm{i}})$ for any $i\in \{2,\mathrm{\dots },g-1\}$, and since there are $2/(\epsilon \delta )$ groups with exactly $(\epsilon \delta /2)W$ slices each, we can charge the total area of $G_1$ to $2/\epsilon$ disjoint sets of $1/\delta$ groups from $G_2,\mathrm{\dots },G_g$. Thus, the total area of discarded tasks, corresponding to tasks in $G_1$ plus the rounding tasks, is at most $(\epsilon /2)\text{area}(\text{OPT}(\mathrm{I}))+(\epsilon /2)\text{area}(\text{OPT}(\mathrm{I}))\le \epsilon \cdot \text{area}(\text{OPT}(\mathrm{I}))$. In conclusion, the obtained schedule for $\tilde{I}$ is feasible and has total area at least $(1-\epsilon )\text{area}(\text{OPT}(\mathrm{I}))$. $◀$

Let $K\in O(1)$ be the number of possible heights in the instance, and $t\in O(1)$ be the maximum number of slices scheduled on any time slot. Similar to the classical dynamic program for makespan minimization (see, e.g., [29]), a configuration is a vector in ${\{0,1,\mathrm{\dots },t\}}^K$ specifying, for each possible height, how many slices of that height are scheduled in a given time slot; in particular, the number of possible configurations is at most ${(t+1)}^K\in O(1)$.

Consider now any feasible schedule for $I$ such that at most $t$ slices are scheduled into each time slot. The number of possible load configurations (i.e., vectors specifying in each coordinate how many time slots follow a given configuration) is at most $T^{{(t+1)}^K}$, and therefore, we can efficiently enumerate all possible load configurations. To conclude, we provide a way to verify whether a given load configuration is feasible, i.e., if the tasks in $I$ can be scheduled such that the solution follows the given load configuration. To see this, we prove that the following greedy algorithm correctly decides whether a load configuration is feasible:

1. (a)

   For each possible height, sort the time slots non-decreasingly according to the total load of slices of that height.

2. (b)

   For a fixed height, and considering the time slots from left to right, iteratively assign a slice from a compatible task (i.e., that has not been assigned yet to that time slot) having the largest remaining width.

If a feasible schedule exists for the tasks, we prove that this procedure computes such a schedule via a simple induction on the number of time slots in the load configuration. As a base case, if there is one time slot, since there is a feasible schedule, every task must have width $1$ and hence the greedy procedure computes the solution. Consider now an instance with $k+1$ time slots, $k\ge 1$, where a feasible schedule exists. Consider the set of tasks whose slices are scheduled into the leftmost time slot. If these tasks have the largest widths in the instance (i.e. they are scheduled exactly as in the greedy procedure), then we can simply apply the inductive hypothesis to the remaining $k$ time slots and the remaining slices. If it is not the case, then there exists some tasks $i,j$, with $w_i>w_j$, such that a slice of $j$ was scheduled into the leftmost time slot but $i$ was not. Since $w_i>w_j$, there must be some time slot where a slice of $i$ was scheduled into but $j$ was not, and hence we can swap them (see Fig. 3). Consequently, we can again apply the inductive hypothesis, concluding the proof. $◀$

To apply Lemma 3, we need to define precisely which tasks we want to include in our solution. The following lemma shows that we can select a set of tasks whose total area is roughly the total area of tall tasks in the optimal solution, and that admits a feasible schedule.

Let $\tilde{I}$ be the set of rounded tall tasks from Lemma 2. Let $h_1,h_2,\mathrm{\dots },h_K$ be the possible heights of tall tasks after rounding, and let ${𝒞}_1,\mathrm{\dots },{𝒞}_K$ be the sets of tasks in $\tilde{I}$ of height $h_i$, for each $i\in \{1,\mathrm{\dots },K\}$, respectively. For each $i\in \{1,\mathrm{\dots },K\}$, let $W_i$ be the total width of tasks from ${𝒞}_i$. We will approximately guess $W_i$, and then select tasks for our solution according to these widths.

We round $W_i$ according to the following procedure. We guess $t\le 1/(\epsilon \delta )+1$ tasks from ${𝒞}_i$, say $\{i_1,\mathrm{\dots },i_t\}$ and consider a value of the form ${\sum }_{j=1}^{t-1}{w}_{i_j}+q\cdot w_{i_t}$, with $q\in \{0,1,\mathrm{\dots },n\}$. $W_i$ will then be rounded down to the closest value $W_i^{\prime }$ of that form. As this requires guessing a constant number of tasks and a number that ranges from zero to $n$, this can be done in polynomial time.

We now prove that there exists a subset of tasks satisfying the requirements of the lemma such that, for each class ${𝒞}_i$, their total width is at most $W_i^{\prime }$. If $|{𝒞}_i|\le 1/(\epsilon \delta )+1$, then $W_i=W_i^{\prime }$ and the proof follows. If not, consider the widest $1/\epsilon +1$ tasks in ${𝒞}_i$ (say $i_1,\mathrm{\dots },i_t$), remove $i_t$ from the set (which is the task of smallest width out of them), and then consider the largest possible value of the form ${\sum }_{j=1}^{t-1}{w}_{i_j}+q\cdot w_{i_t}$ that is not larger than $W_i$. Since $i_t$ is the task of smallest width out of the widest ones, its total area is at most $\epsilon \cdot \delta \cdot \text{area}({𝒞}_{\mathrm{i}})$, proving the claim.

Since $\tilde{I}$ is not known, instead of guessing it exactly we do the following: As before, we guess the $1/(\epsilon \delta )+1$ widest tasks in ${𝒞}_i$, say $\{i_1,\mathrm{\dots },i_t\}$, discard $i_t$, and greedily complete the set until reaching total width $W_i^{\prime }$ using tasks whose width is at most $w_{i_t}$ that are not part of the guessed tasks. Observe that the total width of selected tasks from the group is at least $W_i^{\prime }-w(i_t)\ge (1-\epsilon \delta )W_i^{\prime }$. The union of the selected tasks will be our set $\widehat{I}$.

For each group, suppose now that the guessed tasks are assigned as in the schedule for $\tilde{I}$, and the remaining tasks are iteratively scheduled into the leftmost time slot where they fit (i.e., where there is no slice from the same task already scheduled), using the time slots where original slices of that group were scheduled. Similarly to the proof of Lemma 2, this procedure schedules all the guessed tasks, and every considered task except for at most $1/\delta$ many, and hence the total width of scheduled tasks from the group is at least

In conclusion, the total area of scheduled tasks is at least $(1-4\epsilon )\text{area}({\text{OPT}}_{𝒯})$ thanks to the guarantees from Lemma 2, the load profile is upper bounded by the load profile of the optimal solution restricted to tall tasks, and the set $\widehat{I}$ can be computed in polynomial time as required. $◀$

We can now put the pieces together to obtain our algorithm for tall tasks.

Thanks to Lemma 4, we now have a set of tall tasks with roughly the same total area as ${\text{OPT}}_{𝒯}$, that furthermore can be scheduled respecting its load profile. By means of Lemma 3, this solution can actually be computed, proving the result. $◀$

We can define a relaxation of the problem through an instance of the classical one-dimensional knapsack problem. We define a knapsack instance with capacity $T\cdot C$ and, for each task $i$, we create an item whose size is $h_i\cdot w_i$ and profit is $p_i$. If we solve this instance, we obtain a set of tasks, say $I^{\ast }$, that maximizes its total profit while maintaining its total area below $T\cdot C$. The set $I^{\ast }$ might not admit a feasible schedule, but it satisfies that $p(I^{\ast })\ge p(\text{OPT})$. If we run the PTAS for knapsack due to Lawler [25] on this relaxation, we obtain in polynomial time a set of tasks $I^{\prime }$ satisfying that $p(I^{\prime })\ge (1-\epsilon )p(\text{OPT})$.

We consider an adaptation of Graham’s list scheduling algorithm [15] for makespan minimization. The algorithm considers the tasks in any arbitrary but fixed order and iteratively places the slices of the tasks in the time slot with the lowest current load that does not have a copy of that task. The algorithm continues until a task cannot be included, or until scheduling every task in the instance.

Freund and Naor [11] prove that, if tasks obtained from the knapsack relaxation are sorted non-decreasingly by height and then scheduled according to LF, the solution obtained is $(3+\epsilon )$-approximate even in the presence of general profits. More in detail, the set $I^{\ast }$ can be partitioned into three subsets such that each one of them can be feasibly scheduled according to LF; the best of the three corresponds to the desired solution. We prove now that a similar scheme leads to a PTAS for short tasks under general profits. Our procedure works as follows:

1. 1.

   We compute $I^{\ast }$ by approximately solving the knapsack relaxation restricted to short tasks.

2. 2.

   We sort the tasks in $I^{\ast }$ non-increasingly according to $p_i/(h_i\cdot w_i)$.

3. 3.

   We run the LF algorithm with respect to the previous order, and return the computed solution.

Observe first that, if the algorithm schedules the whole set $I^{\ast }$, we directly obtain the desired guarantee since $p(I^{\ast })\ge (1-\epsilon )p({\text{OPT}}_{𝒮})$. On the other hand, if our algorithm did not schedule all the tasks in $I^{\ast }$, we use the following result due to Freund and Naor: Suppose tasks are placed according to the LF algorithm (regardless of the order in which the tasks are considered), let $h_{\max }$ be the maximum height of a task considered so far. At any given moment during the assignment, it holds that $\mathrm{\ell }(e)-\mathrm{\ell }(e^{\prime })\le h_{\max }$ for any time slots $e,e^{\prime }\in \{1,\mathrm{\dots },T\}$. This implies that for each pair of time slots $e,e^{\prime }\in \{1,\mathrm{\dots },T\}$, $|\mathrm{\ell }(e)-\mathrm{\ell }(e^{\prime })|\le \delta C$, and therefore the total area of the tasks included in the solution is greater than or equal to $(1-2\delta )CT$, since ${\max }_{e\in \{1,\mathrm{\dots },T\}}\mathrm{\ell }(e)>(1-\delta )C$ (otherwise, we would have enough space to include the task that does not fit) and ${\min }_{e\in \{1,\mathrm{\dots },T\}}\mathrm{\ell }(e)\ge (1-2\delta )C$. This already proves the claim for the case of profits being equal to the area (assuming $\delta \le \epsilon /2$) because $\text{area}(\text{OPT})\le \mathrm{CT}$; we will show that this works even for general profits.

Let ALG be the obtained solution. We use the previous facts to show that $p(\mathrm{ALG})\ge p(I^{\ast })\cdot (1-\epsilon )\ge (1-2\epsilon )\cdot p({\text{OPT}}_{𝒮})$. Let $1,\mathrm{\dots },n^{\ast }$ be the tasks of $I^{\ast }$ sorted non-increasingly according to $p_i/(w_i{h}_i)$. Let also $k^{\prime }$ be the last task that ALG included. We partition ALG into groups of total area at least $\epsilon CT$ and at most $(1+\epsilon )\epsilon CT$ by iteratively taking tasks until attaining total area at least $\epsilon CT$. The number of groups that we obtain is at least

where the last inequality holds for every $\epsilon \le 0.4$ and $\delta \le \epsilon /2$. Let $G_1,\mathrm{\dots },G_g$ be the obtained groups, and let $G_{g+1}$ be the tasks in $I^{\ast }\setminus \mathrm{ALG}$. For each $i\in \{1,\mathrm{\dots },g\}$, we have that $p(G_i)\ge p(G_{g+1})$; indeed, thanks to the order of the tasks, it holds that:

where the third inequality holds since the total area of $G_{g+1}$ is at most $\epsilon CT$, and the first and the last inequality follow from the tasks being sorted in non-increasing order according to $p_i/(h_i{w}_i)$. We now compare the total profit of $\mathrm{ALG}$ and ${\text{OPT}}_{𝒮}$. First, we have that $p(I^{\ast })-p(\mathrm{ALG})=p(G_{p+1})$. Since $p(G_i)\ge p(G_{p+1})$ for every $i\in \{1,\mathrm{\dots },g\}$, we have that $p(G_{g+1})\le (p(I^{\ast })-p(G_{g+1}))/g$, which implies that $(g+1)p(G_{g+1})\le p(I^{\ast })$, and hence that $p(G_{g+1})\le p(I^{\ast })/(g+1)\le 10\epsilon \cdot p(I^{\ast })$. In conclusion,

$◀$

We now have all the ingredients required to prove Theorem 1.

We partition the given instance into short and tall tasks as described in the beginning of Section 3.1, using $\delta =\epsilon /2$. We then run the algorithm for tall tasks from Lemma 5 on the tall tasks, and the algorithm for short tasks from Lemma 6 on the short tasks, and return the best of the two solutions. One of them must be a $(2+\epsilon )$-approximate solution for the problem. $◀$