Evaluation of the Parallel Features of Rust for Space Systems
Abstract
The rise in complexity of the algorithms run on space systems, largely attributable to higher resolution instruments which generate a large amount of the data to be processed, as well as to the need for increased autonomy, which relies on Neural Network inference systems in future missions, demand the adoption of more powerful on-board hardware, such as multicores.
At the same time, the correctness and reliability of critical on-board software is of paramount importance for the success of space missions. However, developing such complex software in low-level languages can have a negative impact on these aspects.
For this reason, this paper evaluates the role that the Rust programming language can have in this change, given its memory safety and built in support for parallelism, which allows to better utilise more powerful hardware, in particular multicore cpus, without compromising the programmability and safety of the code.
To this end, the GPU4S benchmarking suite, part of the open source OBPMark benchmarking suite of the European Space Agency (ESA), is ported to Rust, with sequential and parallel implementations. The performance of the ported benchmarks is compared to the existing sequential and parallel implementations in low-level languages to evaluate the trade-offs of the different solutions, and it is evaluated on several multicore platforms which are candidates for future on-board processing systems. A particular focus is put on parallel versions of the benchmarks, where Rust offers solid native support, as well as library support for fast parallelization similar to OpenMP. Finally, in terms of correctness, the Rust implementations are free of recently detected defects in the low-level implementations of the GPU4S benchmarks.
Keywords and phrases:
Rust, Multicore, Space SystemsCopyright and License:
2012 ACM Subject Classification:
Software and its engineering Parallel programming languages ; Applied computing Aerospace ; Software and its engineering Software safetyFunding:
This work was performed within the European Commission’s METASAT Horizon Europe project (grant agreement 101082622). Moreover, it was also partially supported by the Spanish Ministry of Economy and Competitiveness (MINECO) under the grant IJC2020-045931-I.Supplementary Material:
archived at
 swh:1:dir:57ab27fabeccfe138fadcb55e63a5bea6873de21
swh:1:dir:57ab27fabeccfe138fadcb55e63a5bea6873de21
Editors:
Daniele Cattaneo, Maria Fazio, Leonidas Kosmidis, and Gabriele MorabitoSeries and Publisher:
 Open Access Series in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Open Access Series in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
The development of more powerful applications for safety critical missions, together with the growth in the number of cores in commercial processors, requires the software to adapt to use more efficiently the newer platforms. Although in the past Ada – a safe language – dominated the space domain, C/C++ have taken their place, but they are older languages which lack more modern features and in particular safety. Memory safety becomes even more relevant in parallel applications, as it is easier to make mistakes in this context. Other programming languages such as Java and Go, offer better programmability particularly in parallel code, however they are not usable in safety critical systems due to the fact that the garbage collector can cause big latency spikes, and does not allow for Worst Case Execution Time calculations.
In this niche domain, the Rust programming language has a real chance of being the best option. It is a memory safe language without garbage collection, which gets rid of latency spikes [9]. Instead of garbage collection, it uses the RAII (Resource Acquisition Is Initialization) paradigm [6] to insure that memory is freed. It offers modern tools and features, and has native parallelism support within the language. Performance is also one of the biggest focuses of Rust, which is important to compete with C and C++.
In this paper we analyse if the potential that Rust has in theory is carried out in practice, by porting the GPU4S benchmarks [16, 14]. These benchmarks, while they will be useful for platform performance evaluation, in the context of this paper are used instead to show a performance and programmability comparison between Rust and C, both in sequential and parallel code. Our code developed is released as open source at [15] and will be included in the next OBPMark release from ESA.
The paper is divided in 6 sections: Section 2 serves as an introduction to the GPU4S benchmarks. Section 3 presents the hosted (i.e. running on an operating system) version of the benchmarks, both in their sequential and parallel versions. Section 4 discusses the platforms on which the code was evaluated, as well as the performance comparisons and finally Section 5 presents the conclusions and future work.
2 The GPU4S benchmarks
In this section we introduce the GPU4S benchmarks suite [14, 16], also known as OBPMark Kernels, part of the open source OBPMark benchmarking suite [18] of the European Space Agency (ESA) hosted at [12], which are the applications we ported from C to Rust in this work. Next we describe their purpose, design and delve into the benchmarks functionality and relevance.
As the amount of data to be processed on board of spacecraft increases and the type of algorithms to be run expand to allow autonomous operation, the need for performance in the embedded system employed is growing significantly. The GPU4S Bench suite was developed to improve the performance testing capabilities of such systems, with a particular focus on Embedded Graphics Processing Units (GPUs) for satellite on-board processing and other safety critical systems, where existing benchmarks were particularly inadequate.
The complete list of the benchmarks available in the suite is: CIFAR 10, Convolution, Correlation, Fast fourier transform, Fast fourier transform window, Finite impulse response filter, LRN, Matrix multiplication, Max pooling, Memory bandwidth, Relu, Softmax, Wavelet transform.
The benchmarks were chosen as representative algorithms used in space-relevant applications from a survey performed among on-board software divisions of Airbus Defence and Space, Toulouse, France [16], with a look also at applications that will become important in the future, such as Computer Vision and Neural Networks. Although initially focusing on GPU benchmarking, GPU4S Bench has been later ported to several programming models including OpenMP for CPUs (used for comparison in this paper), GPUs and FPGAs, CUDA, OpenCL, HIP, Ada and others and it is used by ESA to drive the selection of hardware platforms for future space missions. To signify this platform independence, it is renamed as OBPMark Kernels, and it is used together with OBPMark applications as contractual requirement for reproducible use cases in ESA- funded projects.
3 Hosted Benchmarks
This section presents the implementation of the hosted version of the benchmarks, which means that they run on top of an OS. First we define the data structures, traits and method implementations of the code to be benchmarked, defined in the obpmark_library crate, before delving in the code of the benchmarks executables.
3.1 Data Structures
The benchmarks from the GPU4S Bench project operate on vectors and matrices, in most cases 2D matrices. As a consequence, the main data structure required is a matrix data structure. While the C version of the benchmarks employs a dynamically allocated one-dimensional buffer for this purpose, we decide to develop two distinct versions of the data structures, to compare performance and ease of use of the two approaches: Matrix1d, that stores the data in a 1D Vector, and Matrix2d, that stores the data in a 2D Vector.
The difference in the memory disposition of the two version depends on the platform and allocator on which the code will run. As the structure will be allocated at the start of the executable, we suspect that the memory will look very similar amongst the different versions. This could make the 2D vector solution preferable, as it will be less bug prone than the 1D version, by allowing an easier use of iterators. We will look further into this when analysing the results of the benchmarks. Listing 1 shows the struct code.
Both structures are generic, so that they can contain any type that implements the trait Number, which we will discuss in detail in the following section.
When analysing the benchmark executables we will see how the Matrix methods will be called from the benchmarks; to allow the benchmark code to not be specialized for the different matrix types, all operations on them are defined in traits. The BaseMatrix trait defines basic operations on matrices:
-
Initialization of a new matrix from a 2D vector representation.
-
Retrieval of a 2D vector representation of the data.
-
Initialization of a new matrix populated with zeroes.
-
Initialization of a new matrix with random contents based on a seed.
-
Input and output operations on files.
-
Conversion to a 1D vector data representation, which is needed for verification.
-
Reshaping the matrix by adjusting its row and column counts.
3.2 The Number trait
The original C code provides the benchmarks with different data types that are selected at compile time. We decided that the library should not need to be compiled to a specific numeric type, but rather should be generic over the content of the matrix. This allows the user of the library to easily have matrices that contain different types in the same context, and makes the library useful also outside of the benchmarks code.
There are four types that we will need to support for the various benchmarks (not all the types are supported for all benchmarks, we will later show how to deal with this):
-
The integer type i32.
-
The single precision floating point type f32.
-
The double precision floating point type f64.
-
The half precision floating point type f16; this is not available in the standard library, so we used the crate half [2]. The inclusion of the f16 version of the benchmarks is for consistency with the C version, however at the moment the support for intrinsics is very limited making the code very slow. This is an area in which Rust is rapidly moving forward and we should expect the situation to be quite different in a short time after the publication of this paper. During the time of writing of this document the hardware support on x86 has changed already. For this reason we will not discuss further this feature, as it is subject to rapid change.
3.2.1 The num_traits crate
The num_traits[3] crate is used to help with definitions of common numerical behaviour in Rust programs. While external to the standard library, it enjoys widespread adoption, and many external numeric types implement the crate’s traits.
The num_traits crate offers many useful traits; here we describe the ones we used in defining our own traits:
-
NumRef: Encompasses basic numeric operations like addition, subtraction, multiplication, and division, both for a type and its reference.
-
NumAssignRef: Adds assignment-based operations to NumRef (e.g. +=, *=).
-
AsPrimitive<f64>: Allows casting to f64,serving as a superset of all types to be implemented.
-
PrimInt: Contains common operations on integer types.
-
Float: Contains common operations on floating point types.
3.2.2 Limitations of num_traits
While the traits discussed are useful to define common behaviour, not all the operations that someone might want to do on a number are covered by the num_traits crate. The crate funty [1] was inspiration for some of the missing traits, in particular for its Fundamental one, that enforces basic behaviour such as Copy, Display and Debug.
Until now we described behaviour that we could anticipate we would need even before writing a single benchmark function, also because they are bundled in existing traits. The additional behaviour we describe from here on was mostly added while developing some specific benchmark. The typical process would be: 1. Do some operation you know you can do on a numeric type, 2. Have the compiler complain that it is not possible for the given bounds, 3. Add a new bound to the existing trait. This can be somewhat frustrating, especially when this is not straight forward, as in some of the cases we will describe later.
The ability to obtain a Number from an iterator of T: Number and &T: Number also needs to be specified as a trait bound. At this point two missing behaviours still remain:
-
Obtain a Number from a sum operation on an iterator of elements of type T where T: Number or &T: Number. This is done with the following trait bounds:
std::iter::Sum<Self>
for<’a> std::iter::Sum<&’a Self>. -
Serialize: A way to serialize the numbers to their bytes representation and back; fundamental numeric types all have this behaviour available but it is not behind a trait, as such we need to implement the trait to call the method defined in the standard library. Since the method name is the same for all types, we can achieve this through a macro rule (Listing 4).
-
RngRange: A way to generate numbers in a given range. In this case a trait does exist (SampleUniform from the rand crate), with some complications for the f16 type.
3.2.3 More specific bounds
The Number trait is designed to work with all the types supported by the benchmarks. However not all benchmarks support all the different types: as an example the Softmax benchmark only works on floating point types. Another situation that sometimes happens is that the implementation is very different amongst different types. To allow for this, two more specific traits are defined, to differentiate between integer and floating point types. Listing 5 shows how this was easily achieved thanks to the num_traits crate.
3.3 Sequential traits
In this section, we will go through the steps required to implement the library code of a benchmark function, and we will analyze a few examples of benchmark traits.
As discussed previously, the matrix methods are defined inside traits, so that the same function can be called on different implementations of the matrix structure from the benchmark code. Each benchmark trait consists of two member functions:
-
The main benchmark function, that is called from the executable and is timed to assess the performance of the hardware.
-
A function that operates on a subsection of the matrix. This often is an extraction of an internal loop of the algorithm.
This code separation does it a little bit less readable, but it allows to reduce code duplication when other implementations, in particular the parallel versions, are coded.
For example, Listing 6 shows the trait for the matrix multiplication operation. In this case the function multiply_row calculates one row of the output given the two input matrices and the index of the row to calculate. The multiply function, on the other hand, is the one that will be benchmarked, that deals with calling multiply_row for each row of the result matrix.
Listing 7 shows the implementation of the multiply_row function for the 1D version of the matrix structure. The code is really straight forward, being the inner two loops of a matrix multiplication function, with the value of the outer loop index being passed as the argument row_idx.
The multiply function then is very easy, since all it has to do is implement the outer loop and call the multiply_row function with the correct arguments. We will discuss this further when analysing the parallel implementations, where the design of the functions will become more relevant.
The matrix multiplication example was chosen because representative of most of the benchmarks available, where the inner function operates on a row of the result and the calculation of each row of the output is completely independent of the others. In benchmarks such as the finite impulse response filter, where the input and output are one-dimensional, the inner loop operates on a single element of the output rather than a row, as we can see from the trait definition in Listing 9.
Another case where the design is somewhat different is where, instead of having only operations that can happen in any order, we have the need to enforce some kind of order amongst operations: this is the case for example in the softmax and the wavelet transform benchmarks, and it will become more relevant in the parallel versions of the benchmarks.
3.4 Parallel versions
The parallel version of the benchmarks comes in two flavours: one that uses only the standard library, and one that uses the Rayon crate [7], which allows Rust to operate in parallel in array elements, with minor code modifications, similar to OpenMP. This way we can assess if the added complexity of dealing with data parallelism ourselves is worth it in some metric, such as performance, code maintenance, etc.
3.4.1 Using the standard library
The easiest way to parallelize the code, is to iterate over the result matrix, and spawn a thread for each row to do the computation. This would look something like the code in Listing 10. The advantages of this approach is the readability and simplicity of the code, which becomes even more evident when comparing it with the one in Listing 8; aside from the thread scope and calling the spawn() method, the code is identical to the sequential version.
We did not comment the chunks_exact_mut() method in the sequential version, because the reason for it being there is the design of the row calculation function, which is suited to parallel code. In the matrix multiplication example in Listing 7, the function modifies the result by receiving mutable slices of its rows, rather than through a mutable reference to the whole result matrix. This is not strictly necessary in the sequential version, as the calls do not overlap with each other. However it is crucial in the parallel versions, because each thread needs a mutable reference to part of the matrix simultaneously: chunks_exact_mut() does exactly this while making sure that there is no overlap amongst the different chunks, which makes sure that to avoid any data race between threads.
The disadvantage of the solution presented is that the number of threads spawned is not constant, rather it grows with the size of the matrix, which significantly degrades the performance of this solution if the number of rows is large.
To improve on this, what we need to do is spawn a proper number of threads, which is usually equal to the number of cores, or hardware threads, available on the platform, and assign multiple rows to each thread. This makes the code only slightly more complicated than the previous case, but improves significantly the performance. As shown in Listing 11, each thread has an internal loop (chunk.chunks_exact_mut(result.cols), so that it can call the row function on each row of the chunk. The use of the method chunks_mut instead of the exact version in the outside loop, allows us to run the code regardless of the number of rows of the matrix, as it does not need to be a multiple of the number of threads.
3.4.2 The Softmax Benchmark
The softmax benchmark, as mentioned before, has a slightly different design than the one presented with the matrix multiplication case. This is because, before we can calculate the element of the final matrix, we need to now the sum of the exponentials of the whole matrix. For this reason the code has two parallel sections, with a synchronization in the middle so that the sum is available to the second parallel section. As shown in Listing 12, this only requires us to have two threads scopes rather than one, so that the threads are joined and the sum is calculated before the start of the second scope.
While the code presented is long, especially when compared to the rayon version as we will see, if we consider only the code specific to the benchmark, without the part to spin the threads presented in the previous section, which is the same in all benchmarks, we can see that the code is indeed very straight forward.
3.4.3 Using Rayon
Rayon is a great tool for dealing with the kind of problems we are working on. This becomes evident when comparing the rayon code with the sequential code, for example for the matrix multiplication function (Listing 13), which we included in its sequential version in Listing 8.
The only modification necessary to the code is using Rayon’s parallel version of the chunks_exact_mut() method from standard library.
The softmax benchmark presented when discussing the standard library versions, is a good example both to show the compactness that Rayon can achieve compared to the standard library code, and to showcase some case where the parallel code is not just adding a par_ in front of the standard library iterator. The Rayon version of the code is available in Listing 14. The second loop is the same as in the sequential version, while the first needs to use the reduce() method for calculating the sum. The syntax of reduce is the typical functional syntax of the method, and allows for the reduction operation itself to be performed in parallel as well, which will not be a major consideration on our target platforms, since they will have relatively few cores (4-8), but could be relevant if we had a very large number of threads. It should be noted that the order in which the reductions will happen is not specified, which means the result could be not exactly the same due to the non-associativity of floating point operations [8], which is why we should use a tolerance when validating the results.
3.4.4 Parallel traits
Just like in the sequential case, the parallel versions of the benchmarks are defined inside traits. The parallel traits are defined inside two modules: rayon_traits for the Rayon versions and parallel_traits for the standard library versions. In this case the traits only require one member, that being the function to be benchmarked, and the naming scheme used is the following: The traits have the same name as their sequential counter-part, preceded by Rayon or Parallel depending on the version. The method defined inside the trait has the same name as the sequential version preceded by rayon_ or parallel_ depending on the version. An example of parallel traits for the rectified linear unit benchmark is shown in Listing 15.
3.5 The Benchmark Code
This section deals with the benchmarks crate, that contains the binaries’ code and utilities used by them. Each benchmark in the project has its own executable that deals with argument parsing, initialization, timing, input/output and validation of the result. Besides the executable, in the benchmarks crate, there is a lib.rs file that defines some common functionalities and helper functions.
3.5.1 Type aliasing
The benchmark_utils module defined in the crate deals with some useful code for the benchmarks. Amongst its functionalities, it deals with defining some types based on arguments passed at compile time, in particular a Number type that is going to be the content of the matrices, and a type Matrix, which is the specific matrix implementation to be used. This is done using #[cfg(feature = ...)] directives, that work similarly to #ifdef directives in C.
Listing 16 shows the code needed to define the correct type for the Number alias. In order to pass the flag using cargo, all it takes is to pass to cargo the flag --features ‘‘feature_name’’, and cargo will then pass the flag to rustc. There is no way yet [5] to have mutually exclusive features, however, if more than one datatype is set we will get a compile error for trying to set a type alias already defined. With the last cfg command, if no type is specified at compilation, we default to f32.
4 Results
4.1 Experimental Setup
The evaluation of the code performance has been carried out on both ARM and x86 hosted platforms. All the evaluated platforms are considered good candidates for upcoming high performance aerospace and avionics systems [17]. This section describes the different platforms characteristics. The platforms selection has been made to add to the evaluations of the existing implementations, however since our code does not make use of GPUs, we only use the multicore CPU on each of the selected platforms.
4.1.1 NVIDIA Jetson AGX Xavier
The NVIDIA Jetson AGX Xavier [4] is an embedded platform from NVIDIA which has 8 CPU cores as well as a GPU. The board has different power-modes (Table 1), that affect both the CPU and GPU. In particular we used power-mode 1 and power-mode 2, which maximises the multicore performance of the platform which keeps the board consumption under 15W which has been identified a thermal limit of on-board processing platforms in the GPU4S ESA-funded project [14]. The selected power modes have respectively 2 and 4 CPU cores active and they are same used in similar multicore performance evaluations [17]. The version of the platform we are using has 32 GB of LPDDR4 shared between the CPU and GPU.
The software on the platform is based on Linux Kernel version: 4.9.140 / L4T 32.3.1, Ubuntu version: Ubuntu 18.04 LTS aarch64 and GCC version: 7.5.0 (Ubuntu/Linaro 7.5.0-3ubuntu1 18.04).
| Mode | |||
| Property | MAXN | 10W | 15W |
| Power budget | n/a | 10W | 15W |
| Mode ID | 0 | 1 | 2 |
| Online CPU | 8 | 2 | 4 |
| CPU maximal frequency (MHz) | 2265.6 | 1200 | 1200 |
| GPU TPC | 4 | 2 | 4 |
| GPU maximal frequency (MHz) | 1377 | 520 | 670 |
4.1.2 AMD Ryzen V1605B
The AMD Ryzen V1605B is part of the Ryzen Embedded V1000 family, which offers high performance platforms with a CPU and a Vega GPU in an SoC.
The V1605B has 4 cores, each with 2 hardware threads each, however in our case we did not see improvements by using 8 threads, so we report our results using 4 threads.
The software used on the platform is: Linux kernel: 5.4.0-42-generic, Ubuntu version: Ubuntu 18.04.5 LTS x86_64, GCC version: 7.5.0 (Ubuntu 7.5.0-3ubuntu1 18.04).
4.2 Performance Results
In this subsection we present the performance results of the Rust code compared to the C implementations. We report the result on the AMD Ryzen V1605B and the NVIDIA Jetson AGX Xavier, so that we have two different architectures. All the benchmarks in this subsection, unless differently specified, use a 4096 size and a single precision floating point type, which means that for benchmarks that operate on vectors rather than matrices (FFT, FIR FFT windowed) the number of elements is very small. The decision on which size and datatype to use is for consistency with the standard sizes defined for the GPU4S Bench/OBPMark Kernels Benchmarking Suite [12], which mainly targets existing space processors which have significantly lower performance and memory. Moreover, the same sizes have been used in multicore evaluation of the same platforms using the same benchmarks presented in [17] under the RTEMS SMP space qualified operating system in sequential C and OpenMP, which are used for comparison with our sequential and parallel Rust implementations.
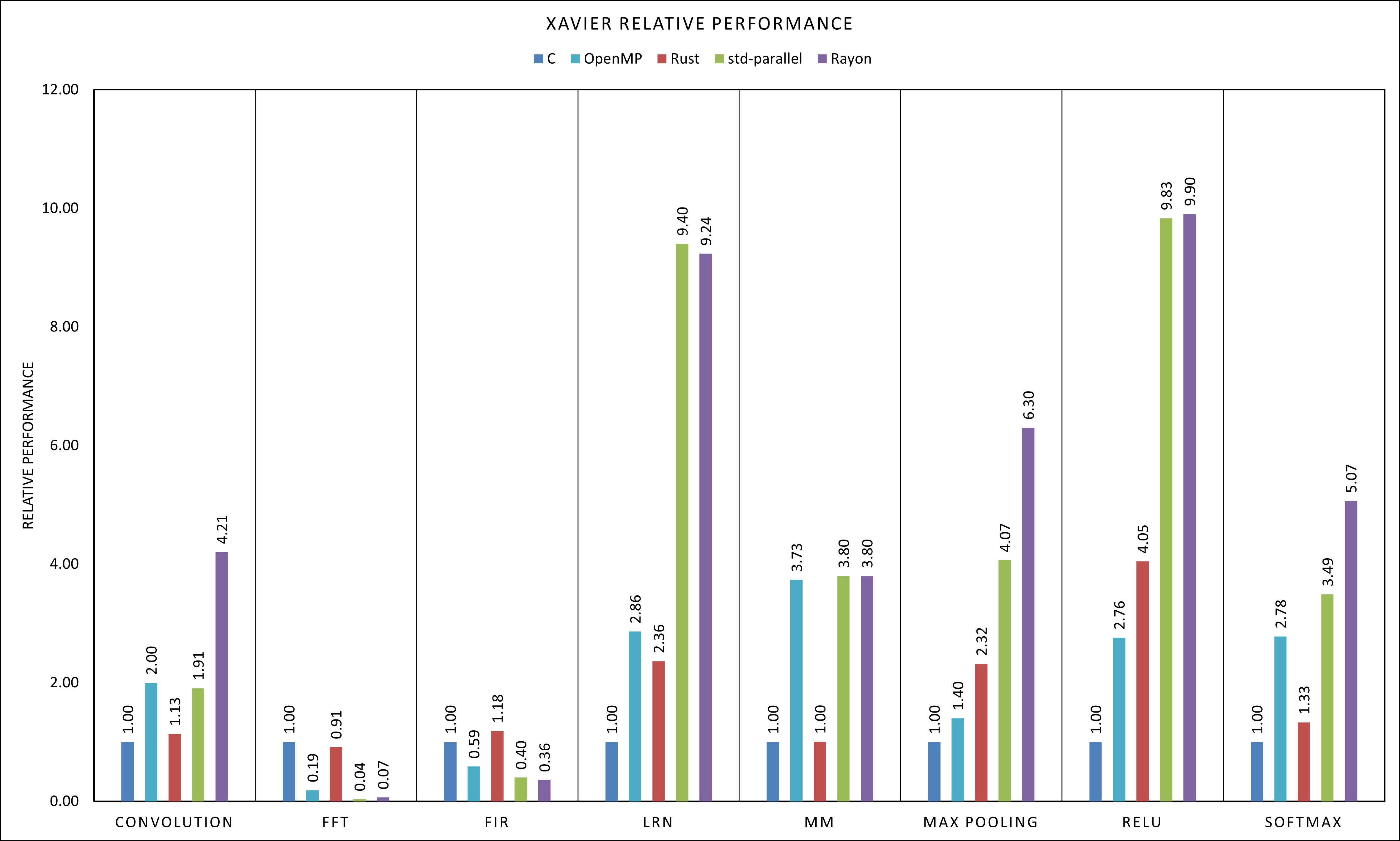
The result on the Xavier in power-mode 2 (so using 4 cores in the parallel benchmarks) are shown in the graphs in Figure 1. If we compare the performance of the sequential versions in C and Rust, we see a few different cases:
-
In FFT and Matrix Multiplication the performance of the two implementations is very close, in the case of Matrix Multiplication almost identical. The small differences are probably attributable to slightly different optimization between LLVM, which is used by Rust and GCC, which is used by RTEMS or different memory arrangements between the different allocators.
-
In Convolution, LRN, Max Pooling, Relu and Softmax the performance of the Rust sequential versions is from 10% all the way to 130% better than that of the C version. This clearly cannot be just slight differences in the compiled code, but requires the code to use significantly different calculations. A few hints have led us to believe that the difference has to be due to the introduction of more vector operations in the Rust compiled code. In particular, while we were not able to identify the specific functionalities of the instructions in the disassembled code, we saw an increase in the number of such operations in the code, as well as in some cases we see the verification to have to be with a tolerance to pass, which suggests that the floating point operations are carried out in some different order compared to the C version.
While in the case of Convolution and Softmax the performance difference is not that large, we are convinced there is a real difference in performance due to the difference in the results for the 2 different parallel implementations. We will discuss this in more detail when analysing the parallel versions. -
In FIR (and perhaps FFT) the performance difference measured is hard to quantify with confidence given the very short execution time of the benchmarks, which is in the 0.5 ms range.
If we now look at the parallel implementations, we see some interesting differences in performance. First, let’s look at the short execution time benchmarks, FIR and FFT: the parallel versions in this case are slower than the sequential version, and this is true both for the Rust and the OpenMP code. This is likely due to the overhead of spinning up the different threads which is not worth the small improvement in execution time. In FFT in particular, we are not actually able to parallelize the code due to complex task dependencies which are not supported in Rayon. Similarly, the OpenMP version of the code uses homogeneous parallelism (i.e. using parallel for) instead of the OpenMP tasking model, because it provides easier certification for multicore contention in aerospace systems [17].
This means that for the parallel code we use the windowed version of the FFT benchmark as in [17], which is much easier to parallelise with homogeneous parallelism, and offers a way to get to an approximated result. This however shows promise for larger vectors, where we can see an actual speedup. The reason for the choice of the sizes is to use the same values from the testing that has been done on the C versions. It should also be noted that the windowed algorithm cannot compete with the library implementation in FFTW, which is highly optimised, making it perhaps not a good candidate for parallelization.
For Matrix Multiplication, we can see that, as in the sequential case, both Rust parallel implementations have extremely similar performance to the OpenMP version, which makes Matrix Multiplication the most consistent benchmarks between the C and Rust implementations, with a very good 3.8x speedup on 4 cores.
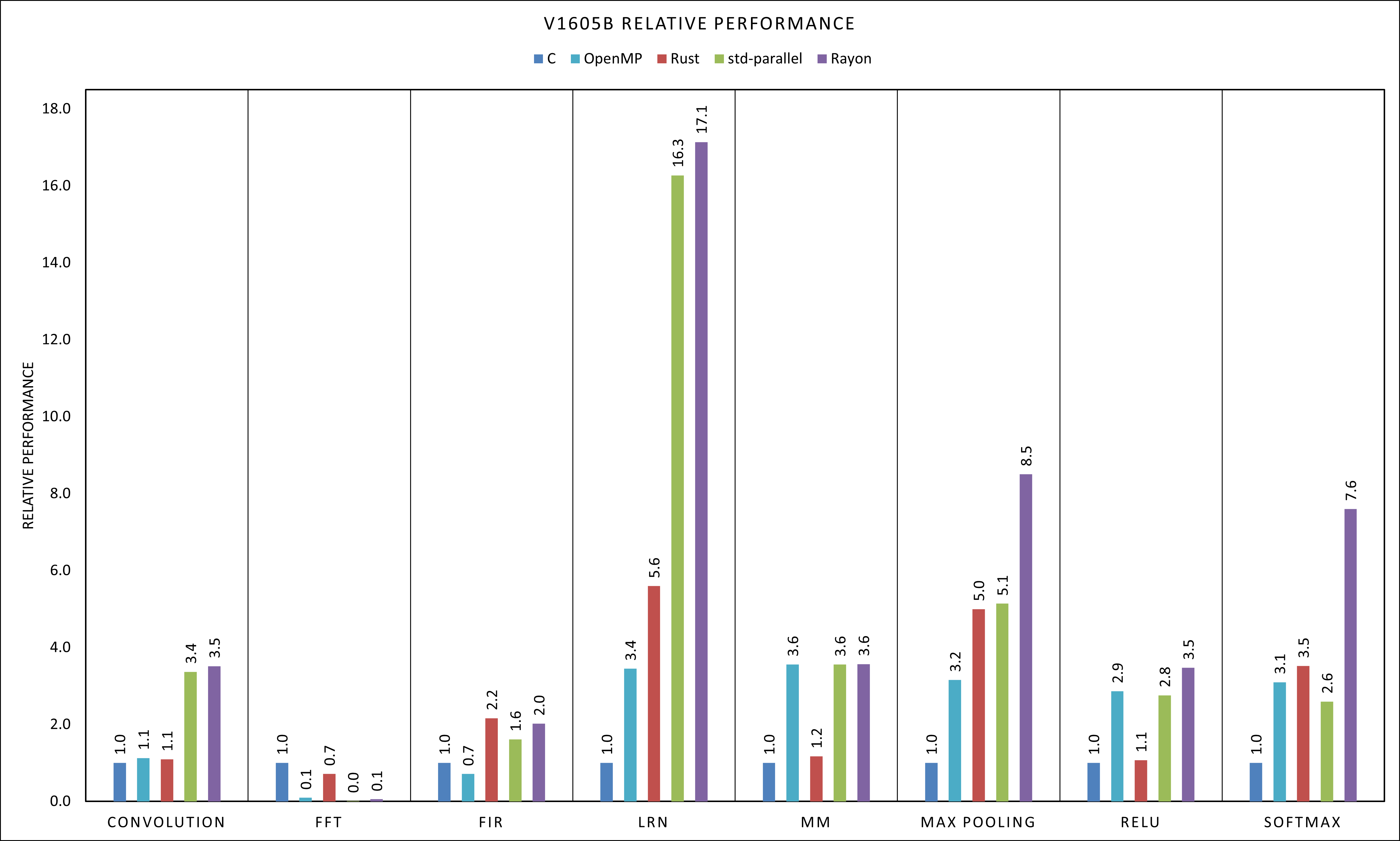
Looking at the AMD platform results we can see that in some cases the results are quite similar to the Xavier platform, while in some other we have very different relative performance. Since we are not particularly interested in the performance difference amongst the platforms we do not report the execution times. However it should be noted that the V1605B has much higher performance, with the benchmark taking usually anywhere from half to to complete execution compared to the Xavier. The behaviour of Matrix multiplication is still very consistent amongst the different implementations, with speedups that approach the linear case both for OpenMP and the parallel Rust implementations. Similar to the Xavier, LRN, Max Pooling and Softmax show much higher sequential performance compared to the C version, in this case performing even better than the OpenMP version, once again thanks to a higher use of vector instructions. Relu, on the other hand, is quite close to the C versions in this case, both in the sequential and parallel execution, with a slight upper hand of the Rayon code. FFT is significantly slower in the parallel versions on the AMD platform too, for the same reasons discussed above, while FIR manages to have better sequential performance compared to the C code, but the parallel code is still slower than the sequential version due to the small sizes on the input.
4.2.1 Taking a closer look to the parallel implementations
As mentioned in the previous section, the two different parallel implementations of the Rust code can have quite different performance depending on the benchmark.
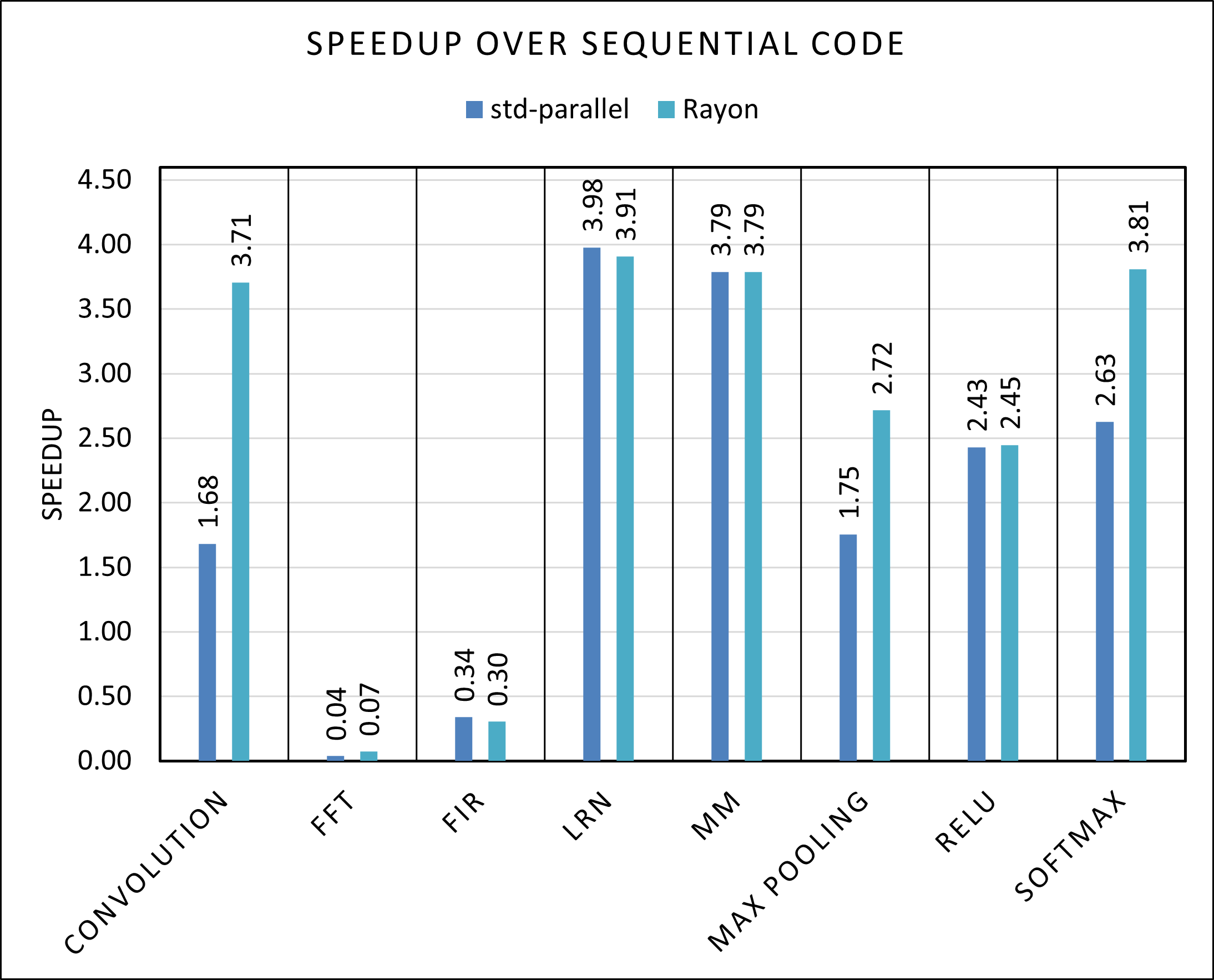
In Figure 3 we see the speedup over the sequential code of the rayon and std-parallel implementations, which seems to favor significantly Rayon, in particular where the vector instructions made the sequential code faster. Our guess to the cause of this behaviour, is that Rayon does a better job keeping the vector operations, as the library can decide, knowing the hardware features available, if it makes sense to make something parallel and to which thread assign each part of the matrix, while in the std-parallel the programmer takes this decision, which can result in suboptimal performance. This is true in particular in the Convolution and Softmax benchmarks, where the std-parallel code has similar performance to the OpenMP one, even though the Rust sequential version is faster. In LRN and Relu this is not the case, with both the std-parallel and Rayon version showing very impressive speed-ups compared to the sequential C version.
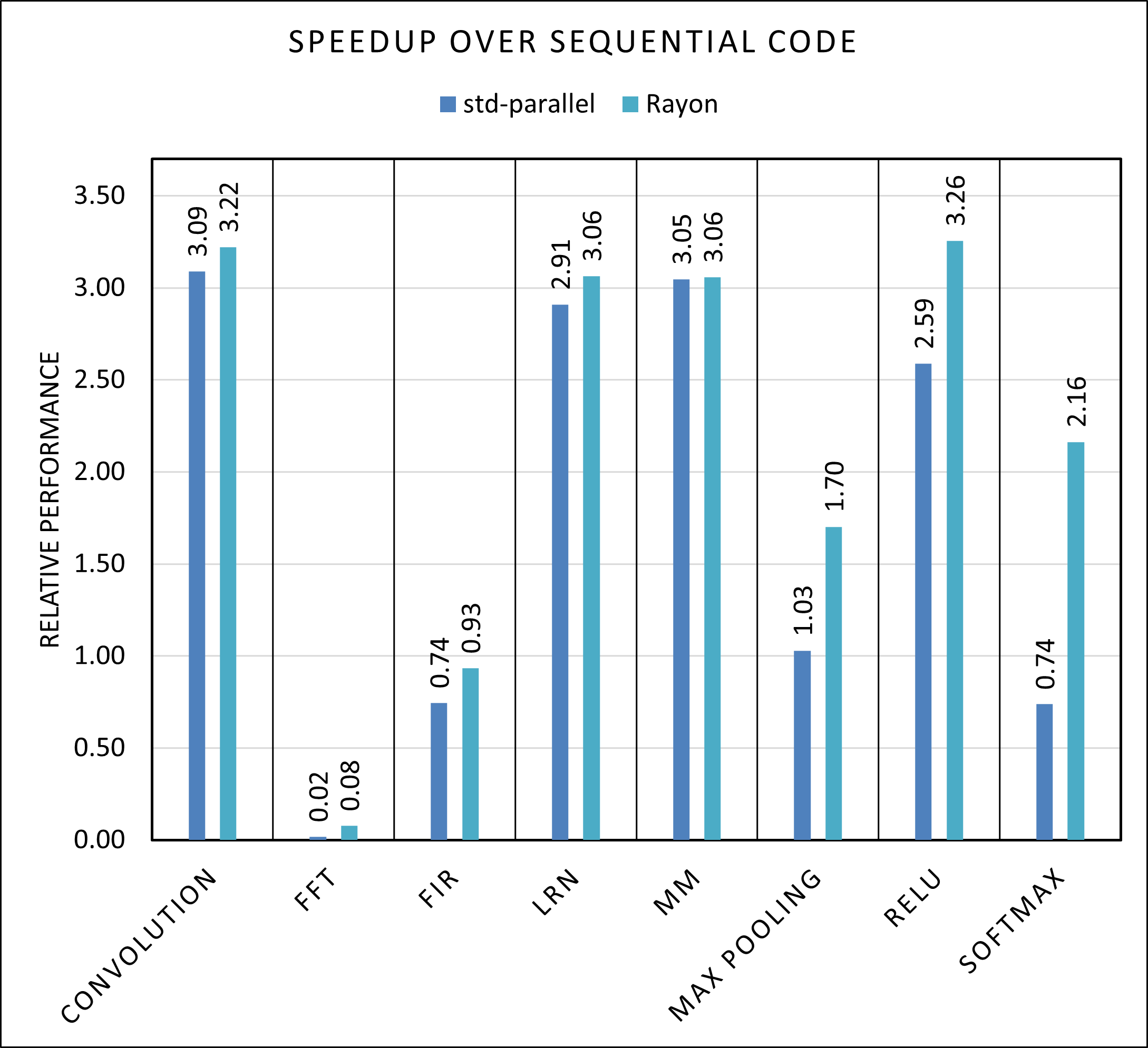
In the AMD results shown in Figure 4, we can see somewhat similar results, but here the std-parallel version of Softmax is slower than the sequential code and in Max Pooling it has a very similar performance, while on the ARM platform we could still see a speedup over the sequential code. As mentioned before, this is likely because the manual subdivision of the input and output matrices to make the parallelization possible interferes with the ability of the compiler to introduce vector instructions, while the more complex Rayon runtime is able to still utilize them. On the other hand, both Rayon and std-parallel manage to perform very well in the LRN benchmark, on both architectures.
Another difference with the performance on the Xavier is that on the V1605B the speedup does not go much higher than three, while in the Xavier case we had some cases, like LRN and Matrix Multiplication, where the performance was close to the theoretical maximum.
4.2.2 2D matrices
Until now we mostly considered the 1D version of the Matrix structure to have a better comparison with the C code, however as we mentioned, we developed also a 2D version which improves on programmability and decreases bugs when manually dealing with identifying rows.
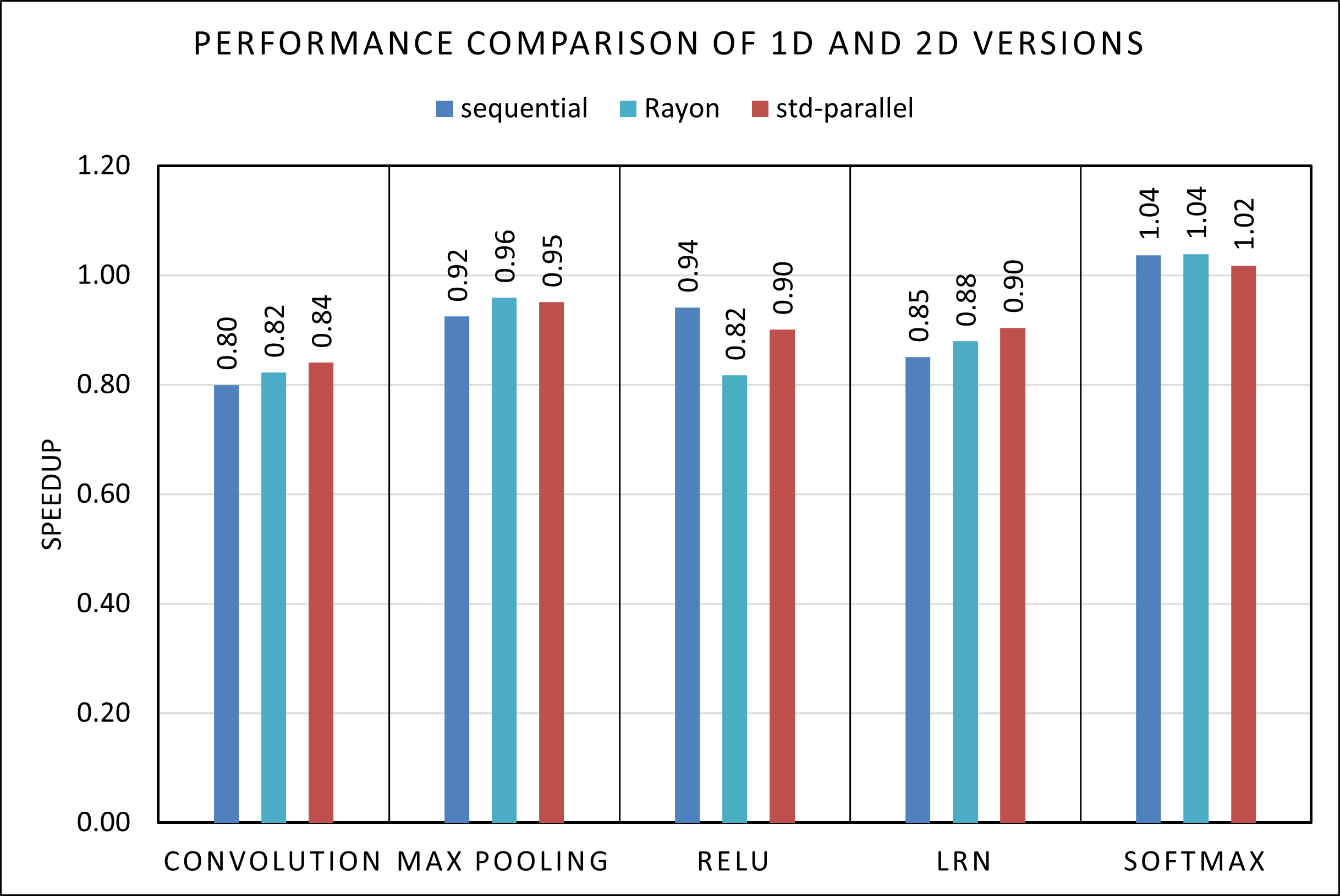
Figure 5 shows the speedup of some 2D Matrix algorithms over their 1D counterparts, and as we can see in general there is a performance deficit by having the rows allocated independently from each other. It seems to be the case that this deficit is not the same for all benchmarks, with Softmax actually showing an improvement, though perhaps not statistically significant. In our results the difference is usually pretty small, making the 2D matrix probably preferable in situations where we don’t care about very small performance differences. It should be noted though that the difference in the real world could be higher, if the structures are allocated during the execution rather than at the start of the program, or with more programs running at the same time, as the OS could place the different rows far away from each other, increasing the cache misses.
5 Conclusions and Future Work
The results presented in the previous section show that the performance of sequential Rust is similar to C in our space-relevant applications. The same holds for the parallel versions, with Rayon showing some of the most promising results both in terms of ease of use and performance. These findings together with the memory safety and easier development of Rust make it a promising technology in the space and other safety critical domains, as well as in embedded systems in general.
Another take away comes from the 2D version of the algorithms, that perform only slightly worse but help a lot with programmability. Throughout the development we caught bugs on the 1D version that stemmed from inadequate testing, as the benchmarks only use square matrices, due to the use of the incorrect dimension in iterators; these bugs did not happen in the 2D versions as the there is no need to manually divide the structure in rows.
Similarly, it is worth noting that during the multicore evaluation performed in our group for the [17] publication, a couple of software defects (out of bounds accesses and incomplete initialisation) were found in the C and OpenMP implementations of the FIR GPU4S benchark, which manifested with a crash only on the GR740 space processor under the RTEMS SMP real-time operating system. These latent defects were masked in all other hardware platforms and operating systems combinations. After investigating and correcting these defects in the GPU4S Bench official repository, we checked whether these defects were also present in our Rust port, as well as in the Ada SPARK versions performed in [10]. Interestingly, these defects were not present in the GPU4S Bench ports in these two safe languages [13, 11], since both languages prevent uninitialised memory and out-of-bound accesses.
Rust has a reputation of being a hard language: we would agree that the learning curve can be somewhat steep in the beginning, but in our opinion the very thing that makes Rust hard, i.e. the compile time checks, is what can make the programmer a lot more confident in the resulting code, since once it compiles we know we are not going to get any segmentation faults. This is even more the case in parallel code, where there is much lower risk of forgetting to release a lock, introducing very hard to debug errors and race conditions.
When compared with OpenMP the comparison in ease of parallel code development is less one sided, especially with the wide use of OpenMP in many applications and the larger feature set compared to Rayon. Still, as we saw in Section 3, the parallel code is very easy to obtain from the sequential one and the results are very good, making Rust a viable option.
Another area where we would like to see further development is in libraries for mathematical abstraction: we considered using some crates for mathematical operations, but did not find one that satisfied our requirements, partly due to limited support. We created the Number trait to deal with some of these problems, and we think a package that can help with this would be instrumental for the use of Rust in high performance parallel applications.
References
- [1] funty – Rust Package Registry – crates.io. URL: https://crates.io/crates/funty.
- [2] half – Rust Package Registry – crates.io. URL: https://crates.io/crates/half.
- [3] num_traits – Rust Package Registry – crates.io. URL: https://crates.io/crates/num_traits.
- [4] NVIDIA Jetson Xavier Series – nvidia.com. URL: https://www.nvidia.com/en-us/autonomous-machines/embedded-systems/jetson-agx-xavier/.
- [5] Pre-RFC: Cargo mutually exclusive features – internals.rust-lang.org. URL: https://internals.rust-lang.org/t/pre-rfc-cargo-mutually-exclusive-features/13182.
- [6] RAII – cppreference.com. URL: https://en.cppreference.com/w/cpp/language/raii.
- [7] rayon – Rust Package Registry – crates.io. URL: https://crates.io/crates/rayon.
- [8] What Every Computer Scientist Should Know About Floating-Point Arithmetic – docs.oracle.com. [Accessed 02-09-2023]. URL: https://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html.
- [9] Why Discord is switching from Go to Rust – discord.com. URL: https://discord.com/blog/why-discord-is-switching-from-go-to-rust.
- [10] Dimitris Aspetakis. Evaluation of the Ada SPARK Language Effectiveness in Graphics Processing Units for Safety Critical Systems. Bachelor’s thesis, Universitat Polytècnica de Catalunya, May 2023. URL: https://upcommons.upc.edu/handle/2117/390672.
- [11] Dimitris Aspetakis, Leonidas Kosmidis, Matina Maria Trompouki, Jose Ruiz, and Gabor Marosy. Formal Methods for High Integrity GPU Software Development and Verification. In Design, Automation & Test in Europe Conference & Exhibition (DATE), 2024.
- [12] D. Steenari et al. On-Board Processing Benchmarks, 2021. https://obpmark.github.io/.
- [13] Leonidas Kosmidis, Dimitris Aspetakis, and Matina Maria Trompouki. Formal methods for GPU Software Development Using Ada SPARK, presentation at the ESA Software Product Assurance Workshop 2023. URL: https://www.cosmos.esa.int/documents/10939403/13962862/3_updated_Leonidas_Kosmidis_2023_Software+Product+Assurance+Workshop+2023_Formal_Methods_GPUs+(1).pdf.
- [14] Leonidas Kosmidis, Iván Rodriguez, Alvaro Jover-Alvarez, Sergi Alcaide, Jérôme Lachaize, Olivier Notebaert, Antoine Certain, and David Steenari. GPU4S: Major Project Outcomes, Lessons Learnt and Way Forward. In Design, Automation & Test in Europe Conference & Exhibition (DATE), 2021.
- [15] Alberto Perugini and Leonidas Kosmidis. GPU4S Benchmarks Rust Port Source Code Repository. swhId: swh:1:dir:57ab27fabeccfe138fadcb55e63a5bea6873de21 (visited on 2025-02-20). URL: https://gitlab.bsc.es/aperugin/gpu4s_rust.
- [16] Ivan Rodriguez, Leonidas Kosmidis, Jerome Lachaize, Olivier Notebaert, and David Steenari. GPU4S Bench: Design and Implementation of an Open GPU Benchmarking Suite for Space On-board Processing. Technical Report UPC-DAC-RR-CAP-2019-1, Universitat Politècnica de Catalunya, 2019. URL: https://www.ac.upc.edu/app/research-reports/public/html/research_center_index-CAP-2019,en.html.
- [17] Marc Solé, Jannis Wolf, Ivan Rodriguez, Alvaro Jover, Matina Maria Trompouki, and Leonidas Kosmidis. Evaluation of the Multicore Performance Capabilities of the Next Generation Flight Computers. In Digital Avionics Systems Conference (DASC), 2023.
- [18] David Steenari, Leonidas Kosmidis, Ivan Rodríguez-Ferrández, Álvaro Jover-Álvarez, and Kyra Förster. OBPMark (On-Board Processing Benchmarks) – Open Source Computational Performance Benchmarks for Space Applications. In 2nd European Workshop on On-Board Data Processing (OBDP), 2021. doi:10.5281/zenodo.5638577.
