ByteSpector: A Verifying Disassembler for EVM Bytecode
Abstract
We present ByteSpector, a tool for constructing and verifying control flow graphs (CFGs) from Ethereum Virtual Machine (EVM) bytecode. CFGs play a crucial role in analyzing smart contract behavior, but resolving dynamic jumps and ensuring CFG correctness remain significant challenges. ByteSpector addresses these challenges by generating formally verified CFGs, i.e., all target jumps have been resolved correctly, which can serve as a foundation for further contract verification.
ByteSpector introduces several key innovation. First, ByteSpector features an efficient algorithm for resolving dynamic jumps that uses a combination of abstract interpretation and semantics reasoning. Second ByteSpector can automatically generate proof objects from EVM bytecode. Proof objects are Dafny programs that encode the semantics of the bytecode, and can be used to prove that computed CFGs over-approximate the contracts execution paths. Third, ByteSpector is written in Dafny and is guaranteed to be free of common runtime errors like array-out-bounds, division-by-zero etc. Moreover, the code and libraries can be automatically translated into multiple languages (e.g., C#, Python, Java, JavaScript), making them reusable in broader verification frameworks.
By generating Dafny proof objects (and verified CFGs), ByteSpector provides a robust foundation for bytecode-level analysis, enabling formal verification of smart contracts beyond high-level source code analysis.
Keywords and phrases:
EVM bytecode, deductive verification, Control Flow Graph2012 ACM Subject Classification:
Theory of computation Logic and verificationEditors:
Diego Marmsoler and Meng XuSeries and Publisher:
 Open Access Series in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Open Access Series in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
The Ethereum Virtual Machine (EVM) is the execution layer of Ethereum, running smart contracts, programs that power decentralized applications (dApps) and manage billions in assets, particularly in DeFi. Smart contracts are typically written in high-level languages like Solidity111https://soliditylang.org and Vyper,222https://vyperlang.org then compiled into EVM bytecode for execution. Smart contract high-level code undergoes testing and audits before deployment. However, since the EVM executes bytecode, not high-level (Solidity or Vyper source) code, verifying bytecode is crucial for several reasons:
- Compiler bugs.
-
Compilers may introduce errors, producing incorrect bytecode. Certora identified several Solidity compiler bugs, including: in 2022, a memory optimisation issue mistakenly removed operations affecting computation [12]; in 2021, a dynamic array bug caused potential memory corruption [7]. Fortunately, the previous bugs were discovered and fixed before being exploited. However, in 2023, a bug [11] in the Vyper compiler was exploited resulting in USD26 Million stolen.
- EVM-specific constraints.
-
The EVM has some specific features that are not present in source code, such as gas and a bounded execution stack. For instance, if we want to guarantee the absence of stack-overflow/underflow exception, or determine the gas requirements to avoid an out-of-gas exception, we need to reason about the bytecode. These safety properties can only be verified at the bytecode level.
The problem we address is enabling formal reasoning about EVM bytecode. To achieve this, we have developed ByteSpector, a tool that extracts Dafny proof objects from EVM bytecode. These proof objects can be analyzed using a Dafny formal semantics of the EVM, leveraging Dafny’s verification capabilities to reason about bytecode behavior. ByteSpector is not intended to replace existing tools for verifying high-level smart contract code. It does not verify that the compiler correctly translates high-level code to bytecode, but rather provides a way to reason about the bytecode itself.
Our contribution
Our contribution is a tool, ByteSpector, that can automatically construct proof objects from EVM bytecode. Proof objects are Dafny (a verification-friendly programming language) programs that encode the semantics of the bytecode, can be instrumented with specifications (e.g., absence of stack underflow) and reasoned about. ByteSpector is itself written in Dafny which has several advantages: the code is free of runtime errors (arithmetic, array-out-of-bounds, division-by-zero, etc.), and always terminates. Moreover, the Dafny code can be automatically translated to several target languages (e.g., C#, Python, Java, JavaScript) using the Dafny backends and re-used in other projects.
2 Overview
In this section we introduce the workflow of ByteSpector and a simple example to highlight the main features of the tool. Figure 1 summarises the main stages: we start with the EVM bytecode of a program, disassemble it into segments of instructions, build a control flow graph (CFG) of the program, and use the CFG to generate a Dafny proof object that can be reasoned about using the Dafny-EVM, a formal semantics [5] of the EVM written in Dafny.
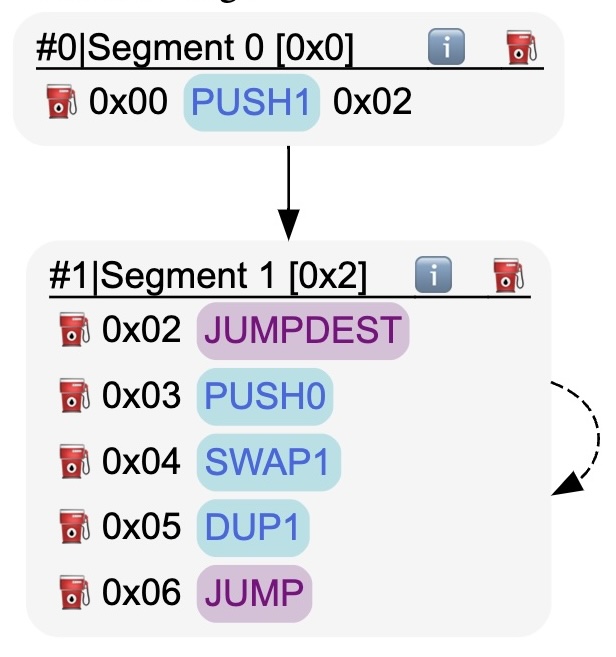
An EVM program is a finite sequence of bytes stored in a contract’s code region starting at address 0x00. This bytecode can be decoded into readable EVM instructions and organised into segments that are non-branching instruction sequences except possibly for the last instruction e.g., JUMP. For example, the bytecode333The prefix 0x indicates hexadecimal encoding. 0x6005600d565b600b600d565b005b56 corresponds to the disassembled TwoCalls program in Listing 1.
To analyze execution flow, we construct a Control Flow Graph (CFG), where nodes represent bytecode segments. Figure 2(a) shows the CFG for TwoCalls, where Segment 3 executes twice, and the JUMP at line 18 has multiple possible targets depending on context. ByteSpector resolves these dynamic jumps and determines all possible execution paths.
The CFG is encoded as a Dafny proof object, a Dafny program defining bytecode semantics for each node and transitions between them. Listing 2 shows the ByteSpector-generated code for nodes #2 and #3. The Dafny code uses Dafny-EVM functions like Jumpdest, Push1, Jump that provide the semantics of the EVM instructions. Preconditions (lines 30–31, 44–45) restrict segment entry points, while function calls (lines 40, 52) define CFG edges. If Dafny successfully verifies the proof object, the CFG is sound444Soundness is formally defined in the next sections. and safely over-approximates the bytecode’s behavior, which is essential for proving safety properties.
3 From EVM bytecode to segments of instructions
In this section we introduce the main features of the EVM, its semantics, and how the bytecode can be partitioned into segments.
3.1 The Ethereum virtual machine
The EVM is a stack machine with a bounded stack for computations. Memory stores temporary data during execution, while global storage retains permanent contract state on the blockchain. Every computation consumes gas, a measure of computational cost, and results in one of the following outcomes:
-
a successful termination, the effect of the computation is stored in the global storage.
-
an abort (exception) e.g., caused by stack overflow, jumps to invalid targets, invalid number of arguments to an instruction, etc.
-
an out-of-gas exception if the gas budget is exhausted before the end of the execution.
3.2 EVM bytecode
The EVM supports around 150 instructions to perform arithmetic or bitwise operations (e.g., ADD, SUB, AND, OR), stack operations (e.g., PUSH0, PUSH1, POP, SWAP1, DUP1), memory store/load operations e.g., MSTORE, MLOAD, global storage operations e.g., SSTORE, SLOAD, unconditional (resp. conditional) jumps, JUMP (resp. JUMPI), as well as blockchain specific operations (e.g., BALANCE, ADDRESS, GASLIMIT). A few instructions, such as PUSHes, have parameters and are encoded on a variable number of bytes. For example PUSH2 pushes two bytes on the stack and expects two bytes as arguments e.g., PUSH2 0x3056. We consider only well-formed EVM bytecode with valid opcodes and correct argument counts. Such bytecode can be decoded into an instruction sequence, as shown in Listing 1 (lines 5–18).
3.3 Semantics of the EVM
The EVM semantics, as per the Yellow Paper [13] define the state transition function of the EVM, that maps an EVM state to a new state . A state includes bytecode, program counter (instruction in the program to be executed next), the stack content , the memory content , gas left for the rest of the computation , global storage, and several other fields that we omit here. We let be the size of the stack, and be the sequence without the first elements. Following the Dafny-EVM [5] semantics, we separate instruction semantics from gas consumption (ignored for now). For instance, if points to a POP instruction, the next state is defined by:555For simplicity, we only define the PC and stack updates.
If the stack is empty, the execution aborts with an error state . Otherwise, the program counter is incremented by one and the top element of the stack is removed.
The jump instructions JUMP and JUMPI (unconditional/conditional jump) are branching instructions that may transfer the control location () to an address that is not the next instruction in the code. However, a nice feature of the EVM is that the target of a jump instruction must be a legal address, i.e., the target address of the jump must be a JUMPDEST instruction. For instance, TwoCalls, Listing 1, has 3 legal target addresses: 0x05, 0x0b, and 0x0d. As a result, given a program , we can compute the set of legal target addresses in by identifying the JUMPDEST instructions. If the instruction at is JUMP, is defined by:
For given bytecode and input , the EVM semantics uniquely define , a finite sequence of EVM states (termination is ensured by the gas limit). The error state has no successors. The set of all possible executions of is: where is the finite set of inputs (the calldata has a maximal size in the EVM).
3.4 Code segments
A segment is a sequence of non-branching consecutive instructions ending at:
-
branching instructions JUMP, JUMPI, or
-
terminal instructions STOP, REVERT, RETURN, or
-
any instruction before a JUMPDEST.
This ensures that ) jump targets start segments, preventing jumps into the middle of a segment and ) there is a unique (linear) execution flow within each segment. Segments are shown in Listing 1 and the CFG of TwoCalls in Figure 2(a). We extend Next to segments to compute the state after executing all instructions in a segment S, returning an error state if execution fails before completion.
4 Control flow graphs for EVM bytecode
ByteSpector builds an intermediate artefact, a control flow graph (CFG) for the EVM bytecode, before extracting the proof object from the CFG. A program’s Control Flow Graph (CFG) represents how the program counter updates during program execution. In this section we define CFGs and their expected properties and show how to build a CFG for EVM bytecode.
4.1 Control flow graph
A CFG is a directed graph with nodes and edges and a designated initial node, . Finite paths in the graph can be constructed by starting at and following the (directed) edges of the CFG. We let be the set of finite paths in from .
A graph is a CFG for program if the nodes of are labelled with segments of bytecode of or an error node to represent the error state . Examples of CFGs for the program TwoCalls are shown in Figure 2, page 2. The nodes of the graph are assigned a unique id (#k, top left of node) and are labelled666Two nodes may be labelled with the same segment, the node/segment mapping is not necessarily 1-1. with segments (0–3).
A path uniquely defines a sequence of control locations, , obtained by concatenating the control locations of the segments on . The set of (finite) sequences of control locations defined by a CFG is: For instance, the path in the CFG of Figure 2(a) defines the sequence of segments and the sequence of control locations [0x00,0x02, 0x04, 0x0d, 0x0e, 0x05, 0x06, 0x08, 0x0a, 0x00d, 0x0e] which is a feasible execution in TwoCalls. In the CFG Figure 2(b), the path defines the sequence of segments which in turn defines the sequence of control locations obtained by expanding and concatenating the locations in each segment. Note that is not feasible in the actual program TwoCalls as they can be only two executions of Segment 3.
An important and desirable property of a CFG is that it over-approximates the set of executions of the program. Given an execution , which is a sequence of EVM states (Section 3.3), we define (the projection) of corresponding sequence of control locations777The error state is mapped to . (program counters), and we define the set of pc-runs of as Given a program and a CFG for :
Definition 1.
A CFG is sound for program if .
This definition does not uniquely define a sound CFG for a program.888There may be an infinite number of sound CFGs for some programs. A CFG is a finite automaton and defines a regular language. The set of executions of a program may not be a regular language and sometimes can be over-approximated by an infinite number of more and more precise regular languages. Both CFGs in Figure 2 are sound. The CFG in Figure 2(a) is more precise than the one in Figure 2(b). The CFG in Figure 2(b) is an over-approximation of the CFG in Figure 2(a) and it contains a cycle that is not present in the CFG in Figure 2(a), and not even feasible in program TwoCalls. The previous observation allows us to define a simple algorithm to build a CFG for EVM bytecode: from each segment ending in a JUMP/JUMPI, we create edges to each segment starting with a JUMPDEST in the code. This over-approximates the set of sequences of control locations and produces a sound CFG but this over-approximation may be too coarse to be of any use (like the CFG in Figure 2(b)). Our objective is to compute sound CFGs that are as precise as possible.
4.2 Abstract semantics of the EVM
To compute precise CFGs, we use abstract semantics (abstract interpretation) that track the program counter and an abstract stack representation. While restrictive, this approach is sound and effective (see Section 6). This works well for two reasons:
-
1.
valid jump targets () are known at compile-time.
-
2.
jump targets for JUMP/JUMPI are usually stored on the stack because: ) computing targets with arithmetic is rare due to gas costs and it is error-prone and ) stack storage is cheaper than memory, so compilers optimise for gas by storing jump targets on the stack.
Since we do not track memory, CFG construction might fail if target addresses are stored there. However, experiments (Section 6) confirm this rarely occurs in practice.
An (EVM) abstract state of type EState is a pair : is the program counter, and is an abstract stack, with elements either or which is the unknown/arbitrary value. The abstract representation of the stack captures the size of the stack, and the target addresses of JUMP/JUMPI instructions.
The abstract semantics of EVM instructions (Figure 3) is given by the function999The complete definition of the Nextα function can be found in the code base here. . The abstract semantics may contain more than one successor states for some instructions like JUMPI that have two possible successors: one for the case when the condition is true and one for the case when the condition is false. Other instructions are deterministic and have a single successor. What is captured in the semantics in Figure 3 is that the result of an addition operation “add and pop the two values at the top of the stack, and push the result” is abstracted as . It is not likely to be a target jump. For some instructions like POP, Nextα is identical to Next. The abstract semantics101010The PC advances by as PUSHk instructions have bytes as arguments. of PUSHk instructions track the concrete values that are pushed on the stack, but only if they are in . For jump instructions, the abstract semantics check if the target address is a valid jump target and if the stack is not empty. This implies that if , the target of the jump is not known, we end up in an error (abstract) state .
4.3 CFG computation
Given a segment S, and an abstract state such that the start address of S is , we let be the abstract states obtained after executing the segment S from .
To compute the CFG of program , we perform a standard Depth First Search (DFS) traversal of the graph defined by Nextα starting from the initial abstract state (0x00, []). It is not guaranteed that the DFS will terminate, as the stack may grow indefinitely.
To ensure termination, we limit the DFS to a given maximum depth (e.g., 100). If the maximum depth is reached (indicated by the result of the DFS), we can try a larger bound and iterate until the CFG fits within the bound. We write for the CFG of program as computed by our DFS algorithm on abstract states.
The DFS algorithm completes the exploration of a branch when it encounters a previsoulsy visited node with the same abstract state. However, in some cases, this may lead to non-termination regardless of the maximum depth limit, as the abstract stack may grow arbitrarily large. In the next section we provide a sufficient condition to test whether two abstract states are equivalent and can be safely merged.
4.4 Loop detection
The bytecode in Listing 3 is a simple program that contains an unbounded loop. The CFG for this program is depicted in Figure 4. After execution of the JUMP instruction, the abstract stack content at PC location 0x02 is with unknown values.
The DFS algorithm introduced previously will not terminate for any maximum depth limit. However, we can see that the part of the stack that grows arbitrarily large is made of elements and this has no impact on the target of the JUMP instruction, which remains constant and equal to 0x02. For instance when we run the DFS algorithm we explore the path . If we execute Segment 1 from the state , we end up in a state where the top of the stack is still 0x02. The state can be merged with the state because every future execution after is covered by executions starting from . To identify such configurations, we need to determine that every execution of Segment 1 results in the JUMP at its end always targeting 0x02.
We can provide a sufficient condition to test whether this is the case:
-
1.
Compute the weakest precondition that ensures that at the end of Segment 1 the value of the PC is 0x02;
-
2.
check whether this weakest precondition is invariant when executing Segment 1.
Assume we want to prove that after executing the JUMP instruction at 0x06 (line 11, Figure 4), the program counter is 0x02. As a JUMP instruction updates the program counter to the value at the top element of the stack, the least we can require is that, before we execute the JUMP instruction, the top of the stack contains 0x02. Any other choice would fail to result in pc == 0x02 after the JUMP. If execution begins in a state where the top of the stack holds 0x02, represented by the predicate , then executing a JUMP instruction guarantees that the next instruction to execute is at location 0x02.
To check the previous condition, we can compute the weakest precondition that ensures that executing a JUMP instruction leads to the postcondition pc==0x02. Weakest preconditions are standard concepts in formal verification and we illustrate the computation of weakest preconditions with a simple example. We let denote the weakest precondition (a predicate) for instruction to ensure that (a post condition) holds after the execution of the instruction. For instance, for the JUMP instruction, we have:
Computing weakest preconditions for sequences of instructions amounts to propagating the weakest preconditions backwards. For a sequence of instructions , and a predicate , with . If we perform this computation for all the instructions in Segment 1, we obtain condition :
To decide whether we can add a loop edge from node #1 to node #1 in the CFG of the program, we are going to check whether is preserved by Segment 1. If this is the case we have an invariant and a proof that any future execution of Segment 1 will end up in a state that satisfies . To check whether is preserved by Segment 1, we can compute the postcondition of after executing Segment 1. If it implies then it is an invariant. We have implemented this check in the DFS algorithm, and we can successfully build a CFG for programs with unbounded stacks similar to Listing 3.
4.5 Minimisation
Finally, we apply a minimisation algorithm after the DFS to collapse nodes that are language-equivalent. Minimising the CFG amounts to minimising an automaton and can be done with standard techniques to partition the set of of nodes in equivalence classes. We have implemented a minimisation algorithm (a mixture of Moore and Hopcroft algorithms) that can generate a minimised version of the CFG. In the experiments the minimisation stage provides marginal benefits. It minimises very short subgraphs of the CFG, mostly nodes that contain segments STOP or REVERT instructions.
5 Soundness test for CFGs
We formally verify that ByteSpector’s CFGs are sound, ensuring they can be reliably used for code analysis, auditing, and inspection. Since the CFG algorithm relies on abstract semantics, errors could arise from opcode interpretation or other parts of the code. The CFG computation itself is not certified, it is not inherently proven to always produce sound CFGs. To address this, we perform soundness checks, making ByteSpector a certifying CFG generator, as per the definition in [9].
5.1 Soundness proof
Given a program , a node in corresponds to an abstract state . The component is a list of either concrete values (target of jumps) or . As a result we can view as a finite set of contraints , of the form , with and write a node/abstract state in the form . The constraints enforces that some elements of the stack have some specific values.
To prove that is sound, we need to show that it simulates the executions of the program . To do so we prove the following:
- Condition 1
-
The initial EVMState state of the execution of in the EVM satisfies the constraints of the initial node , i.e., and satisfies the constraints .
- Condition 2
-
For any node in , and any concrete EVMState state that satisfies the constraints of i.e., and satisfies the constraints , if then there exists a (direct) successor node of in such that and satisfies .
Proving these two properties for all nodes of the CFG ensures (by induction) that the CFG is sound. Condition 1 relating the initial state of the EVM and the initial node of the CFG is straightforward to prove: the initial state of the EVM starts at and an empty stack, and the initial node of the CFG is associated with the segment of code starting at and an empty stack. In the Section 5.3 we explain how to prove the second condition.
5.2 Proof objects for EVM bytecode
To prove the soundness of a CFG, we generate a Dafny proof object that encodes the bytecode semantics and node transitions.
The Dafny-EVM library provides functions like PUSH0, DUP, and POP to represent EVM instructions as state transformations, and EVMState that models the EVM state. Listing 4 shows the proof object for SimpleLoop, and Figure 5 shows the CFG for SimpleLoop. The semantics of Segment is implemented in ExecuteFromCFGNode_s0 lines 2-11. This function maps an EVM state,111111The gas parameter is explained later. s0: EVMState to a state s’: EVMState obtained after executing the segment.
Each function has a precondition (requires) ensuring the in the initial state s0 matches the segment start address. The CFG of SimpleLoop indicates that the successor of node is node , so the line 10 is a call to the execution of the next node/segment, ExecuteFromCFGNode_s1. When we verify the proof object, Dafny checks that for all input states s0 that satisfy the precondition of ExecuteFromCFGNode_s0, the precondition of ExecuteFromCFGNode_s1 is satisfied at the callsite in line 10. If Dafny successfully verifies ExecuteFromCFGNode_s0 the condition 2 is verified for node . The encoding of the other nodes and edges follow the same pattern.
Dafny requires proof of termination. For CFGs with loops, we use a gas parameter that strictly decreases with each transition in the CFG, proving that all paths terminate. This effectively verifies soundness for every path of arbitrary length, not actual gas usage.
Note that with our encoding and Dafny-EVM semantics, we prove more than soundness. In the Dafny-EVM, each operation e.g., Pop(s0) at line 38, may have some preconditions: e.g., the stack must not be empty, otherwise the POP operation results in a error state (stack underflow). In our encoding, we ensure that the stack preconditions of each Dafny-EVM function (Pop, PushN, Swap,…) in the code are satisfied. To do so, we add some constraints, for example, for ExecuteFromCFGNode_s1 to execute without error, we require that the stack on entry has more than two elements requires s0.Operands() >= 2.
To summarise, given a CFG, we can build a Dafny program, a proof object, that encodes the semantics of the bytecode in each node, and the transitions between nodes. If the proof object verifies, we have a proof that the CFG is sound (and no stack underflow exceptions121212The absence of stack overflows can be guaranteed by adding a requirement on the capacity of the stack in the initial state. occurs.) This provides a soundness test for CFGs generated by ByteSpector.
5.3 Efficient soundness test
The technique we have described previously has some limitations:
-
for large segments of code, Dafny may be unable to verify some functions of the proof object due to the complexity of the code. Indeed, the Dafny-EVM semantics is quite complex for some opcodes (and the state has several components) and the verification of the proof object may require a lot of resources, and time out.
-
some opcodes correspond to calls to other contracts e.g., CALL, DELEGATECALL, STATICCALL. In the CFG generation algorithm, the effects of these calls are abstracted, only taking into account the effect on the stack. The Dafny-EVM semantics of these instructions is more complex, involving the memory, storage, and the return value of the call.
The solution to these problems is to use an abstract version of the Dafny-EVM semantics. The abstract version is restricted to tracking the (abstract) stack and the program counter, and does include the memory, storage, etc.
For calls to other contracts, we encode the visible effect of the call on the stack: from the caller point of view, a CALL instruction pops arguments from the stack and pushes one return value (that could be an error code) if it does not abort. As a result the semantics of call instructions can be abstracted as a simple stack operation as shown in Listing 5.
To preserve soundness, we can prove that the abstract semantics simulate the Dafny-EVM semantics, and the proof can be written in Dafny. The proof for the POP instruction is specified in Listing 6.
6 Evaluation
ByteSpector is implemented in Dafny [8] and available at https://github.com/franck44/evm-dis. In our experiments, ByteSpector can successfully construct provably sound CFGs for 978 out of 1048 contracts (93.3% success rate).
6.1 Implementation
ByteSpector consists of 6 modules, 36 files, 6000 lines of code, and 2200 lines of comments. The implementation is formally verified, ensuring no division-by-zero, out-of-bounds errors, or non-terminating functions. We use pre/postconditions and datatype constraints to enforce functional correctness. For example, the segment types in Dafny (JUMPSeg, STOPSeg) are constrained to end with the corresponding EVM instructions (JUMP, STOP) and this property is statically verified on the Dafny code. In our experimental evaluation, we have used the Java backend to generate a Java version of ByteSpector.
6.2 Experiments
For experimental evaluation we use a dataset from the project EVMLiSA [2], available at https://github.com/lisa-analyzer/evm-lisa.
The initial dataset less_than_3000_opcode.txt has 1704 EVM bytecode contracts’ addresses. The contracts are published on Ethereum, live, and their bytecodes can be retrieved using the etherscan.io API. Each contracts has less than opcodes. In our experiments we excluded the contracts containing the recently introduced instructions RJUMP, RJUMPI, RJUMPV and set the maximum depth to 100 for the CFG generation algorithm. These instructions do not present major difficulties and are already partially supported in our code base, but we have not yet fully integrated them in the CFG generation algorithm. Overall there are 1048/1704 contracts that 1) do not contain RJUMPs instructions and 2) the maximum depth is not reached during the generation of the CFG. With our technique we can generate and verify the CFG for almost all the contracts. A few of them contain jump targets that are stored in memory (probably using an old version of the Vyper compiler).
7 Related work and conclusion
Decompiling low-level code and building CFGs has a long history. We refer the reader to [4] for an history of decompilation. More specifcally, for the decompilation of EVM bytecode, most of the tools use static analysis techniques (and value sets) or symbolic execution and SMT-solvers to generate CFGs. Tools like Oyente [3], EthIR [1], Mythril [10] and EtherSolve [6] use symbolic execution and/or SMT-solvers to compute CFGs. Some of these tools are not maintained anymore and it is not possible to compare our results with them.
EVMLiSA [2] is a tool with a large set of benchmarks. The technique used in EVMLiSA relies on stack abstraction too, but the abstraction is more complicated than the one we presented in this paper: it tracks sets of stacks.
Our contribution goes beyond the computation of CFGs and outperforms the previous tools in several aspects: ) the CFGs are certified (formally verified); ) the proof objects can be instrumented with specifications to capture more complicated functional requirements and ) the source code (https://github.com/franck44/evm-dis) is written in Dafny, verified, and artefacts available in several target languages (Java, Python, C#) and can be integrated in existing code bases.
References
- [1] Elvira Albert, Pablo Gordillo, Benjamin Livshits, Albert Rubio, and Ilya Sergey. EthIR: A Framework for High-Level Analysis of Ethereum Bytecode. In Shuvendu K. Lahiri and Chao Wang, editors, Automated Technology for Verification and Analysis, pages 513–520, Cham, 2018. Springer International Publishing. doi:10.1007/978-3-030-01090-4_30.
- [2] Vincenzo Arceri, Saverio Mattia Merenda, Greta Dolcetti, Luca Negrini, Luca Olivieri, and Enea Zaffanella. Towards a sound construction of EVM bytecode control-flow graphs. In Luca Di Stefano, editor, Proceedings of the 26th ACM International Workshop on Formal Techniques for Java-like Programs, FTfJP 2024, Vienna, Austria, 20 September 2024, pages 11–16. ACM, 2024. doi:10.1145/3678721.3686227.
- [3] Syed Badruddoja, Ram Dantu, Yanyan He, Kritagya Upadhayay, and Mark Thompson. Making smart contracts smarter. In 2021 IEEE International Conference on Blockchain and Cryptocurrency (ICBC), pages 1–3, 2021. doi:10.1109/ICBC51069.2021.9461148.
- [4] Zion Leonahenahe Basque. 30 years of decompilation and the unsolved structuring problem: Parts 1 & 2. Blog Post. Accessed 2024-10-11. URL: https://mahaloz.re/dec-history-pt1.
- [5] Franck Cassez, Joanne Fuller, Milad K. Ghale, David J. Pearce, and Horacio Mijail Anton Quiles. Formal and executable semantics of the ethereum virtual machine in dafny. In Marsha Chechik, Joost-Pieter Katoen, and Martin Leucker, editors, Formal Methods - 25th International Symposium, FM 2023, Lübeck, Germany, March 6-10, 2023, Proceedings, volume 14000 of Lecture Notes in Computer Science, pages 571–583. Springer, 2023. doi:10.1007/978-3-031-27481-7_32.
- [6] Filippo Contro, Marco Crosara, Mariano Ceccato, and Mila Dalla Preda. Ethersolve: Computing an accurate control-flow graph from ethereum bytecode. In 29th IEEE/ACM International Conference on Program Comprehension, ICPC 2021, Madrid, Spain, May 20-21, 2021, pages 127–137. IEEE, 2021. doi:10.1109/ICPC52881.2021.00021.
- [7] Uri Kirstein. Bug Disclosure – Solidity Code Generation Bug Can Cause Memory Corruption. Medium Post by Certora, 2021. Accessed 2024-10-11. URL: https://medium.com/certora/bug-disclosure-solidity-code-generation-bug-can-cause-memory-corruption-bf65468d2b34.
- [8] K. Rustan M. Leino. Accessible software verification with Dafny. IEEE Softw., 34(6):94–97, 2017. doi:10.1109/MS.2017.4121212.
- [9] Xavier Leroy. A formally verified compiler back-end. J. Autom. Reason., 43(4):363–446, 2009. doi:10.1007/s10817-009-9155-4.
- [10] Bernhard Mueller. Smashing smart contracts, 2018. 9th HITB Security Conference. URL: https://tinyurl.com/y827tk72.
- [11] Natachi Nnamaka. The Vyper Compiler Saga: Unraveling the Reentrancy Bug that Shook DeFi. Medium Post by Rektify AI, 2023. Accessed 2024-10-10. URL: https://medium.com/rektify-ai/the-vyper-compiler-saga-unraveling-the-reentrancy-bug-that-shook-defi-86ade6c54265.
- [12] John Toman. Overly Optimistic Optimizer – Certora Bug Disclosure. Medium Post by Certora, 2022. Accessed 2024-10-10. URL: https://medium.com/certora/overly-optimistic-optimizer-certora-bug-disclosure-2101e3f7994d.
- [13] David Wood. Ethereum: a secure decentralised generalised transaction ledger, 2022. Berlin version d77a387 - 2022-04-26. URL: https://ethereum.github.io/yellowpaper/paper.pdf.
