Formal Verification of a Fail-Safe Cross-Chain Bridge
Abstract
Cross-chain bridges are financial services that interconnect blockchains. High monetary values flow through these bridges, and their security must be safeguarded. However, designing real-world cross-chain bridges is a difficult endeavor. Due to blockchain’s closed-world nature, tokens cannot be transferred from a sender to a receiver chain; on the contrary, they need complex logic that maintains an equilibrium on both chains, even if either the chains or the bridge fail. This paper formally verifies a model of a novel fail-safe cross-chain bridge to ensure correctness. We define formal requirements and prove the bridge is safe using the Isabelle/HOL proof assistant.
Keywords and phrases:
Cross-Chain Bridge, Formal Verification, Logic, SecurityCopyright and License:
2012 ACM Subject Classification:
Software and its engineering Software verificationAcknowledgements:
We want to thank Sonic Labs engineers Jan Kalina and Jirka Malek for designing and implementing the fail-safe bridge. Without their insights and explanations, we would not have been able to build the model.Editors:
Diego Marmsoler and Meng XuSeries and Publisher:
 Open Access Series in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Open Access Series in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
The blockchain ecosystem has rapidly evolved over the last decade, most notably with the rise of Ethereum [32] and Bitcoin [23]. At the end of 2024, the top 636 smart contract blockchains had a market cap of 2.9 trillion dollars [11].
As the blockchain ecosystem continues to grow, it has become increasingly heterogeneous, consisting of blockchains with unique designs and varying characteristics (proof-of-work, proof-of-stake, costs, performance, programming languages, etc.). Thus, each blockchain provides users with a diverse experience, security guarantees, and financial incentives, making it unlikely that a single dominant blockchain design will emerge [7].
Unfortunately, without a method of communication between blockchains, the advantages of a multichain world are limited. Since blockchains have closed-world assumption about their tokens, digital assets are not universal entities and cannot exist outside of their chains.
To this end, decentralized cross-chain bridges have been proposed (e.g., [33]) to provide interoperability between blockchains. Given two blockchains, a cross-chain bridge allows users to transfer tokens from a sender chain to a receiver chain . When an asset is transferred from to , the asset is locked on , and a new asset is minted on , representing the original asset on . When the newly created asset is transferred back to chain , the corresponding asset on is burned, and the locked asset on is released. Smart contracts on both blockchains implement this protocol, and a relay network is used to establish communication between the two chains.
Given the various security exploits targeting bridges [18, 19, 34], designing a safe bridge is paramount. Developing a safe bridge involves guaranteeing several safety and liquidity invariants. For instance, we want to ensure that there is always a 1-to-1 relationship between locked and minted assets. Otherwise, double-spending [17] attacks may arise. Liquidity invariants guarantee that the user can always perform an action to access the their asset. The bridge has fail safety, i.e., that all tokens will be unlocked in a blockchain if blockchain irrecoverably crashes.
Standard audit and testing methods can be employed to increase the likelihood of safety on the bridge. However, these methods, due to their inability to account for all possible behaviors, are insufficient. This is evidenced by the fact that bridges have become notorious targets for hackers. As of 2024, bridge-related hacks cost more than $2.8 billion, representing approximately 40% of all hacks in the Web3 [16]. Given the potential for sizable losses, relying only on ad-hoc testing and auditing techniques is perilous. A more rigorous method to ensure bridge safety is to employ formal verification. Here, we construct mathematical objects describing the bridge behavior and mathematical proofs to ensure the bridge protocol is correct for all possible inputs and configurations.
This paper presents an industrial case study in which we formally prove the safety of the formal abstract model of Sonic Gateway. This cross-chain bridge provides interoperability between the Ethereum and Sonic blockchains. While formal methods have been employed for individual blockchain components [6], to the best of our knowledge, our work is the first to prove the safety of a fail-safe cross-chain bridge model formally.
We formalize the bridge within the interactive theorem prover Isabelle/HOL [25] and establish safety by identifying and proving several fundamental safety properties. We perform our verification using a stepwise refinement approach [31, 9]: We start with an abstract model and then refine it by adding more and more implementation details. This process has verified the final Sonic Gateway design and contributed to the design of cross-chain bridges by identifying essential properties that are pervasive to all fail-safe cross-chain bridges.
Our contributions are summarized as follows:
-
1.
A detailed formal description of the fail-safe Sonic Gateway cross-chain bridge including safety properties,
-
2.
A formal specification and correctness proof for the Sonic Gateway cross-chain bridge,
-
3.
Experimental evaluation and experience of the verification effort.
This paper is structured as follows. Section 2 describes the Sonic Gateway bridge. In Section 3, we detail the formal specification of the Sonic Gateway bridge, and in Section 4, we provide a corresponding proof of its safety. We evaluate the verification process in Section 5, and Section 6 details related work. We conclude in Section 7.
2 The Fail Safe Bridge
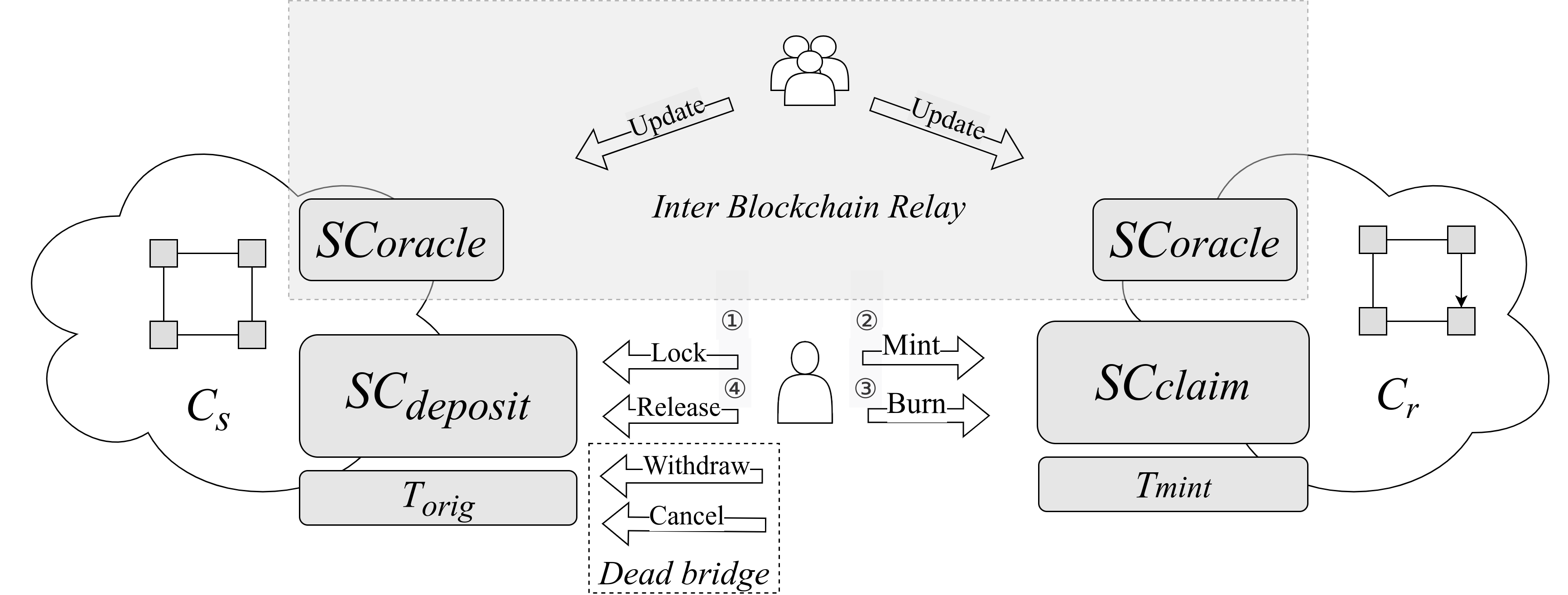
This section describes the Sonic Gateway fail-safe cross-chain bridge. A detailed example of bridge operations is given in Appendix A. The bridge is illustrated in Figure 1. Here, the bridge operates on a pair of blockchains and , where is the sender chain, used to deposit (aka. lock) tokens, and is the receiver chain, used to claim (aka. mint) tokens. The blockchain has a smart contract , and has a smart contract . For simplicity, we assume that users transfer fungible tokens from an ERC20 [29] contract (although these could also be native tokens of ) to , where they are represented by tokens on a dedicated ERC20 contract .
2.1 Token Exchange
During normal bridge operations, users can exchange original tokens on for minted tokens on . At any time, the minted tokens can be converted back to the original tokens in . Token transfers from to operate using a pair of transactions denoted as Lock and Mint. Assuming that a user already has at least tokens available on , the user invokes a Lock transaction on (step ①) to transfer tokens from their balance to the balance. To verify that a Lock transaction has been successfully executed, keeps a log , containing data about all executed lock transactions (a unique transaction ID is mapped to data about the caller, token, and amount, usually combined into a hash value). Before tokens can be issued by on (using a Mint, step ②), the solvency needs to be ensured. issues new tokens only if the user has locked tokens on . This requires (operating on ) to read the state of from a different blockchain (), which it cannot do directly. To enable this, the bridge uses a Merkle proof (a path of a Merkle tree [15]), which acts as a trusted witness for blockchain of the existence of a specific transaction (or its effect) at a block height on blockchain . This Merkle proof is an argument for the Mint transaction. Simultaneously, the state root hash of the world state of is shipped via the trusted channel, which we call the Inter-Blockchain Communication (IBC) Relay. We assume that a special contract keeps track of state root hashes and that a consensus of trusted users regularly updates it by invoking Update transactions. When executing a Mint transaction, the contract on verifies that the Lock transaction took place on at block height using the Merkle proof and state root hash of read from , which confirm that the log contains valid data about the Lock transaction. If the proof verification succeeds, the user’s balance of is increased by ( tokens are minted “out of thin air”). To prevent double claims of the same deposit, keeps a directory of minted deposits. Once the user obtains tokens on , they can trade with them as with all other ERC20 tokens.
At any point, a user with tokens on can exchange them for the same amount of on . This is done by performing a sequence of Burn and Release operations, which are pretty similar to Lock and Mint, so we do not describe them in detail. The user invokes a Burn transaction (step ③), which removes tokens from their balance on , and the information about this is logged in the log on on . After has been informed about the root of the world state of , the user can invoke a Release transaction (step ④) in that contains a Merkle tree proof confirming that the Burn transaction has been successfully executed. Once the proof verification succeeds, tokens are transferred from the balance to the user’s one.
2.2 Fail-Safety
What is unique to the Sonic Gateway is that it implements a mechanism that enables users to retrieve their funds on , even if the bridge goes out of operation (if or contracts or even the blockchain stop operating). The bridge is declared dead once the contract (on ) does not execute a state root update transaction within a fixed amount of time (e.g., 7 days). The bridge is declared dead by setting a flag in the contract and by copying the last known state root of from to . Once the bridge is declared dead, this status cannot be undone. When the bridge is dead, users retrieve their assets using Withdraw and Cancel transactions. Furthermore, note that Release transactions do not depend on and are executed similarly, regardless of whether the bridge is dead.
The last known state root hash of enables verifying the user’s balance of . If the user had tokens of on at the point when the last state root was given to the , they can generate a Merkle Tree proof for that and invoke a Withdraw transaction on . When the proof verification succeeds, tokens of are transferred from the contract to the user’s balance. Every withdrawal transaction is logged in the array to prevent double withdrawals.
Finally, it is possible that the user has deposited and locked some tokens of on , but has not yet claimed them, or they claimed them but there was no state root update after that claim, so there are no corresponding tokens on that they could retrieve using the Withdraw operation. A Cancel transaction must be used in such cases. With this transaction, the user provides a Lock transaction ID (which can be easily checked to exist using the log of on ) and the Merkle tree proof that there was no corresponding Mint on on in the last known state (verified by checking the log). Once the Cancel transaction is successful, to prevent double cancellation, the information about the canceled Lock transaction is removed from the log.
3 Specification
This section briefly outlines the Isabelle/HOL specification of the Sonic fail-safe bridge.
Due to space constraints, many details are omitted. For full details, we refer the reader to
the Isabelle/HOL source, available at https://github.com/filipmaric/bridge_formalization.
We expressed the Sonic bridge implementation, originally in Solidity, as a purely functional program in Isabelle/HOL.
Translation from Solidity to Isabelle/HOL is done manually, trying to be as close as possible to Solidity’s semantics.
For simplicity, the basic types of Solidity (uint256, bytes32, address) are all modeled as natural numbers in Isabelle/HOL, ignoring overflow issues.
In Solidity, mappings storing natural numbers default to 0 for non-existent keys.
The function lookup_nat (and similarly lookup_bool) that we define and use mimics that behavior. An Isabelle/HOL record models the internal state of each contract.
The balances mapping in the ERC20State assigns token amounts to user addresses. In the SCDepositState, the locks mapping records all successful Lock transactions, mapping transaction IDs to hash values derived from the sender address, token, and amount. The withdrawals mapping tracks users who executed Withdraw transactions to retrieve balances from the dead bridge. The address of is stored in SCOracleAddr, while deadState holds the last valid state root before the bridge failure (0 indicates the bridge is not declared dead). States of other contracts (e.g., SCClaimState) are similarly defined.
The storage states of all contracts define the blockchain state, mapping contract addresses to their respective states. Due to the Isabelle/HOL type system, each smart contract type requires a separate mapping.
We define functions to read and modify smart contract states. For example, the following helper function reads a user’s balance from the specified ERC20 contract state.
As in Solidity, contract functions can be called on a chain via a contract address. For instance,
Each call may fail, e.g., if no valid contract exists at the given address.
In such cases, the chain state remains unchanged.
We defined an Isabelle/HOL counterpart for each contract function by following our Solidity implementation closely.
For example, the following Solidity function in the SCDeposit contract checks whether the bridge is dead. The last valid state root hash is stored in the deadState field when the bridge fails.
This function is implemented in Isabelle/HOL as follows:
The function returns a triple: the first element indicates success or failure, the second whether the bridge is dead, and the third the updated state. Monad syntax could remove explicit state passing and status checks.
In our Solidity implementation, some contract functions verify Merkle tree proofs to confirm the presence of specific memory content in another chain, ensuring a key-value pair exists in a mapping. Our specification follows a stepwise refinement approach, omitting proof details and instead postulating axioms that these proofs must satisfy. These axioms are expressed as Isabelle/HOL [4]. First, we postulate that the following functions can be defined so that they satisfy the two given axioms:
-
generateStateRoot creates a state root hash value,
-
generateLockProof generates a proof for the fact that lock[ID] = val,
-
verifyLockProof verifies if the given proof is valid for the given state root.
We also postulate the honesty assumption for the consensus of users who perform the regular state root updates, by assuming that whenever an Update operation succeeds the state root hash given to the oracle is indeed the state root hash of the current blockchain state (as generated by the generateStateRoot function).
This is sufficient to define the token mint operation and prove its properties (for other operations, in the same manner we introduce mint proofs, burn proofs, balance proofs etc.). A concrete implementation for these three abstract functions should be provided at later stages. This implementation can be based on Merkle-tree proofs (as used in our Solidity implementation), but other types of proofs, such as zero-knowledge proofs, could also be used. For illustration, we present our specifications for the mint function.
A blockchain state is considered reachable from a starting state if a sequence of successful operations (steps, transactions) exists that leads to the final state when executed starting from the initial state. To define this relation, we first introduce a representation of the steps (with comments after each step type indicating the step parameters).
Each step is executed by calling its corresponding function on some chain contract.
Finally, we inductively define reachability between two blockchain states. Each state is reachable from itself by the empty list of steps. If is reachable from by a list steps, and executing step reaches from , then is reachable from by the list obtained by joining steps and step.
Steps issued by a specific caller are interleaved with steps issued by other users. When distinguishing between them is important, we use the predicate reachableInterlaved caller stepsCaller stepsOther, which is also defined inductively. The following function, defined by primitive recursion, checks whether the given list of steps can be successfully executed, regardless of the steps taken by other users.
4 Correctness proofs
We have proven numerous properties of our bridge, beginning with simple, low-level technical properties and culminating in high-level properties that express user safety. The proof concludes with the central fail-safety theorem, which states that even when the bridge is dead, every user can execute a series of transactions to retrieve all their assets (i.e., the tokens they locked, plus the tokens received from others, minus the tokens transferred to others). Our fail-safety features ensure this guarantee and the primary challenge was to prove it formally. The main idea of the proof is as follows.
-
If the bridge is alive, after the deposit by a LOCK, the user can make a MINT, then a BURN, and finally RELEASE to retrieve their tokens on the sender chain.
-
Assume that the bridge is dead and that the last valid state known on SCDeposit is (that is the state when the last UPDATE happened before the bridge became unresponsive).
-
–
If only the LOCK occurred before , and the tokens have not been claimed (or if MINT occurred after the last state update), the user can retrieve their funds using the CANCEL_WD operation.
-
–
If a MINT is recorded in , and there was no BURN after it (or if it occurred after the last state update), the user has minted tokens in , and can retrieve them using the WITHDRAW_WD operation.
-
–
Finally, if a BURN is recorded in , the user can retrieve their tokens using the standard RELEASE operation (just as they would while the bridge is active).
-
–

Many theorems share assumptions describing the situation where the bridge is dead. Instead of repeating these assumptions in every theorem and deriving their consequences in each proof, we used Isabelle/HOL locales [4]. We defined the locale BridgeDead to describe the state of a dead bridge. This situation is depicted in Fig. 2. The execution begins in some initial state . For simplicity, we assume that the first operation after the bridge is deployed is a state UPDATE, which transitions it to state . After this, the bridge operates normally, executing a sequence of steps denoted by stepsInit. At some state , the final state UPDATE occurs, leading to state . Following that, additional steps (denoted by stepsNoUpdate) are executed before the bridge becomes inactive. The step that indicates the bridge is dead is denoted by stepDeath. At this point, the field deadState in the SCDeposit contract is set to the state root of the last known valid state, which in this case is . Subsequently, more steps (denoted by steps) are executed on the SCDeposit contract, leading to the current state . The complete sequence of all steps from to is denoted by stepsAll.
Several auxiliary functions are defined to compute token amounts to formulate the central fail-safety theorem.
-
depositedAmountTo – this function calculates the total amount of tokens that a caller has deposited into by executing Lock transactions.
-
retrievedAmountFrom – this function calculates the total amount of tokens that a caller has retrieved from the contract by executing Release, Withdraw, and Cancel transactions.
-
transferredAmountFrom – this function calculates the total amount of minted tokens on the bridge that the caller has transferred to other users, while the function transferredAmountTo calculates the total amount of that other users have transferred to the caller.
When the bridge dies, contains a state root that encodes aggregated information about all transactions that occurred before the last update before the bridge’s failure (i.e., transactions in the list stepsInit in Figure 2). After this update, transactions (including mints, burns, and transfers) are ignored. We consider a user to have retrieved all their assets if the total amount of tokens they invested (defined as the sum of they locked up to the current state and the they transferred to other users before the last update) is equal to the total amount of tokens they gained (defined as the sum of they retrieved via a Release, Withdraw, or Cancel transaction and the they received from other users before the last update).
Our central theorem demonstrates that, from any state in which the bridge is dead, each user can issue a list of transactions that will be executable regardless of the transactions made by other users. Moreover, executing these transactions will always result in a state where the user has retrieved all of their tokens.
The steps in the list stepsAll lead from to . The steps interleaveSteps steps stepsOther, obtained by interleaving the unpredictable steps of other users stepsOther with the steps steps issued by the current user, lead from to , where all tokens have been successfully retrieved.
Note that a similar, less interesting theorem can be proven when the bridge is not dead (under some additional assumptions on the frequency of updates). In this scenario, the caller only needs to issue MINT, BURN, and RELEASE transactions. However, there is no guarantee that the bridge will not fail during the execution of these transactions. If this occurs, the user must switch to the recovery strategy used when the bridge is dead.
Many necessary lemmas contribute to the proof of the central theorem. We formulated and proved lemmas that ensure the executability of each specific operation. For instance, the following theorem guarantees lock cancellation is possible if no claim of minted tokens was made before the last update before the bridge became inactive and if no cancellation occurred before the current state.
Theorems for other “rescue” operations are similar. It is typically necessary to prove that a particular step is possible by showing that some data is set in the required manner. For example, canceling a deposit ID by a caller who requests a specific token amount is only possible if the proof that guarantees that locks[ID] = hash(caller, token, amount) can be verified. It is proved (by induction) that this data guarantees that there was a prior LOCK operation from the caller for the given amount of the give token (assuming that hash function is injective, which is a widespread assumption in a blockchain setting). However, repaying tokens for a canceled deposit also requires enough tokens in the SCDeposit contract balance. This is the most challenging part of the entire proof, as it requires careful analysis of the “cash flow” across all parts of the bridge, considering all operations and steps. Such invariants are proven both globally (characterizing the SCDeposit contract balance after transactions from all users) and on a per-user basis (characterizing and balances for each user). Due to space constraints, we will describe only the former. We introduce the following quantities (all are natural numbers, so they are non-negative):
-
SCDepositBalance – the current token balance of the given address.
-
locked / canceled / withdrawn / released – the total sum of amounts in all LOCK / CANCEL_WD / WITHDRAW_WD / RELEASE steps for a given address and token.
-
mintedBeforeDeath – the total sum of amounts in all MINT steps executed before the last update before the bridge becomes inactive.
-
nonMintedBeforeDeath – the total sum of amounts in all LOCK steps whose ID is not claimed (minted) before the last update before the bridge becomes inactive.
-
nonCanceledNonMintedBeforeDeath – the total sum of amounts in all LOCK steps whose ID is not minted before the last update before the bridge becomes inactive and which has not been canceled.
-
nonWithdrawnNonBurnedMintedBeforeDeath – the total amount of tokens produced by MINT steps that have not been burned before the last update before the bridge becomes inactive, and have not been withdrawn.
-
burnedBeforeDeath – the total sum of amounts in BURN steps for a given address and token that were executed before the last update, when the bridge becomes inactive.
-
nonReleasedBurnedBeforeDeath – the total sum of amounts in all BURN steps for a given address and token, that were executed before the last update before the bridge becomes inactive whose ID has not yet been released.
Then, we proved the following five invariants.
-
1.
locked = SCDepositBalance + canceled + withdrawn + released
-
2.
locked = mintedBeforeDeath + nonMintedBeforeDeath
-
3.
nonMintedBeforeDeath = canceled + nonCanceledNonMintedBeforeDeath
-
4.
mintedBeforeDeath = withdrawn + nonWithdrawnNonBurnedMintedBeforeDeath +
burnedBeforeDeath
-
5.
burnedBeforeDeath = released + nonReleasedBurnedBeforeDeath
The first invariant is proved by induction by analyzing the transactions that change the token deposit balance. The second invariant is trivial. The others focus on specific operations and are proven by induction and case analysis of the last applied step, where most steps are irrelevant (for example, only MINT and CANCEL_WD operations are relevant for the third invariant). Combining these four invariants yields
SCDepositBalance = nonCanceledNonMintedBeforeDeath +
nonWithdrawnNonBurnedMintedBeforeDeath + nonReleasedBurnedBeforeDeath
From this, we can guarantee sufficient funds for each rescue operation. For instance, when proving that a cancel step is possible, there is a deposit that was not claimed before the last update before the bridge died and that has not yet been canceled. Therefore, the it’s amount is included in the nonCanceledNonMintedBeforeDeath quantity, which, by the previous invariant, is less than or equal to the SCDepositBalance, i.e., the current token balance of the SCDeposit contract. Since the amount the caller requires must match the amount they deposited (which we know from the value of locks[ID] = hash(caller, token, amount), and the assumed injectivity of the hash function), the contract contains the required tokens, making the payback possible. Similar reasoning applies to all other operations.
Many other lower-level properties had to be proven to support the correctness proof. For example, each Mint must be preceded by a Lock, only the entity who made a lock can mint the tokens, once the bridge dies, it can never become life again, etc. We refer readers to the Isabelle/HOL proof documents for their formalization.
5 Evaluation and Discussion
The Isabelle formalization was completed by a single individual who had worked part-time on this project for over six months. A rough estimate suggests the formalization required approximately 2–3 full person-months of effort. Isabelle’s definition of the bridge’s formal model comprises around 900 lines of code (LOC), including approximately 50 defined functions, while the accompanying proofs span roughly 15,000 LOC. The current proof contains approximately 750 lemmas and theorems. The proof-checking process takes around 8 minutes on a standard laptop computer (Intel(R) Core(TM) i5-8265U CPU @ 1.60GHz, 8GB of RAM). However, this time could be significantly reduced by replacing several time-consuming, fully automated proofs with more detailed manual proofs.
Several underlying assumptions in our model pose threats to validity and must be addressed to ensure the total correctness of a real-world bridge implementation. Some of these assumptions can be easily ensured through a correct deployment process.
-
It is assumed that contracts are correctly deployed and initialized, i.e., that all addresses are correctly set up.
-
It is assumed that each bridge and original token has a dedicated minted token, i.e., that minted tokens are not shared.
-
It is assumed that users initially have no minted tokens after the bridge is deployed.
-
It is assumed that an UPDATE operation occurs immediately after the bridge is deployed, i.e., that the bridge never operates in a state where state roots are uninitialized.
Other assumptions include the following:
-
It is assumed that arithmetic overflows will not occur while the bridge is in operation. This is reasonable, as the only arithmetic operations involve updating user token balances.
-
It is assumed that the hash function is injective (i.e., no hash collisions) and always produces a nonzero value. This is a common assumption underlying blockchain security.
-
It is assumed that (Merkle-tree) proof checking is fully sound. This is also reasonable, as the correctness of Merkle trees has been formally verified.
-
Transaction fees and gas prices are not included in our model.
-
Reentrancy attacks are not considered. Although reentrancy poses a significant threat in Solidity smart contracts, it can be prevented through careful implementation (e.g., by following the checks-effects-interactions pattern).
-
It is assumed that updates are reliable, i.e., that validators are always honest. This assumption may be the most problematic, as many successful bridge attacks have been carried out by corrupting validators [34]. While specifying the details of a validation protocol can help relax this assumption, some risks will always remain. For example, private keys must be kept secure.
6 Related Work
BFT consensus protocols have been verified using interactive theorem provers. The work in [6] develops a modular proof in TLA+ for DAG-based consensus protocols. The work in [26] uses the IVy interactive theorem prover [1] to formally verify a variant of the Moonshine consensus protocol [26]. The work in [21] uses IVy and Isabelle/HOL [24] to verify the Stellar Consensus Protocol [20]. The Algorand [13] consensus protocol has been verified using Coq [12]. The safety of several non-Byzantine protocols, such as variants of Paxos [10, 28] has been verified using interactive theorem proving. To the best of our knowledge, we are the first to propose formal proof for a cross-chain bridge, particularly bridge failure safety.
There has been foundational work in the verification of Ethereum smart contracts. These contracts are compiled into Ethereum Virtual Machine (EVM) bytecode, formally defined for use with interactive theorem provers [14]. A sound program logic at the bytecode level has also been developed [3]. Typically, smart contracts are written in the Solidity programming language, with formal semantics defined in Isabelle/HOL [22]. Another proposed approach in smart contract verification is to define them in specialized languages converted to low-level byte code using verified compilers. For example, Britten’s PhD thesis [8] explores techniques to improve the reliability and security of smart contracts by leveraging formal verification methods through interactive theorem proving in Coq, combined with a verified compiler from the language DeepSEA [30]. In [27], Ribeiro defines the imperative language soli within Isabelle/HOL that captures a significant subset of Solidity, and develops big-step, Hoare logic, and a proof system for it, with soundness and completeness results formally established.
Our approach differs in that the formal bridge model is currently represented as a functional program within Isabelle/HOL, derived through manual translation from Solidity. Consequently, our current work establishes only the correctness of a high-level bridge model, leaving the verification of its Solidity implementation for future work.
Various automated tools analyze Solidity code and detect bugs or violations of specific safety properties (for example, since 2019, the Solidity compiler has included a model checker, SolCMC [2]). However, a key limitation of these tools is their lack of effectiveness in expressing and verifying liquidity properties. Some automated tools are also designed explicitly for verifying liquidity properties, such as Solvent [5].
Our decision to use the interactive theorem prover Isabelle/HOL instead of automated tools was influenced by our prior experience and the fact that any limitations in automated prover support can be overcome by reverting to manual proofs. One possible research direction would be to examine whether state-of-the-art automated tools are capable of proving the liquidity properties of large-scale projects such as a crypto-bridge.
7 Conclusion
This paper describes the Sonic Gateway fail-safe bridge design and its formalization in Isabelle/HOL. We have formally proven that users can still retrieve all their assets on the sender chain even if the bridge becomes unresponsive on the receiver chain.
Our current abstract model does not account for numerous essential real-world issues, such as gas consumption, potential overflows, reentrancy vulnerabilities, and other Solidity-specific implementation challenges. Addressing these practical concerns will be an integral part of our efforts to ensure that the model reflects these complexities and security requirements in a real-world deployment. Therefore, we plan to bridge the gap between the current abstract Isabelle/HOL bridge model and its real Solidity implementation in our future work. To achieve this, we must provide a detailed description of the Inter-Blockchain Communication (IBC) Relay, which utilizes Merkle-tree proofs and whose correctness is currently only assumed in our formalization. Additionally, we plan to leverage the formal semantics of Solidity in Isabelle/HOL [22] to verify our bridge up to the Solidity implementation level fully formally.
References
- [1] Ki Yung Ahn and Ewen Denney. Testing first-order logic axioms in program verification. In Gordon Fraser and Angelo Gargantini, editors, Tests and Proofs - 4th International Conference, TAP@TOOLS 2010, Málaga, Spain, July 1-2, 2010. Proceedings, volume 6143 of Lecture Notes in Computer Science, pages 22–37. Springer, 2010. doi:10.1007/978-3-642-13977-2_4.
- [2] Leonardo Alt, Martin Blicha, Antti E. J. Hyvärinen, and Natasha Sharygina. Solcmc: Solidity compiler’s model checker. In Computer Aided Verification: 34th International Conference, CAV 2022, Haifa, Israel, August 7–10, 2022, Proceedings, Part I, pages 325–338, Berlin, Heidelberg, 2022. Springer-Verlag. doi:10.1007/978-3-031-13185-1_16.
- [3] Sidney Amani, Myriam Bégel, Maksym Bortin, and Mark Staples. Towards verifying ethereum smart contract bytecode in isabelle/hol. In Proceedings of the 7th ACM SIGPLAN International Conference on Certified Programs and Proofs, CPP 2018, pages 66–77, New York, NY, USA, 2018. Association for Computing Machinery. doi:10.1145/3167084.
- [4] Clemens Ballarin. Interpretation of Locales in Isabelle: Theories and Proof Contexts. In Mathematical Knowledge Management, MKM, Proceedings, pages 31–43, 2006. doi:10.1007/11812289_4.
- [5] Massimo Bartoletti, Angelo Ferrando, Enrico Lipparini, and Vadim Malvone. Solvent: Liquidity verification of smart contracts. In Nikolai Kosmatov and Laura Kovács, editors, Integrated Formal Methods, pages 256–266, Cham, 2025. Springer Nature Switzerland.
- [6] Nathalie Bertrand, Pranav Ghorpade, Sasha Rubin, Bernhard Scholz, and Pavle Subotic. Reusable formal verification of dag-based consensus protocols. CoRR, abs/2407.02167, 2024. doi:10.48550/arXiv.2407.02167.
- [7] Bloomberg. Multi-chain future likely as ethereum’s defi dominance declines. https://www.bloomberg.com/professional/insights/data/multi-chain-future-likely-as-ethereums-defi-dominance-declines/, February 2022.
- [8] Daniel Britten. Building trustworthy smart contracts using interactive theorem proving. Doctor of philosophy (phd) thesis, The University of Waikato, 2024. Supervisors: Steve Reeves, Vimal Kumar. URL: https://hdl.handle.net/10289/16566.
- [9] Dominique Cansell. Foundations of the B method. Computers and Informatics, 22, January 2003.
- [10] Saksham Chand, Yanhong A. Liu, and Scott D. Stoller. Formal verification of multi-paxos for distributed consensus. In John S. Fitzgerald, Constance L. Heitmeyer, Stefania Gnesi, and Anna Philippou, editors, FM 2016: Formal Methods - 21st International Symposium, Limassol, Cyprus, November 9-11, 2016, Proceedings, volume 9995 of Lecture Notes in Computer Science, pages 119–136, 2016. doi:10.1007/978-3-319-48989-6_8.
- [11] CoinGecko. Top smart contract platform coins by market cap. https://www.coingecko.com/en/categories/smart-contract-platform, November 2024.
- [12] Thierry Coquand and Gérard P. Huet. The calculus of constructions. Inf. Comput., 76(2/3):95–120, 1988. doi:10.1016/0890-5401(88)90005-3.
- [13] Yossi Gilad, Rotem Hemo, Silvio Micali, Georgios Vlachos, and Nickolai Zeldovich. Algorand: Scaling Byzantine agreements for cryptocurrencies. In Proceedings of SOSP 2017, pages 51–68. ACM, 2017. doi:10.1145/3132747.3132757.
- [14] Yoichi Hirai. Defining the ethereum virtual machine for interactive theorem provers. In Michael Brenner, Kurt Rohloff, Joseph Bonneau, Andrew Miller, Peter Y.A. Ryan, Vanessa Teague, Andrea Bracciali, Massimiliano Sala, Federico Pintore, and Markus Jakobsson, editors, Financial Cryptography and Data Security, pages 520–535, Cham, 2017. Springer International Publishing. doi:10.1007/978-3-319-70278-0_33.
- [15] Kamil Jezek. Ethereum data structures. CoRR, abs/2108.05513, 2021. doi:10.48550/arXiv.2108.05513.
- [16] Defi Lama. Hacks. https://defillama.com/hacks, November 2024.
- [17] Sung-Shine Lee, Alexandr Murashkin, Martin Derka, and Jan Gorzny. Sok: Not quite water under the bridge: Review of cross-chain bridge hacks. CoRR, abs/2210.16209, 2022. doi:10.48550/arXiv.2210.16209.
- [18] Sung-Shine Lee, Alexandr Murashkin, Martin Derka, and Jan Gorzny. Sok: Not quite water under the bridge: Review of cross-chain bridge hacks. In 2023 IEEE International Conference on Blockchain and Cryptocurrency (ICBC), 2023. doi:10.1109/ICBC56567.2023.10174993.
- [19] Ningran Li, Minfeng Qi, Zhiyu Xu, Xiaogang Zhu, Wei Zhou, Sheng Wen, and Yang Xiang. Blockchain cross-chain bridge security: Challenges, solutions, and future outlook. Distrib. Ledger Technol., October 2024. Just Accepted. doi:10.1145/3696429.
- [20] Marta Lokhava, Giuliano Losa, David Mazières, Graydon Hoare, Nicolas Barry, Eli Gafni, Jonathan Jove, Rafal Malinowsky, and Jed McCaleb. Fast and secure global payments with stellar. In Tim Brecht and Carey Williamson, editors, Proceedings of the 27th ACM Symposium on Operating Systems Principles, SOSP 2019, Huntsville, ON, Canada, October 27-30, 2019, pages 80–96. ACM, 2019. doi:10.1145/3341301.3359636.
- [21] Giuliano Losa and Mike Dodds. On the formal verification of the stellar consensus protocol. In Bruno Bernardo and Diego Marmsoler, editors, 2nd Workshop on Formal Methods for Blockchains, FMBC@CAV 2020, July 20-21, 2020, Los Angeles, California, USA (Virtual Conference), volume 84 of OASIcs, pages 9:1–9:9. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2020. doi:10.4230/OASICS.FMBC.2020.9.
- [22] Diego Marmsoler and Achim D. Brucker. Isabelle/solidity: A deep embedding of solidity in isabelle/hol. Form. Asp. Comput., October 2024. Just Accepted. doi:10.1145/3700601.
- [23] Satoshi Nakamoto. Bitcoin: A peer-to-peer electronic cash system, May 2009. URL: http://www.bitcoin.org/bitcoin.pdf.
- [24] Tobias Nipkow, Lawrence C. Paulson, and Markus Wenzel. Isabelle/HOL - A Proof Assistant for Higher-Order Logic, volume 2283 of Lecture Notes in Computer Science. Springer, 2002. doi:10.1007/3-540-45949-9.
- [25] Tobias Nipkow, Markus Wenzel, and Lawrence C. Paulson. Isabelle/HOL: a proof assistant for higher-order logic. Springer-Verlag, Berlin, Heidelberg, 2002.
- [26] M. Praveen, Raghavendra Ramesh, and Isaac Doidge. Formally verifying the safety of pipelined moonshot consensus protocol. In Bruno Bernardo and Diego Marmsoler, editors, 5th International Workshop on Formal Methods for Blockchains, FMBC 2024, April 7, 2024, Luxembourg City, Luxembourg, volume 118 of OASIcs, pages 3:1–3:16. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2024. doi:10.4230/OASIcs.FMBC.2024.3.
- [27] Maria Saraiva de Campos Mendes Ribeiro. Formal Verification of Ethereum Smart Contracts Using Isabelle/HOL. Master’s thesis, Instituto Superior Técnico, 2019. Supervisors: Paulo Alexandre Carreira Mateus, Pedro Miguel dos Santos Alves Madeira Adão. URL: https://fenix.tecnico.ulisboa.pt/downloadFile/1689244997260666/tese_maria_ribeiro.pdf.
- [28] William Schultz, Ian Dardik, and Stavros Tripakis. Formal verification of a distributed dynamic reconfiguration protocol. In Andrei Popescu and Steve Zdancewic, editors, CPP ’22: 11th ACM SIGPLAN International Conference on Certified Programs and Proofs, Philadelphia, PA, USA, January 17 - 18, 2022, pages 143–152. ACM, 2022. doi:10.1145/3497775.3503688.
- [29] Rudrapatna K. Shyamasundar. Erc20: Correctness via linearizability and interference freedom of the underlying smart contract. In Proceedings of the 20th International Conference on Security and Cryptography - Volume 1: SECRYPT, pages 557–566. INSTICC, SciTePress, 2023. doi:10.5220/0012145800003555.
- [30] Vilhelm Sjöberg, Kinnari Dave, Daniel Britten, Maria A Schett, Xinyuan Sun, Qinshi Wang, Sean Noble Anderson, Steve Reeves, and Zhong Shao. Foundational verification of smart contracts through verified compilation, 2024. doi:10.48550/arXiv.2405.08348.
- [31] Niklaus Wirth. Program development by stepwise refinement. Commun. ACM, 14(4):221–227, April 1971. doi:10.1145/362575.362577.
- [32] Gavin Wood. Ethereum: A secure decentralised generalised transaction ledger, 2014. EIP-150 Revision. URL: https://ethereum.github.io/yellowpaper/paper.pdf.
- [33] Tiancheng Xie, Jiaheng Zhang, Zerui Cheng, Fan Zhang, Yupeng Zhang, Yongzheng Jia, Dan Boneh, and Dawn Song. zkbridge: Trustless cross-chain bridges made practical. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, CCS ’22, pages 3003–3017, New York, NY, USA, 2022. Association for Computing Machinery. doi:10.1145/3548606.3560652.
- [34] Mengya Zhang, Xiaokuan Zhang, Yinqian Zhang, and Zhiqiang Lin. Security of cross-chain bridges: Attack surfaces, defenses, and open problems. In Proceedings of the 27th International Symposium on Research in Attacks, Intrusions and Defenses, RAID ’24, pages 298–316, New York, NY, USA, 2024. Association for Computing Machinery. doi:10.1145/3678890.3678894.
Appendix A Detailed Bridge Example
An example showing basic bridge operations is shown in Figure 3. Bridge operations are supported by two smart contracts on the sender chain (our custom contract SCDeposit and an ERC20 contract Token), and two smart contracts on the receiver chain (our custom contract SCClaim and an ERC20 contract MintedToken).
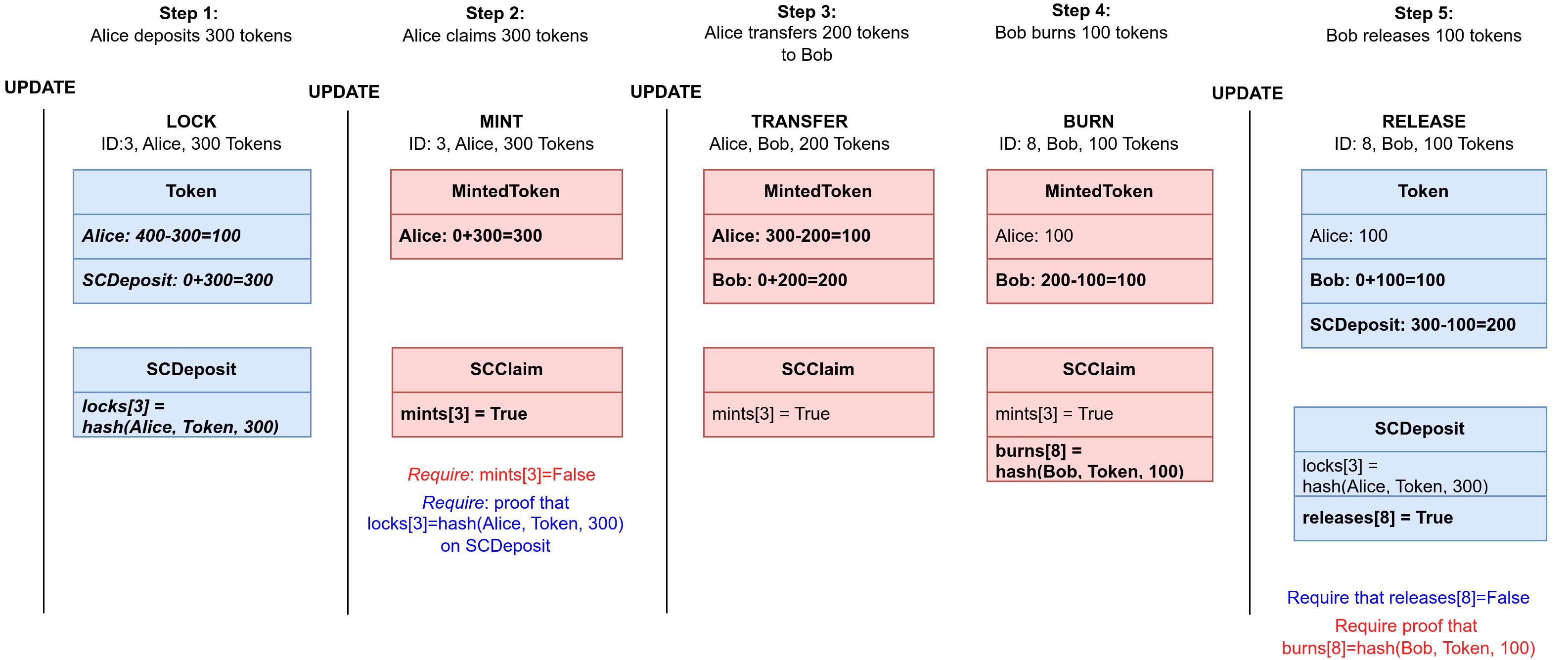
We assume that Alice has 400 tokens on the sender chain and she wants to transfer 300 tokens to the receiver chain. She invokes a LOCK operation on the SCDeposit contract on the sender chain, that transfers 300 tokens from her balance to the SCDeposit contract balance. Information about this transaction is logged in the SCDeposit contract, in a special locks mapping, by assigning a hash value that combines information about the caller (Alice, i.e., her unique address), the currency (Token, i.e., its unique address), and the amount (300) to the unique transaction ID (it is 3, in this example). This information is later used to confirm that this transaction occurred.
In the next step, Alice invokes a MINT transaction on the SCClaim contract on the receiver chain. If that transaction succeeds, 300 tokens will be added to her balance on the MintedToken contract (,,minted out of thin air”). However, for this to be possible, (1) these 300 tokens should be justified by the 300 tokens deposited on the sender chain, and (2) it should be ensured that she can do this only once. For this, it is assumed that she sends the ID of the original LOCK transaction (the value 3) as a parameter of this claim. Requirement (2) is easily ensured by maintaining a special mints mapping in the SCClaim contract. Before the claim, the value mints[ID] must be False, and is set to True once the minting is done. Requirement (1) is harder to achieve, because it requires information about the data stored in the sender chain. From the value assigned to the key ID in the locks log of the SCDeposit contract, we can check that Alice was the one who deposited 300 tokens (assuming that there are no hash collisions, which is a rather common assumption). To be able to do this, we rely on Merkle-tree proofs and consensus on the root hash of the sender chain. During regular updates, a consensus of trusted verifiers agrees on the root hash value and writes it to a special place (for this, a special StateOracle contract is used). When Alice wants to claim the minted tokens, she provides a Merkle tree proof for the value assigned to locks[ID]. The Bridge contract then verifies if this value is equal to the hash value that combines her address, the token address, and the deposited amount, and if it is, the transaction succeeds.
Next, we assume that Alice transfers 200 minted to Bob. It is a regular ERC20 transfer operation, and no additional checks and loggings are performed.
Next, we assume that Bob wants to transfer 100 of these minted tokens back to the sender chain. For this, he must first burn the tokens on the receiver chain. He invokes a BURN operation which reduces his balance (minted tokens are “burned and destroyed”), and then logs this information by assigning the hash that combines the information about the caller (Bob), the currency (Token) and the amount (100) to the unique transaction ID (it is 8 in this example) in a special burns mapping in the SCClaim contract.
Finally, Bob releases 100 tokens on the sender chain, by transferring them from the SCDeposit balance in the Token contract to his balance. Again, it must be ensured that (1) these are covered by the burned 100 tokens on the bridge, and that (2) this release is done exactly once. Requirement (2) is easily ensured by using a special releases mapping in the SCDeposit contract (the value True is assigned to the unique transaction ID once the release is done). To ensure (1), we again use Merkle-tree proofs and the state root set by the consensus of verifiers in the UPDATE operation (this time sender chain must be informed about the state root of the receiver chain at certain block height). Bob must supply a Merkle-proof that the value burns[ID] is equal to the hash value of the caller (Bob), the currency (Token) and the amount 100. If the Merkle-tree proof verification succeeds, we know that Bob really burned his 100 tokens on the receiver chain, so we can transfer him the required 100 tokens.
Our bridge has a fail-safety mechanism that enables users to retrieve their funds on the sender chain, even when the contracts on the receiver chain become unresponsive. An example of this feature in operation is shown in Fig. 4.

We assume that the first three steps are the same as in the previous example. Next, we assume that Carol makes a deposit and locks 500 tokens on the sender chain, and that after that she makes a successful claim and mints those 500 tokens on the receiver chain. For this to succeed, there must have been an UPDATE step in between in which the StateOracle contract has been informed about the state roots of the chains. Just after the MINT step, the bridge dies and becomes unresponsive. If someone tries to release the funds on the sender chain, he would be able to do this only if the burned them prior to that last UPDATE (since, the effect of those BURN operations is encoded in the current state root). However, users that have funds on the failed receiver bridge that have not been burned before that update, cannot retrieve them. The operations that happened after that last UPDATE step are not visible from the sender chain, so it is assumed that the state of the receiver chain in the moment of that last UPDATE step is its last valid state, also called the dead state (it is the state after the step 3 in Fig. 4). After some predetermined time period in which there are no new updates, the sender chain realizes that the bridge is dead and switches to fail-safe mode. This is irreversible, since, even if the bridge becomes operational again, the contract on the sender chain will not take that into account. In the fail-safe mode, all users who had minted tokens in the last valid state can withdraw them as original tokens on the sender chain.
We assume that Bob wants to withdraw his 200 tokens that he got from Alice, so he invokes a special withdraw while dead (WITHDRAW_WD) operation. He can do this only once, and For this, he must provide a Merkle-tree proof that he had exactly 200 minted tokens in the last valid state. If this proof successfully verifies, he is given his 200 tokens from the TokenDeposit contract balance, and this is logged in a special withdrawals mapping (the value withdrawals[Bob] is set to True, guaranteeing that Bob has withdrawn all his funds an will not be able to do this again.
However, there is a problem with Carol. She has made a successful claim while the bridge was alive, but the bridge died before another UPDATE step, so from the sender chain, it is not visible that she has some minted tokens, and she cannot invoke WITHDRAW_WD operation to retrieve her funds. However, since the last valid state was prior to her claim, it is also not visible from the sender chain. Therefore, she has the same status as the users that have made a deposit, but did not claim them before the bridge died. The do not have minted tokens, and cannot withdraw them by proving their balance in the last valid state. Therefore another special operation is introduced.
We assume that Carol invokes the special cancel deposit while dead (CANCEL_WD) operation. She can do this only once and she must provide the unique ID of the original transaction (in this example, ID=5) along with the proof that she has not claimed the funds before the last valid state (i.e., that mints[ID]=False in the last valid state). The hash value assigned to locks[5] in the SCDeposit contract verifies that Carol was the one that really deposited 500 tokens. If these two verifications succeeds, the deposit is canceled, she is given back 500 tokens, and it is recorded that the deposit with the ID=5 has been canceled (by setting locks[5]=0, and assuming that 0 cannot be a valid hash value), so Carol cannot repeat this operation more than once.
