A DSL for Swarm Intelligence Algorithms
Abstract
We propose a domain-specific language to simplify the expression of Swarm Intelligence algorithms. These algorithms are typically introduced through metaphors, requiring practitioners to manually translate them into low-level implementations.This process can obscure intent and hinder reproducibility. The proposed DSL bridges this gap by capturing algorithmic behavior at a higher level of abstraction. We demonstrate its expressiveness in a few lines of code and evaluate its feasibility through a reference implementation. A discussion is presented that includes empirical comparisons with traditional implementations and future directions of the proposed DSL.
Keywords and phrases:
Domain Specific Languages, Swarm Intelligence, Global OptimizationFunding:
Kevin Martins: Kevin Martins thanks FCT for the grant SFRH/BD/151434/2021.Copyright and License:
2012 ACM Subject Classification:
Software and its engineering Domain specific languagesFunding:
This work has been supported by FCT – Fundação para a Ciência e Tecnologia within the R&D Unit Project Scope UID/00319/Centro ALGORITMI (ALGORITMI/UM).Editors:
Jorge Baptista and José BarateiroSeries and Publisher:
 Open Access Series in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Open Access Series in Informatics, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
Optimization is a popular research field that aims to find the best solution to a given problem by minimizing or maximizing an objective. It is a fundamental aspect of many disciplines, including mathematics, computer science, and engineering [11].
In the presence of gradient-based information, optimization problems can be solved efficiently. However, in many cases, this information is not available or is difficult to obtain. In these scenarios, metaheuristics represent a popular alternative as they are a black-box method for finding near-optimal solutions.
These black-box methods have become popular tools in many fields such as digital image processing, computer vision, networks and communications, power and energy management, machine learning, robotics, medical diagnosis, and others [7].
A particular category of metaheuristics that has attracted much interest in the last two decades is Swarm Intelligence (SI) [26]. SI algorithms are population-based metaheuristics that take inspiration from nature by mimicking the intelligent behavior that emerges from a population of simple organisms in self-organized systems.
In recent years, due to the considerable number of these types of algorithms in the literature, the research community has expressed concerns about the field [34, 31, 33]. The dependence on metaphors as the main motivation behind the inner workings of algorithms can hide similarities between them, leading to duplication of research effort. Furthermore, there is a tendency to reimplement these algorithms from scratch, which hinders reproducibility and replicability [34].
However, the no-free lunch (NFL) theorem [39] suggests that the main problem in this field is that these algorithms are not necessarily good at solving all kinds of problems. In fact, these algorithms often need to be configured and tested to discover which algorithm is most suitable to discover the best solution to a given optimization problem.
This paper proposes a domain-specific language (DSL) for expressing SI algorithms. The goal is to demonstrate the feasibility and practicality of using a purpose-built DSL as a unified and intuitive framework for researchers and practitioners to develop, analyze, combine, and systematically compare SI algorithms.
We show that the proposed DSL captures the essence of SI algorithms at a higher level of abstraction, independent of any specific programming language. Most importantly, it provides a clear separation between metaphor and core algorithmic concepts, such as recombination, probability distributions, and interactions between individuals. This structured representation improves the ability to identify algorithmic similarities, assess novelty, and support reproducibility.
Since optimization is a broad topic, this study focuses on SI algorithms applied to continuous single-objective optimization in real domains.
2 Background
The use of metaphors blurs the specific mechanism in the solution domain, making it difficult to determine the novelty of the contribution of an algorithm [34, 31]. For example, it has been argued that the Harmony Search algorithm can be formulated as a variation of Evolution Strategies [33], the Cuckoo search algorithm as well [5], and the Firefly Algorithm is argued to be similar to Particle Swarm Optimization with a grouping mechanism inspired by the behavior of fireflies [18]. It was also argued that for some algorithms, the metaphor, the mathematical model, and the algorithm are almost entirely different [5, 2].
This overlay between algorithms suggests that metaheuristics have common components that can be combined or that specific parts of these algorithms can be changed to create new variations. Due to the NFL theorem, we argue that this fact is a feature, not a bug, since algorithms can be fine-tuned or modified for a specific optimization problem. In recent years, several approaches have been proposed to automatize the creation and tuning of metaheuristics, which seems to support this fact [23, 4, 10, 20].
Furthermore, the research agenda proposed in [33] advocates that a pure functional description is vital to standardize metaheuristics, opening up opportunities to compose heuristics in novel ways. Although in a more narrow scope, this approach was taken in [29].
Functional programming (FP) is characterized by: (1) the use of pure functions, that is, given the same input, the same output is always produced, and (2) by having no side effects, that is, functions only compute the output and make no changes outside its scope.
Higher-order functions and lazy evaluation are two powerful features with significant contributions to the modularity of functional programming, since they allow modules/functions to be composed, acting like a kind of ’glue’ [14]. Therefore, this approach seems well suited for gluing parts of SI algorithms.
FP and DSL are natural partners since both emphasize expressiveness and modularity [13]. Instead of focusing on computing, DSL makes programming in a domain more efficient since expressiveness is bounded by a purpose-built language [12]. Therefore, DSL allows computing-specific improvements and techniques to be detached from the domain, allowing scientific advances in computing and the domain to be seamlessly adopted without disrupting existing code or workflows. This perspective aligns with the proposed DSL; that is, using functional programming principles to model SI algorithms modularity allows domain and computational advances to evolve independently.
DSL can be internal or external [12]. While external DSL is parsed independently of the underlying programming language, internal DSL represents an Application Programming Interface (API) for the underlying programming language. This study focuses on external DSL, however, the scope of the objective function of the proposed in the DSL is limited. That is, certain specificities of objective functions such as access and manipulation of external files or databases are not addressed in this proposal.
Libraries such as Opytimizer [6], NiaPy [38], and MEALPy [37] offer prebuilt algorithm templates and utilities for benchmarking, but remain grounded in imperative, metaphor-centric programming paradigms. As a result, algorithm implementations often involve boilerplate code and tight coupling between search strategies and problem-specific logic.
In contrast, the proposed purpose-built DSL adopts a high-level declarative approach that abstracts away low-level implementation details. By emphasizing mechanism-first design over metaphor-driven structures, it enables practitioners to express, compose, and hybridize algorithmic components more concisely and flexibly. In addition, it supports contextualized declarative integration of auxiliary features such as parameter tuning, making the language naturally extensible.
The following sections will describe the components of the SI algorithms that were identified and the proposed DSL.
3 Components of Swarm Intelligence algorithms
Many real-world problems can be rewritten as the minimization or maximization of some objective. As stated in [35], these problems can be defined by the couple , where is the set of feasible solutions and is the objective function to optimize. maps every feasible solution to a real number representing the quality of the solution.
At a higher level, every SI algorithm comprises two main components: the search space and the search strategy. The search space is represented by . On the other hand, the search strategy is responsible for finding the optimal solution by iteratively generating new solutions that are submitted for evaluation to the search space that, in turn, responds with the respective quality mapped.
Individuals explore/exploit the search space by generating new solutions. Depending on the number of individuals involved in the search process, metaheuristics can be classified into two types: single-solution, where only one individual explores and exploits the search space, and population-based, where multiple individuals search for the best solution in parallel. SI algorithms adopts a population-based approach.
| Algorithm | Reference |
|---|---|
| Artificial Bee Colony (ABC) | [15] |
| Cuckoo Search (CS) | [43] |
| Differential Evolution (DE) | [32] |
| Particle Swarm Optimization (PSO) | [17] |
| Barebones Particle Swarm (BB) | [16] |
| Fully Informed Particle Swarm (FIPS) | [22] |
| Firefly Algorithm (FF) | [41] |
| Jaya | [27] |
| Sine Cosine Algorithm (SCA) | [24] |
| Grey Wolf Optimizer (GWO) | [25] |
| Teaching Learning based Optimization (TLBO) | [28] |
The purpose of the search strategy is to use the quality of the solutions generated by the individuals as a guide to find the optimal solution . The search process begins with a set of initial solutions in which every individual generates and holds a solution. Then, the individuals engage in an iterative process, using information about the population to generate new solutions. In some algorithms, individuals maintain the best solution, thus maintaining the current solution if it is better than the candidate.
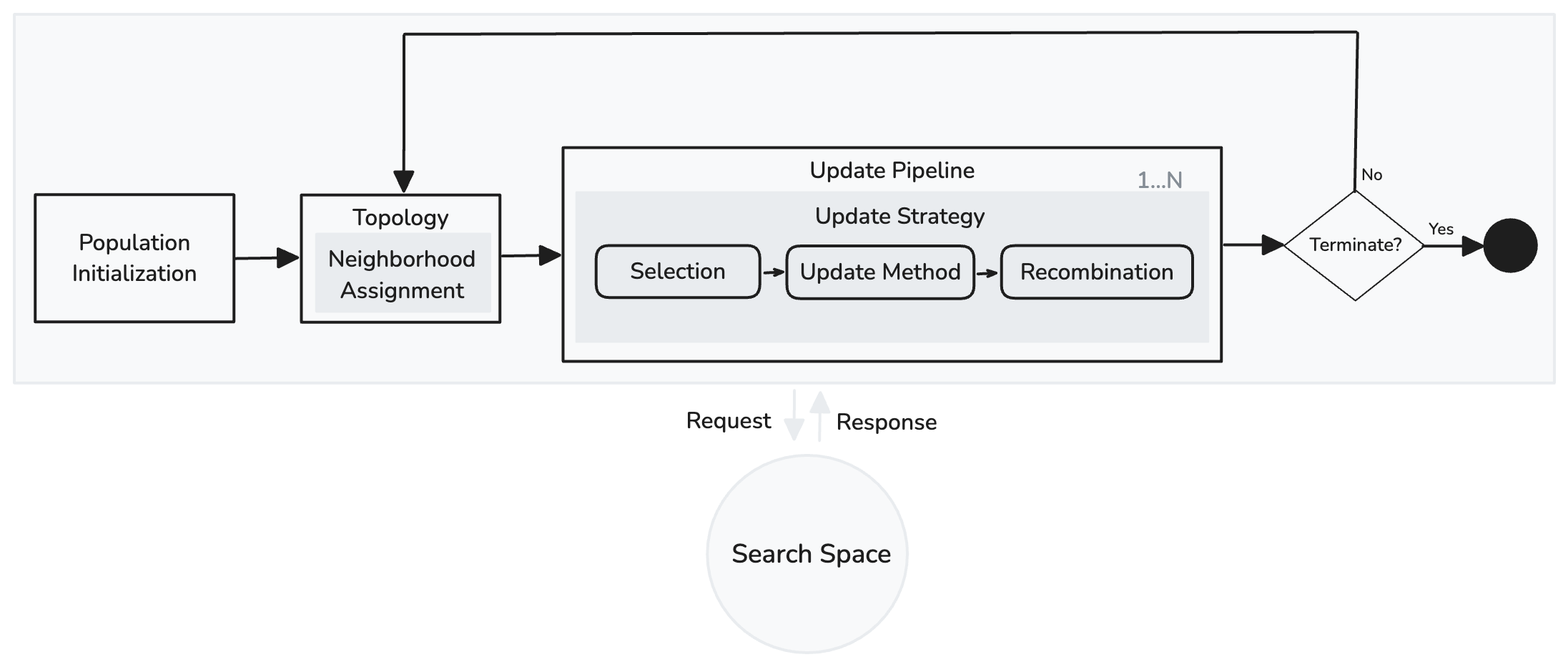
As illustrated in Fig. 1, the search strategy can be divided into three main components: population initialization, topology, and update pipeline. The search process will stop once the termination criterion has been satisfied. This study treats these components as functions with specific input and output constraints that must be satisfied. Thus, a valid component implementation can be any function that satisfies its constraints.
With this approach, the search process can be generalized so that building blocks can be swapped in and out to compose new or hybrid strategies.The following sections detail the inner workings of these components. The described building blocks were identified after analyzing the metaheuristics shown in Table 1.
FIPS and BB are variants of PSO, but are included in this study due to their distinct internal mechanisms. FIPS relies on a neighborhood topology in which each particle is influenced by all its neighbors, rather than just the global or local best. BB, on the other hand, eliminates velocity updates and samples new positions using a Gaussian distribution - representing an implicit model that contrasts with the explicit mathematical formulations typical of most SI algorithms.
In addition, although DE is not traditionally classified as a swarm intelligence algorithm, it is a population-based metaheuristic that shares similarities with SI algorithms such as stochasticity and information sharing. It was included in this study because of its distinctive use of crossover mechanisms.
Although this study does not include the latest LSHADE variants, recognized in [19] for their strong empirical performance, the identified components are general enough to model such algorithms. In particular, adaptive population size and historical memory can be expressed as modular functions or higher-order constructs within the proposed framework, preserving its applicability to advanced strategies.
3.1 Population initialization
The search process begins with the initialization of a population of individuals. Initializing the population with a diverse and representative set of solutions that effectively cover the solution space is recommended.
Population initialization generates an initial set of candidate solutions. This can be formalized as a function , where is the size of the population, and is the resulting set of solutions.
Usually, random number generation methods are used to initialize the population. Random number generation can be generated from any probability distribution depending on the problem.
3.2 Topology
Individuals in the population can be organized so that it is possible to manipulate the dissemination of information throughout the population [3]. Individuals can be grouped into neighborhoods, limiting their access to information to the assigned neighborhood. Although this method is popular in the PSO community, it can be generalized to other population-based metaheuristics.
A topology function can be any function that, given the population of individuals as input, produces as output the set of neighborhood where represents the set of individuals of a given neighborhood.
Usually, all individuals in the population have information about the entire population. This topology is termed globally oriented (GBest). In contrast, locally oriented (LBest) is defined when the adjacent population members are arranged in neighborhoods [21, 8].
Only LBest and GBest topologies were employed in this study. However, since the topology function is triggered in every iteration , our approach remains valid even when the topology is dynamic, that is, the organization changes over the iterations.
3.3 Update pipeline
In every iteration , selected individuals update their solution by generating new candidate solutions based on the information provided by their neighborhood. Usually, one update per individual takes place in every generation. Others, like TLBO and ABC, perform multiple updates based on some selection mechanism. Thus, a pipeline where one or more updates occur can be generalized, i.e., in every iteration, a set of updates occurs sequentially.
Every update method in the pipeline can be defined by the couple , where is the selection function and is the update function, that is, only selected individuals can generate new candidate solutions.
The selection process can be generalized by a function such that, given the population , it returns the selected individuals . Examples of selection procedures include:
-
All: All individuals are selected.
-
Random: individuals are randomly selected.
-
Probabilistic: individuals are selected based on some fixed probability or proportionally to their fitness, that is, better/worst-fitted individuals have higher chances of being selected.
-
Rule-based: The selection of an individual is governed by a set of rules.
Then, the selected individuals engage in the process of updating their position (solution). The update process can be generalized by a higher order function where is the generated solution vector with dimensions, represents the function responsible for the calculation of candidate solutions and the recombination method.
To generate the solution vector, equations are applied using information about the search space collected by the neighborhood, for example, the best and worst solutions. The equations usually include random perturbations to promote exploration and exploitation of the search space.
The generated solution is then recombined using some specific method , that is, applying the generated solution to dimensions of the current solution of the individual . This process is referred to as recombination. Usually, the generated solution is applied to all dimensions. Other methods include:
-
Binomial: Based on a predefined probability, the dimensions will be randomly selected and updated with the new solution.
-
Exponential: Starting with a randomly chosen index of the circularly arranged set of dimensions, adjacent indices are selected and updated with the new solution until we fail a probability roll [9].
-
Random: A fixed number of dimensions are updated randomly.
-
Probabilistic: An approach similar to the binomial method. However, a maximum of dimensions are updated.
The candidate solution generated from the update method is then evaluated. Some algorithms are elitist, discarding the candidate solution if it is not better than the individual’s best-known solution.
From the algorithms studied, a function evaluation is performed for every update, with FF representing the only gray area. In the proposal paper pseudocode [41], FF has an iterative process in that, in each generation, an individual calculates a new solution and performs function evaluations for every other individual with a better fitness value. However, in the MATLAB code [42], the author suggests that the update method is applied iteratively whenever the individual finds another one with better fitness, and at the end only one evaluation of the objective function evaluation is made.
In order to make our proposal more easily adaptable in parallel computing scenarios, this study assumes that each update method only undergoes one objective function evaluation per individual. This approach allows for the decoupling of the objective function evaluation from the update method, that is, the user provides the update pipeline, and internally the system takes care of the solution evaluation task after each update. Thus, parallel execution of the evaluation task and the update method can be enabled among individuals for every iteration .
4 Swarm Domain Language
The components identified in the previous chapter can be leveraged to construct a DSL for SI algorithms, which we refer to as Swarm Domain Language (SDL).
Parameter settings are crucial for the performance of an algorithm when searching for solutions to optimization problems. Although purposeful configurations can produce consistent results for a specific problem, they do not guarantee success for all problems. This makes selecting the appropriate parameters a challenging task. Hence, the parameter-tuning feature is also included in this DSL proposal.
Listing 1 presents a high-level overview of SDL. For better understanding, the following preliminary syntax is introduced:
-
::= is used to express how placeholders, e.g., search_space, are syntactically defined.
-
{...} is used to define the required components.
-
[...] is used to define optional components.
-
| is used to define the list of alternative expressions that can be used.
-
+ indicates that a specific expression can be repeated, that is, one or more if used in conjunction with {...} and zero or more if used in conjunction with [...].
-
Numbers are referred as number.
-
Numbers are referred as integer.
-
equation is used whenever a mathematical equation is expected. Arithmetic and trigonometric operations are allowed.
-
expression is used whenever is expected a number, parameter, equation or other production rules that will be described in this section.
-
comparison is used when comparing two values to determine their relationship: equality (=), inequality (!=), greater/less than (>, <), or greater/less than or equal to (>=, <=).
In the following sections, we will focus on the language definition of the search space, the search strategy, and the termination criteria.
4.1 Search space statement
The search space statement is shown in Listing 2. It begins with the declaration of one or more variables. A variable can be a vector; in this case, the size should be specified. The lower and upper bounds of each variable are specified using real numbers.
When specifying the objective function, the goal of the optimization should be declared. That is, MINIMIZE or MAXIMIZE should be used to specify the optimization goal.
4.2 Search strategy statement
The search strategy statement is shown in Listing 3. First, the parameter declaration occurs and is optional since some algorithms do not require parameters. Parameters can be set statically, using numbers or integers, dynamically set using expressions, or, in addition, automatically set using AUTO. Then, the process described in Section 3 follows.
To perform parameter tuning, replace the static parameter expression with the automatic one as shown in Listing 4. Integer and real numbers are supported to define the boundaries of the search space where parameter tuning should occur. It is worth pointing out that when automatic parameters are defined, the statement TUNE UNTIL(...) must be specified, and the maximum number of generation (trials) should be provided, i.e. how many evaluations of the SI algorithm are allowed during parameter tuning.
The population initialization instruction follows the parameter declaration. The size expression defines the number of individuals of the population, while initialization instructs which method to use. Listing 5 shows the currently supported methods.
The topology of the population is optional. When specifying a Lbest topology, the default size of the neighborhoods is 2 when not provided by the user.
Before moving further, let us introduce the individual memory. It contains a set of properties that are managed internally throughout generations. It is made up of the following properties:
-
POS: The current position of the individual.
-
BEST: The best position the individual found.
-
DELTA: The size of the last step taken by the individual, that is, the difference in position between the current and the previous position.
-
FIT: The current fitness of the individual.
-
IMPROVED: If the current position represents an improvement in fitness compared to the previous one.
-
TRIALS: The number of trials that an individual has performed without improving its fitness.
-
NDIMS: The number of dimensions that compose the position vector.
-
INDEX: The index of the individual in the population.
For the update pipeline, the selection, update, and recombination methods are supported. In the selection expression, the selectors in Listing 6 can be optionally specified. If specific selectors are provided, WHERE and ORDER BY must be omitted; otherwise, these clauses can be used with individual properties in the comparison expression.
Since in some algorithms, the update method can have several instructions, helper variables can be specified as needed. For example, in PSO, velocity can be defined as a helper variable to aid in position calculation. The position of the individual, POS, is always required in the update method, as it defines the new position of the individual in the search space. However, with the statement WHEN, specific conditions can be defined to update the individual. For example, to update the individual position only if the new position is better than the previous position.
By default, search space helper variables are also available allowing the use of context-specific search space variables. MAX\_GEN and CURR\_GEN return the maximum and current generation, respectively. The same logic is also applied to MAX\_EVALS and CURR\_EVAL.
Both helper and POS are defined using expression where mathematical operations can be performed using information derived from the population. In addition, the constructs reference, aggregation, utility_function, and perturbation are allowed as shown in Listing 7.
In SI algorithms, the common requirement for calculating a candidate’s position is to use the information provided by the population or neighborhood. Thus, reference can be used for this purpose. Here, when SWARM_BEST or SWARM_WORST is used without specifying the size, the best or worst individual in the neighborhood is returned, respectively. Otherwise, the best/worst will be returned. In addition, the UNIQUE clause ensures that individuals are selected without duplication on the update method. Random and roulette selection can be done with or without replacement.
Although in this proposal SUM, AVG, MIN, and MAX are the aggregation operators proposed, additional ones could be added. However, utility functions MAP and REDUCE are supported and can be used to specify more complex aggregation operations.
In fact, complex logic is sometimes required in SI algorithms. FILTER, MAP, and REDUCE provide a way to execute operations on an expression that evaluates into a collection. FILTER constructs a new collection by including only the elements of the original collection for which a specified expression evaluates to true. MAP transforms each collection element using expression, producing a new collection of transformed values. REDUCE computes a single result for the collection elements using the acc parameter as the aggregator of results.
The individual and its properties can be accessed in the key parameter. For example, for an operation performed on a collection of individuals, if individual is defined as the name of the parameter key, the expression individual.fit gives the fitness of the individual being evaluated.
DISTANCE calculates the euclidean distance between two expressions, for example, the positions of two individuals. REPEAT returns a list of the first expression parameter repeated the number of times specified by the second expression.
Finally, perturbations can be used to define the new position of the individual. These are the identical probabilistic distributions allowed in the initialization step. However, here, the size of the random number generation can be specified while in initialization its by definition given by the number of dimensions of the search space.
4.3 Termination criteria statement
Listing 8 shows the termination criteria statement. EVALUATIONS and GENERATION define the maximum allowed number of evaluations and generations, respectively. FITNESS defines the minimum or maximum fitness value that must be achieved before termination. If more than one condition is specified, the termination will occur whenever one of them is reached.
5 Discussion
This section discusses the practical use and evaluation of the proposed DSL.
We first demonstrate its expressiveness through example implementations of SI algorithms using SDL, then present comparative results with traditional approaches. Finally, we highlight the opportunities for extensibility and future directions identified during this study.
5.1 SDL examples
To illustrate the expressiveness and practical utility of the proposed DSL, we present implementations of GWO and BB using SDL. Both algorithms are applied to the Sphere function, a well-known benchmark in continuous optimization.
The Sphere function is defined by:
| (1) |
where and for all . It is a simple, convex, and continuous function with a single global minimum of , at .
As shown in Listings 9 and 10, with 13 and 17 lines of SDL for BB and GWO respectively, it was possible to express not only the algorithms but also the objective function, showing the prototyping capabilities of such DSL.
Due to space constraints, the implementation of the remaining algorithms used in this study is available at: https://github.com/kafm/swarmist/tree/main/examples. These examples illustrate the expressiveness and practicality of the proposed SDL. Each algorithm can be implemented in a concise and readable manner, with high-level constructs that clearly capture the intended behavior demonstrating the language’s effectiveness in reducing boilerplate and improving clarity.
Another key aspect of such approach is that we can create hybrid algorithms, but using building blocks from other algorithms. For instance, we can apply the binomial crossover from DE to BB as shown in Listing 11.
5.2 Experimental Evaluation
To demonstrate the feasibility of the proposal DSL, an example implementation was developed and is available on GitHub: https://github.com/kafm/swarmist. Although built using Python, the same principles can be used to port the DSL to other programming languages.
Lark [30] was used as the parsing library. A complete machine-readable grammar for SDL in EBNF format can be found at https://github.com/kafm/swarmist/blob/main/swarmist/sdl/grammar.py, which defines every nonterminal, token, and production rule needed for parsing, thus satisfying the requirement for a formal and unambiguous DSL specification.
For parameter tuning, the example implementation used Optuna [1], however, different implementations can use different frameworks or methods.
This implementation was then used to perform the following experiments: 1) comparative results with traditional implementations; and 2) parameter tuning performance evaluation.
We used benchmark functions of the CEC-2017 competition (F1 to F20) [40] with 30 dimensions for all experiments. Opfunu [36], a Python library that implements these benchmark functions, was used. In addition, we set the termination criteria to 2500 epochs and the population size was set to 40 individuals for all algorithms.
5.2.1 Comparative results with traditional implementations
To ensure that the SDL results are consistent with traditional metaheuristic implementations, we compared the SDL results with the Mealpy results, an open source Python library with more than 160 algorithms implemented [37]. For simplicity, we only selected the SI algorithms in our study with single update pipelines, that is, PSO, DE, JAYA, FF, GWO, SCA, and WO.
The same parameters were used for SDL and Mealpy. Regarding PSO, a different variation is implemented in Mealpy since the function receives a minimum and maximum inertia weight as parameters. Thus, we set the minimum at 0.45 and the maximum at 0.73.
We independently ran the Mealpy implementation for each algorithm and their static settings 30 times each and applied the Wilcoxon rank-sum test with to check whether there was a statistically significant difference between the Mealpy-implemented algorithms and the SDL ones. Holm corrections were applied to the p-values because several tests were performed.
We could not statistically conclude that the two settings differ in performance for DE, SCA, and WO (). SDL implementations of PSO, JAYA, and GWO were significantly better than Mealpy (). In contrast, for FF, the Mealpy implementation yielded better results (). The differences found in performance may be related to the specific implementations of the algorithms, for example, the variation of PSO implemented by Mealpy.
Regarding FF, SDL was significantly worse in all problems. By analyzing the Mealpy implementation, we found that a function evaluation was performed wherever an individual found a better solution for every generation, that is, the Mealpy implementation performed many more function evaluations than SDL. Thus, the experiment could have been more fair.
5.2.2 Parameter setting performance evaluation
To assess the effectiveness of parameter tuning capabilities, we compared the results of SDL with tuned parameters with those found in the SDL vs. Mealpy experiment. We excluded FF from this experiment because of the objective function evaluation problem already explained.
We independently performed the SDL parameter settings tuning for each algorithm, running it 30 times. To check for any significant differences between the SDL with parameter tuning, the static SDL settings, and Mealpy, we applied the Wilcoxon rank-sum tests with . Since we were performing multiple tests, we used the Holm correction for the p-values. As expected, SDL with parameter settings tuned was statistically better than static settings and Mealpy in all benchmark problems ().
5.3 Extensibility and Future Directions
The SDL proposed in this study leverages high-level constructs to abstract common SI mechanisms. This abstraction facilitates implementation by reducing the need for imperative code and enabling modular composition of algorithms. In practice, this led to more concise, readable, and reusable definitions.
Although the current work focuses on the definition and execution of algorithms, further extensibility could enhance the long-term utility of the language. For example, the ability to persist and reuse complete algorithm definitions would allow practitioners to encapsulate algorithmic logic once and reuse it across different problems. Listing 12 illustrates a hypothetical SDL syntax for persisting an algorithm, while Listing 13 shows how such an algorithm could be reused.
A similar mechanism could also apply to lower-level abstractions, such as reusable expressions for parameter adaptation or recombination strategies. This would further promote the construction of hybrid algorithms by mixing building blocks at different abstraction levels, ultimately improving the language’s expressiveness and extensibility.
Based on these insights, we hypothesize that SDL could support the emergence of an evolving, reusable library of SI algorithm components. This collection, combined with automatic tuning and composition mechanisms, could form the basis for automated algorithm design tailored to specific problem classes.
Although these capabilities were not addressed in this study, they represent promising directions for future work. However, their implementation involves complex design challenges that will require further investigation.
Learning a new language may not be ideal for practitioners, and one may argue that visual interfaces may be preferred over DSLs. However, the textual nature of SDL offers precise version-controlled specifications that improve systematic design and auditing of optimization models.
6 Conclusion
This study introduced a purpose-built DSL designed to support the development and experimentation of SI algorithms. The DSL provides a dedicated and expressive framework that frees researchers from the constraints of metaphor-driven representations, enabling them to model search strategies, set parameters, and combine algorithmic components with greater clarity and flexibility.
The proposed DSL offers a high-level declarative framework for the development and experimentation of SI algorithms by abstracting low-level implementation details and focusing on reusable mechanisms rather than metaphors. Thus, it enables clear, flexible, and concise representations of various algorithmic strategies.
Through illustrative examples and empirical evaluation, we showed that the DSL maintains performance comparable to traditional implementations, while significantly improving clarity, modularity, and reproducibility.
In general, the DSL establishes a foundation for a more systematic design and analysis of SI algorithms, supporting both rigorous experimentation and scalable reuse of algorithmic components.
References
- [1] Takuya Akiba, Shotaro Sano, Toshihiko Yanase, Takeru Ohta, and Masanori Koyama. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2019.
- [2] Claus Aranha, Christian L Camacho Villalón, Felipe Campelo, Marco Dorigo, Rubén Ruiz, Marc Sevaux, Kenneth Sörensen, and Thomas Stützle. Metaphor-based metaheuristics, a call for action: the elephant in the room. Swarm Intelligence, 16(1):1–6, 2022. doi:10.1007/S11721-021-00202-9.
- [3] Tim Blackwell and James Kennedy. Impact of communication topology in particle swarm optimization. IEEE Transactions on Evolutionary Computation, 23(4):689–702, 2018. doi:10.1109/TEVC.2018.2880894.
- [4] Anna Bogdanova, Jair Pereira Junior, and Claus Aranha. Franken-swarm: grammatical evolution for the automatic generation of swarm-like meta-heuristics. In proceedings of the genetic and evolutionary computation conference companion, pages 411–412, 2019. doi:10.1145/3319619.3321902.
- [5] Christian L Camacho-Villalón, Marco Dorigo, and Thomas Stützle. An analysis of why cuckoo search does not bring any novel ideas to optimization. Computers & Operations Research, 142:105747, 2022. doi:10.1016/J.COR.2022.105747.
- [6] Gustavo H de Rosa, Douglas Rodrigues, and João P Papa. Opytimizer: A nature-inspired python optimizer. arXiv preprint arXiv:1912.13002, 2019.
- [7] Tansel Dokeroglu, Ender Sevinc, Tayfun Kucukyilmaz, and Ahmet Cosar. A survey on new generation metaheuristic algorithms. Computers & Industrial Engineering, 137:106040, 2019.
- [8] Russell Eberhart and James Kennedy. A new optimizer using particle swarm theory. In MHS’95. Proceedings of the sixth international symposium on micro machine and human science, pages 39–43. Ieee, 1995.
- [9] Andries P Engelbrecht. Computational intelligence: an introduction. John Wiley & Sons, 2007.
- [10] Iztok Fajfar, Árpád Bűrmen, and Janez Puhan. Grammatical evolution as a hyper-heuristic to evolve deterministic real-valued optimization algorithms. Genetic programming and evolvable machines, 19:473–504, 2018. doi:10.1007/S10710-018-9324-5.
- [11] Christodoulos A Floudas and Panos M Pardalos. Encyclopedia of optimization. Springer Science & Business Media, 2008.
- [12] Martin Fowler. Domain-specific languages. Pearson Education, 2010.
- [13] Jeremy Gibbons. Functional programming for domain-specific languages. In Central European Functional Programming School, pages 1–28. Springer, 2013. doi:10.1007/978-3-319-15940-9_1.
- [14] John Hughes. Why functional programming matters. The computer journal, 32(2):98–107, 1989. doi:10.1093/COMJNL/32.2.98.
- [15] Dervis Karaboga and Bahriye Basturk. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (abc) algorithm. Journal of global optimization, 39(3):459–471, 2007. doi:10.1007/S10898-007-9149-X.
- [16] James Kennedy. Bare bones particle swarms. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium. SIS’03 (Cat. No. 03EX706), pages 80–87. IEEE, 2003. doi:10.1109/SIS.2003.1202251.
- [17] James Kennedy and Russell Eberhart. Particle swarm optimization. In Proceedings of International Conference on Neural Networks (ICNN’95), Perth, WA, Australia, November 27 - December 1, 1995, pages 1942–1948. IEEE, 1995. doi:10.1109/ICNN.1995.488968.
- [18] Michael A Lones. Metaheuristics in nature-inspired algorithms. In Proceedings of the Companion Publication of the 2014 Annual Conference on Genetic and Evolutionary Computation, pages 1419–1422, 2014. doi:10.1145/2598394.2609841.
- [19] Zhongqiang Ma, Guohua Wu, Ponnuthurai Nagaratnam Suganthan, Aijuan Song, and Qizhang Luo. Performance assessment and exhaustive listing of 500+ nature-inspired metaheuristic algorithms. Swarm and Evolutionary Computation, 77:101248, 2023. doi:10.1016/J.SWEVO.2023.101248.
- [20] Kevin Martins and Rui Mendes. Cherry-picking meta-heuristic algorithms and parameters for real optimization problems. In Progress in Artificial Intelligence: 21st EPIA Conference on Artificial Intelligence, EPIA 2022, Lisbon, Portugal, August 31–September 2, 2022, Proceedings, pages 500–511. Springer, 2022. doi:10.1007/978-3-031-16474-3_41.
- [21] Rui Mendes, James Kennedy, and José Neves. Watch thy neighbor or how the swarm can learn from its environment. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium. SIS’03 (Cat. No. 03EX706), pages 88–94. IEEE, 2003. doi:10.1109/SIS.2003.1202252.
- [22] Rui Mendes, James Kennedy, and José Neves. The fully informed particle swarm: simpler, maybe better. IEEE transactions on evolutionary computation, 8(3):204–210, 2004. doi:10.1109/TEVC.2004.826074.
- [23] Pericles BC Miranda, Ricardo BC Prudêncio, and Gisele L Pappa. H3ad: A hybrid hyper-heuristic for algorithm design. Information Sciences, 414:340–354, 2017. doi:10.1016/J.INS.2017.05.029.
- [24] Seyedali Mirjalili. Sca: a sine cosine algorithm for solving optimization problems. Knowledge-based systems, 96:120–133, 2016. doi:10.1016/J.KNOSYS.2015.12.022.
- [25] Seyedali Mirjalili, Seyed Mohammad Mirjalili, and Andrew Lewis. Grey wolf optimizer. Advances in engineering software, 69:46–61, 2014. doi:10.1016/J.ADVENGSOFT.2013.12.007.
- [26] Anand Nayyar, Dac-Nhuong Le, and Nhu Gia Nguyen. Advances in swarm intelligence for optimizing problems in computer science. CRC press, 2018.
- [27] R Rao. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. International Journal of Industrial Engineering Computations, 7(1):19–34, 2016.
- [28] R Venkata Rao, Vimal J Savsani, and DP Vakharia. Teaching–learning-based optimization: a novel method for constrained mechanical design optimization problems. Computer-aided design, 43(3):303–315, 2011. doi:10.1016/J.CAD.2010.12.015.
- [29] Richard Senington and David Duke. De composing metaheuristic operations. In Implementation and Application of Functional Languages: 24th International Symposium, IFL 2012, Oxford, UK, August 30-September 1, 2012, Revised Selected Papers 24, pages 224–239. Springer, 2013. doi:10.1007/978-3-642-41582-1_14.
- [30] Erez Shinan. Lark: A modern parsing toolkit for Python. https://github.com/lark-parser/lark, 2020. Version 0.14.0 (2023).
- [31] Kenneth Sörensen. Metaheuristics—the metaphor exposed. International Transactions in Operational Research, 22(1):3–18, 2015.
- [32] Rainer Storn and Kenneth Price. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of global optimization, 11(4):341–359, 1997. doi:10.1023/A:1008202821328.
- [33] Jerry Swan, Steven Adriaensen, Mohamed Bishr, Edmund K Burke, John A Clark, Patrick De Causmaecker, Juanjo Durillo, Kevin Hammond, Emma Hart, Colin G Johnson, et al. A research agenda for metaheuristic standardization. In Proceedings of the XI metaheuristics international conference, pages 1–3. Citeseer, 2015.
- [34] Jerry Swan, Steven Adriaensen, Alexander EI Brownlee, Kevin Hammond, Colin G Johnson, Ahmed Kheiri, Faustyna Krawiec, Juan Julián Merelo, Leandro L Minku, Ender Özcan, et al. Metaheuristics “in the large”. European Journal of Operational Research, 297(2):393–406, 2022.
- [35] El-Ghazali Talbi. Metaheuristics: from design to implementation. John Wiley & Sons, 2009.
- [36] Nguyen Van Thieu. Opfunu: an open-source python library for optimization benchmark functions. Journal of Open Research Software, 12(1), 2024.
- [37] Nguyen Van Thieu and Seyedali Mirjalili. Mealpy: An open-source library for latest meta-heuristic algorithms in python. Journal of Systems Architecture, 139:102871, 2023. doi:10.1016/J.SYSARC.2023.102871.
- [38] Grega Vrbančič, Lucija Brezočnik, Uroš Mlakar, Dušan Fister, and Iztok Fister. Niapy: Python microframework for building nature-inspired algorithms. Journal of Open Source Software, 3(23):613, 2018. doi:10.21105/JOSS.00613.
- [39] David H Wolpert and William G Macready. No free lunch theorems for optimization. IEEE transactions on evolutionary computation, 1(1):67–82, 1997. doi:10.1109/4235.585893.
- [40] Guohua Wu, Rammohan Mallipeddi, and Ponnuthurai Nagaratnam Suganthan. Problem definitions and evaluation criteria for the cec 2017 competition on constrained real-parameter optimization. National University of Defense Technology, Changsha, Hunan, PR China and Kyungpook National University, Daegu, South Korea and Nanyang Technological University, Singapore, Technical Report, 2017.
- [41] Xin-She Yang. Firefly algorithms for multimodal optimization. In International symposium on stochastic algorithms, pages 169–178. Springer, 2009. doi:10.1007/978-3-642-04944-6_14.
- [42] Xin-She Yang. Firefly algorithm matlab implementation. MATLAB Central File Exchange. Retrieved June 19, 2023., 2011. URL: https://www.mathworks.com/matlabcentral/fileexchange/29693-firefly-algorithm.
- [43] Xin-She Yang and Suash Deb. Cuckoo search via lévy flights. In 2009 World congress on nature & biologically inspired computing (NaBIC), pages 210–214. Ieee, 2009. doi:10.1109/NABIC.2009.5393690.
