Limited-Preemption EDF Scheduling for Multi-Phase Secure Tasks
Abstract
Safety-critical embedded systems such as autonomous vehicles typically have only very limited computational capabilities on board that must be carefully managed to provide required enhanced functionalities. As these systems become more complex and inter-connected, some parts may need to be secured to prevent unauthorized access, or isolated to ensure correctness.
We propose the multi-phase secure (MPS) task model as a natural extension of the widely used sporadic task model for modeling both the timing and the security (and isolation) requirements for such systems. Under MPS, task phases reflect execution using different security mechanisms which each have associated execution time costs for startup and teardown. We develop corresponding limited-preemption EDF scheduling algorithms and associated pseudo-polynomial schedulability tests for constrained-deadline MPS tasks. In doing so, we provide a correction to a long-standing schedulability condition for EDF under limited-preemption. Evaluation shows that the proposed tests are efficient to compute for bounded utilizations. We empirically demonstrate that the MPS model successfully schedules more task sets compared to non-preemptive approaches.
Keywords and phrases:
real-time systems, limited-preemption scheduling, trusted execution environmentsCopyright and License:
2012 ACM Subject Classification:
Computer systems organization Real-time systemsAcknowledgements:
We, the authors, would like to thank the reviewers for their constructive remarks.Funding:
This research was supported in part by NSF Grants CPS-1932530, CNS-2141256, CNS-2229290, IIS-1724227, CNS-2038609, CCF-2118202, CNS-2211641, and CPS-2038726.DOI:
10.4230/LITES.10.1.3Received:
2024-08-19Accepted:
2025-03-31Published:
2025-05-15Part Of:
TGDK, Volume 10, Issue 1Journal and Publisher:
 Leibniz Transactions on Embedded Systems, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
Leibniz Transactions on Embedded Systems, Schloss Dagstuhl – Leibniz-Zentrum für Informatik
1 Introduction
In today’s interconnected world, the security of real-time systems has emerged as a primary concern, e.g., [41, 23, 26, 20, 37, 44, 31], given the widespread integration of electronic devices into various aspects of daily life. However, the implementation of security measures often introduces additional resource requirements, such as increased computational overhead, or imposes specific constraints on application behaviors; for example, this could involve necessitating computation that requires isolation or cannot be preempted.
For example, control flow integrity (CFI) checks may be needed to ensure correct program execution. However, such checks, which require CPU time in addition to normal code execution, must be carried out at specific time points (e.g., after branching) and allowing for preemption may result in an arbitrary computation being performed but not detected. As another example, a task that is responsible for taking sensor readings may need to execute in isolation in order to ensure that another task cannot deduce when an event of interest occurs [31].
Since implementing security measures requires some of the same resources that the real-time tasks need to advance their execution, a co-design approach that explicitly considers security cost/requirements along with real-time requirements is potentially more effective at managing limited computational resources. For instance, trusted execution environments (TEEs) provide isolation of code and data in hardware at the expense of startup and teardown costs. A scheduling approach that does not consider this specific security-driven overhead may elect to switch between the secure world (i.e., executing in TEE) and the normal world (no TEE) indiscriminately. This may result in an excessive amount of overhead incurred by, e.g., hardware mode switching, saving and restoring the stack, and copying data, resulting in deadline misses. A security-cognizant scheduler, on the other hand, would make judicious decisions based on both security and real-time requirements, e.g., by bundling up multiple TEE executions and executing them one immediately after the other so as to have to pay for startup and teardown cost only once [32].
A recent ISORC paper [5] proposed and developed algorithms that are able to provide provable correctness of both the timing and some security properties. We believe that such a scheduling-based approach to achieving security in safety-critical systems is possible, and indeed, necessary in embedded systems that are particularly cost- and SWaP-constrained and hence need to be implemented in a resource-efficient manner. However, we consider it unlikely that a “one size fits all” solution exists; instead, security-cognizant scheduling must first explicitly identify the kinds of threats that are of concern by precisely defining a threat model, and design scheduling strategies that can be proved to be resistant to attacks under the identified threat model. We consider the research in [33] to be particularly noteworthy in this regard, in their explicit and methodical modeling of different threats in the context of the sporadic task model, and their analysis of vulnerabilities of current strategies (including security-agnostic fixed-priority scheduling [1] and the randomization-based schedule obfuscation approaches, e.g., the one in [44]) to such threats.
Security-Cognizant Scheduling.
We believe the methodology formalized and used in [33] holds great promise as a means of integrating security and timing correctness concerns within a common framework. This methodology was articulated in [5] as follows: security for safety-critical real-time embedded systems can be achieved by (i) explicitly representing specific security considerations within the same formal frameworks that are currently used for specifying real-time workloads, thereby extending notions of correctness to incorporate both the timing and the security aspects; and (ii) extending previously-developed techniques for achieving provable timing correctness to these models, thus assuring that both timing and security properties are correct.
This Work.
This paper extends our prior work in [3], which applied the methodology articulated in [5] to the following problem in system design for real-time + security. We consider computer platforms upon which multiple different security mechanisms (such as TEEs, encryption/decryption co-processors, FPGA-implemented secure computations, etc.) co-exist. Depending upon their security requirements, different pieces/parts of the (real-time) code may need to use different security mechanisms at different times. We therefore assume that the code is broken up into phases, with different consecutive phases needing to use different sets of security mechanisms – the security mechanisms used by each phase are specified for the phase. We assume that there is a startup/teardown overhead cost (for data communication, initialization, etc.) expressed as an execution duration, associated with switching between different security mechanisms. In other words, there is a time overhead associated with switching between the execution of different phases.
Contributions.
As in our prior work that this paper extends [3], we formalize the workload model discussed above as the Multi-Phase Secure (MPS) task model, with multiple independent recurrent processes of this kind that are to execute upon a single shared preemptive processor. We start out in Section 4 assuming that each recurrent process is represented using the widely-used 3-parameter sporadic task model [7]. For this model, we represent the problem of ensuring timeliness plus security as a schedulability analysis problem, which we then solve by adapting results obtained in prior work (e.g., [4, 9, 13, 34, 14]) on limited-preemption scheduling. Later in Section 5, we propose a generalization that models conditional execution within each recurrent process. Its original treatment in [3] makes a simplifying assumption that was later addressed in another extension; we therefore present the conditional model and the simplifying assumption in this paper, but leave the analysis for conditional execution to the more accurate treatment in [38].
We emphasize that although the designs of these models are motivated by security considerations – they arose out of some security-related projects that we are currently working on – we are proposing a scheduling model and associated algorithms, not a complete solution to a particular security problem. That is, although our model draws inspiration from security concerns, it (i) does not claim a perfect match to all security requirements; and (ii) it should have applicability beyond the security domain – indeed, we suggest that the results presented in this paper be looked upon as a generalization of the rich body of real-time scheduling theory literature on limited-preemption scheduling.
Extensions to the Prior Work.
This paper extends, corrects, and clarifies our prior results in [3], making the following new contributions. Section 3.2 presents a correction to the condition in [4, 9] for EDF schedulability of limited-preemption tasks. Section 4 leverages the corrected condition to introduce pseudo-polynomial schedulability analysis for sets of MPS tasks, improving the execution time of the associated algorithms originally proposed in [3], especially for tasks with implicit deadlines. With these improvements, we are able to evaluate larger sets of tasks with more realistic ranges of periods. We also address inconsistencies in [3] between the theoretical model and its implementation by using a continuous-time representation of the algorithms. These are reflected in the new results in Section 6, which more clearly demonstrate the advantages of our approach over non-preemptive schedulers.
Organization.
The remainder of this manuscript is organized as follows. After briefly discussing some related scheduling-theory results in Section 2, Section 3.2 presents the correction to the limited-preemption EDF schedulability condition of [4, 9]. We then motivate and formally define the MPS sporadic tasks model in Section 4, and provide both pre-runtime analysis and a run-time scheduling algorithm for MPS sporadic task systems upon preemptive uniprocessor platforms. In Section 5 we further generalize the workload model to be able to represent conditional execution. We have performed schedulability experiments to evaluate both the effectiveness of our algorithms and the performance improvements over their original implementations in [3]. We report the results in Section 6. We conclude in Section 8 by pointing out some directions in which we intend to extend this work, and by placing our results within a larger context on the timing- and security-aware synthesis of safety-critical systems.
2 Some Real-Time Scheduling Background
2.1 The Sporadic Task Model [7]
In this model, recurrent processes are represented as sporadic tasks . Each task has three defining characteristics: worst-case execution requirement (WCET) , relative deadline , and period (minimum inter-arrival duration) . The sporadic task generates a series of jobs, with inter-arrival times of at least . Each job must be completed within a scheduling window, which starts at the job’s release time and ends time units later, and the job’s execution time is limited to units. A sporadic task system is made up of multiple independent sporadic tasks. We assume without loss of generality that tasks are indexed in non-decreasing relative deadline order (i.e., if then ).
Processor Demand Analysis (PDA).
A sporadic task system can be scheduled optimally by the Earliest Deadline First (EDF) [24] scheduling algorithm, given a preemptive uniprocessor. To determine whether a specific task system can be correctly scheduled by EDF, Processor Demand Analysis (PDA) [8] can be utilized. PDA is a necessary and sufficient algorithm that is also optimal. The key idea of PDA is built upon the demand bound function (dbf). Given an interval length of such that , the dbf for a sporadic task can be represented by : the maximum possible aggregate execution time required by jobs of task such that they arrive in and have deadlines before . The following equation was derived in [7] to compute its value:
| (1) |
For a task system to be correctly scheduled by EDF, the following was derived in [7] as a necessary and sufficient condition for all :
| (2) |
The Testing Set.
A naïve application of PDA requires testing the validity of Equation 2 for all intervals. However, a more efficient approach, outlined in [7], involves checking only values of that follow the pattern for some non-negative integer and some .
Furthermore, it suffices to test such values that are less than the least common multiple of all the parameters. The collection of all such values of for which it is necessary to verify that Condition 2 holds true in order to confirm EDF-schedulability is referred to as the testing set for the sporadic task system , often denoted as .
It is worth noting [7] that, in general, the size of the testing set can be exponential in the representation of . However, it has been proven [8, Theorem 3.1] that for bounded-utilization task systems – i.e., systems that fulfill the additional requirement that for some fixed constant strictly less than 1 – it is sufficient to check a smaller testing set with pseudo-polynomial cardinality relative to the representation of , consisting of all values of the form not exceeding
| (3) |
where is the least common multiple of all , and is the maximum of all parameters. We note that for bounded-utilization implicit-deadline tasks – those for which for every task – this bound reduces to . In this extension, we apply this smaller testing set to our scheduling algorithms for MPS tasks.
Since we can check Condition 2 in linear () time for any given value of , these observations imply that we can perform an exponential-time EDF-schedulability test for general task systems and a pseudo-polynomial-time one for bounded-utilization systems.
2.2 Limited-Preemption Scheduling
The limited-preemption sporadic task model, as introduced by Baruah et al. [4], adds to the task specification a chunk-size parameter in addition to the regular parameters , , and . This parameter indicates that each job of task may need to execute non-preemptively for up to time units.
To schedule tasks in the limited-preemption sporadic task model, the limited-preemption EDF scheduling algorithm was proposed [4, 9]. Like its preemptive counterpart, the limited-preemption EDF algorithm prioritizes jobs based on their (absolute) deadlines. If a job of task with remaining execution time is executing and a new job with an earlier deadline arrives, then ’s job may execute for an additional time units before incurring a preemption.
Baruah and Bertogna [4, 9] showed that a task system is not schedulable under the limited-preemption EDF model if and only if either of the following conditions are true:
| (4) |
or
| (5) |
Noting that when , we combine and invert the two conditions, giving a necessary and sufficient condition for successfully scheduling a limited-preemption sporadic task system upon a single preemptive processor using the limited-preemption EDF algorithm:
| (6) |
Unlike the exact test for preemptive uniprocessor EDF-schedulability (Equation 2), Equation 6 contains an additional term on the left-hand side of the inequality that accounts for blocking due to later-deadline (and hence lower-priority) jobs. Specifically, the term is a blocking term that captures the potential delay caused by lower-priority jobs that were already executing at the start of the interval, for a duration of up to their chunk size. Since we assume that all tasks have non-negative execution time, this blocking term is always non-negative.
In this extension to the prior work in [3], we use a continuous-time representation of the blocking term in Equation 6. The prior work used a discrete-time representation, , which requires both task periods and execution times to be represented as integers. This introduces several challenges. First, it is more difficult to reason about the effect of inserting preemption points; blocking times (chunk sizes) must also be represented as integers, but the number of “chunks” might not evenly divide the execution time. Second, there is a tradeoff when choosing the precision at which to represent execution time units. If the unit of time is coarse, then the execution time of each phase and its corresponding startup/teardown time must be rounded up. If the unit of time is very short – such as a single processor tick – to achieve higher precision, then the testing set grows rapidly as the representations of the task periods become larger. By using continuous time, this extension removes these limitations, and modifies the expression to allow execution times to take any non-negative real value.
Based on this observation, the Processor Demand Analysis (PDA) algorithm has been extended to apply to limited-preemption systems as well [4]. The extension is straightforward: Equation 6 replaces Equation 2 in the algorithm, and the algorithm proceeds as usual.
However, we note that Expression 6 cannot hold true for values of of the form
| (7) |
where , suggesting incorrectly that a set of tasks is not EDF schedulable if any task has non-zero blocking time. In the next section of this extension, we present a corrected condition that addresses this issue, which we then apply to scheduling of MPS tasks in Section 4.
3 The Corrected Limited-Preemption EDF Schedulability Condition
In this section, we present a correction to the condition of Baruah and Bertogna [4, 9] for EDF schedulability of limited-preemption tasks.
3.1 The Problem
As discussed in the prior section, in [4, 9], Baruah and Bertogna claimed as a necessary and sufficient condition for scheduling a limited-preemption sporadic task system upon a single preemptive processor using EDF that
| (8) |
where is the blocking due to limited preemption induced by task .
From the definition of the demand bound function in Equation 1, we observe that for . Then for (i.e., for all tasks ), the above condition requires ; as we are already considering the case that , this can be simplified to .
This implies that for values of such that , the above condition cannot hold true if does not also exceed for all tasks . More simply, the condition cannot hold true for values of of the form shown in Expression 7. Because processor demand analysis requires that the condition hold true for all values of , this would deem any set of limited-preemption tasks with non-zero blocking time to be unschedulable by EDF.
3.2 The Correction
As this is obviously not true – i.e., there are limited-preemption task sets that are schedulable by EDF, we now set out to correct the above condition. We do so by pointing out a subtlety to the proof in [4] of the condition in Expression 6.
That proof constructs the blocking time condition by defining a minimal unschedulable set of jobs for which represents the earliest arrival time of those jobs and is the time at which the first deadline miss occurs. Additionally, for each job , it defines as representing an upper bound on the time for which can execute non-preemptively. In this system, there is exactly one job with a deadline after ; we let be the task that generates this job. If is the time at which that job begins to execute non-preemptively and is when it stops executing, then [4, Equation 4] states that
As is a bound on the non-preemptive execution time, the proof in [4] then claims that . We observe that since , it also follows that . We can therefore combine these inequalities to make the statement that . In light of this, we modify the rest of the proof in [4]. Now, it follows that
We then replace the expression with a time . Since , it follows that ; the dbf of will therefore be zero at and we can rewrite the condition as:
This condition checks whether some task causes excessive blocking at times ; to determine if the system is schedulable, we can therefore test whether the following condition holds for any task at any time , considering blocking times from just those tasks for which :
| (9) |
Then when , the dbf for each task is , so the condition will always be satisfied. Furthermore, when , , and so the condition cannot be satisfied when . We can therefore begin the testing set of our implementation at , and only check the blocking time when determining whether the condition is violated.
4 Systems of Multi-Phase Secure (MPS) Sporadic Tasks
In this section we extend the sporadic task model to consider the setting where the workload of each task comprises an ordered sequence of different phases, with each phase required to use a different security mechanism.222Note that we consider a unique combination of security mechanisms to be its own security mechanism. Thus, a portion of a task subject to multiple overlapping security mechanisms would execute in its own phase. Therefore, switching between phases or between jobs incurs some teardown/startup overhead, which translates to an additional execution duration. We are given a system of multiple such independent tasks that are to be scheduled upon a shared preemptive processor. If an executing task is preempted within a phase, the assumption that the tasks in the system are independent of one another implies that we must conservatively assume that the preempting task may be executing using a different security mechanism; hence, the teardown/startup overhead may be incurred again. In some systems, the cost of a preemption may be less than the full startup/teardown cost of a phase; this can be accounted for by adding any additional cost to the execution time of the phase. When a phase of a task is selected for execution we assign it responsibility for taking care of both the startup that must happen at that point in time, and the subsequent teardown that occurs when it either completes execution or is preempted by a higher-priority task. Hence a phase with execution duration that is preempted times is responsible for (and hence should have been budgeted for) a total execution duration of
| (10) |
A Motivating Example.
To motivate the MPS task model, consider the case of trusted execution environments (TEEs), a hardware feature that provides strong isolation of code and data. Although this isolation has significant security benefits, broadly-used TEE implementations such as OP-TEE [35] are sometimes limited to using only a small fraction of the available system memory [36] and code running in a TEE has limited access to common system APIs. In addition, placing more functionality inside a TEE increases the probability that an unidentified vulnerability compromises the isolated TEE environment; a number of works based on TEEs have cited minimization of the trusted computing base (TCB) as a key design concern [25, 29, 39]. A fine-grained minimization of the code placed in a TEE can lead to the existence of tasks that span multiple “worlds” – for example, a task may begin execution in the normal world (i.e. no TEE), switch to the secure world (executing in the TEE) to perform a sensitive cryptographic operation, and then return to the normal world to complete its work. In some cases, switching across worlds can also be used as a workaround for TEE memory limitations. For example, large neural networks may be executed securely by copying a single layer into the TEE, computing and storing an intermediate result, and then returning to the normal world to retrieve the next layer [2].
However, switching between worlds induces TEE startup and teardown costs, the impact of which varies depending on the choice of processor and TEE software implementation; one implementation based on an Arm Cortex-M development board saw costs on the order of microseconds [30], while an implementation using OP-TEE on a Raspberry Pi with a Cortex-A processor saw overheads ranging from hundreds of microseconds to tens of milliseconds [32]. A scheduling approach that does not consider these significant context-switching costs may preempt execution for higher-priority jobs indiscriminately, resulting in missed deadlines due to the overheads incurred by frequent startup/teardown.
4.1 Task Model
We have a task system comprising independent recurrent tasks , to be scheduled upon a single preemptive processor. The task is characterized by a period/inter-arrival separation parameter and a relative deadline . The body of the task – the work that must be executed each time the task is invoked – comprises phases, denoted , that must execute in sequence upon each job release of the task:
As previously discussed, we assume that successive phases are required to execute using different security mechanisms (i.e., and execute using different security mechanisms for all , ). Let denote the WCET of phase , and denote the sum of the startup cost and the teardown cost associated with the security mechanism within which phase is to execute. The aggregate WCET of all phases of this task during its execution is thus given by the following expression
However, suppose that during some execution of task the ’th phase is preempted times for each , ; as discussed above (Equation 10), the cumulative WCET of all phases of this task during this execution is then given by the expression
The figure below depicts a 2-phase job, denoted by and , which is preempted once in the first phase and twice in the second phase. The shaded region denotes the startup and teardown costs for each phase of the job.
4.2 Overview of Approach
Given a task system comprising multiple independent MPS tasks to be scheduled upon a single preemptive processor, we will first execute a schedulability analysis algorithm to determine whether this system is schedulable, i.e., whether we can guarantee to schedule it to always meet all deadlines, despite the costs incurred by startup/teardown. This schedulability analysis algorithm essentially constructs a limited-preemption task corresponding to each task , and determines whether the resulting limited-preemption task system can be scheduled by the limited-preemption EDF scheduling algorithm [4, 9] to always meet all deadlines. If so, then during run-time the original task system is scheduled using the limited-preemption EDF scheduling algorithm, with chunk-sizes as determined for the corresponding constructed limited-preemption tasks. We point out that if a chunk-size is determined for the limited-preemption task , then the ’th phase of ’s jobs will execute in no more than contiguous time-intervals (i.e., it would experience at most preemptions); equivalently, the cumulative WCET of all the phases of each of task ’s jobs will be no more than
Assumption of Fixed-Preemption Points.
We make the conservative assumption that once the chunk-size is determined for each task then the preemption points in the code are statically determined prior to run-time. That is, once the chunk-size is determined for a task , a preemption is statically inserted into the task’s code after the code has executed non-preemptively for no more than time units; this is referred to as the fixed-preemption point model [42]. Once ’s program reaches this statically-placed preemption point, the security mechanism for the task’s current phase must
-
1.
complete a teardown (e.g., a flush of the cache, or ending a TEE session) to ensure task execution integrity during preemption;
-
2.
invoke the operating system’s scheduler to see if there are any high-priority tasks awaiting execution; and
-
3.
upon resuming execution as the highest-priority task the security mechanism must perform a startup (e.g., starting a new TEE session from the task’s last executed instruction).
Since the preemption points are statically inserted into the code, we must perform the teardown/startup for a phase each time a preemption point is encountered (even if there is no other task active in the system at that time). While clearly this approach suffers from potentially performing unnecessary preemptions, it is often used in safety-critical settings due the precise predictability that fixed-preemption points provide. In future work, we will explore the floating preemption point model and other models that would permit the system to avoid unnecessary preemptions and teardowns/startups.
4.3 The Schedulability Test
We now describe our schedulability test. As discussed above, our approach is to construct for each task a corresponding limited-preemption task . This limited-preemption task is assigned the same relative deadline parameter value (i.e., ) and the same period parameter value (i.e., ) as ; its WCET and its chunk-size parameter are computed as described below, and in pseudo-code form in Algorithm 1.
We introduce integer variables for each , , and for each , , to denote the maximum number of contiguous time-intervals in which the ’th phase of may need to execute. Then , the WCET of each job of task , can be written as
| (11) |
where the second term within the summation represents the maximum preemption overhead (the startup cost plus the teardown cost) that is incurred by the ’th phase of task .
It remains to specify the values we will assign to the variables. We will start out assuming that each phase of each task executes non-preemptively – i.e., in one contiguous time-interval. We do this by initially assigning each the value ; we will describe below how the values are updated if enforcing such non-preemptive execution may cause deadlines to be missed. With each assigned the value , it is evident that the largest duration for which task will execute non-preemptively is equal to ; we initialize the chunk-size parameters – the values – accordingly: for each task ,
| (12) |
In this manner, we have instantiated the parameters for one limited-preemption task corresponding to each task . We must now check whether the limited-preemption task system so obtained is schedulable using the limited-preemption EDF scheduling algorithm [4, 9]. We do so by checking whether Equation 9 holds for values of in the testing set , considered in increasing order; we motivate this ordering below in (5). First, we split into two sets, containing all values up to and including , and containing all values thereafter. Then, we initialize to denote the smallest value in , and perform the following steps.
-
1.
If Equation 9 is satisfied for , we set to be the next-smallest value in , and repeat this step.
-
2.
If Equation 9 is violated for and the first term in the LHS of Equation 9 is , then we conclude that the system is not schedulable and return.
Suppose, however, that a violation of Equation 9 occurs due to the blocking term in Equation 9. That is, the first term in the LHS of Equation 9 is when Equation 9 is instantiated with , but the sum of the first and second terms exceeds . For this to happen, it must be the case that some with is blocking ‘too much;’ we must reduce the amount of blocking each such task can cause (i.e., reduce its parameter). Below, we describe how to do so.
-
3.
Let denote the amount of blocking that can be tolerated at without causing a deadline miss:
(13) As discussed above, each with must ensure that its blocking term, , is no greater than . For each such task with currently greater than , we may need to increase , the number of contiguous time-intervals in which its ’th phase may execute for each of its phases , in the following manner:
(14) That is, we reduce blocking in order to satisfy Equation 9 for by potentially increasing the number of preemptions (and thereby incurring additional teardown/startup overhead). In prior work [3], we assumed that tasks had integer execution times and hence used as the blocking term; here, we use continuous time and therefore do not subtract a time segment.
-
4.
Such additional overhead must be accounted for; this requires that , the WCET parameter of the limited-preemption task , must be updated (i.e., potentially increased) by recomputing it using Equation 11 (reproduced below):
(Notice that since some of the values may have increased, the value of may also increase.)
-
5.
Recall that we have been checking the validity of Equation 9 for values of in , the partial testing set of , considered in increasing order. Since we are currently considering , we have therefore already validated that Equation 9 previously held for values of in the testing set. The crucial observation now is that the increase in the value of for any with does not invalidate Equation 9 for any , because the increased values only contribute to the cumulative demand (the first term in the LHS of Equation 9) for values of . Hence, we do not need to go back and re-validate Equation 9 for values of smaller than .
- 6.
-
7.
Once reaches , there are no remaining tasks with , and so we are done updating the cnt variables. At this point, we check if the total utilization of the system, . If it is, the system cannot be scheduled.
-
8.
For an implicit-deadline system with , we prove in Lemma 2 that the slack will never be at any later time. Therefore, we know that the system is schedulable and can return immediately.
-
9.
For a constrained-deadline system, we check the slack at each remaining point in the testing set up to and including the testing set’s upper bound, described by Expression 3. If the slack is found to be , the system is unschedulable, and we return immediately. Otherwise, is system is deemed to be schedulable.
Computational Complexity.
The number of iterations of the for-loops of Lines 6 and 23 dominate the computational complexity; the other loops in the algorithm are polynomial in the number of tasks or number of vertices in a chain. The number of iterations of Line 6 is proportional to ; for implicit-deadline systems, this is the only loop that executes. For constrained-deadline systems, the combined number of iterations for both loops is the number of testing set points. In general, for constrained-deadline sporadic task systems scheduled on a single processor, the testing set can be exponential in the number of tasks, but is psuedo-polynomial as long as the utilization is bounded by a fixed constant strictly less than 1 [8]. For MPS sporadic tasks, the utilization can change as we add preemption points. However, because we only continue to add preemption points as the testing set is traversed up to , the testing set remains pseudo-polynomial in size unless the utilization reaches exactly 1, in which case it becomes exponential (bounded by the least-common multiple of the task periods).
Proof of Correctness/Optimality.
We now provide formal arguments that our approach for chains yields a correct assignment of values for all tasks (Theorem 3) and is optimal in the sense that if the approach returns the system is not schedulable, then there is no assignment of s that would cause the system to become schedulable (Theorem 4).
Before we prove the two main theorems of the section, we prove a useful invariant for the for-loop in Line 6 of Algorithm 1. The remainder of this section assumes the fixed-preemption model where a preemption is always taken at a fixed-preemption point (i.e., incurring the teardown/startup costs). In this model, it can be shown that Equation 9 remains a necessary and sufficient condition for limited-preemption EDF schedulability. However, under other preemption models where we may skip/delay preemptions, Equation 9 is only a sufficient condition. Thus, only the correctness theorem will hold, and we leave an investigation of optimality for these more dynamic settings to future research.
Lemma 1.
At the beginning of each iteration of the for-loop at Line 6 with being the current testing set interval considered, the following statements hold:
-
1.
For any , Equation 9 is satisfied for the current set of values.
-
2.
For any such that , the value of set by the algorithm is maximum (over all possible schedulable chunk-size configurations of ).
Proof.
Lemma 1 is, as expected, proved by induction.
Initialization.
Initially equals ; the minimum deadline is the first non-zero value of the dbf function for all tasks. Thus, Statement 1 is true since at all prior timepoints the first term of Equation 9 is zero and Equation 9 reduces to per the arguments in Section 3.2. Statement 2 is also vacuously true since is set to its largest possible value by the previous loop and does not affect schedulability as cannot block any other task (by nature of having the smallest relative deadline).
Maintenance.
Let us consider the current testing-set point . Let be the testing-set point considered in the previous iteration of the for-loop. Assume that Statements 1 and 2 were true at the beginning of the for-loop for point ; we will show that the statements will hold for .
For Statement 1, we must show that Equation 9 is not invalidated when we execute the for-loop for . As was previously argued, for , the dbf values are unchanged as any changes made to values in the iteration for only affect the of tasks with . Thus, Statement 1 continues to hold for all by assumption. We only need to show that the previous iteration will set the corresponding values such that Equation 9 will also be true at . However, this obviously holds since for each with , either already satisfied Equation 9 (and does not change) or it is set by Line 12 of Algorithm 1 to the largest value that satisfies Equation 9 for the current values of .
Statement 2 follows from the last observation of the previous paragraph and by the assumption that values for all with are set to their maximum value by assumption and cannot change at or after. Therefore, the values that contribute to the dbf in Equation 9 at are as small as possible. It therefore follows that any with has either already had its value set to the largest possible to satisfy Equation 9 for some or has its value set to the largest possible to satisfy Equation 9 at .
Termination.
Let be the last testing set interval considered by the for loop in Line 6. During the execution of the loop, the algorithm may return the system is not schedulable. In the case that not schedulable is returned, Statements 1 and 2 hold for all testing set intervals up to (and including) , but not necessarily after . If the algorithm completes execution of the loop without returning, the Statements 1 and 2 are guaranteed to hold for all testing set intervals in (by properties of testing-sets for Equation 9 and that the last testing set point must be at least ).
Lemma 2.
In an implicit-deadline task system, Equation 9 will be satisfied at all points if .
Proof.
By contradiction. Consider some in the testing set at which Equation 9 fails to hold. At this point, there are no tasks where , and so Equation 9 becomes . From the definition of the dbf:
Since for an implicit-deadline task system, for all tasks ,
From which it follows that
As and are both positive:
which implies that .
Theorem 3.
If the schedulability test returns the system is schedulable, then assignment of values by the algorithm in Algorithm 1 ensures that the task system meets all deadlines when scheduled by limited-preemption EDF.
Proof.
The termination argument of Lemma 1 argues that Statement 1 and therefore Equation 9 hold for all testing set points in . If the system is an implicit-deadline system, then by the check in line 18, the system utilization must be ; by Lemma 2, Statement 1 will continue to hold for all points in . If the system is a constrained-deadline system, the loop in Line 23 will complete and return the system is schedulable if and only if Equation 9 holds for all points in .
Since Equation 9 is sufficient (and necessary for the fixed-preemption model), the task system is schedulable by limited-preemption EDF when the assigned chunk-sizes are used.
Theorem 4.
If the schedulability test returns the system is not schedulable, then there does not exist an assignment of values such that Equation 6 is satisfied.
Proof.
If the system is not schedulable is returned while processing a testing-set interval in then either or for some and . In either case, Statement 2 of Lemma 1 implies that the ’s set prior to are as large as possible with respect to for Equation 9. Therefore, if is true, it is not possible to find another assignment of ’s to make this false. Otherwise, if , the fact that was set to its maximum value means there does not exist a larger possible to successfully fit task execution into given the startup/teardown costs of the phase .
If the system is not schedulable is returned while processing a testing-set interval in , then Equation 9 is false for some . The right-side term of equation 9 considers only tasks where ; as begins past , there can be no tasks matching this condition and therefore no assignment of that would reduce the right-side term. Per Statement 2 of Lemma 1, each has already been maximized when considering ; reducing some can only increase the number of preemption points required and therefore increase the dbf of some task in the left-side term of Equation 9. Therefore, there is no alternative assignment of ’s that would reduce the left side of Equation 9 and cause the system to become schedulable.
5 Systems of Conditional MPS Sporadic Tasks
In Section 4 we considered recurrent tasks representing “linear” workflows: each task models a piece of straight-line code comprising a sequence of phases that are to be executed in order. In many event-driven real-time application systems, however, the code modeled by a task may include conditional constructs (‘if-then-else’ statements) in which the outcome of evaluating a condition depends upon factors (such as the current state of the system, the values of certain external variables, etc.), which only become known at run-time, and indeed may differ upon different invocations of the task. Hence the precise sequence of phases that is to be executed when a task is invoked is not known a priori. It is convenient to model such tasks as directed acyclic graphs (DAGs) in which the vertices represent execution of straight-line code, and a vertex representing a piece of straight-line code ending in a conditional expression has out-degree – see Figure 1 for an example. In this figure the vertex denotes a piece of straight-line code that ends with the execution of a conditional expression. Depending upon the outcome of this execution, the code represented by either the vertex or the vertex executes, after which the code represented by the vertex is executed. In this section, we briefly explain how our proposed Multi-Phase Secure (MPS) workload model may be further extended (i.e., beyond the aspects discussed in Section 4) to accommodate recurrent tasks that may include such conditional constructs.
5.1 Model
We now provide a more formal description of the conditional MPS sporadic task model. Each task is characterized by a 3-tuple where and are the relative deadline and period, and is a DAG: with . Each vertex represents a phase of computation, which must execute using a specified security mechanism. The interpretation of each edge depends upon the outdegree (i.e., the number of outgoing edges) of vertex :
-
1.
If this outdegree , then the edge denotes a precedence constraint: vertex may only begin to execute after vertex has completed execution.
-
2.
If this outdegree is , then all the outgoing edges from collectively denote the choices available upon the execution of a conditional construct: after completes execution, exactly one of the vertices for which becomes eligible to start executing. It is not known beforehand which one this may be, and different ones may become eligible upon different invocations of the task.
A WCET function is specified, with denoting the WCET of node . An overhead function is specified, with denoting the startup/teardown cost associated with the security mechanism using which vertex is to execute.
In the original model presented in [3], a simplifying assumption was made that teardown and setup costs are always incurred when transitioning between any two jobs, regardless of whether they use the same or different security mechanisms. This assumption was conservative, as it did not account for cases where both jobs use the same security mechanism, in which case the teardown and setup costs would not actually be incurred.
5.2 A Subtlety
A subtle issue arises when dealing with conditional code, which was not present in the consideration of linear workflows in Section 4. Specifically, during the execution of conditional code, it is not known at compile time which branch will be taken at runtime, and different invocations may take different paths. In hard real-time systems, it is necessary to ensure that tasks meet their deadlines under all possible runtime conditions. Thus, during pre-runtime schedulability analysis, a conservative approach is adopted, assuming that each invocation of the task follows the “longest” path – the one with the maximum cumulative execution requirement.
Standard algorithms are known for identifying the longest path through a DAG that have running time linear in the representation of the DAG. Under limited-preemption scheduling, however, identifying the path through the DAG that has maximum cumulative execution requirement is not entirely straightforward. Let us consider again the example DAG of Figure 1.
-
If the chunk size for this task were , then both branches can be executed non-preemptively. The upper branch incurs a cost of while for the lower branch the cost is ; therefore, the upper branch is the computationally more expensive one.
-
Now suppose . Then the upper branch may need to execute in or 3 contiguous pieces, for a cumulative cost of . The lower branch may need to execute in or 3 contiguous pieces, for a cumulative cost of , and is hence the more expensive branch.
This example illustrates that the computationally most expensive path through a DAG that represents conditional execution depends upon the value of the chunk size parameter (the parameter of the task). As we saw in Section 4, the approach to scheduling MPS sporadic tasks has been to convert each task to a limited-preemption sporadic task. The procedure for doing so (Algorithm 1) repeatedly changes the values of the parameters of the tasks. As we adapt the techniques of Section 4 to schedulability analysis of conditional MPS tasks, it is important to note that the necessary improvements to handle conditional execution, including the correct analysis of teardown and setup costs, have already been addressed in a separate extension paper [38]. In that work, the unnecessary conservatism in the assumption that teardown and setup costs are always incurred during transitions between jobs, regardless of whether they use the same security mechanism is eliminated. This refinement leads to a more precise schedulability analysis, ensuring that only the relevant overheads are considered and optimizing the overall analysis of conditional MPS tasks. Thus, while this paper focuses on the linear task model and its optimization, the more accurate treatment of conditional execution is fully covered in [38].
6 Empirical Evaluation
In the previous sections, we have developed algorithms to introduce preemptions into the execution of the phases of multi-phase secure tasks. While these preemptions reduce the blocking that higher-priority phases/jobs experience at runtime, they come at a cost – increased overhead due to the additional teardown/startup costs that must be performed before and after every inserted preemption. Thus, while the limited-preemption approach proposed in this paper theoretically dominates the non-preemptive approach (i.e., each phase is executed non-preemptively and preemptions are permitted only between phases of a task), it is unclear how much schedulability improvement on average we can expect a system designer to obtain from using our proposed approach.
In this section, we provide an empirical analysis on that topic via the application of the schedulability tests of Section 4 over synthetically-generated MPS task systems. We compare the proposed schedulability tests with existing limited-preemption scheduling where each phase of a task is executed fully non-preemptively.
By using the refined algorithms presented in this work that permit pseudo-polynomial running times for bounded utilization task sets, and correcting implementation issues identified in our earlier work [3], we were able to extend our experiments to a broader parameter space and larger task sets. We also directly evaluate the running times of our algorithms and implementation, and compare them to the original versions from [3].
As before, we limit our scope to evaluating linear task sequences; we refer readers interested in further evaluation, analysis, and refinement of the conditional model to [38].
6.1 Experimental Setup
The evaluation was conducted using a C++ simulation. All tests were performed on a a server with two Intel Xeon Gold 6130 (Skylake) processors running at 2.1 GHz, and with 64GB of memory. Multiple task sets were evaluated in parallel; each task set was given a single thread on which to run. We evaluate task sets for many parameter variations, including the task count, number of phases per task, utilization, and task periods. In some cases, the number of phases per task is fixed; where it is not fixed, we select the number of phases for each task following a uniform distribution in the given range. Task periods are selected either from a uniform distribution within the period range specified for each test or, where specified below, a log-uniform distribution. For each combination of fixed parameters, we generate 1000 random task systems. For each system, we use the UUniFast algorithm [12], first to assign a total utilization to each task and then to distribute the task’s total allotted time between the execution times and startup/teardown overhead for each of its phases. We note that compared to the prior work in [3] that this paper extends, we have adjusted this distribution to be more consistent and to be independent of the number of phases in the task. We then evaluate each task set against three algorithms: chains, the algorithm presented in section 4, phase NP, in which there is a static preemption point between each phase but no additional preemption points can be inserted, and fully NP, in which the entire task runs as a single non-preemptive chunk.
We evaluate both implicit-deadline and constrained-deadline task systems. In an implicit-deadline system, for each task. In a constrained-deadline system, we choose a random value for each that is uniformly distributed between the task’s execution time and its period . For implicit-deadline systems, we evaluate at increments of in . We note that, compared to the prior version of this work in [3], the improvement to the testing set described in Section 4 allows us to evaluate these systems in a reasonable amount of time even for large numbers of tasks; to understand the impact of this optimization, we also test the exponential set presented in the original version on systems with 8 tasks or fewer and compare their execution times. For constrained-deadline systems, the testing set is bounded by a term that is determined in part by a factor ; as , the testing set size becomes very large and becomes infeasible to evaluate. We therefore limit our evaluation of constrained-deadline systems to utilizations in .
6.2 Schedulability Analysis Results
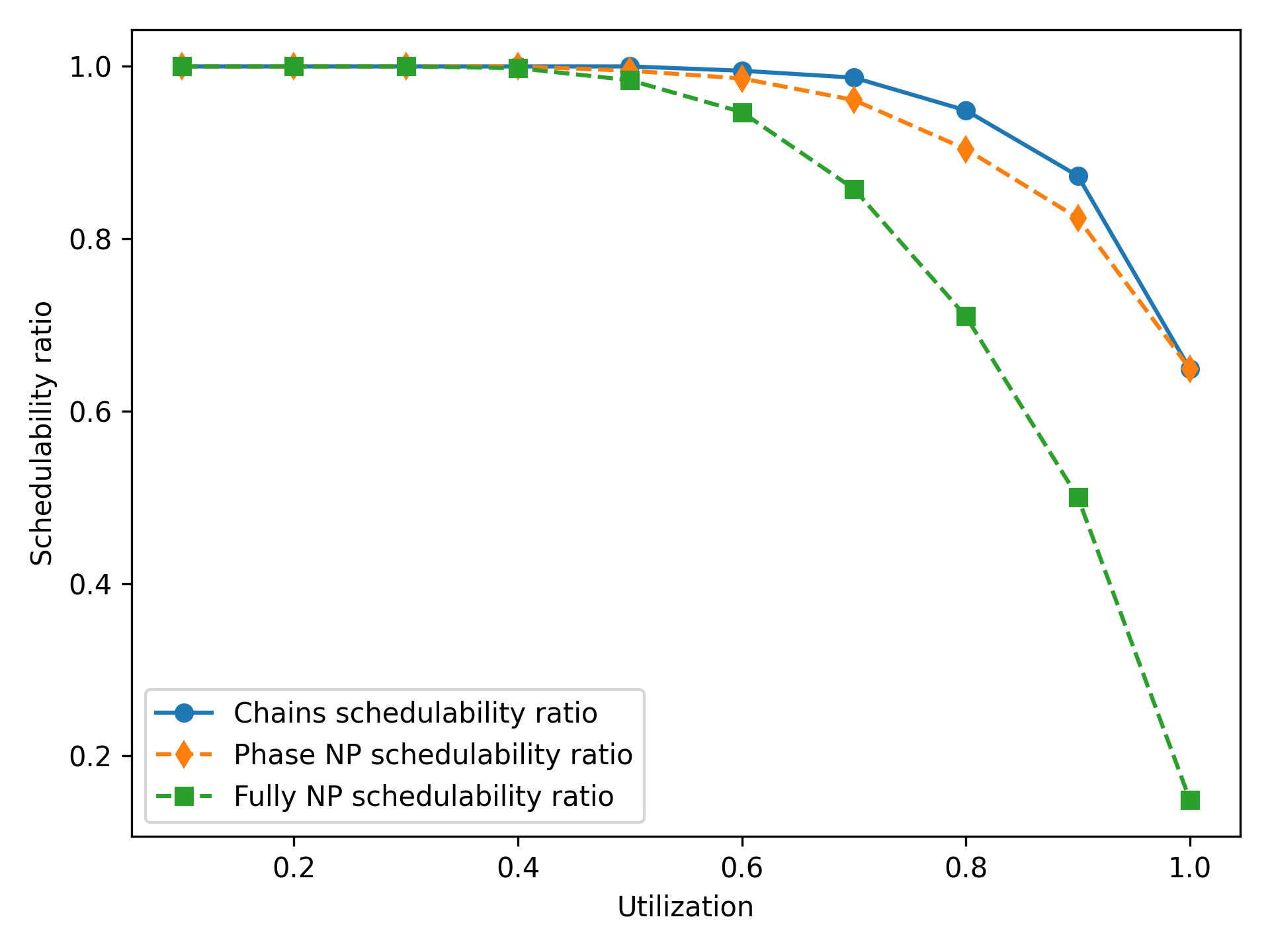

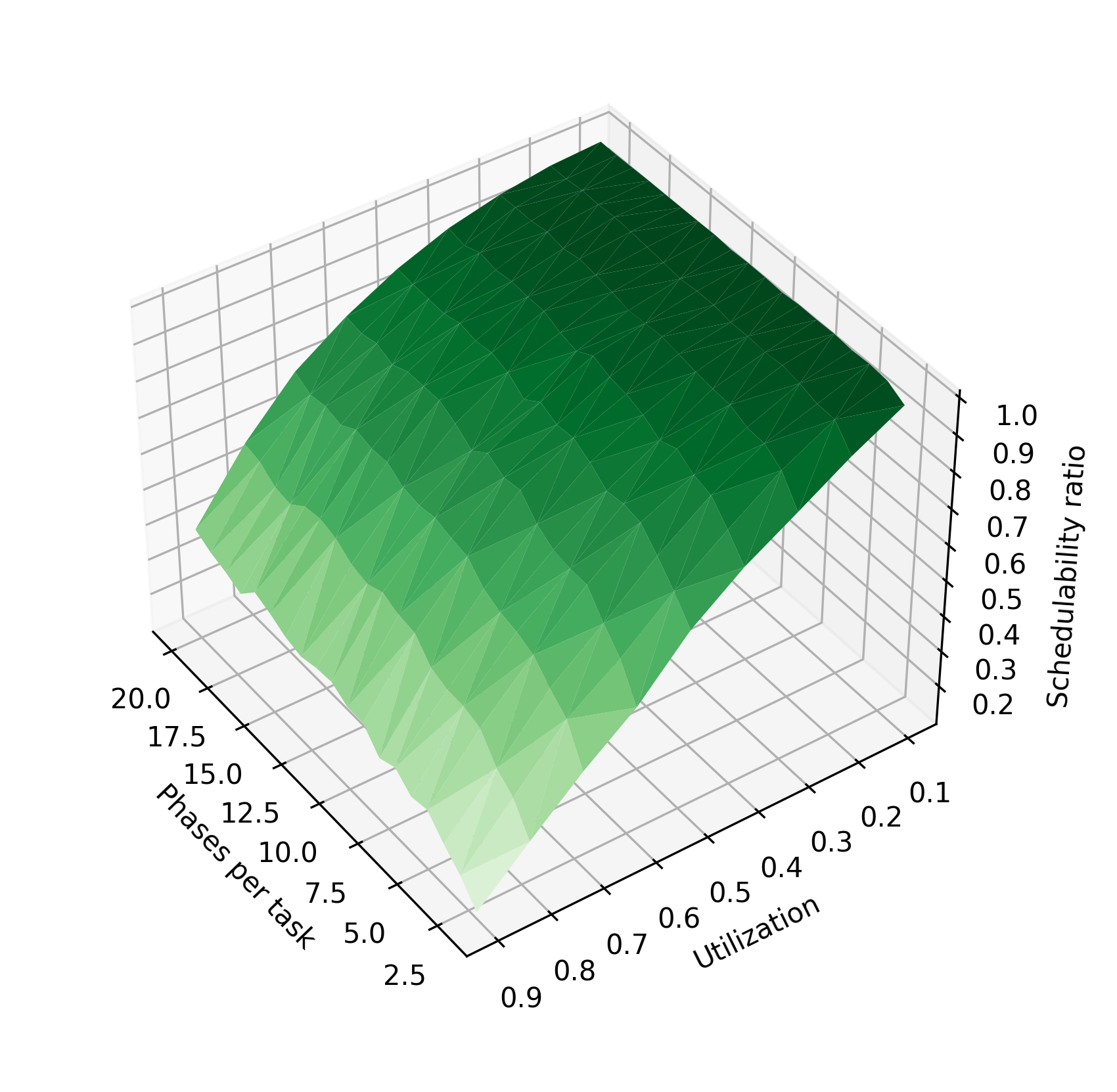
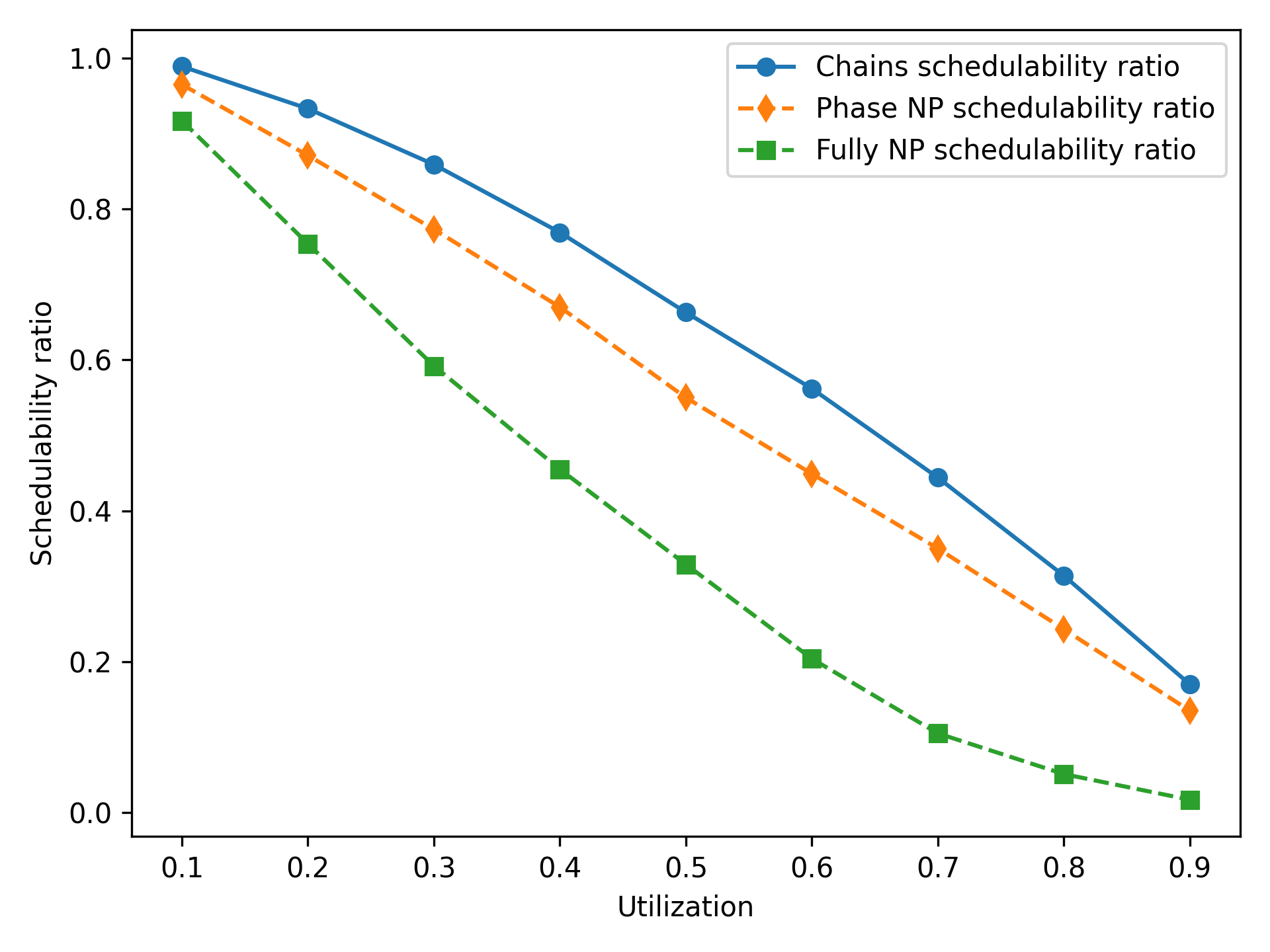
Schedulability of Implicit-Deadline Systems.
Figure 2 shows the schedulability ratio of each of the three tests described above – chains, phase NP, and fully NP. For each test, tasks with low utilization are all schedulable, but schedulability decreases as the utilization of the system increases. By inserting additional preemption points, the chains algorithm is able to obtain a schedulability improvement over a phase NP approach on these higher-utilization tasks. Once utilization reaches 1, it is not possible to insert any preemption points, as inserting a preemption point would increase the startup/teardown overhead and cause the utilization to exceed 1; therefore, the chains algorithm does not lead to a schedulability improvement. Tasks with 1-6 phases have a slightly higher schedulability ratio than tasks with 1-4 phases; we explore this effect more in the paragraph below.
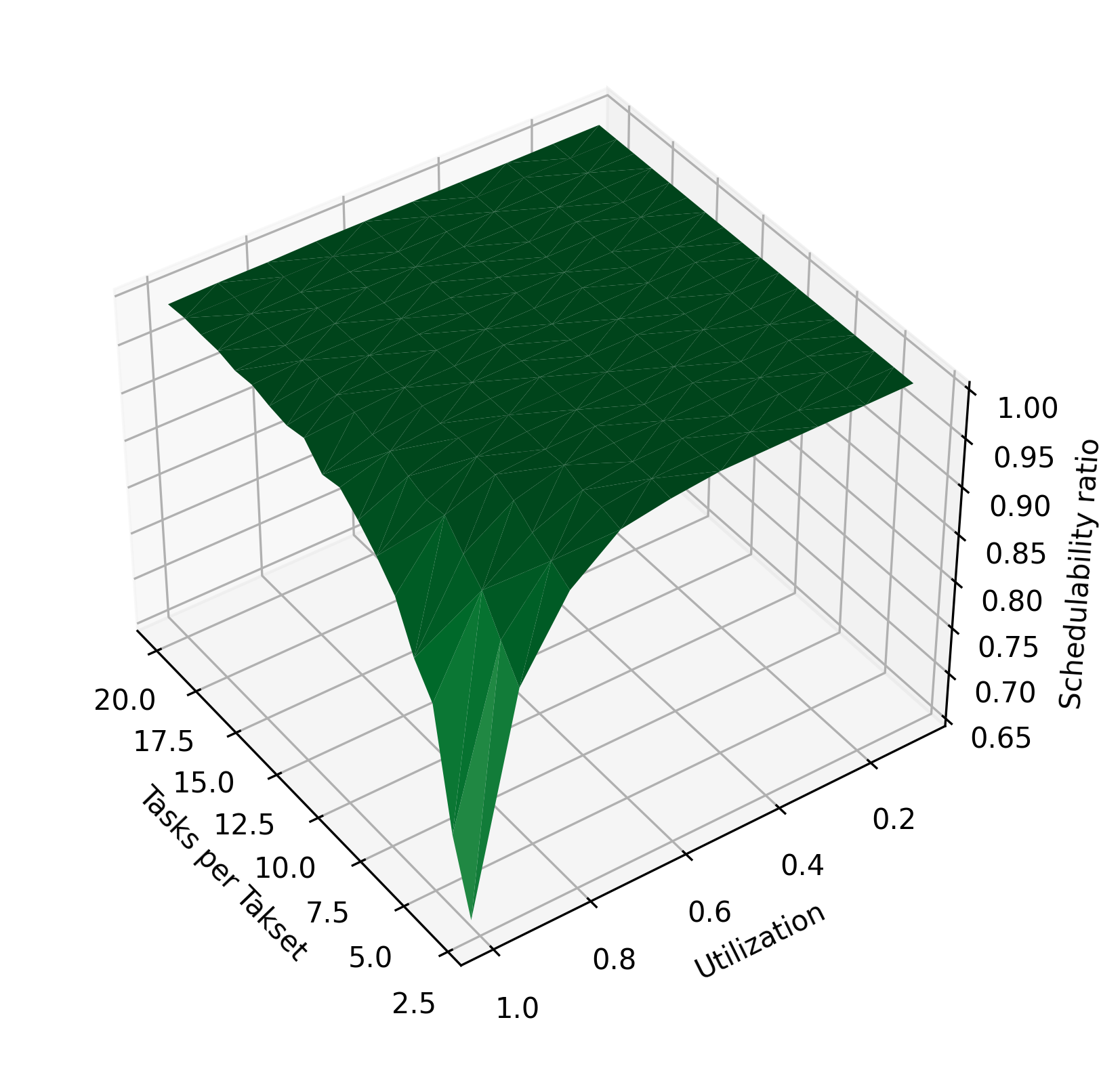
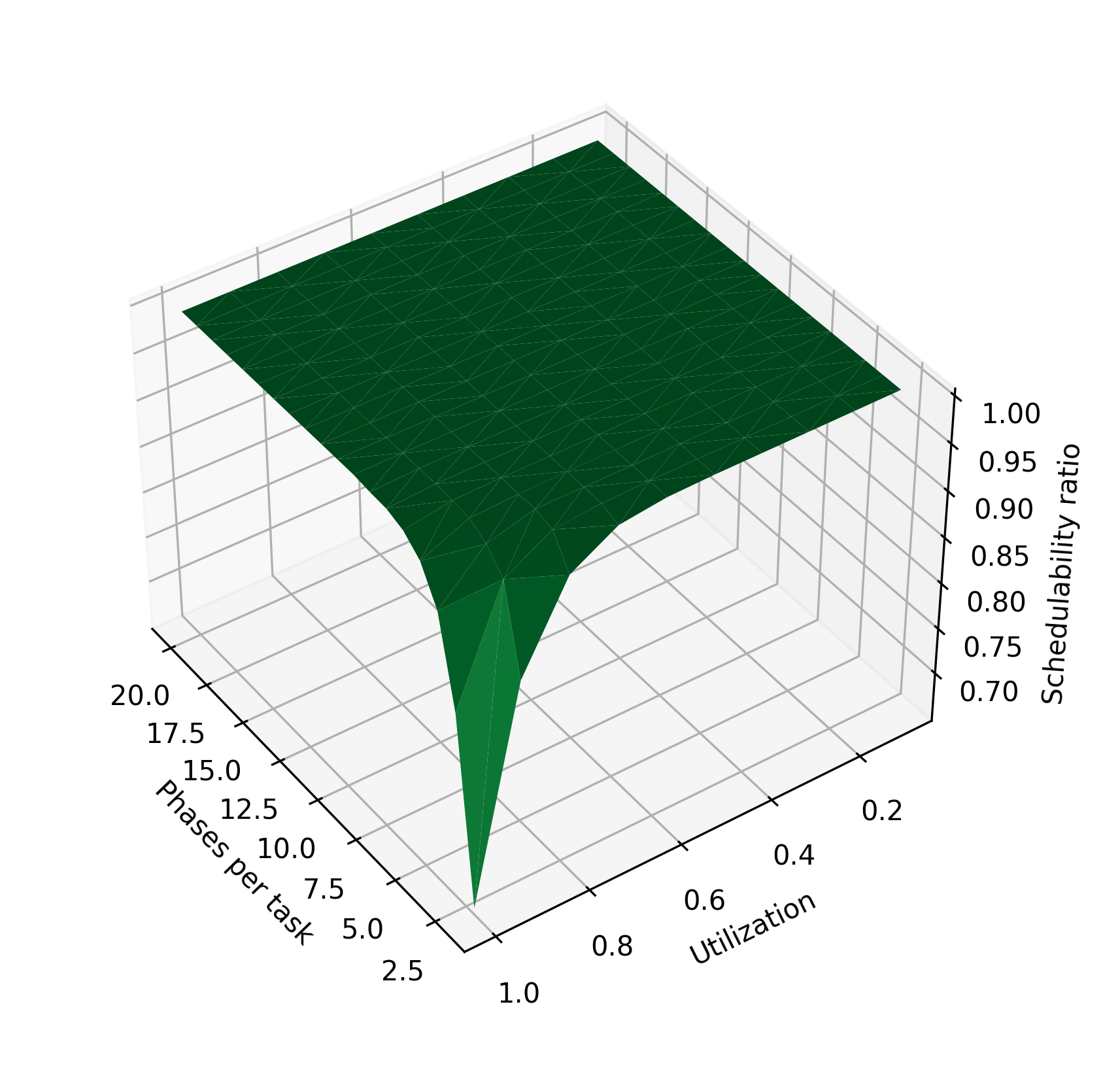
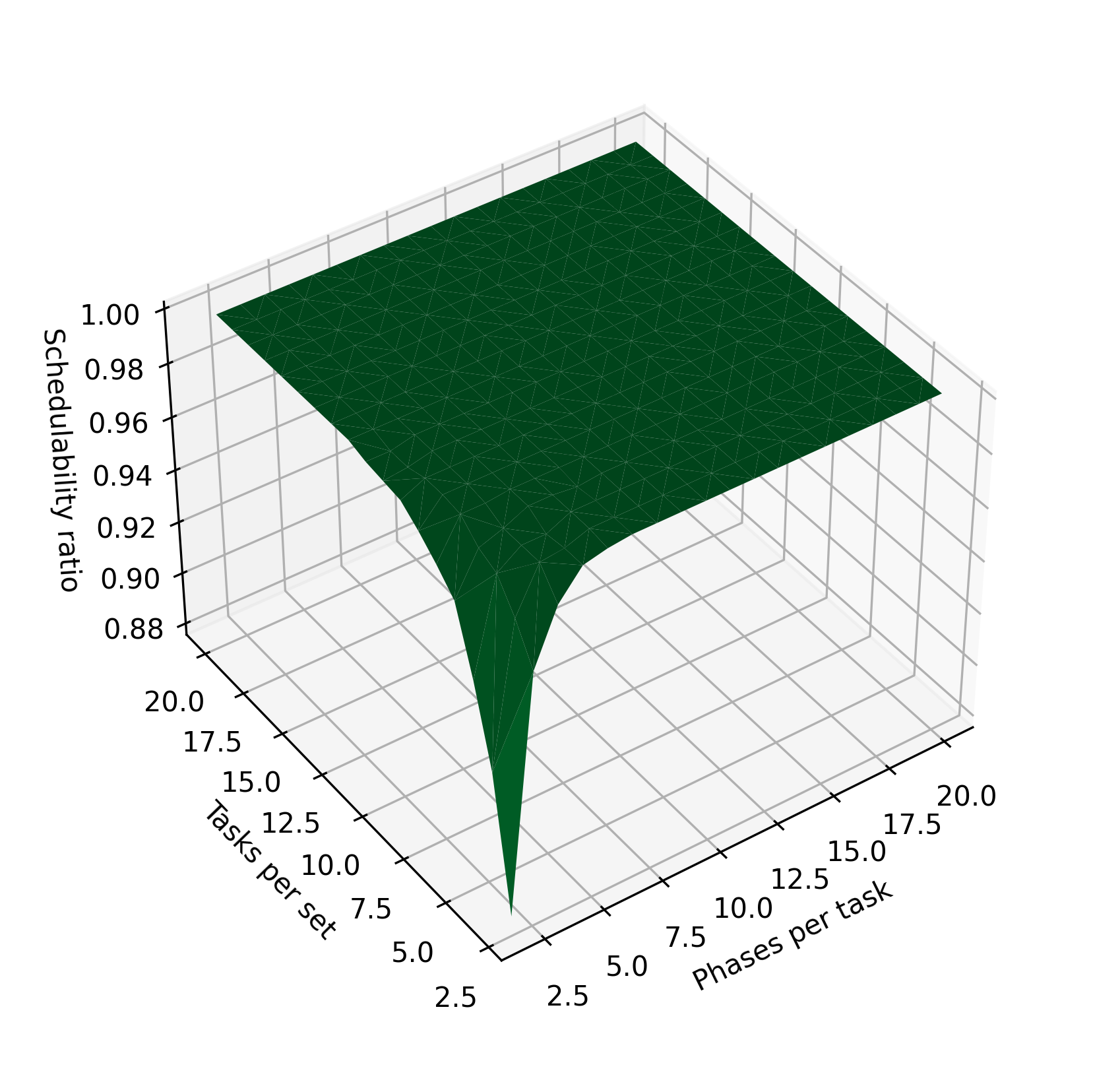
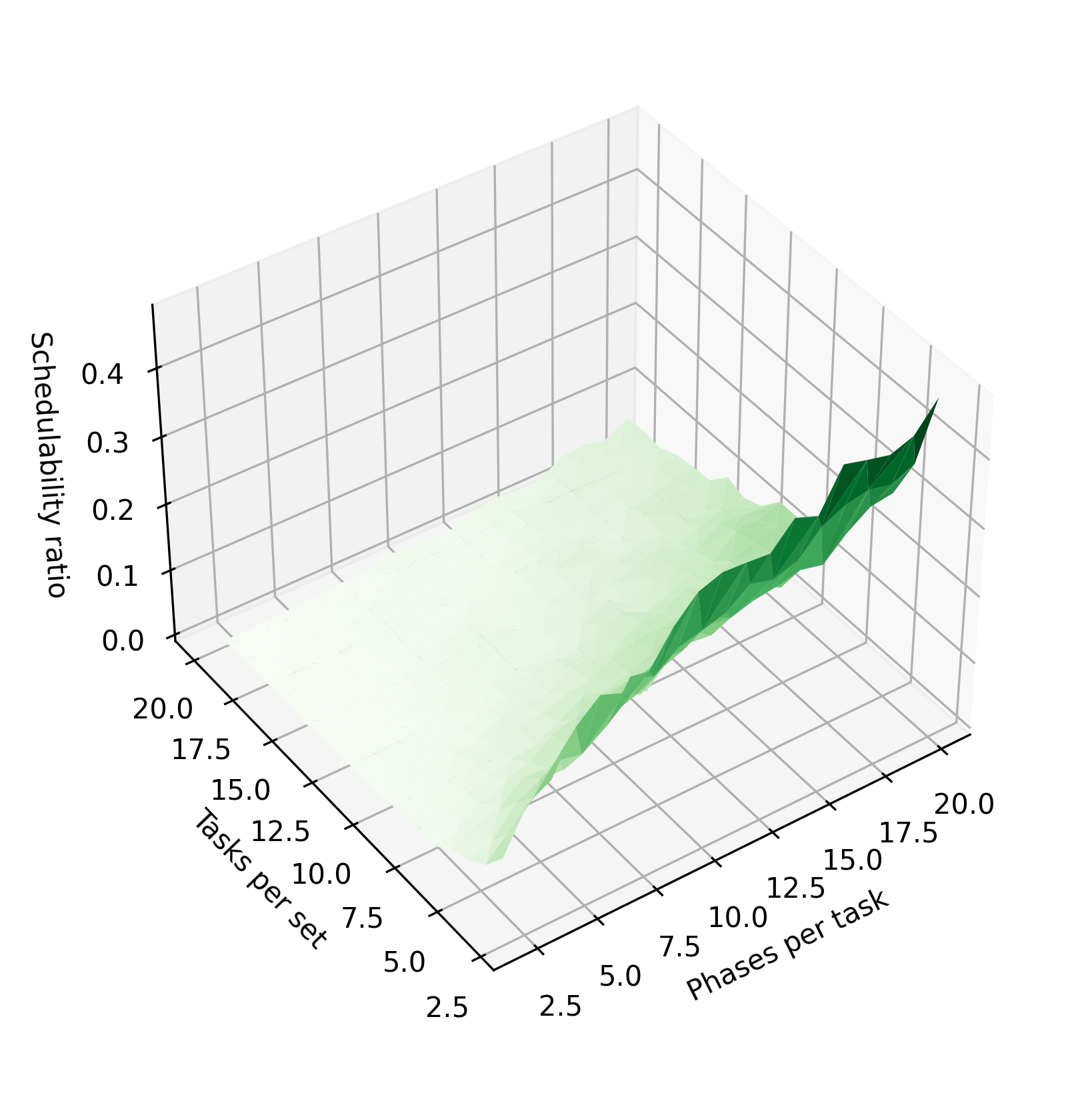
Figure 3 shows the impact of various parameters of the task system on the schedulability ratio using the chains algorithm and periods of 10–30 time units. In Figure 3(a), tasks are randomly assigned 1-4 phases, while the utilization and tasks per taskset are varied. In Figure 3(c), the number of tasks is held constant at 3, and each taskset is assigned a fixed number of phases, varying from 2 to 20 phases per task. In Figure 3(e), the utilization is held constant at 0.9. As in Figure 2, increasing utilization reduces the schedulability ratio. Here, it is clearly visible that increasing the number of tasks or number of phases per task improves the schedulability ratio. When these parameters are increased, the system’s total execution time is divided among more tasks or among more phases, so that each task has a lower blocking time. The reduction in blocking time makes the system more likely to be schedulable.
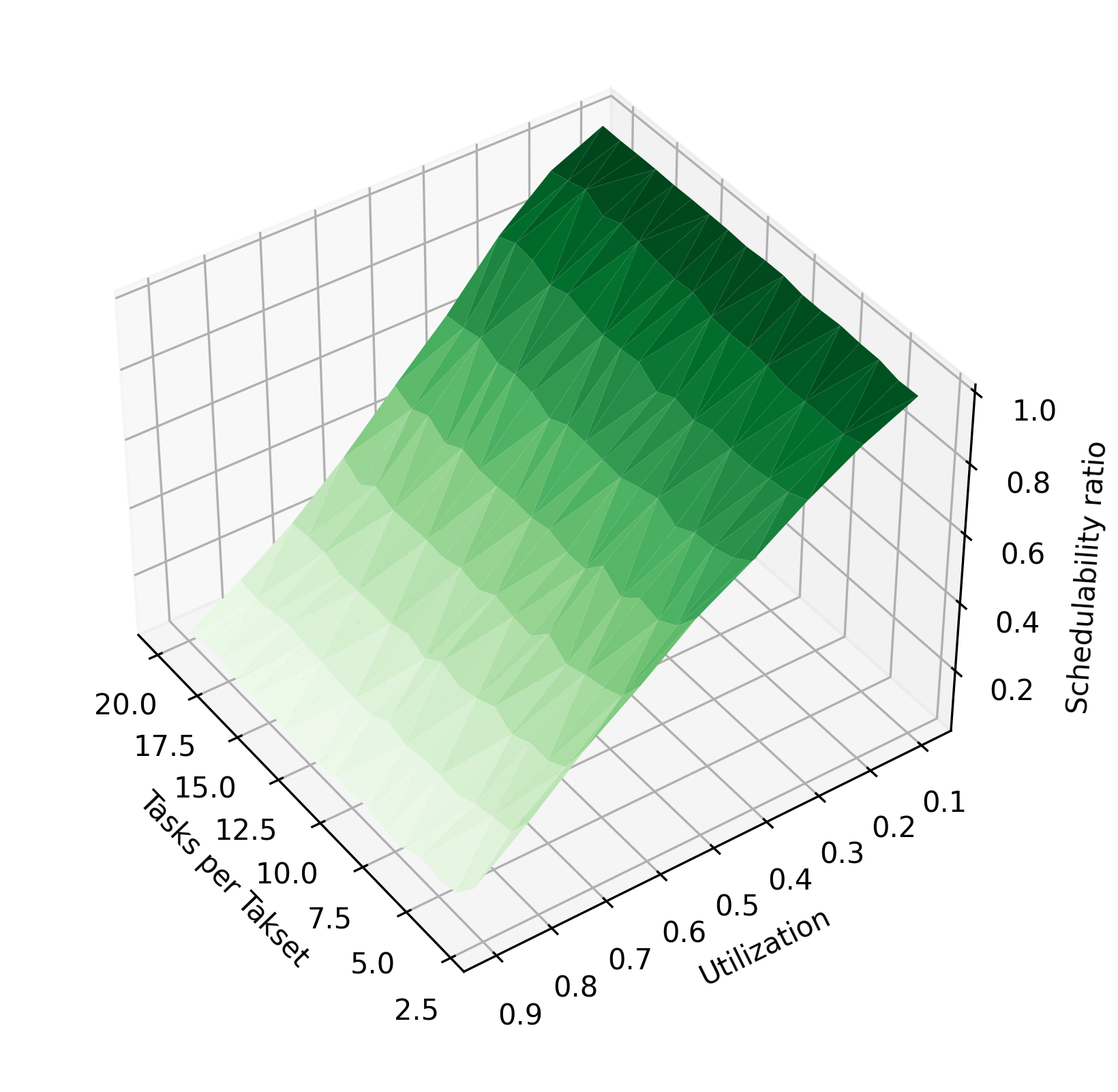
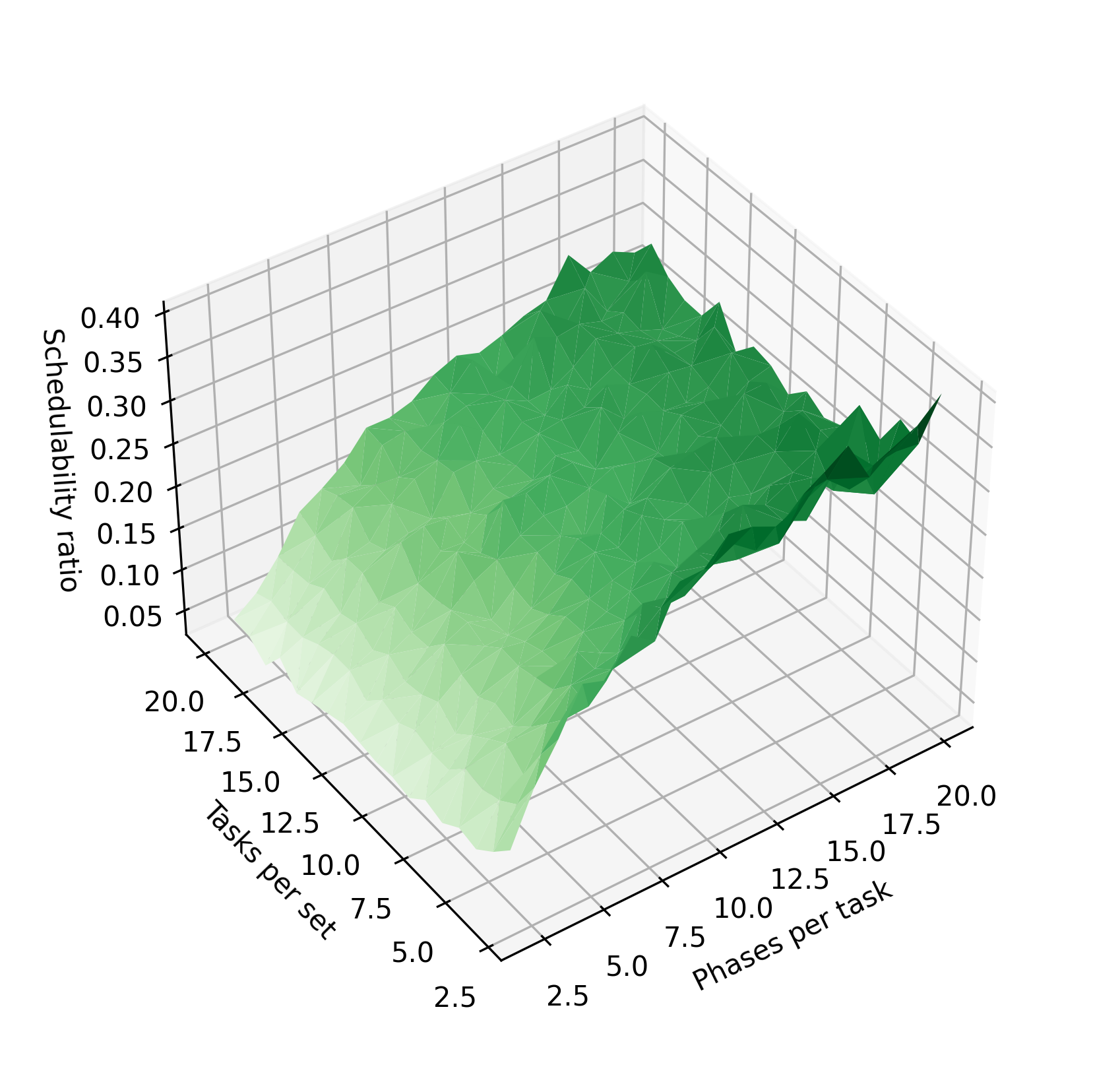
For completeness, we also evaluate the performance of the algorithm on a wider 1–1000 time unit period range, using both a uniform distribution of periods within this range, as well as the log-uniform distribution recommended in [19]. Figure 4 shows how the schedulability of these task sets compares to the tasksets with 10–30 unit periods. The schedulability of the sets with the wider period range is much lower; in particular, tasksets containing a task with a small period are less likely to be schedulable. We hypothesize that this is due to these high-frequency tasks having less ability to expand their execution time as preemption points are inserted. This trend is also apparent in Figure 5; unlike tasks with 10–30 unit periods, increasing the number of tasks increases the probability of generating a high-frequency task and therefore causes the schedulability ratio to decrease.


Schedulability of Constrained-Deadline Systems.
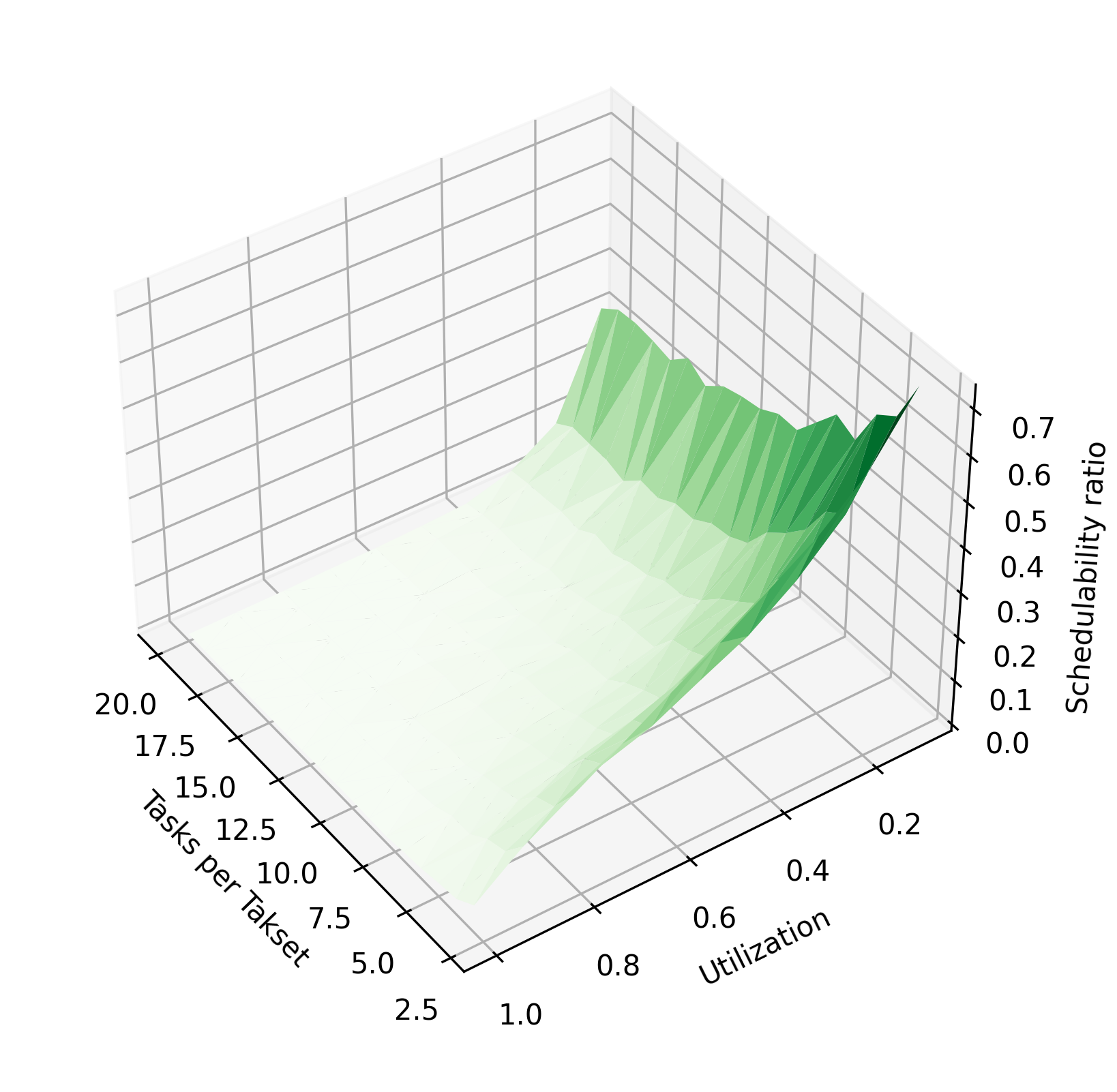
Figure 6 shows the schedulability ratio for each of the three scheduling algorithms on constrained-deadline tasksets, in which all other task parameters follow the same configuration as Figure 2. In a constrained-deadline system, the chains algorithm is also able to obtain a schedulability improvement over a phase NP approach, by inserting additional preemption points to reduce the blocking time. As the tasks in these systems have shorter deadlines than the implicit-deadline systems, all three algorithms obtain a lower schedulability ratio.
The right column of Figure 3 shows the effect of varying different taskset parameters for the constrained-deadline task sets, which otherwise have the same parameter configurations as the implicit-deadline systems. For constrained-deadline tasks, the schedulability ratio is generally lower, and the effect of increasing the phase count is smaller. Increasing the number of tasks has only a very small effect on the schedulability ratio. We hypothesize that, although increasing the task count still tends to reduce the system’s blocking times, it also increases the probability that one or more tasks will have a tightly-constrained deadline, which reduces the chance that the system will be schedulable.

6.3 Runtime Performance
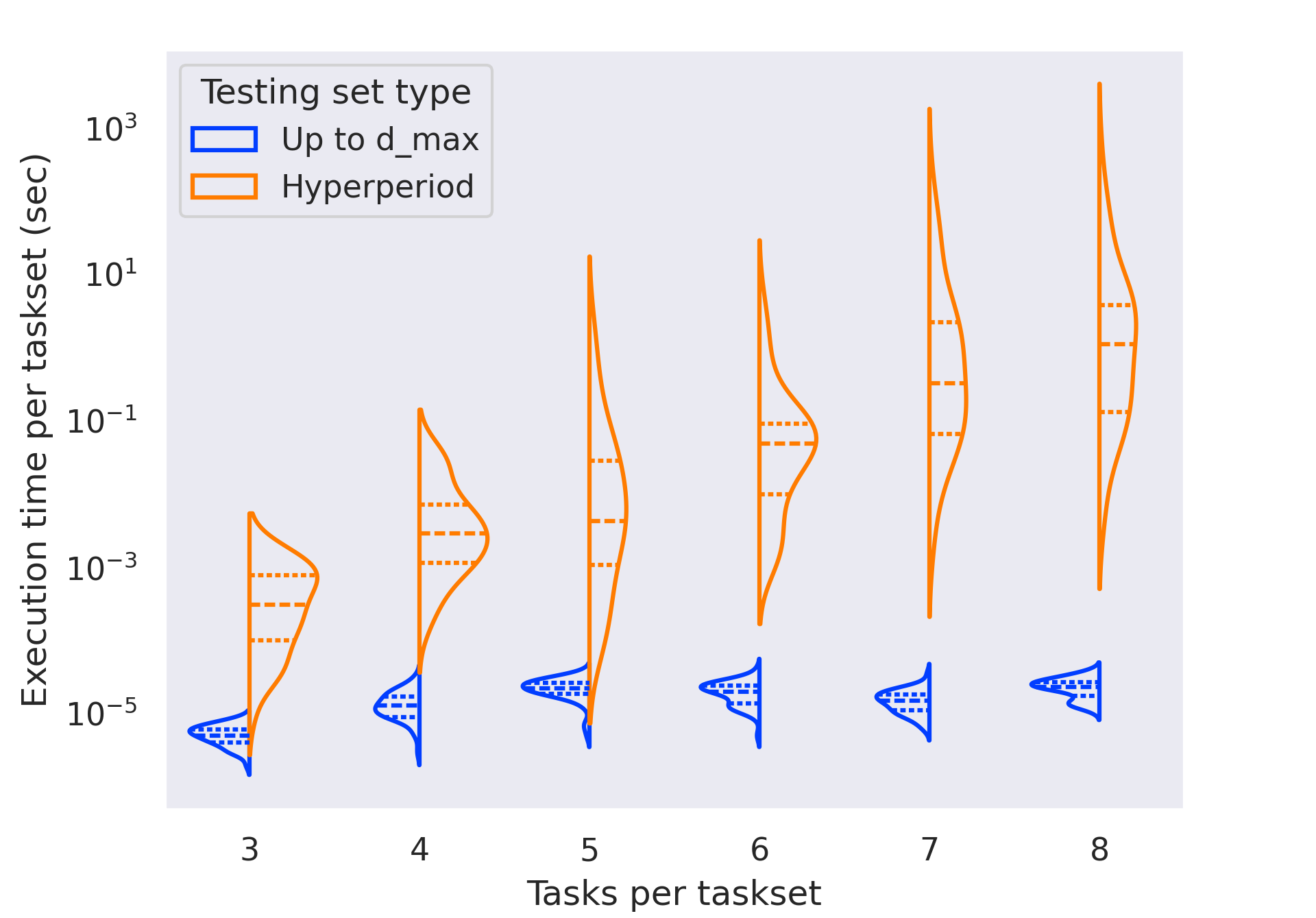
The implementation of the algorithm in our prior work [3] could only evaluate sets of a few tasks in a reasonable amount of time. In this work, we rewrite the original Python-based simulation using C++, and correct an implementation issue with the original construction of the hyperperiod-bounded testing set. These changes lead to significant performance improvements on their own. In Figure 7 we randomly generate and test 50 task sets with either 3 or 4 tasks each; the original implementation is compared to the rewritten one, which is configured to test points in the full, exponentially-sized testing set. For sets of 3 tasks, the median execution time improves by approximately and the mean execution time improves by around . For sets of 4 tasks, the median improves by around and the mean execution time by more than . These improvements enable testing larger task sets, as shown in the following sections.
In this work, we also introduce an optimization for implicit-deadline task systems that allows us to avoid testing timepoints past . In Figure 9, we analyze the impact of this optimization. Using the full, exponential testing set from the prior work, our implementation is able to test tasksets with 6 tasks in only a few seconds, but the time needed still scales exponentially with the number of tasks; past eight tasks per set, the analysis once again takes an unreasonable amount of time to run. Using the optimization for implicit-deadline systems, evaluating schedulability is orders of magnitude faster, and the evaluation times also become more consistent for each taskset. This optimization allows us to determine the schedulability ratio for systems of up to 20 tasks, the results of which are displayed in Figure 3. As the time needed to determine schedulability now scales much more slowly with respect to the number of tasks, we believe that evaluating even larger task sets is also possible.
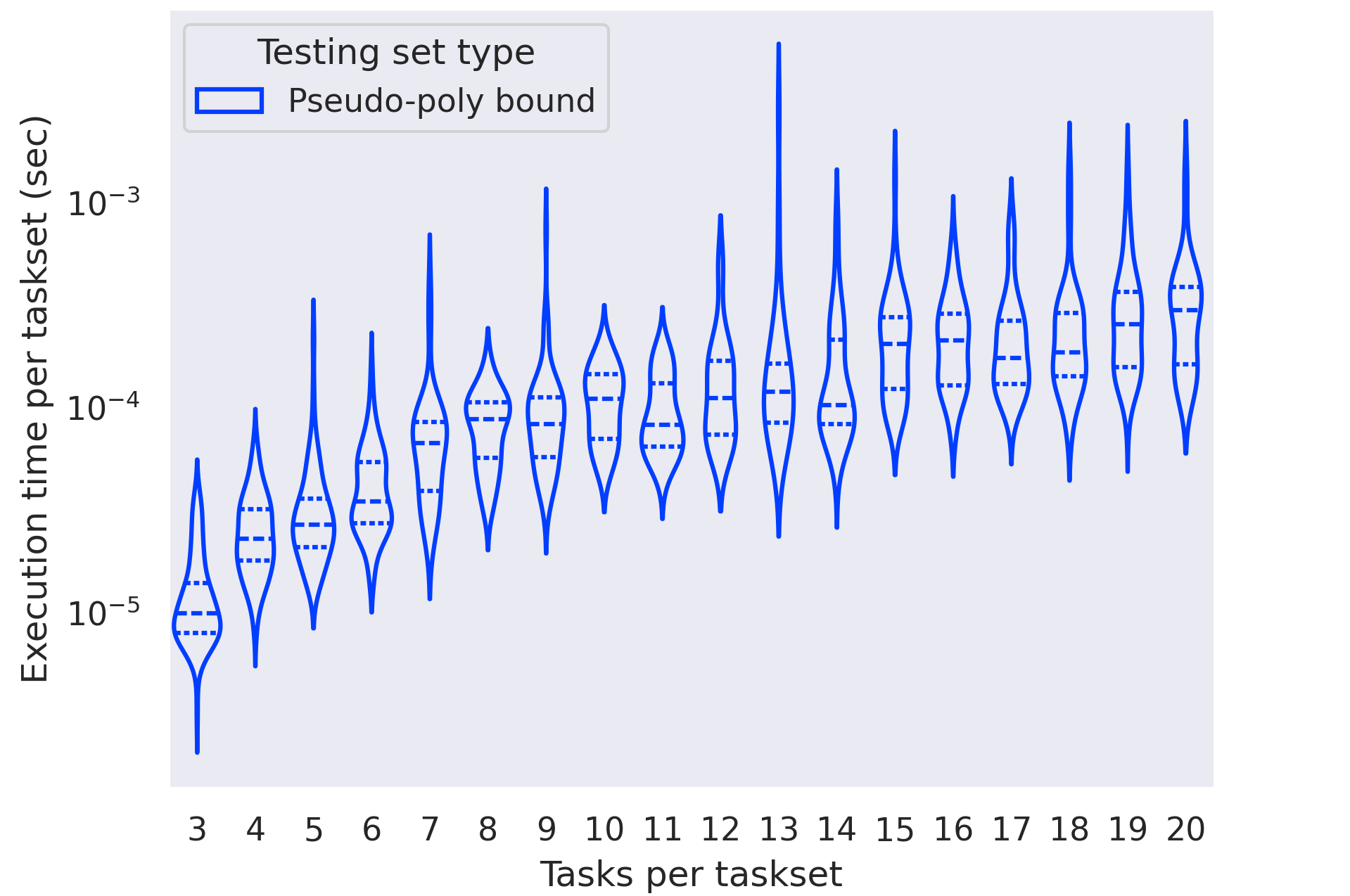
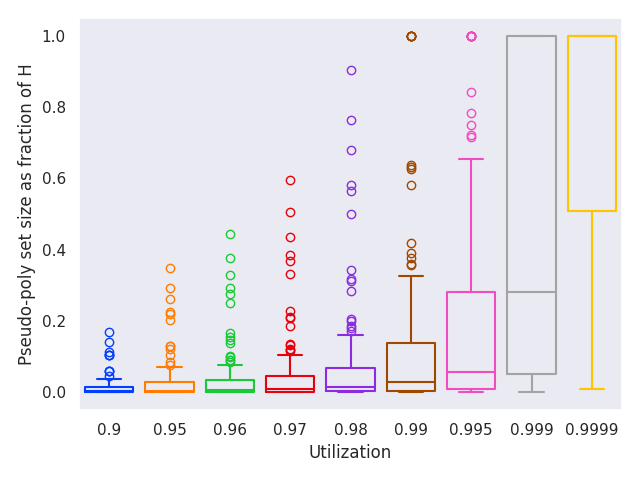
In Figure 9, we evaluate the performance of determining schedulability of constrained-deadline task sets using the pseudo-polynomial bound on the testing set identified in [7]. Compared to the full hyperperiod testing set, running the evaluation with this testing set is much faster. However, we note that it is still slower than the optimized implicit-deadline bound from Figure 9. Moreover, the distribution of execution times exhibits high variability. Perhaps most importantly, our evaluation is on task sets where , at which the pseudo-polynomial bound is still reasonably small. As shown in Figure 10, when , the size of the pseudo-polynomial set approaches the hyperperiod set, and it becomes increasingly less feasible to iterate over the entire testing set.
7 Related Work
The trade-off between security and timing constraints in real-time, IoT, and edge computing environments is crucial as it involves balancing robust security measures with the need for real-time performance. Several studies have explored these trade-offs. For instance, Leonardi et al. [22] and Lemieux-Mack et al [21] present mixed-integer linear programming approaches to optimize security and schedulability in real-time embedded systems under cyber-attacks. Wang et al. [40] consider the trade-off between security and overhead for pointer integrity checks. These papers attempt to maximize security without overloading the target system, but do not consider preemption-related overhead induced by the startup/teardown costs of the selected security mechanisms.
Limited-preemption scheduling, surveyed in 2013 by Buttazzo et al. [13], balances the increased blocking times of non-preemptive execution with the increased overheads caused by context switching. The original models of Baruah and Bertogna minimize context switching by finding the longest time each task may execute non-preemptively without compromising schedulability [4, 9], but do not account for the worst-case overhead due to the resulting preemptions.
Later approaches account for both blocking time and preemption overheads by defining instants that preemption can occur during task execution (called preemption points) to guarantee schedulability. In [10], Bertogna et al. develop an algorithm to find preemption points for tasks scheduled with EDF under the assumption that the preemption overhead for each task is constant. In contrast, in our MPS task model, individual task phases have unique preemption costs. A similar model to that of [10], but for fixed-priority (FP) scheduling, again with constant preemption overheads for each task, was developed by Yao et al. in [43].
In [11], Bertogna et al. model tasks as sequences of “basic blocks,” and present algorithms for selecting preemption points between those blocks for both EDF and FP scheduling. Although less flexible than the earlier “floating” preemption point models where a preemption point can be placed anywhere, that model allows different preemption costs between blocks. The latter is similar to the algorithm in [10], but supports domain-specific preemption costs rather than a constant overhead per task.
8 Conclusions
We believe that the concurrent consideration of timing and security properties within a single unified framework is an effective means of extending the rigorous approach of real-time scheduling theory to guaranteeing appropriately-articulated security properties in resource-constrained embedded systems. In real-time scheduling theory, pre run-time verification of timing correctness is performed using models of run-time behavior; these models are carefully crafted for specific purposes: e..g, the sporadic task model [7] has been designed to represent recurrent processes for which it is safe to assume a minimum duration between successive invocations and for which timing correctness is defined as the ability to meet all deadlines.
In this work, as in [3], we have extended the sporadic task model in a security-cognizant manner, to deal with a particular kind of security-cognizant workload model. For the specific model that we have proposed, we have developed algorithms that are able to provide provable correctness of both the timing and the security properties that are considered.
In this extension to our original work in [3], we have corrected the long-standing condition of Baruah and Bertogna [4, 9] for EDF schedulability of limited-preemption tasks. Leveraging this, we reduced the execution time complexity of our algorithm, and demonstrated that in an implicit-deadline task system, it can run quickly even for large numbers of tasks.
We note that the improvements made to the algorithm in this extension also apply to the generalization of the model to conditional code that we presented in [3]. In an already-published extension to that work [38], we further improve on the conditional execution model by removing the assumption that startup/teardown costs are paid at every phase transition and analyze its performance.
The complexity improvements made in this extension, in combination with a more efficient implementation of the algorithm, allowed us to evaluate larger and more complex task systems. We have also illustrated the scaling properties of the algorithm’s execution time for both constrained- and implicit-deadline systems, and shown how its ability to schedule tasks is affected by varying their properties. Finally, we have clarified several details of our algorithm and have provided a more complete demonstration of the improved schedulability offered by our algorithm over a phase or fully non-preemptive approach.
Although the work described in this manuscript arose out of our related projects in embedded systems security, we emphasize that we are not claiming that our algorithms solve any security problems; rather, they solve a scheduling problem that may arise from a class of security problems for which an adequate protective response gives rise to execution environments with bounded-cost startup/teardown operations. As future work, we intend to evaluate these scheduling models in conjunction with real-world attack/defense models.
On the other hand, we believe that our results are relevant beyond just security considerations: that they may, in fact, be considered to be further contributions to the real-time scheduling theory literature dealing with limited-preemption scheduling. They may also be extended to other limited-preemption scheduling frameworks, e.g., for multi-core platforms.
References
- [1] N. C. Audsley, A. Burns, R. I. Davis, K. W. Tindell, and A. J. Wellings. Fixed priority preemptive scheduling: An historical perspective. Real-Time Systems, 8:173–198, 1995. doi:10.1007/BF01094342.
- [2] Mohammad Fakhruddin Babar and Monowar Hasan. DeeptrustˆRT: Confidential deep neural inference meets real-time! In Rodolfo Pellizzoni, editor, 36th Euromicro Conference on Real-Time Systems, ECRTS 2024, July 9-12, 2024, Lille, France, volume 298 of LIPIcs, pages 13:1–13:24. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2024. doi:10.4230/LIPIcs.ECRTS.2024.13.
- [3] Sanjoy Baruah, Thidapat Chantem, Nathan Fisher, and Fatima Raadia. A scheduling model inspired by security considerations. In 2023 IEEE 26th International Symposium on Real-Time Distributed Computing (ISORC), pages 32–41, 2023. doi:10.1109/ISORC58943.2023.00016.
- [4] Sanjoy K. Baruah. The limited-preemption uniprocessor scheduling of sporadic task systems. In 17th Euromicro Conference on Real-Time Systems (ECRTS 2005), 6-8 July 2005, Palma de Mallorca, Spain, Proceedings, pages 137–144. IEEE Computer Society, 2005. doi:10.1109/ECRTS.2005.32.
- [5] Sanjoy K. Baruah. Security-cognizant real-time scheduling. In 25th IEEE International Symposium On Real-Time Distributed Computing, ISORC 2022, Västerås, Sweden, May 17-18, 2022, pages 1–9. IEEE, 2022. doi:10.1109/ISORC52572.2022.9812766.
- [6] Sanjoy K. Baruah and Nathan Fisher. Choosing preemption points to minimize typical running times. In Proceedings of the 27th International Conference on Real-Time Networks and Systems, RTNS 2019, Toulouse, France, November 06-08, 2019, RTNS ’19, pages 198–208, New York, NY, USA, 2019. Association for Computing Machinery. doi:10.1145/3356401.3356407.
- [7] Sanjoy K. Baruah, Aloysius K. Mok, and Louis E. Rosier. Preemptively scheduling hard-real-time sporadic tasks on one processor. In Proceedings of the Real-Time Systems Symposium - 1990, Lake Buena Vista, Florida, USA, December 1990, pages 182–190, Orlando, Florida, 1990. IEEE Computer Society. doi:10.1109/REAL.1990.128746.
- [8] Sanjoy K Baruah, Louis E Rosier, and Rodney R Howell. Algorithms and complexity concerning the preemptive scheduling of periodic, real-time tasks on one processor. Real-Time Syst., 2(4):301–324, November 1990. doi:10.1007/BF01995675.
- [9] Marko Bertogna and Sanjoy K. Baruah. Limited preemption EDF scheduling of sporadic task systems. IEEE Trans. Ind. Informatics, 6(4):579–591, 2010. doi:10.1109/TII.2010.2049654.
- [10] Marko Bertogna, Giorgio Buttazzo, Mauro Marinoni, Gang Yao, Francesco Esposito, and Marco Caccamo. Preemption Points Placement for Sporadic Task Sets. In 2010 22nd Euromicro Conference on Real-Time Systems, pages 251–260, 2010. doi:10.1109/ECRTS.2010.9.
- [11] Marko Bertogna, Orges Xhani, Mauro Marinoni, Francesco Esposito, and Giorgio Buttazzo. Optimal selection of preemption points to minimize preemption overhead. In 2011 23rd Euromicro Conference on Real-Time Systems, pages 217–227. IEEE, 2011. doi:10.1109/ECRTS.2011.28.
- [12] Enrico Bini and Giorgio C Buttazzo. Measuring the performance of schedulability tests. Real-Time Systems, 30(1-2), 2005. doi:10.1007/s11241-005-0507-9.
- [13] Giorgio C Buttazzo, Marko Bertogna, and Gang Yao. Limited preemptive scheduling for real-time systems. a survey. IEEE Trans. Industr. Inform., 9(1):3–15, February 2013. doi:10.1109/TII.2012.2188805.
- [14] John Cavicchio and Nathan Fisher. Integrating preemption thresholds with limited preemption scheduling. In 2020 IEEE 26th International Conference on Embedded and Real-Time Computing Systems and Applications (RTCSA). IEEE, August 2020. doi:10.1109/RTCSA50079.2020.9203646.
- [15] Friedrich Eisenbrand and Thomas Rothvoß. EDF-schedulability of synchronous periodic task systems is coNP-hard. In Moses Charikar, editor, Proceedings of the Twenty-First Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2010, Austin, Texas, USA, January 17-19, 2010, pages 1029–1034. SIAM, January 2010. doi:10.1137/1.9781611973075.83.
- [16] Pontus Ekberg. Models and Complexity Results in Real-Time Scheduling Theory. PhD thesis, Uppsala University, Sweden, 2015. URL: https://nbn-resolving.org/urn:nbn:se:uu:diva-267017.
- [17] Pontus Ekberg and Wang Yi. Uniprocessor feasibility of sporadic tasks remains conp-complete under bounded utilization. In 2015 IEEE Real-Time Systems Symposium, RTSS 2015, San Antonio, Texas, USA, December 1-4, 2015, pages 87–95. IEEE Computer Society, 2015. doi:10.1109/RTSS.2015.16.
- [18] Pontus Ekberg and Wang Yi. Uniprocessor feasibility of sporadic tasks with constrained deadlines is strongly conp-complete. In 27th Euromicro Conference on Real-Time Systems, ECRTS 2015, Lund, Sweden, July 8-10, 2015, pages 281–286. IEEE Computer Society, 2015. doi:10.1109/ECRTS.2015.32.
- [19] P. Emberson, R. Stafford, and R.I. Davis. Techniques for the synthesis of multiprocessor tasksets. In WATERS workshop at the Euromicro Conference on Real-Time Systems, pages 6–11, July 2010. 1st International Workshop on Analysis Tools and Methodologies for Embedded and Real-time Systems ; Conference date: 06-07-2010.
- [20] Ke Jiang, Adrian Alin Lifa, Petru Eles, Zebo Peng, and Wei Jiang. Energy-aware design of secure multi-mode real-time embedded systems with FPGA co-processors. In Michel Auguin, Robert de Simone, Robert I. Davis, and Emmanuel Grolleau, editors, 21st International Conference on Real-Time Networks and Systems, RTNS 2013, Sophia Antipolis, France, October 17-18, 2013, pages 109–118. ACM, October 2013. doi:10.1145/2516821.2516830.
- [21] Cailani Lemieux-Mack, Kevin Leach, Ning Zhang, Sanjoy Baruah, and Bryan C Ward. Optimizing runtime security in real-time embedded systems. In Proc. of Workshop on Optimization for Embedded and Real-time Systems (OPERA), December 2024.
- [22] Sandro Di Leonardi, Federico Aromolo, Pietro Fara, Gabriele Serra, Daniel Casini, Alessandro Biondi, and Giorgio C. Buttazzo. Maximizing the security level of real-time software while preserving temporal constraints. IEEE Access, 11:35591–35607, 2023. doi:10.1109/ACCESS.2023.3264671.
- [23] M. Lin, L. Xu, L.T. Yang, X. Qin, N. Zheng, Z. Wu, and M. Qiu. Static security optimization for real-time systems. IEEEII, 5(1):22–37, February 2009. doi:10.1109/TII.2009.2014055.
- [24] C. Liu and J. Layland. Scheduling algorithms for multiprogramming in a hard real-time environment. Journal of the ACM, 20(1):46–61, 1973. doi:10.1145/321738.321743.
- [25] Yin Liu, Siddharth Dhar, and Eli Tilevich. Only pay for what you need: Detecting and removing unnecessary TEE-based code. Journal of Systems and Software, 188:111253, 2022. Publisher: Elsevier. doi:10.1016/j.jss.2022.111253.
- [26] Yue Ma, Wei Jiang, Nan Sang, and Xia Zhang. ARCSM: A distributed feedback control mechanism for security-critical real-time system. In 10th IEEE International Symposium on Parallel and Distributed Processing with Applications, ISPA 2012, Leganes, Madrid, Spain, July 10-13, 2012, pages 379–386. IEEE Computer Society, July 2012. doi:10.1109/ISPA.2012.56.
- [27] Filip Markovic, Jan Carlson, Radu Dobrin, Bjorn Lisper, and Abhilash Thekkilakattil. Probabilistic response time analysis for fixed preemption point selection. In 2018 IEEE 13th International Symposium on Industrial Embedded Systems (SIES), pages 1–10, 2018. doi:10.1109/SIES.2018.8442099.
- [28] Filip Marković, Jan Carlson, and Radu Dobrin. Cache-aware response time analysis for real-time tasks with fixed preemption points. In 2020 IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS), pages 30–42, 2020. doi:10.1109/RTAS48715.2020.00-19.
- [29] Jonathan M McCune, Bryan J Parno, Adrian Perrig, Michael K Reiter, and Hiroshi Isozaki. Flicker: An execution infrastructure for TCB minimization. In Proceedings of the 3rd ACM SIGOPS/EuroSys European Conference on Computer Systems 2008, pages 315–328, 2008. doi:10.1145/1352592.1352625.
- [30] Tanmaya Mishra, Thidapat Chantem, and Ryan M. Gerdes. Teecheck: Securing intra-vehicular communication using trusted execution. In 28th International Conference on Real Time Networks and Systems, RTNS 2020, Paris, France, June 10, 2020, RTNS 2020, pages 128–138, New York, NY, USA, 2020. Association for Computing Machinery. doi:10.1145/3394810.3394822.
- [31] Sibin Mohan, Man Ki Yoon, Rodolfo Pellizzoni, and Rakesh Bobba. Real-time systems security through scheduler constraints. In Proceedings of the 2014 Agile Conference, AGILE ’14, pages 129–140, 2014. doi:10.1109/ECRTS.2014.28.
- [32] Anway Mukherjee, Tanmaya Mishra, Thidapat Chantem, Nathan Fisher, and Ryan M. Gerdes. Optimized trusted execution for hard real-time applications on COTS processors. In Proceedings of the 27th International Conference on Real-Time Networks and Systems, RTNS 2019, Toulouse, France, November 06-08, 2019, RTNS ’19, pages 50–60, New York, NY, USA, 2019. Association for Computing Machinery. doi:10.1145/3356401.3356419.
- [33] M. Nasri, T. Chantem, G. Bloom, and R. M. Gerdes. On the pitfalls and vulnerabilities of schedule randomization against schedule-based attacks. In 2019 IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS), pages 103–116, April 2019. doi:10.1109/RTAS.2019.00017.
- [34] Mitra Nasri, Geoffrey Nelissen, and Gerhard Fohler. A new approach for limited preemptive scheduling in systems with preemption overhead. In 28th Euromicro Conference on Real-Time Systems, ECRTS 2016, Toulouse, France, July 5-8, 2016, pages 25–35. IEEE Computer Society, July 2016. doi:10.1109/ECRTS.2016.15.
- [35] OP-TEE. URL: https://www.trustedfirmware.org/projects/op-tee/.
- [36] OP-TEE Documentation: Core: Pager. URL: https://optee.readthedocs.io/en/latest/architecture/core.html#pager.
- [37] Miroslav Pajic, Nicola Bezzo, James Weimer, Rajeev Alur, Rahul Mangharam, Nathan Michael, George J. Pappas, Oleg Sokolsky, Paulo Tabuada, Stephanie Weirich, and Insup Lee. Towards synthesis of platform-aware attack-resilient control systems. In Linda Bushnell, Larry Rohrbough, Saurabh Amin, and Xenofon D. Koutsoukos, editors, 2nd ACM International Conference on High Confidence Networked Systems (part of CPS Week), HiCoNS 2013, Philadelphia, PA, USA, April 9-11, 2013, pages 75–76. ACM, April 2013. doi:10.1145/2461446.2461457.
- [38] Fatima Raadia, Nathan Fisher, Thidapat Chantem, and Sanjoy Baruah. An improved security-cognizant scheduling model. In 2024 IEEE 27th International Symposium on Real-Time Distributed Computing (ISORC), pages 1–8. IEEE, 2024. doi:10.1109/ISORC61049.2024.10551349.
- [39] Jinwen Wang, Ao Li, Haoran Li, Chenyang Lu, and Ning Zhang. Rt-tee: Real-time system availability for cyber-physical systems using arm trustzone. In 2022 IEEE Symposium on Security and Privacy (SP), pages 352–369. IEEE, 2022. doi:10.1109/SP46214.2022.9833604.
- [40] Yujie Wang, Cailani Lemieux-Mack, Thidapat Chantem, Sanjoy Baruah, Ning Zhang, and Bryan C Ward. Partial context-sensitive pointer integrity for real-time embedded systems. In 2024 IEEE Real-Time Systems Symposium (RTSS), pages 415–426. IEEE Computer Society, 2024. doi:10.1109/RTSS62706.2024.00042.
- [41] T. Xie and X. Qin. Scheduling security-critical real-time applications on clusters. IEEE Transactions on Computers, 55(7):864–879, July 2006. doi:10.1109/TC.2006.110.
- [42] Gang Yao, Giorgio Buttazzo, and Marko Bertogna. Feasibility analysis under fixed priority scheduling with fixed preemption points. In 2010 IEEE 16th International Conference on Embedded and Real-Time Computing Systems and Applications, pages 71–80, 2010. doi:10.1109/RTCSA.2010.40.
- [43] Gang Yao, Giorgio Buttazzo, and Marko Bertogna. Feasibility analysis under fixed priority scheduling with limited preemptions. Real-Time Systems, 47(3):198–223, 2011. Publisher: Springer. doi:10.1007/s11241-010-9113-6.
- [44] Man-Ki Yoon, Sibin Mohan, Chien-Ying Chen, and Lui Sha. Taskshuffler: A schedule randomization protocol for obfuscation against timing inference attacks in real-time systems. In 2016 IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS), Vienna, Austria, April 11-14, 2016, pages 111–122. IEEE, IEEE Computer Society, 2016. doi:10.1109/RTAS.2016.7461362.
