Rule Learning over Knowledge Graphs: A Review

In this subsection, we introduce the basics of knowledge graphs and rules.

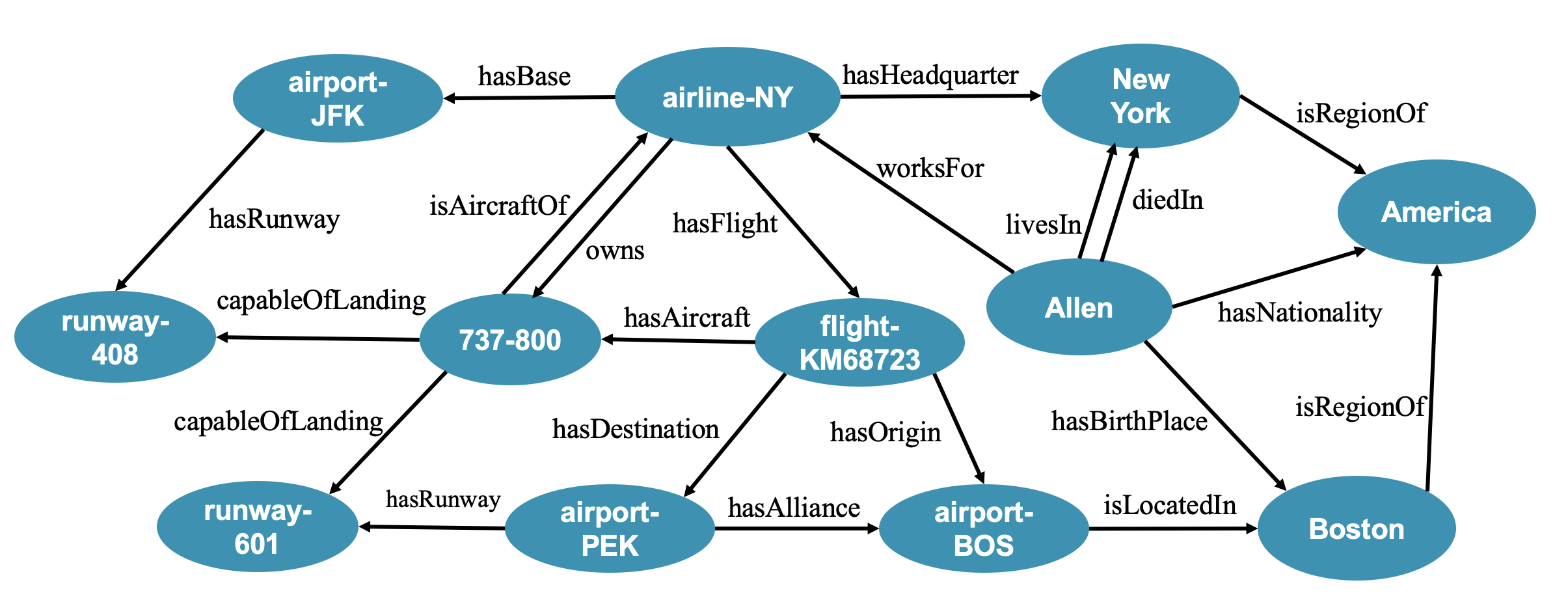
Knowledge graphs represent real-world entities, such as persons and places, and binary relations among them. A knowledge graph (KG) is often expressed as a set of triples of the form $(s,p,o)$, where entities $s$ and $o$ are called the subject and object of the triple, respectively, and $p$ is the relation. A KG is essentially a directed multi-relational graph by viewing the entity (the subjects and objects) as the vertices and a triple $(s,p,o)$ as an edge from $s$ to $o$ with the label $p$. For instance, a triple $(\mathrm{𝖺𝗂𝗋𝗅𝗂𝗇𝖾}\text{-}\mathrm{𝖭𝖸},\mathrm{𝗁𝖺𝗌𝖡𝖺𝗌𝖾},\mathrm{𝖺𝗂𝗋𝗉𝗈𝗋𝗍}\text{-}\mathrm{𝖩𝖥𝖪})$ describes that the two entities $\mathrm{𝖺𝗂𝗋𝗅𝗂𝗇𝖾}\text{-}\mathrm{𝖭𝖸}$ and $\mathrm{𝖺𝗂𝗋𝗉𝗈𝗋𝗍}\text{-}\mathrm{𝖩𝖥𝖪}$ are connected by the relation $\mathrm{𝗁𝖺𝗌𝖡𝖺𝗌𝖾}$. Following the convention in knowledge representation, a triple is also denoted as a fact $p(s,o)$.

Formally, let $ℰ$ and $𝒫$ be respectively the sets of entities and relations in a KG $𝒢$. For a relation $p$, $p^{-}$ denotes its inverse, i.e., triple $(\mathrm{𝗋𝗎𝗇𝗐𝖺𝗒}\text{-}\mathrm{𝟦𝟢𝟪},{\mathrm{𝗁𝖺𝗌𝖱𝗎𝗇𝗐𝖺𝗒}}^{-1},\mathrm{𝖺𝗂𝗋𝗉𝗈𝗋𝗍}\text{-}\mathrm{𝖩𝖥𝖪})$ is equivalent to $(\mathrm{𝖺𝗂𝗋𝗉𝗈𝗋𝗍}\text{-}\mathrm{𝖩𝖥𝖪},\mathrm{𝗁𝖺𝗌𝖱𝗎𝗇𝗐𝖺𝗒},\mathrm{𝗋𝗎𝗇𝗐𝖺𝗒}\text{-}\mathrm{𝟦𝟢𝟪})$. And ${𝒫}^{\ast }$ denotes the set of the relations and their inverse relations, i.e., $𝒫\cup \{p^{-}|p\in 𝒫\}$. In this paper, we consider the class of first-order Horn rules, which is sufficiently expressive for many practical applications in the Semantic Web and AI, and allows efficient reasoning algorithms. Moreover, in KGs, only binary and unary relations are considered. While a binary relation connects two entities, a unary relation represents a type (or class) of entities. In first-order logic, a relation is expressed as a predicate. Whenever no confusion is caused, we use these two terms alternatively.

A term is either an entity or a variable. If $p$ is a binary relation, $p(t_1,t_2)$ is an atom, where $t_1$ and $t_2$ are terms. Similarly, if $p$ is a unary relation, $p(t)$ is an atom, where $t$ is a term.

A first-order Horn rule $r$ is of the form

where $h,b_1,\mathrm{\dots },b_n$ are atoms. The atom $h$ is the head of $r$, denoted $head(r)$, and the conjunction of atoms $b_1,\mathrm{\dots },b_n$ is the body of $r$, denoted $body(r)$. Intuitively, the rule $r$ reads that if $b_1$, $\mathrm{\dots }$, and $b_n$ hold, then $h$ holds too. The length of the above rule body is $n$ (the number of body atoms in the rule).

Due to the enormous search space of first-order Horn rules over large KGs, existing rule learning approaches often adopt certain language biases to restrict the forms of rules to learn, such as constraining the maximum length of rules, to effectively reduce the search space. This enables the rule-learning algorithm to be more efficient and applicable in practical scenarios. These constraints strike a balance between the size of the search space and the expressiveness of rules.

A most common language bias is to learn rules that represent path patterns in KGs, that is, the class of closed-path (CP) rules [81, 51]. Intuitively, in a CP rule, the body atoms form a path from the subject to the object of the head atom (involving only variables not entities). Formally, a closed-path rule is of the form

where $p\in 𝒫,$ $p_i\in {𝒫}^{\ast }$ ($1\le i\le n$) and $x_j$’s ($0\le j\le n$) are variables. Note that CP rules allow recursion, i.e., the head predicate can occur in the body. The advantage of closed-path rules lies in their ability to capture specific and meaningful patterns in the data. These rules can reveal intricate dependencies, cyclic patterns, and sequential behaviours present in the data, providing deeper insights into the underlying associations. Focusing on CP rules reduces the search for candidate rules to the problem of path finding and ranking in KGs. This type of rules have been widely adopted by major rule learners [88, 25, 13, 51, 56].

As the class of CP rules is too limited for some applications, one way to expand the class of CP rules is to allow rules that are closed and connected. Two atoms in a rule are connected if they share a variable or an entity. A rule is connected if every atom in the rule is connected to another atom. A variable in a rule is closed if it appears at least twice in the rule. A rule is closed if all of its variables are closed.

To avoid learning rules with unrelated atoms, some methods, such as AMIE and its variants [24, 23, 37], require that the graphs of learned rules to be connected. In addition, to avoid having variables with existential quantifier in the rule head, a learned rule must be closed. For example, the rule $p_1(x_0,x_1)\wedge p_2(x_1,x_2)\to p(x_0,x_1)$ is connected but not closed, while the rule $p_1(x_0,x_1)\wedge p_2(x_2,x_2)\to p(x_0,x_1)$ is closed but not connected. By the definition, it is clear that a CP rule is both connected and closed, but not vice versa. For example, $p_1(x_0,x_1)\wedge p_2(x_1,x_2)\wedge p_3(x_0,x_1)\to p(x_0,x_2)$ is both connected and closed, but not a CP rule.

Another natural extension of CP rules is to allow unary predicates, i.e., classes (or types), in the rules [82]. Such a rule also describes a path pattern in the KG, but allows to specify the classes (or types) of the nodes on the paths. The rule $\mathrm{𝗉𝖾𝗋𝗌𝗈𝗇}(x_0)\wedge \mathrm{𝗁𝖺𝗌𝖡𝗂𝗋𝗍𝗁𝖯𝗅𝖺𝖼𝖾}(x_0,x_1)\wedge \mathrm{𝖼𝗂𝗍𝗒}(x_1)\wedge \mathrm{𝗂𝗌𝖱𝖾𝗀𝗂𝗈𝗇𝖮𝖿}(x_1,x_2)\wedge \mathrm{𝖼𝗈𝗎𝗇𝗍𝗋𝗒}(x_2)\to \mathrm{𝗁𝖺𝗌𝖭𝖺𝗍𝗂𝗈𝗇𝖺𝗅𝗂𝗍𝗒}(x_0,x_2)$ is a typed rule. It specifies the classes (types) of $x_0,x_1,x_2$ to be $\mathrm{𝖯𝖾𝗋𝗌𝗈𝗇},\mathrm{𝖢𝗂𝗍𝗒},\mathrm{𝖢𝗈𝗎𝗇𝗍𝗋𝗒}$.

Some rule learners can learn more expressive rules beyond first-order Horn rules, allowing negations [21, 31, 75], numeric values [54, 77], temporal values [52, 42], etc. Such extensions are useful for practical applications. Specifically, some approaches can learn rules that involve comparisons among numeric values, for example, $\mathrm{𝗁𝖺𝗌𝖡𝗂𝗋𝗍𝗁𝖸𝖾𝖺𝗋}(x,v_0)\wedge \mathrm{𝗁𝖺𝗌𝖡𝗂𝗋𝗍𝗁𝖸𝖾𝖺𝗋}(y,v_1)\wedge v_0>v_1\to \mathrm{𝗒𝗈𝗎𝗇𝗀𝖾𝗋}(x,y)$. This rule says if a person $x$ was born after another person $y$, then $x$ is younger than $y$. Here, the relation $\mathrm{𝗁𝖺𝗌𝖡𝗂𝗋𝗍𝗁𝖸𝖾𝖺𝗋}$ takes literal numbers as its object datatype. Some approaches focus on learning nonmonotonic rules (or negated rules) with negated atoms in the rule body, such as $\mathrm{𝖻𝗈𝗋𝗇𝖨𝗇}(x,y)\wedge \mathrm{𝐧𝐨𝐭}\mathrm{𝗂𝗆𝗆𝗂𝗀𝗋𝖺𝗍𝖾}(x,z)\to \mathrm{𝗅𝗂𝗏𝖾𝗌𝖨𝗇}(x,y)$ says that a person $x$ who was born in a place $y$ and is not known to have migrated to $z$ lives in $y$. Moreover, temporal rules can be learned over temporal KGs where every atom has a timestamp. For example, the rule $\mathrm{𝖻𝗈𝗋𝗇𝖨𝗇}(x,y,t)\to \mathrm{𝖽𝗂𝖾𝖽𝖨𝗇}(x,y,t+80)$ indicates that if a person $x$ born in city $y$ at timestamp $t$ usually die in the same place at time $t+80$.

The task of rule learning is to automatically extract a set of first-order logic Horn rules over a given KG. Formally, given a KG $𝒢$, a rule learning system, a.k.a. rule learner, learns a set of rules $r$ of the form $b_1\wedge \mathrm{\dots }\wedge b_n\to h$ with a confidence degree $0\le {\alpha }_r\le 1$ associated with each rule $r$. The relations and (possibly) entities in $r$ are from $𝒢$, and $r$ is considered plausible if there are many instances of $r$ obtained by substituting the variables in $r$ with entities in $𝒢$, such that the atoms in these instances are facts occurring in the KG $𝒢$. The more such instances exist the more plausible $r$ is. The confidence degree ${\alpha }_r$ is calculated to reflect the plausibility of $r$, i.e., the more plausible $r$ is the higher ${\alpha }_r$ should be.

Rule learning involves both learning the rule structures and estimating their plausibility. For example, in traditional Inductive Logic Programming, rule structure learning is achieved by systematically exploring the rule space by adding, updating, or deleting atoms at a time in the rule bodies. Rule plausibility is measured via example coverage by the set of learned rules. That is, given two sets of positive examples (true facts in the data) and negative examples (false or absent facts), the rule learner aims to induce a set of rules that cover as many positive examples and as few negative examples as possible. Yet, due to the large sizes and the lack of negative examples in KGs, the traditional ILP methods of traversing rule space for structure learning and measuring example coverage for plausibility estimation are not directly applicable to KGs.

To handle the large sizes, complexity, incompleteness and dynamics of KGs, many novel and efficient rule learners have been developed. We classify them by two dimensions as shown in Figure 2, according to their structure learning and confidence measure methods.

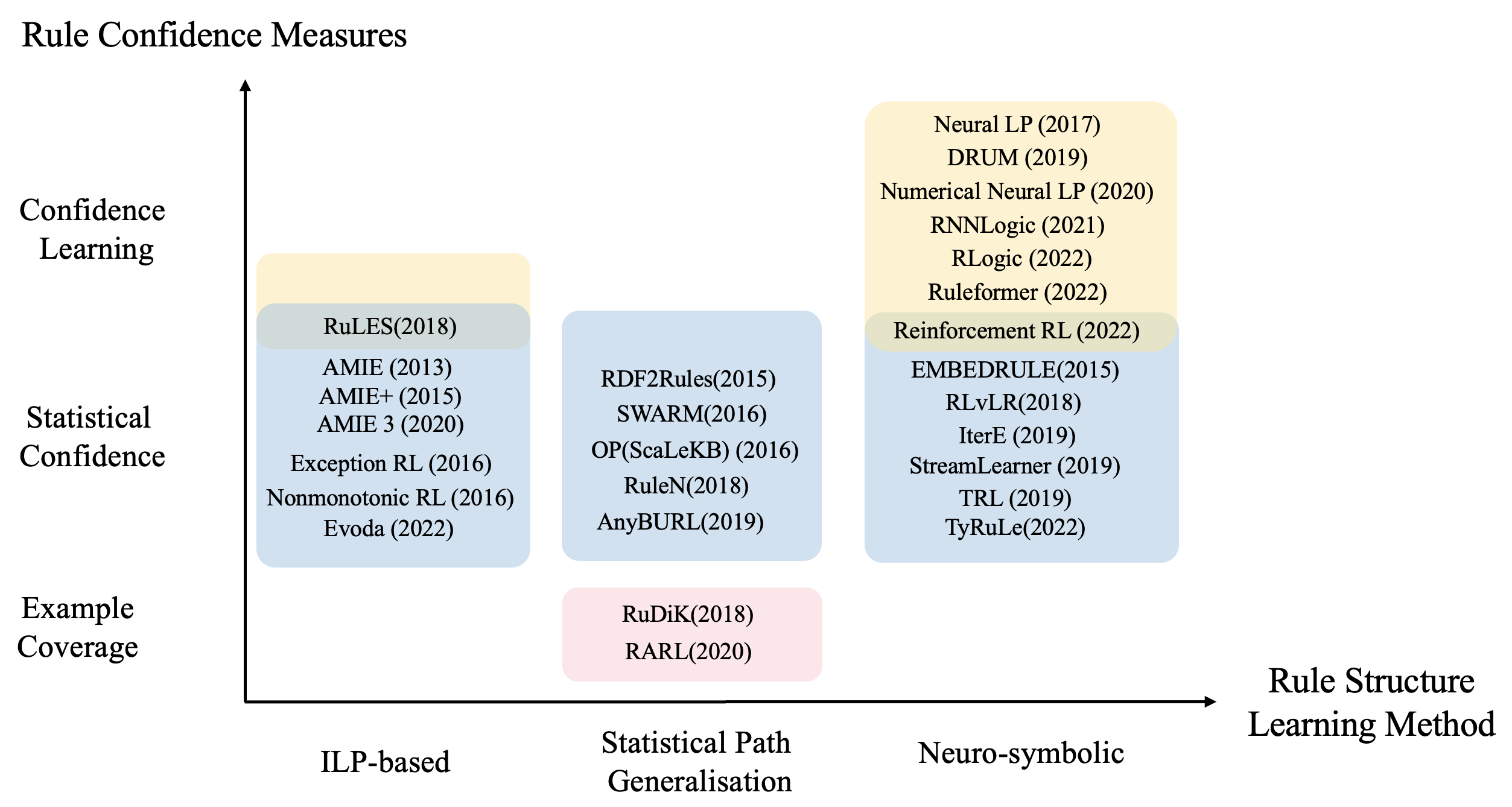
According to the rule structure learning methods, we can broadly categorise existing methods into three groups: the inductive logic programming (ILP)-based approaches, which use refinement operators to guide the search in the rule space, the statistical path generalisation methods, which extract frequent patterns from sampled paths or sub-graphs of the KGs, and the neuro-symbolic approaches, which directly or indirectly utilise neural networks to learn rules. We will introduce these three groups of methods with their representative works in Sections 3, 4, and 5.

According to the confidence measures, we classify the existing methods into three groups: the example coverage measures, which are in the same spirit as ILP approaches, by generating negative examples from KGs via a form of closed world assumption; the statistical confidence measures, which adapt statistical measures from association rule mining to address the lack of negative examples; and the confidence learning approaches, which learn confidence degrees as parameters of some neural networks. We will discuss these confidence measures in further detail in the remainder of this section.

Generally speaking, earlier works on KG rule learning are mostly ILP-based or statistical path generalisation methods, while most recent ones are largely neuro-symbolic methods. Statistic confidence measures are the most widely used, as they do not rely on the existence of negative examples and have better interpretability, i.e., statistical meanings. While confidence learning is only adopted by neuro-symbolic methods, example coverage measures have also been employed in statistical path generalisation methods. Interestingly, we have not found an ILP-based rule learner for KGs that adopts the example coverage measure which originates from ILP.

Rule confidence measures play a crucial role in rule learning, as they indicate the plausibility of the learned rules, and the accuracy of such measures is critical for downstream tasks based on the learned rules. There are three main approaches for rule confidence measures, example coverage, statistical, and confidence learning measures.

As traditional ILP methods cannot handle rule learning due to the scale of search space and the lack of negative examples, recent ILP-based rule learners such as AMIE [24, 23, 37] tackle these challenges in rule learning over KGs by employing certain language biases and new confidence measures adapted form association rule mining. AMIE, especially its extension AMIE+ [23] is one of the earliest and most widely referenced KG rule learners.

To reduce the search space, AMIE learns connected and closed rules. The rule structure learning process of AMIE is a standard ILP top-down search to explore the rule search space. Top-down rule search starts with a general rule and then refines it by progressively adding more atoms. Based on defined refinement operators, such as adding atoms to make the rule closed and connected, it iteratively expands rules. Instead of using standard confidence (SC), AMIE calculates rule confidence under partial completeness assumption (PCA). If the rule satisfies the confidence measure thresholds, the rule is selected as a candidate rule.

AMIE+ and AMIE 3 [37] are the extensions of AMIE with a series of improvements and optimisations that allow the system to run over large-scale KGs. Specifically, AMIE+ speeds up the rule refinement phase for specific kinds of rules, simplifies the query of support, and approximates the PCA computations by an upper bound; AMIE 3 utilises an in-memory database and parallel computation to store and process large-scale KGs.

Some other rule learning methods use enhanced refinement operators for rule search. For example, Evoda [84] uses a Genetic Logic Programming algorithm that is combined with Evolutionary Algorithms (EA) to define refinement operators. Hence, three rule transformation operators are proposed, mutation, crossover and selection. This allows Evoda to learn rules that are not necessarily closed, e.g., it can learn a rule like $\mathrm{𝗈𝗐𝗇𝗌}(x_0,x_1)\wedge \mathrm{𝖼𝖺𝗉𝖺𝖻𝗅𝖾𝖮𝖿𝖫𝖺𝗇𝖽𝗂𝗇𝗀}(x_1,x_2)\to \mathrm{𝗂𝗌𝖠𝗂𝗋𝖼𝗋𝖺𝖿𝗍𝖮𝖿}(x_1,x_0)$, which says if $x_0$ owns $x_1$ that can land on $x_2$, then $x_1$ may be the aircraft of the airline $x_0$. Evoda also adopts the PCA measure for rule confidence estimation.

Some other approaches address the lack of negative examples by generating them, this is particularly necessary for learning rules with negations, traditionally known as nonmonotonic logic programs [33, 64]. Such rules can express a form of exceptions and support nonmonotonic reasoning.

Exception-Enriched Rule Learning [21] is an ILP-based method that refines learned Horn rules by adding negated atoms (i.e., exceptions) into their rule bodies. They primarily focus on mining rules over unary predicates, by converting binary predicates into multiple unary ones. For example, the binary predicate $\mathrm{𝗁𝖺𝗌𝖮𝗋𝗂𝗀𝗂𝗇}(\cdot ,\cdot )$ can be translated into several unary ones like $\mathrm{𝗁𝖺𝗌𝖮𝗋𝗂𝗀𝗂𝗇𝖯𝖤𝖪}(\cdot )$ and $\mathrm{𝗁𝖺𝗌𝖮𝗋𝗂𝗀𝗂𝗇𝖡𝖮𝖲}(\cdot )$. This is because unary predicates are easier to search for negated atoms. But this makes KG a flattened representation containing just unary facts. To overcome this problem, Nonmonotonic Relational Learning [75] extends [21] to learn exception rules with binary predicates in KGs.

The lack of negative examples is essentially related to the incompleteness and noisiness of KGs, and approaches like RuLES [31] address this through KG embeddings. Compared to AMIE+, RuLES has two more refinement operators to allow negated atoms in a rule body. From Figure 2, we can see the rule evaluation for RuLES is a hybrid combination of statistical and embedding-guided confidence. A weight is used to allow one to choose whether to rely more on the classical measure ${\mu }_1$ (like standard or PCA confidence), or on the embedding-based measure ${\mu }_2({𝒢}_r,\varphi )$. ${𝒢}_r$ extends $𝒢$ with facts derived from $𝒢$ by applying rule $r$. So, ${\mu }_2({𝒢}_r,\varphi )$ capture the information about facts missing in $𝒢$ that are relevant for $r$ by loss function $\varphi (\cdot )$ pre-trained by KG embedding and text corpus models.

This group of approaches generate candidate rules by directly exploring paths in KGs using heuristic strategies, and these approaches typically focus on learning CP rules generalised from KG paths. As many KGs contain scheme-level (a.k.a., ontological) knowledge such as entity types as well as relation domains and ranges, which is different from instance-level knowledge about relations between individual entities. So, a KG containing ontological knowledge can be split into the ontology graph and the instance (sub)graph.

Given a KG $𝒢={𝒢}_O\cup {𝒢}_I$, ${𝒢}_O$ is the ontology graph and ${𝒢}_I$ is the instance graph. The instance graph ${𝒢}_I$ has entities as vertices and describes instance-level knowledge about entities and their relations; for instance, a triple $(\mathrm{𝖺𝗂𝗋𝗅𝗂𝗇𝖾}\text{-}\mathrm{𝖭𝖸},\mathrm{𝗁𝖺𝗌𝖡𝖺𝗌𝖾},\mathrm{𝖺𝗂𝗋𝗉𝗈𝗋𝗍}\text{-}\mathrm{𝖩𝖥𝖪})$ describes that the two entities $\mathrm{𝖺𝗂𝗋𝗅𝗂𝗇𝖾}\text{-}\mathrm{𝖭𝖸}$ and $\mathrm{𝖺𝗂𝗋𝗉𝗈𝗋𝗍}\text{-}\mathrm{𝖩𝖥𝖪}$ are associated by the relation $\mathrm{𝗁𝖺𝗌𝖡𝖺𝗌𝖾}$. ${𝒢}_I$ also describes the classes of entities, such as a triple $(\mathrm{𝖺𝗂𝗋𝗅𝗂𝗇𝖾}\text{-}\mathrm{𝖭𝖸},\mathrm{𝗋𝖽𝖿}\text{:}\mathrm{𝗍𝗒𝗉𝖾},\mathrm{𝖠𝗂𝗋𝗅𝗂𝗇𝖾})$ expressing that $\mathrm{𝖺𝗂𝗋𝗅𝗂𝗇𝖾}\text{-}\mathrm{𝖭𝖸}$ is a member of the class $\mathrm{𝖠𝗂𝗋𝗅𝗂𝗇𝖾}$. The ontology graph ${𝒢}_O$, on the other hand, has classes as vertices and describes schema-level (or ontological) knowledge about the relations between classes. For example, triple $(\mathrm{𝖠𝗂𝗋𝗅𝗂𝗇𝖾},\mathrm{𝗋𝖽𝖿𝗌}\text{:}\mathrm{𝗌𝗎𝖻𝖢𝗅𝖺𝗌𝗌𝖮𝖿},\mathrm{𝖮𝗋𝗀𝖺𝗇𝗂𝗌𝖺𝗍𝗂𝗈𝗇})$ says that class $\mathrm{𝖠𝗂𝗋𝗅𝗂𝗇𝖾}$ is a subclass of $\mathrm{𝖮𝗋𝗀𝖺𝗇𝗂𝗌𝖺𝗍𝗂𝗈𝗇}$. Also, the two triples $(\mathrm{𝗁𝖺𝗌𝖡𝖺𝗌𝖾},\mathrm{𝗋𝖽𝖿𝗌}\text{:}\mathrm{𝖽𝗈𝗆𝖺𝗂𝗇},\mathrm{𝖠𝗂𝗋𝗅𝗂𝗇𝖾})$ and $(\mathrm{𝗁𝖺𝗌𝖡𝖺𝗌𝖾},\mathrm{𝗋𝖽𝖿𝗌}\text{:}\mathrm{𝗋𝖺𝗇𝗀𝖾},\mathrm{𝖠𝗂𝗋𝗉𝗈𝗋𝗍})$ state that relation $\mathrm{𝗁𝖺𝗌𝖡𝖺𝗌𝖾}$ has a domain type $\mathrm{𝖠𝗂𝗋𝗅𝗂𝗇𝖾}$ and a range type $\mathrm{𝖠𝗂𝗋𝗉𝗈𝗋𝗍}$. This can be expressed as an edge $(\mathrm{𝖠𝗂𝗋𝗅𝗂𝗇𝖾},\mathrm{𝗁𝖺𝗌𝖡𝖺𝗌𝖾},\mathrm{𝖠𝗂𝗋𝗉𝗈𝗋𝗍})$ in the ontology graph.

A path is a sequence of triples $(s_1,p_1,o_1),$ $(s_2,p_2,o_2),\mathrm{\dots },(s_n,p_n,o_n)$ in $𝒢$ where $o_i=s_{i+1}$ (). There are two kinds of paths in KGs. A instance path (resp., ontological path) is a path where $s_i,o_i$ are entities (resp., classes). Existing path exploration methods can thus be classified by whether the paths are from the ontology graph or the instance graph. Generalising instance paths to form rule patterns is also called a bottom-up approach, while generating rules from ontological paths is called a top-down approach.

Some techniques in association rule mining have been adapted to first-order rule learning [81, 4, 5]. Such techniques are originally developed to discover meaningful relationships or associations among items in a dataset and thus, they are modified to generate first-order rules by identifying statistically frequent patterns occurring in KGs.

RDF2Rules [81] samples the so-called frequent predicate cycles (FPCs). A predicate cycle is a sequence of variables and predicates of the form $(x_0,p_1,x_1,\mathrm{\dots },p_n,x_0)$, which are essentially generalised instance paths. If a predicate cycle has a sufficient number of instance paths in the KG as its instantiations, it is called a frequent predicate cycle. Rules can be generated from FPCs. For instance, a FPC $(x_0,{\mathrm{𝗁𝖺𝗌𝖮𝗋𝗂𝗀𝗂𝗇}}^{-1},x_1,\mathrm{𝗁𝖺𝗌𝖣𝖾𝗌𝗍𝗂𝗇𝖺𝗍𝗂𝗈𝗇},x_2,\mathrm{𝗁𝖺𝗌𝖠𝗅𝗅𝗂𝖺𝗇𝖼𝖾},x_0)$ can generate three rules $\mathrm{𝗁𝖺𝗌𝖣𝖾𝗌𝗍𝗂𝗇𝖺𝗍𝗂𝗈𝗇}(x_1,x_2)\wedge \mathrm{𝗁𝖺𝗌𝖠𝗅𝗅𝗂𝖺𝗇𝖼𝖾}(x_2,x_0)\to \mathrm{𝗁𝖺𝗌𝖮𝗋𝗂𝗀𝗂𝗇}(x_1,x_0)$, $\mathrm{𝗁𝖺𝗌𝖮𝗋𝗂𝗀𝗂𝗇}(x_1,x_0)\wedge {\mathrm{𝗁𝖺𝗌𝖠𝗅𝗅𝗂𝖺𝗇𝖼𝖾}}^{-1}(x_0,x_2)\to \mathrm{𝗁𝖺𝗌𝖣𝖾𝗌𝗍𝗂𝗇𝖺𝗍𝗂𝗈𝗇}(x_1,x_2)$, and ${\mathrm{𝗁𝖺𝗌𝖣𝖾𝗌𝗍𝗂𝗇𝖺𝗍𝗂𝗈𝗇}}^{-1}(x_2,x_1)\wedge \mathrm{𝗁𝖺𝗌𝖮𝗋𝗂𝗀𝗂𝗇}(x_1,x_0)\to \mathrm{𝗁𝖺𝗌𝖠𝗅𝗅𝗂𝖺𝗇𝖼𝖾}(x_2,x_0)$. RDF2Rules uses a greedy algorithm to iteratively mine FPCs.

SWARM [4, 5] converts triples in KGs into transaction data to apply association rule mining. Association rules capture frequent items in transaction data. As for KG, they convert a triple $(s,p,o)$ into a 2-tuple $(s,(p,o))$ or $(o,(p^{-1},s))$. Here both of the $s$ or $(p,o)$ can be seen as items, also the fact tuple $(s,(p,o))$ can be one transaction where these two items appear at the same time. The frequent transaction items can be generalised to rule patterns. For example, we found two frequent transaction items having a common or mostly overlapping item set like $(\{\mathrm{𝖠𝗅𝗅𝖾𝗇},\mathrm{𝖠𝗅𝗅𝗒}\},(\mathrm{𝗅𝗂𝗏𝖾𝗌𝖨𝗇},\mathrm{𝖭𝖾𝗐𝖸𝗈𝗋𝗄}))$ and $(\{\mathrm{𝖠𝗅𝗅𝖾𝗇},\mathrm{𝖠𝗅𝗅𝗒}\},(\mathrm{𝖽𝗂𝖾𝖽𝖨𝗇},\mathrm{𝖭𝖾𝗐𝖸𝗈𝗋𝗄}))$. They can be generalised to the association rule $\{\mathrm{𝖠𝗅𝗅𝖾𝗇},\mathrm{𝖠𝗅𝗅𝗒}\}:(\mathrm{𝗅𝗂𝗏𝖾𝗌𝖨𝗇},\mathrm{𝖭𝖾𝗐𝖸𝗈𝗋𝗄})\to (\mathrm{𝖽𝗂𝖾𝖽𝖨𝗇},\mathrm{𝖭𝖾𝗐𝖸𝗈𝗋𝗄})$. Using the type information like $\mathrm{𝗋𝖽𝖿}\text{:}\mathrm{𝗍𝗒𝗉𝖾}$ and $\mathrm{𝗋𝖽𝖿𝗌}\text{:}\mathrm{𝗌𝗎𝖻𝖢𝗅𝖺𝗌𝗌𝖮𝖿}$ in the ontology graph, they could generate the rule $\{\mathrm{𝖯𝖾𝗋𝗌𝗈𝗇}\}:(\mathrm{𝗅𝗂𝗏𝖾𝗌𝖨𝗇},\mathrm{𝖢𝗂𝗍𝗒})\to (\mathrm{𝖽𝗂𝖾𝖽𝖨𝗇},\mathrm{𝖢𝗂𝗍𝗒})$.

In this subsection, we discuss about approaches that use DNNs to learn rules directly by optimising objective functions that roughly correspond to plausible path patterns.

Representation learning for KGs has attracted intensive interest, which maps entities, relations, and types to low-dimensional vector or matrix spaces, called embedding [61, 35], to capture semantic associations between them. Another stream of rule learning approaches use existing or new KG embeddings to learn rule structures and combine them with other rule search strategies and/or rule confidence measures. Utilising embeddings enhances the efficiency of rule learning to allow the handling of large KGs and improves the interpretability of DNN-based rule learning methods.

The authors of [88] were among the first to suggest using KG embeddings extracted from DNNs for rule structure learning, called EMBEDRULE [88]. In EMBEDRULE, the plausibility of rules will be first estimated via an embedding-based scoring function before the more expensive computation of PCA confidence. It first embeds entities $e\in ℰ$ and predicates $p\in {𝒫}^{\ast }$ as respectively vectors $𝐞\in {ℝ}^d$ and diagonal matrices $𝐏\in {ℝ}^{d\times d}$. Similar to the bilinear transformation of Neural LP, the embeddings satisfy ${𝐞}_1^T\cdot 𝐏\cdot {𝐞}_2\approx 1$ for each fact $p(e_1,e_2)$ in the KG; that is, ${𝐞}_1^T\cdot 𝐏\approx {𝐞}_2^T$. Consider a CP rule $r$ of the form $p_1(x_0,x_1)\wedge p_2(x_1,x_2)\wedge \mathrm{\cdots }\wedge p_n(x_{n-1},x_n)\to p(x_0,x_n)$, there should be many instance paths that support it, i.e., $p_1(e_0,e_1),p_2(e_1,e_2),\mathrm{\dots },p_n(e_{n-1},e_n)$ and $p(e_0,e_n)$ in the KG. Hence, the embeddings satisfy ${𝐞}_0^T\cdot {𝐏}_1\approx {𝐞}_1^T$, ${𝐞}_1^T\cdot {𝐏}_2\approx {𝐞}_2^T$, $\mathrm{\dots }$, ${𝐞}_{n-1}^T\cdot {𝐏}_n\approx {𝐞}_n^T$, and ${𝐞}_0^T\cdot 𝐏\approx {𝐞}_n^T$; that is, ${𝐞}_0^T\cdot {𝐏}_1\cdot {𝐏}_2\mathrm{\cdots }{𝐏}_n\approx {𝐞}_n^T\approx {𝐞}_0^T\cdot 𝐏$. Since rule $r$ must hold for many such entities $e_0$, the rule can be captured by ${𝐏}_1\cdot {𝐏}_2\mathrm{\cdots }{𝐏}_n\approx 𝐏$. The scoring function for $r$ is defined via embeddings as follows:

and the similarity between two matrices $sim({𝐌}_1,{𝐌}_2)$ can be defined in various ways such as the Frobenius norm, i.e., $sim({𝐌}_1,{𝐌}_2)=exp(-{\Vert {𝐌}_1-{𝐌}_2\Vert }_F)$. Based on similar intuitions, different scoring functions via embeddings for rule learning.

RLvLR [51] uses a KG sampling strategy and path embedding methods, which enables it to handle large-scale KGs like DBpedia or Wikidata. The step of sampling based on $n$-hop paths (for rules with maximum length $n$) can effectively reduce the search space and can handle massive benchmarks efficiently. The sampled smaller KG contains only those entities and facts that are relevant to the target predicate $p$. Then, RLvLR uses the proposed co-occurrence scoring function to guide and prune the search for plausible rules. The selected candidates are kept for the final evaluation by standard confidence and head coverage. The co-occurrence means that for a rule of the form $p_1(x_0,x_1)\wedge p_2(x_1,x_2)\wedge \mathrm{\cdots }\wedge p_n(x_{n-1},x_n)\to p(x_0,x_n)$, the objects of $p_i$ share many common entities with the subjects of $p_{i+1}$, where embeddings of the subjects and objects of $p_i$, denoted ${𝐩}_i^s$ and ${𝐩}_i^s$, are defined as the averages of the embeddings of the entities occurring in the corresponding positions. Their co-occurrence scoring function is defined as:

Later approaches focus on improving the embedding methods to further enhance rule learning performance [83, 94, 53] or learn more expressive forms of rules [52, 82]. In particular, R-Linker [83] improves RLvLR with a hierarchical sampling and lightweight embedding method, and IterE [94] improves the KG embeddings of (especially sparse) KGs through an iterative enhancement process. Rules are learned from embedding with traverse and select strategies, while embedding is refined according to new triples inferred by rules. StreamLearner [52] extends RLvLR to learn temporal rules, and TyRuLe [82] extends the embedding to learn rules with entity type information. Finally, embeddings have been used to transfer rules from one KG to another KG [53].

Many existing KGs are large-scale and subject to regular updates. Yet the knowledge contained in them is still far from complete and contains noise. Manual maintenance of large-scale KGs is costly, if not impossible. Hence, automated reasoning for KG completion and verification is essential, including common tasks such as link prediction and fact checking. While link prediction aims to discover missing links between entities, fact-checking focuses on validating existing triples. Both tasks are important for building KGs and enhancing the quality of existing KGs.

There has been a heightened interest in the interpretability of AI models, as understanding how and why a model arrives at a particular decision is pivotal for trust and transparency in decision-making. Logic rules, with their inherent ability to support human-comprehensible reasoning processes, have emerged as a valuable tool in diverse fields.

Several domains are actively exploring the use of automatically learned rules to complement and enhance existing AI models. Rules can naturally be applied to other tasks related to KGs, such as entity alignment [10, 36] and knowledge base question answering (KBQA) [70]. In the entity alignment task, RTEA-RA [36] enhances the embeddings of individual entities by injecting the grounded rules into the model to produce hybrid embeddings. MuGNN [10] reconciles the structural differences of two KGs before entity alignment by employing rules induced by AMIE+ for KG completion and pruning. Also, these rules are transferred between KGs based on the knowledge invariant assumption.

As for KBQA, RuKBC-QA [70] uses rule-based knowledge base completion (KBC) in general question answering (QA) systems. Both the origin knowledge base and inferred missing facts by selected rules are used as input of RuKBC-QA for predicting the answers.

Beyond the tasks with KGs as the primary forms of data, several attempts involving rules have been made in the context of natural language processing (NLP), computer vision (CV), and biomedical applications. For NLP, RuleBERT [63] tries to teach the pre-trained language models (PLMs) with the common-sense knowledge provided by Horn rules. KoRC [91] uses rules learned by background KGs to construct the reasoning chain for Reading Comprehension.

Rule learning has also found applications in computer vision, like reasoning in the sub-graph extracted from the images. LOGICDEF [90] constructs a defence model that uses first-order logic rules mined from the extracted scene graph, to explain the object classification and detect the attacks of the adversarial vision model. The document image model [59] uses inductive rules by extracting textual subgraphs corresponding to the text entities in the documents for information extraction.

In the biomedical domain, rule learning has also shown promising applications. In drug discovery [66], generating the explanation paths by Horn rules for drug-disease (entity) pairs. As for drug-gene interaction prediction [2], rules can predict missing links between drug and gene nodes in a graph that contains relevant biomedical knowledge.

These studies collectively showcase the versatility and potential of rule learning across diverse domains, addressing various challenges and improving outcomes in different application areas.

Despite the rapid advancements in rule learning techniques over KGs, this is still a relatively new research area, with a lot of potential for further development in several aspects, including the complexity and quality of learned rules, evaluation metrics, and rule learning and reasoning strategies.

First of all, the complexity of learned rules can be enhanced by expanding the form of rules (i.e., the language bias) to be learned. Most existing rule learning approaches focus on rules that represent path patterns in KGs. While path patterns capture important structural information in KGs, more complex structural patterns such as sub-graph patterns can reveal more refined knowledge and first-order Horn rules can express complex sub-graph patterns. Scalability of rule learning and identification of the most useful sub-graph patterns remain major challenges in learning more complex rules. Besides, learning rules that can capture more useful information such as attributes or more complex logical connections in KGs is another aspect of rule complexity.

Also, the form of rules and their learning strategies can be tailored according to the applications. For instance, to learn domain-specific rules that are designed to express prior knowledge in specific domains, can potentially lead to more scalable, accurate, and robust performance in the concerned applications. This is especially relevant for applications in knowledge-intensive domains such as biomedical science, healthcare, finance, or legal applications, which involve domain-specific knowledge and specialised applications.

Moreover, to enhance the quality of learned rules, it is crucial to establish effective and robust rule quality evaluation measures. Existing rule confidence measures often lack sufficient granularity or interpretability. Yet designing suitable rule quality metrics has received less attention in the literature. Meanwhile, there has been insufficient emphasis on evaluating the semantic validity of learned rules, that is, to measure how meaningful the learned rules are to human beings. This is particularly important for learning domain-specific rules, and it is desirable to develop quality measures that take into consideration both the data semantics and data distributions.

Finally, new rule learning and reasoning strategies that tightly integrate symbolic AI and deep learning techniques hold great promise. This line of research may involve developing hybrid models that leverage the strengths of both rule-based reasoning and data-driven neural networks. Yet a tighter integration of them has always been a pursuit of the academic communities and the industry. With the recent development of neuro-symbolic approaches, where neural networks are used for symbolic rule learning and reasoning, the other direction is gaining increasing interest, that is, to apply symbolic knowledge, logical constraints, and rule guidance in neural network predictions. This research direction also foresees a tighter coupling of rule learning and prediction models that utilise KGs.

In this paper, we have provided a systematic review of state-of-the-art rule learning for knowledge graphs. We studied major categories of logic rule learning approaches over knowledge graphs, including the ILP-based, statistical path generalisation, and neuro-symbolic approaches, with discussions on their developments and limitations. Besides, we also discussed the rule confidence measures, which play a crucial role in rule learning. As for the applications of rule learning, we introduced applications of rule-based knowledge graph inferences, as well as wider applications in natural language processing, computer vision, and biomedical science. Finally, we pointed out several promising future directions for rule learning research.