Logics for Conceptual Data Modelling: A Review

Fillottrani, Pablo R.; Keet, C. Maria

doi:10.4230/TGDK.2.1.4

Logics for Conceptual Data Modelling: A Review

Pablo R. Fillottrani

Universidad Nacional del Sur, Bahía Blanca, Argentina
Comisión de Investigaciones Científicas, Provincia de Buenos Aires, Argentina C. Maria Keet¹¹1Corresponding author

Department of Computer Science, University of Cape Town, South Africa

Abstract

Information modelling for databases and object-oriented information systems avails of conceptual data modelling languages such as EER and UML Class Diagrams. Many attempts exist to add logical rigour to them, for various reasons and with disparate strengths. In this paper we aim to provide a structured overview of the many efforts. We focus on aims, approaches to the formalisation, including key dimensions of choice points, popular logics used, and the main relevant reasoning services. We close with current challenges and research directions.

Keywords and phrases:

Conceptual Data Modelling, EER, UML, Description Logics, OWL

Category:

Survey

Copyright and License:

2012 ACM Subject Classification:

Information systems

\rightarrow

Database design and models ; Computing methodologies

\rightarrow

Description logics ; Software and its engineering

\rightarrow

Formal language definitions ; Software and its engineering

\rightarrow

Unified Modeling Language (UML) ; Theory of computation

\rightarrow

Data modeling

DOI:

10.4230/TGDK.2.1.4

Received:

2023-09-14

Accepted:

2024-02-08

Published:

2024-05-03

Part Of:

TGDK, Volume 2, Issue 1 (Trends in Graph Data and Knowledge - Part 2)

Journal and Publisher:

Transactions on Graph Data and Knowledge, Schloss Dagstuhl – Leibniz-Zentrum für Informatik

1 Introduction

Information modelling or conceptual modelling plays an essential role in computing by providing a structured and abstract representation of complex data that sustains each software system. It serves as a foundational step in the development lifecycle, facilitating communication and understanding among stakeholders from the identification of requirements to maintenance. In addition, it promotes a shared vision and a common understanding of the system’s domain information that facilitates interoperability with other systems in unforeseen ways at development time. The latest curriculum recommendations²²2Accessible at https://www.acm.org/education/curricula-recommendations include conceptual modelling in the undergraduate curriculum and pertinent dimensions are listed with multiple terms in the ACM classification codes, notably, among others: Information management, Data Modeling, Model development and analysis, Enterprise modeling, Entity relationship model, and Unified Modeling Language (UML).

Storey et al. recently described conceptual modelling as “an activity that occurs during information systems development and use that involves capturing, abstracting, and representing relevant aspects of reality, to support understanding, communication, design, and decision making. Conceptual models are comprised of constructs, such as entities, events, goals, attributes, relationships, roles, and processes, connected by well-defined rules.” (emphasis in original) [116]. Here, we focus specifically on conceptual data modelling (and thus excluding process and goal modelling) and within that, what has been called structural conceptual data models [56] (and thus excluding behavioural aspects like UML’s methods). Popular modelling languages over the years include Extended Entity-Relationship (EER) diagrams for database design [36] and the Natural language Information Analysis Method that evolved into Object-Role Modeling (ORM) [59], design for object-oriented programming with Unified Modeling Language’s (UML) Class Diagrams³³3The first standard listed is version 1.1 from 1997, at https://www.omg.org/spec/UML/1.1; last accessed: 30 Sept. 2023., and the Semantics of Business Vocabulary and Business Rules [93] that reuses ORM.

Albeit only one of many topics in computing, conceptual data modelling has been investigated widely. This has also resulted in several surveys and scoping reviews on conceptual data modelling broadly but without logics [116], on ontology-driven conceptual modelling aspects from a modelling side [130, 131] rather than logics, on verification topics for UML class diagrams specifically [52, 109], or only for conceptual model-like artefacts as it pertains to reasoning in the context of scalable data management [107]. Those reviews also indicate that conceptual modelling may span (sub)disciplines. Among others, the human aspects of the modelling process may be assumed to be within the scope of information systems and their formal aspects are within the scope of the computing discipline. The latter involves their quality assessment, and algorithms to, among others, convert such specifications into databases and software applications. Conceptual data models are also used in Artificial Intelligence (AI) to drive the design of intelligent information systems, provided they are given a logic-based specification. By being formalised, complex knowledge – entity types, relationships, attributes, and constraints holding over them – can be captured accurately and passed on to a range of computational tasks. Example tasks include using automated reasoners for classification and satisfiability checking and querying data by making use of, e.g., a Description Logics reasoner [12], test data generation (e.g., [110]), optimising query compilation [124], and explainable machine learning processes [83, 117].

This logic-based conceptual data modelling, thus far, has focussed on a number of subtopics, such as which logic to use to formalise the graphical elements and diagram grammar, which features of which conceptual data modelling language to include, and whether one could just have one logic that maps to all major diagram-based conceptual data modelling languages and therewith functioning as a precise interlingua in the back-end – and that for each purpose or assumed application. Figure 1 shows three main strands of investigation and related work programmes with particular aims for logic-based conceptual data modelling together with a few key moments or the publication of pertinent languages and concepts. They are, roughly:

Figure 1: Timeline of the three identified strands and a selection of the key moments regarding languages, logics and semantics of the formalisations, and applications. Regarding the latter: ICOM was the first automated reasoner-enabled conceptual modelling tool, Mastro and QuOnto realised OBDA initially, Google’s positioning of KGs helped boost graph-based approaches, and recently FaCIL combines languages and techniques.

$\blacksquare$

logic-based reconstructions⁴⁴4 The term “reconstruction” captures the process more accurately than “formalisation”. We understand by reconstruction an attempt to get a complete description of information available early at design time, which goes beyond creating just one of many possible formal representations. It includes also, among others, assessment of the graphical design’s implicit assumptions and approach to formalisation. Put differently, the formalisation step forms a part of the reconstruction. of conceptual data models (CDMs⁵⁵5The abbreviation is well known; tracing it to its origins among the many mentions, it appeared at least already in 1991 [37]. Before that, the CDM abbreviation was also used for Common Data Model or Content Data Model.) and conceptual data modelling languages (CDMLs) in expressive logics targeting precision and automated reasoning over them, since around 1990.
$\blacksquare$

runtime usage of CDMs since the early 2000s: ontology-driven information systems including Ontology-Based Data Access (OBDA) where the ontology is de facto a CDM due to being tailored to one application, query optimisation, and verification.
$\blacksquare$

reach-out to a broader IT scope and to end users since the mid 2010s, which necessarily simplifies and upscales it, where the broader access may have to be tolerant of conflicting information in the model.

Each strand brings with it a different set of requirements for AI theory and techniques, which we will discuss in detail in the paper, and are summarised as follows. The first strand is mostly based on a waterfall design approach: design the model well and shelve it once the system is being implemented. Modellers and domain experts generally develop models only in a graphical language with none or ambiguous semantics that should be formalised. Those logic-based reconstructions focus on formalisations to be as expressive as possible. The more features the better, since the more precision the better, in line with feature extensions from ER to EER [122], ORM to ORM2 [60], and OWL DL to OWL 2DL [38]. In summary, more expressive logics are also more interesting for a broader range of automated reasoning tasks to further help improve a model’s quality.

The second strand of research shifted the focus to leaner languages, designing computationally “well-behaved” fragments of the logics used for the formalisation. The key goal is scalability, not expressiveness, with the logic-based CDM as a component of more advanced AI-driven software systems. It did not focus on reasoning over the CDM itself, but rather the reasoning service as part of querying the data using the conceptual model.

The third, and most recent, strand is ongoing, and might be dubbed “modelling for the masses” and may bifurcate further into new usages. Here, not only scalability is important, but also ease of use and possibly also permitting contradictions, and thus also lower quality models. The latter may happen because the representation language can be too weak to be able to detect quality issues and contradictions. While it may focus on simple queries at most, such basic large models can be of use already in machine learning and natural language processing (NLP) and neuro-symbolic approaches for knowledge graph (KG) embeddings to enhance NLP. Example initiatives that closely relate to CMDs include schema.org, linked data with RDF and optionally with ShEx [13] and SHACL [77] for constraint validation, and the data and modelling component of the community-driven Abstract Wikipedia [132]. This line of work runs in parallel with the first two and may be the most prominent currently.

The different aims of logic-based formalisations, however, do affect how “best” to define that construction, because what “best” entails is relative to the aim. On top of these different aims and tasks, including reasoning tasks, there are various formalisation decisions on how to give semantics to the elements of the diagrammatic notation of the CDM, which, in turn, can affect the computational complexity and therewith the tasks one actually can use the conceptual model for. Owing to the diverse lines of work with their aims for formalising CDMs, different approaches are necessary for assessing a given formalisation in conceptual data modelling. In this condensed review, using the means of a qualitative narrative review, we zoom in on the evaluation of the aspects that arise in selecting, developing, and applying logic-based semantics in this context. We seek to answer the following questions:

Q1:

What are the tasks and challenges in that formalisation?
Q2:

Which logics are popular for which (sub-)aim?
Q3:

What are the known benefits of a logic-based reconstruction in terms of the outcome and in terms of reasoning services that one may use once a CDM is formalised?
Q4:

What are some of the outstanding problems in logic-based conceptual data modelling?

The remainder of the paper is structured as follows. We first describe related work on reviews on conceptual data models in Section 2. Section 3 covers decision points for a formalisation, the logics used for different purposes, and it outlines the two key different processes to do so, covering questions Q1 and Q2. Section 4 identifies and evaluates possible reasoning services that can be applied to CDMs, illustrating with examples two of them. We therewith deal with Q3. Current challenges and future directions related to Q4 are described in Section 5 and we close with conclusions in Section 6.

2 Related Work

Several reviews of the state of the art in conceptual data modelling and logic-based reconstructions of languages exist, but they either cover only the early years or the first strand of the development of the area [66, 115, 118, 102, 119] or the first and the beginnings of the second strand of the area [2, 39] and are, by now, outdated. New applications of CDMs since those reviews introduce distinctive challenges that were not considered before. Key differences are the uptake of Semantic Web technologies with scalable reasoning over CDMs and runtime usage of CDMs especially for querying data.

Scoping the related work on reviews for CDM to the last 10-15 years, they focus on the non-logical aspects [134, 86, 131, 130, 116]. Wen et al. [134] analysed several quality aspects of conceptual models, such as expressivity, clarity, and semantics, and they evaluated effectiveness of modelling languages in different fields of applications. The formalisation of the languages is generally described, i.e., without logical translations, and no detailed comparison of alternative representations is done.

Other reviews assess CDM from the ontology modelling angle. McDaniel et al. [86] reviewed publications on domain ontology evaluation. Their work concentrates on the evaluation process, and even though domain ontologies are related to conceptual data modelling, the modelling language and their formalisation is not part of the analysed characteristics. Verdonck et al. [131, 130] conducted a systematic literature mapping and review on the domain of ontology-based conceptual modelling. They consider ontology-driven conceptual modelling as the utilisation of ontological techniques, like formal ontology, cognitive science and philosophical logics, to the practice of conceptual modelling. This analyses CDMs in general, not only those approaches related to ontologies.

There are also reviews on the collaborations of the field of conceptual modelling with artificial intelligence [18, 19, 127, 84]. These reviews focus on identifying new research directions and do not address formalisation details.

Gonzalez et al. [52] conducted a systematic literature review of formal verification of structural software models in UML, complemented or not with constraints expressed in textual languages like the Object Constraint Language (OCL). The scope were papers describing research initiatives on model-driven engineering tools that ensure software correctness, and the results classify the type of input models, the reasoning support of the tools, and the completeness of the automatic verification process. The way models are formalised, and how the tools help to develop this formalisation is not analysed, only listing the formal languages used. Shaik et al. [109] presents a more recent literature review with similar aims. They describe language coverage and formalisation techniques in more depth, but the scope is limited to only verifying UML class diagrams, so new applications such as querying are not considered and language coverage is limited to classes, associations, generalisations, compositions, and aggregations. Also, the complexity of formalizations is missing. While such quantitative surveys are useful, they lack in-depth content assessments.

The most recent review, by Storey et al. [116], presents a comprehensive systematic review of the literature in conceptual modelling in general with as aim to identify relevant topics and future research directions. It has a much broader scope including not only static (structural) modelling but also process and collaboration modelling. They recognise the need to support an always increasing variety of users and interconnected domains. Another noteworthy result is that they found out that over the last 15 years, process modelling prevails over data modelling on the research topics. Being a systematic review of a huge amount of literature with semiautomatic tools, there is, however, no reference to logic-based semantic constructions.

There is thus no review on logics for conceptual data modelling specifically, let alone on assessing logic-based formalisations for CDM in view of the current demands and applications not only from the formal point of view, but also on the design decisions that influence data-driven applications across different domains.

Refer to caption — Figure 2: Example EER diagram of Example 1.

3 On formalising conceptual data models

Logic-based reconstructions of CDMs and their languages (CDMLs) used to represent them are motivated by two main key usage scenarios: 1) precision in representation and automated reasoning over them (and, implicitly: quality) and 2) their use at runtime as part of an intelligent information system. It also may be the case that the CDML angle is only a possible scenario and the main aim is to design more logics, whereas from our perspective, the CDMs and CDMLs are the key focus.

This section will summarise the component tasks and types of challenges first, since they set the stage for the logics, subsequently discuss the popular logics used for that, and finally describe the two main approaches typically taken carrying out that task.

3.1 Decision points before the formalisation

This section zooms in on considerations when designing or selecting a logic for creating a logic-based reconstruction of a conceptual data model or modelling language and the decision points involved in it.

In a recent empirical survey, Valle Souza et al. [128] identify six types of functional goals, and five types of quality goals for using conceptual data modelling in practice. Before formalising a CDM, it is important to understand both which subset of the all possible functional goals and which balance of all quality goals are adequate for the context. Different model properties are relevant for achieving these goals, mainly reusability, correctness, comprehensibility, completeness, confinement, and maintainability. Correctness can be further split into precision and coverage.

On the surface, it seems straightforward to formalise CDMs, as something that can be done promptly with little effort, but to get it right for either the whole CDML or an “interesting” fragment requires attention to detail and a substantial amount of knowledge and time. This is due to two key reasons:

$\blacksquare$

the purpose or reason for the formalisation that influences the design process of a language and therewith the many variations in outcome [46];
$\blacksquare$

where to set the cut-off point for feature (constraint) inclusion, since if a feature is added, it will be used by someone somewhere and perceived as needed [75].

Purposes such as reusability, comprehensibility, and maintainability favour leaner logics for better performance. In contrast, a purpose of precision requires a more expressive logic to maximise coverage of CDML constraints in the ontologically best possible way, which concerns both higher precision so that more unintended models are excluded [55] and philosophical decisions embedded in the logic [47]. Feature inclusion decisions can be split up into two categories. One is modelling features, which concerns whether to include attributes and multi-attribute identifiers, with or without data properties and data types (concrete domains), and which semantics to choose for shared and composite aggregation – among the 23 types of elements and 49 types of constraints across the three main CDML families [76]. The other concerns those that affect the automated reasoning outputs, notably Open World Assumption vs Closed World Assumption and whether to honour the implicit disjointness of classes except when they are in a hierarchy.

In addition to these feature decisions where the logic does not adequately cover all the CDML’s constraints it should be able to express, there is generally a discrepancy in the other direction as well. This concerns the confinement model property, which refers to the degree to which a model has only the necessary information to fulfill its purpose [128]. Here, the logic may permit more than is possible to declare in a diagram due to composition rules of the CDML, with the effect that the logic falls in a higher complexity class than strictly needed.

An overview of the key dimensions of choice points is included in Table 1, which the authors created by combining an assessment of the published logic-based reconstructions (see also Section 3.2) and the top-down approach of the language design procedure introduced in [47]. The first row in Table 1 describes the main aim of the reconstruction, which aligns with the strands 1 vs 2 and 3 introduced in Section 1. The second row presents two approaches to the formalisation: rule based and mapping based. The choice of the approach commits the modeller to a given process, with different tools and outcomes. A detailed analysis for this choice is presented in Section 3.3 and it is further illustrated in the Appendix. Different syntactic and semantic representations for the underlying logic are shown in the third and fourth rows respectively, which summarises the various options that are further discussed in Section 3.2. The next three rows show alternative formalisations for relationship, class disjointness, and how negation is to be treated (closed world view). Finally, the last row describes the influence of the logic-basic constituents in the formalisation, which varies greatly across the published logic-based reconstructions (discussed in Section 3.2.1). The following example illustrates some of these issues, in particular regarding roles and relationships and disjointness.

Table 1: Key dimensions to choose for creating a logic-based reconstruction of a conceptual data model (see Section 3.1 for details).

Dimension	Options	Comments
Main aim	High feature coverage for [precision/automated reasoning], limited features for runtime usage	Mainly a choice between computationally “well-behaved” logic or not
Approach to formalisation	Algorithmic/rules, mappings	See Section 3.3 for details
Syntax	Graphical, textual, both	See Section 3.2 for details
Semantics	Set-based, model-theoretic, graph-based, other	First two are most popular; see Section 3.2 for details
Relationships	See formalisation options in Example 1	Often not stated explicitly which option is chosen
Class disjointness	Classes outside a class hierarchy are disjoint, or not	Most formalisations do not make them disjoint (although assumed in the CDM)
World view	Open, Closed World	Most formalisations are with Open World Assumption
Language feature inclusion	Choose types of elements and constraints to include	A unifying metamodel for EER, UML class diagrams, and ORM2 identified 23 types of elements and 49 constraint types [76] to choose from; see also Section 3.2.1

Example 1.

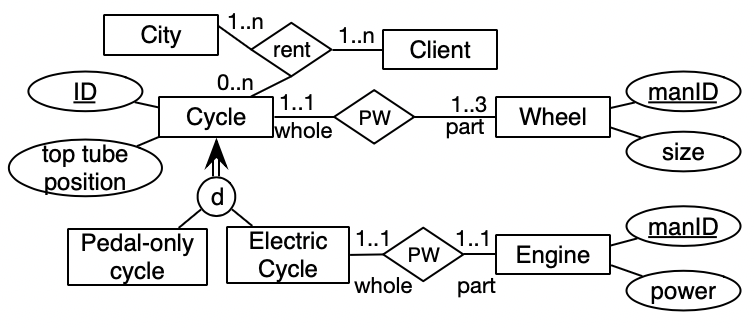
A sample conceptual data model in one of the EER notations is included in Figure 2 (incomplete with respect to the universe of discourse). There are only regular and electric bicycles (which are disjoint) that all have a number of wheels and where the latter has an engine as part. Clients can rent bicycles in a city. Bicycles, engines, and wheels are identified by their respective ID. The first step is to decide how to formalise this in which logic.

Consider the relationship between the Electric bicycle and Engine. There are multiple options that may have consequences for the logic and the resultant computational complexity of popular automated reasoning tasks:

1.

One-directional binary relationship; choose either partOf or hasPart.
2.

Two-directional binary relationships, partOf and hasPart; choose whether to declare them inverses or not.
3.

One non-directional binary relationship with two roles (as part of the relation) that the participating entities play, named, say partwhole with as roles [part] and [whole]; choose whether to define the relationship as having those roles as part.
4.

Reify the relationship to a new class and add two new binary relationships to each participating entity type, e.g., Parthood with as new relationships partOf and hasPart that must have as domain Parthood; choose whether to approximate the reification (i.e., add only mandatory or only functional (“at most one”) constraints or both on the two new binaries) or demand logical equivalence (i.e., also have the external identifier, as in ORM, or owner entity identifier, as in ER).
5.

Acknowledge that relationships in CDMs are local rather than reused like they are in ontologies, so the parthood relationships between Electric bicycle and Engine and between Cycle and Wheel must have unique names; choose whether to declare them equivalent or not.

Regarding option 2: adding inverses may or may not change the worst-case computational complexity of a language: e.g., the Description Logic (DL) $\mathcal{ALCQ}$ and $\mathcal{ALCQI}$ are both ExpTime-complete [123], whereas $\mathcal{EL}$ (the basis of the OWL 2 EL profile [90]) does not have inverse properties and is PTime-complete, but adding inverses increases complexity [58].

Option 3 requires more machinery in the logic, specifically roles (called role components in DLs) as core elements and functions to relate the role player to the role, which is used for more convenient processing. Defining relationships, such as defining (familial) aunt to be precisely one’s parent’s sister ( ${\sf aunt\equiv hasParent\circ hasSister}$ ), pushes the logic into undecidability in most cases [85, 135, 106]. The reification-based approach of option 4 is used by, e.g., Wikidata’s data model⁶⁶6Reification such as described by [62]. See also the data model at https://www.mediawiki.org/wiki/Wikibase/DataModel; last accessed on 2-1-2024.. Logical equivalence with a binary relationship requires an advanced identifier constraint that is currently only available in $\mathcal{DLR}_{\mbox{\emph{{{\footnotesize ifd}}}}}$ [31] and $\mathcal{CFDI}^{\forall-}_{\textit{\it nc}}$ [125] DLs and in full first order logic, but not in OWL that has ample software infrastructure.

For the disjointness, one could either capture that as the complement or as full disjointness, i.e., as ${\sf Bicycle\sqsubseteq\neg Electrical\,bicycle}$ or as ${\sf Bicycle\sqcap Electrical\,bicycle\sqsubseteq\bot}$ , respectively. Diagrams show disjointness declared on the subsumption relation rather than between the entity types, however, and it thus can be declared only in a class hierarchy, not any number of arbitrary classes in the CDM.

There are more choices for other elements, which, taken together with the myriad of logics, easily can lead to a combinatorial explosion of the combination of formalisation choices with the logic chosen, and which subset of constraints of the CDML is honoured in the formalisation. For instance, OWL DL [87] does not have qualified cardinality constraints to be able to capture the constraint on Wheel fully; OWL 2 DL [91] does. $\lrcorner$

The different options for this one example are illustrations of how to formalise a particular element, constraint, or combination thereof. CDMs have only a limited set of such patterns and this can be defined algorithmically so that the logic-based reconstruction can be done systematically and a repeat reconstruction will result in the same formalisation, provided the same vocabulary is used where vocabulary needs to be provided. The designers of the different algorithms have made different formalisation choices, and thus their corresponding tools will not necessarily result in the same formalisation given the same CDM.

Finally, an element of the CDML may not be unambiguous and therefore it may be formalised differently across formalisations. The common example of such an issue is UML’s aggregation association that was a “semantic variation point” according to the UML v2.4 standard [94] and its semantics is left to the implementer to specify.

3.2 Popular logics for logic-based reconstructions

Most research has focussed on the motivation of the first strand, expressiveness and model quality, both from a conceptual modelling and from a logics perspective, such as [7, 15, 59, 120, 70, 104]. Popular logics to give the graphical elements a formal semantics and to use that for automated reasoning over them at least in theory, are Description Logics (DL) languages but also other logics have been used (e.g., [7, 15]). Several of those other logics, notably those with some tooling support, include UML’s object constraint language (OCL) [103], common logic interchange format CLIF (an ISO-standardised first order logic) [98], Alloy (also first-order logic) [21], and Z (a typed first order logic) [67]. Conversely, there are also multiple formalisations for one CDML; e.g., logic-based reconstructions of ORM include, among others, [48, 50, 59, 120, 71, 133] and for ER and EER both from a modeller’s perspective [36, 111, 122] and from the logicians’ one with the $\mathcal{DLR}$ family [29, 30, 31] and $DL\mbox{-}Lite$ family [28] of languages.

Alternative approaches consider the verification problem, for which constraint programming is used [25, 26], and there are a few graph-based approaches [20]. Also, there is the deductive databases approach based on logic programming [88], in which the concepts of closed world assumption (CWA) and unique name assumption were first introduced. ConceptBase⁷⁷7https://conceptbase.sourceforge.net is a tool that adds conceptual modelling and metamodelling features based on the same logical representation. Deductive databases focus on a logic-based representation and inference within an already deployed database system, however, where all choices and decisions about the formalisation are already made, while conceptual modelling is concerned with creating a high-level, technology-independent representation of the entire information system during the early stages of development where there are still plenty of open points to formalise. Although it is possible to do conceptual modelling in this context, it is not in the main interest of the deductive databases area. Other attempts, such as exploring category theory [120] for a precise specification, are also considered out of scope for this review.

The next three paragraphs elaborate on the main trends.

Table 2: Popular logics for CDMLs and a set of features (adapted and extended from [42]). “–”: negative/absent; “+”: positive/present; “feature mismatch” refers to the number of constraints (e.g, disjointness) that can be captured in the logic; roles sensu DL role components or FOL argument places in relations and relationships.

DL-Lite_A (Approx. OWL 2 QL)	$\mathcal{DLR}_{\mbox{\emph{{{\footnotesize ifd}}}}}$	OWL 2 DL	FOL
Selection of features
– without roles	+ with roles	– without roles	– without roles
– no $n$ -aries	+ has $n$ -aries	– no $n$ -aries	+ has $n$ -aries
+ attributes	+ attributes	+ attributes	– no attributes
+ has datatypes	+ has datatypes	+ has datatypes	– no datatypes
– very few language features; large mismatch	+ little feature mismatch	$\pm$ some feature mismatch, with overlapping sets	+ little feature mismatch
– logic-based reconstructions to complete	+ logic-based reconstructions exist	– logic-based reconstructions to complete	$\pm$ logic-based reconstructions exist
+ modularity (import statements etc)	– modularity	+ modularity (import statements etc)	– modularity
UNA / no UNA	no UNA	no UNA	no UNA
$\pm$ OWA	$\pm$ OWA	$\pm$ OWA	$\pm$ OWA
Computation and implementability
+ PTIME (TBox); AC⁰ (ABox)	$\pm$ ExpTime-complete	$\pm$ N2ExpTime-complete	– undecidable
+ very scalable (TBox and ABox)	$\pm$ somewhat scalable (TBox)	$\pm$ somewhat scalable (TBox)	– not scalable
+ relevant automated reasoners available	– no implementation	+ relevant automated reasoners available	$\pm$ limited automated reasoners (see text for detail)
+ linking with ontologies doable	– no interoperability	+ linking with ontologies doable	– no interoperability with widely used infrastructures
+ modularity infrastructure	– modularity infrastructure	+ modularity infrastructure	– modularity infrastructure

3.2.1 Coverage and DLs

We shall focus on DLs since they are relatively popular thanks to the OWL standard [87, 91], which is largely based on them [65]⁸⁸8OWL DL 2 is based on $\mathcal{SROIQ}$ [64], OWL 2 QL is based on $DL\mbox{-}Lite$ [28], OWL 2 EL on $\mathcal{EL}^{++}$ [11], and OWL 2 RL was inspired by both Description Logic Programs [53] and pD^∗ [121]., the software tooling ecosystem that it fostered, more research has been carried out on logic-based reconstructions into a DL or a DL-based OWL species than for other logic families, and they enjoy ample insights into the computational complexity of language feature combinations.

Most logic-based reconstructions consider only one CDML family at a time. Well-known logics for this purpose are DL-Lite and $\mathcal{DLR}_{\mbox{\emph{{{\footnotesize ifd}}}}}$ for EER [7] and UML class diagrams [15], and OWL for (fragments of) ORM and UML class diagrams [133]. The formalisations are typically incomplete with respect to the full CDML due to limited expressiveness of the logic; among others, omitting ER’s identifiers (aka keys) [34], excluding $n$ -ary relationships where $n$ may also be $\geq 3$ [7, 133], or no special semantics for UML’s aggregation association nor for its qualified associations [15]. To some extent, this is unavoidable: ORM and its extended ORM2 are undecidable due to arbitrary projections over $n$ -aries and due to the acyclic role constraint, and probably also due to the antisymmetric role constraint. An advantage of all these formalisations in the different logics covering different features, is that it provides good insight into the computational complexity of the CDMLs. Table 2 lists these and related aspect for four logics, three of which are expressive ones. The for CDMLs relatively well-suited $\mathcal{DLR}$ family – meaning that there is a comparatively good language feature alignment of the logics with CDMLs – are all ExpTime-complete. It varies for the many flavours of $DL\mbox{-}Lite$ for different EER fragments [7]. $DL\mbox{-}Lite$ is included in the comparison because it is popular in ontology-based data access, where the ontology has to resemble a CDM for seamless query formulation and execution. OWL 2 DL is included for its popularity, given that it is standardised and a reconstruction provides instant access to ample software infrastructure. Their respective language feature sets have some overlap, but either has features that the other one does not have; among others, OWL does not have $n$ -aries proper, no external uniqueness/multi-attribute identifiers or qualified associations, no compound attributes, and no acyclicity, whereas the CDMLs notably do not have property chains and no defined classes. FOL is a common and very expressive language at least on paper and therefore included. Its status of “limited” automated reasoners refers to their plug ’n play level of maturity and the reasoning services they currently offer, as compared to DL-based automated reasoners.

Adding the missing features to any of $DL\mbox{-}Lite$ , $\mathcal{DLR}$ or DL-based OWL species is likely to push them straight into undecidability, if they were not already. This also negatively affects obtaining interesting results in unifying the CDMLs through one logic foundation as the central point from which to pivot between graphical CDMs. The typical approach is to identify a common fragment with features that all CDMLs have in common and devise a suitable logic for that, such as the DL $\mathcal{ALUNI}$ [34] and the tailor-made DLs in the same low expressiveness range for evidence-based unification of CDMLs [42]. An exception is the framework for the Distributed Ontology, model, and specification Language (DOL) that uses institutions to provide a framework to let different languages cooperate, including a logic-based reconstruction of UML class diagrams, OWL, and CLIF [89, 54].

Given that one easily arrives at a logic that is ExpTime-complete even without covering all CDML features, little has been done to venture into CDML extensions, although this is also in part because there are not many temporal or spatial conceptual data modelling languages. The main line of research where attempts have been made, concerns expressive temporal DLs like $\mathcal{DLR}_{\mathcal{US}}$ [9] that serves as a basis for the temporal EER $ER{{}_{VT}}$ [10]. $\mathcal{DLR}_{\mathcal{US}}$ was also explored in context of the MADS spatio-temporal modelling language [99], and $ER{{}_{VT}}$ has been extended into $EER{{}_{VT}^{++}}$ [95] and Trend [74], all of which still can be reconstructed into $\mathcal{DLR}_{\mathcal{US}}$ . While $\mathcal{DLR}_{\mathcal{US}}$ turned out to be undecidable [9], this does not need to be the case for all temporal conceptual data models in existence. Only those that have, among others, the following modelling features, are: disjointness and covering (total) constraints, sub-relationships, timestamping, and evolution (i.e., object migration) constraints [6]. Without them, a modeller lacks the ability to represent temporal constraints such as, e.g., “each alumnus must have been a graduating student before”.

3.2.2 CDM runtime usage and DLs

The second strand of research into logic-based reconstructions of CDMLs, runtime usage, focuses on (very) lean fragments for scalability. The software system then uses at least the conceptual model’s vocabulary, relationships, and possibly also its constraints or a subset thereof. Practically, the CDM is then deemed so-called “background knowledge” of the system, rather than the traditional view on it as a starting point for software design from a requirements specification. Popular runtime usages are test data generation for verification and validation [92, 110], query answering with the principal aim of query execution or user-centred query design [16, 33, 35, 82, 113], and database query execution during query compilation [124].

Query answering has received most attention in AI under the name of ontology-based data access (OBDA) [100] and related implementations generally [136, 17, 82, 124, 3], and specific use cases such as EPNet [27] whose “ontologies” are de facto conceptual data models (see for a comparison, e.g., [73]). An alternative approach to the same problem uses transformations rather than a mapping layer, availing of the DL $\mathcal{CFDI}^{\forall-}_{\textit{\it nc}}$ and an abstract relational model [125, 105]. $\mathcal{CFDI}^{\forall-}_{\textit{\it nc}}$ has been shown to cover a substantial number of constraints used in ORM in its $\mbox{ORM2}_{\mbox{\emph{{{\scriptsize cfd}}}}}$ fragment [48] and the approach fits well also with EER [47]. Thanks to the transformations and the assumption of materialising deductions, the expressivity of the logic for the CDML may be higher in this configuration compared to the logic for the CDML in the OBDA approach; other trade-offs are discussed in [47].

For the computationally “well-behaved” lean logics, the key challenge is that the formalisation of a CDM becomes so complicated that it borders cognitive overload for the modeller, if they have to do it all at once. That is, to have to combine in one view and all at the same time the understanding of the universe of discourse, to model it right in the CDM, to know enough of logics, and be fully conversant with its workarounds, convoluted encodings, and approximations. In theory, this should be solvable with good modelling software.

As with the CDM reconstructions that focus on coverage, also here there are steps toward lean temporal fragments, which are motivated mainly by spatio-temporal stream queries with OBDA [69, 40, 97].

3.3 Approaches to the formalisation

Once the CDML, or a fragment thereof, and the logic are chosen there are two main ways to create the logic-based reconstruction, whose components and their interactions are illustrated in Figure 3. The distinction between the two is important, because they meet different sets of formalisation and deployment requirements. One option is to do it algorithmically with a series of rules stating what axiom(s) must be added to the knowledge base for each element encountered in the CDM that needs to be formalised (e.g., [15, 42, 103]). This is like converting an existing informal CDM to the logic. Practically, a particular model is deconstructed into component parts where each component – a pattern or unit for formalisation – may be formalised in a single axiom or several axioms, depending on the pattern and logic, which are then added one-by-one to a logical theory. This resultant logical theory may be a semantically complete reconstruction of the original CDM or only resembling the original CDM, for it may be missing an element (e.g., a cardinality of “2-4” appears as “ $\exists$ ” in the logical theory) or approximating one (e.g., reification of an $n$ -ary without the identification constraint).

The other option is to declare a new textual syntax of the modelling language, map that syntax to the graphical elements of the CDML, specify the semantics for the syntax, and then show it can be represented in the chosen logic (e.g., [7, 48]). In this second option, the graphical elements in the CDM are effectively a syntactic sugar coating in the modelling process that is already logic-based from the start. With the mapping based approach, it is fully reconstructed by design if the mapping were 1:1 and any excluded features could not be used to begin with, else it is also only an approximation. That is: the details of the reconstruction into the logic vary by proposal and are embedded in the creation of the mapping.

Figure 3: Conceptual model describing the characteristics of the two main approaches used for creating logic-based reconstructions of conceptual data models: Mapping-based and rule-based.

The rules-based approach is illustrated in Appendix A.1, where we adapt the “positionalist core profile” $\mathcal{DC}_{p}$ of [42] for the occasion, which contains the features used most across UML class diagrams, EER, and ORM2, into DL syntax (and thus semantics) [12] with the specific DL role component notation as in the $\mathcal{DLR}$ family of DLs [29]. The mapping-based approach is illustrated in Appendix A.2, also with the $\mathcal{DC}_{p}$ language. It is clearly more verbose in its specification than the rules-based one, and takes more time to specify. We illustrate some formalisations with both approaches in the following example.

Example 2.

Consider again the bicycles of Figure 2. Let us formalise a section of it into the DL fragment for $\mathcal{DC}_{p}$ , using the rules listed in Appendix A.1:

\begin{array}[]{rcl}\geq 1[whole]PW&\sqsubseteq&ElectricBicycle\\ \geq 1[part]PW&\sqsubseteq&Engine\\ Engine&\sqsubseteq&\exists power.T\,\sqcap\leq 1\,power\\ ElectricBicycle&\sqsubseteq&Cycle\\ ElectricBicycle&\sqsubseteq&\leq 1[whole]PW\,\sqcap\geq 1\,[whole]PW\\ \end{array}

The same section of the model can be formalised a different set of rules for a different logic. For instance, let us take the same section in OWL 2 DL: we first need to somehow add directionality to the nondirectional PW relationship. Further, one could argue about whether the PW relationship should be typed with a domain and range axiom, since it is used twice and so without typing, one can then obtain a more elegant formalisation. If so, it would be, at least:

\begin{array}[]{cl}&\mathtt{SubClassOf}(\mathtt{ObjectSomeValuesFrom}(\mathtt{% ex:hasPart})\ \ \mathtt{ex:ElectricBicycle})\\ &\mathtt{SubClassOf}(\mathtt{ObjectSomeValuesFrom}(\mathtt{ex:isPartOf})\ \ % \mathtt{ex:Engine})\\ &\mathtt{SubClassOf}(\mathtt{ex:Engine}\ \ (\mathtt{ObjectIntersectionOf}\ \ (% \mathtt{DataSomeValuesFrom}(\mathtt{ex:power})\\ &\ \ \ \ \ \mathtt{FunctionalDataProperty}(\mathtt{ex:power})))\\ &\mathtt{SubClassOf}(\mathtt{ex:ElectricBicycle}\ \ \mathtt{ex:Cycle})\\ &\mathtt{SubClassOf}(\mathtt{ex:ElectricBicycle}\ \ \mathtt{% ObjectExactValuesFrom}(1\mathtt{ex:hasPart}))\\ \end{array}

and optionally with the additional assertion that hasPart is the inverse of isPartOf. If one were to decide against typing relationships in the rules-based approach, still for OWL 2 DL, then the following set of axioms approximates it by exploiting the qualified cardinality constraint feature:

\begin{array}[]{cl}&\mathtt{SubClassOf}(\mathtt{ex:Engine}\ \ (\mathtt{% ObjectIntersectionOf}\ \ (\mathtt{DataSomeValuesFrom}(\mathtt{ex:power})\\ &\ \ \ \ \ \ \mathtt{FunctionalDataProperty(ex:power})))\\ &\mathtt{SubClassOf}(\mathtt{ex:ElectricBicycle}\ \ \mathtt{ex:Cycle})\\ &\mathtt{SubClassOf}(\mathtt{ex:ElectricBicycle}\ \ \mathtt{% ObjectExactValuesFrom}(1\ \mathtt{ex:hasPart}\ \mathtt{ex:Engine}))\\ \end{array}

The mapping approach, on the other hand, is laborious to define (recall Appendix A.2), but then results in a succinct notation in the formalisation, for one can use the textual version of the CDML. The same model snippet is then:

\begin{array}[]{rcl}\mbox{\sc rel}\mathcal{}(\mathtt{PW})&=&\{whole:\mathtt{% ElectricBicycle},part:\mathtt{Engine}\}\\ \mbox{\sc att}\mathcal{}(\mathtt{Engine})&=&\{power:T\}\\ \mathbin{\mbox{\sc isa}\mathcal{}}(\mathtt{ElectricBicycle},\mathtt{Cycle})\\ \mbox{\sc cmin}\mathcal{}(\mathtt{ElectricBicycle},\mathtt{PW},whole)&=&1\\ \mbox{\sc cmax}\mathcal{}(\mathtt{ElectricBicycle},\mathtt{PW},whole)&=&1\\ \end{array}

This notation is likely to be more readable for users who are not logicians, because a term like att for attribute or, say, Attribute in full, is closer to common terminology than FunctionalDataProperty, and likewise a simple comma to separate the part and whole versus a “ $\sqcap$ ” symbol. $\lrcorner$

As can be seen in the example, a different set of rules may result in a knowledge base that is never equivalent, regardless whether that was into the same logic or into different logics with an isomorphism. For instance, with the “bumping up the role names”-approach rather than the roles-based approach, it would not be equivalent due to having created two independent OWL object properties, hasP and isofP, whereas there is only one relationship (PW) in the $\mathcal{DC}_{p}$ -based knowledge base. This also motivates that each CDM-to-logic-X converter would need to be explicit on the rules the algorithm uses.

It must be noted that the resultant logic needed to encode all $\mathcal{DC}_{p}$ knowledge bases, those language features in that DL syntax allow formulas that are not $\mathcal{DC}_{p}$ knowledge bases, or: this logic is more expressive than $\mathcal{DC}_{p}$ . For example, a knowledge base using that DL fragment may contain $A\sqsubseteq\exists a.T\sqcap\leq 1a\sqcap\forall a.T$ , but it cannot be obtained from the translation of any conceptual data model that has only $\mathcal{DC}_{p}$ ’s elements. This is a feature that holds for all such reconstructions: it is a one-way direction from conceptual data model into the logic, but not vice versa.

Observe that since a rule-based construction procedure is linear in the number of elements in the CDM, as most of them are, the overall complexity of translation and any subsequent automated reasoning on the theory remains the same as for the logic. The overall complexity of the mapping-based approach depends on its realisation. If one can model only with what is declared in that mapping, then the complexity is the same as in the logic, which is more efficient than the rules-based approach thanks to not having to do the linear translation. If one can model independently from the CDML in the mapping, then one has to add the pattern-finding complexity to the complexity for the logic.

The approaches also can be merged. For instance, a rules-based approach that transforms EER to an intermediary abstract relational model [47], which has its own syntax that is closer to the relational model with its semantics and a mapping from that abstract relational model to a logic (a DL in the case of [17, 82, 124]).

Table 3: Summary of differences between the rule-based and mapping-based approaches, principally emanating from both the different components and relations between them (see Figure 3) and from how the two approaches are currently realised (see the Appendix for an illustration).

Rule-based	Mapping-based
Logic is more expressive than the CDML	The logic is/can be as expressive as the CDML
When mapped into that logic, the only semantics is that of that logic	Can swap the semantics or declare multiple and choose, like set-based for model-theoretic
Formalisation decisions “hidden” in the algorithm/rules	Ontological commitments explicit in the text-based version and what maps to what
May be with information loss (i.e., less in the formalisation than was modelled in the diagram)	Typically, it is information-preserving
Relatively quick specifications for the formalisation	It is more verbose in its specification and takes more time to specify
Goes in one direction only, from diagram to the axioms	Two-way direction between the CDM and logic
Executed post hoc after completion of the model, or needs to be re-run each time a change has been made	Formalised at modelling time with formalisation and diagram updated in real-time. Computationally faster than re-running the formalisation in the rule-based approach
Graphical elements in the CDM take precedence	Graphical elements in the CDM are effectively a syntactic sugar coating in the modelling process that is already logic-based from the start

4 Reasoning over and with Conceptual Data Models

Depending on the aims of the modeller, it may already suffice to have a logic-based reconstruction for precision and elimination of ambiguity of the language. It may also be the case that the CDM is formalised in order to use it with automated reasoning services. The principal reasoning tasks assumed for DL-formalised CDMs are the so-called standard reasoning services for DL knowledge bases and OWL ontologies: satisfiability, consistency, instance checking, and querying [12]. Satisfiability and consistency are interesting theoretically, and deducing implicit information can improve on the model’s quality, but for this to be useful during the modelling stage, the available CDML features need to be used more often than currently done [75]. In particular: disjointness constraints, cardinalities beyond 1, and role and relationship subsumption ought, or would need, to be used more often to obtain most benefits. Discovering unsatisfiable classes are useful because if undetected, they result in necessarily empty database tables in a database or OOP classes in the application cannot have any objects. Upfront correction before implementation is better than revising after unit test failures. Detecting implicit cardinality constraints is useful so that they can be made explicit in the database or application, which enhances data integrity. These benefits can be obtained thanks to having formalised the CMD in order to enable automated reasoning over it, which results in a better quality CDM. This is illustrated in the next example.

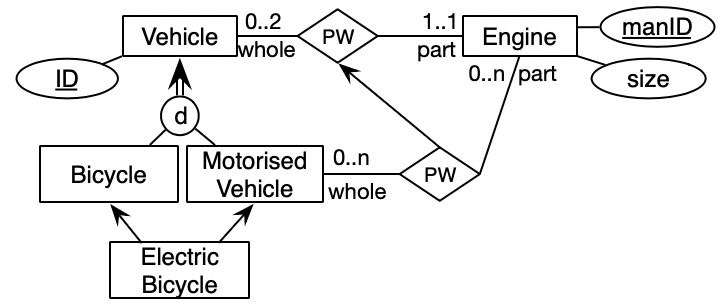
Example 3.

Consider the CDM about bicycles in Figure 4: Vehicles may have at most two engines as part and each engine is part of exactly one vehicle. Bicycles and motorised vehicles (which are disjoint) are vehicles, and electric bicycles are both a type of bicycle and a type of motorised vehicle. In addition, the modeller created a part-whole relationship between motorised vehicle and engine, declared it a subrelationship of the former, but forgot to specify the cardinality constraints, which defaults to 0..n. A logic-based reconstruction of the EER diagram is straightforward in either of the languages in the $\mathcal{DLR}$ family as well as in OWL 2 and thus also in first order predicate logic, be it following the rules-based or mapping-based approach.

Running the automated reasoner, there are three deductions, which are highlighted in Figure 5. First, the Electric Bicycle class is unsatisfiable: no individual electric bicycle can be both a bicycle and a motorised vehicle, according to this model, because of the disjointness constraint on the entity type subsumption. Additionally, thanks to the subsumption axiom between the PW between vehicle and engine and motorised vehicle and engine, we obtain two more deductions: the subsumed PW relationship inherits two stronger cardinality constraints declared over the parent relationship. $\lrcorner$

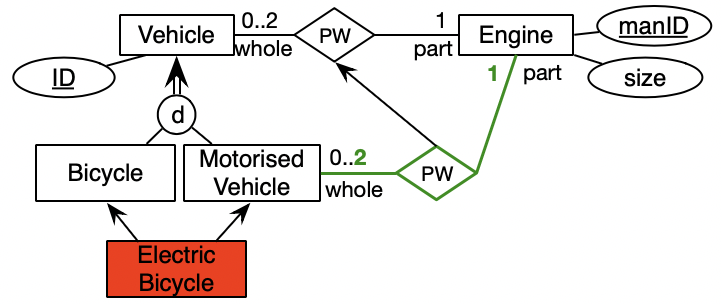
Example 3 is a variation on examples and tooling that exists since 2000 with the ICom tool for EER diagrams [49], its evolution with its own notation⁹⁹9There are other tools that provide a diagrammatic interface to OWL that resemble EER, UML or ORM to a greater or lesser extent, most recently by [79], but the reverse is a different problem and outside the scope of this review, as are graphical notations that are not conceptual data models. and better module management to declare inter-model assertions [43], and subsequent bifurcation into ORMie for reasoning over ORM2 diagrams [114] and crowd2 that supports reasoning over ORM2, EER, and UML class diagrams and swapping between them [23]. They mostly use the DL $\mathcal{ALCQI}$ either directly or they use a behind-the-scenes reification of $n$ -aries by rewriting them into $n$ binaries in case $n\geq 3$ . That is, common automated reasoners for OWL 2 DL, such as HermiT [51] or Racer [57], can be, and are, used in these implementations.

The notion of finite satisfiability – i.e., the problem of deciding whether a knowledge base has a finite non-empty model – in the context of DL-based formalisations is sometimes also considered [14, 15]. If so, this is done more often from the viewpoint of model verification in software engineering and also availing of constraint programming or OCL besides, or instead of, FOL, DL, or HOL, it is focussed on UML class diagrams only, and the majority has only a Yes/No type of output [25, 26, 52, 109].

The reasoning service of instance checking in the DL and OWL sense is not relevant in conceptual model development, for it is focussed on type-level information only, i.e., the TBox in DL terminology. Where instances can, and do, feature in the modelling processes are all in different tasks, being: 1) in the specification of small sample populations to help derive the participation constraints [60], 2) automatic test data generation from CDMs [110], and 3) in a test-driven development method [126]. Because of the absence of an ABox and considering regular conceptual modelling practices, it is hard to obtain an inconsistent CDM and therefore it is, to the best of our knowledge, fully ignored in the research.

Querying over a CDM has not received particular attention, unlike the Query-By-Diagram idea since 1990 [4] and the scalable ontology-based data access that evolved from it [100], which includes using a graphical conceptual data model for it, notably ORM and ORM-like notations (e.g., [33, 35]; see [112] for a review). The first basic task is to use the conceptual data model to “point and click” to select the elements to query, which is then translated into a SPARQL query and from there into SQL, or straight to SQL, to fetch the data from the data store. The more advanced option uses the knowledge represented in the CDM to enhance the query. The enhancement can occur at the level of the TBox, where the query itself is rewritten taking the logic-based reconstruction of the CDM into account, or it is used to compute the deductions over the instances to subsequently materialise the results (i.e., append to the database), which is then queried with the plain query. The general idea is illustrated in Example 2.

Example 4.

Consider the following simple conceptual data model $\mathcal{CDM}$ that consists of a fragment of the EER diagram in Figure 4:
$\mathcal{CDM}=\{{\sf Bicycle\sqsubseteq Vehicle},{\sf MotorisedVehicle% \sqsubseteq Vehicle},{\sf Bicycle\sqsubseteq\neg MotorisedVehicle}\}$
A corresponding database may have three tables, assuming each entity type has its own database table, and at least one instance each:
$\mathcal{DB}=\{{\sf Bicycle(b1)},{\sf MotorisedVehicle(mv1)},{\sf Vehicle(v1)}\}$
Consider now the query “Retrieve all vehicles”, i.e., SELECT * FROM Vehicle for a relational database. A regular RDBMS returns only {v1} as answer, it being the only tuple in that table.

Now consider OBDA with the query rewriting approach. The abstract representation of the query is: $q(x)\leftarrow Vehicle(x)$ . In evaluating the query, it first consults $\mathcal{CDM}$ : the algorithm detects the two subsumption axioms and rewrites the query as $q(x)\leftarrow Vehicle(x)\lor Bicycle(x)\lor MotorisedVehicle(x)$ . This rewritten query is converted into SQL, which amounts to a union of SELECT * FROM Vehicle, SELECT * FROM MotorisedVehicle, and SELECT * FROM Bicycle. It returns {b1, mv1, v1}, which is what a typical user would expect when asking for all the vehicles.

Consider again the same query, but now we incorporate the knowledge of the $\mathcal{CDM}$ in the database before we run the same query, also called ABox rewriting or the combined approach. The algorithm detects the ${\sf Bicycle\sqsubseteq Vehicle}$ and updates the database:

$\mathcal{DB}=\{{\sf Bicycle(b1)},{\sf MotorisedVehicle(mv1)},{\sf Vehicle(v1)}% ,{\sf Vehicle(b1)}\}$
and likewise for the motorised vehicle:

$\mathcal{DB}=\{{\sf Bicycle(b1)},{\sf MotorisedVehicle(mv1)},{\sf Vehicle(v1)}% ,{\sf Vehicle(b1)},{\sf Vehicle(mv1)}\}$
The query $q(x)\leftarrow Vehicle(x)$ translates to SELECT * FROM Vehicle, but now that table has the other instances as well, and so the query answer is {b1, mv1, v1} as well. This approach permits more advanced queries, such as with path queries that have been shown to be more effective [82]. $\lrcorner$

Notwithstanding that the intuitive idea is seemingly straightforward, the logics and algorithms for the various options are rather involved and depend on the logic used for the TBox; for an early overview on query rewriting see [100], for the first database completion, see [81], and an overview with many further references can be found in Section 3.1 of Schneider and Simkus’ recent review on linking ontologies to databases [107]. In addition, each option has its pros and cons regarding computational complexity, query expressiveness, expressivity of the logic for the $\mathcal{CDM}$ , and optimal usage scenarios [47].

Finally, two orthogonal choices that affect reasoning are choosing between the Closed (CWA) vs Open (OWA) world assumptions and whether to choose for the unique name assumption (UNA) or not. No UNA negatively affects computational complexity especially for the lean OBDA logics [8]. CWA vs OWA principally affects the deductions and it is mostly left implicit that the logic-based reconstructions use OWA since logics in AI assume this unless stated otherwise. CWA is often used in situations where the knowledge is assumed to be complete and where uncertainty is not explicitly represented or tolerated. OWA is used in situations where uncertainty is explicitly acknowledged and where it is important to represent and reason about incomplete information. OWA is more flexible and allows for the representation of unknown or partially known facts. In principle, a CDM may include both approaches.

5 Challenges and future directions

We describe some challenges that emerge from the discussion in previous sections. We classify them along three lines of inquiry: CDM languages, CDM integration with related areas, and CDM applications.

5.1 CDML design

In this section, we analyse challenges in formalisation and expressivity of CDML design. The formalisation space to a logic of choice is crowded with many attempts and assigning semantics to a CDML appears a solved problem, or if not solved, admitted to be intractable in the sense that it will never meet all demands at the same time – good in the formalisation, good in tooling support, and effective use throughout applications. Yet another formalisation of plain EER, ORM2, or UML class diagrams in yet another logic may only make a marginal contribution to the body of knowledge. Also the CDM interoperability, or logic as unifier, task has been well explored (see [42, 22] and references therein), albeit with limited tools and mostly covering a small set of constraints. From our own experiences by both authors, it is tedious, time-consuming, and difficult to publish because from the outside it looks like just more of the same without an appreciation of the thorny finer details and principal differences and consequences thereof. There may be a higher chance of more impact by considering extensions, notably logic-based temporal conceptual data modelling for stream processing or for process mining, and to investigate how to transform a logic-based temporal CDM into a temporal database. This may also connect with the process modelling that Storey et al.’s review highlighted as a general trend in conceptual data modelling [116].

The different clusters of formalisations have different sets of shortcomings and one that they all share, except for the CDML profiles in [42]: none of them is evidence-based regarding what features conceptual modellers use and to prioritise accordingly. In addition, user evaluations on usability and understandability are mostly lacking. When carried out, it is about the non-logical additional graphical or textual notation, such as for the logic-based Trend temporal conceptual data modelling language [74] or diagrammatic preferences only (e.g., [129]). Among others, neither the effects of using an automated reasoner in a conceptual data modelling task has been investigated with human modellers, nor the perceptions of modelling for OBDA. To attain scientific progress, such experiences need to go beyond anecdotes in a few use cases and they need to be tested in a controlled setting, or at least documented and analysed systematically when pooling together a set of use cases.

In addition, to the best of our knowledge, there are no methodologies that incorporate logic-based reconstructions and automated reasoning over the CDM, other than stating it as part of a workflow in FaCiL [22] and it is alluded to in test-driven development of CDM in [126]. Perhaps these gaps contribute to the, to date, limited uptake of logic-based conceptual data modelling in industry. Another reason for that may be that modellers do not use as many language features as they ought to [75] to get the most out of the automated reasoning and thus may need to be trained better in logic-based conceptual data modelling. Another reason may be the relative immaturity of the sparse logic-based conceptual data modelling tools that are mostly of the level of proof-of-concept or prototype [21, 23, 41, 43, 114], rather than full-fledged end-user and commercial-level applications. The underlying issues and opportunities are still unexplored.

Recently, there has been a decline in interest to develop logic-based reasoners [1], most of them being nowadays discontinued in their development. It seems that the mere availability of reasoners is not enough for widespread usage. Much effort is necessary to develop tools that integrate reasoning with real world applications. CDMs may present an opportunity to investigate new tools that demand reasoning services, with the objective to improve the modelling process and enhance the quality of conceptual models, and, just as important, their runtime usage in intelligent information systems.

5.2 CDM integration with related research areas

Ontologies and knowledge graphs are well established research areas that are closely related to CDMs. There are numerous practices that attempt to blur the lines between CDMs and ontologies [45], both in OBDA and elsewhere, as well as recognising the differences but then facing the challenge of how exactly how to relate the two artefacts (e.g., [32, 68]). This involves both how to map between the two at the language level and at the modelling pattern level, and the processes for the various use cases. For instance, top-down generation of candidate CDMs from an ontology, as Jarrar et al.’s aim was [68], requires different procedures from the original motivation for ontologies, as a bottom-up approach to provide a common vocabulary that all CDMs can link to [73]. Their precise interaction – why, when, and how – may be informally clear to some, but that is still non-trivial to apply in practice and does not appear to be clear to the practitioner community. What exactly is missing to fully resolve it both in theory, including with which methods and techniques, and for deployment, is yet to be addressed fully.

This review being a narrative review about the logics rather than a systematic review of both logics and automated reasoning services that are more popular in the ontology engineering field, there is the risk of some bias in the selection of sources. For Section 4, this was intentionally limited to “standard” reasoning services to illustrate some benefits of a logic-based approach. A systematic or broader narrative review about reasoning services for logic-based CDMs may provide additional insight.

From a different angle, and looking at both older and more recent techniques and standards than the most popular – by a large margin in terms of research efforts – logic-based reconstructions, are knowledge graphs that also do relate in some way to CDMs and the logics. Graph-based approaches are expected to (re)gain in popularity. We do not refer to choosing a graph-based semantics after transforming a CDM into OWL or OWL 2 syntax [87, 91], though possible, but the transformation of the CDMs into graphs directly or them being graphs from the outset. The former was proposed by Boyd and McBrian who used hypergraphs for interoperability among the established CDMLs [20] that is based on their graph-based data model [101]. An example of the latter is the TEGeL modelling language, which is a type graph from the outset and has a set of new icons; its formalisation is only assumed in [108], however, and its aim is specifically for a translation into a graph database only. One could link it to the formal definitions in Appendix B of [63], to RDF [61] or RDFS [24], and with or without constraints, be they with ShEx [13] or SHACL [77] or their logic-based foundation (see [96] for a recent brief overview and references therein), or another approach, such as extending a DL with more options for attributes, as in [78]. This is fertile ground for research whose outcomes may, in turn, feed into the neuro-symbolic strand of usage through KG embeddings that presumably would be improved by such logic-enhanced KGs and it would offer new means for quality control of the information represented in the KG.

5.3 CDM applications in other and new contexts

Other subtopics within the scope of logic-based CDMs are automated content learning, evolution of CDMs, and automated adaptation of CDMs and their database based on the queries posed. Automated CDM content learning should be able to leverage the advances made on corpus-based KG and ontology learning and may also make use of research on automated database-driven logic-based CDM creation that maintains the intermediate state [80]. Dynamic CDM optimisation from database usage patterns concerns updating the CDM by taking into account what data is queried from the database [137]. For instance, if only a fraction of the attributes are queried most of the time, the rarely used ones can be relegated to a separate entity type, like given a Person with attributes tel.no and address where only their tel.no is queried in 95% of the queries, then the optimisation suggestion would be to create a separate entity type Address with a binary relationship to Person. This can save time in query answering and possibly simplify the query interface of an OBDA system.

Further automation in creation, quality control, and use of CDMs does receive interest, as noted in Section 2 and with recent reviews such as [109] on verification. They all do need a formalised CDM to ensure correct operation, yet more such UML advances are still to be ported to other CDMLs and embedded in CDM development methodologies and usage process.

CDM evolution has been well-researched under the term schema evolution at least since the 1990s with renewed interest in the 2000s thanks to ontology evolution and those logics specifically. Ontology evolution is known to be far from trivial, however, which carries over to logic-based CDMs at least to some extent. Given that CDMs have a more restrictive grammar than most of the logics used, it may be less hard, and use cases with current relevance should be specified to limit the possibilia to increase the possibility to find a solution.

Finally, multilingual modelling may become an area of interest, as it is in ontology development for the past 15 years and increasingly for knowledge graphs as well, but it has received little attention in combination with logic-based conceptual modelling [5].

6 Conclusions

Information modelling with conceptual data modelling languages such as EER, UML Class Diagrams, and ORM has been augmented with logic-based reconstructions mainly for precision, quality, and runtime usage for querying and verification. Many logics have been used for many different conceptual data modelling fragments, having used either a rules-based or a mapping-based approach to the formalisation. This paper provided a succinct overview of key choice points in the aims to formalise, approaches to the formalisation, popular logics used, and the principal relevant reasoning services. Current challenges and research directions include the modeller’s perspective (with user evaluations), interaction with ontologies, and a renewed interest in graph-based approaches.

References

[1] Sunitha Abburu. A survey on ontology reasoners and comparison. International Journal of Computer Applications, 57(17):33–39, 2012.
[2] Miguel I. Aguirre-Urreta and George M. Marakas. Comparing conceptual modeling techniques: a critical review of the eer vs. oo empirical literature. ACM SIGMIS Database: The DATABASE for Advances in Information Systems, 39(2):9–32, 2008. doi:10.1145/1364636.1364640.
[3] Lina Al-Jadir, Christine Parent, and Stefano Spaccapietra. Reasoning with large ontologies stored in relational databases: The OntoMinD approach. Data & Knowledge Engineering, 69:1158–1180, 2010. doi:10.1016/j.datak.2010.07.006.
[4] Michele Angelaccio, Tiziana Catarci, and Giuseppe Santucci. QBD*: A graphical query language with recursion. IEEE Transactions on Software Engineering, 16(10):1150–1163, 1990. doi:10.1109/32.60295.
[5] Kutz Arrieta, Pablo R. Fillottrani, and C. Maria Keet. Cosmo: A constructor specification language for abstract wikipedia’s content selection process. Technical report, aug 2023. doi:10.48550/arXiv.2308.02539.
[6] Alessandro Artale. Reasoning on temporal conceptual schemas with dynamic constraints. In Proceedings. 11th International Symposium on Temporal Representation and Reasoning, 2004. TIME 2004., pages 79–86. IEEE, 2004. doi:10.1109/time.2004.1314423.
[7] Alessandro Artale, Diego Calvanese, Roman Kontchakov, Vladislav Ryzhikov, and Michael Zakharyaschev. Reasoning over extended ER models. In Christine Parent, Klaus-Dieter Schewe, Veda C. Storey, and Bernhard Thalheim, editors, Proceedings of the 26th International Conference on Conceptual Modeling (ER’07), volume 4801 of LNCS, pages 277–292. Springer, 2007. Auckland, New Zealand, November 5-9, 2007. doi:10.1007/978-3-540-75563-0_20.
[8] Alessandro Artale, Diego Calvanese, Roman Kontchakov, and Michael Zakharyaschev. DL-Lite without the unique name assumption. In Proceedings of the 22nd International Workshop on Description Logic (DL’09), volume 477 of CEUR-WS, 2009. URL: http://ceur-ws.org/Vol-477/paper_11.pdf.
[9] Alessandro Artale, Enrico Franconi, Frank Wolter, and Michael Zakharyaschev. A temporal description logic for reasoning about conceptual schemas and queries. In S. Flesca, S. Greco, N. Leone, and G. Ianni, editors, Proceedings of the 8th Joint European Conference on Logics in Artificial Intelligence (JELIA-02), volume 2424 of LNAI, pages 98–110. Springer Verlag, 2002. doi:10.1007/3-540-45757-7_9.
[10] Alessandro Artale, Christine Parent, and Stefano Spaccapietra. Evolving objects in temporal information systems. Annals of Mathematics and Artificial Intelligence, 50(1-2):5–38, 2007. doi:10.1007/s10472-007-9068-z.
[11] Franz Baader, Sebastian Brandt, and Carsten Lutz. Pushing the EL envelope. In Proceedings of the 19th Joint International Conference on Artificial Intelligence (IJCAI’05), volume 5, pages 364–369, 2005. URL: http://ijcai.org/Proceedings/05/Papers/0372.pdf.
[12] Franz Baader, Diego Calvanese, Deborah L. McGuinness, Daniele Nardi, and Peter F. Patel-Schneider, editors. The Description Logics Handbook – Theory and Applications. Cambridge University Press, 2 edition, 2008.
[13] Thomas Baker and Eric Prud’hommeaux. Shape expressions (shex) 2.1 primer – final community group report. W3C Recommendation, 2019. URL: http://shex.io/shex-primer/.
[14] Mira Balaban and Azzam Maraee. A UML-based method for deciding finite satisfiability in description logics. In Franz Baader, Carsten Lutz, and Boris Motik, editors, Proceedings of the 21st International Workshop on Description Logics (DL’08), volume 353 of CEUR-WS, 2008. Dresden, Germany, May 13–16, 2008. URL: https://ceur-ws.org/Vol-353/BalabanMaraee.pdf.
[15] Daniela Berardi, Diego Calvanese, and Giuseppe De Giacomo. Reasoning on UML class diagrams. Artificial Intelligence, 168(1-2):70–118, 2005. doi:10.1016/j.artint.2005.05.003.
[16] Anthony C. Bloesch and Terry A. Halpin. Conceptual Queries using ConQuer-II. In Proceedings of ER’97: 16th International Conference on Conceptual Modeling, volume 1331 of LNCS, pages 113–126. Springer, 1997. doi:10.1007/3-540-63699-4_10.
[17] Alexander Borgida, David Toman, and Grant Weddell. On referring expressions in information systems derived from conceptual modelling. In Isabelle Comyn-Wattiau, Katsumi Tanaka, Il-Yeol Song, Shuichiro Yamamoto, and Motoshi Saeki, editors, Conceptual Modeling (ER’16), volume 9974 of LNCS, pages 183–197. Springer, 2016. doi:10.1007/978-3-319-46397-1_14.
[18] Dominik Bork. Conceptual modeling and artificial intelligence: Challenges and opportunities for enterprise engineering: Keynote presentation at the 11th enterprise engineering working conference (eewc 2021). In Enterprise Engineering Working Conference, pages 3–9. Springer, 2021. doi:10.1007/978-3-031-11520-2_1.
[19] Dominik Bork, Syed Juned Ali, and Ben Roelens. Conceptual modeling and artificial intelligence: A systematic mapping study. Technical report, 2023. doi:10.48550/arXiv.2303.06758.
[20] Michael Boyd and Peter McBrien. Comparing and transforming between data models via an intermediate hypergraph data model. Journal on Data Semantics, IV:69–109, 2005. doi:10.1007/11603412_3.
[21] Bernardo F. B. Braga, João P. A. Almeida, Giancarlo Guizzardi, and Alessander Botti Benevides. Transforming OntoUML into Alloy: towards conceptual model validation using a lightweight formal methods. Innovations in Systems and Software Engineering, 6(1-2):55–63, 2010. doi:10.1007/s11334-009-0120-5.
[22] Germán Braun, Pablo R. Fillottrani, and C. Maria Keet. A framework for interoperability between models with hybrid tools. Journal of Intelligent Information Systems, 60:437–462, 2023. doi:10.1007/s10844-022-00731-7.
[23] Germán Braun, Giuliano Marinelli, Emiliano Rios Gavagnin, Laura A. Cecchi, and Pablo R. Fillottrani. Web interoperability for ontology development and support with crowd 2.0. In 30th International Joint Conference on Artificial Intelligence, IJCAI’21, pages 4980–4983, 2021. doi:10.24963/ijcai.2021/707.
[24] Dan Brickley and R. V. Guha. Rdf schema 1.1. Standard, W3C, 2014. URL: https://www.w3.org/TR/2014/REC-rdf-schema-20140225/.
[25] Jordi Cabot, Robert Clarisó, and Daniel Riera. Verification of UML/OCL class diagrams using constraint programming. In Model Driven Engineering, Verification, and Validation: Integrating Verification and Validation in MDE (MoDeVVA 2008), 2008. doi:10.1109/ICSTW.2008.54.
[26] Marco Cadoli, Diego Calvanese, Giuseppe De Giacomo, and Toni Mancini. Finite model reasoning on UML class diagrams via constraint programming. In Proc. of AI*IA 2007, volume 4733 of LNAI, pages 36–47. Springer, 2007. doi:10.1007/978-3-540-74782-6_5.
[27] Diego Calvanese, Benjamin Cogrel, Sarah Komla-Ebri, Roman Kontchakov, Davide Lanti, Martin Rezk, Mariano Rodriguez-Muro, and Guohuia Xiao. Ontop: Answering SPARQL queries over relational databases. Semantic Web Journal, 8(3):471–487, 2017. doi:10.3233/SW-160217.
[28] Diego Calvanese, Giuseppe De Giacomo, Domenico Lembo, Maurizio Lenzerini, and Riccardo Rosati. Tractable reasoning and efficient query answering in description logics: The DL-Lite family. Journal of Automated Reasoning, 39(3):385–429, 2007. doi:10.1007/s10817-007-9078-x.
[29] Diego Calvanese, Giuseppe De Giacomo, and Maurizio Lenzerini. On the decidability of query containment under constraints. In Proceedings of the 17th ACM SIGACT SIGMOD SIGART Symposium on Principles of Database Systems (PODS’98), pages 149–158, 1998. doi:10.1145/275487.275504.
[30] Diego Calvanese, Giuseppe De Giacomo, and Maurizio Lenzerini. Reasoning in expressive description logics with fixpoints based on automata on infinite trees. In Proceedings of the 16th International Joint Conference on Artificial Intelligence (IJCAI’99), pages 84–89, 1999. doi:10.5555/1624218.1624231.
[31] Diego Calvanese, Giuseppe De Giacomo, and Maurizio Lenzerini. Identification constraints and functional dependencies in description logics. In Bernhard Nebel, editor, Proc. of the 17th Int. Joint Conf. on Artificial Intelligence (IJCAI 2001), pages 155–160. Morgan Kaufmann, 2001. Seattle, Washington, USA, August 4-10, 2001. doi:10.5555/1642090.1642111.
[32] Diego Calvanese, Tahir Emre Kalayci, Marco Montali, Ario Santoso, and Wil van der Aalst. Conceptual schema transformation in ontology-based data access. In Catherine Faron Zucker, Chiara Ghidini, Amedeo Napoli, and Yannick Toussaint, editors, Proceedings of the 21st International Conference on Knowledge Engineering and Knolwedge Management, volume 11313 of LNAI. Springer, 2018. 12-16 Nov 2018, Nancy, France. doi:10.1007/978-3-030-03667-6_4.
[33] Diego Calvanese, C. Maria Keet, Werner Nutt, Mariano Rodríguez-Muro, and Giorgio Stefanoni. Web-based graphical querying of databases through an ontology: the WONDER system. In Sung Y. Shin, Sascha Ossowski, Michael Schumacher, Mathew J. Palakal, and Chih-Cheng Hung, editors, Proceedings of ACM Symposium on Applied Computing (ACM SAC’10), pages 1389–1396. ACM, 2010. March 22-26 2010, Sierre, Switzerland. doi:10.1145/1774088.1774384.
[34] Diego Calvanese, Maurizio Lenzerini, and Daniele Nardi. Unifying class-based representation formalisms. Journal of Artificial Intelligence Research, 11:199–240, 1999. doi:10.5555/3013545.3013550.
[35] Diego Calvanese, Pietro Liuzzo, Alessandro Mosca, José Remesal, Martin Rezk, and Guillem Rull. Ontology-based data integration in epnet: Production and distribution of food during the roman empire. Engineering Applications of Artificial Intelligence, 51:212–229, 2016. doi:10.1016/j.engappai.2016.01.005.
[36] Peter P. Chen. The entity-relationship model—toward a unified view of data. ACM Transactions on Database Systems, 1(1):9–36, 1976. doi:10.1145/320434.320440.
[37] HD Crockett, J Guynes, and CW Slinkman. Framework for development of conceptual data modelling techniques. Information and Software Technology, 33(2):134–142, 1991. doi:10.1016/0950-5849(91)90058-J.
[38] Bernardo Cuenca Grau, Ian Horrocks, Boris Motik, Bijan Parsia, Peter Patel-Schneider, and Ulrike Sattler. OWL 2: The next step for OWL. Journal of Web Semantics: Science, Services and Agents on the World Wide Web, 6(4):309–322, 2008. doi:10.1016/j.websem.2008.05.001.
[39] Islay Davies, Peter Green, Michael Rosemann, Marta Indulska, and Stan Gallo. How do practitioners use conceptual modeling in practice? Data & Knowledge Engineering, 58(3):358–380, 2006. doi:10.1016/j.datak.2005.07.007.
[40] Thomas Eiter, Josiane Xavier Parreira, and Patrik Schneider. Spatial ontology-mediated query answering over mobility streams. In E. Blomqvist et al., editors, Proceedings of the 13th Extended Semantic Web Conference (ESWC’17), volume 10249 of LNCS, pages 219–237. Springer, 2017. 30 May - 1 June 2017, Portoroz, Slovenia. doi:10.1007/978-3-319-58068-5_14.
[41] Carles Farré, Anna Queralt, Guillem Rull, Ernest Teniente, and Toni Urpí. Automated reasoning on UML conceptual schemas with derived information and queries. Information and Software Technology, 55(9):1529–1550, 2013. doi:10.1016/j.infsof.2013.02.010.
[42] Pablo Fillotrani and C. Maria Keet. Evidence-based lean conceptual data modelling languages. Journal of Computer Science and Technology, 21(2):e10, oct 2021. doi:10.24215/16666038.21.e10.
[43] Pablo R. Fillottrani, Enrico Franconi, and Sergio Tessaris. The ICOM 3.0 intelligent conceptual modelling tool and methodology. Semantic Web Journal, 3(3):293–306, 2012. doi:10.3233/SW-2011-0038.
[44] Pablo R. Fillottrani and C. Maria Keet. Conceptual model interoperability: a metamodel-driven approach. In A. Bikakis et al., editors, Proceedings of the 8th International Web Rule Symposium (RuleML’14), volume 8620 of LNCS, pages 52–66. Springer, 2014. August 18-20, 2014, Prague, Czech Republic. doi:10.1007/978-3-319-09870-8_4.
[45] Pablo R. Fillottrani and C. Maria Keet. Dimensions affecting representation styles in ontologies. In 1st Iberoamerican conference on Knowledge Graphs and Semantic Web (KGSWC’19), volume 1029 of CCIS, pages 186–200. Springer, 2019. 24-28 June 2019, Villa Clara, Cuba. doi:10.1007/978-3-030-21395-4_14.
[46] Pablo R. Fillottrani and C. Maria Keet. An analysis of commitments in ontology language design. In B. Brodaric and F. Neuhaus, editors, Proceedings of the 11th International Conference on Formal Ontology in Information Systems (FOIS’20), volume 330 of Frontiers in Artificial Intelligence and Applications, pages 46–60, 2020. doi:10.3233/FAIA200659.
[47] Pablo R. Fillottrani and C. Maria Keet. KnowID: An architecture for efficient knowledge-driven information and data access. Data Intelligence, 2(4):487–512, 2020. doi:10.1162/dint_a_00060.
[48] Pablo R. Fillottrani, C. Maria Keet, and David Toman. Polynomial encoding of orm conceptual models in $\mathcal{CFDI}_{nc}^{\forall-}$ . In Diego Calvanese and B. Konev, editors, Proceedings of the 28th International Workshop on Description Logics (DL’15), volume 1350 of CEUR-WS, pages 401–414, 2015. 7-10 June 2015, Athens, Greece. URL: https://ceur-ws.org/Vol-1350/paper-50.pdf.
[49] E. Franconi and G. Ng. The ICOM tool for intelligent conceptual modelling. In 7th Workshop on Knowledge Representation meets Databases (KRDB’00), 2000. Berlin, Germany, 2000. doi:10.5555/2590200.2590206.
[50] Enrico Franconi, Alessandro Mosca, and Dmitry Solomakhin. The formalisation of ORM2 and its encoding in OWL2. KRDB Research Centre Technical Report KRDB12-2, Faculty of Computer Science, Free University of Bozen-Bolzano, Italy, mar 2012.
[51] Birte Glimm, Ian Horrocks, Boris Motik, and Giorgos Stoilos. Optimising ontology classification. In The Semantic Web–ISWC 2010: 9th International Semantic Web Conference, ISWC 2010, Shanghai, China, November 7-11, 2010, Revised Selected Papers, Part I 9, pages 225–240. Springer, 2010. doi:10.1007/978-3-642-17746-0_15.
[52] Carlos A. González and Jordi Cabot. Formal verification of static software models in mde: A systematic review. Information and Software Technology, 56(8):821–838, 2014. doi:10.1016/j.infsof.2014.03.003.
[53] Benjamin N. Grosof, Ian Horrocks, Raphael Volz, and Stefan Decker. Description logic programs: Combining logic programs with description logic. In Proceedings of the 12th International World Wide Web Conference (WWW’03), pages 48–57, 2003. Budapest, Hungary. doi:10.1145/775157.775160.
[54] Object Management Group. Distributed ontology, model, and specification language, feb 2018. URL: http://www.omg.org/spec/DOL/.
[55] Nicola Guarino. Formal ontology and information systems. In N. Guarino, editor, Proceedings of Formal Ontology in Information Systems (FOIS’98), Frontiers in Artificial intelligence and Applications, pages 3–15. Amsterdam: IOS Press, 1998.
[56] Giancarlo Guizzardi. Ontological Foundations for Structural Conceptual Models. Phd thesis, University of Twente, The Netherlands. Telematica Instituut Fundamental Research Series No. 15, 2005.
[57] Volker Haarslev, Kay Hidde, Ralf Möller, and Michael Wessel. The racerpro knowledge representation and reasoning system. Semantic Web Journal, 3(3):267–277, 2012. doi:10.3233/SW-2011-0032.
[58] Christoph Haase and Carsten Lutz. Complexity of subsumption in the EL family of description logics: Acyclic and cyclic tboxes. In Malik Ghallab, Constantine D. Spyropoulos, Nikos Fakotakis, and Nikolaos M. Avouris, editors, ECAI 2008 - 18th European Conference on Artificial Intelligence, Patras, Greece, July 21-25, 2008, Proceedings, volume 178 of Frontiers in Artificial Intelligence and Applications, pages 25–29. IOS Press, 2008. doi:10.3233/978-1-58603-891-5-25.
[59] Terry Halpin. A logical analysis of information systems: static aspects of the data-oriented perspective. PhD thesis, University of Queensland, Australia, 1989. URL: https://search.library.uq.edu.au/permalink/f/l3gdeh/61UQ_ALMA2179989800003131.
[60] Terry Halpin and Tony Morgan. Information modeling and relational databases. Morgan Kaufmann, 2nd edition, 2008.
[61] Patrick J. Hayes and Peter F. Patel-Schneider. RDF 1.1 Semantics. W3c recommendation, World Wide Web Consortium, feb 2014. URL: http://www.w3.org/TR/rdf11-mt/.
[62] Daniel Hernández, Aidan Hogan, and Markus Krötzsch. Reifying RDF: what works well with wikidata? In Thorsten Liebig and Achille Fokoue, editors, Proceedings of the 11th International Workshop on Scalable Semantic Web Knowledge Base Systems 2015), volume 1457 of CEUR-WS, pages 32–47. CEUR-WS.org, 2015. Bethlehem, PA, USA, October 11, 2015. URL: https://ceur-ws.org/Vol-1457/SSWS2015_paper3.pdf.
[63] Aidan Hogan, Eva Blomqvist, Michael Cochez, Claudia d’Amato, Gerard de Melo, Claudio Gutiérrez, José Emilio Labra Gayo, Sabrina Kirrane, Sebastian Neumaier, Axel Polleres, Roberto Navigli, Axel-Cyrille Ngonga Ngomo, Sabbir M. Rashid, Anisa Rula, Lukas Schmelzeisen, Juan F. Sequeda, Steffen Staab, and Antoine Zimmermann. Knowledge graphs. Technical report, 2020. doi:10.48550/arXiv.2003.02320.
[64] Ian Horrocks, Oliver Kutz, and Ulrike Sattler. The even more irresistible $\mathcal{SROIQ}$ . In Proceedings of the Tenth International Conference on Principles of Knowledge Representation and Reasoning (KR’06), KR’06, pages 57–67. AAAI Press, 2006. URL: http://www.aaai.org/Library/KR/2006/kr06-009.php.
[65] Ian Horrocks, Peter F. Patel-Schneider, and Frank van Harmelen. From SHIQ and RDF to OWL: The making of a web ontology language. Journal of Web Semantics, 1(1):7, 2003. doi:10.1016/j.websem.2003.07.001.
[66] Richard Hull and Roger King. Semantic database modeling: Survey, applications, and research issues. ACM Computing Surveys (CSUR), 19(3):201–260, 1987. doi:10.1145/45072.45073.
[67] Amir Jahangard Rafsanjani and Seyed-Hassan Mirian-Hosseinabadi. A Z Approach to Formalization and Validation of ORM Models. In Ezendu Ariwa and Eyas El-Qawasmeh, editors, Digital Enterprise and Information Systems, volume 194 of CCIS, pages 513–526. Springer, 2011. doi:10.1007/978-3-642-22603-8_45.
[68] Mustafa Jarrar, Jan Demey, and Robert Meersman. On using conceptual data modeling for ontology engineering. Journal on Data Semantics, 2003. doi:10.1007/978-3-540-39733-5_8.
[69] Elem Güzel Kalayci, Guohui Xiao, Vladislav Ryzhikov, Tahir Emre Kalayci, and Diego Calvanese. Ontop-temporal: A tool for ontology-based query answering over temporal data. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management, CIKM 2018, Torino, Italy, October 22-26, 2018, pages 1927–1930, 2018. doi:10.1145/3269206.3269230.
[70] Ken Kaneiwa and Ken Satoh. Consistency checking algorithms for restricted uml class diagrams. In Jürgen Dix and Stephen J. Hegner, editors, Foundations of Information and Knowledge Systems, pages 219–239, Berlin, Heidelberg, 2006. Springer. doi:10.1007/11663881_13.
[71] C. Maria Keet. Mapping the Object-Role Modeling language ORM2 into Description Logic language $\mathcal{DLR}_{ifd}$ . Technical Report 0702089v2, KRDB Research Centre, Free University of Bozen-Bolzano, Italy, apr 2009. arXiv:cs.LO/0702089v2. doi:10.48550/arXiv.cs/0702089.
[72] C. Maria Keet. Ontology-driven formal conceptual data modeling for biological data analysis. In Mourad Elloumi and Albert Y. Zomaya, editors, Biological Knowledge Discovery Handbook: Preprocessing, Mining and Postprocessing of Biological Data, chapter 6, pages 129–154. Wiley, 2013. doi:10.1002/9781118617151.ch06.
[73] C. Maria Keet. An introduction to ontology engineering, volume 20 of Computing. College Publications, UK, 2018. 334p.
[74] C. Maria Keet and Sonia Berman. Determining the preferred representation of temporal constraints in conceptual models. In H.C. Mayr et al., editors, 36th International Conference on Conceptual Modeling (ER’17), volume 10650 of LNCS, pages 437–450. Springer, 2017. 6-9 Nov 2017, Valencia, Spain. doi:10.1007/978-3-319-69904-2_33.
[75] C. Maria Keet and Pablo R. Fillottrani. An analysis and characterisation of publicly available conceptual models. In P. Johannesson, M. L. Lee, S.W. Liddle, A. L. Opdahl, and O. Pastor López, editors, Proceedings of the 34th International Conference on Conceptual Modeling (ER’15), volume 9381 of LNCS, pages 585–593. Springer, 2015. 19-22 Oct, Stockholm, Sweden. doi:10.1007/978-3-319-25264-3_45.
[76] C. Maria Keet and Pablo R. Fillottrani. An ontology-driven unifying metamodel of UML Class Diagrams, EER, and ORM2. Data & Knowledge Engineering, 98:30–53, 2015. doi:10.1016/j.datak.2015.07.004.
[77] Holger Knublauch and Dimitris Kontokostas. Shapes constraint language (shacl). W3C Recommendation, 2017. https://www.w3.org/TR/shacl/.
[78] Markus Krötzsch, Maximilian Marx, Ana Ozaki, and Veronika Thost. Attributed description logics: Reasoning on knowledge graphs. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI’18), pages 5309–5313. International Joint Conferences on Artificial Intelligence Organization, jul 2018. doi:10.24963/ijcai.2018/743.
[79] Domenico Lembo, Valerio Santarelli, Domenico Fabio Savo, and Giuseppe De Giacomo. Graphol: A graphical language for ontology modeling equivalent to owl 2. Future Internet, 14(3), 2022. doi:10.3390/fi14030078.
[80] Lina Lubyte and Sergio Tessaris. Automated extraction of ontologies wrapping relational data sources. In Proceedings of International Conference on Database and Expert Systems Applications (DEXA’09), pages 128–142. Springer, 2009. doi:10.1007/978-3-642-03573-9_10.
[81] Carsten Lutz, David Toman, and Frank Wolter. Conjunctive query answering in the description logic el using a relational database system. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI’09), pages 2070–2075. ACM, 2009. URL: http://ijcai.org/Proceedings/09/Papers/341.pdf.
[82] Weicong Ma, C. Maria Keet, Wayne Oldford, David Toman, and Grant Weddell. The utility of the abstract relational model and attribute paths in sql. In Catherine Faron Zucker, Chiara Ghidini, Amedeo Napoli, and Yannick Toussaint, editors, Proceedings of the 21st International COnference on Knowledge Engineering and Knowledge Management (EKAW’18)), volume 11313 of LNAI, pages 195–211. Springer, 2018. 12-16 Nov. 2018, Nancy, France. doi:10.1007/978-3-030-03667-6_13.
[83] Wolfgang Maass, Arturo Castellanos, Monica C. Tremblay, Roman Lukyanenko, and Veda C. Storey. AI explainability: Embedding conceptual models. In Niels Bjørn-Andersen, Roman Beck, Stacie Petter, Tina Blegind Jensen, Tilo Böhmann, Kai-Lung Hui, and Viswanath Venkatesh, editors, Proceedings of the 43rd International Conference on Information Systems, ICIS 2022, Digitization for the Next Generation, Copenhagen, Denmark, December 9-14, 2022. Association for Information Systems, 2022. URL: https://aisel.aisnet.org/icis2022/data_analytics/data_analytics/12.
[84] Wolfgang Maass and Veda C Storey. Pairing conceptual modeling with machine learning. Data & Knowledge Engineering, 134:101909, 2021. doi:10.1016/j.datak.2021.101909.
[85] Fabio Massacci. Decision procedures for expressive description logics with intersection, composition, converse of roles and role identity. In Proceedings of the 17th International Joint Conference on Artificial Intelligence (IJCAI’2001), pages 193–198, 2001.
[86] Melinda McDaniel and Veda C Storey. Evaluating domain ontologies: clarification, classification, and challenges. ACM Computing Surveys (CSUR), 52(4):1–44, 2019. doi:10.1145/3329124.
[87] Deborah L. McGuinness and Frank van Harmelen. OWL Web Ontology Language Overview. W3C Recommendation., 2004. URL: http://www.w3.org/TR/owl-features/.
[88] Jack Minker. Foundations of deductive databases and logic programming. Morgan Kaufmann, 2014.
[89] Till Mossakowski, Christoph Lange, and Oliver Kutz. Three semantics for the core of the Distributed Ontology Language. In Michael Grüninger, editor, Proceedings of the 7th International Conference on Formal Ontology in Information Systems (FOIS’12). IOS Press, 2012. 24-27 July, Graz, Austria. doi:10.3233/978-1-61499-084-0-337.
[90] Boris Motik, Bernardo Cuenca Grau, Ian Horrocks, Zhe Wu, Achille Fokoue, and Carsten Lutz. OWL 2 Web Ontology Language Profiles. W3C recommendation, W3C, 27 October 2009. URL: http://www.w3.org/TR/owl2-profiles/.
[91] Boris Motik, Peter F. Patel-Schneider, and Bijan Parsia. OWL 2 web ontology language structural specification and functional-style syntax. W3c recommendation, W3C, 27 October 2009. URL: http://www.w3.org/TR/owl2-syntax/.
[92] Matthew Nizol, Laura K. Dillon, and R. E. K. Stirewalt. Toward tractable instantiation of conceptual data models using non-semantics-preserving model transformations. In Proceedings of the 6th International Workshop on Modeling in Software Engineering (MiSE’14), pages 13–18. ACM Conference Proceedings, 2014. Hyderabad, India, June 02-03, 2014. doi:10.1145/2593770.2593771.
[93] Object Management Group. Semantics of Business Vocabulary and Rules (SBVR) – OMG released versions of SBVR, formal/2008-01-02, jan 2008. URL: http://www.omg.org/spec/SBVR/1.0.
[94] Object Management Group. Superstructure specification. Standard 2.4.1, Object Management Group, 2012. URL: http://www.omg.org/spec/UML/2.4.1/.
[95] E. A. N. Ongoma. Formalising temporal attributes in temporal conceptual data models. Msc thesis, Department of Computer Science, 2015.
[96] Magdalena Ortiz. A short introduction to SHACL for logicians. In Helle Hvid Hansen, Andre Scedrov, and Ruy J. G. B. de Queiroz, editors, Proceedings of the 29th International Workshop on Logic, Language, Information, and Computation (WoLLIC’23), volume 13923 of LNCS, pages 19–32. Springer, 2023. Halifax, NS, Canada, July 11-14, 2023. doi:10.1007/978-3-031-39784-4_2.
[97] Özgür Lütfü Özçep, Ralf Möller, and Christian Neuenstadt. Stream-query compilation with ontologies. In Bernhard Pfahringer and Jochen Renz, editors, Proceedings of the 28th Australasian Joint Conference on Advances in Artificial Intelligence (AI’15), volume 9457 of LNCS, pages 457–463. Springer, 2015. Canberra, ACT, Australia, November 30 – December 4, 2015. doi:10.1007/978-3-319-26350-2_40.
[98] Wen-Lin Pan and Da-xin Liu. Mapping object role modeling into common logic interchange format. In Proceedings of the 3rd International Conference on Advanced Computer Theory and Engineering (ICACTE’10), volume 2, pages 104–109. IEEE Computer Society, 2010. doi:10.1109/ICACTE.2010.5579141.
[99] Christine Parent, Stefano Spaccapietra, and Esteban Zimányi. Conceptual modeling for traditional and spatio-temporal applications—the MADS approach. Berlin Heidelberg: Springer Verlag, 2006. doi:10.1007/3-540-30326-X.
[100] Antonella Poggi, Domenico Lembo, Diego Calvanese, Giuseppe De Giacomo, Maurizio Lenzerini, and Riccardo Rosati. Linking data to ontologies. Journal on Data Semantics, X:133–173, 2008. doi:10.1007/978-3-540-77688-8_5.
[101] Alexandra Poulovassilis and Peter McBrien. A general formal framework for schema transformation. Data & Knowledge Engineering, 28(1):47–71, 1998. doi:10.1016/s0169-023x(98)00013-5.
[102] Sandeep Purao and Veda C. Storey. A multi-layered ontology for comparing relationship semantics in conceptual models of databases. Applied Ontology, 1(1):117–139, 2005. URL: http://content.iospress.com/articles/applied-ontology/ao000011.
[103] Anna Queralt, Alessandro Artale, Diego Calvanese, and Ernest Teniente. OCL-Lite: Finite reasoning on UML/OCL conceptual schemas. Data & Knowledge Engineering, 73:1–22, 2012. doi:10.1016/j.datak.2011.09.004.
[104] Anna Queralt and Ernest Teniente. Decidable reasoning in UML schemas with constraints. In Zohra Bellahsene and Michel Léonard, editors, Proceedings of the 20th International Conference on Advanced Information Systems Engineering (CAiSE’08), volume 5074 of LNCS, pages 281–295. Springer, 2008. Montpellier, France, June 16-20, 2008. doi:10.1007/978-3-540-69534-9_23.
[105] Jason Saint Jacques, David Toman, and Grant E. Weddell. Object-relational queries over cfdi ${}_{\mbox{nc}}$ knowledge bases: OBDA for the sql-literate. In Subbarao Kambhampati, editor, Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, IJCAI 2016, New York, NY, USA, 9-15 July 2016, pages 1258–1264. IJCAI/AAAI Press, 2016. URL: http://www.ijcai.org/Abstract/16/182.
[106] Manfred Schmidt-Schauß. Subsumption in KL-ONE is undecidable. In Proceedings of the 1st International Conference on Principles of Knowledge Representation and Reasoning, pages 421–431, 1989.
[107] Thomas Schneider and Mantas Šimkus. Ontologies and data management: A brief survey. KI-Künstliche Intelligenz, 34(3):329–353, 2020. doi:10.1007/s13218-020-00686-3.
[108] Matthias Sedlmeier and Martin Gogolla. Design and prototypical implementation of an integrated graph-based conceptual data model. In Bernhard Thalheim, Hannu Jaakkola, Yasushi Kiyoki, and Naofumi Yoshida, editors, Proceedings of the 24th International Conference Information Modelling and Knowledge Bases (EJC’14), volume 272 of FAIA, pages 376–395. IOS Press, 2014. doi:10.3233/978-1-61499-472-5-376.
[109] Asadullah Shaikh, Abdul Hafeez, Asif Ali Wagan, Mesfer Alrizq, Abdullah Alghamdi, and Mana Saleh Al Reshan. More than two decades of research on verification of UML class models: A systematic literature review. IEEE Access, 9:142461–142474, 2021. doi:10.1109/ACCESS.2021.3121222.
[110] Yannis Smaragdakis, Christoph Csallner, and Ranjith Subramanian. Scalable satisfiability checking and test data generation from modeling diagrams. Automated Software Engineering, 16:73–99, 2009. doi:10.1007/s10515-008-0044-6.
[111] Il-Yeol Song and Peter P. Chen. Entity relationship model. In Ling Liu and M. Tamer Özsu, editors, Encyclopedia of Database Systems, volume 1, pages 1003–1009. Springer, 2009. doi:10.1007/978-0-387-39940-9_148.
[112] Ahmet Soylu, Martin Giese, Ernesto Jimenez-Ruiz, Evgeny Kharlamov, Dmitriy Zheleznyakov, and Ian Horrocks. Ontology-based end-user visual query formulation: Why, what, who, how, and which? Universal Access in the Information Society, 16(2):435–467, jun 2017. doi:10.1007/s10209-016-0465-0.
[113] Ahmet Soylu, Evgeny Kharlamov, Dimitry Zheleznyakov, Ernesto Jimenez Ruiz, Martin Giese, Martin G. Skjaeveland, Dag Hovland, Rudolf Schlatte, Sebastian Brandt, Hallstein Lie, and Ian Horrocks. OptiqueVQS: a visual query system over ontologies for industry. Semantic Web Journal, 9(5):627–660, 2018. doi:10.3233/sw-180293.
[114] Francesco Sportelli and Enrico Franconi. Formalisation of orm derivation rules and their mapping into owl. In OTM Conferences in Computer Science, volume 10033, pages 827–843, 2016. doi:10.1007/978-3-319-48472-3_52.
[115] Veda C. Storey. Relational database design based on the entity-relationship model. Data & knowledge engineering, 7(1):47–83, 1991. doi:10.1016/0169-023X(91)90033-T.
[116] Veda C. Storey, Roman Lukyanenko, and Arturo Castellanos. Conceptual modeling: Topics, themes, and technology trends. ACM Comput. Surv., 55(14s), jul 2023. doi:10.1145/3589338.
[117] Veda C. Storey, Roman Lukyanenko, Wolfgang Maass, and Jeffrey Parsons. Explainable AI. Commun. ACM, 65(4):27–29, 2022. doi:10.1145/3490699.
[118] Vijayan Sugumaran and Veda C Storey. Ontologies for conceptual modeling: their creation, use, and management. Data & knowledge engineering, 42(3):251–271, 2002. doi:10.1016/S0169-023X(02)00048-4.
[119] Vijayan Sugumaran and Veda C Storey. The role of domain ontologies in database design: An ontology management and conceptual modeling environment. ACM Transactions on Database Systems (TODS), 31(3):1064–1094, 2006. doi:10.1145/1166074.1166083.
[120] Arthur H. M. ter Hofstede and Henderik A. Proper. How to formalize it? formalization principles for information systems development methods. Information and Software Technology, 40(10):519–540, 1998. doi:10.1016/S0950-5849(98)00078-0.
[121] Herman J. ter Horst. Completeness, decidability and complexity of entailment for rdf schema and a semantic extension involving the owl vocabulary. Journal of Web Semantics, 3(2):79–115, 2005. doi:10.1016/j.websem.2005.06.001.
[122] Bernhard Thalheim. Extended entity relationship model. In Ling Liu and M. Tamer Özsu, editors, Encyclopedia of Database Systems, volume 1, pages 1083–1091. Springer, 2009. doi:10.1007/978-0-387-39940-9_157.
[123] Stephan Tobies. Complexity Results and Practical Algorithms for Logics in Knowledge Representation. PhD thesis, RWTH Aachen, 2001. URL: http://sylvester.bth.rwth-aachen.de/dissertationen/2001/082/01_082.pdf.
[124] David Toman and Grant E. Weddell. Fundamentals of Physical Design and Query Compilation. Synthesis Lectures on Data Management. Morgan & Claypool, 2011. doi:10.1007/978-3-031-01881-7.
[125] David Toman and Grant E. Weddell. On adding inverse features to the description logic CFD ${}^{\mbox{{$\forall$}}}$ ${}_{\mbox{nc}}$ . In PRICAI 2014: Trends in Artificial Intelligence - 13th Pacific Rim International Conference on Artificial Intelligence, Gold Coast, QLD, Australia, December 1-5, 2014., pages 587–599, 2014. doi:10.1007/978-3-319-13560-1_47.
[126] Albert Tort, Antoni Olivé, and Maria-Ribera Sancho. An approach to test-driven development of conceptual schemas. Data & Knowledge Engineering, 70:1088–1111, 2011. doi:10.1016/j.datak.2011.07.006.
[127] Juan Trujillo, Karen C Davis, Xiaoyong Du, Ernesto Damiani, and Veda C. Storey. Conceptual modeling in the era of big data and artificial intelligence: Research topics and introduction to the special issue, 2021. doi:10.1016/j.datak.2021.101911.
[128] Isadora Valle Sousa, Tiago Prince Sales, Eduardo Guerra, Luiz Olavo Bonino da Silva Santos, and Giancarlo Guizzardi. What do I get from modeling? an empirical study on using structural conceptual models. In International Conference on Enterprise Design, Operations, and Computing, pages 21–38. Springer, 2023. doi:10.1007/978-3-031-46587-1_2.
[129] John R. Venable and John C. Grundy. Integrating and supporting entity relationship and object role models. In Mike P. Papazoglou, editor, Proceedings of the 14th International Conference on Object-Oriented and Entity-Relationship Modelling (ER’95), volume 1021 of LNCS, pages 318–328. Springer, 1995. doi:10.1007/BFb0020543.
[130] Michaël Verdonck, Frederik Gailly, and Sergio de Cesare. Comprehending 3d and 4d ontology-driven conceptual models: an empirical study. Information Systems, 93:101568, 2020. doi:10.1016/j.is.2020.101568.
[131] Michaël Verdonck, Frederik Gailly, Sergio De Cesare, and Geert Poels. Ontology-driven conceptual modeling: A systematic literature mapping and review. Applied Ontology, 10(3-4):197–227, 2015. doi:10.3233/AO-150154.
[132] Denny Vrandecic. Building a multilingual Wikipedia. Communications of the ACM, 64(4):38–41, 2021. doi:10.1145/3425778.
[133] Heba M. Wagih, Doaa S. El Zanfaly, and Mohamed M. Kouta. Mapping Object Role Modeling 2 schemes into $\mathcal{SROIQ}(d)$ description logic. International Journal of Computer Theory and Engineering, 5(2):232–237, 2013. doi:10.7763/ijcte.2013.v5.684.
[134] Kunmei Wen, Yong Zeng, Ruixuan Li, and Jianqiang Lin. Modeling semantic information in engineering applications: a review. Artificial Intelligence Review, 37:97–117, 2012. doi:10.1007/s10462-011-9221-2.
[135] Michael Wessel. Obstacles on the way to qualitative spatial reasoning with description logics: some undecidability results. In Carole A. Goble, Deborah L. McGuinness, Ralf Möller, and Peter F. Patel-Schneider, editors, Proceedings of the International Workshop in Description Logics (DL’01), volume 49 of CEUR WS, 2001. Stanford, CA, USA, August 1-3, 2001. URL: https://ceur-ws.org/Vol-49/Wessel-122start.ps.
[136] Guohui Xiao, Linfang Ding, Benjamin Cogrel, and Diego Calvanese. Virtual knowledge graphs: An overview of systems and use cases. Data Intelligence, 1:201–223, 2019. doi:10.1162/dint_a_00011.
[137] Tilmann Zäschke, Stefania Leone, Tobias Gmünder, and Moira C. Norrie. Optimising conceptual data models through profiling in object databases. In Wilfred Ng, Veda C. Storey, and Juan Trujillo, editors, Proceedings of the 32th International Conference on Conceptual Modeling (ER’13), volume 8217 of LNCS, pages 284–297. Springer, 2013. Hong-Kong, November 11-13, 2013. doi:10.1007/978-3-642-41924-9_24.

Appendix A Examples of both approaches to the logic-based reconstruction

Since both approaches for CDM or CDML formalisation work in principle for any conceptual data modelling language, as described in Section 3.3, we first harmonise terminology across such CDMLs, using the unified metamodel [76]: Relationship (also called association or fact type), Role (relationship component, association end), Object Type (entity type, class), Attribute¹⁰¹⁰10ORM does not have “attribute” as such, but a value type has an attribute, it being a binary relation between a class and a data type. This is a straight-forward conversion procedure; see [44] for details., and Data Type. Second, the different properties of the rules-based vs. the mapping-based approach, as also depicted in Figure 3, practically result in different sequences of steps for how to create that logic-based reconstruction. The ones we followed in this appendix are graphically depicted in Figure 6, where steps 2 and 3 are illustrated in this appendix; step 1 was taken from other work and steps 4 and 5 are realised in crowd2. Note that the aim is to illustrate the way these logic-based reconstructions are done in the literature and these two approaches are our distillation of the two key distinct approaches researchers have taken. It is not meant to be prescriptive and there is no official or investigated method for carrying out this task.

We use the $\mathcal{DC}_{p}$ “positionalist core profile” of [42] to illustrate both approaches, because it respects the positionalist ontological commitment of those languages and it is a relatively simple language with few features that are those that have been shown to be used most in UML class diagrams, EER, and ORM2. Specifically, based on the analysis of the 101 publicly available CDMs [75], the feature list of $\mathcal{DC}_{p}$ is expressive enough to include 87.57% of the entities (elements and constraints) used in all the 101 models analysed, and 91,88% of the entities in the UML models, 73.29% of the contents of the ORM and ORM2 models, and 94.64% of the ER and EER models [42].

Figure 6: Possible sequences of steps for creating logic-based reconstructions of conceptual data models.

A.1 Rule-based approach

First, we specify the rules for the algorithmic conversion for any CDM within the $\mathcal{DC}_{p}$ feature list:

Definition 5 (Syntax of $\mathcal{DC}_{p}$ [42]).

Given a conceptual model in any of UML class diagrams, EER, and ORM2, take the set of all object types ranging over symbols $A$ , $B$ , …, binary relationships $P$ , datatypes $T$ and attributes $a$ in the conceptual data model as the basic elements in the knowledge base. Then construct a knowledge base in $\mathcal{DC}_{p}$ by applying the rules:

1.

For each relationship $P$ between object types $A$ and $B$ , add to the knowledge base
$\geq 1[1]P\sqsubseteq A$ and $\geq 1[2]P\sqsubseteq B$
2.

For each attribute $a$ of datatype $T$ within an object type $A$ (including the transformation of ORM’s Value Type following the rule in [44]), add
$A\sqsubseteq\exists a.T\sqcap\leq 1a$
3.

Subsumption between two object types $A$ and $B$ is formalised by adding the assertion
$A\sqsubseteq B$
4.

For each object type cardinality $m . . n$ in relationship $P$ with respect to its $i$ -th component $A$ , add
$A\sqsubseteq\,\leq n[i]P\,\sqcap\geq m[i]P$
5.

Add for each mandatory constraints of a concept $A$ in a relationship $P$ either the axiom
$A\sqsubseteq\,\geq 1[1]P$ or $A\sqsubseteq\,\geq 1[2]P$
depending on the position played by $A$ in $P$ . This is a special case of the previous one, with $n=1$ .
6.

For each single identification in object type $A$ with respect to an attribute $a$ of datatype $T$ , add
$\mathsf{id}\,A\,a$

Given the formalisation rules in Definition 5, the DL for $\mathcal{DC}_{p}$ would result in the following syntax: starting from atomic elements, we can construct binary relationships $R$ , arbitrary concepts $C$ and axioms $X$ as follows:

	$\displaystyle C\longrightarrow$	$\displaystyle\top\,\|\,A\,\|\,\leq k[i]R\,\|\,\geq k[i]R\,\|\,\forall a.T\,\|\,% \exists a.T\,\|\,$
		$\displaystyle\leq 1\,a\,\|\,C\sqcap D$
	$\displaystyle R\longrightarrow$	$\displaystyle\top_{2}\,\|\,P\,\|\,(i:C)$
	$\displaystyle X\longrightarrow$	$\displaystyle C\sqsubseteq D\,\|\,\mathsf{id}\,C\,a$

where $i=1,2$ and $0<k$ (roles may be numbered or named, and are not ordered).

Then, for the second step in the algorithmic procedure, the semantics. For DLs, it can avail of the model-theoretic semantics with its customary notation, as included in Definition 6:

Definition 6 (Semantics of $\mathcal{DC}_{p}$ [42]).

An $\mathcal{DC}_{p}$ interpretation $\cal{I}=(\Delta_{C}^{\cal{I}},\Delta_{T}^{\cal{I}},\cdot^{\cal{I}})$ for a knowledge base in $\mathcal{DC}_{p}$ consists of a set of objects $\Delta_{C}^{\cal{I}}$ , a set of datatype values $\Delta_{T}^{\cal{I}}$ , and a function $\cdot^{\cal{I}}$ satisfying the constraints shown in Table 4. It is said that $\cal{I}$ satisfies the assertion $C\sqsubseteq D$ iff $C^{\cal{I}}\subseteq D^{\cal{I}}$ ; and it satisfies the assertion $\mathsf{id}\,C\,a$ iff there exists $T$ such that $C^{\cal{I}}\subseteq(\exists a.T\sqcap\leq 1a)^{\cal{I}}$ (mandatory 1) and for all $v\in T^{\cal{I}}$ it holds that $\#\{c|c\in\Delta_{C}^{\cal{I}}\wedge(c,v)\in a^{\cal{I}}\}\leq 1$ (inverse functional).

Table 4: Semantics of

\mathcal{DC}

_p (Source: [42]).

\top^{\cal{I}}\subseteq\Delta_{C}^{\cal{I}}

A^{\cal{I}}\subseteq\top^{\cal{I}}

\top_{2}^{\cal{I}}=\top^{\cal{I}}\times\top^{\cal{I}}

P^{\cal{I}}\subseteq\top_{2}^{\cal{I}}

T^{\cal{I}}\subseteq\Delta_{T}^{\cal{I}}

a^{\cal{I}}\subseteq\top^{\cal{I}}\times\Delta^{\cal{I}}_{T}

(C\sqcap D)^{\cal{I}}=C^{\cal{I}}\cap D^{\cal{I}}

(\leq k[i]R)^{\cal{I}}=\{c\in\Delta_{C}^{\cal{I}}|\#\{(d_{1},d_{2})\in R^{\cal% {I}}.d_{i}=c\}\leq k\}

(\geq k[i]R)^{\cal{I}}=\{c\in\Delta_{C}^{\cal{I}}|\#\{d_{1},d_{2})\in R^{\cal{% I}}.d_{i}=c\}\geq k\}

(\exists a.T)^{\cal{I}}=\{c\in\Delta_{C}^{\cal{I}}|\exists v\in\Delta^{\cal{I}% }_{T}.(c,v)\in a^{\cal{I}}\wedge v\in T^{\cal{I}}\}

(\forall a.T)^{\cal{I}}=\{c\in\Delta_{C}^{\cal{I}}|\forall v\in\Delta^{\cal{I}% }_{T}.(c,v)\in a^{\cal{I}}\rightarrow v\in T^{\cal{I}}\}

(\leq 1\,a)^{\cal{I}}=\{c\in\Delta_{C}^{\cal{I}}|\#\{(c,v)\in a^{\cal{I}}\}% \leq 1\}

(i:C)^{\cal{I}}=\{(d_{1},d_{2})\in\top_{2}^{\cal{I}}|d_{i}\in C^{\cal{I}}\}

An alternative option is to choose either of the five relationship formalisation options described in Example 1, create a conversion algorithm from the positionalist relationships of conceptual data models to that choice, and then create a different profile accordingly with, say, OWL in the formalisation rules. The “bumping up the role names to relationships” choice and DL OWL2 syntax then would add the following axioms to the knowledge base, respectively in the same order as in Definition 5:

1.

SubClassOf(ObjectSomeValuesFrom(ex:hasP) ex:A) and
SubClassOf(ObjectSomeValuesFrom(ex:isOfP) ex:B)
2.

SubClassOf(ex:A (ObjectIntersectionOf (DataSomeValuesFrom(ex:a)
FunctionalDataProperty(ex:a)))
3.

SubClassOf(ex:A ex:B)
4.

SubClassOf(ex:A ObjectIntersectionOf(ObjectMinCardinality(n ex:hasP)
ObjectMaxCardinality(m ex:hasP)))
5.

SubClassOf(ex:A ObjectSomeValuesFrom(ex:hasP)) or
SubClassOf(ex:A ObjectSomeValuesFrom(ex:isOfP))
6.

SubClassOf(ex:A DataExactCardinality(1 ex:a)) and
SubClassOf(ex:A DataSomeValuesFrom(ex:a))

Alternatively, the relationship is not typed but qualified cardinality constraints are used, or hasP and isOfP are declared inverses, or only one of the two is introduced with an inverse feature where needed.

An example of this approach with a concrete CDM is illustrated in Example 2.

A.2 Mapping-based approach

The first step in the mapping approach is to declare the textual syntax which, if that were to have been done for $\mathcal{DC}_{p}$ , would have looked like as in Definition 7. For comprehensiveness, a table with textual elements mapping to the respective graphical elements of the selected modelling language should be done as well (Figure 7), then to declare the semantics (Definition 8). It can stop here, or be mapped into a a logic of choice to obtain either a precise or approximate indication of the computational complexity of the language needed for the CDM or chosen fragment thereof, as shown in Definition 9 for a DL. The ones here are based on [72], but includes only those features that are in $\mathcal{DC}_{p}$ to facilitate a comparison with the first approach.

Definition 7 (Conceptual Data Model $\mathcal{DC}_{p}$ syntax)).

A $\mathcal{DC}_{p}$ conceptual data model is a tuple $\Sigma\mathcal{}=(\mathcal{L},\mbox{\sc rel}\mathcal{},\mbox{\sc att}\mathcal{% },\mbox{\sc card}\mathcal{}_{R},\mbox{\sc card}\mathcal{}_{A},\mathbin{\mbox{% \sc isa}\mathcal{}},\mbox{\sc id}\mathcal{})$ such that:

1.

$\mathcal{L}$ is a finite alphabet partitioned into the sets: $\mathcal{C}$ (class symbols), $\mathcal{A}$ (attribute symbols), $\mathcal{R}$ (relationship symbols), $\mathcal{U}$ (role symbols), and $\mathcal{D}$ (domain symbols); the tuple $(\mathcal{C},\mathcal{A},\mathcal{R},\mathcal{U},\mathcal{D})$ is the signature of the conceptual model $\Sigma\mathcal{}$ .
2.

att is a function that maps a class symbol in $\mathcal{C}$ to an $\mathcal{A}$ -labeled tuple over $\mathcal{D}$ , $\mbox{\sc att}\mathcal{}:\mathcal{A}\mapsto\mathcal{D}$ , so that $\mbox{\sc att}\mathcal{}(C)=\{A_{1}:D_{1},\ldots,A_{h}:D_{h}\}$ where $h$ a non-negative integer.
3.

rel is a function that maps a relationship symbol in $\mathcal{R}$ to an $\mathcal{U}$ -labeled tuple over $\mathcal{C}$ , $\mbox{\sc rel}\mathcal{}(R)=\{U_{1}:C_{1},U_{2}:C_{2}\}$ , if $(U_{i},C_{i})\in\mbox{\sc rel}\mathcal{}(R)$ (with $i=\{1,2\}$ ), then $\mbox{\sc player}\mathcal{}(R,U_{i})=C_{i}$ and $\mbox{\sc role}\mathcal{}(R,C_{i})=U_{i}$ . The signature of the relation is $\sigma_{R}=\langle\mathcal{U},\mathcal{C},\mbox{\sc player}\mathcal{},\mbox{% \sc role}\mathcal{}\rangle$ , where for all $U_{i}\in\mathcal{U}$ , $C_{i}\in\mathcal{C}$ , if $\sharp U\geq\sharp C$ then for each $u_{i}$ , $c_{i}$ , $\mbox{\sc rel}\mathcal{}(R)$ , we have $\mbox{\sc player}\mathcal{}(R,U_{i})=C_{i}$ and $\mbox{\sc role}\mathcal{}(R,C_{i})=U_{i}$ , and if $\sharp U>\sharp C$ then $\mbox{\sc player}\mathcal{}(R,U_{i})=C_{i}$ , $\mbox{\sc player}\mathcal{}(R,U_{i+1})=C_{i}$ and $\mbox{\sc role}\mathcal{}(R,C_{i})=U_{i},U_{i+1}$ .
4.

$\mbox{\sc card}\mathcal{}_{R}$ is a function $\mbox{\sc card}\mathcal{}_{R}:\mathcal{C}\times\mathcal{R}\times\mathcal{U}% \mapsto\mathbb{N}\times(\mathbb{N}\cup\{\infty\})$ denoting cardinality constraints. We denote with $\mbox{\sc cmin}\mathcal{}(C,R,U)$ and $\mbox{\sc cmax}\mathcal{}(C,R,U)$ the first and second component of $\mbox{\sc card}\mathcal{}_{R}$ .
5.

$\mbox{\sc card}\mathcal{}_{A}$ is a function $\mbox{\sc card}\mathcal{}_{A}:\mathcal{C}\times\mathcal{A}\mapsto\mathbb{N}% \times(\mathbb{N}\cup\{\infty\})$ denoting multiplicity constraints for attributes. We denote with $\mbox{\sc cmin}\mathcal{}(C,A)$ and $\mbox{\sc cmax}\mathcal{}(C,A)$ the first and second component of $\mbox{\sc card}\mathcal{}_{A}$ , and $\mbox{\sc card}\mathcal{}_{A}(C,A)$ may be defined only if $(A,D)\in\mbox{\sc att}\mathcal{}(C)$ for some $D\in\mathcal{D}$ ;
6.

$\mathbin{\mbox{\sc isa}\mathcal{}}$ is a binary relationship $\mathbin{\mbox{\sc isa}\mathcal{}}\subseteq\mathcal{C}\times\mathcal{C}$ .
7.

id is a function, $\mbox{\sc id}\mathcal{}:\mathcal{C}\mapsto\mathcal{A}$ , that maps a class symbol in $\mathcal{C}$ to its key attribute and $A\in\mathcal{A}$ is an attribute already defined in $\mbox{\sc att}\mathcal{}(C)$ , i.e., $\mbox{\sc id}\mathcal{}(C)$ may be defined only if $(A,D)\in\mbox{\sc att}\mathcal{}(C)$ for some $D\in\mathcal{D}$ .

Figure 7: Sample mapping of the

\mathcal{DC}_{p}

textual elements from Definition 7 to graphical elements of one of the EER notational flavours and to UML Class Diagram elements.

Definition 8 ( $\mathcal{DC}_{p}$ Semantics).

Let $\Sigma\mathcal{}$ be a $\mathcal{DC}_{p}$ conceptual data model. An interpretation for the conceptual model $\Sigma\mathcal{}$ is a tuple ${\mathcal{I}}=(\Delta^{\cal I}\/\cup\Delta_{D}^{\cal I}\/,\cdot^{\cal I}\/)$ , such that:

$\blacksquare$

$\Delta^{\cal I}\/$ is a nonempty set of abstract objects disjoint from $\Delta_{D}^{\cal I}\/$ ;
$\blacksquare$

$\Delta_{D}^{\cal I}\/=\bigcup_{D_{i}\in\mathcal{D}}\Delta_{D_{i}}^{\cal I}\/$ is the set of basic domain values used in $\Sigma\mathcal{}$ ; and
$\blacksquare$
$\cdot^{\cal I}\/$ is a function that maps:
- –
  
  Every basic domain symbol $D\in\mathcal{D}$ into a set $D^{\cal I}\/=\Delta_{D_{i}}^{\cal I}\/$ .
- –
  
  Every class $C\in\mathcal{C}$ to a set $C^{\cal I}\/\subseteq\Delta^{\cal I}\/$ .
- –
  
  Every relationship $R\in\mathcal{R}$ to a set $R^{\cal I}\/$ of $\mathcal{U}$ -labeled tuples over $\Delta^{\cal I}\/$ – i.e. let $R$ be an binary relationship connecting the classes $C_{1},C_{2}$ , $\mbox{\sc rel}\mathcal{}(R)=\{U_{1}:C_{1},U_{2}:C_{2}\}$ , then, $r\in R^{\cal I}\/\to(r=\{U_{1}:o_{1},U_{2}:o_{2}\}\land\forall i\in\{1,2\}% \textbf{.}o_{i}\in C_{i}^{\cal I}\/)$ .
- –
  
  Every attribute $A\in\mathcal{A}$ to a set $A^{\cal I}\/\subseteq\Delta^{\cal I}\/\times\Delta_{D}^{\cal I}\/$ , such that, for each $C\in\mathcal{C}$ , if $\mbox{\sc att}\mathcal{}(C)=\{A_{1}:D_{1},\ldots,A_{h}:D_{h}\}$ , then, $o\in C^{\cal I}\/\to(\forall i\in\{1,\ldots,h\},\exists d_{i}\textbf{.}$ $\langle o,d_{i}\rangle\in A_{i}^{\cal I}\/\land\forall d_{i}\textbf{.}\langle o% ,d_{i}\rangle\in A_{i}^{\cal I}\/\to d_{i}\in\Delta_{D_{i}}^{\cal I}\/)$ .

$\mathcal{I}$ is said a legal database state or legal application software state if it satisfies all of the constraints expressed in the conceptual data model:

$\blacksquare$

For each $C_{1},C_{2}\in\mathcal{C}$ : if $C_{1}\mathbin{\mbox{\sc isa}\mathcal{}}_{C}C_{2}$ , then $C_{1}^{\cal I}\/\subseteq C_{2}^{\cal I}\/$ .
$\blacksquare$

For each $R\in\mathcal{R}$ with $\mbox{\sc rel}\mathcal{}(R)=\{U_{1}:C_{1},U_{2}:C_{2}\}$ : all instances of $R$ are of the form $\{U_{1}:o_{1},U_{2}:o_{2}\}$ where $o_{i}\in C_{i}^{\cal I}\/$ , $U_{i}\in U_{i}^{\cal I}\/$ , and $1\leq i\leq 2$ .
$\blacksquare$

For each cardinality constraint $\mbox{\sc card}\mathcal{}_{R}(C,R,U)$ , then:
$o\in C^{\cal I}\/\to\mbox{\sc cmin}\mathcal{}(C,R,U)\leq\#\{r\in R^{\cal I}\/% \mid r[U]=o\}\leq\mbox{\sc cmax}\mathcal{}(C,R,U)$ .
$\blacksquare$

For each multiplicity constraint $\mbox{\sc card}\mathcal{}_{A}(C,A)$ , then:
$o\in C^{\cal I}\/\to\mbox{\sc cmin}\mathcal{}(C,A)\leq\#\{(o,a)\in A^{\cal I}% \/\}\leq\mbox{\sc cmax}\mathcal{}(C,A)$ .
$\blacksquare$

For each $C\in\mathcal{C},A\in\mathcal{A}$ such that $\mbox{\sc id}\mathcal{}(C)=A$ , then $A$ is an attribute and $\forall d\in\Delta_{D}^{\cal I}\/\textbf{.}\#\{o\in C^{\cal I}\/\mid\langle o,% d\rangle\in A^{\cal I}\/\}\leq 1$ .

Definition 9 (Mapping $\mathcal{DC}_{p}$ into $\mathcal{DLR}$ ).

Let $\Sigma=(\mathcal{L},\mbox{\sc rel}\mathcal{},\mbox{\sc att}\mathcal{},\mbox{% \sc card}\mathcal{}_{R},\mbox{\sc card}\mathcal{}_{A},\mathbin{\mbox{\sc isa}% \mathcal{}},\mbox{\sc id}\mathcal{})$ be a $\mathcal{DC}_{p}$ conceptual data model. The $\mathcal{DLR}$ knowledge base, $\mathcal{K}$ , mapping $\Sigma$ is as follows.

$\blacksquare$

For each $A\in\mathcal{A}$ , then, $A\sqsubseteq{\tt From}\!:\!\top\sqcap{\tt To}\!:\!\top\in\mathcal{K}$ ;
$\blacksquare$

If $C_{1}\mathbin{\mbox{\sc isa}\mathcal{}}C_{2}\in\Sigma\mathcal{}$ , then, $C_{1}\sqsubseteq C_{2}\in\mathcal{K}$ ;
$\blacksquare$

If $\mbox{\sc rel}\mathcal{}(R)=\{U_{1}\!:\!C_{1},U_{2}\!:\!C_{2}\}\in\Sigma% \mathcal{}$ , then $R\sqsubseteq U_{1}\!:\!C_{1}\sqcap U_{2}\!:\!C_{2}\in\mathcal{K}$ ;
$\blacksquare$

If $\mbox{\sc att}\mathcal{}(C)=\{A_{1}:D_{1},\ldots,A_{h}:D_{h}\}\in\Sigma% \mathcal{}$ , then, $C\sqsubseteq\exists[{\tt From}]A_{1}\sqcap\ldots\sqcap\exists[{\tt From}]A_{h}% \sqcap\forall[{\tt From}](A_{1}\to{\tt To}:D_{1})\sqcap\ldots\sqcap\forall[{% \tt From}](A_{h}\to{\tt To}:D_{h})\in\mathcal{K}$ ;
$\blacksquare$

If $\mbox{\sc card}\mathcal{}_{C}(C,R,U)=(m,n)\in\Sigma\mathcal{}$ , then, $C\sqsubseteq\exists^{\geq m}[U]R\sqcap\exists^{\leq n}[U]R\in\mathcal{K}$ ;
$\blacksquare$

If $\mbox{\sc card}\mathcal{}_{A}(C,A)=(m,n)\in\Sigma\mathcal{}$ , then, $C\sqsubseteq\exists^{\geq m}[U]R\sqcap\exists^{\leq n}[U]R\in\mathcal{K}$ ;
$\blacksquare$

If $\mbox{\sc id}\mathcal{}(C)=A\in\Sigma\mathcal{}$ , then, $\mathcal{K}$ contains: $C\sqsubseteq\exists^{=1}[{\tt From}]{A}$ ; $\top\sqsubseteq\exists^{\leq 1}[{\tt To}](A\sqcap[{\tt From}]:C)$ ;

An example of this approach with a concrete CDM is illustrated in Example 2.

[bib.bib1] [1] Sunitha Abburu. A survey on ontology reasoners and comparison. International Journal of Computer Applications, 57(17):33–39, 2012.

[bib.bib2] [2] Miguel I. Aguirre-Urreta and George M. Marakas. Comparing conceptual modeling techniques: a critical review of the eer vs. oo empirical literature. ACM SIGMIS Database: The DATABASE for Advances in Information Systems, 39(2):9–32, 2008. doi:10.1145/1364636.1364640.

[bib.bib3] [3] Lina Al-Jadir, Christine Parent, and Stefano Spaccapietra. Reasoning with large ontologies stored in relational databases: The OntoMinD approach. Data & Knowledge Engineering, 69:1158–1180, 2010. doi:10.1016/j.datak.2010.07.006.

[bib.bib4] [4] Michele Angelaccio, Tiziana Catarci, and Giuseppe Santucci. QBD*: A graphical query language with recursion. IEEE Transactions on Software Engineering, 16(10):1150–1163, 1990. doi:10.1109/32.60295.

[bib.bib5] [5] Kutz Arrieta, Pablo R. Fillottrani, and C. Maria Keet. Cosmo: A constructor specification language for abstract wikipedia’s content selection process. Technical report, aug 2023. doi:10.48550/arXiv.2308.02539.

[bib.bib6] [6] Alessandro Artale. Reasoning on temporal conceptual schemas with dynamic constraints. In Proceedings. 11th International Symposium on Temporal Representation and Reasoning, 2004. TIME 2004., pages 79–86. IEEE, 2004. doi:10.1109/time.2004.1314423.

[bib.bib7] [7] Alessandro Artale, Diego Calvanese, Roman Kontchakov, Vladislav Ryzhikov, and Michael Zakharyaschev. Reasoning over extended ER models. In Christine Parent, Klaus-Dieter Schewe, Veda C. Storey, and Bernhard Thalheim, editors, Proceedings of the 26th International Conference on Conceptual Modeling (ER’07), volume 4801 of LNCS, pages 277–292. Springer, 2007. Auckland, New Zealand, November 5-9, 2007. doi:10.1007/978-3-540-75563-0_20.

[bib.bib8] [8] Alessandro Artale, Diego Calvanese, Roman Kontchakov, and Michael Zakharyaschev. DL-Lite without the unique name assumption. In Proceedings of the 22nd International Workshop on Description Logic (DL’09), volume 477 of CEUR-WS, 2009. URL: http://ceur-ws.org/Vol-477/paper_11.pdf.

[bib.bib9] [9] Alessandro Artale, Enrico Franconi, Frank Wolter, and Michael Zakharyaschev. A temporal description logic for reasoning about conceptual schemas and queries. In S. Flesca, S. Greco, N. Leone, and G. Ianni, editors, Proceedings of the 8th Joint European Conference on Logics in Artificial Intelligence (JELIA-02), volume 2424 of LNAI, pages 98–110. Springer Verlag, 2002. doi:10.1007/3-540-45757-7_9.

[bib.bib10] [10] Alessandro Artale, Christine Parent, and Stefano Spaccapietra. Evolving objects in temporal information systems. Annals of Mathematics and Artificial Intelligence, 50(1-2):5–38, 2007. doi:10.1007/s10472-007-9068-z.

[bib.bib11] [11] Franz Baader, Sebastian Brandt, and Carsten Lutz. Pushing the EL envelope. In Proceedings of the 19th Joint International Conference on Artificial Intelligence (IJCAI’05), volume 5, pages 364–369, 2005. URL: http://ijcai.org/Proceedings/05/Papers/0372.pdf.

[bib.bib12] [12] Franz Baader, Diego Calvanese, Deborah L. McGuinness, Daniele Nardi, and Peter F. Patel-Schneider, editors. The Description Logics Handbook – Theory and Applications. Cambridge University Press, 2 edition, 2008.

[bib.bib13] [13] Thomas Baker and Eric Prud’hommeaux. Shape expressions (shex) 2.1 primer – final community group report. W3C Recommendation, 2019. URL: http://shex.io/shex-primer/.

[bib.bib14] [14] Mira Balaban and Azzam Maraee. A UML-based method for deciding finite satisfiability in description logics. In Franz Baader, Carsten Lutz, and Boris Motik, editors, Proceedings of the 21st International Workshop on Description Logics (DL’08), volume 353 of CEUR-WS, 2008. Dresden, Germany, May 13–16, 2008. URL: https://ceur-ws.org/Vol-353/BalabanMaraee.pdf.

[bib.bib15] [15] Daniela Berardi, Diego Calvanese, and Giuseppe De Giacomo. Reasoning on UML class diagrams. Artificial Intelligence, 168(1-2):70–118, 2005. doi:10.1016/j.artint.2005.05.003.

[bib.bib16] [16] Anthony C. Bloesch and Terry A. Halpin. Conceptual Queries using ConQuer-II. In Proceedings of ER’97: 16th International Conference on Conceptual Modeling, volume 1331 of LNCS, pages 113–126. Springer, 1997. doi:10.1007/3-540-63699-4_10.

[bib.bib17] [17] Alexander Borgida, David Toman, and Grant Weddell. On referring expressions in information systems derived from conceptual modelling. In Isabelle Comyn-Wattiau, Katsumi Tanaka, Il-Yeol Song, Shuichiro Yamamoto, and Motoshi Saeki, editors, Conceptual Modeling (ER’16), volume 9974 of LNCS, pages 183–197. Springer, 2016. doi:10.1007/978-3-319-46397-1_14.

[bib.bib18] [18] Dominik Bork. Conceptual modeling and artificial intelligence: Challenges and opportunities for enterprise engineering: Keynote presentation at the 11th enterprise engineering working conference (eewc 2021). In Enterprise Engineering Working Conference, pages 3–9. Springer, 2021. doi:10.1007/978-3-031-11520-2_1.

[bib.bib19] [19] Dominik Bork, Syed Juned Ali, and Ben Roelens. Conceptual modeling and artificial intelligence: A systematic mapping study. Technical report, 2023. doi:10.48550/arXiv.2303.06758.

[bib.bib20] [20] Michael Boyd and Peter McBrien. Comparing and transforming between data models via an intermediate hypergraph data model. Journal on Data Semantics, IV:69–109, 2005. doi:10.1007/11603412_3.

[bib.bib21] [21] Bernardo F. B. Braga, João P. A. Almeida, Giancarlo Guizzardi, and Alessander Botti Benevides. Transforming OntoUML into Alloy: towards conceptual model validation using a lightweight formal methods. Innovations in Systems and Software Engineering, 6(1-2):55–63, 2010. doi:10.1007/s11334-009-0120-5.

[bib.bib22] [22] Germán Braun, Pablo R. Fillottrani, and C. Maria Keet. A framework for interoperability between models with hybrid tools. Journal of Intelligent Information Systems, 60:437–462, 2023. doi:10.1007/s10844-022-00731-7.

[bib.bib23] [23] Germán Braun, Giuliano Marinelli, Emiliano Rios Gavagnin, Laura A. Cecchi, and Pablo R. Fillottrani. Web interoperability for ontology development and support with crowd 2.0. In 30th International Joint Conference on Artificial Intelligence, IJCAI’21, pages 4980–4983, 2021. doi:10.24963/ijcai.2021/707.

[bib.bib24] [24] Dan Brickley and R. V. Guha. Rdf schema 1.1. Standard, W3C, 2014. URL: https://www.w3.org/TR/2014/REC-rdf-schema-20140225/.

[bib.bib25] [25] Jordi Cabot, Robert Clarisó, and Daniel Riera. Verification of UML/OCL class diagrams using constraint programming. In Model Driven Engineering, Verification, and Validation: Integrating Verification and Validation in MDE (MoDeVVA 2008), 2008. doi:10.1109/ICSTW.2008.54.

[bib.bib26] [26] Marco Cadoli, Diego Calvanese, Giuseppe De Giacomo, and Toni Mancini. Finite model reasoning on UML class diagrams via constraint programming. In Proc. of AI*IA 2007, volume 4733 of LNAI, pages 36–47. Springer, 2007. doi:10.1007/978-3-540-74782-6_5.

[bib.bib27] [27] Diego Calvanese, Benjamin Cogrel, Sarah Komla-Ebri, Roman Kontchakov, Davide Lanti, Martin Rezk, Mariano Rodriguez-Muro, and Guohuia Xiao. Ontop: Answering SPARQL queries over relational databases. Semantic Web Journal, 8(3):471–487, 2017. doi:10.3233/SW-160217.

[bib.bib28] [28] Diego Calvanese, Giuseppe De Giacomo, Domenico Lembo, Maurizio Lenzerini, and Riccardo Rosati. Tractable reasoning and efficient query answering in description logics: The DL-Lite family. Journal of Automated Reasoning, 39(3):385–429, 2007. doi:10.1007/s10817-007-9078-x.

[bib.bib29] [29] Diego Calvanese, Giuseppe De Giacomo, and Maurizio Lenzerini. On the decidability of query containment under constraints. In Proceedings of the 17th ACM SIGACT SIGMOD SIGART Symposium on Principles of Database Systems (PODS’98), pages 149–158, 1998. doi:10.1145/275487.275504.

[bib.bib30] [30] Diego Calvanese, Giuseppe De Giacomo, and Maurizio Lenzerini. Reasoning in expressive description logics with fixpoints based on automata on infinite trees. In Proceedings of the 16th International Joint Conference on Artificial Intelligence (IJCAI’99), pages 84–89, 1999. doi:10.5555/1624218.1624231.

[bib.bib31] [31] Diego Calvanese, Giuseppe De Giacomo, and Maurizio Lenzerini. Identification constraints and functional dependencies in description logics. In Bernhard Nebel, editor, Proc. of the 17th Int. Joint Conf. on Artificial Intelligence (IJCAI 2001), pages 155–160. Morgan Kaufmann, 2001. Seattle, Washington, USA, August 4-10, 2001. doi:10.5555/1642090.1642111.

[bib.bib32] [32] Diego Calvanese, Tahir Emre Kalayci, Marco Montali, Ario Santoso, and Wil van der Aalst. Conceptual schema transformation in ontology-based data access. In Catherine Faron Zucker, Chiara Ghidini, Amedeo Napoli, and Yannick Toussaint, editors, Proceedings of the 21st International Conference on Knowledge Engineering and Knolwedge Management, volume 11313 of LNAI. Springer, 2018. 12-16 Nov 2018, Nancy, France. doi:10.1007/978-3-030-03667-6_4.

[bib.bib33] [33] Diego Calvanese, C. Maria Keet, Werner Nutt, Mariano Rodríguez-Muro, and Giorgio Stefanoni. Web-based graphical querying of databases through an ontology: the WONDER system. In Sung Y. Shin, Sascha Ossowski, Michael Schumacher, Mathew J. Palakal, and Chih-Cheng Hung, editors, Proceedings of ACM Symposium on Applied Computing (ACM SAC’10), pages 1389–1396. ACM, 2010. March 22-26 2010, Sierre, Switzerland. doi:10.1145/1774088.1774384.

[bib.bib34] [34] Diego Calvanese, Maurizio Lenzerini, and Daniele Nardi. Unifying class-based representation formalisms. Journal of Artificial Intelligence Research, 11:199–240, 1999. doi:10.5555/3013545.3013550.

[bib.bib35] [35] Diego Calvanese, Pietro Liuzzo, Alessandro Mosca, José Remesal, Martin Rezk, and Guillem Rull. Ontology-based data integration in epnet: Production and distribution of food during the roman empire. Engineering Applications of Artificial Intelligence, 51:212–229, 2016. doi:10.1016/j.engappai.2016.01.005.

[bib.bib36] [36] Peter P. Chen. The entity-relationship model—toward a unified view of data. ACM Transactions on Database Systems, 1(1):9–36, 1976. doi:10.1145/320434.320440.

[bib.bib37] [37] HD Crockett, J Guynes, and CW Slinkman. Framework for development of conceptual data modelling techniques. Information and Software Technology, 33(2):134–142, 1991. doi:10.1016/0950-5849(91)90058-J.

[bib.bib38] [38] Bernardo Cuenca Grau, Ian Horrocks, Boris Motik, Bijan Parsia, Peter Patel-Schneider, and Ulrike Sattler. OWL 2: The next step for OWL. Journal of Web Semantics: Science, Services and Agents on the World Wide Web, 6(4):309–322, 2008. doi:10.1016/j.websem.2008.05.001.

[bib.bib39] [39] Islay Davies, Peter Green, Michael Rosemann, Marta Indulska, and Stan Gallo. How do practitioners use conceptual modeling in practice? Data & Knowledge Engineering, 58(3):358–380, 2006. doi:10.1016/j.datak.2005.07.007.

[bib.bib40] [40] Thomas Eiter, Josiane Xavier Parreira, and Patrik Schneider. Spatial ontology-mediated query answering over mobility streams. In E. Blomqvist et al., editors, Proceedings of the 13th Extended Semantic Web Conference (ESWC’17), volume 10249 of LNCS, pages 219–237. Springer, 2017. 30 May - 1 June 2017, Portoroz, Slovenia. doi:10.1007/978-3-319-58068-5_14.

[bib.bib41] [41] Carles Farré, Anna Queralt, Guillem Rull, Ernest Teniente, and Toni Urpí. Automated reasoning on UML conceptual schemas with derived information and queries. Information and Software Technology, 55(9):1529–1550, 2013. doi:10.1016/j.infsof.2013.02.010.

[bib.bib42] [42] Pablo Fillotrani and C. Maria Keet. Evidence-based lean conceptual data modelling languages. Journal of Computer Science and Technology, 21(2):e10, oct 2021. doi:10.24215/16666038.21.e10.

[bib.bib43] [43] Pablo R. Fillottrani, Enrico Franconi, and Sergio Tessaris. The ICOM 3.0 intelligent conceptual modelling tool and methodology. Semantic Web Journal, 3(3):293–306, 2012. doi:10.3233/SW-2011-0038.

[bib.bib44] [44] Pablo R. Fillottrani and C. Maria Keet. Conceptual model interoperability: a metamodel-driven approach. In A. Bikakis et al., editors, Proceedings of the 8th International Web Rule Symposium (RuleML’14), volume 8620 of LNCS, pages 52–66. Springer, 2014. August 18-20, 2014, Prague, Czech Republic. doi:10.1007/978-3-319-09870-8_4.

[bib.bib45] [45] Pablo R. Fillottrani and C. Maria Keet. Dimensions affecting representation styles in ontologies. In 1st Iberoamerican conference on Knowledge Graphs and Semantic Web (KGSWC’19), volume 1029 of CCIS, pages 186–200. Springer, 2019. 24-28 June 2019, Villa Clara, Cuba. doi:10.1007/978-3-030-21395-4_14.

[bib.bib46] [46] Pablo R. Fillottrani and C. Maria Keet. An analysis of commitments in ontology language design. In B. Brodaric and F. Neuhaus, editors, Proceedings of the 11th International Conference on Formal Ontology in Information Systems (FOIS’20), volume 330 of Frontiers in Artificial Intelligence and Applications, pages 46–60, 2020. doi:10.3233/FAIA200659.

[bib.bib47] [47] Pablo R. Fillottrani and C. Maria Keet. KnowID: An architecture for efficient knowledge-driven information and data access. Data Intelligence, 2(4):487–512, 2020. doi:10.1162/dint_a_00060.

[bib.bib48] [48] Pablo R. Fillottrani, C. Maria Keet, and David Toman. Polynomial encoding of orm conceptual models in $\mathcal{CFDI}_{nc}^{\forall-}$ . In Diego Calvanese and B. Konev, editors, Proceedings of the 28th International Workshop on Description Logics (DL’15), volume 1350 of CEUR-WS, pages 401–414, 2015. 7-10 June 2015, Athens, Greece. URL: https://ceur-ws.org/Vol-1350/paper-50.pdf.

[bib.bib49] [49] E. Franconi and G. Ng. The ICOM tool for intelligent conceptual modelling. In 7th Workshop on Knowledge Representation meets Databases (KRDB’00), 2000. Berlin, Germany, 2000. doi:10.5555/2590200.2590206.

[bib.bib50] [50] Enrico Franconi, Alessandro Mosca, and Dmitry Solomakhin. The formalisation of ORM2 and its encoding in OWL2. KRDB Research Centre Technical Report KRDB12-2, Faculty of Computer Science, Free University of Bozen-Bolzano, Italy, mar 2012.

[bib.bib51] [51] Birte Glimm, Ian Horrocks, Boris Motik, and Giorgos Stoilos. Optimising ontology classification. In The Semantic Web–ISWC 2010: 9th International Semantic Web Conference, ISWC 2010, Shanghai, China, November 7-11, 2010, Revised Selected Papers, Part I 9, pages 225–240. Springer, 2010. doi:10.1007/978-3-642-17746-0_15.

[bib.bib52] [52] Carlos A. González and Jordi Cabot. Formal verification of static software models in mde: A systematic review. Information and Software Technology, 56(8):821–838, 2014. doi:10.1016/j.infsof.2014.03.003.

[bib.bib53] [53] Benjamin N. Grosof, Ian Horrocks, Raphael Volz, and Stefan Decker. Description logic programs: Combining logic programs with description logic. In Proceedings of the 12th International World Wide Web Conference (WWW’03), pages 48–57, 2003. Budapest, Hungary. doi:10.1145/775157.775160.

[bib.bib54] [54] Object Management Group. Distributed ontology, model, and specification language, feb 2018. URL: http://www.omg.org/spec/DOL/.

[bib.bib55] [55] Nicola Guarino. Formal ontology and information systems. In N. Guarino, editor, Proceedings of Formal Ontology in Information Systems (FOIS’98), Frontiers in Artificial intelligence and Applications, pages 3–15. Amsterdam: IOS Press, 1998.

[bib.bib56] [56] Giancarlo Guizzardi. Ontological Foundations for Structural Conceptual Models. Phd thesis, University of Twente, The Netherlands. Telematica Instituut Fundamental Research Series No. 15, 2005.

[bib.bib57] [57] Volker Haarslev, Kay Hidde, Ralf Möller, and Michael Wessel. The racerpro knowledge representation and reasoning system. Semantic Web Journal, 3(3):267–277, 2012. doi:10.3233/SW-2011-0032.

[bib.bib58] [58] Christoph Haase and Carsten Lutz. Complexity of subsumption in the EL family of description logics: Acyclic and cyclic tboxes. In Malik Ghallab, Constantine D. Spyropoulos, Nikos Fakotakis, and Nikolaos M. Avouris, editors, ECAI 2008 - 18th European Conference on Artificial Intelligence, Patras, Greece, July 21-25, 2008, Proceedings, volume 178 of Frontiers in Artificial Intelligence and Applications, pages 25–29. IOS Press, 2008. doi:10.3233/978-1-58603-891-5-25.

[bib.bib59] [59] Terry Halpin. A logical analysis of information systems: static aspects of the data-oriented perspective. PhD thesis, University of Queensland, Australia, 1989. URL: https://search.library.uq.edu.au/permalink/f/l3gdeh/61UQ_ALMA2179989800003131.

[bib.bib60] [60] Terry Halpin and Tony Morgan. Information modeling and relational databases. Morgan Kaufmann, 2nd edition, 2008.

[bib.bib61] [61] Patrick J. Hayes and Peter F. Patel-Schneider. RDF 1.1 Semantics. W3c recommendation, World Wide Web Consortium, feb 2014. URL: http://www.w3.org/TR/rdf11-mt/.

[bib.bib62] [62] Daniel Hernández, Aidan Hogan, and Markus Krötzsch. Reifying RDF: what works well with wikidata? In Thorsten Liebig and Achille Fokoue, editors, Proceedings of the 11th International Workshop on Scalable Semantic Web Knowledge Base Systems 2015), volume 1457 of CEUR-WS, pages 32–47. CEUR-WS.org, 2015. Bethlehem, PA, USA, October 11, 2015. URL: https://ceur-ws.org/Vol-1457/SSWS2015_paper3.pdf.

[bib.bib63] [63] Aidan Hogan, Eva Blomqvist, Michael Cochez, Claudia d’Amato, Gerard de Melo, Claudio Gutiérrez, José Emilio Labra Gayo, Sabrina Kirrane, Sebastian Neumaier, Axel Polleres, Roberto Navigli, Axel-Cyrille Ngonga Ngomo, Sabbir M. Rashid, Anisa Rula, Lukas Schmelzeisen, Juan F. Sequeda, Steffen Staab, and Antoine Zimmermann. Knowledge graphs. Technical report, 2020. doi:10.48550/arXiv.2003.02320.

[bib.bib64] [64] Ian Horrocks, Oliver Kutz, and Ulrike Sattler. The even more irresistible $\mathcal{SROIQ}$ . In Proceedings of the Tenth International Conference on Principles of Knowledge Representation and Reasoning (KR’06), KR’06, pages 57–67. AAAI Press, 2006. URL: http://www.aaai.org/Library/KR/2006/kr06-009.php.

[bib.bib65] [65] Ian Horrocks, Peter F. Patel-Schneider, and Frank van Harmelen. From SHIQ and RDF to OWL: The making of a web ontology language. Journal of Web Semantics, 1(1):7, 2003. doi:10.1016/j.websem.2003.07.001.

[bib.bib66] [66] Richard Hull and Roger King. Semantic database modeling: Survey, applications, and research issues. ACM Computing Surveys (CSUR), 19(3):201–260, 1987. doi:10.1145/45072.45073.

[bib.bib67] [67] Amir Jahangard Rafsanjani and Seyed-Hassan Mirian-Hosseinabadi. A Z Approach to Formalization and Validation of ORM Models. In Ezendu Ariwa and Eyas El-Qawasmeh, editors, Digital Enterprise and Information Systems, volume 194 of CCIS, pages 513–526. Springer, 2011. doi:10.1007/978-3-642-22603-8_45.

[bib.bib68] [68] Mustafa Jarrar, Jan Demey, and Robert Meersman. On using conceptual data modeling for ontology engineering. Journal on Data Semantics, 2003. doi:10.1007/978-3-540-39733-5_8.

[bib.bib69] [69] Elem Güzel Kalayci, Guohui Xiao, Vladislav Ryzhikov, Tahir Emre Kalayci, and Diego Calvanese. Ontop-temporal: A tool for ontology-based query answering over temporal data. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management, CIKM 2018, Torino, Italy, October 22-26, 2018, pages 1927–1930, 2018. doi:10.1145/3269206.3269230.

[bib.bib70] [70] Ken Kaneiwa and Ken Satoh. Consistency checking algorithms for restricted uml class diagrams. In Jürgen Dix and Stephen J. Hegner, editors, Foundations of Information and Knowledge Systems, pages 219–239, Berlin, Heidelberg, 2006. Springer. doi:10.1007/11663881_13.

[bib.bib71] [71] C. Maria Keet. Mapping the Object-Role Modeling language ORM2 into Description Logic language $\mathcal{DLR}_{ifd}$ . Technical Report 0702089v2, KRDB Research Centre, Free University of Bozen-Bolzano, Italy, apr 2009. arXiv:cs.LO/0702089v2. doi:10.48550/arXiv.cs/0702089.

[bib.bib72] [72] C. Maria Keet. Ontology-driven formal conceptual data modeling for biological data analysis. In Mourad Elloumi and Albert Y. Zomaya, editors, Biological Knowledge Discovery Handbook: Preprocessing, Mining and Postprocessing of Biological Data, chapter 6, pages 129–154. Wiley, 2013. doi:10.1002/9781118617151.ch06.

[bib.bib73] [73] C. Maria Keet. An introduction to ontology engineering, volume 20 of Computing. College Publications, UK, 2018. 334p.

[bib.bib74] [74] C. Maria Keet and Sonia Berman. Determining the preferred representation of temporal constraints in conceptual models. In H.C. Mayr et al., editors, 36th International Conference on Conceptual Modeling (ER’17), volume 10650 of LNCS, pages 437–450. Springer, 2017. 6-9 Nov 2017, Valencia, Spain. doi:10.1007/978-3-319-69904-2_33.

[bib.bib75] [75] C. Maria Keet and Pablo R. Fillottrani. An analysis and characterisation of publicly available conceptual models. In P. Johannesson, M. L. Lee, S.W. Liddle, A. L. Opdahl, and O. Pastor López, editors, Proceedings of the 34th International Conference on Conceptual Modeling (ER’15), volume 9381 of LNCS, pages 585–593. Springer, 2015. 19-22 Oct, Stockholm, Sweden. doi:10.1007/978-3-319-25264-3_45.

[bib.bib76] [76] C. Maria Keet and Pablo R. Fillottrani. An ontology-driven unifying metamodel of UML Class Diagrams, EER, and ORM2. Data & Knowledge Engineering, 98:30–53, 2015. doi:10.1016/j.datak.2015.07.004.

[bib.bib77] [77] Holger Knublauch and Dimitris Kontokostas. Shapes constraint language (shacl). W3C Recommendation, 2017. https://www.w3.org/TR/shacl/.

[bib.bib78] [78] Markus Krötzsch, Maximilian Marx, Ana Ozaki, and Veronika Thost. Attributed description logics: Reasoning on knowledge graphs. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI’18), pages 5309–5313. International Joint Conferences on Artificial Intelligence Organization, jul 2018. doi:10.24963/ijcai.2018/743.

[bib.bib79] [79] Domenico Lembo, Valerio Santarelli, Domenico Fabio Savo, and Giuseppe De Giacomo. Graphol: A graphical language for ontology modeling equivalent to owl 2. Future Internet, 14(3), 2022. doi:10.3390/fi14030078.

[bib.bib80] [80] Lina Lubyte and Sergio Tessaris. Automated extraction of ontologies wrapping relational data sources. In Proceedings of International Conference on Database and Expert Systems Applications (DEXA’09), pages 128–142. Springer, 2009. doi:10.1007/978-3-642-03573-9_10.

[bib.bib81] [81] Carsten Lutz, David Toman, and Frank Wolter. Conjunctive query answering in the description logic el using a relational database system. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI’09), pages 2070–2075. ACM, 2009. URL: http://ijcai.org/Proceedings/09/Papers/341.pdf.

[bib.bib82] [82] Weicong Ma, C. Maria Keet, Wayne Oldford, David Toman, and Grant Weddell. The utility of the abstract relational model and attribute paths in sql. In Catherine Faron Zucker, Chiara Ghidini, Amedeo Napoli, and Yannick Toussaint, editors, Proceedings of the 21st International COnference on Knowledge Engineering and Knowledge Management (EKAW’18)), volume 11313 of LNAI, pages 195–211. Springer, 2018. 12-16 Nov. 2018, Nancy, France. doi:10.1007/978-3-030-03667-6_13.

[bib.bib83] [83] Wolfgang Maass, Arturo Castellanos, Monica C. Tremblay, Roman Lukyanenko, and Veda C. Storey. AI explainability: Embedding conceptual models. In Niels Bjørn-Andersen, Roman Beck, Stacie Petter, Tina Blegind Jensen, Tilo Böhmann, Kai-Lung Hui, and Viswanath Venkatesh, editors, Proceedings of the 43rd International Conference on Information Systems, ICIS 2022, Digitization for the Next Generation, Copenhagen, Denmark, December 9-14, 2022. Association for Information Systems, 2022. URL: https://aisel.aisnet.org/icis2022/data_analytics/data_analytics/12.

[bib.bib84] [84] Wolfgang Maass and Veda C Storey. Pairing conceptual modeling with machine learning. Data & Knowledge Engineering, 134:101909, 2021. doi:10.1016/j.datak.2021.101909.

[bib.bib85] [85] Fabio Massacci. Decision procedures for expressive description logics with intersection, composition, converse of roles and role identity. In Proceedings of the 17th International Joint Conference on Artificial Intelligence (IJCAI’2001), pages 193–198, 2001.

[bib.bib86] [86] Melinda McDaniel and Veda C Storey. Evaluating domain ontologies: clarification, classification, and challenges. ACM Computing Surveys (CSUR), 52(4):1–44, 2019. doi:10.1145/3329124.

[bib.bib87] [87] Deborah L. McGuinness and Frank van Harmelen. OWL Web Ontology Language Overview. W3C Recommendation., 2004. URL: http://www.w3.org/TR/owl-features/.

[bib.bib88] [88] Jack Minker. Foundations of deductive databases and logic programming. Morgan Kaufmann, 2014.

[bib.bib89] [89] Till Mossakowski, Christoph Lange, and Oliver Kutz. Three semantics for the core of the Distributed Ontology Language. In Michael Grüninger, editor, Proceedings of the 7th International Conference on Formal Ontology in Information Systems (FOIS’12). IOS Press, 2012. 24-27 July, Graz, Austria. doi:10.3233/978-1-61499-084-0-337.

[bib.bib90] [90] Boris Motik, Bernardo Cuenca Grau, Ian Horrocks, Zhe Wu, Achille Fokoue, and Carsten Lutz. OWL 2 Web Ontology Language Profiles. W3C recommendation, W3C, 27 October 2009. URL: http://www.w3.org/TR/owl2-profiles/.

[bib.bib91] [91] Boris Motik, Peter F. Patel-Schneider, and Bijan Parsia. OWL 2 web ontology language structural specification and functional-style syntax. W3c recommendation, W3C, 27 October 2009. URL: http://www.w3.org/TR/owl2-syntax/.

[bib.bib92] [92] Matthew Nizol, Laura K. Dillon, and R. E. K. Stirewalt. Toward tractable instantiation of conceptual data models using non-semantics-preserving model transformations. In Proceedings of the 6th International Workshop on Modeling in Software Engineering (MiSE’14), pages 13–18. ACM Conference Proceedings, 2014. Hyderabad, India, June 02-03, 2014. doi:10.1145/2593770.2593771.

[bib.bib93] [93] Object Management Group. Semantics of Business Vocabulary and Rules (SBVR) – OMG released versions of SBVR, formal/2008-01-02, jan 2008. URL: http://www.omg.org/spec/SBVR/1.0.

[bib.bib94] [94] Object Management Group. Superstructure specification. Standard 2.4.1, Object Management Group, 2012. URL: http://www.omg.org/spec/UML/2.4.1/.

[bib.bib95] [95] E. A. N. Ongoma. Formalising temporal attributes in temporal conceptual data models. Msc thesis, Department of Computer Science, 2015.

[bib.bib96] [96] Magdalena Ortiz. A short introduction to SHACL for logicians. In Helle Hvid Hansen, Andre Scedrov, and Ruy J. G. B. de Queiroz, editors, Proceedings of the 29th International Workshop on Logic, Language, Information, and Computation (WoLLIC’23), volume 13923 of LNCS, pages 19–32. Springer, 2023. Halifax, NS, Canada, July 11-14, 2023. doi:10.1007/978-3-031-39784-4_2.

[bib.bib97] [97] Özgür Lütfü Özçep, Ralf Möller, and Christian Neuenstadt. Stream-query compilation with ontologies. In Bernhard Pfahringer and Jochen Renz, editors, Proceedings of the 28th Australasian Joint Conference on Advances in Artificial Intelligence (AI’15), volume 9457 of LNCS, pages 457–463. Springer, 2015. Canberra, ACT, Australia, November 30 – December 4, 2015. doi:10.1007/978-3-319-26350-2_40.

[bib.bib98] [98] Wen-Lin Pan and Da-xin Liu. Mapping object role modeling into common logic interchange format. In Proceedings of the 3rd International Conference on Advanced Computer Theory and Engineering (ICACTE’10), volume 2, pages 104–109. IEEE Computer Society, 2010. doi:10.1109/ICACTE.2010.5579141.

[bib.bib99] [99] Christine Parent, Stefano Spaccapietra, and Esteban Zimányi. Conceptual modeling for traditional and spatio-temporal applications—the MADS approach. Berlin Heidelberg: Springer Verlag, 2006. doi:10.1007/3-540-30326-X.

[bib.bib100] [100] Antonella Poggi, Domenico Lembo, Diego Calvanese, Giuseppe De Giacomo, Maurizio Lenzerini, and Riccardo Rosati. Linking data to ontologies. Journal on Data Semantics, X:133–173, 2008. doi:10.1007/978-3-540-77688-8_5.

[bib.bib101] [101] Alexandra Poulovassilis and Peter McBrien. A general formal framework for schema transformation. Data & Knowledge Engineering, 28(1):47–71, 1998. doi:10.1016/s0169-023x(98)00013-5.

[bib.bib102] [102] Sandeep Purao and Veda C. Storey. A multi-layered ontology for comparing relationship semantics in conceptual models of databases. Applied Ontology, 1(1):117–139, 2005. URL: http://content.iospress.com/articles/applied-ontology/ao000011.

[bib.bib103] [103] Anna Queralt, Alessandro Artale, Diego Calvanese, and Ernest Teniente. OCL-Lite: Finite reasoning on UML/OCL conceptual schemas. Data & Knowledge Engineering, 73:1–22, 2012. doi:10.1016/j.datak.2011.09.004.

[bib.bib104] [104] Anna Queralt and Ernest Teniente. Decidable reasoning in UML schemas with constraints. In Zohra Bellahsene and Michel Léonard, editors, Proceedings of the 20th International Conference on Advanced Information Systems Engineering (CAiSE’08), volume 5074 of LNCS, pages 281–295. Springer, 2008. Montpellier, France, June 16-20, 2008. doi:10.1007/978-3-540-69534-9_23.

[bib.bib105] [105] Jason Saint Jacques, David Toman, and Grant E. Weddell. Object-relational queries over cfdi ${}_{\mbox{nc}}$ knowledge bases: OBDA for the sql-literate. In Subbarao Kambhampati, editor, Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, IJCAI 2016, New York, NY, USA, 9-15 July 2016, pages 1258–1264. IJCAI/AAAI Press, 2016. URL: http://www.ijcai.org/Abstract/16/182.

[bib.bib106] [106] Manfred Schmidt-Schauß. Subsumption in KL-ONE is undecidable. In Proceedings of the 1st International Conference on Principles of Knowledge Representation and Reasoning, pages 421–431, 1989.

[bib.bib107] [107] Thomas Schneider and Mantas Šimkus. Ontologies and data management: A brief survey. KI-Künstliche Intelligenz, 34(3):329–353, 2020. doi:10.1007/s13218-020-00686-3.

[bib.bib108] [108] Matthias Sedlmeier and Martin Gogolla. Design and prototypical implementation of an integrated graph-based conceptual data model. In Bernhard Thalheim, Hannu Jaakkola, Yasushi Kiyoki, and Naofumi Yoshida, editors, Proceedings of the 24th International Conference Information Modelling and Knowledge Bases (EJC’14), volume 272 of FAIA, pages 376–395. IOS Press, 2014. doi:10.3233/978-1-61499-472-5-376.

[bib.bib109] [109] Asadullah Shaikh, Abdul Hafeez, Asif Ali Wagan, Mesfer Alrizq, Abdullah Alghamdi, and Mana Saleh Al Reshan. More than two decades of research on verification of UML class models: A systematic literature review. IEEE Access, 9:142461–142474, 2021. doi:10.1109/ACCESS.2021.3121222.

[bib.bib110] [110] Yannis Smaragdakis, Christoph Csallner, and Ranjith Subramanian. Scalable satisfiability checking and test data generation from modeling diagrams. Automated Software Engineering, 16:73–99, 2009. doi:10.1007/s10515-008-0044-6.

[bib.bib111] [111] Il-Yeol Song and Peter P. Chen. Entity relationship model. In Ling Liu and M. Tamer Özsu, editors, Encyclopedia of Database Systems, volume 1, pages 1003–1009. Springer, 2009. doi:10.1007/978-0-387-39940-9_148.

[bib.bib112] [112] Ahmet Soylu, Martin Giese, Ernesto Jimenez-Ruiz, Evgeny Kharlamov, Dmitriy Zheleznyakov, and Ian Horrocks. Ontology-based end-user visual query formulation: Why, what, who, how, and which? Universal Access in the Information Society, 16(2):435–467, jun 2017. doi:10.1007/s10209-016-0465-0.

[bib.bib113] [113] Ahmet Soylu, Evgeny Kharlamov, Dimitry Zheleznyakov, Ernesto Jimenez Ruiz, Martin Giese, Martin G. Skjaeveland, Dag Hovland, Rudolf Schlatte, Sebastian Brandt, Hallstein Lie, and Ian Horrocks. OptiqueVQS: a visual query system over ontologies for industry. Semantic Web Journal, 9(5):627–660, 2018. doi:10.3233/sw-180293.

[bib.bib114] [114] Francesco Sportelli and Enrico Franconi. Formalisation of orm derivation rules and their mapping into owl. In OTM Conferences in Computer Science, volume 10033, pages 827–843, 2016. doi:10.1007/978-3-319-48472-3_52.

[bib.bib115] [115] Veda C. Storey. Relational database design based on the entity-relationship model. Data & knowledge engineering, 7(1):47–83, 1991. doi:10.1016/0169-023X(91)90033-T.

[bib.bib116] [116] Veda C. Storey, Roman Lukyanenko, and Arturo Castellanos. Conceptual modeling: Topics, themes, and technology trends. ACM Comput. Surv., 55(14s), jul 2023. doi:10.1145/3589338.

[bib.bib117] [117] Veda C. Storey, Roman Lukyanenko, Wolfgang Maass, and Jeffrey Parsons. Explainable AI. Commun. ACM, 65(4):27–29, 2022. doi:10.1145/3490699.

[bib.bib118] [118] Vijayan Sugumaran and Veda C Storey. Ontologies for conceptual modeling: their creation, use, and management. Data & knowledge engineering, 42(3):251–271, 2002. doi:10.1016/S0169-023X(02)00048-4.

[bib.bib119] [119] Vijayan Sugumaran and Veda C Storey. The role of domain ontologies in database design: An ontology management and conceptual modeling environment. ACM Transactions on Database Systems (TODS), 31(3):1064–1094, 2006. doi:10.1145/1166074.1166083.

[bib.bib120] [120] Arthur H. M. ter Hofstede and Henderik A. Proper. How to formalize it? formalization principles for information systems development methods. Information and Software Technology, 40(10):519–540, 1998. doi:10.1016/S0950-5849(98)00078-0.

[bib.bib121] [121] Herman J. ter Horst. Completeness, decidability and complexity of entailment for rdf schema and a semantic extension involving the owl vocabulary. Journal of Web Semantics, 3(2):79–115, 2005. doi:10.1016/j.websem.2005.06.001.

[bib.bib122] [122] Bernhard Thalheim. Extended entity relationship model. In Ling Liu and M. Tamer Özsu, editors, Encyclopedia of Database Systems, volume 1, pages 1083–1091. Springer, 2009. doi:10.1007/978-0-387-39940-9_157.

[bib.bib123] [123] Stephan Tobies. Complexity Results and Practical Algorithms for Logics in Knowledge Representation. PhD thesis, RWTH Aachen, 2001. URL: http://sylvester.bth.rwth-aachen.de/dissertationen/2001/082/01_082.pdf.

[bib.bib124] [124] David Toman and Grant E. Weddell. Fundamentals of Physical Design and Query Compilation. Synthesis Lectures on Data Management. Morgan & Claypool, 2011. doi:10.1007/978-3-031-01881-7.

[bib.bib125] [125] David Toman and Grant E. Weddell. On adding inverse features to the description logic CFD ${}^{\mbox{{$\forall$}}}$ ${}_{\mbox{nc}}$ . In PRICAI 2014: Trends in Artificial Intelligence - 13th Pacific Rim International Conference on Artificial Intelligence, Gold Coast, QLD, Australia, December 1-5, 2014., pages 587–599, 2014. doi:10.1007/978-3-319-13560-1_47.

[bib.bib126] [126] Albert Tort, Antoni Olivé, and Maria-Ribera Sancho. An approach to test-driven development of conceptual schemas. Data & Knowledge Engineering, 70:1088–1111, 2011. doi:10.1016/j.datak.2011.07.006.

[bib.bib127] [127] Juan Trujillo, Karen C Davis, Xiaoyong Du, Ernesto Damiani, and Veda C. Storey. Conceptual modeling in the era of big data and artificial intelligence: Research topics and introduction to the special issue, 2021. doi:10.1016/j.datak.2021.101911.

[bib.bib128] [128] Isadora Valle Sousa, Tiago Prince Sales, Eduardo Guerra, Luiz Olavo Bonino da Silva Santos, and Giancarlo Guizzardi. What do I get from modeling? an empirical study on using structural conceptual models. In International Conference on Enterprise Design, Operations, and Computing, pages 21–38. Springer, 2023. doi:10.1007/978-3-031-46587-1_2.

[bib.bib129] [129] John R. Venable and John C. Grundy. Integrating and supporting entity relationship and object role models. In Mike P. Papazoglou, editor, Proceedings of the 14th International Conference on Object-Oriented and Entity-Relationship Modelling (ER’95), volume 1021 of LNCS, pages 318–328. Springer, 1995. doi:10.1007/BFb0020543.

[bib.bib130] [130] Michaël Verdonck, Frederik Gailly, and Sergio de Cesare. Comprehending 3d and 4d ontology-driven conceptual models: an empirical study. Information Systems, 93:101568, 2020. doi:10.1016/j.is.2020.101568.

[bib.bib131] [131] Michaël Verdonck, Frederik Gailly, Sergio De Cesare, and Geert Poels. Ontology-driven conceptual modeling: A systematic literature mapping and review. Applied Ontology, 10(3-4):197–227, 2015. doi:10.3233/AO-150154.

[bib.bib132] [132] Denny Vrandecic. Building a multilingual Wikipedia. Communications of the ACM, 64(4):38–41, 2021. doi:10.1145/3425778.

[bib.bib133] [133] Heba M. Wagih, Doaa S. El Zanfaly, and Mohamed M. Kouta. Mapping Object Role Modeling 2 schemes into $\mathcal{SROIQ}(d)$ description logic. International Journal of Computer Theory and Engineering, 5(2):232–237, 2013. doi:10.7763/ijcte.2013.v5.684.

[bib.bib134] [134] Kunmei Wen, Yong Zeng, Ruixuan Li, and Jianqiang Lin. Modeling semantic information in engineering applications: a review. Artificial Intelligence Review, 37:97–117, 2012. doi:10.1007/s10462-011-9221-2.

[bib.bib135] [135] Michael Wessel. Obstacles on the way to qualitative spatial reasoning with description logics: some undecidability results. In Carole A. Goble, Deborah L. McGuinness, Ralf Möller, and Peter F. Patel-Schneider, editors, Proceedings of the International Workshop in Description Logics (DL’01), volume 49 of CEUR WS, 2001. Stanford, CA, USA, August 1-3, 2001. URL: https://ceur-ws.org/Vol-49/Wessel-122start.ps.

[bib.bib136] [136] Guohui Xiao, Linfang Ding, Benjamin Cogrel, and Diego Calvanese. Virtual knowledge graphs: An overview of systems and use cases. Data Intelligence, 1:201–223, 2019. doi:10.1162/dint_a_00011.

[bib.bib137] [137] Tilmann Zäschke, Stefania Leone, Tobias Gmünder, and Moira C. Norrie. Optimising conceptual data models through profiling in object databases. In Wilfred Ng, Veda C. Storey, and Juan Trujillo, editors, Proceedings of the 32th International Conference on Conceptual Modeling (ER’13), volume 8217 of LNCS, pages 284–297. Springer, 2013. Hong-Kong, November 11-13, 2013. doi:10.1007/978-3-642-41924-9_24.

	$\displaystyle C\longrightarrow$	$\displaystyle\top\,\|\,A\,\|\,\leq k[i]R\,\|\,\geq k[i]R\,\|\,\forall a.T\,\|\,% \exists a.T\,\|\,$
		$\displaystyle\leq 1\,a\,\|\,C\sqcap D$
	$\displaystyle R\longrightarrow$	$\displaystyle\top_{2}\,\|\,P\,\|\,(i:C)$
	$\displaystyle X\longrightarrow$	$\displaystyle C\sqsubseteq D\,\|\,\mathsf{id}\,C\,a$

Logics for Conceptual Data Modelling: A Review

Abstract

Keywords and phrases:

Category:

Copyright and License:

2012 ACM Subject Classification:

DOI:

Received:

Accepted:

Published:

Part Of:

Journal and Publisher:

1 Introduction

2 Related Work

3 On formalising conceptual data models

3.1 Decision points before the formalisation

Example 1.

3.2 Popular logics for logic-based reconstructions

3.2.1 Coverage and DLs

3.2.2 CDM runtime usage and DLs

3.3 Approaches to the formalisation

Example 2.

4 Reasoning over and with Conceptual Data Models

Example 3.

Example 4.

5 Challenges and future directions

5.1 CDML design

5.2 CDM integration with related research areas

5.3 CDM applications in other and new contexts

6 Conclusions

References

Appendix A Examples of both approaches to the logic-based reconstruction

A.1 Rule-based approach

Definition 5 (Syntax of 𝒟⁢𝒞p [42]).

Definition 6 (Semantics of 𝒟⁢𝒞p [42]).

A.2 Mapping-based approach

Definition 7 (Conceptual Data Model 𝒟⁢𝒞p syntax)).

Definition 8 (𝒟⁢𝒞p Semantics).

Definition 9 (Mapping 𝒟⁢𝒞p into 𝒟⁢ℒ⁢ℛ).

Definition 5 (Syntax of $\mathcal{DC}_{p}$ [42]).

Definition 6 (Semantics of $\mathcal{DC}_{p}$ [42]).

Definition 7 (Conceptual Data Model $\mathcal{DC}_{p}$ syntax)).

Definition 8 ( $\mathcal{DC}_{p}$ Semantics).

Definition 9 (Mapping $\mathcal{DC}_{p}$ into $\mathcal{DLR}$ ).